An on-the-fly deep neural network for simulating time-resolved spectroscopy: predicting the ultrafast ring opening dynamics of 1,2-dithiane

Abstract

Revolutionary developments in ultrafast light source technology are enabling experimental spectroscopists to probe the structural dynamics of molecules and materials on the femtosecond timescale. The capacity to investigate ultrafast processes afforded by these resources accordingly inspires theoreticians to carry out high-level simulations which facilitate the interpretation of the underlying dynamics probed during these ultrafast experiments. In this Article, we implement a deep neural network (DNN) to convert excited-state molecular dynamics simulations into time-resolved spectroscopic signals. Our DNN is trained on-the-fly from first-principles theoretical data obtained from a set of time-evolving molecular dynamics. The train-test process iterates for each time-step of the dynamics data until the network can predict spectra with sufficient accuracy to replace the computationally intensive quantum chemistry calculations required to produce them, at which point it simulates the time-resolved spectra for longer timescales. The potential of this approach is demonstrated by probing dynamics of the ring opening of 1,2-dithiane using sulphur K-edge X-ray absorption spectroscopy. The benefits of this strategy will be more markedly apparent for simulations of larger systems which will exhibit a more notable computational burden, making this approach applicable to the study of a diverse range of complex chemical dynamics.

---

1 Introduction

Modern light sources and optics have led to a dramatic increase in sophisticated time-resolved experimental techniques that can reveal fine details about the excited-state dynamics of molecules and materials on the atomic scales of time (femtosecond) and length (Angström). Methodologies such as ultrafast multidimensional spectroscopy,¹ femtosecond stimulated Raman spectroscopy,² ultrafast electron diffraction (UED),³ and time-resolved X-ray absorption spectroscopy (TR-XAS)^4,5 offer complimentary insights into the competition between different photochemical and photophysical channels, couplings between key vibrational modes and electronic states, and the electronic and nuclear structural dynamics which underpin the functional properties of the molecules and materials under study. However, the complexity of these experiments and their data are such that extracting the dynamics from the experimentally-obtained observables can be extremely challenging and, in practice, often requires strong support from theory and computation.

This support often focuses on the simulation of quantities such as electronic state population kinetics; which can be compared directly to time constants extracted from fitting kinetic models to the experimentally-obtained observables. While useful, these theoretical quantities are not guaranteed to be directly related to any of the experimental observables, and previous works⁶ have highlighted the importance of simulating the experimental observables directly to avoid the misinterpretation of the data. Ultimately, the direct evaluation of experimental observables using simulations provides the critical connection between experiment and theory that is required to maximise the reliable information extracted from the experiment. It also supplies a common vocabulary for theoreticians and experimentalists working on light-triggered processes to exchange and develop meaningful interpretations of experimental data.

A time-dependent theoretical framework which describes excited-state non-adiabatic nuclear dynamics is often essential to reproduce accurately the experimental observables. When it comes to carrying out simulations under such a framework, trajectory-based approaches [e.g. trajectory surface hopping (TSHD),⁷ab initio multiple spawning (AIMS),⁸ or variational multi-configurational Gaussian (VMCG) dynamics⁹] are appealing since they circumvent the challenge presented by the exponential scaling of quantum dynamics.^10–12 Indeed, as both the potential and experimental observables can be calculated on-the-fly with trivial parallelisation as and when (and only where) they are required, trajectory-based approaches make it easier to translate the quantum dynamics performed in higher dimensional space into time-resolved spectra. Specifically, in the context of X-ray spectroscopy^13,14 – the focus of the present work – on-the-fly trajectory-based approaches have been used to great effect to model the ultrafast photochemical ring-opening reaction of 1,3-cylohexadiene,¹⁵ the excited state relaxation of pyrazine,^16,17 and the non-radiative relaxation of ethene via a conical intersection (CI).¹⁸ However, while trajectory-based approaches can reduce the computational cost compared to traditional grid-based quantum dynamics approaches,^19,20 there remains still a significant computational cost associated with carrying out an (X-ray) spectral simulation at each time step; this cost is preclusive for larger systems, especially where high-accuracy quantum-chemical calculations are required to describe satisfactorily complex effects.

We have previously developed^21,22 and deployed^25–27 a deep neural network (DNN) – XANESNET²⁸ – for predicting the lineshape of X-ray absorption (XAS)^21,22,29 and emission (XES)²³ spectra. XANESNET predicts spectral lineshapes using only local information about the coordination geometry of the absorbing atom. It can be optimised in as little as a minute and predicts instantaneously, making it a powerful tool for reducing the computational cost associated with simulating time-resolved spectra. Towards developing DNNs for this kind of application, there are two distinct approaches: one can either develop a ‘Type I’ DNN, trained for generality in the sense that it is able to simulate an XAS/XES spectrum for an arbitrary absorbing atom in any coordination environment at a given absorption edge (our previous work has, to date, focused on this approach^21,22), or a ‘Type II’ DNN, trained for a specific (time-dependent) problem. A general ‘Type I’ model might be a sub-optimal solution for the prediction of the fine structure that can typically be acquired in modern ultrafast experiments. Consequently, in this Article, we work with a ‘Type II’ DNN and apply our model to investigate theoretically the ultrafast excited-state ring-opening dynamics of 1,2-dithiane (for structure see Fig. 1) as studied with sulphur K edge XAS. Our results show that our ‘Type II’ DNN, trained on-the-fly using first-principles geometric and XAS spectral data obtained from excited-state TSHD, offers an accurate, affordable, and computationally efficient approach for translating nuclear dynamics into time-resolved experimental observables.

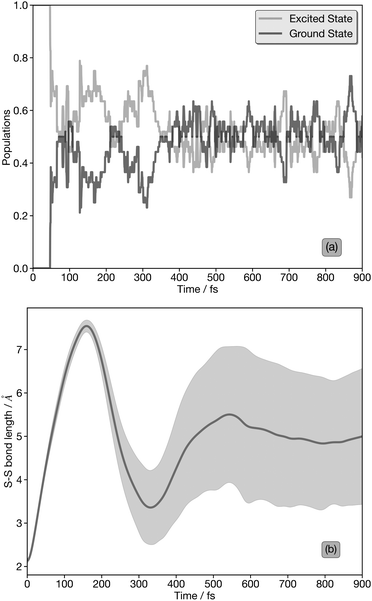Fig. 1 (a) Electronic state population kinetics obtained from the first 900 fs of TSHD simulations. (b) Average (line) and standard deviation (shaded region) of the S–S internuclear distance obtained from the first 900 fs of TSHD simulations. TSHD simulations were propagated following the transformation of 51 initial conditions sampled from a ground-state (S₀) Wigner-distributed ensemble into the first electronically-excited (S₁; 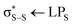) state. Data were obtained from ref. 30.

2 Method and computational details

2.1 Trajectory surface-hopping dynamics of 1,2-dithiane

Nonadiabatic TSHD simulations of the ultrafast excited-state ring-opening dynamics of 1,2-dithiane have been previously published in ref. 30, and the complete computational details are contained therein. Briefly: 51 independent initial conditions sampled from a ground-state (S₀) Wigner-distributed ensemble were transformed into the first electronically-excited (S₁; ) state according to their computed transition energies and moments, and then trajectories were propagated classically over the excited state potential energy surface for 1 ps using a 0.5 fs integration time step via the velocity-Verlet algorithm. The nonadiabatic transition probabilities were accounted for using the the fewest-switches algorithm.³¹

Fig. 1(a) shows the population kinetics of the S₀ (ground state) and S₁ and S₂ (together, as the excited states) over the first 900 fs post-photoexcitation to the S₁ state. The excited state population in Fig. 1(a) couples together both the S₁ and S₂ states since the latter has only a minor contribution in the early part of the dynamics and the two form a degenerate pair of states at later times, so we do not represent the states separately. In the XAS spectral simulations, the treatment of the S₁ and S₂ states is discussed in more detail below.

Fig. 1(b) shows the average (with one standard deviation covered by the shaded area) S–S internuclear distance as a function of time obtained from the TSHD simulations. An initial coherent oscillation with a temporal period of ≈350 fs is observed, followed by a significant increase in the standard deviation and a damping of the oscillation which indicates vibrationally-hot incoherent motion occurring across the S₀- and S₁/S₂-state potential energy surfaces at later times. This behaviour, discussed in detail in ref. 30, agrees well with previous experimental observations obtained via time-resolved ion spectroscopy.³²

2.2 Sulphur K-edge XAS simulations

Sulphur K-edge XAS spectra were simulated using restricted-excitation-window time-dependent density functional theory (REW-TDDFT)³³ within the approximation(s) of the BP86 exchange-and-correlation functional^34,35 as implemented in the ORCA³⁶ quantum chemistry package. The REW-TDDFT equations were solved for 60 states under the Tamm-Dancoff approximation (TDA),³⁷ and the interaction with the X-ray field was accounted for under the electric quadrupole approximation.³³ The scalar relativistic effects were described using a Douglas–Kroll–Hess (DKH) Hamiltonian of 2nd order.³⁸ The DKH-def2-TZVP³⁹ basis set was used throughout.

To calculate the sulphur K-edge XAS spectra of the electronically-excited states (S₁/S₂), the reference wavefunction for the valence-excited states was approximated using the lowest-lying triplet electronically-excited state (T₁) of 1,2-dithiane, which has very similar electronic structure to the lowest-lying electronically-excited singlet states (S₁/S₂) and represents a tractable approximation due to the lack of spin sensitivity in XAS.⁴⁰ As detailed in ref. 30, the S₁ and S₂ states correspond to transitions which are close in energy (near degenerate at later times in the TSHD simulations) and, given the similarity of their character, should be expected to exhibit similar sulphur K-edge XAS spectra. The T₁ state, which we use as a proxy, also corresponds to a transition and approximates the character of the S₁ and S₂ states well – certainly sufficiently well for the scope of the present work which aims primarily to establish the effectiveness of training our ‘Type II’ DNN on the fly.

2.3 Deep neural network

The architecture of the ‘Type II’ DNN used in this Article closely follows that of XANESNET,²⁸ as detailed in ref. 22. XANESNET is a deep multilayer perceptron (MLP) machine-learning model comprising an input layer, two hidden layers, and an output layer. All layers are dense, i.e. fully connected, and each hidden layer performs a nonlinear transformation using the rectified linear unit (ReLU) activation function. Featurisation is performed via dimensionality reduction using the wACSF descriptor of Gastegger and Marquetand et al.⁴¹ As constructed in this Article, the input layer contained 49 neurons comprising a ‘global’ (G¹) function, 16 radial (two-body; G²) functions, and 32 angular (three-body; G⁴) functions, and the first hidden layer contained 256 neurons with each subsequent hidden layer reducing in size by 50% relative to the size of the preceding layer. The linear output layer contained 359 neurons from which the discretised sulphur K-edge XAS spectrum was retrieved. The internal weights, W, were optimised via iterative feed-forward and backpropagation cycles to minimise the empirical loss, J(W), defined here as the mean-squared error (MSE) between the predicted, μ_predict, and target, μ_target, sulphur K-edge XAS spectra over the reference dataset, i.e. an optimal set of internal weights, W*, was sought to satisfy .

Gradients of the empirical loss with respect to the internal weights, δJ(W)/δW, were estimated over minibatches of 32 samples and updated iteratively according to the Adaptive Moment Estimation (ADAM)⁴² algorithm. The learning rate for the ADAM algorithm was set to 1 × 10⁻⁴. The internal weights were initially set according to the He⁴³ uniform distribution. Unless explicitly stated in this Article, optimisation was carried over 2000 epochs. Regularization was implemented to minimise the propensity of overfitting; batch standardisation and dropout were applied at each hidden layer. The probability of dropout at each epoch was set to 0.30.

The XANESNET DNN is programmed in Python 3 with the TensorFlow⁴⁴/Keras⁴⁵ API and integrated into a Scikit-Learn⁴⁶ (sklearn) data pre- and post-processing pipeline via the KerasRegressor wrapper for Scikit-Learn. The Atomic Simulation Environment⁴⁷ (ase) API is used to handle and manipulate molecular structures. The code is publicly available under the GNU Public License (GPLv3) on GitLab.²⁸

In this Article, the objective is to develop a ‘Type II’ DNN to translate the TSHD simulations described above into time-resolved XAS spectroscopic signals. The DNN is trained on the fly from first-principles data (geometries and sulphur K-edge XAS spectra) obtained/calculated at each time step, and is then used to predict all future timesteps. After each iteration of this process, the DNN predictions are assessed for accuracy (Fig. 2). We aim to find the timestep at which the DNN can provide predictions that substitute for the time-consuming quantum-chemical calculations which would otherwise be required to obtain the time-resolved sulphur K-edge XAS spectra at later times. At each timestep, two DNN are trained using data from the preceding timesteps: one for the electronic ground state (S₀) and one for the electronically-excited states (S₁/S₂, using the T₁ as a proxy). The two DNNs are then used to predict the sulphur K-edge XAS spectra for all future timesteps, the choice of DNN depending on whether the trajectory is in the S₀ or S₁/S₂ state at that timestep. We assess the point at which the DNN can substitute for the quantum-chemical calculations in two ways. Firstly, we use a cosine similarity metric to quantify the difference between the predictions and quantum-chemical calculations at each time step after the point up to which the DNNs were trained; while this provides an appropriately accurate assessment for this proof-of-concept work, the obvious limitation is that this approach requires the quantum-chemical calculations to already be available for all future timesteps. Secondly, and, principally, to circumvent this requirement, we also assess the cutoff using the model uncertainty evaluated using the ensembling methodology.²³ Principally, ensembling exploits the fact that there is no guarantee that there exists a single unique set of internal weights, W*, for a DNN which satisfy . Practically, ensembling involves training multiple (N) instances of each DNN using the same reference dataset but different statistical initialisations for W. The ensemble of N DNNs is then used to produce N independent predictions from which a mean prediction and standard deviation for each input can be derived. The latter is used to quantify the ensemble uncertainty for the predictions. In this present Article, ensembling is performed at each timestep and the point at which the DNN is sufficiently capable of substituting for the quantum-chemical calculations is taken to be the point at which the standard deviation converges to its minimum value.

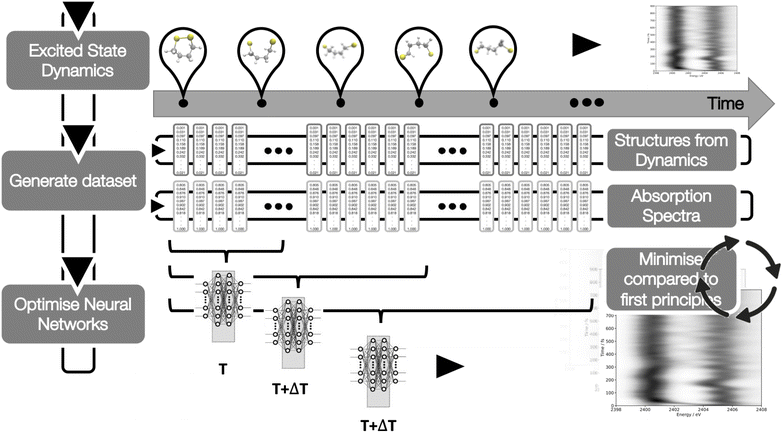Fig. 2 A schematic of the workflow used in this Article. The DNN takes as input geometries obtained from the TSHD simulations of 1,2-dithiane, carried out in ref. 30, and the calculated sulphur K-edge XAS spectra for these geometries up until some time, T, after excitation. These pairs of geometries and sulphur K-edge XAS spectra constitute the reference dataset on which the DNN carries out supervised learning. The optimised DNN is used to predict the sulphur K-edge XAS spectra for all future timesteps up until the final timestep, and the error – or loss – associated with the predictions is quantified by the cosine similarity between the theoretical target and DNN-predicted sulphur K-edge XAS spectra. This process is repeated at sequential timesteps, T + ΔT, until the cosine similarity between the theoretical target and DNN-predicted sulphur K-edge XAS spectra converges.

3 Results and discussion

3.1 Time-resolved sulphur K-edge XAS spectra from first principles

Fig. 3(a) and (b) show the ground- (S₀) and excited-state (S₁/S₂) sulphur K-edge XAS spectra as a function of the S–S internuclear distance along the ring-opening coordinate. The S₀-state sulphur K-edge XAS spectrum corresponding to the (initial; equilibrium) ring-closed structure of 1,2-dithiane exhibits a main band at 2404 eV with a shoulder on the high-energy front. This main band, within a single-electron picture, corresponds to transitions from each of the S 1 s orbitals into the low-lying unoccupied orbital. The shoulder corresponds to transitions into the orbitals, with the latter being weaker transitions than the former as a consequence of the reduced spatial overlap between these orbitals and the S 1 s orbitals. Upon photoexcitation into the S₁ state – a HOMO–LUMO transition – an additional band appears at ≈2401 eV (Fig. 3(b)), corresponding to transitions from the S 1 s orbitals into the sulphur ‘lone pair’ (LP_S) orbitals which now contain holes as a consequence of the photoexcitation process. There is also a reduction in the energy gap between the and 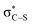orbitals. For the ring-opened structure, both the S₀- and S₁/S₂-state sulphur K-edge XAS spectra show a distinct low-energy feature similar to the excited-state sulphur K-edge XAS spectrum of the ring-closed structure. This is because the ring-opened structure contains two terminal sulphur radicals and the lowest-energy unoccupied orbitals, similarly, are of the LP_S type. The highly localised nature of the LP_S orbitals and the initial S 1 s core electron means that these transitions are much less sensitive to changes in geometry than the other features present in the sulphur K-edge XAS spectrum.

Fig. 3 Evolution of the sulphur K-edge XAS spectrum along the ring-opening coordinate in (a) the electronic ground state (S₀) and (b) the lowest-lying electronically-excited states (S₁/S₂, using the T₁ state as a proxy). Calculated using REW-TDDFT at the DKH-BP86/def2-TZVP level.

In the S₀ state (Fig. 3(a)) a shift of the first feature towards lower energy occurs as ring opening proceeds. This reflects the elongation of the S–S bond. In the S₁/S₂ states (Fig. 3(b)), the low-energy feature at 2401 eV is already present at the equilibrium/Franck–Condon geometry and so little change in this peak with S–S bond length is observed. A similar observation is made with respect to the main band shifting towards lower energy. However, in contrast to what we observe for the S₀ state, the shift is weaker. It is noted that both the S₀- and S₁/S₂-state sulphur K-edge XAS spectra are very similar at longer S–S internuclear distances as a consequence of the near-degeneracy of the three states at the ring-opened geometries.

Fig. 4 shows the temporal evolution of the sulphur K-edge XAS spectra from the ensemble average of the 51 TSHD trajectories over 900 fs post-photoexcitation to the S₁ state. Fig. S1–S51 – found in the ESI† – show the temporal evolution of the sulphur K-edge XAS spectra for each of the 51 TSHD trajectories individually. Fig. 4 shows two distinct and temporally-evolving bands centred around 2401 and 2405 eV, consistent with the static simulations along the ring-opening coordinate (Fig. 3).

Fig. 4 Time-resolved sulphur K-edge XAS spectrum associated with the ultrafast excited-state ring-opening dynamics of 1,2-dithiane. Calculated using REW-TDDFT at the DKH-BP86/def2-TZVP level.

At early times, the band at 2401 eV shows oscillatory behaviour with a period of ≈150 fs. This mirrors the population kinetics (Fig. 3(a)). As shown in Fig. 3, this first transition exhibits quite different behaviour in the ground and excited state and therefore it is unsurprising that the oscillations in this band reflects the population kinetics. In contrast, the peak at 2405 eV shows oscillations with two distinct time periods, one of ∼50 fs and another ∼340 fs. The latter is consistent with changes in the S–S bond length, which as expected from Fig. 1(b) shows one distinct oscillation before being damped from the loss of coherence. The former 50 fs component corresponds to oscillations in C–S bond lengths, while coherence is reduced during the dynamics, these oscillations remain more visible throughout the first 900 fs. This peak does not exhibit any kinetics associated with the population kinetics as the spectral shape is less sensitive to the fine details of the electronic state populated than geometric changes occurring during the dynamics. Both of the bands show little clear variation after ≈400 fs, consistent with the dephasing of the coherent nuclear motion (Fig. 1(b)) after the first ring-opening/ring-closing cycle and the progression of the system towards vibrationally-hot incoherent motion occurring across the S₀- and S1/S₂-state potential energy surfaces at later times.

3.2 Predicting the sulphur K-edge XAS signal using XANESNET

Having established the time evolution of the sulphur K-edge XAS spectra using quantum-chemical calculations, we turn our attention towards reproducing the same spectral simulations using our ‘Type II’ DNN. As described in the Methods section, we train two DNNs at each timestep: one for the S₀ state, and one for the S₁/S₂ states. The training data comprises, in each case, all of the geometric and sulphur K-edge XAS spectral data calculated until the current timestep, T. The two DNNs are then used to predict the sulphur K-edge XAS spectra for all future timesteps. Fig. 5 shows the mean cosine similarity of all spectra predicted from timestep T to T = 900 fs. We acknowledge that, although the cosine similarity metric ignores differences in magnitude between the predicted and target sulphur K-edge XAS spectra, our focus here is on reproduction of the spectral shape alone as all of our sulphur K-edge XAS spectra have been normalised to the largest value during their dynamics. The cosine similarity shows a rapid improvement from 0.86 to 0.94 within the first 100 fs, followed by a subsequent plateau suggesting that 100 fs of first-principles data is sufficient to predict satisfactorily the sulphur K-edge XAS spectra for all future timesteps. 100 fs is a surprisingly short timescale for this data to be acquired over, but it corresponds approximately to the time required for the S–S internuclear distance to reach its maximum value (Fig. 1(b)). Suggesting that in this case, once a DNN is trained on first principles sampling the full range of S–S bond length, it has sufficient information to predict the remaining spectra up to the 900 fs studied in this work. This is discussed in more detail in Section 3.3.

Fig. 5 Evolution of the cosine similarity loss metric as a function of the training set size; the training set comprises all timesteps up to the training time (T; on the x axis).

This is supported in Fig. 6 which shows a plot of the principal t-distributed stochastic neighbour embedding (t-SNE) components of the wACSF descriptor encoding each local geometry at every timestep (colour bar) of the dynamics. t-SNE is a statistical approach for reducing the dimensionality of datasets.²⁴ In contrast to the more commonly-used linear dimensionality reduction approach of principal component analysis (PCA), t-SNE is a non-linear dimensionality reduction approach which, unlike PCA, seeks to preserve the local structure of data by minimizing the Kullback–Leibler (KL) divergence between distributions with respect to the locations of the points in the map. In contrast to PCA, t-SNE is not a black box, but instead requires user-defined hyperparameters: the perplexity, learning rate, and the number of iterations (which, to produce Fig. 6, were set to 50, 60, and 1000, respectively). The t-SNE visualisation presented in Fig. 6 shows that the wACSF embeddings describing the equilibrium/Franck–Condon structures are centred around 20 (t-SNE₁), 0 (t-SNE₂). During the first 200 fs post-photoexciation, t-SNE₁ gradually transforms to −20, while t-SNE₂ initially decreases, suddenly increases at ≈100 fs, and then subsequently decreases again to 0 at ≈200 fs. Post-350 fs t-SNE₁ and t-SNE₂ disperse over the entire t-SNE component space, reflecting the vibrationally-hot incoherent dynamics that take over the TSHD simulations at later times. This illustrates, consistent with the analysis performed in the previous paragraph, that a significant amount of the t-SNE₁ and t-SNE₂ space has been covered within the first 100 fs, which explains the convergence observed in Fig. 5.

Fig. 6 t-SNE embedding of the wACSF feature vectors (encoding the local geometries around the absorbing atoms) for all geometries across all timesteps and all trajectories. Embeddings are colour-coded according to their timestep. The initialisation of the t-SNE embedding was performed via PCA, the learning rate was set to 50, the perplexity was set to 60, and 1000 iterations were carried out.

Fig. 7(a) and (b) show theoretical (target) and DNN-predicted time-resolved sulphur K-edge XAS spectra over the first 900 fs post-photoexcitation, respectively. Percentage errors between the theoretical (target) and DNN-predicted time-resolved sulphur K-edge XAS spectra are tabulated in Table 1. In contrast to Fig. 4, the first 120 fs are left blank in Fig. 7(a) and (b) as this timeframe contains the first-principles data from which the DNN learns and on which no predictions are made (see Fig. 5). Overall, we observe good agreement (particularly at early times) between the theoretical and DNN-predicted sulphur K-edge XAS spectra: the oscillatory behaviour of both bands – associated with the population kinetics and changes in S–S internuclear distance – is successfully reproduced by the DNN. However, any comparison between the theoretical and DNN-predicted sulphur K-edge XAS spectra for the trajectory ensemble at later times (e.g. t > 500 fs) is complicated by the vibrationally-hot nuclear wavepacket and the progression of incoherent dynamics. Consequently, we focus our analysis of the performance of the DNN on individual trajectories from the trajectory ensemble which, we assert, are a more stringent test of the quality of the DNN predictions.

Fig. 7 Time-resolved sulphur K-edge XAS ensemble-averaged spectrum associated with the ultrafast excited-state ring-opening dynamics of 1,2-dithiane. (a) Calculated using REW-TDDFT at the DKH-BP86/def2-TZVP level. (b) Predicted using the DNN detailed in this Article. Plots are shown from 120 fs onwards, as the DNN has been trained on the data from all timesteps up until 120 fs.

Table 1 Percentage errors averaged over the duration of the trajectory for each of trajectories 1, 2, and 3 (Fig. 8), and for the full trajectory ensemble; also tabulated are the percentage errors averaged over four time windows: I (100–300 fs), II (300–500 fs), III (500–700 fs) and IV (700–900 fs). The corresponding table for the remaining trajectories in the trajectory ensemble is found in the ESI (Table S1)

Trajectory	Overall	I	II	III	IV
1	8.4	3.7	8.7	10.1	11.1
2	8.7	5.1	7.6	11.7	10.2
3	11.5	6.0	14.1	14.8	10.9
Overall	10.2	5.2	11.3	11.7	12.7

---

Fig. 8 shows a comparison between the theoretical and DNN-predicted time-resolved sulphur K-edge XAS spectra for three individual trajectories. The corresponding plots for the remaining trajectories are shown in Fig. S55–S102 (ESI†). These show much more fine detail in the dynamics than is visible at the trajectory ensemble level and – importantly – in each case show good agreement between the theoretical DNN-predicted sulphur K-edge XAS spectra. Fig. 8(a) and (b) show the theoretical and DNN-prredicted sulphur K-edge XAS spectra for Trajectory 1 and the percentage error between the two simulations is tabulated in Table 1. The oscillations present in the theoretical simulations are also observed in the DNN simulations with an overall percentage error under 10%. The merging of the two peaks observed at ≈300 and ≈700 fs are associated with the reformation of the S–S bond at these timescales. Similar behaviour is observed for Trajectory 2 in Fig. 8(c) and (d); in this case, the S–S bond reforms at ≈300 and ≈600 fs. Fig. 8(e) and (f), showing the time-resolved sulphur K-edge XAS spectra for Trajectory 3, illustrate different behaviour: once the S–S bond reforms after ≈300 fs, non-radiative internal conversion returns the molecule to the S₀ state in a vibrationally hot condition and rapid oscillations are observed, corresponding to vibrational activity of the S–S stretching mode.

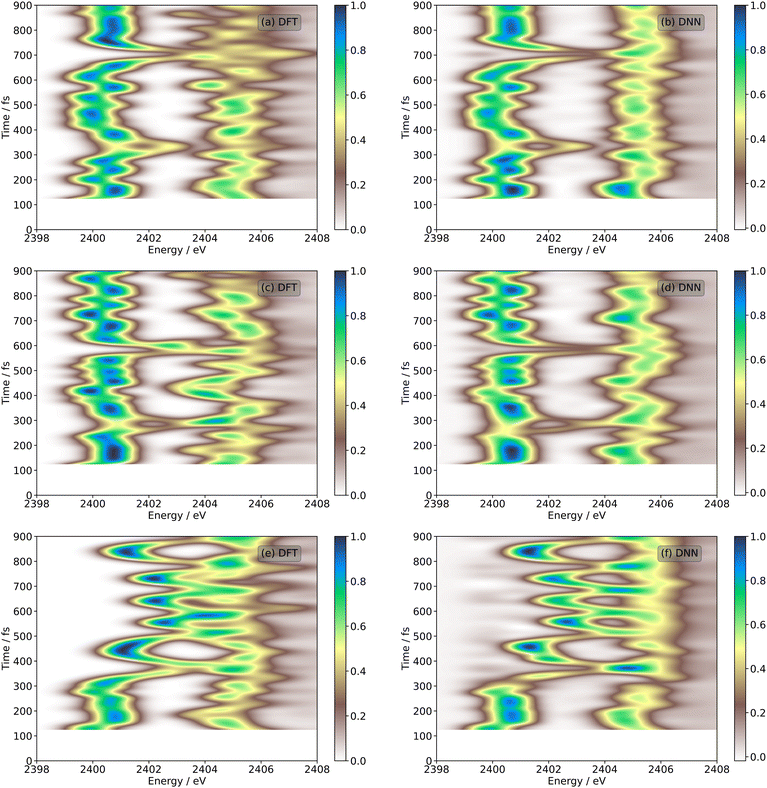Fig. 8 Time-resolved sulphur K-edge XAS spectra associated with the ultrafast excited-state ring-opening dynamics of 1,2-dithiane for three individual trajectories (1, 2, and 3) taken from the trajectory ensemble average shown in Fig. 7. (a), (c), (e) Calculated using REW-TDDFT at the DKH-BP86/def2-TZVP level. (b), (d), (f) Predicted using the DNN detailed in this Article. The remaining individual trajectories are shown in the ESI.† Plots are shown from 120 fs onwards, as the DNN has been trained on the data from all timesteps up until 120 fs.

To quantify the error between the calculated and DNN predicted time-resolved spectra, Table 1 shows the overall percentage error and the error in 4 time windows for the overall ensemble and the trajectories shown in Fig. 8. The corresponding table for the remaining trajectories is shown in the Table S1 (ESI†). For the individual trajectories the overall percentage error is ∼10%, with the error being smaller in the first two time-windows and increasing slightly in the final two. The overall percentage error of the ensemble (shown in Table 1) is larger than the error of most of the individual trajectories, indicating (i) the influence of the worst trajectories and (ii) that combining each of the individual trajectories into the ensemble can compound the overall error. This influence of individual trajectories makes it interesting to consider the weighting given to each trajectory in the ensemble. For TSH dynamics used here each trajectory should have equal weights for all time-step, alternatively for Gaussian based methods, the weighting of the trajectory basis functions is dynamic and calculated during the dynamics.^16,18,48 An alternative approach adopted to analyse time-resolved scattering experiments used the weighting as a free parameter to fit the experimental spectra.¹⁵ This would provide one criteria to eliminate trajectories exhibiting large errors and the weighings determined to achieve a good agreement with experimental data could be used to establish the dominant photochemical pathways from an ensemble of trial trajectories.

3.3 Determining if a model is sufficiently trained for an unknown system

Up until this point, we have assessed whether the DNN is sufficiently trained to predict future timesteps based on an evaluation of the cosine similarity metric between the theoretical and DNN-predicted sulfur K-edge XAS spectra for those future timesteps (Fig. 5). However, this approach is not particularly useful in practice as it requires that quantum-chemical calculations have already been carried out for all timesteps – this then makes the DNN redundant. Consequently, a metric which supplies an error/uncertainty, enabling one to judge when the DNN model is sufficiently capable and confident in a prediction, is required.

One approach could be to execute quantum-chemical calculations to assess the prediction error for a limited time window after the DNN model has been developed up until the prediction error is minimised. However, such an approach would likely fail to account for scenarios where the system explores a region of the potential energy surface which is significantly different to region(s) explored in the early timesteps with which the DNN was trained. Another approach could be to execute a small number of quantum-chemical calculations distributed throughout the future time window for the purposes of assessing the prediction error at specific future times, and to assume that these samples cover sufficiently the space of the potential energy surface that is explored. However, this is certainly not straightforward to assume.

Alternatively, we can implement a broader uncertainty awareness into the DNN itself using an ensembling approach.^23,49 Practically, ensembling involves training multiple (N) instances of each DNN using the same reference dataset but different statistical initialisations for W. The ensemble of N DNNs is then used to produce N independent predictions from which a mean prediction and standard deviation for each input can be derived. The latter is used to quantify the ensemble uncertainty for the predictions. The concept behind this interpretation is that different W* obtained from the N models in the ensemble will tend towards similar predictions when the inputs are similar to those found in the reference data. This is because W* for each DNN instance, even if/when different, have been optimised for comparable data. In contrast, if the inputs are dissimilar to the inputs found in the reference dataset, each of the N independent predictions will be more greatly affected by W* and a higher standard deviation will consequently be observed. The deviation of ensembled predictions hence provides, to the end user, a barometer of the ‘dependability’ of the DNN for an application with their own dataset.

Fig. 9(a) shows the median relative standard deviation for the ensembled predictions as a function of the training time. This shows a rapid decrease with convergence observed around 100 fs, in close agreement with that shown in Fig. 5. This indicates that for general application where all of the first principles calculations do not exist, this metric could be used to assess the point at which convergence is reached. For this case study, the convergence around 100 fs is consistent with previous analysis of the convergence this time window sufficiently covers the full range of S–S bond distances covered throughout the rest of the dithiane ring-opening dynamics.

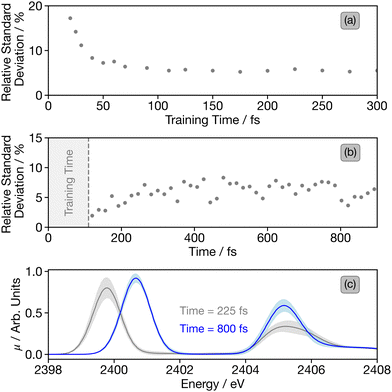Fig. 9 (a) Median relative standard deviations of the DNN-predicted time-resolved sulphur K-edge XAS spectra at timesteps greater than the model training time. (b) Median relative standard deviations as a function of time for the spectra trained up to 110 fs, as shown in Fig. 7. (c) Sulphur K-edge XAS spectra at 225 and 800 fs, including 2σ uncertainty (shaded region) calculated via the ensembling approach.

For more detail, Fig. 9(b) shows the relative standard deviation as a function of time for the spectra trained up to 110 fs. This shows a small increase between 120–400 fs followed by a plateau for the remaining time of the simulations. A comparison for models with shorter training times can be found in Fig. S54 (ESI†), which show a much greater increase in the relative standard deviation. To exemplify the uncertainty obtained from the ensembling models, Fig. 9(c) shows two spectra with ±2σ, calculated from the ensembling technique.

4 Conclusions

In this Article, we have applied the XANESNET DNN to transform excited-state TSHD simulations into time-resolved experimental sulphur K-edge XAS spectral signals. Taking advantage of the accurate, affordable, and instantaneous predictions produced by the XANESNET DNN, we bypass the intensive quantum-chemical calculations that are usually necessary to simulate time-evolving XAS spectra from (excited-state) molecular dynamics simulations. We have shown that our ‘on-the-fly’ train-test procedure, iterated at each timestep of the TSHD simulation, converges quickly and is able to substitute effectively for (otherwise) time-consuming quantum-chemical calculations. Consequently, we anticipate that this approach could become an important auxiliary tool for simulating and interpreting time-resolved XAS spectra.

For the present example presented in this article – the ultrafast excited-state ring-opening dynamics of 1,2-dithiane – we find that ≈100 fs of TSHD simulation provides sufficient first-principles data to train a DNN which is then able to predict accurately the sulphur K-edge XAS spectra at future (unseen) timesteps in the TSHD simulation. In this particular case – the periodic ring-opening/ring-closing dynamics of 1,2-dithiane – this training time window can be rationalised as it covers the time required for the S–S bond to break post-photoexcitation to an 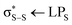state and survey subsequently a significant amount of coordinate space. However, for future applications, where convergence may be less straightforward, we have also demonstrated that the ensembling approach can be used to assess the uncertainty of the DNN, providing an indication of whether or not the DNN is sufficiently trained to reproduce reliably and accurately the pertinent signals of the XAS spectra. In the present formulation, the DNN maps (local) structure onto the XAS spectral lineshape and, consequently, any interpretation drawn from using the DNN will be in terms of how the nuclear wavepacket or ensemble dynamics map onto the (experimental) spectroscopic observables. The DNN is therefore unable to provide – directly, at least – information on the electronic wavepacket dynamics and, under the present framework, such information would still require first-principle quantum-chemical calculations; however, these could be carried out at reduced computational cost in a targeted manner, e.g. at critical geometries/times identified from the experimental and/or DNN-predicted dynamics.

Overall, this Article demonstrates a particularly promising new approach for the simulation and interpretation of time-resolved X-ray spectroscopic signals. Extension to systems of higher dimensionality is straightforward under the present framework, and our ‘on-the-fly’ train-test procedure should have broad applicability to trajectory-based approaches for simulating time-resolved X-ray spectroscopic signals for a diverse range of chemical dynamics – particularly dynamics on longer timescales and for larger systems that the computational cost of these simulations presently precludes.

Data availability

The data that support the findings of this study are openly available in Open Data Commons Open Database License at 10.25405/data.ncl.21931509.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research described in this Article was funded by the Leverhulme Trust (project no. RPG-2020-268) and EPSRC (grant no. EP/S022058/1, EP/R021503/1, EP/X035514/1, and EP/R51309X/1). This research made use of the Rocket High Performance Computing (HPC) service at Newcastle University.

Notes and references

1. T. A. Oliver, R. Soc. Open Sci., 2018, 5, 171425.
2. D. R. Dietze and R. A. Mathies, ChemPhysChem, 2016, 17, 1224–1251.
3. J. Yang, X. Zhu, J. P. F. Nunes, J. K. Yu, R. M. Parrish, T. J. Wolf, M. Centurion, M. Gühr, R. Li and Y. Liu, et al. , Science, 2020, 368, 885–889.
4. D. Garratt, L. Misiekis, D. Wood, E. W. Larsen, M. Matthews, O. Alexander, P. Ye, S. Jarosch, C. Ferchaud and A. Bakulin, et al. , Nat. Commun., 2021, 13, 3414.
5. Y. Uemura, A. S. Ismail, S. H. Park, S. Kwon, M. Kim, H. Elnaggar, F. Frati, H. Wadati, Y. Hirata and Y. Zhang, et al. , J. Phys. Chem. Lett., 2022, 13, 4207–4214.
6. H. Tao, T. Allison, T. Wright, A. Stooke, C. Khurmi, J. Van Tilborg, Y. Liu, R. Falcone, A. Belkacem and T. Martinez, J. Chem. Phys., 2011, 134, 244306.
7. J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572.
8. M. Ben-Nun, J. Quenneville and T. J. Martnez, J. Phys. Chem. A, 2000, 104, 5161–5175.
9. G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308.
10. B. F. Curchod and T. J. Martnez, Chem. Rev., 2018, 118, 3305–3336.
11. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068.
12. G. Capano, T. J. Penfold, M. Chergui and I. Tavernelli, Phys. Chem. Chem. Phys., 2017, 19, 19590–19600.
13. T. J. Penfold, C. Milne and M. Chergui, Adv. Chem. Phys., 2013, 153, 1–41.
14. C. D. Rankine and T. J. Penfold, J. Phys. Chem. A, 2021, 20, 4276–4293.
15. M. Minitti, J. Budarz, A. Kirrander, J. Robinson, D. Ratner, T. Lane, D. Zhu, J. Glownia, M. Kozina and H. Lemke, et al. , Phys. Rev. Lett., 2015, 114, 255501.
16. T. Northey, J. Norell, A. E. Fouda, N. A. Besley, M. Odelius and T. J. Penfold, Phys. Chem. Chem. Phys., 2020, 22, 2667–2676.
17. V. Scutelnic, S. Tsuru, M. Pápai, Z. Yang, M. Epshtein, T. Xue, E. Haugen, Y. Kobayashi, A. I. Krylov and K. B. Møller, et al. , Nat. Commun., 2021, 12, 1–8.
18. S. P. Neville, M. Chergui, A. Stolow and M. S. Schuurman, Phys. Rev. Lett., 2018, 120, 243001.
19. G. Capano, C. Milne, M. Chergui, U. Rothlisberger, I. Tavernelli and T. Penfold, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 214001.
20. T. Penfold, M. Pápai, T. Rozgonyi, K. B. Møller and G. Vankó, Faraday Discuss., 2016, 194, 731–746.
21. C. D. Rankine, M. M. M. Madkhali and T. J. Penfold, J. Phys. Chem. A, 2020, 124, 4263–4270.
22. C. D. Rankine and T. Penfold, J. Chem. Phys., 2022, 156, 164102.
23. T. Penfold and C. Rankine, Mol. Phys., 2022, e2123406.
24. L. Van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 11.
25. M. M. M. Madkhali, C. D. Rankine and T. J. Penfold, Molecules, 2020, 25, 2715.
26. M. M. M. Madkhali, C. D. Rankine and T. J. Penfold, Phys. Chem. Chem. Phys., 2021, 23, 9259–9269.
27. E. Falbo, C. Rankine and T. Penfold, Chem. Phys. Lett., 2021, 780, 138893.
28. XANESNET, 2021, gitlab.com/conor.rankine/xanesnet.
29. L. Watson, C. D. Rankine and T. J. Penfold, Phys. Chem. Chem. Phys., 2022, 24, 9156–9167.
30. C. D. Rankine, J. P. F. Nunes, M. S. Robinson, P. D. Lane and D. A. Wann, Phys. Chem. Chem. Phys., 2016, 18, 27170–27174.
31. S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667.
32. A. B. Stephansen, R. Y. Brogaard, T. S. Kuhlman, L. B. Klein, J. B. Christensen and T. I. Sølling, J. Am. Chem. Soc., 2012, 134, 20279–20281.
33. S. D. George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965–972.
34. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
35. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
36. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
37. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
38. M. Reiher, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 139–149.
39. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
40. S. Eckert, J. Norell, R. M. Jay, M. Fondell, R. Mitzner, M. Odelius and A. Föhlisch, Chem. – Eur. J., 2019, 25, 1733–1739.
41. M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, J. Chem. Phys., 2018, 148, 241709.
42. D. P. Kingma and J. L. Ba, arXiv, 2014, preprint, arXiv:1412.6980.
43. K. He, X. Zhang, S. Ren and J. Sun, arXiv, 2015, preprint, arXiv:1502.01852.
44. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean and M. Devinet al., TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems, 2015, tensorflow.org/.
45. Keras, 2015, github.com/keras-team/keras.
46. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830.
47. A. Hjorth Larsen, J. Jorgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002.
48. T. Northey, J. Duffield and T. Penfold, J. Chem. Phys., 2018, 149, 124107.
49. A. Ghose, M. Segal, F. Meng, Z. Liang, M. S. Hybertsen, X. Qu, E. Stavitski, S. Yoo, D. Lu and M. R. Carbone, Phys. Rev. Res., 2023, 5, 013180.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00510k

---