 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capillary forces exerted by a water bridge on cellulose nanocrystals: the effect of an external electric field†
Nabin Kumar
Karna
 *ab,
Jakob
Wohlert
*ab,
Jakob
Wohlert
 bc,
Anna
Hjorth
bc,
Anna
Hjorth
 ab and
Hans
Theliander
a
ab and
Hans
Theliander
a
aChalmers University of Technology, Chalmersplatsen-4, Sweden. E-mail: nabin@chalmers.se
bWallenberg Wood Science Center, The Royal Institute of Technology, Chalmers University of Technology and Linköping University, SE-10044 Stockholm, Sweden
cKTH Royal Institute of Technology, Stockholm, Sweden
First published on 24th January 2023
Abstract
Capillary forces play an important role during the dewatering and drying of nanocellulosic materials. Traditional moisture removal techniques, such as heating, have been proved to be deterimental to the properties of these materials and hence, there is a need to develop novel dewatering techniques without affecting the desired properties of materials. It is, therefore, important to explore novel methods for dewatering these high-added-value materials without negatively influencing their properties. In this context, we explore the effect of electric field on the capillary forces developed by a liquid–water bridge between two cellulosic surfaces, which may be formed during the water removal process following its displacement from the interfibrillar spaces. All-atom molecular dynamics (MD) simulations have been used to study the influence of an externally applied electric field on the capillary force exerted by a water bridge. Our results suggest that the equilibrium contact angle of water and the capillary force exerted by the water bridge between two nanocellulosic surfaces depend on the magnitude and direction of the externally applied electric fields. Hence, an external electric field can be applied to manipulate the capillary forces between two particles. The close agreement between the capillary forces measured through MD simulations and those calculated through classical equations indicates that, within the range of the electric field applied in this study, Young–Laplace equations can be safely employed to predict the capillary forces between two particles. The present study provides insights into the use of electric fields for drying of nanocellulosic materials.
1 Introduction
Capillary forces are dominant when particles are in contact with each other via liquid bridges.1,2 These liquid bridges induce an adhesive force due to the pressure difference between the liquid and the gas phases and due to the surface tension of liquid–gas interfaces.3–5 Surface forces have a great influence on particle–particle interactions and hence the behavior of bulk materials like agglomeration, powder flow, etc. These effects are very important in many scientific and technological areas like materials science,6–9 colloids10,11 and other engineering processes such as drying12,13 and evaporation.14,15. For instance, the gradual removal of water from wet pulp fibers during the formation of sheets creates liquid bridges with a specific radius between the fibers during the pressing and drying operations. Although the total volume of water decreases during dewatering, the water–air surface area increases, resulting in a significant increase in the capillary forces.16 This leads to higher adhesive energy, and results in high process energy.17 Yet, another such example is the drying process of two phase materials such as cellulose nanofibril gels18,19 and cellulose foams. The formation of particle–liquid bridges creates high capillary pressures which may induce shape deformation of foams upon drying and generation of cracks.20Nanofibrillated cellulose (CNF) has attracted great attention in materials engineering and technology due to its exceptional properties such as high specific strength and elastic modulus, a large specific surface area, a low coefficient of thermal expansion, a high aspect ratio, low cost and biodegradabilty. Many suitable applications have been proposed based on the mentioned properties.21–24 One of the major challenges in the production of commercially feasible CNFs, irrespective of the fiber disintegration methods applied, is the necessity to dewater the CNF solutions. The conventional dewatering process, which involves the gradual removal of water through filtration, or assisted filtration techiques and subsequent evaporation, may create an air–water–CNF interface, which can give rise to a sufficient attractive capillary force to displace the CNFs from their original positions.25 This, among other phenomena, may result in the collapse of CNFs and agglomerate irreversibly26 which makes it difficult to redisperse in solvents of interest. These phenomena are inherent to nanoscale systems where the surface forces are the dominant forces.27,28
As the characteristic length of the system decreases to the nanoscale, the capillary forces created between two particles due to a liquid bridge can be of several orders of magnitude. It has previously been shown that the classical equations which describe the capillary forces are still valid at the nanoscale.29–31 The generation of capillary pressures as described using the Young–Laplace (Y–L) equation depends on the surface tension of the air–water interface, γlg, and the radius of the liquid bridge meniscus as shown in eqn (1).
 | (1) |
Consider a system consisting of two parallel slabs with a water drop forming a capillary bridge in between them as shown in Fig. 1. In the system, lx is the width of the slabs and the separation between the slabs is 2d. Similarly, ly represents the length of the particle that is in contact with water and θ is the angle made by the water meniscus with the slab walls. Furthermore, if the pressure inside the liquid meniscus is uniform, the slabs are subjected to a force (Fpz) due to the water pressure and is given by eqn (2).
| Fpz = Ac·ΔP | (2) |
Fγz = −γ·lx·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (3) |
Combining eqn (1)–(3), the total capillary force exerted by the liquid bridge under this configuration on the top slab is given by1
 | (4) |
The application of an external electric field across the interfaces seems to be an effective method to tune the wettability of a surface.30,37 This induces a change in the surface tension of a liquid–gas interface and the interfacial free energy at the solid–liquid interface.38 The contact angle made by the liquid–gas interface with the solid under the influence of an external electric field can be predicted using the Young–Lipmann equation (YLE) as shown in eqn (5), and has been discussed elsewhere.39–41
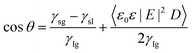 | (5) |
In eqn (5), θ is the equilibrium contact angle, D is the thickness of the solid–liquid interface, γ is the surface tension, E is the applied electric field strength, ε is the dielectric constant of the liquid and ε0 is the permittivity of the free space. The subscripts l, g and s refer to the liquid, gas and solid, respectively, and the angular bracket stands for the average over D. The Young–Lipmann equation, as shown above, predicts the lowering of the contact angle with an increase in the electric field independent of the field direction; however, deviations from this behavior have been reported at the nanoscale.37,41 The externally applied electric field not only affects the solid–liquid contact angle, but also affects other properties such as viscosity,42 surface tension,43–45 and dieletric constant46 which makes it challenging to predict the effect of electric field on a hydrated system. Moreover, phenomena related to hydrogen bond stretching which is inherent to high electric field at the interfaces are neglected using the YLE equation. For a more detailed explanation of YLE, the readers are referred to an extensive review on electrowetting by Mugele and Baret.47
In this work, we explore the effect of an externally applied static electric field on the capillary force exerted by a water bridge between two chains of cellulose nanocrystals (CNCs) using molecular dynamics (MD) simulations. The strength of the applied E-field ranges from 0 to 0.75 V nm−1 and is applied in parallel and perpendicular directions to the CNC slabs. The range used in this study is found in biological ion channels, charged electrodes,48 AFM studies,49 and electroporation processes.50 It has been shown elsewhere51 that the range of the electric field used in this study does not cause disintegration of water molecules.
2 Methodology
A series of MD simulations have been conducted using GROMACS2019, an MD package that has widely been used to investigate the molecular interaction phenomena for systems involving biomolecules.30,52,53 A time step of 2 fs (2 × 10−15 s) was used in all simulations. It has been suggested that the cut-off distance for truncating the van der Waals force should be greater than 0.8 nm;1 hence, we used a cut-off distance of 1 nm in our study. Long range electrostatic interactions were calculated using the Smooth Particle Mesh Ewald (SPME) method.54 All the equilibration and production simulations were carried out in the canonical (NVT) ensemble at 300 K, unless otherwise mentioned. The temperature was controlled using the velocity rescaling version of the Berendsen thermostat55 to isolate athermal effects as much as possible56–58 and the periodic boundary condition was applied in all directions throughout all the simulations.Two rectangular crystalline cellulose slabs were placed in a computational domain of 6.96 nm × 20.44 nm × 24.91 nm3 as shown in Fig. 1. The initial distance between the slabs (2d) was maintained constant at 7 nm. Cellulose 1β cystals were modeled with chains formed by repeating cellobiose units as shown in Fig. 2 and was based on the structure predicted by Nishiyama et al.59 Apart from the atomic configurations for the initial system, it is also very important to choose a forcefield (FF) based on the nature of simulation systems. Although various FFs like AMBER,60 CHARMM,61 and GROMOS62 have been reported for carbohydrate systems, we chose to implement the GLYCAM0663 FF, which has been reported to be consistent with a larger biomolecular context. This FF has also been employed in condensed phase simulations of biomolecules in aqueous media to represent biopolymers and crystalline lattice properties in previous studies and has been proved to successfully predict the surface and mechanical characteristics of nanocrystalline cellulose and its interaction with an aqueous medium.64
Water molecules were described using the simple point charge SPC/E model65 which has successfully been used in studies involving water–cellulose systems.66 We have chosen the SPC/E water model not only to give consistency to the previous studies29,31,67,68 but also due to its quantitative agreement with experiments to yield water reorientation and hydrogen bond (HB) dynamics.69 Moreover, it has been shown that the value of the surface tension for the SPC/E model is in good agreement with the experimental results.70
To create a drop of water, a fixed number of water molecules were energy minimised. After energy minimization, the system was subjected to the NVT ensemble at 300 K for 3 ns and subsequently to the NVE ensemble for next 3 ns. The water–cellulose interaction parameters were described using Lorentz–Bertholet (LB) mixing rules.71 For further details of the potentials used here, we refer readers to Matthews et al.72 and Kirschner et al.63
To study the effect of an electric field on the capillary force exerted by a water bridge confined between two cellulose particles, we first of all construct the CNC slabs composed of cellulose chains. The CNC slabs were then equilibrated in the NVT ensemble for 5 ns and the output was subjected to the NVE ensemble for the next 5 ns. Two CNC slabs were then put in a computational box with the chain axis parallel to the y-axis of the box (cf.Fig. 1).
Thereafter, we proceed to calculate the capillary force exerted by a water bridge under the effect of an externally applied electric field and confined between two CNC slabs separated by predetermined spacing. We first equilibrate the cellulose and the water systems separately, and subsequently introduce water between the CNC slabs. During this time period, the water drop spreads on the internal CNC walls and hence creates an equilibrated water bridge. Subsequently, we run further equilibration under the NVT ensemble at 300 K for 3 ns. After equilibration of the water bridge confined between two CNC surfaces, we apply electric fields of varying strength in parallel and perpedicular directions (along y and z axes respectively in Fig. 1) to the water bridge for 3 ns. During these steps, we restrict the motion of the CNC slabs in all directions using position restraints.
To measure the capillary force between two slabs connected by a water bridge, we anchored the surface C6 atoms of the cellulose chains of the top CNC slab at one end forming a parallel combination of springs whose other end is fixed, as shown in Fig. 3. The water bridge draws the top slab towards the bottom under the influence of the capillary force which can be directly calculated from the Hookes law (eqn 6), i.e. the force (F) exerted by the bridge is the product between the elastic constant of the spring (κ) and the stretching of the i-springs due to the capillary force (δx).
 | (6) |
 | ||
| Fig. 3 Schematic representation of the strategy considered to calculate the contact angle of water with the CNC slabs. | ||
The details of this method is elaborated in the study by Valenzuela et al 2016.2
3 Results and discussion
3.1 Measurement of contact angles on cellulose surfaces
The 2D density profile was plotted based on the average molecular density profile of the water bridge averaged over the last 5000 configurations divided into 5 blocks to estimate the deviations in the measurement. The points in the air–water interface where the density was less than 0.6 g cm−3 were discarded. An arc was fitted to the points near the interface where the water density was equal to or above 0.6 g cm−3 as shown in Fig. 4. The contact angle of the water bridge with the slabs was assumed to be the tangent to the arc at the “apparent” contact plane. The adsorbed water molecules at the solid–liquid interface form a rigid layer of highly structured molecules. In the present study, this layer was assumed to be solidified layers and the height of this layer was substracted from the actual height of the CNC channel. The apparent contact plane is, thus, made at the imaginary plane parallel to the CNC surface (Fig. 3). The effective contact angle was taken as the mean value of angles made by the water bridge on the top left side and the bottom left side of the CNC slab. The errors bars correspond to the contact angle deviation over the last 5 blocks as mentioned above. These errors correspond to the thermal and mechanical fluctuations of the interfacial water density. | ||
| Fig. 4 Graphical representation of the contact angle determination from the 2D water bridge density profile. The color bar on the right hand side of the above figure is expressed in kg m−3. | ||
Eqn (5) suggests a gradual reduction of the contact angle of a liquid on a solid substrate with an increasing magnitude of an external electric field. However, it should be noted that at the nanoscale, the direction along with the magnitude of an electric field has a significant effect on the formation of the contact angle and is shown in Fig. 5.41 The physical mechanisms behind the dynamics of capillary bridge formation under the effect of an electric field can be rather complex owing to the interplay of factors like the dipole–electric field interactions, the hydrogen bond dynamics at the interfaces in the presence of an electric field, surface tension and viscosity effects and each term may affect the contact angle formation in a particular way. Therefore, to assess the overall effect of an applied electric field on the capillary bridge formation, the dynamic contact angle (DCA) during the formation of a stable capillary bridge was measured (cf.Fig. 6).
 | ||
| Fig. 6 Dynamic contact angle of the water droplet on CNC walls under the influence of external static electric fields. The electric fields are applied parallel to the CNC slab. | ||
The DCAs measured, both, in the presence and absence of an external electric field are consistent with the WCA value reported in our previous study.38 However, it seems that a higher the magnitude of the externally applied electric field reduces the time required to attain the equilibrium contact angle. Nevertheless, the equilibrium contact angle is attained approximately 1 ns after the application of the external field. The main reason behind the faster response of the DCA at a higher electric field may be understood by relating the ultrafast reorientation of the water dipoles with the applied field and also the subsequent change in the hydrogen bond structure.73 It is well established that the water molecules orient in the direction of the applied electric field with the water dipole pointing towards the field direction.30,37,58 Using DFT-based ab initio MD to explore the structural and dynamic responses of the hydrogen bond (HB) network in water, Elgabarty et al.73 showed that in the field–dipole interaction that is much stronger than the HB potential energy well (∼ 8kBT, kB = Boltzmann constant and T = temperature), the molecules will reorient in a ballastic manner. This preferential orientation of water molecules with respect to the externally applied electric field results in the change in interfacial free energies of the system which affects the overall wetting properties and hence causes variations in the observed water contact angle.38
3.2 Capillary force measurements
The force balance eqn (4) is dependent principally on the following factors: (i) surface tension of the air–water interface (γlg), (ii) separation between the CNC slabs (2d) and (iii) the contact angle made by the water droplet with the walls of the CNC slabs (θ).The surface tension of water varies depending on the magnitude and direction of the applied electric field and has been shown in our previous studies.38 The values of surface tensions at various external electric fields from our previous study have been used in eqn (4) to calculate the theoretical values of the capillary force.
 | ||
| Fig. 7 Force on the bottom CNC slab in the z-direction due to a liquid bridge for different separation distances. The filled square dots are the values of forces extracted from MD simulations, while the empty ones are those predicted by eqn (4). The results above corresponds to the averages over 5 reruns of each simulations. | ||
The observed decrease in the force is due to the increase in the radius of the curvature (rm) of the capillary bridge as the remaining parameters are maintained constant. This increased rm contributes to a decrease in the capillary pressure exerted by the bridge that in turn results in the decrease in the capillary force.
3.3 Influence of the external electric field on the capillary force
In this section, we are mainly interested in the forces due to non-bonded interactions of the drop of water molecules and the CNC slabs. For this purpose, we choose a system with a CNC separation distance of 7 nm. After the steady state equilibrium is reached, i.e. after the fluctuations in the force becomes neglible, the forces are calculated based on Hooke's law at different applied electric fields. The maximum extension of the “harmonic spring” was observed to be less than 0.27 nm which preserved the approximate radius of the curvature of the water bridge between the slabs; hence the capillary forces calculated for different cases could be compared. CNC slabs are hydrophilic; hence, a film of adsorbed water was always present at equilibrium when a stable water bridge was obtained. This physically adsorbed film influenced the theoretical calculation of forces using eqn (4) and has been considered as solidified water layers; hence, the effective height of the CNC channel is considered to be the total height excluding the height of the adsorbed water layer i.e. 2(H − he) as shown in Fig. 3. Similarly, the area of the adsorbed film was excluded from the total wetted area.The capillary force measured directly from simulations showed lower variations with the different field strengths when the external field was applied in the direction parallel to the CNC slabs and are shown in Fig. 8. This could possibly be due to the relatively lower variation in contact angles at the range of applied field.38 The other factor that might also have influenced the lesser variation observed in the capillary forces is the low variability in the surface tension of the air–water interface of the water bridge in the applied field range.38
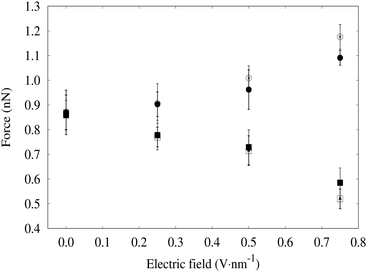 | ||
| Fig. 8 Average capillary force exerted by the water bridge on the CNC slabs under the influence of an external electric field. The filled dots are the simulated values of the capillary forces while the hollow dots are the values calculated using eqn (4). Similarly, the round dots are the cases where the electric field is applied in the parallel direction to the CNC slabs while the square dots are the cases with the electric field applied perpendicular to the CNC surface. The results shown above corresponds to the averages over 5 reruns of each simulations. | ||
We found that the average force in the perpendicular direction for the CNC slabs decreases with the increasing magnitude of the electric field as shown in Fig. 8. However, the decrease in the average force is not linear. The average values of the forces under various magnitudes of the electric field is inline with those predicted by eqn (4). This suggests that the determining factor for the capillary force of a water bridge under the influence of an static external electric field depends on the characteristics of the system like separation between the particles and solid–liquid contact areas together with the interfacial tensions.
While a study performed at the molecular level can be useful to gain deeper insights into the influence of an external electric field on the interparticular capillary forces which directly affect the drying process, its application in an industrial process requires the experimental validation and optimization of the field strength and direction during the process design. Furthermore, a CNF matrix is a complex structure with plethora of fibril orientations, large variations in interfibrillar distances and fibril–fibril entanglements. Hence, the direct extrapolation of MD results to such a complex material matrix is not straight forward. Nevertheless, the capillary forces obtained by MD simulations of two extreme cases of the external field suggest that the overall decrease in capillary forces is larger under a perpendicular applied field as compared to the increase in capillary forces under a parallel field applied to the CNF surface at the same field strength (c.f.Fig. 8) which indicates that a higher magnitude of the electric field when directed perpendicular to the CNF surface, which might be possible by the continuous change of the cake orientation, is suitable for the removal of the trapped water between the cellulosic surfaces.
4 Conclusions
By employing the MD simulation techniques, we have studied the effect of an externally applied electric field on the capillary force exerted by a bridge of pure water between two CNC slabs at 300 K. We found that the contact angle of water on a CNC slab is dependent on the magnitude and direction of the applied electric field.30,74 We attribute this to the preferential orientation of water molecules in the electric field.30 Our results suggest that the variation in the capillary force with an increase in the magnitude of the applied electric field is primarily due to the variation in the contact angle of the water drops on the CNC surface. The variation in the capillary forces when the electric field was applied in the perpendicular direction to the CNC surface was more pronounced as compared to the cases where it was applied in the parallel direction. The results predicted by the classical force balance equation including the Young–Laplace equations indicate that the Young–Laplace equation remains valid at the nanoscale. Although the direct extrapolation of the MD results in the drying process might not be trivial, the present study paves a path for an experimental exploration of the effect of electric field in the drying process of hard-to-dewater materials like CNFs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computations/data handling were enabled by the resources provided by the Swedish National Infrastructure for Computing (SNIC) in NSC at Linköping university partially funded by the Swedish Research Council through the grant agreement no. 2018-05973.References
- P. M. Amarasinghe, A. Anandarajah and P. Ghosh, Appl. Clay Sci., 2014, 88–89, 170–177 CrossRef CAS.
- G. E. Valenzuela, J. H. Saavedra, R. E. Rozas and P. G. Toledo, Phys. Chem. Chem. Phys., 2016, 18, 11176–11183 RSC.
- M. Dormann and H.-J. Schmid, Langmuir, 2014, 30, 1055–1062 CrossRef PubMed.
- S. Cheng and M. O. Robbins, Langmuir, 2016, 32, 7788–7795 CrossRef CAS PubMed.
- L. Vagharchakian, F. Restagno and L. Léger, J. Phys. Chem. B, 2009, 113, 3769–3775 CrossRef CAS PubMed.
- M. M. Kohonen, D. Geromichalos, M. Scheel, C. Schier and S. Herminghaus, Phys. A, 2004, 339, 7–15 CrossRef.
- L. Wang and T. J. McCarthy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2664–2669 CrossRef CAS PubMed.
- L. Siebert, T. Schaller, F. Schüt, S. Kaps, J. Carstensen, S. Shree, J. Bahr, Y. K. Mishra, H.-H. Sievers and R. Adelung, Nanoscale Horiz., 2019, 4, 947–952 RSC.
- X. Zhang, Y. Liu, Y. Liu and S.-U. Ahmed, Chin. Sci. Bull., 2009, 54, 1648–1654 Search PubMed.
- H. Stark, J.-i Fukuda and H. Yokoyama, Phys. Rev. Lett., 2004, 92, 205502 CrossRef PubMed.
- P. A. Kralchevsky and N. D. Denkov, Curr. Opin. Colloid Interface Sci., 2001, 6, 383–401 CrossRef CAS.
- E. W. Comings and T. K. Sherwood, Ind. Eng. Chem., 1934, 26, 1096–1098 CrossRef CAS.
- P. Faure and P. Coussot, Phys. Rev. E, 2010, 82, 036303 CrossRef CAS PubMed.
- R. Roth and K. M. Kroll, J. Phys.: Condens. Matter, 2006, 18, 6517–6530 CrossRef CAS PubMed.
- A. I. Rusanov, Prot. Met. Phys. Chem. Surf., 2015, 51, 36–40 CrossRef CAS.
- T. G. M. van de Ven, Ind. Eng. Chem. Res., 2008, 47, 7250–7256 CrossRef CAS.
- S. Stenström, Drying Technol., 2020, 38, 825–845 CrossRef.
- M. J. Lundahl, A. G. Cunha, E. Rojo, A. C. Papageorgiou, L. Rautkari, J. C. Arboleda and O. J. Rojas, Sci. Rep., 2016, 6, 1–21 CrossRef PubMed.
- K. J. De France, T. Hoare and E. D. Cranston, Chem. Mater., 2017, 29, 4609–4631 CrossRef CAS.
- K. Gordeyeva, H. Voisin, N. Hedin, L. Bergström and N. Lavoine, Mater. Chem. Front., 2018, 2, 2220–2229 RSC.
- K. Missoum, M. Belgacem and J. Bras, Materials, 2013, 6, 1745–1766 CrossRef PubMed.
- T. Keplinger, X. Wang and I. Burgert, J. Mater. Chem. A, 2019, 7, 2981–2992 RSC.
- H. A. Khalil, Y. Davoudpour, M. N. Islam, A. Mustapha, K. Sudesh, R. Dungani and M. Jawaid, Carbohydr. Polym., 2014, 99, 649–665 CrossRef PubMed.
- S. Li and P. S. Lee, Sci. Technol. Adv. Mater., 2017, 91–102 Search PubMed.
- Y. Peng, D. J. Gardner and Y. Han, Cellulose, 2012, 19, 91–102 CrossRef CAS.
- A. Bohumil, V. Alois, H. d O. Marcius and G. d V. Theo, Nord. Pulp Pap. Res. J., 2006, 21, 653–658 CrossRef.
- A. Rana, A. Patra, M. Annamalai, A. Srivastava, S. Ghosh, K. Stoerzinger, Y.-L. Lee, S. Prakash, R. Y. Jueyuan, P. S. Goohpattader, N. Satyanarayana, K. Gopinadhan, M. M. Dykas, K. Poddar, S. Saha, T. Sarkar, B. Kumar, C. S. Bhatia, L. Giordano, Y. Shao-Horn and T. Venkatesan, Nanoscale, 2016, 8, 15597–15603 RSC.
- Nanoscale Surface Force Measurement, 2005, pp. 781–782.
- N. K. Karna, E. Oyarzua, J. H. Walther and H. A. Zambrano, Phys. Chem. Chem. Phys., 2016, 18, 31997–32001 RSC.
- N. K. Karna, A. Rojano Crisson, E. Wagemann, J. H. Walther and H. A. Zambrano, Phys. Chem. Chem. Phys., 2018, 20, 18262–18270 RSC.
- E. Oyarzua, J. H. Walther, A. Mejia and H. A. Zambrano, Phys. Chem. Chem. Phys., 2015, 17, 14731–14739 RSC.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- R. D. Hazlett, J. Colloid Interface Sci., 1990, 137, 527–533 CrossRef CAS.
- R. J. Good, J. Adhes. Sci. Technol., 1992, 6, 1269–1302 CrossRef CAS.
- A. Depalo and A. C. Santomaso, Colloids Surf., A, 2013, 436, 371–379 CrossRef CAS.
- L. J. Jallo, Y. Chen, J. Bowen, F. Etzler and R. Dave, J. Adhes. Sci. Technol., 2011, 25, 367–384 CrossRef CAS.
- F. Song, L. Ma, J. Fan, Q. Chen, G. Lei and B. Q. Li, Phys. Chem. Chem. Phys., 2018, 20, 11987–11993 RSC.
- N. K. Karna, J. Wohlert, A. Liden, T. Mattsson and H. Theliander, J. Colloid Interface Sci., 2021, 589, 347–355 CrossRef CAS PubMed.
- T. Krupenkin and J. A. Taylor, Nature, 2011, 2, 448 Search PubMed.
- C. D. Daub, D. Bratko, K. Leung and A. Luzar, J. Phys. Chem. C, 2007, 111, 505–509 CrossRef CAS.
- C. D. Daub, D. Bratko and A. Luzar, in Nanoscale Wetting Under Electric Field from Molecular Simulations, ed. B. Kirchner and J. Vrabec, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 155–179 Search PubMed.
- D. Zong, H. Hu, Y. Duan and Y. Sun, J. Phys. Chem. B, 2016, 120, 4818–4827 CrossRef CAS PubMed.
- A. Bateni, A. Ababneh, J. Elliott, A. Neumann and A. Amirfazli, Adv. Space Res., 2005, 36, 64–69 CrossRef CAS.
- V. B. Warshavsky and X. C. Zeng, Phys. Rev. Lett., 2002, 89, 246104 CrossRef CAS PubMed.
- B. A. Pethica, Langmuir, 1998, 14, 3115–3117 CrossRef CAS.
- I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 110, 7935–7942 CrossRef CAS.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS.
- Z. Wang, D. L. Olmsted, M. Asta and B. B. Laird, J. Phys.: Condens. Matter, 2016, 28, 464006 CrossRef PubMed.
- N. Balke, S. Jesse, B. Carmichael, M. B. Okatan, I. I. Kravchenko, S. V. Kalinin and A. Tselev, Nanotechnology, 2017, 28, 065704 CrossRef PubMed.
- T.-H. Yen, Mol. Simul., 2012, 38, 509–517 CrossRef CAS.
- A. M. Saitta, F. Saija and P. V. Giaquinta, Phys. Rev. Lett., 2012, 108, 207801 CrossRef PubMed.
- S. Paavilainen, T. R'og and I. Vattulainen, J. Phys. Chem. B, 2011, 115, 3747–3755 CrossRef CAS PubMed.
- S. Kishani, T. Benselfelt, L. Wårberg and J. Wohlert, J. Colloid Interface Sci., 2021, 588, 485–493 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- N. J. English and J. M. D. MacElroy, J. Chem. Phys., 2003, 119, 11806–11813 CrossRef CAS.
- N. J. English and C. J. Waldron, Phys. Chem. Chem. Phys., 2015, 17, 12407–12440 RSC.
- Z. Futera and N. J. English, J. Chem. Phys., 2017, 147, 031102 CrossRef PubMed.
- Y. Nishiyama, P. Langan and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074–9082 CrossRef CAS PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmuller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- L. Pol Fachin, V. H. Rusu, H. Verli and R. D. Lins, J. Chem. Theory Comput., 2012, 8, 4681–4690 CrossRef CAS PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- M. Bergenstråhle, L. A. Berglund and K. Mazeau, J. Phys. Chem. B, 2007, 111, 9138–9145 CrossRef PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- B. Stenqvist, E. Wernersson and M. Lund, Nord. Pulp Pap. Res. J., 2015, 30, 26–31 CrossRef CAS.
- H. A. Zambrano, J. H. Walther and R. L. Jaffe, J. Mol. Liq., 2014, 198, 107–113 CrossRef CAS.
- E. Wagemann, E. Oyarzua, J. H. Walther and H. A. Zambrano, Phys. Chem. Chem. Phys., 2017, 19, 8646–8652 RSC.
- J. Schmidt, S. Roberts, J. Loparo, A. Tokmakoff, M. Fayer and J. Skinner, Chem. Phys., 2007, 341, 143–157 CrossRef CAS.
- C. Vega and E. de Miguel, J. Chem. Phys., 2007, 126, 154707 CrossRef CAS PubMed.
- D. Boda and D. Henderson, Mol. Phys., 2008, 106, 2367–2370 CrossRef CAS.
- J. F. Matthews, G. T. Beckham, M. Bergenstråhle-Wohlert, J. W. Brady, M. E. Himmel and M. F. Crowley, J. Chem. Theory Comput., 2012, 8, 735–748 CrossRef CAS PubMed.
- H. Elgabarty, N. K. Kaliannan and T. D. Kühne, Sci. Rep., 2019, 9, 10002 CrossRef PubMed.
- F. H. Song, B. Q. Li and Y. Li, Phys. Chem. Chem. Phys., 2015, 17, 5543–5546 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05563e |
| This journal is © the Owner Societies 2023 |



