Physical properties and nanostructuring of long-chained homobaric imidazolium ionic liquids

Abstract

Understanding the structure–property relationship and nanoscopic behaviour of ionic liquids is of utmost importance for their potential applications. Focusing these studies on sets of homobaric ionic liquids could provide important insight into the effects of specific chemical groups on the overall interaction profile, bringing researchers one step closer to succesfully designing ionic liquids which are tailor-made for specific applications. This work focuses on ionic liquids with 12 total carbons on their side chains, studying both their bulk physical properties (such as densities and viscosities) and their nanostructuring. The results reveal that by keeping the total number of carbons constant, but arranging them differently around the imidazolium ring, either in a linear or in a branched-chain formation, can result in compounds with quite distinct properties. Some of those (such as diffusivity) appear to be more sensitive to symmetry variations, while others (such as density) are not significantly affected. X-ray scattering is used in order to get a clearer understanding of the nanostructuring of the studied compounds and to investigate to what extent the observed macroscopic properties are directly linked to the nanoscale ordering.

---

Introduction

The study and development of non-traditional solvent systems, such as ionic liquids, has extended the available solvent-specific effects on chemical reactions, and nowadays getting a desired reaction outcome could be conditional upon just choosing the right solvent.¹ In order to achieve appropriate solvent selection it is important to understand specific solvent–solvent and solvent–solute interactions, as they are primarily responsible for the observed effects.²

Researchers working with ionic liquids know well that structure–property relationship studies are often challenging and lead to inconclusive results.³ The main reason for this is the structural complexity of these systems, which for ionic liquids is demonstrated, for example, by the formation of nanostructured domains. These nanodomains can have very distinct sets of interactions, which are defined by the atoms and the functional groups that participate in their formation.⁴

Molecular symmetry is a crucial parameter affecting the properties and nanostructuring of ionic liquids. Early in ionic liquid research, it was proposed that symmetry is a defining parameter for the properties of ionic liquids, with the lower melting points of alkylimidazolium ionic liquids compared to alkylpyridinium ionic liquids attributed to the asymmetric nature of the former.⁵ The N-alkylpyridinium cation has a C₂ symmetry (one symmetric rotational axis), while the 1-alkyl-3-methylimidazolium cation has C₁ symmetry (no rotational axis).

Expanding on this hypothesis would mean that symmetric 1,3-dialkylimidazolium cations should lead to ionic liquids with higher melting points compared to their asymmetric analogues. This was indeed proved with studies on 1,3-dialkylimidazolium ionic liquids with varying alkyl chain lengths, which showed that only few of the symmetric ionic liquids were liquid around room temperature.^6,7 Studies on a homologous series of symmetrical 1,3-dialkylimidazolium hexafluorophosphate ionic liquids revealed a common pattern, with the compounds with short alkyl chains (1 to 3 carbons) being solid, the compounds with intermediate chain lengths (4 to 10 carbons) being low-melting point solids, while the longer-chained compounds showed liquid-crystalline behaviour.^7,8

Following from these early observations, several studies have been published showing that ionic liquids with symmetric cations ([C_(n/2)C_(n/2)im]⁺) show higher local ordering compared to their asymmetric analogues ([C_(n−1)C₁im]⁺).^9,10 Small- and wide-angle X-ray scattering have shown that structural heterogeneity in symmetric dialkylimidazolium ionic liquids occupies smaller domains compared to their asymmetric counterparts, as indicated by the increased q-values in the scattering experiment.^8,11 These characteristics of the symmetric dialkylimidazolium ionic liquids make them promising candidates for a wide range of applications, such as catalysis as ‘pre-organised ionic solvents’.¹²

The properties of such symmetrical ionic liquids have been widely studied by different groups with an emphasis on viscosities and densities,⁸ volatility,¹³ tribology,¹⁴ surface tension¹⁵etc. However, all the studies revolve around a similar axis, studying a homologous series of increasing alkyl chain lengths and comparing the properties of interest. This approach does not resolve the question of when does molecular (a)symmetry start affecting the property of ionic liquids? Are these ‘special’ effects exclusive to the totally symmetric [C_(n/2)C_(n/2)im]⁺ cations and how do they get affected if we start introducing small asymmetries to the system?

In order to answer these questions, we have performed a systematic structure–property relationship study on a set of homobaric ionic liquids (Fig. 1) with a large number of alkyl chain carbons (12 carbons in total). As a model cation we used 1-undecyl-3-methylimidazolium ([C₁₁C₁im]⁺), as this offers a large number of structural isomers and could prove useful to show how gradual increase of the symmetry translates into the macroscopic properties (viscosity, density, thermal decomposition) or the nanostructuring of the ionic liquids. As can be seen from Fig. 1, we have synthesised 11 cations, 10 of which are direct structural isomers for [C₁₁C₁im]⁺, by re-arranging the alkyl chain; [C₇CycloC₅]⁺ is not strictly a structural isomer of [C₁₁C₁im]⁺, as it has one less hydrogen atom. The studied dataset consists of 8 cations with linear chains, 2 of which have a methylated C² position, 3 cations with one branched alkyl chain with different lengths and 1 cation with a cyclic chain. It is important to emphasise here that this dataset does not represent all the possible structural isomers of the model cation, as according to the cation isomer enumeration performed by Koutsoukos et al.,³ for a dialkylimidazolium cation with 12 total alkyl chain carbons with no heteroatoms present, there are more than 70 000 structural isomers.

Fig. 1 Cation structures studied in this work and their abbreviations.

Materials and methods

The ionic liquids studied in this work were prepared based on the procedures described in detail in previous works.^16,17 Detailed descriptions of the synthetic procedures can be found in the ESI.†

All ionic liquids were dried for several days in vacuo before their use and the water content, as tested by coulometric Karl Fischer titration, was always below 100 ppm. The water content of the ionic liquids was also tested after the measurements and is shown in the ESI,† Table S5.

Thermogravimetric analysis (TGA)

The TGA measurements were performed on a PerkinElmer Pyris1 TGA, equipped with a microbalance. All the measurements were performed under a 20 mL min⁻¹ nitrogen flow, using less than 5 mg of sample. The samples were heated from 30 to 600 °C with a rate of 5 °C min⁻¹.

Densities and viscosities measurements

The densities (ρ) and viscosities (η) of the samples were measured in an Anton Paar coupled density meter DMA 5000 M and microviscometer LOVIS 2000 ME, respectively. The density meter is based in a U-shaped vibrating-tube, that is electronically excited to oscillate at its characteristic frequency. The characteristic frequency changes depending on the density of the filled sample. Via a precise measurement of the characteristic frequency, the true density of the sample is determined. The calibration of the equipment was performed before the sample measurements with two substances of the precisely known densities, air and the Anton Paar density standard ultra-pure water. The precision of the measurements is 0.000050 g mL⁻¹ in the density and 0.001 °C in the temperature. Linear fits were performed to the density measurements, with an R² > 0.9999 in all cases. The raw density data, as well as the fitted lines, are shown in the ESI,† Tables S1 and S2.

The microviscometer is based on Hoeppler's falling ball principle that measures the rolling time of a ball through transparent and opaque liquids confined in a glass microcapillary. The accuracy of this module is 0.05% in the viscosity and 0.02 °C in the temperature. A 1.8 mm diameter capillary was calibrated in order to cover the whole range of the sample viscosities in the temperature range of the analysis. The calibration was performed with a substance of precisely known viscosities, APN26, and a ball with specific and known material, geometry and density. The viscosity data were successfully fitted to the Vogel – Fulcher – Tammann (VFT) equation (eqn (S4), ESI†).¹⁸ The raw viscosity data, as well as the fitted curves are shown in the ESI,† Tables S3 and S4.

Self-diffusion coefficients

The pulsed-field gradient stimulated echo (PFGSTE) spectra were measured at 297 K using a Bruker Avance III HD 500 NMR equipped with a 5 mm BBO SmartProbe. All measurements were performed on neat, dried and degassed ionic liquids with a DMSO-d₆ capillary insert. The full procedure is explained in detail in the work published by Philippi et al.¹⁹

Small- and wide-angle X-ray scattering

Small- (SAXS) and wide-angle (WAXS) X-ray scattering experiments were performed on I22 beamline at Diamond Light Source.²⁰ The X-ray energy was set to 18 keV (0.69 Å wavelength) and the sample-to-detector distance to 1.99 m (SAXS) and 0.17 m (WAXS). The resulting q range was 0.004 to 0.45 Å⁻¹ on the SAXS detector and 0.01 to 7.20 Å⁻¹ on the WAXS detector. 2D scattering patterns were recorded on Pilatus P3-2M detectors (both for SAXS and WAXS), using silver behenate to calibrate the SAXS detector and NBS silicon to calibrate the WAXS detector. The samples were loaded into polycarbonate capillaries. All measurements were performed at room temperature (25 °C). The DAWNDiamond (v2.26.0) software²¹ was used to integrate the scattering patterns to give 1D scattering plots of intensity against scattering vector, q (where q is the scattering vector defined as q = 2π/d, with d representing a real space distance) and subtract the background scattering from an empty polycarbonate capillary tube.

Results and discussions

TGA analysis

Four temperature-related data have been extracted from the TGA measurements and are presented in Table 1. These are: T_on: onset temperature, calculated as the temperature point with 10% weight loss, which indicates the decomposition initiation; T_max.rate: point of maximum decomposition rate, as indicated by the first derivative of the thermogram; T_1/2: temperature point of 50% sample mass loss and the carbonaceous residue at the end of the ionic liquid's decomposition. The full thermograms can be found in the ESI,† Fig. S1–S3.

Table 1 TGA data of the studied ionic liquids

Ionic liquid	T on (°C)	T 1/2 (°C)	T max.rate (°C)	Carb. residue (% weight)
[C11C1im][NTf2]	370.9	415.2	429.4	0.1
[C10C2im][NTf2]	400.7	442.3	462.5	0.2
[C10C1C1im][NTf2]	406.2	451.2	466.1	0.2
[C9C3im][NTf2]	374.6	415.8	428.9	0.2
[C9C2,1im][NTf2]	370.9	407.2	420.4	0.1
[C8C4im][NTf2]	377.2	427.0	438.0	0
[C8C3,1im][NTf2]	377.6	409.3	429.9	0.1
[C7C5im][NTf2]	374.1	418.0	433.3	0.1
[C7C4,1im][NTf2]	371.6	427.3	445.6	0
[C7C4C1im][NTf2]	397.1	447.7	463.1	0
[C7CycloC5im][NTf2]	360.5	396.0	417.1	0.1
[C6C6im][NTf2]	372.9	414.1	427.6	0.1

---

Comparing the ionic liquids with linear alkyl chains and no C²-methylation (Fig. S1, ESI†) it is apparent that all linear-chain ionic liquids have approximately the same decomposition temperature (decomposition starts around 370 °C), with the exception of [C₁₀C₂im][NTf₂], which decomposes at approximately 30 °C higher temperature. It seems that replacing the side methyl group with an ethyl group increases the thermal stability, an effect that is cancelled when longer alkyl chains are used.

Adding a branched chain to the ionic liquid (Fig. S2, ESI†) does not significantly affect the decomposition onset, but it does affect the decomposition rate. When the branched chain is closer to the imidazolium ring ([C₉C_2,1im][NTf₂]), the decomposition is sharper, while increasing this distance ([C₈C_3,1im][NTf₂] and [C₇C_4,1im][NTf₂]) gradually makes the decomposition broader. Adding a cyclic chain ([C₇CycloC₅][NTf₂]) reduces the thermal stability of the ionic liquid; combining this observation with the also reduced onset of [C₉C_2,1im][NTf₂] shows that the existence of a secondary carbon attached directly to an imidazolium's nitrogen promotes the decomposition reaction.

Methylation of the C²-position of the ring gives results similar to those reported in previous publications,¹⁶ with the methylation increasing the decomposition temperature of the compound. However, unlike the non-methylated analogues, the distribution of carbons on the alkyl chain does affect the decomposition profile of these compounds, with [C₇C₄C₁im][NTf₂] having a lower decomposition temperature compared to [C₁₀C₁C₁im][NTf₂]. This could be an indication that the decomposition mechanism of the methylated analogues deviates from that of the non-methylated, otherwise the alkyl chain effect should have similar trend between the two cases.

The decomposition mechanism for [NTf₂]⁻ ionic liquids is still uncertain, with only limited published experimental studies. Existing TGA/MS data show that during the thermal decomposition of [C_xC_yim][NTf₂] ionic liquids, the cation remains intact unless it contains ‘fragile’ groups, such as unsaturated bonds on the alkyl chain.^22,23 There are studies reporting that in those cases the [NTf₂]⁻ anion decomposes first via elimination of the SO₂ from the anion, leading to the formation of a more volatile neutral ion pair with the cation.²⁴ Our study shows that the existence of a secondary carbon attached to the imidazolium ring makes the product more volatile, enabling the decomposition product to be removed from the system more easily.

Densities and viscosities

Fig. 2 shows the primary measured density data and the fitted lines for the ionic liquids studied in this work. The first observation from those data is that, as expected, the re-arrangement of carbons in the side chains does not affect density. It has been shown that the molar volume, and so the density, of a pure ionic liquid is additive with that of its monovalent ions, making possible the description and prediction of the density using group contribution methods with maximum relative deviations in the order of 1%.^25,26 The densities essentially overlap for all the ionic liquids with non-methylated C² positions, regardless of the presence of a linear or branched chain. The compounds with the most significant density difference are [C₁₁C₁im][NTf₂] (1.257 g mL⁻¹ at 298 K) and [C₇C₅im][NTf₂] (1.263 g mL⁻¹ at 298 K), but this difference could be considered negligible as it is less than 1% and could be attributed to small fluctuations in the water content.

Fig. 2 Densities of the ionic liquids studied in this work. Error bars not included for simplicity; standard deviations are below 0.5%.

In previous work on the physical properties of short-chained imidazolium ionic liquids it was shown that the density was not affected neither when going from a linear to a branched chain, nor when going to a more symmetric system.¹⁶ Both observations are still true for long-chained systems presented in this work. It seems that density is not sensitive to symmetry variations and is only affected by the total number of carbons in the chain.

Methylation of the C²-position of the imidazolium ring increased the density of the resulting ionic liquids. However, it seems that this increase is a result solely due to methylation (as also reported in other works),^27,28 but it is not affected by symmetry as the densities of both C²-methylated analogues ([C₁₀C₁C₁im][NTf₂] and [C₇C₄C₁im][NTf₂]) completely overlap.

[C₇CycloC₅im][NTf₂] represents an exception to these observations, as it shows the largest density among the ionic liquids studied in this work. Since the cations are of equal molecular weight, the higher density of this ionic liquid can arise from either the [C₇CycloC₅im] cation itself being smaller (e.g. lower van der Waals surface) and/or from the presence of less ‘free space’ in this ionic liquid. The existence of the ring makes the cation more ‘compact’, occupying less space than it would in the case of a freely flexible side chain, so leading to more efficient packing. It is known that for ionic liquids with large number of alkyl carbons, the side chains tend to orient towards each other, favouring the formation of hydrophobic domains dominated by van der Waals interactions.^29,30 According to those reports, it is not expected that the alkyl chains of an ionic liquid will be constantly linearly oriented; in an unrestricted system they will have a distribution of orientations. However, folding back on itself entirely to have a conformation akin to the cyclopentyl chain would both be extremely unlikely, being one orientation of the many possible, and would disrupt the non-polar channel formation. Further discussion on the orientation and the structuring of these ionic liquids, supported by the SAXS/WAXS measurements is given below.

Fig. 2 (also see ESI†) shows that all the studied temperature-dependent densities are fitted to straight lines with the same slope, meaning that all the studied ionic liquids have the same isobaric thermal expansivity. This observation is consistent with our previous work on short-chained ionic liquids, as the temperature-dependent densities of these ionic liquids are also parallel to each other, regardless of the presence of heteroatoms on the alkyl chain. However, between the two homobaric sets the densities slopes are different, indicating that the density reduction is practically determined by the molecular weight of the ionic liquid. Expanding on that would mean that if one has the temperature dependent density trend of one ionic liquid, and thus the slope, one could predict the density trend of their homobaric analogues just by knowing the density at a single temperature.

On the other hand, the viscosity data (Fig. 3) present different trends compared to densities. The ionic liquids with linear chains and non-methylated C²-positions have very similar viscosities, with [C₁₀C₂im][NTf₂] showing the lowest viscosity among them, while [C₆C₆im][NTf₂] shows the highest; their difference is statistically significant (around 15% at 20 °C) but essentially small. From this behaviour we can extract two important pieces of information: first, increasing symmetry reduces the fluidity of the ionic liquid and, second, adding an ethyl chain on the ring ([C₁₀C₂im][NTf₂]) improves the fluidity compared to the model compound, probably because the additional carbon is more efficient in disrupting the ion–ion interactions between the charged cores (as will also be shown below with the X-ray scattering experiments), while simultaneously it is short enough to prevent any alkyl chain segregation of this side of the ring.

Fig. 3 Viscosities of the ionic liquids studied in this work. Error bars not included for simplicity; standard deviations are below 0.5%.

Adding a branched chain increases the viscosity of the ionic liquids following the trend of [C₁₁C₁im][NTf₂] < [C₉C_2,1im][NTf₂] < [C₇C_4,1im][NTf₂] < [C₈C_3,1im][NTf₂]. It seems that the effect of the branched chain on viscosity is related to its proximity to the imidazolium ring, with the property being affected the most when the branching has a distance of two carbons from the ring, while further increasing this distance reduces its significance. The addition of a cyclic chain does not seem to affect the viscosity significantly, as [C₇C₅im][NTf₂] and [C₇CycloC₅im][NTf₂] have very similar behaviours; this observation is counter-intuitive, as it is widely accepted that conformational flexibility is key parameter for reducing the viscosity,^31,32 but although [C₇C₅im][NTf₂] is more flexible than [C₇CycloC₅im][NTf₂], this is not determining the viscosity in this case.

As was expected, methylation of C²-position increases the viscosity of the ionic liquid. However, in this case the results are somewhat contradicting compared to the non-methylated cases. [C₁₀C₁C₁im][NTf₂] is significantly more viscous than [C₇C₄C₁im][NTf₂], indicating that for a methylated ring the distribution of carbons affects fluidity, with more symmetric chains having lower viscosity. However, in order to extract more detailed information about this behaviour, more C²-methylated analogues would have to be studied.

Another interesting observation of this series of ionic liquids regards the temperature dependence of viscosity. Although the viscosity differences at lower temperatures are significant, increasing the temperature above 70 °C results in all the ionic liquids having the same viscosity (14 mPa s). As expected from the Vogel–Fulcher–Tammann equation (eqn (S4), ESI†), viscosity is reducing with temperature, however it is not expected that all the systems will converge to the same value. The reasoning behind this is probably that all the interactions affecting viscosity (such as hydrogen bonding and π-interactions)³³ become less significant, leading to a ‘residual’ viscosity which is primarily determined by the molecular weight of the ions themselves. Just as a comparison for this we can use data on n-hexadecane, which at 20 °C has a viscosity of 3.49 mPa s reducing to 1.24 mPa s at 70 °C (reduction by a factor of 3),³⁴ while for the same temperature range [C₁₁C₁im][NTf₂] goes from 142 mPa s to 14 mPa s (reduction by a factor of 10). This example shows that for a non-hydrogen bonding system, the viscosity reduction with temperature is much lower than that of ionic liquids. The high-temperature viscosity reduction factor usually increases for more associating hydrogen bonding systems; relevant examples are 1-nonanoic acid, for which viscosity reduces from 8.22 mPa s at 20 °C to 2.07 mPa s at 70 °C (reduction by 3.6), while for 1-nonanol it reduces from 11.57 mPa s at 20 °C to 2.15 mPa s at 70 °C (reduction by 5.4).^35,36 The fact that all the studied compounds, regardless of the carbon distribution, converge to the same viscosity is a strong indication that regardless of the flexibility, symmetry or hydrodynamic radius of the ions, the molecular weight (size) itself contributes to their mobility. At lower temperatures viscosity is strongly dependent on the size of the alkyl chains and the position of the branching (higher viscosity when branching is closer to the imidazolium ring), but at higher temperatures these interactions become less relevant.

Self-diffusion of ions

NMR diffusometry with Pulsed Field Gradient Stimulated Echo (PFGSTE) is a valuable and sensitive technique to determine the self-diffusion coefficients of the system's constituents. In order to verify the accuracy of the measurements, all ionic liquids were synthesised and measured independently in triplicate, leading to less than 2% experimental deviation. The experimental data have been fitted to the Stejskal–Tanner equation³⁷ with an R² > 0.9999 for all cases.

Table 2 shows the calculated self-diffusion coefficients of the studied ionic liquids. The first observation here is that in this set of compounds, the diffusion coefficient of the cation is smaller than that of the anion for most compounds. There are several published studies demonstrating similar results in long-chained ionic liquids.^38,39 Specifically, Tokuda et al. published a study investigating the anion and cation self-diffusion coefficients of [C_nC₁im][NTf₂] for n ranging from 1 to 8 and they all show cation diffusion coefficients larger than the anion's, with the difference gradually reducing as the alkyl chain length increases; finally in the case of [C₈C₁im][NTf₂] the two coefficients are almost equal. It is therefore expected that for ionic liquids with longer alkyl chain, the cation will diffuse slower than the anion. [C₁₀C₂im]⁺ and [C₇CycloC₅im]⁺ do not follow this trend, as the self-diffusion coefficients of the cations are larger than those of the anions. This behaviour is reproducible over different samples, but not completely explained with the measurements performed in this study. Our current hypothesis for [C₇CycloC₅im]⁺ is that the rigid bulky cyclic chain of the cation acts as a ‘barrier’ for the anion, forcing it to diffuse slower. However this requires further investigation in the future to extract solid results.

Table 2 Cation and anion self-diffusion coefficients at 25 °C, as calculated with the Stejskal–Tanner equation. Standard deviations are ± 0.1 × 10⁻¹² m² s⁻¹

Ionic liquid	Cation D+ (10^−12 m^2 s^−1)	Anion D− (10^−12 m^2 s^−1)
[C11C1im][NTf2]	7.7	9.2
[C10C2im][NTf2]	10.1	8.4
[C10C1C1im][NTf2]	4.6	4.8
[C9C3im][NTf2]	9.3	9.5
[C9C2,1im][NTf2]	9.0	9.3
[C8C4im][NTf2]	9.4	9.5
[C8C3,1im][NTf2]	6.0	6.4
[C7C5im][NTf2]	9.1	10.0
[C7C4,1im][NTf2]	7.5	8.2
[C7C4C1im][NTf2]	6.5	6.7
[C7CycloC5im][NTf2]	9.1	7.9
[C6C6im][NTf2]	8.7	8.9

---

Looking at the diffusion coefficients of the cations, for the linear-chained ionic liquids [C₁₁C₁im][NTf₂] has a rate of 7.7 × 10⁻¹² m² s⁻¹, which rises to 10.1 × 10⁻¹² m² s⁻¹ for [C₁₀C₂im][NTf₂]. After that, the diffusion coefficient reduces by increasing symmetry, with [C₆C₆im][NTf₂] having the lowest coefficient (8.7 × 10⁻¹² m² s⁻¹). Adding a branched chain makes all the cations diffuse slower compared to their linear analogues. Similar to the effects observed for viscosity, when the branching is close to the imidazolium ring ([C₉C_2,1im][NTf₂]) the diffusion is almost identical to the linear analogue ([C₉C₃im][NTf₂]), while [C₈C_3,1im][NTf₂] shows a sharp reduction in diffusion rate which then is again increased for [C₇C_4,1im][NTf₂].

Methylation of the C²-position of the ring makes the ions diffuse slower, which comes in agreement with the viscosity observations, as viscosity and ionic mobility are highly correlated. In the previous section it was shown that [C₁₀C₁C₁im][NTf₂] is significantly more viscous than [C₇C₄C₁im][NTf₂], a behaviour that is also shown on the diffusion rates. This result could be related to the increased flexibility of [C₇C₄C₁im][NTf₂] due to the existence of two long alkyl chains, compared to [C₁₀C₁C₁im][NTf₂].⁴⁰

Nanostructuring studies

So far in this work we have mentioned several times the concept of nanostructuring and how this would affect the different studied physical properties. It is therefore important to characterise this nanoscale ordering and how this changes in the studied homobaric series. SAXS and WAXS are probably the most appropriate methods for characterising the ionic liquid environments, as even for a macroscopically homogeneous liquid they are able to detect persistent interactions, which are then translated to atom distances with high statistical occurrence. Fig. 4, 6 and 7 show the X-ray scattering patterns of the studied ionic liquids from the WAXS detector. For q-values lower than 0.4 Å⁻¹ the SAXS detector is normally preferred, as it offers higher resolution, however, the maximum q recorded on the SAXS detector in this case was 0.35 Å⁻¹ and since the first observed peak in most samples is in the range of 0.4–0.6 Å⁻¹, it was not always observable by SAXS. The SAXS measurements of all samples are shown in the ESI,† Fig. S4–S6.

Fig. 4 SAXS/WAXS scattering patterns of the linear-chained ionic liquids.

Fig. 4 shows the SAXS/WAXS scattering patterns of the linear-chained ionic liquids. All the patterns are normalised to the 1.38 Å⁻¹ peak, as this appears to be almost identical across all samples. The scattering patterns show the 3 main peaks that are characteristic for ionic liquids, which are attributed to specific inter- and intramolecular interactions.⁴¹ The first peak (low q-values) is the ionic liquid prepeak (peak I) which is dependent on the interactions between distinct polar (charged cation or anion headgroup) and non-polar (cation's alkyl chains) components of the ionic liquids and is considered to be the strongest indication of nanoscale heterogeneity.⁴² The peak at intermediate q-values (peak II, typically 0.8 to 1 Å⁻¹) is attributed to charge alternation, which is usually translated to cation–cation or anion–anion repeat distances. The third peak (peak III, typically at 1 to 2 Å⁻¹) is the adjacency peak, which is attributed to intermolecular interactions and is considered characteristic of neighbouring anion–cation distances.^43,44 Fig. S4–S6 in the ESI† show the SAXS data for the same ionic liquids, but since the SAXS is measured for the q range of 0.004 to 0.35 Å⁻¹, not all the prepeaks are visible in this range.

[C₁₁C₁im][NTf₂] and [C₁₀C₂im][NTf₂] show strong prepeaks at 24.2 Å, a reasonable result since long-chained ionic liquids such as those presented in this work are expected to show strong polar–non polar domain segregation. However, from [C₉C₃im][NTf₂] onwards, the prepeak is reduced to a shoulder on the scattering pattern. This reduction can be explained by taking into account the interactions that contribute to the formation of the prepeak. According to Araque et al., polar–polar interactions and non-polar–non-polar interactions contribute positively towards the prepeak, while the polar–non-polar interactions create an antipeak.⁴³ In practice this translates to the fact that the existence of strong polar–non-polar interactions could indicate the lack of segregation into distinct domains. However, this is not expected to be the case for our ionic liquids here, since the alkyl chains still remain long enough to observe nanostructuring (typically the limit is 5 carbons^29,45). Probably what is happening in this case is that increasing the number of carbons on the 3-position of the imidazolium ring actively increases the polar–non-polar interactions, and as a result the antipeak effect, as the anion is ‘forced’ to interact with the alkyl carbons due to their proximity.

Table 3 shows the calculated distances based on the data presented on Fig. 4. The distance reduction of peak I indicates that the polarity interaction does not take into account the whole length of the molecule (as this would remain essentially the same); the distance indicated by peak I most probably takes into account only the charged imidazolium core and the length of the longest alkyl chain. Peak II shows a small increase, from 7.4 to 8.1 Å, showing that the charge interactions are also sensitive to the carbon distribution, with more symmetric cations increasing the space between charge alternations.

Table 3 Calculated distances from the SAXS/WAXS data of Fig. 4. The patterns were fitted to Gaussian bell functions and the peaks were calculated from the fitting

Ionic liquid	Peak I (Å)	Peak II (Å)	Peak III (Å)
[C11C1im][NTf2]	24.2	7.4	4.6
[C10C2im][NTf2]	24.2	7.7	4.6
[C9C3im][NTf2]	17.8	7.9	4.6
[C8C4im][NTf2]	15.1	8.0	4.6
[C7C5im][NTf2]	13.8	8.1	4.6
[C6C6im][NTf2]	13.7	8.1	4.6

---

Comparing the observed peaks to literature values for [C_xC₁im][NTf₂] ionic liquids where x is the same as the longest alkyl chain (e.g. comparing [C₉C₃im][NTf₂] with [C₉C₁im][NTf₂]),⁴⁶ we observe that the position of peak I is shifted to lower q-values for the [C_xC₁im][NTf₂] compounds, while the positions of peak II and III remain practically unchanged. This shows that the formed nanodomains are larger for the [C_xC₁im][NTf₂] ionic liquids, probably due to a preference of the alkyl chains toward linear orientations, while in the [C_xC_yim][NTf₂] ionic liquids a more curled or U-shaped configuration is preferred (Fig. 5).⁴⁷

Fig. 5 From left to right: linear, V- and U-shaped orientations of a 1,3-dialkylimidazolium cation. Figure redrawn from ref. 45.

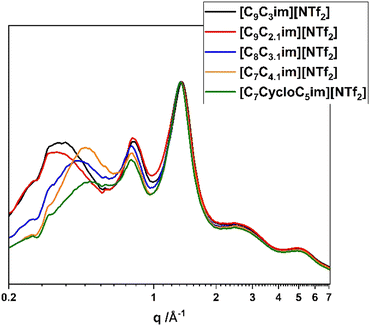
Fig. 6 shows the SAXS/WAXS patterns for the branch-chained ionic liquids and compares them with [C₉C₃im][NTf₂]. The overall profiles look similar, with peak III still being unchanged. Increasing the length of the branched chain causes peak I to reduce in intensity and shift to higher q-values (calculated distances shown in Table 4), while peak II also decreases in intensity. This observation makes sense taking into account again the polar–non-polar interactions; the branching is always on the terminal group of the alkyl chain and increasing its length probably ‘forces’ it to be in contact with the polar domains, increasing again the antipeak I. Increasing the interactions between anions and cations also gives rise to a charge antipeak,⁴⁸ which explains the reduction in peak II intensity too. [C₇CycloC₅im][NTf₂] appears to have almost completely lost its prepeak, something that has been observed previously in pyrrolidinium ionic liquids with attached cyclic chains,⁴⁸ and is again relevant to the mixing of the bulky non polar chain with the charged anion core.

Fig. 6 SAXS/WAXS scattering patterns of the branch-chained ionic liquids.

Table 4 Calculated distances from the SAXS/WAXS data of Fig. 5 and 6. The patterns were fitted to Gaussian bell functions and the peaks were calculated from the fitting

Ionic liquid	Peak I (Å)	Peak II (Å)	Peak III (Å)
[C9C2,1im][NTf2]	18.7	7.9	4.6
[C8C3,1im][NTf2]	14.7	8.0	4.6
[C7C4,1im][NTf2]	13.6	8.0	4.6
[C7CycloC5im][NTf2]	13.1	8.1	4.6
[C10C1C1im][NTf2]	23.0	7.3	4.8
[C7C4C1im][NTf2]	13.8	7.9	4.7

---

Fig. 7 shows the scattering patterns for the 2 C²-methylated ionic liquids, compared to their non-methylated analogues (calculated distances shown in Table 4). The prepeaks of the C²-methylated compounds are very similar to the corresponding non-methylated analogues (especially for [C₇C₄C₁im][NTf₂] and [C₇C₅im][NTf₂] the prepeaks look identical), indicating that the methylation of C² position of the ring does not affect significantly the polarity alternation. Peaks II and III seem more affected by the methylation. In both studied cases, peak II of the methylated compounds appears to have higher intensity and being shifted to higher q-values compared to the non-methylated analogues. These changes, compared to the fact that the prepeak is not significantly affected, indicate that the methylation does not contribute to the polar–non-polar interactions, instead it brings the ion pairs slightly closer together, probably helping them to arrange more tightly. Peak III is different for the methylated ionic liquids compared to the non-methylated analogues, being broader and slightly shifted towards lower q-values. Since peak III is related to the distances between neighbouring molecules, methylation of C² position acts as an extra spacer unit, pushing the molecules slightly apart.

Fig. 7 SAXS/WAXS scattering patterns of the C²-methylated ionic liquids versus their non-methylated analogues.

Conclusions

This work studied the effects of symmetry and alkyl chain re-arrangement on the physical properties and nanostructuring of a series of 12 synthesised dialkylkimidazolium ionic liquids. The model cation ([C₁₁C₁im]⁺) has a molecular weight of 237.4 g mol⁻¹ and all the studied analogues are direct structural isomers with identical molecular weight, with the exception of [C₇CycloC₅im]⁺, which has one hydrogen atom less due to the cyclic chain.

When the studied alkyl chain is linear and the C² position of the ring is not methylated, then then distribution of carbons in the alkyl chains does not significantly affect the thermal decomposition, density or viscosity. The exception to that is [C₁₀C₂im][NTf₂] which shows higher thermal stability compared to the other analogues. When the C² position is methylated, then the distribution of carbons affects the decomposition temperatures and viscosity, but not density. Both [C₁₀C₁C₁im][NTf₂] and [C₇C₄C₁im][NTf₂] have almost identical densities. NMR diffusometry shows a slightly different trend compared to the other properties, with [C₁₁C₁im][NTf₂] diffusing slower than the others; introducing a side ethyl group in [C₁₀C₂im][NTf₂] makes the cation diffuse faster, while all the other arrangement combinations show practically identical diffusion rates. C²-methylated ionic liquids diffuse slower than the non-methylated, with the distribution of carbons affecting the results here as well – the methylated analogues show significantly reduced diffusion rates compared to the non-methylated.

Introducing a branched or cyclic chain to the cation has different effects depending to the studied property. Thermal stability is mostly affected in terms of the decomposition rate, while the onset temperatures are not significantly affected. The densities of the branched ionic liquids do not show significant differentiations compared to their linear analogues, with the exception of [C₇CycloC₅im][NTf₂] which shows the highest density of all the other analogues, indicating that the cyclic chain leads to more efficient packing of the molecules. Regarding their rheological behaviour, the branched-chain ionic liquids appear more viscous compared to their linear analogues at lower temperatures, but above 70 °C this effect is negated and all viscosities converge to the same value. For the branched-chain ionic liquids diffusivity remains unaffected when the branching is closer to the ring ([C₉C_2,1im][NTf₂]) and then is reduced when the branching is farther from the ring, showing a minimum value for ([C₈C_3,1im][NTf₂]).

The X-ray scattering measurements provide insight about the interactions and the nanostructuring of the studied compounds. The ionic liquids with the shorter chains on the 3-position of the ring ([C₁₁C₁im][NTf₂] and [C₁₀C₂im][NTf₂]) show significant signs of nanodomain segregation, as revealed by the strong prepeak. As the side chain on the 3-position gradually becomes longer though, the prepeak is significantly reduced, even almost absent for [C₇CycloC₅im][NTf₂]; this reduction is believed to be due to the mixing of the previously strictly polar domain with the now longer alkyl chains of the 3-position, which gives rise to a polarity antipeak. Methylation of the C²-position does not seem to affect significantly the polarity alternation, its major effects are related to the charge alternation and the distances between adjacent species.

This work clearly demonstrates that the many–body interactions inherent for the ionic liquids significantly affect their physical properties, even when minor alterations are introduced on the structure. Not all properties are equally affected by the symmetry though, as for example although the SAXS/WAXS data show clear differentiations in the nanostructuring even for the linear analogues, macroscopic viscosities and densities are not significantly affected. Expanding the studied dataset to include more examples, possibly with introducing alkylations of the C^4/5 positions of the imidazolium ring or by studying ionic liquids with different sizes of alkyl chains, could help understanding better the effects of symmetry on the physical properties of ionic liquids and even create models which can help structure-property relationship predictions.

Author contributions

Conceptualisation S. K., T. W.; supervision T. W.; investigation S. K., J. A.; methodology S. K., J. A.; writing – original draft preparation S. K.; writing – review & editing, S. K., J. A., M. C. G., N. J. B., T. W.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Lisa Haigh for the mass spectrometry measurements and Dr Peter Haycock and Imperial College's NMR Suite for the PFGSTE NMR measurements. We acknowledge the Diamond Light Source for the time on the Beamline I22 under proposal SM29165 and thank Dr Andy Smith for his assistance during our experiments. J. A. and M. C. G. thank IDEX Lyon (ANR-16-IDEX-0005) for financial support.

Notes and references

1. J. B. Harper, B. Kirchner, P. Pavez and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 26028–26029.
2. T. Welton and C. Reichardt, Solvents and solvent effects in organic chemistry, John Wiley & Sons, 2011.
3. S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843.
4. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
5. K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356.
6. K. Lee, C. Lee and I. B. Lin, Chem. Commun., 1997, 899–900.
7. S. V. Dzyuba and R. A. Bartsch, Chem. Commun., 2001, 1466–1467.
8. W. Zheng, A. Mohammed, L. G. Hines Jr, D. Xiao, O. J. Martinez, R. A. Bartsch, S. L. Simon, O. Russina, A. Triolo and E. L. Quitevis, J. Phys. Chem. B, 2011, 115, 6572–6584.
9. M. A. Rocha, C. M. Neves, M. G. Freire, O. Russina, A. Triolo, J. A. Coutinho and L. M. Santos, J. Phys. Chem. B, 2013, 117, 10889–10897.
10. D. Xiao, L. G. Hines Jr, S. Li, R. A. Bartsch, E. L. Quitevis, O. Russina and A. Triolo, J. Phys. Chem. B, 2009, 113, 6426–6433.
11. S. Raju and S. Balasubramanian, J. Phys. Chem. B, 2010, 114, 6455–6463.
12. A. V. Yermalayeu, M. A. Varfolomeev and S. P. Verevkin, J. Mol. Liq., 2020, 317, 114150.
13. M. A. Rocha, J. A. Coutinho and L. M. Santos, J. Phys. Chem. B, 2012, 116, 10922–10927.
14. G. Yu, S. Yan, F. Zhou, X. Liu, W. Liu and Y. Liang, Tribol. Lett., 2007, 25, 197–205.
15. H. F. Almeida, M. G. Freire, A. M. Fernandes, J. A. Lopes-da-Silva, P. Morgado, K. Shimizu, E. J. Filipe, J. N. Canongia Lopes, L. M. Santos and J. A. Coutinho, Langmuir, 2014, 30, 6408–6418.
16. S. Koutsoukos, F. Philippi, D. Rauber, D. Pugh, C. W. Kay and T. Welton, Phys. Chem. Chem. Phys., 2022, 24, 6453–6468.
17. S. Koutsoukos, J. Becker, A. Dobre, Z. Fan, F. Othman, F. Philippi, G. J. Smith and T. Welton, Nat. Rev. Methods Primers, 2022, 2, 1–18.
18. S. Jiang, Y. Hu, Y. Wang and X. Wang, J. Phys. Chem. Ref. Data, 2019, 48, 033101.
19. F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, Chem. Sci., 2020, 11, 6405–6422.
20. A. Smith, S. Alcock, L. Davidson, J. Emmins, J. Hiller Bardsley, P. Holloway, M. Malfois, A. Marshall, C. Pizzey and S. Rogers, J. Synchrotron Radiat., 2021, 28, 939–947.
21. M. Basham, J. Filik, M. T. Wharmby, P. C. Chang, B. El Kassaby, M. Gerring, J. Aishima, K. Levik, B. C. Pulford and I. Sikharulidze, J. Synchrotron Radiat., 2015, 22, 853–858.
22. M. C. Kroon, W. Buijs, C. J. Peters and G.-J. Witkamp, Thermochim. Acta, 2007, 465, 40–47.
23. C. Maton, N. De Vos and C. V. Stevens, Chem. Soc. Rev., 2013, 42, 5963–5977.
24. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
25. J. Jacquemin, R. Ge, P. Nancarrow, D. W. Rooney, M. F. Costa Gomes, A. A. Pádua and C. Hardacre, J. Chem. Eng. Data, 2008, 53, 716–726.
26. Y. Deng, S. Morrissey, N. Gathergood, A. M. Delort, P. Husson and M. F. Costa Gomes, ChemSusChem, 2010, 3, 377–385.
27. Z. J. Chen and J.-M. Lee, J. Phys. Chem. B, 2014, 118, 2712–2718.
28. A. S. Rodrigues, M. A. Rocha, H. F. Almeida, C. M. Neves, J. A. Lopes-da-Silva, M. G. Freire, J. A. Coutinho and L. M. Santos, J. Phys. Chem. B, 2015, 119, 8781–8792.
29. J. N. Canongia Lopes and A. A. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335.
30. J. N. Canongia Lopes, M. F. Costa Gomes and A. A. Pádua, J. Phys. Chem. B, 2006, 110, 16816–16818.
31. F. Philippi, D. Rauber, O. Palumbo, K. Goloviznina, J. McDaniel, D. Pugh, S. Suarez, C. C. Fraenza, A. Padua and C. W. Kay, Chem. Sci., 2022, 13, 9176–9190.
32. D. Rauber, F. Philippi, B. Kuttich, J. Becker, T. Kraus, P. Hunt, T. Welton, R. Hempelmann and C. W. Kay, Phys. Chem. Chem. Phys., 2021, 23, 21042–21064.
33. O. Hollóczki, F. Malberg, T. Welton and B. Kirchner, Phys. Chem. Chem. Phys., 2014, 16, 16880–16890.
34. T. Klein, S. Yan, J. Cui, J. W. Magee, K. Kroenlein, M. H. Rausch, T. M. Koller and A. P. Fröba, J. Chem. Eng. Data, 2019, 64, 4116–4131.
35. A. Guzmán-López, G. A. Iglesias-Silva, F. Reyes-García, A. Estrada-Baltazar and M. Ramos-Estrada, J. Chem. Eng. Data, 2017, 62(2), 780–795.
36. X. Wang, T. Sun and A. S. Teja, J. Chem. Eng. Data, 2016, 61, 2651–2658.
37. E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292.
38. T. M. Koller, J. Ramos, P. S. Schulz, I. G. Economou, M. H. Rausch and A. P. Fröba, J. Phys. Chem. B, 2017, 121, 4145–4157.
39. T. Burankova, E. Reichert, V. Fossog, R. Hempelmann and J. P. Embs, J. Mol. Liq., 2014, 192, 199–207.
40. P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288.
41. N. J. Brooks, F. Castiglione, C. M. Doherty, A. Dolan, A. J. Hill, P. A. Hunt, R. P. Matthews, M. Mauri, A. Mele and R. Simonutti, Chem. Sci., 2017, 8, 6359–6374.
42. H. V. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838–16846.
43. J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740.
44. C. C. Weber, N. J. Brooks, F. Castiglione, M. Mauri, R. Simonutti, A. Mele and T. Welton, Phys. Chem. Chem. Phys., 2019, 21, 5999–6010.
45. D. W. Bruce, C. P. Cabry, J. N. Canongia Lopes, M. L. Costen, L. A. D’Andrea, I. Grillo, B. C. Marshall, K. G. McKendrick, T. K. Minton and S. M. Purcell, J. Phys. Chem. B, 2017, 121, 6002–6020.
46. O. Russina, A. Triolo, L. Gontrani, R. Caminiti, D. Xiao, L. G. Hines, R. A. Bartsch, E. L. Quitevis, N. Plechkova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121.
47. O. Renier, G. Bousrez, M. Yang, M. Hölter, B. Mallick, V. Smetana and A.-V. Mudring, CrystEngComm, 2021, 23, 1785–1795.
48. H. K. Kashyap, C. S. Santos, N. S. Murthy, J. J. Hettige, K. Kerr, S. Ramati, J. Gwon, M. Gohdo, S. I. Lall-Ramnarine and J. F. Wishart, J. Phys. Chem. B, 2013, 117, 15328–15337.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed procedures for the syntheses of the studied ionic liquids, ¹H and ¹³C NMR, mass spectrometry measurements, water content of the ionic liquids, TGA thermograms, raw data of the physical measurements and fitted curves, SAXS patterns. See DOI: https://doi.org/10.1039/d2cp05783b

---