Tuning the optical properties of the metal–organic framework UiO-66 via ligand functionalization

Abstract

Metal–organic frameworks (MOFs) are a promising class of materials for optical applications, especially due to their modular design which allows fine-tuning of the relevant properties. The present theoretical study examines the Zr-based UiO-66-MOF and derivatives of it with respect to their optical properties. Starting from the well-known monofunctional amino- and nitro-functionalized UiO-66 derivatives, we introduce novel UiO-66-type MOFs containing bifunctional push–pull 1,4-benzenedicarboxylate (bdc) linkers. The successful synthesis of such a novel UiO-66 derivative is also reported. It was carried out using a para-nitroaniline (PNA)-based bdc-analogue linker. Applying density functional theory (DFT), suitable models for all UiO-66-MOF analogues were generated by assessing different exchange–correlation functionals. Afterwards, HSE06 hybrid functional calculations were performed to obtain the electronic structures and optical properties. The detailed HSE06 electronic structure calculations were validated with UV-Vis measurements to ensure reliable results. Finally, the refractive index dispersion of the seven UiO-66-type materials is compared, showing the possibility to tailor the optical properties by the use of functionalized linker molecules. Specifically, the refractive index can be varied over a wide range from 1.37 to 1.78.

---

Introduction

Metal–organic frameworks (MOFs) are an important class of porous organic–inorganic hybrid materials built up by metal ions or metal-oxide clusters as inorganic building units (IBUs) connected by organic ligands acting as linkers.^1,2 Based on the intrinsic porosity of the frameworks, MOFs have been discussed intensively with regard to classical applications of such materials, like catalysis, gas separation, gas storage, or gas sensing.^3–5

More recently, the use of MOFs for optical applications has gathered increasing attention.^6–10 Due to their modular design, the electronic and optical properties of MOFs can be tailored by making use of the possibilities to employ different metal centers, different linkers, and to exploit the pore space for storing guest molecules.^11–13 This versatility and adaptability enables the development of new materials for optical components with precisely adjusted properties. Compared to classical optical materials like glasses, MOFs furthermore offer the advantage of low temperature preparation routes, thus simplifying and cheapening the production processes of optical systems. Further work is needed in order to prepare MOF entities with optical quality, e.g. as highly transparent thin films, generated, e.g., via layer-by-layer synthesis, direct crystallisation or spin-coating techniques.^7,13–15

Zr-based frameworks represent a promising family of MOFs, consisting of numerous different compounds, most of which feature exceptional chemical and thermal stability, promoting Zr-based MOFs for materials development.¹⁶ In this study we focus on the Zr-based MOF UiO-66 and its functionalized derivatives. The UiO-66 framework is built up from zirconium-oxo-hydroxo clusters [Zr₆O₄(OH)₄] which are 12-fold coordinated by 1,4-benzenedicarboxylate (bdc) forming an expanded cubic closed-packed structure.¹⁷ The use of amino- or nitro-functionalized bdc linkers results in the well-established UiO-66-NH₂ and UiO-66-NO₂ MOFs sharing the UiO-66 topology and exhibiting a high stability as well.^18,19 While the framework topology remains, these derivatives show differences in the porosity and chemical nature of the pores, as well as different electronic, spectral and optical properties.^20–22

This study aims to gain a better understanding of a basic optical property of MOFs, namely the refractive index. The refractive index is of importance in many optical applications, but in the case of MOFs has been somewhat overlooked. Only in the last few years, the interest in the evaluation of the refractive index of MOFs has increased somewhat.^7,13 Changes in refractive index have been measured, mostly via ellipsometry on thin films (not all of which were of optical quality), often with the idea to use the measured variations as sensor signals.^15,23–29 In a similar vein, variations in signal intensities on waveguides covered with MOFs were measured.^30,31 These experiments thus used the empty pore space of the MOFs.

Here, we focus instead on the linker chemistry to test its influence on the refractive index of the frameworks themselves. Especially, we want to determine the range of accessible refractive indices which can be achieved by the addition of functional groups to a “standard” MOF linker, namely terephthalate. For this purpose, we calculate the electronic properties of UiO-66 derivatives containing linkers with additional functional groups which give the linker molecules push–pull properties. These linker molecules contain “push” groups like amino (NH₂) or dimethylamino (N(Me)₂) and “pull” groups like nitro (NO₂) or dicyanovinyl (DCV) and are shown in Fig. 1d–f. Results obtained on UiO-66-MOF structures with these linkers will be compared to those gained on the simpler congeners UiO-66, UiO-66-NH₂ and UiO-66-NO₂, containing the linkers depicted in Fig. 1a–c. The introduction of push–pull-linkers allows advanced band gap modulation and leads to materials with tailored optical properties. The electronic and optical properties of UiO-66 MOFs containing the linker molecules depicted in Fig. 1 are characterized by applying density functional theory (DFT). Assessing different exchange–correlation functionals and dispersion corrections within the (meta) generalized gradient approximation (GGA, mGGA) we obtain adequate structural descriptions of the UiO-66 analogues. Subsequently, we use the range-separated hybrid functional HSE06 to determine both, the electronic structure and optical properties of UiO-66 and its derivatives with high accuracy.^32–35 To the best of our knowledge, this is the first study of MOFs examining the electronic and optical properties relying completely on hybrid DFT calculations. To gain full benefit of this high level of theory calculations and reliable results, we use carefully converged plane-wave basis sets and fully relaxed models with a precise representation of the studied structures eliminating influences of the basis set size and variations of the cell volume on the calculated optical properties.

Fig. 1 Linkers in the UiO-66 MOFs investigated with (a) no functionalization, (b) NO₂ group (c) NH₂ group; and novel bifunctional linker molecules with (d) NH₂ and NO₂, (e) N(Me)₂ and NO₂, (f) NH₂ and DCV and (g) N(Me)₂ and DCV groups.

Furthermore, in the experimental part of the work, we report the synthesis of a novel bifunctional UiO-66 derivative featuring a terephthalate-based para-nitroaniline linker (pnadc: 2-amino-5-nitrobenzene-1,4-dicarboxylate) introducing amino- and nitro-groups into the framework within one linker. We fully characterize this novel MOF which is only the second framework containing this special linker.³⁶

With the novel UiO-66-(NH₂,NO₂), UiO-66-MOFs with the linkers depicted in Fig. 1a–d are available for experimental investigations. We have determined the band gaps of these substances experimentally from their UV-Vis spectra and compare the obtained values to the calculated ones.

With a better understanding of how the various modular components – metal oxide clusters, linkers, guest molecules – influence the refractive index, MOFs can qualify as optical materials beyond the application of guest-selective coatings. They can be employed as coatings for mirrors and lenses, or as optical media in more complex devices like waveguiding elements, optical filters or in Fabry–Pérot devices.

Methods

Experimental details

UiO-66 was synthesized according to the synthetic route of Shearer et al.³⁷ All three UiO-66 derivatives were synthesized in a 100 mL Pyrex glass vessel by dissolving specific amounts of a Zr(IV)-source, water, modulator and linker successively in DMF. The exact values are given in ESI,† Section S1. The glass vessels were sealed and heated at 120 °C for 24 h (150 °C and 12 h for UiO-66-(NH₂,NO₂)). After cooling to room temperature, the precipitate was separated via centrifugation, washed with DMF and acetone and dried under vacuum. To further purify the material, each powder was Soxhlet-extracted with acetone for 24 h and activated at 150 °C under vacuum.

Powder X-Ray diffraction (PXRD) was carried out in transmission mode using a Stoe Stadi-P diffractometer operated with Ge (111)-monochromatized CuKα₁ radiation (λ = 1.54060 Å). A Mythen 1K detector was used and the diffractograms were recorded from 5 to 50° 2θ. UV-Vis diffuse reflectance spectroscopy (UV-Vis DRS) was performed on the MOF powders using a Praying Mantis device on a Cary 4000 from Agilent Technologies. For this purpose, the MOF powder was mortared with BaSO₄ to gain better quality measurements. For further characterization, MOF samples were digested according to the procedure of Chu et al. and transferred to liquid-state ¹H-NMR-spectroscopy.³⁸ For this instance, 15 mg of MOF were digested in 1 M NH₄CO₃ solution in D₂O for 2 h. ¹H-NMR spectra were recorded on a Bruker Ascend 400 MHz Spectrometer. Argon physisorption measurements were performed at 87 K on a 3Flex instrument from micromeritics. The samples (25 mg) were activated at 150 °C under secondary vacuum for 20 h. For the analysis of the data the associated software was used. BET areas were determined by the BET-auto function of the software and total pore volumes were calculated with single-point method at a relative pressure of 0.95. Scanning electron microscope (SEM) images were recorded with a JEOL JSM-6700F microscope using an accelerating voltage of 2 kV with a working distance of 8 mm. The SEM samples were prepared by dispersion of small amounts of MOF powder in ethanol using an ultrasonic bath. The dispersion was dropped onto a polished graphite block and dried at room temperature. Thermogravimetric measurements were performed on a Netzsch STA 449 F5 Jupiter in synthetic air (N₂, O₂) with a heating rate of 5 K min⁻¹ using 10 mg of MOF powder.

Computational details

Kohn–Sham density functional theory calculations were performed using the CASTEP code (version 20.1) employing a plane-wave basis set in combination with pseudopotentials.^39,40 UiO-66 and its analogues were modelled with primitive cells of the fcc lattice with 114 to 198 atoms depending on the functionalisation. The convergence of the plane-wave kinetic energy cutoff and the Brillouin zone sampling were examined with respect to the lattice parameters (see ESI,† Section S2) and set to 1000 eV for UiO-66 and 800 eV for the derivatives with Γ-point sampling. The pseudopotentials were generated on-the-fly with the Koelling–Harmon method to incorporate relativistic effects into the generated pseudopotentials.⁴¹ The PBEsol exchange–correlation functional was used to fully relax the structures using “on-the-fly” generated ultra-soft pseudopotentials with an SCF convergence criterion of 5.0 × 10⁻⁷ eV per atom.⁴² Applying a low-memory Broyden–Fletcher–Goldfarb–Shanno (LBGFS) algorithm, structures with an energy change of less than 5.0 × 10⁻⁶ eV per atom and a maximal force of 0.01 eV Å⁻¹ were obtained. The convergence threshold of the stress and maximal atom displacement were 0.02 GPa and 5.0 × 10⁻⁴ Å, respectively.

Subsequently three different exchange–correlation (XC) functionals were assessed with regard to the lattice parameters of the UiO-66 and its analogues to obtain precise structural models for further characterisation. To determine suitable XC functionals, full cell relaxations were performed using the parameters described above. The benchmark included the generalized gradient approximation (GGA) functional of Perdew, Burke, and Ernzerhof (PBE) with D2 and TS dispersion correction, respectively, the PBE expansion for solids (PBEsol) and its dispersion corrected form (PBEsol-TS), and the rSCAN meta-GGA functional.^42–47

Using the optimized models, single point HSE06 hybrid DFT calculations were performed to obtain the band structures, the corresponding density of states (DOS) and the dispersion of the refractive index.³² All calculations were carried out using Γ-point Brillouin zone sampling with the determined plane-wave kinetic energy cutoff values and a SCF convergence criterion of 10⁻⁹ eV per atom. The optical properties were calculated applying the tools provided within CASTEP to evaluate the electronic structure, obtain the complex dielectric function and subsequently the dispersion of the index of refraction.⁴⁸

Results and discussion

This study is concerned with UiO-66-type MOFs containing the linker molecules depicted in Fig. 1. Of these, UiO-66 as well as its amino and nitro derivative are well-known. In addition, we have synthesized the novel UiO-66-(NH₂,NO₂) with the pnadc push–pull linker. We first describe the results of the characterization of these experimentally accessible MOFs prior to focussing on the results of the calculations of the electronic and optical properties of MOFs with all the linkers depicted in Fig. 1.

Experimental studies on UiO-66-type MOFs

UiO-66 derivatives were synthesized via the standard synthesis route with DMF as solvent and using the modulation approach which was introduced for the synthesis of Zr-MOFs by our group.⁴⁹ By using this approach the well-known UiO-66 derivatives, as well as the novel UiO-66-(NH₂,NO₂), were obtained with a high crystallinity as proven by the PXRD measurements depicted in Fig. 2 left. UV-Vis DRS measurements show that unfunctionalized UiO-66 only exhibits absorption in the UV region, whereas its derivatives all feature a second adsorption maximum at a higher wavelength which is contributed by the functional groups introduced into the framework (Fig. 2 right). Whereas this additional absorption is only weak in the case of UiO-66-(NO₂), it is pronounced upon the incorporation of amino groups into the framework. The successful incorporation of the linker molecules into the framework and the complete removal of solvents during work-up were verified with ¹H-NMR-spectroscopy on digested samples (see ESI,† Fig. S4). The recorded spectra substantiate that the phase-pure samples were solvent-free and that the linker molecules were not altered during the solvothermal synthesis.

Fig. 2 PXRD patters (left) and UV-Vis spectra (right) of UiO-66, its monofunctionalized derivatives UiO-66-NO₂ and UiO-66-NH₂, and of the novel bifunctional UiO-66-(NH₂,NO₂).

Further analysis via argon physisorption measurements on the novel UiO-66-(NH₂,NO₂) reveals the intact porosity of this framework after solvent exchange and activation (see ESI,† Fig. S1). A typical type I isotherm, characteristic for microporous materials like UiO-66 derivatives, was obtained, with a BET area of 932 m² g⁻¹ and a pore volume of 0.385 cm³ g⁻¹. Thermogravimetric analysis suggests that the framework has thermal stability up to 300 °C (see ESI,† Fig. S2). Scanning electron microscope (SEM) images of UiO-66-(NH₂,NO₂) show that the material appears as intergrown octahedral particles with a size in the nanometer range (see ESI,† Fig. S3).

Structure of UiO-66 and its analogues

This comprehensive DFT study includes UiO-66, its well-known amino- and nitro-derivatives and four novel MOFs containing push–pull linkers. With one of the push–pull linkers, amino–nitro benzene dicarboxylate, a UiO-66-MOF was also obtained experimentally for the first time (see above). The “push” units included here are amino and dimethylamino, the “pull” units employed are nitro and dicyanovinyl groups.

UiO-66 crystallizes in space group F4̄3m with an experimental lattice parameter of a = 20.747 Å containing four primitive triclinic cells (a_P = 14.670 Å).⁵⁰ As the PXRD diagrams in Fig. 2 show, the two synthesized monofunctional derivatives (UiO-66-NO₂, UiO-66-NH₂) and the novel bifunctional (UiO-66-(NH₂,NO₂)) derivative are topologically equivalent with UiO-66 and have closely matching lattice parameters. It was assumed that also the in silico-designed bifunctional derivatives will share the UiO-66 topology and lattice parameters. Relying on this hypothesis, suitable XC functionals were assessed to describe the structures with suitable models by comparing the calculated lattice parameters with experimental ones of the pure UiO-66 (see ESI,† Section S3). It was found, that the PBEsol and rSCAN functionals lead to fully optimized structures with an error of less than 1% for the average lattice parameter a_P while the use of the PBEsol functional with TS dispersion correction (PBEsol-TS) consistently results in structures with less than 0.2% error (see Table 1). Only in the case of the unmodified UiO-66 the meta-GGA rSCAN functional outperforms the PBEsol-TS functional, proving the improved performance of dispersion-corrected GGA functionals and the capability of the PBEsol functional regarding the accurate description of crystal structures.

Table 1 Details of the DFT study and generated structural models of UiO-66 derivatives: plane-wave kinetic energy cutoff, exchange–correlation functional, average lattice parameter of the optimized primitive cell and its deviation compared with the experimental UiO-66 value

MOF	Abbreviation	E cutoff/eV	XC functional	a P/Å	Deviation/%
UiO-66 (exp.)^50				14.670
UiO-66	H	1000	rSCAN	14.677	0.050
UiO-66-NO2	NO2	800	PBEsol-TS	14.652 ± 0.004	0.123
UiO-66-NH2	NH2	800	PBEsol-TS	14.647 ± 0.010	0.154
UiO-66-(NH2,NO2)	NH2, NO2	800	PBEsol-TS	14.674 ± 0.023	0.025
UiO-66-(N(Me)2,NO2)	N(Me)2, NO2	800	PBEsol-TS	14.691 ± 0.021	0.146
UiO-66-(NH2,DCV)	NH2, DCV	800	PBEsol-TS	14.675 ± 0.074	0.034
UiO-66-(N(Me)2,DCV)	N(Me)2, DCV	800	PBEsol-TS	14.669 ± 0.023	0.006

---

In this study, all UiO-66 derivatives were modelled within space group P1, which introduces higher degrees of freedom during the cell relaxation. As a result, the lattice constants are optimized independently and an average lattice parameter a_P was introduced. Although slight distortions of the primitive cells occurred compared to UiO-66, the shape of the primitive cells basically remained unchanged and stayed comparable to the one of UiO-66, confirming that the functionalisation of the UiO-66 leads to isostructural derivatives with nearly unchanged lattice parameters. This underlines the stability of the UiO-66 topology regarding the use of functionalized linker molecules and shows that even linkers carrying large push–pull motifs can be incorporated. Additionally, the fact that calculated lattice parameters lie close to experimental ones shows that the careful convergence of the basis set allows very precise structural descriptions of the examined MOFs.

Electronic structure of UiO-66 and its analogues

It has been repeatedly shown that the electronic structure of UiO-66 derivatives can be altered by introducing further functional groups on the bdc linker. Thus, also the optical properties of UiO-66 depend on the type of functionalisation.^8,12,22,51 In this section we focus on the electronic structure of UiO-66 and its analogues to evaluate the effect of the mono- and bifunctional linker functionalisation.

We carried out electronic structure calculations on hybrid DFT level (see ESI,† Section S4) and validated the results with regard to band gaps extracted from solid state UV-Vis DRS (see Fig. 2 right) determined using Tauc plots (see ESI,† Fig. S5) of phase-pure samples of the experimentally accessible MOFs. The calculated band gaps are compared with the experimental ones in Fig. 3. The HSE06 calculations reproduce the experimental trend and are in good agreement with the measured band gaps; additionally, the calculated values are coherent with the HSE06 studies of UiO-66 and UiO-66-NH₂ in literature.^8,12,52,53 Moreover, we report the first HSE06 electronic structure calculation of UiO-66-NO₂. The calculated band gap is in accordance with the published HSE03-based study of Flage-Larsen et al.²² The band structure calculation of UiO-66-(NH₂,NO₂) yields a band gap of 2.78 eV, which compares well to the experimental value of 2.91 eV. Furthermore the predicted small difference in the band gap values of UiO-66-NH₂ and UiO-66-(NH₂,NO₂) was observed in the experiment.

Fig. 3 Comparison of calculated (HSE06) and experimental (exp.) band gaps.

In general, the functionalisation of UiO-66 reduces the band gap. In particular, electron-donating “push” substituents lower the band gap more than electron-withdrawing “pull” ones. A direct look on the calculated band structures as depicted in Fig. 4 gives further information. Electron-donating groups like the amino group mainly introduce new states above the valence band maximum (VBM) of unfunctionalized UiO-66, basically forming band gap states with regard the parent UiO-66 band structure. On the contrary, electron withdrawing groups like the nitro group only introduce states located near to the VBM, resulting in a discernible, but smaller influence on the band gap (see Fig. 4). By analysing the projected density of states (PDOS), it becomes clear, that the small influence of the electron-withdrawing substituents on the band gap originates from the strongly bound electrons forming localized states. In the case of the NO₂-functionalisation, the VBM states belong to the oxygen atoms of the nitro-groups (O_NO2) while the nitrogen atom forms unoccupied states in the conduction band. The strongly bound electrons of O_NO2 lead to eigenstates with just slightly more energy than those of the oxygen atoms forming the IBU (O_IBU). This increases the density of states at the top of the valence band but has only a small effect on the band gap. In contrast, the band gap states introduced by the electron-donating substituents are generated by unbound delocalized electrons, which in the case of the amino-substituents are formed by the free electron pair of the nitrogen atoms and the electrons of the benzene ring. These states have a significant higher energy compared to the O_IBU states, leading to the formation of separated states which increase the VBM and correspondingly lower the band gap notably.

Fig. 4 Band structures with density of states (DOS) and projected density of states (PDOS) of UiO-66, UiO-66-NO₂, UiO-66-NH₂ and UiO-66-(NH₂,NO₂). The valence band maximum (VBM) and band gap states (BGS) are highlighted.

Using the characteristics of the nitro- and amino-model systems, we proceed with describing the electronic structures of UiO-66 derivatives containing bifunctional linkers featuring an electron-withdrawing and an electron-donating substituent within the same linker molecule. This leads to the insertion of further band gap states and of states at the conduction band minimum (CBM), both influencing the band gap and thus allowing for tuning the resulting optical properties. For instance, the bifunctional UiO-66-(NH₂,NO₂) features the VBM states characteristics of the amino-functionalisation and the CBM states typical of the nitro-functionalisation. Insertion of these states results in a smaller band gap while increasing the number of states at the CBM and VBM. This should lead to a higher refractive index in the visible range, due on the one hand to the red shift and on the other to the higher intensity of the absorption coupled with an increased polarizability which allows the tailoring of UiO-66-based optical materials using bifunctional linkers.

To analyze the effect of the different bifunctional linkers on the electronic structure of the resulting MOFs, the PDOS of the IBU and the corresponding linker including the oxygen atoms of the carboxylate are compared (Fig. 5). In the case of UiO-66-(NH₂,NO₂) the PDOS of the linker highlights the increased number of VBM and CBM states with regard to the MOFs with monofunctional linkers. The projected electron density of the UiO-66-(NH₂,NO₂) band gap states reveals the influence of the free electrons originating from the nitrogen atom of the electron-donating amino group and underlines that the electron-withdrawing nitro group with its free electrons located at the oxygen atoms also contributes to the VBM. Thus, the use of a bifunctional push–pull-linker enables band gap tuning by altering the VBM and CBM states simultaneously.

Fig. 5 Left: Projected density of states of IBU (grey) and of linker atoms (red) with highlighted band gap states. Right: Projected electron density of UiO-66-(NH₂,NO₂) band gap states (isosurface value 0.03 e Å⁻³).

With the introduction of our novel bifunctional linkers, the number of band gap and CBM states were extended inducing a further reduction of the band gap. Especially, the expansion of the VBM states occurring in all systems with N(Me)₂- and DCV-groups enhances the polarizability of the linker, leading to a more intense absorption and thus promoting a higher index of refraction, regardless of the small changes in the band gap.

Optical properties of UiO-66 and its analogues

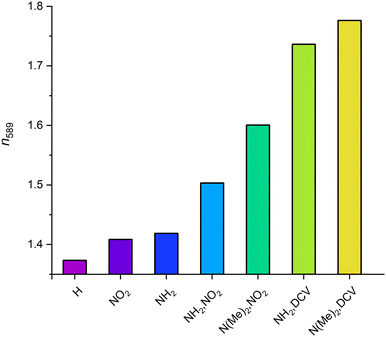
We used hybrid DFT calculations to determine the dielectric function and obtain the dispersion of the refractive index (RI) of the studied UiO-66 materials. Fig. 6 shows impressively the broad range of RI values accessible with one framework topology via modification of the linker functionalisation. The parent UiO-66 shows a band gap larger than 4 eV leading to a typical RI dispersion in the visible range for an insulator. At 589 nm UiO-66 exhibits a RI of 1.37 increasing towards shorter wavelengths (due to the upcoming absorption in the UV) and decreasing monotonically with longer wavelengths to finally become constant. Our HSE06-based calculation of the optical properties results in a static RI of about 1.35. This is below the reported values of 1.5 and 1.47 presented in previous studies using the PBE functional with an applied scissors operator to correct the underestimated band gap.^9,54 The latter values might be overestimated, because the sole application of the scissors operator without further correction to satisfy the sum rule can lead to overrated amplitudes in the dielectric function and thus to a shifted refractive index.⁵⁵ Using the PBE functional without a scissors operator results in even larger RI values due to the well-known underestimation of the band gap by the PBE functional (see ESI,† Section S6).

Fig. 6 Calculated complex refractive index dispersion. Left: Extinction coefficient (imaginary part); right: refractive index (real part).

The monofunctional UiO-66 derivatives show reduced band gaps and higher electron densities at the VBM and CBM, respectively, in comparison to bare UiO-66, leading to a redshift of the maximum of the extinction coefficient (see Fig. 6) and thus to slightly higher indices of refraction, namely 1.41 and 1.42 for UiO-66-NH₂ and UiO-66-NO₂, respectively (see Fig. 7). In general, all dispersion curves exhibit a comparable trend. At the low energy end of the dispersion the amino- and nitro-derivatives are very similar, but they diverge towards higher energies. The plateau visible in the dispersion curve of UiO-66-NH₂ around 400 nm is caused by the lower band gap of that congener resulting in the absorption of light with wavelengths just below the visible range. This corresponds to the increased extinction in the visible range caused by a maximum at around 360 nm. In contrast, the UiO-66-NO₂ shows a dispersion profile similar to UiO-66, as its band gap is larger than that of UiO-66-NH₂ and polarizability is lower.

Fig. 7 Comparison of the calculated refractive indices of UiO-66 and its analogues at 589 nm.

On the contrary, UiO-66-(NH₂,NO₂) has a significantly higher RI (1.50 at 589 nm) due to its smaller band gap and the larger number of states at the CBM and VBM, elevating the polarizability of the linker and enabling more excitations with an energy just above the band gap to take place; this leads to a more intense absorption corresponding to a strong increase in the extinction coefficient. This absorption takes place in the blue region of the visible light due to the smaller band gap. The absorption of visible light corresponds to the yellow colour of this compound which was also investigated experimentally. However, such an absorption in the visible range might prevent the application of the UiO-66-(NH₂,NO₂) in certain devices where materials which are transparent in the visible range of the light are needed; nevertheless, UiO-66-(NH₂,NO₂) provides a robust material with reasonably high RI for optical systems applied at longer wavelengths.

The bifunctional UiO-66 analogues with more extended electron-donating or -withdrawing groups follow the trend of the UiO-66-(NH₂,NO₂) and show higher RIs while having a larger bathochromic shift (see ESI,† Table S2). A comparison of the extinction coefficients of UiO-66-(NH₂,NO₂) and UiO-66-(NMe₂,NO₂) reveals that the substitution of the hydrogen atoms at the amino group with methyl groups causes only small changes in the amplitude of the extinction coefficient. Nevertheless, the RI is increased significantly due to the lower band gap and the increased number of VBM and CBM states, leading to high values of the extinction coefficient in a broader spectral range. This effect ranges far into the visible region.

The substitution of nitro with the DCV groups of UiO-66-(NH₂,NO₂) has an even larger impact on the refractive index than the aforementioned methyl substitution at the amino group. This is due to the higher polarizability of the DCV group and the larger number of states introduced. The resulting extinction coefficient has a massively increased amplitude and shows elevated values in the visible range leading to an RI of 1.74 at 589 nm (see Fig. 7). Compared to the refractive index of the pristine UiO-66 this is an increase of almost 0.4 demonstrating the broad tuneability of the optical properties of one MOF structure by manipulating its linkers.

The highest RI values are accessible with the UiO-66-(N(Me)₂,DCV) which, however, is also non-transparent for roughly half of the visible spectrum. This can be ascribed to the small band gap and the large polarizability. Despite that, it might be used as a highly refractive material for applications in the near infra-red regime.

Altogether, UiO-66 and its derivatives are promising materials for optical applications based on their high chemical stability and the tuneability of their RIs. They enable the construction of optical systems using light from the upper half of the visible range and from the near IR region. The wide range of refractive indices allows the design of complex optical systems needing materials with different RIs, for example optical filter or coatings.

Conclusions

The electronic structure and the resulting optical properties of the Zr-based UiO-66 MOF and of mono- and bifunctional derivatives have been investigated using the hybrid HSE06 DFT functional. Four novel bifunctional push–pull linkers were introduced for theoretical calculations; for one of those linkers, the successful synthesis of the novel UiO-66-(NH₂,NO₂)-MOF is reported which contains the bdc analogue of para-nitroaniline.

Utilising carefully converged plane-wave basis sets, periodic models were fully relaxed with different functionals to assess a suitable and precise representation of each material. The lattice parameters of the resulting functionalized structures are comparable with the ones of the pristine UiO-66 showing the broad possibilities for substitution within the isostructural UiO-66 family. These structural models were then used to conduct electronic structure calculations. The approach used here is based on carefully converged basis sets and an XC functional benchmark for each structure. To the best of our knowledge, this is the first work that fully relies on computationally demanding hybrid DFT calculations to obtain optical properties of MOFs. The method was validated by comparing the calculated band gaps with experimentally determined ones obtained from DRS UV-Vis measurement. The good agreement shows that high-level precise electronic structure calculations are able to provide reliable values for the band gap. Precise electronic structures also ensure the calculation of trustworthy values of the refractive index as a major optical material property. Incorporating bifunctional linker molecules, the band gaps were found to be drastically reduced. Further analysis via the PDOS of the materials showed that the reduction of the band gap occurs due to the introduction of numerous states at the CBM and in the band gap of the parent UiO-66, resulting for the derivatives in a new CBM at lower energies as well as a new VBM. Subsequently, the dispersion curves of the refractive index were calculated for each material. This reveals the direct influence of, on the one hand, the band gap energy on the refractive index; on the other hand, it also becomes clear that higher density of states at the VBM and CBM lead to significantly increased extinction coefficients, in turn also giving rise to higher refractive indices.

In total, the wide range spanned by the indices of refraction determined in this work demonstrates the capabilities offered by MOFs as optical materials. Their modular design allows to obtain materials tuned for specific optical applications, also ones which require high refractive indices. In particular, the functionalisation of linker molecules has been presented as simple and effective method to generate materials with the same topology and similar synthesis protocols, but featuring distinct optical properties.

The MOFs treated here, based on push–pull systems, are very well suited for applications in the near IR. The absorption in the visible range of wavelengths may, however, cause problems in applications addressing this range of wavelengths. From our study we propose that future work to circumvent this problem should focus on providing linker functions with high polarizabilities, but without the introduction of extended push–pull systems. MOFs with such linkers should provide high refractive indices combined with band gaps above 3 eV. Thus, the extinction maximum lies in the UV region and the resulting material should be transparent in the visible range.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the support of the cluster system team at the Leibniz University of Hannover, Germany in the production of this work. This work is funded by the DFG under Germany's Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453). A. H. is grateful for being funded by the Hannover School for Nanotechnology (HSN) at the Laboratory of Nano and Quantum Engineering (LNQE). The HSN is funded by the Ministry of Science and Culture of Lower Saxony.

Notes and references

1. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O’Keeffe, M. Paik Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 710.
2. J. L. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3.
3. A. Dhakshinamoorthy, Z. Li and H. Garcia, Chem. Soc. Rev., 2018, 47, 8134.
4. H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Mater. Today, 2018, 21, 108.
5. L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105.
6. Y. Zheng, F.-Z. Sun, X. Han, J. Xu and X.-H. Bu, Adv. Opt. Mater., 2020, 8, 2000110.
7. Y. Huang, C.-A. Tao, R. Chen, L. Sheng and J. Wang, Nanomaterials, 2018, 8, 676.
8. B. Ni, W. Sun, J. Kang and Y. Zhang, J. Phys. Chem. C, 2020, 124, 11595.
9. H. Li, L. Zhang, H. He, Y. Yang, Y. Cui and G. Qian, Sci. China Mater., 2021, 64, 698.
10. K.-T. Hsu, P. Thanasekaran, T.-W. Hsu, C.-H. Su, B.-C. Chang, Y.-H. Liu, C.-H. Hung and K.-L. Lu, CrystEngComm, 2021, 23, 824.
11. M. A. Syzgantseva, C. P. Ireland, F. M. Ebrahim, B. Smit and O. A. Syzgantseva, J. Am. Chem. Soc., 2019, 141, 6271.
12. K. Hendrickx, D. E. P. Vanpoucke, K. Leus, K. Lejaeghere, A. van Yperen-De Deyne, V. van Speybroeck, P. van der Voort and K. Hemelsoet, Inorg. Chem., 2015, 54, 10701.
13. W. Yin, C.-A. Tao, F. Wang, J. Huang, T. Qu and J. Wang, Sci. China Mater., 2018, 61, 391.
14. K. Müller, K. Fink, L. Schöttner, M. Koenig, L. Heinke and C. Wöll, ACS Appl. Mater. Interfaces, 2017, 9, 37463.
15. N. C. Keppler, K. D. J. Hindricks and P. Behrens, RSC Adv., 2022, 12, 5807.
16. Y. Bai, Y. Dou, L.-H. Xie, W. Rutledge, J.-R. Li and H.-C. Zhou, Chem. Soc. Rev., 2016, 45, 2327.
17. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850.
18. S. J. Garibay and S. M. Cohen, Chem. Commun., 2010, 46, 7700.
19. M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632.
20. G. E. Cmarik, M. Kim, S. M. Cohen and K. S. Walton, Langmuir, 2012, 28, 15606.
21. F. Vermoortele, M. Vandichel, B. van de Voorde, R. Ameloot, M. Waroquier, V. van Speybroeck and D. E. de Vos, Angew. Chem., Int. Ed., 2012, 51, 4887.
22. E. Flage-Larsen, A. Røyset, J. H. Cavka and K. Thorshaug, J. Phys. Chem. C, 2013, 117, 20610.
23. W. Vandezande, K. P. F. Janssen, F. Delport, R. Ameloot, D. E. de Vos, J. Lammertyn and M. B. J. Roeffaers, Anal. Chem., 2017, 89, 4480.
24. K.-J. Kim, P. Lu, J. T. Culp and P. R. Ohodnicki, ACS Sens., 2018, 3, 386.
25. A. Demessence, C. Boissière, D. Grosso, P. Horcajada, C. Serre, G. Férey, G. J. A. A. Soler-Illia and C. Sanchez, J. Mater. Chem., 2010, 20, 7676.
26. O. Dalstein, D. R. Ceratti, C. Boissière, D. Grosso, A. Cattoni and M. Faustini, Adv. Funct. Mater., 2016, 26, 81.
27. P. Horcajada, C. Serre, D. Grosso, C. Boissière, S. Perruchas, C. Sanchez and G. Férey, Adv. Mater., 2009, 21, 1931.
28. E. Redel, Z. Wang, S. Walheim, J. Liu, H. Gliemann and C. Wöll, Appl. Phys. Lett., 2013, 103, 91903.
29. W. Yin, C.-A. Tao, X. Zou, F. Wang, T. Qu and J. Wang, Nanomaterials, 2017, 7, 242.
30. L. Zheng, N. Keppler, H. Zhang, A. Günther, P. Behrens and B. Roth, in Integrated Optics: Devices, Materials, and Technologies XXVI, SPIE, 2022, p. 15.
31. L. Zheng, N. Keppler, H. Zhang, P. Behrens and B. Roth, Adv. Mater. Technol., 2022, 7, 2200395.
32. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
33. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 125, 249901.
34. A. J. Garza and G. E. Scuseria, J. Phys. Chem. Lett., 2016, 7, 4165.
35. M. Nishiwaki and H. Fujiwara, Comput. Mater. Sci., 2020, 172, 109315.
36. K. Markey, M. Krüger, T. Seidler, H. Reinsch, T. Verbiest, D. E. de Vos, B. Champagne, N. Stock and M. A. van der Veen, J. Phys. Chem. C, 2017, 121, 25509.
37. G. C. Shearer, S. Chavan, J. Ethiraj, J. G. Vitillo, S. Svelle, U. Olsbye, C. Lamberti, S. Bordiga and K. P. Lillerud, Chem. Mater., 2014, 26, 4068.
38. J. Chu, F.-S. Ke, Y. Wang, X. Feng, W. Chen, X. Ai, H. Yang and Y. Cao, Commun. Chem., 2020, 3, 5.
39. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
40. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
41. D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107.
42. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
44. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
45. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 73005.
46. W. A. Al-Saidi, V. K. Voora and K. D. Jordan, J. Chem. Theory Comput., 2012, 8, 1503.
47. A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101.
48. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, Comput. Phys. Commun., 2014, 185, 1477.
49. A. Schaate, P. Roy, A. Godt, J. Lippke, F. Waltz, M. Wiebcke and P. Behrens, Chem. – Eur. J., 2011, 17, 6643.
50. S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370.
51. T. Musho, J. Li and N. Wu, Phys. Chem. Chem. Phys., 2014, 16, 23646.
52. K. Hendrickx, D. E. P. Vanpoucke, K. Leus, K. Lejaeghere, A. van Yperen-De Deyne, V. van Speybroeck, P. van der Voort and K. Hemelsoet, Inorg. Chem., 2015, 54, 10701.
53. K. L. Svane, J. K. Bristow, J. D. Gale and A. Walsh, J. Mater. Chem. A, 2018, 6, 8507.
54. L.-M. Yang, E. Ganz, S. Svelle and M. Tilset, J. Mater. Chem. C, 2014, 2, 7111.
55. M. Nishiwaki and H. Fujiwara, Comput. Mater. Sci., 2020, 172, 109315.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis procedures, argon sorption isotherm, TG analysis, NMR analysis, UV-Vis spectra, details of DFT calculations. See DOI: https://doi.org/10.1039/d2cp03746g

---