 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A volume-based description of transport in incompressible liquid electrolytes and its application to ionic liquids†
Franziska
Kilchert
 ab,
Martin
Lorenz
c,
Max
Schammer
ab,
Martin
Lorenz
c,
Max
Schammer
 ab,
Pinchas
Nürnberg
c,
Monika
Schönhoff
ab,
Pinchas
Nürnberg
c,
Monika
Schönhoff
 c,
Arnulf
Latz
c,
Arnulf
Latz
 abd and
Birger
Horstmann
abd and
Birger
Horstmann
 *abd
*abd
aGerman Aerospace Center, Wilhelm-Runge-Straße 10, 89081 Ulm, Germany. E-mail: birger.horstmann@dlr.de
bHelmholtz Institute Ulm, Helmholtzstraße 11, 89081 Ulm, Germany
cUniversity of Münster, Corrensstraße 28/30, 48149 Münster, Germany
dUlm University, Albert-Einstein-Allee 47, 89081 Ulm, Germany
First published on 27th July 2023
Abstract
Transference numbers play an important role in understanding the dynamics of electrolytes and assessing their performance in batteries. Unfortunately, these transport parameters are difficult to measure in highly concentrated liquid electrolytes such as ionic liquids. Also, the interpretation of their sign and magnitude has provoked an ongoing debate in the literature further complicated by the use of different languages. In this work, we highlight the role of the reference frame for the interpretation of transport parameters using our novel thermodynamically consistent theory for highly correlated electrolytes. We argue that local volume conservation is a key principle in incompressible liquid electrolytes and use the volume-based drift velocity as a reference. We apply our general framework to electrophoretic NMR experiments. For ionic liquid based electrolytes, we find that the results of the eNMR measurements can be best described using this volume-based description. This highlights the limitations of the widely used center-of-mass reference frame which for example forms the basis for molecular dynamics simulations – a standard tool for the theoretical calculation of transport parameters. It shows that the assumption of local momentum conservation is incorrect in those systems on the macroscopic scale.
1. Introduction
The large majority of technical applications for energy storage employ concentrated liquid electrolytes, including standard electrolytes with around 1 mol L−1 of solute and those with higher salt concentrations.1 With modeling we can provide deeper insights into the internal transport processes. Here, transport parameters like the transference number play a major role as performance indicators. In principle, the transference number tα = Iα/I of a species is defined as the fraction of current Iα, carried by the respective species, with respect to the overall current I. However, the determination of transference numbers in highly concentrated electrolytes such as ionic liquids (ILs) is challenging.A multitude of measurement techniques have been developed over time, in part assisted by modeling approaches. This variety together with diverse nomenclature hampers the comparability of experimental results. One prominent example is the recent discovery of negative transference numbers for several highly concentrated electrolytes and the resulting debate.2–9 Next, we summarize the diversity of experimental and theoretical methods in this domain.
On the experimental side, electrochemical methods are the most widespread. Here, potentiostatic polarization (PP) developed by Bruce and Vincent and based on the classical Hittorf method10–13 and galvanostatic polarization (GP) by Newman and co-workers2 are prominent techniques besides some more recent developments that aim at reducing the number of experiments needed to obtain a full set of independent transport parameters.14–17 Another approach uses very-low frequency impedance spectroscopy (VLF-EIS).18–21 It is common sense that ideal ion dissolution in concentrated electrolytes is not a valid assumption and, thus, quantities obtained from PFG-NMR via the Nernst–Einstein relation cannot be considered “true” transference numbers. However, they are still calculated in many cases as comparative figures.4,18,20,22 The relatively new technique of electrophoretic NMR (eNMR), however, is a valuable tool for analyzing highly concentrated electrolytes.6,23,24 Here, the mobilities of each species in the system can be measured directly and, thus, used to determine transference numbers.
Physiochemical models, on the other hand, can supplement experimental techniques and are a valuable tool to rationalize the different definitions for transference numbers proposed in the literature. Different parameter definitions and experimental set-ups can be exactly quantified with sufficient effort, e.g. the relationship between VLF-EIS and eNMR.25
Transference numbers depend on the adopted frame of reference determined by the underlying theory. The choice of the reference frame specifies the ion flux densities which are defined relative to the corresponding drift velocity of the reference frame. This well-known fact has been described extensively in the literature.26–28 Kirkwood et al. first stated coherently the reference frame dependence of equations to test Onsager's reciprocal relationships for isothermal diffusion in multi-component systems.29 Flux densities and constraints are given in the local center-of-mass (CM), local volume and local species-based reference frame. However, no electric currents were considered. Miller showed in great detail the connection between Onsager coefficients and transport parameters for binary to N-component systems focusing on the species-based reference frame.30–32 Transformations between reference frames are also considered early on, e.g. by Schönert who discusses Onsager coefficients in the solvent- and CM-based frames.33 In the battery-modelling community, the most widely used descriptions are based on the center-of-mass motion34–36 or the solvent-based species-frame.36–38 In contrast, the volume-based description has been discussed only rarely in the literature.39–44
For a certain application one reference frame is more convenient for describing observed phenomena than another. For example, in the presence of an excess solvent species, e.g. in aqueous electrolytes or polymer electrolytes, the species velocity of the solvent is the natural reference. Also, the aforementioned Hittorf method for determining transference numbers relates to the solvent-fixed reference frame30 and models based on the Stefan–Maxwell theory, like the widespread concentrated solution theory, are formulated in this frame.45–47 Another choice for the reference frame often used in the literature is the mass-based frame where the ion flux densities are expressed relative to the center-of-mass (CM) motion. Because the corresponding drift velocity equals the bulk momentum per unit mass, this description is inherently related to momentum balance and applies to highly viscous liquids where momentum dissipation due to frictional forces must be taken into account.48 For describing bulk transport in IL electrolytes using an Onsager approach, the mass-based description is the natural choice of ref. 49. This frame also forms the reference description used in molecular dynamics (MD) simulations.50 Here, structural and dynamical properties can be directly accessed from the atomic or molecular structure of the system evolving with time. Then, parameters like the transference number can be calculated using analytical tools.8,51,52
With our work, we want to shed some light on recent discussions about reference frames and corresponding transference numbers in concentrated liquid electrolytes to help improving the mutual understanding. Here, we use thermodynamically consistent modeling based on an Onsager approach which assumes that the thermodynamic flux densities are linear functions of the electrochemical forces.26,49 Thermodynamic flux densities are usually defined relative to the internal dynamics of some excess bulk quantity. These internal flux densities differ from the external flux densities by a convective correction, where the choice of drift velocity defines the corresponding frame of reference. In this flux-explicit description, the Onsager coefficients determine the transport parameters. As a consequence, all transport parameters are defined with respect to a specific frame of reference, i.e. choice for the drift velocity. At the beginning of our theory section, we recapitulate the basic frame-dependent flux density definitions. As we show in detail, using the volume-based drift velocity as a reference can be a convenient ansatz for electrolytes where the volume does not change under pressure variation, i.e. incompressible electrolytes. Since electrolytes are hardly compressible, this is usually a good approximation.53 In contrast to the CM-based frame of reference, this description models species transport via volume-preserving flux densities and, thus, facilitates the transport equation for drift velocity. Furthermore, we derive simple transformation rules between the descriptions.
In highly concentrated electrolytes, strong ion correlations and conservation laws such as charge conservation lead to constraints on the dynamics of the electrolyte species. In the volume-based description, volume conservation replaces the typical momentum conservation from CM-based frames as the governing principle. The resulting constraints transfer to the thermodynamic flux densities such that only a reduced number of internal flux densities is independent (N − 1 in the case of N species). Furthermore, this implies that not all Onsager coefficients are independent. Thus, only a reduced number of transport parameters are independent and can be measured independently. For example, in the case of transference numbers, there are two constraints. First, an ion flux density determines a designated species. Second, the transference numbers of the remaining species sum up to unity.49 As a consequence, there exist only N − 2 independent transference numbers in the internal description of an N-component electrolyte solution. This can lead to confusion regarding the sign and magnitude of the transport parameters when different descriptions from the literature are compared. Hence, it is important to clearly state the reference frame for the transport description. Interestingly, as pointed out by Harris,54 these issues were clearly understood for molten salt systems already in the 1950s.55–64
In this work, we rationalize the relevance of reference frames on the sign and magnitude of transference numbers, identify the set of independent parameters, and discuss alternative definitions for the transference numbers. Our joint theoretical/experimental work described here focuses on theoretical aspects and is accompanied by a second publication of the same authors which focuses on the experimental aspects.65 Here, we show that our volume-based description is for example applicable to porous electrode theory as an electrolyte modeling framework. For incompressible electrolytes, the volume-based representation facilitates the volume velocity equation. We, finally, apply it to eNMR experiments where the volume-based reference frame turns out to be especially beneficial due to the vanishing volume flux boundary condition of the system. Furthermore, we show that incompressible electrolytes are better described with local volume conservation and how we can explain experimental findings with our theory. We build the theoretical framework based on irreversible thermodynamics and focus on transference numbers. Our complementary publication, see ref. 65, focuses on the experimental aspects of our collaboration and provides eNMR and density data to experimentally validate the theoretical concepts.
2. Theory
Recently, Schammer et al. proposed a novel transport theory for highly correlated electrolytes.49 It captures the cell dynamics of electrochemical devices on a macro-scale, e.g. in the electroneutral bulk,49 but also for strong electrostatic correlations in crowded environments, e.g. in the electrochemical double layer (EDL).66,67 The focal quantity in this modeling framework is the Helmholtz free energy, which incorporates the material-specific properties, and determines the description of the system in the form of constitutive equations. Here, we apply the framework outlined in great detail in ref. 49 and focus on the transport parameters.We structure this theory part as follows. First, in Section 2.1, we briefly summarize how the flux densities are defined in different internal reference frames. We put emphasis on the dominant conservation laws and resulting constraints appearing in strongly correlated electrolytes, which reduce the number of independent parameters, and on the frame-dependence of the transport parameters. This is followed by two sections in which we focus on two different reference frames. In Section 2.2, we outline the canonical approach where the center-of-mass motion is used as drift velocity. In Section 2.3, we discuss an alternative description based on the volume motion. In Section 2.4, we show how to transform between reference frames. Finally, in Section 2.5, we focus on transference numbers and their reference frame dependence.
To facilitate the readability of this theory section, we provide a list of symbols at the end of the manuscript.
2.1 Internal frames of reference
Our transport theory describes the evolution of state variables. It is based on the dynamics of species flux densities that relate to some reference frame. Mutual couplings between these flux densities, e.g. due to balancing laws, impose flux constraints and reduce the number of independent fluxes.Our framework applies to electrolyte mixtures composed of N different constituent species. We express the corresponding flux densities as Nψα = cα(vα − vψ), where cα is the species amount concentrations, via the relative motion between the species velocities vα and the bulk motion of some internal electrolyte quantity, i.e. drift velocity, vψ. Usually, the drift velocity vψ is defined as linear function of some internal electrolyte quantity ψα which exists in bulk-excess,  . Thus, in our description, vψ constitutes an “internal” reference frame, which highlights the special role of the drift velocity. Here, we assume that the expansion coefficients are normalized,
. Thus, in our description, vψ constitutes an “internal” reference frame, which highlights the special role of the drift velocity. Here, we assume that the expansion coefficients are normalized, 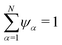 . By construction, this implies a universal flux constraint,42
. By construction, this implies a universal flux constraint,42
 | (1) |
In the literature, many different expressions for the drift velocity exist.26,27,29 The relevance of specific choices depends upon the physical system, i.e. the experimental set-up and boundary conditions. Common examples include the velocity of the center-of-mass motion,34–36,49 the volume-based velocity,39–44 or internal species velocities like the solvent motion.36–38 However, accounting for the bulk motion of the electrolyte in the dynamical description implies that vψ becomes a dynamical variable. This requires that the system of transport equations must be supplemented by an additional drift velocity equation.
The widely used CM description is based on the CM drift velocity  , where
, where
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 and gives rise to flux densities
and gives rise to flux densities | (6) |
 | (7) |
Finally, we discuss the description based on an internal species velocity, i.e. where the drift velocity is given by the velocity of one designated electrolyte species. By convention, we set α = 1 for the designated species such that vs = v1 (thus, ψα = δ1α). This description is a common choice in the presence of a dominant solvent species, where vs defines the “solvent-fixed frame”, or for polymer electrolytes, where the polymer would be the designated species. The flux densities then take the form
| Nsα = cα(vα − vs) = cα(vα − v1), | (8) |
2.2 Mass-based description
In this section, we focus on the mass-based description, i.e. the reference frame constituted by the center of mass motion (see Section 2.1).The framework of rational thermodynamics obeys the second law of thermodynamics using the entropy production rate R, where thermodynamic consistency demands that the quantity R is strictly non-negative. Hence, the entropy production rate measures the deviation from thermodynamic equilibrium and expresses a balance of entropy production. As we show in ref. 49, R comprises a contribution due to internal friction, i.e. viscosity, and a flux term
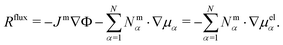 | (9) |
 . Next, we evaluate the flux constraint eqn (4) and reduce the flux-explicit expansion of R appearing on the right of eqn (9) to the set of independent fluxes,
. Next, we evaluate the flux constraint eqn (4) and reduce the flux-explicit expansion of R appearing on the right of eqn (9) to the set of independent fluxes,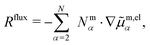 | (10) |
 | (11) |
 | (12) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) mαβ is semi-positive definite (see eqn (S1) in the ESI† for a matrix expression).
mαβ is semi-positive definite (see eqn (S1) in the ESI† for a matrix expression).
All macroscopic transport parameters follow directly from the Onsager matrix. Note that the sum on the right side starts at counter two, which restricts the number of independent Onsager coefficients, i.e. transport parameters (the choice for the electrolyte species which is set to α = 1 can be motivated with respect to the physical set-up, see ref. 49). Altogether, symmetry and thermodynamic consistency reduce the number of independent transport coefficients appearing in an N-component electrolyte mixture to N(N + 1)/2. This statement is generally true in any internal reference frames.
The Euler equation for the volume, eqn (5), and charge continuity  reduce the set of variables which is necessary for the complete dynamical description of highly concentrated electrolytes.49 Hence, c1 and c2 are functions of (να, q, c3, …, cN) (see eqn (S9) and (S10), ESI†). Similarly, from the universal flux constraint follows that
reduce the set of variables which is necessary for the complete dynamical description of highly concentrated electrolytes.49 Hence, c1 and c2 are functions of (να, q, c3, …, cN) (see eqn (S9) and (S10), ESI†). Similarly, from the universal flux constraint follows that  , such that Nm1 and Nm2 are functions of the independent fluxes (Jm, Nm3, …, NmN), where
, such that Nm1 and Nm2 are functions of the independent fluxes (Jm, Nm3, …, NmN), where
 | (13) |
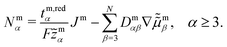 | (14) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) m2/F
m2/F![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 2 is an chemo-electrical potential,36,69 and κm and Dmαβ are the conductivity and diffusion coefficient (derived from Onsager coefficients, see ref. 49) in the mass-based frame,69 respectively. The transference numbers appearing in eqn (13) and (14) satisfy the normalization
2 is an chemo-electrical potential,36,69 and κm and Dmαβ are the conductivity and diffusion coefficient (derived from Onsager coefficients, see ref. 49) in the mass-based frame,69 respectively. The transference numbers appearing in eqn (13) and (14) satisfy the normalization  and constitute the set of N − 2 independent parameters in the CM description. Furthermore, we introduced
and constitute the set of N − 2 independent parameters in the CM description. Furthermore, we introduced | (15) |
| ∂tq = −∇Jm − ∇(ρvm), | (16) |
| ∂tcα = −∇Nmα − ∇(cαvm), α ≥ 3, | (17) |
 | (18) |
| q = −εRε0ΔΦ, | (19) |
 | (20) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) α,
α, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) α, …) emerge naturally in all other descriptions based on different internal frames of references as artefacts of redundant fluxes.
α, …) emerge naturally in all other descriptions based on different internal frames of references as artefacts of redundant fluxes.
2.3 Volume-based description
In this section, we discuss the volume-based frame defined in Section 2.1 (see eqn (6) and (7)).Our rationale here is similar to the CM-based description discussed in Section 2.2. The corresponding transport equations are analogous to eqn (16)–(19), with the exception of different flux densities and a different drift velocity. Similar to the CM-based description, we apply charge continuity, 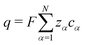 and the volumetric flux constraint, eqn (7), to reduce our description for these flux densities. For this purpose, we introduce reduced quantities involving corrections due to volume ratios,
and the volumetric flux constraint, eqn (7), to reduce our description for these flux densities. For this purpose, we introduce reduced quantities involving corrections due to volume ratios,
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) vα = zα − z1·να/ν1, and vα = zα − z1·να/ν1, and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) vα = μα − μ1·να/ν1. vα = μα − μ1·να/ν1. | (21) |
 , such that
, such that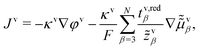 | (22) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) v2/F
v2/F![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) 2 both in the volume description, and
2 both in the volume description, and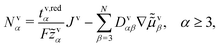 | (23) |
 | (24) |
The drift velocity equation in the volume-based description becomes (see Section S1.2, ESI†)
 | (25) |
When the partial molar volumes do not depend on pressure, i.e. for incompressible electrolytes, the volume-based drift velocity is spatially constant,26
| ∇vv = 0. | (26) |
 , where rα is the reaction rate of the species α at the electrodes.
, where rα is the reaction rate of the species α at the electrodes.
2.4 Flux transformations between different reference frames in incompressible electrolytes
In this section, we state transformation rules for the drift velocities, flux densities and current densities between different reference frames. To improve readability, we state the results in the main text and provide a complete derivation in the ESI,† see Section S1.4. Here, we focus on the two cases of the CM-based description and the volume-based description discussed in Sections 2.2 and 2.3. In addition, we discuss transformation rules with respect to the species-based reference frame in the ESI,† see Section S1.5. From now on, we focus on incompressible electrolytes where the partial molar volumes do not depend on the pressure and assume that ∇να = 0.It is a fundamental assumption of physics that the dynamical evolution of a macroscopic system is independent of the internal description, i.e. the choice of reference frame. This implies that frame transformations are symmetries of the macroscopic description. However, in contrast to the macroscopic description, internal quantities, e.g. flux densities, depend on the reference frame, and simple frame transformations exist.
The transformation of the drift velocities between the CM-based description and the volume-based description reads (see Section S1.4 in the ESI†)
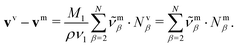 | (27) |
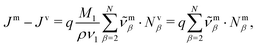 | (28) |
 | (29) |
2.5 Transference numbers
In this section, we focus on the concept of the transference numbers. We discuss different definitions for these transport coefficients and derive the corresponding number of independent quantities. Here, we restrain our discussion mainly to the volume-based description. However, this discussion generalizes to any internal reference frame. Finally, we state the transformation rules for the transference numbers between different internal reference frames.The N − 1 transference numbers tv,redα for an N-component electrolyte introduced above, see eqn (23), follow directly from the Onsager coefficients via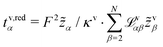 (see eqn (12)).49 By construction, they sum up to unity,
(see eqn (12)).49 By construction, they sum up to unity, 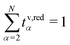 , such that only N − 2 independent parameters exist.
, such that only N − 2 independent parameters exist.
Commonly, transference numbers are understood as a measure for the ratio of current density that is carried by one species, i.e. the contribution of Nvα to the overall current density J. However, there are two important aspects regarding this interpretation. First, we emphasize that the flux densities Nvα relate to the internal reference frame given by the volume-averaged drift velocity, i.e. comprise a drift-correction Nvα = cαvα − cαvv (in the electroneutral case, or if the drift velocity vanishes, 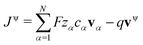 is the same in all frames, and equals the electric current defined relative to external coordinates,30i.e. the lab-frame). Second, due to the relation eqn (23), the above interpretation of the transference numbers applies more directly to the quantity tv,redα/
is the same in all frames, and equals the electric current defined relative to external coordinates,30i.e. the lab-frame). Second, due to the relation eqn (23), the above interpretation of the transference numbers applies more directly to the quantity tv,redα/![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) vα than to the quantities tv,redα itself. Also, the quantities
vα than to the quantities tv,redα itself. Also, the quantities ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) vα can take counterintuitive values, as even uncharged species can get
vα can take counterintuitive values, as even uncharged species can get ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) vα ≠ 0.49 Hence, we argue that the N − 1 flux ratios defined by
vα ≠ 0.49 Hence, we argue that the N − 1 flux ratios defined by
 | (30) |
In contrast to the N − 1 transference numbers tv,redα, we can extend the set of N − 1 quantities (τ2, …, τN) and N − 1 quantities (t2, …, tN) by a quantity τ1 and tv1, relating to the flux contribution of Nv1. For this purpose, we use eqn (7),  , and express the flux densities Nv2, …, NvNvia Jv assuming chemical equilibrium,
, and express the flux densities Nv2, …, NvNvia Jv assuming chemical equilibrium,
 | (31) |
 | (32) |
 | (33) |
It has to be noted though, that, similar to the quantities tv,redα, the quantities τvα measure the species contribution to the overall current density Jv in the volume-based reference frame, which differs from the electric current measured in the resting laboratory frame.
This discussion for the volume-based description generalizes to any other description based on an arbitrary internal frame of reference. In particular, the normalization eqn (32) holds in any frame, whereas eqn (33) takes a slightly different form in different frames (as a consequence of differing flux constraints eqn (1)). For example, in the CM-based description, we find constraints
 | (34) |
 | (35) |
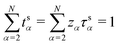 .
.
Our description rationalizes the role of the transference numbers in an electrolyte with only two ion constituents. For such electrolytes, the sign and magnitude of the transference numbers become arbitrary, as they are completely determined by the frame-specific form of the two constraints discussed above.56,62,70 In the volume-based description, the transference numbers are completely determined by the partial molar volumes viaeqn (32) and (33),56
| tv1 = (1 + ν1/ν2)−1, tv2 = (1 + ν2/ν1)−1. | (36) |
| tm1 = (1 + M1/M2)−1, tm2 = (1 + M2/M1)−1. | (37) |
Finally, we state the transformation rules of the transference numbers between the volume-based description and the CM-based description for electroneutral systems where q = 0 (see Section S1.4.4 in the ESI† for details),
 | (38) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) mβ/zβ can become negative.
mβ/zβ can become negative.
The corresponding transformation into the species-based reference frame depends upon the relative species concentrations (see Section S1.5 in the ESI.†)
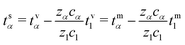 | (39) |
Note that, by construction, ts1= 0.
3. Application to eNMR measurements
In the following, we apply our description to eNMR experiments. We structure this chapter as follows. First, in Section 3.1, we briefly sketch the experimental set-up and introduce species mobilities. The experimental details can be found in ref. 65. Next, in Section 3.2, we present our theoretical description of eNMR experiments and state the underlying assumptions. Furthermore, we show how mobilities from eNMR are related to transference numbers and highlight the reference frame dependence of those transport parameters. In Section 3.3, we shortly discuss the measurements on pure ILs and validate our assumption of a vanishing volume flux focusing on the theoretical aspects. In Section 3.4, we consider electrolytes with three ion constituents. Instead of discussing the mobilities,65 we here put emphasis on the transference numbers, which are important transport parameters for continuum models. Finally, in Section 3.5 we compare transference numbers in different reference frames.Note that another possible application of our theory is given in the ESI,† namely the modeling of electrochemical systems, e.g. batteries, with porous electrode theory. We state the respective modeling equations in Section S2.
3.1 Experimental set-up and species mobilities
In this section, we briefly sketch the experimental set-up of eNMR measurements and discuss the species mobilities. For more details regarding the experimental aspects, we refer to ref. 65, 23 and 71.In electrophoretic NMR, a canonical PFG NMR experiment is performed with additional electric field pulses. The external field Eext induces a constant force upon the ions, such that after a negligibly short acceleration period, a charged species will exhibit a constant drift velocity, which is proportional to the external field, vdriftα = uαEext. The species mobilities uα can be obtained from varying the electric field strength Eext and evaluating the phase shift of the NMR signal, which is caused by the uniform displacement of this species in space. As the encoding of space is performed by magnetic field gradients, the species velocities vα are generally determined in the laboratory frame. We identify the drift velocity of the ions with the species velocities, such that uαEext = vdriftα = vα = Nvα/cα + vv.
The electric conductivity κ of all electrolyte mixtures was measured experimentally using impedance spectroscopy (see ref. 65 for details) and the values are listed in Tables S2 and S4 in the ESI.†
3.2 Model: assumptions and parameters
In this section, we state our model assumptions for this system and discuss the mobilities and transport parameters.We assume that, during the eNMR experiment, the bulk electrolyte remains electroneutral (q = 0) and that all concentration profiles are constant (∇μvα = 0).65 Because this implies that the electric current density and the electric conductivity are equal in all frames, we omit the labels for these two quantities. Furthermore, we assume a boundary condition for the electric field of the electrolyte, where E = Eext. This constitutes chemical equilibrium, i.e. Nvα = tvα/Fzα·J, where the electric current density simplifies to J = −κ∇Φ = κE. Altogether, we thus find a relation between the species mobilities and the transport parameters,
 | (40) |

 | (41) |
 , viz.
, viz. . Below we discuss the transference numbers of Li in the two other frames of reference described above. In particular, we find for the mass-based quantities
. Below we discuss the transference numbers of Li in the two other frames of reference described above. In particular, we find for the mass-based quantities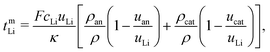 | (42) |
 | (43) |
The experimental set-up consists of long vertical glass capillaries for thermal convection control with electrodes below and above immersed in a reservoir of electrolyte.23 Because the measurement area of the eNMR measurement is located inside the capillaries, the electrodes themselves are outside the expected range of influence. This suggests that we set the boundary conditions right on top and below the glass capillaries, thus excluding electrode effects. Because the excess liquid above the capillaries leads to strong hydrostatic pressures at the end of the capillaries, we expect that there is no volume flux out of the measurement area.
We define the transference numbers derived in the laboratory frame from eNMR and conductivity measurements as
| teNMRα = Fcαzα·uα/κ. | (44) |
 . Therefore, the quantities τeNMRα = teNMRα/zα measure the species contribution to the electric current density as observed in the laboratory frame, and the quantities τeNMRα equal exactly the intuitive interpretation discussed in Section 2.5. In particular, no specific knowledge of the partial molar volumes is needed for the calculation of the teNMRα.
. Therefore, the quantities τeNMRα = teNMRα/zα measure the species contribution to the electric current density as observed in the laboratory frame, and the quantities τeNMRα equal exactly the intuitive interpretation discussed in Section 2.5. In particular, no specific knowledge of the partial molar volumes is needed for the calculation of the teNMRα.
We want to validate that the volume flux vanishes. Thus, we check the two constraints eqn (32) and (33) on the transference numbers. With eqn (44), they transfer to,
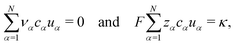 | (45) |
Apparently, the electric conductivity of the electrolyte is completely determined by the species' mobilities and the species' concentrations. Note that the experimental determination of the conductivity κ is comparatively straightforward using, e.g. impedance spectroscopy as in this work. Thus, the second constraint in eqn (45) can be used conveniently for a consistency check of the results obtained from eNMR measurements, which is a standard procedure to ensure high quality eNMR measurements.6,23,24 Furthermore, the second constraint in eqn (45) implies that all transference numbers can be calculated from eNMR mobilities alone via (see eqn (44))
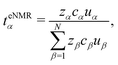 | (46) |
The eqn (44) and (46) reproduce the expression used in the experimental literature for the calculation of transference numbers from mobilities, see e.g., eqn (7) in ref. 6.
3.3 Validation: pure ionic liquids
In this section, we apply our description to eNMR measurements of pure ionic liquids (ILs). First, we show that in our description of the binary case, the two species mobilities are completely determined by either the conductivity and the partial molar volumes (according to the volume-based description) or the conductivity and the molar masses (CM-based description). Second, we apply the volume- and the mass-based description to experimental data for different pure ILs. Finally, we discuss that the volume-based approach yields a better description of incompressible electrolytes.We assume that the pure IL dissociates into two ionic species which are oppositely charged, XY → X+ + Y−. We label the cation species by cX+ = c+ and the anion species by cY− = c−. In the electroneutral state, the two ion concentrations of a pure IL have the same bulk concentration cb and valencies z+ = −z−. However, due to the Euler equation for the volume, eqn (5), the bulk concentration is completely determined by the partial molar volumes, such that c+ = c− = cb = 1/(ν+ + ν−).
In our transport theory, electric conductivity is the only independent transport parameter in an electrolyte with two ion constituents. In particular, the transference numbers become arbitrary in the case of pure ILs and can be determined by, e.g. the molar masses (according to the mass-based description), or by the partial molar volumes (according to the volume-based description), see Section 2.5. In the volume description, the two constraints κ = Fcbz+(u+ − u−) and ν+u+ + ν−u− = 0 determine the species mobilities (see eqn (45)),
| u+ = ν−·κ/F and u− = −ν+·κ/F, | (47) |
| |u+/u−| = ν−/ν+. | (48) |
| |u+/u−| = M−/M+. | (49) |
This makes the mobility ratio a simple and straightforward parameter to identify the relevant boundary condition.65,72
We use these simple relations, eqn (48) and (49), to validate our assumption for the right boundary condition in comparison with experimental data for a wide range of different pure ILs.
Here, we use the experimental data first published in ref. 65, supplemented by data first published in ref. 23 (we restate relevant data in Tables S2, ESI†). The partial molar volumes να were consistently calculated from density measurements, as detailed in ref. 65. The species mobilities uα were determined via eNMR measurements, see Section 3.1.
First, we probe the constraint eqn (48). Fig. 1 shows the absolute values for the mobility ratios |u+/u−| as function of the relative partial molar volumes ν−/ν+ for the different IL electrolytes. The error bars stem from the systematic evaluation of all measurement uncertainties, see Section S3.1 (ESI†). The diagonal line corresponds to the case where |u+/u−| = ν−/ν+. Apparently, for most systems, the results (including the error bars) lie on the diagonal line. This validates our assumption that vv = 0.
 | ||
| Fig. 1 Ratio of mobilities versus ratio of partial molar volumes plotted for various ILs. Open circles: data from Gouverneur et al.23; Filled circles: data from Lorenz et al.65. Diagonal line: analytical prediction (see eqn (48)). The chemical acronyms are listed in Table S1 in the ESI.†. | ||
In contrast, as we show in Fig. S1 (ESI†) (see also ref. 65 and 72), the mobility ratios do not align close to the diagonal line when plotted as functions of the ratio of molar masses. Hence, the experimental results contradict the constraint in eqn (49). Thus, the assumption of vanishing drift velocity vm, i.e. vanishing momentum flux, is badly chosen.
We highlight the relevance of the volume-based description for the eNMR experiment in Fig. 2, where we compare the analytical results for the species mobilities, as calculated from the partial molar volumes and the conductivity viaeqn (47), with the species mobilities obtained from eNMR measurements. Fig. 2 shows the corresponding set of eNMR mobilities for the ILs used in Fig. 1, where circles represent the positive cation values and squares the negative anion mobilities. Furthermore, experimental results are shown in orange and the analytically predicted mobilities in blue. Apparently, there is a high quantitative agreement between the experimental and theoretical results for the majority of the systems. This confirms our conclusion from above.
 | ||
| Fig. 2 Comparison of the measured eNMR mobilities (orange) with the predicted mobilities from eqn (47) (blue) for various ILs; Circles: cation mobilities; Squares: anion mobilities; Open symbols: data from Gouverneur et al.;23 filled symbols: data from Lorenz et al.65 (cf.Fig. 1). The chemical acronyms are listed in Table S1 in the ESI.† | ||
In summary, we find that the volume-based description subject to the assumption that vv = 0 is quantitatively in very good agreement with the experimental data. In contrast, the mass-based description subject to the assumption of vanishing momentum flux does not reproduce the experimental results in a satisfactory manner. This confirms that the assumption of vanishing volume-based drift velocity is better justified than the assumption of local momentum conservation. As a consequence, the volume-based model provides a better description for eNMR experiments in pure ILs than the mass-based description. Furthermore, we conclude that species diffusion in an incompressible electrolyte preserves, by definition, a very good approximation of local thermodynamic volume elements, but not the local momentum density. Indeed, in an incompressible mixture of components with different mass densities, volume conservation implies a center-of-mass motion and, thus, transport of momentum but no volume changes.
3.4 Validation: ionic liquid + Li-salt mixtures
Here, we focus on electrolyte mixtures composed of pure ILs with Li-salt with a common anion. In contrast to the previous section (where the transference numbers were arbitrary and we focused on the species mobilities), we now put emphasis on the transference numbers. We apply our volume-based description and validate our modeling assumptions concerning the relevant boundary condition for systems with three ionic constituents.There exist three independent transport parameters in an electrolyte mixture composed of three different constituents. These are the electric conductivity, one transference number, and one diffusion coefficient. However, here we assume chemical equilibrium in the eNMR experiments, and thus neglect diffusion. As a consequence, the set of independent transport parameters reduces to the electric conductivity κ (which is frame-invariant in the electroneutral case, see section 3.2), and one transference number (i.e. τv3 or tv3 or tv,red3) or one mobility.
For all electrolyte mixtures, we assume dissociation of the IL, XY → X+ + Y−, and of the Li-salt LiY → Li+ + Y−. Thus, each electrolyte mixture gives rise to three independent ion species. By convention, we label the common anion species as the first species by cY− = can, the cation species of the IL as the second species by cX+ = ccat and Li as the third species by cLi. Hence, in our description, the only independent transference number is tLi.
In order to validate our model assumptions concerning a vanishing volume drift velocity for systems with three ion constituents, we check the two constraints eqn (32) and (33) on the transference numbers obtained from eNMR viaeqn (44) for each IL mixture stated in Table S3 (ESI†).6,65,73 The teNMRα values are listed in Table S4 (ESI†).
First, we focus on the constraint imposed by the assumption of charge conservation,  (see eqn (32)). Fig. 3 illustrates this sum for all IL + Li-salt electrolyte mixtures listed in Table S3.† The horizontal line marks the theoretically predicted value of one. To improve the readability, we group similar systems with varying salt concentrations by color. The assigned error bars stem mainly from errors made in eNMR measurements of the mobilities. Apparently, for nearly all systems, the analytical prediction lies well within the error of the experimental results. However, for the Pyr12O1 FTFSI systems, a small deviation is clearly visible. We attribute this anomalous behaviour to an underestimation of the corresponding error made in the eNMR experiment. The partial molar volumes for the FTFSI− anion and, thus, also the density values had to be interpolated for those systems,65 resulting in slightly higher uncertainties than for the other mixtures. Apart from this singular deviation, there is in general a very good agreement with the analytical prediction. Note that the constraint eqn (32) is already used as quality check for the eNMR measurements (see Section 3.2 and ref. 6, 23 and 24).
(see eqn (32)). Fig. 3 illustrates this sum for all IL + Li-salt electrolyte mixtures listed in Table S3.† The horizontal line marks the theoretically predicted value of one. To improve the readability, we group similar systems with varying salt concentrations by color. The assigned error bars stem mainly from errors made in eNMR measurements of the mobilities. Apparently, for nearly all systems, the analytical prediction lies well within the error of the experimental results. However, for the Pyr12O1 FTFSI systems, a small deviation is clearly visible. We attribute this anomalous behaviour to an underestimation of the corresponding error made in the eNMR experiment. The partial molar volumes for the FTFSI− anion and, thus, also the density values had to be interpolated for those systems,65 resulting in slightly higher uncertainties than for the other mixtures. Apart from this singular deviation, there is in general a very good agreement with the analytical prediction. Note that the constraint eqn (32) is already used as quality check for the eNMR measurements (see Section 3.2 and ref. 6, 23 and 24).
 | ||
| Fig. 3 Probing charge conservation for various IL + Li-salt mixtures with common anion, see eqn (33). The horizontal line represents the analytical prediction. Data is based on mobilities from ref. 6, 65 and 73. Error bars result from measurement errors of the mobilities and conductivity. Chemical compositions are listed in Table S3 in the ESI† and teNMRα in Table S4. | ||
As the second step, we probe the assumption of vanishing volume drift velocity (vv = 0), which leads to the constraint in eqn (33) applying to teNMRα. For this purpose, we calculate the residual quantity
 | (50) |
 .
.
Fig. 4 illustrates the quantity Δ for all IL + Li-salt electrolyte mixtures (see also Table S3, ESI†), where similar systems with varying salt concentrations are grouped by color. Apparently, all up to two investigated systems fulfill the volume constraint very well. Only the first two EMIM BF4 systems show a significant deviation from the analytical prediction (horizontal line at zero), which indicates a non-trivial drift velocity vv for these systems. However, it was already argued in ref. 65 that this deviation may result from side reactions occurring at the electrodes. If the partial molar volumes of the electrolyte species are different, these can cause unbalanced faradaic productions of volume fractions, resulting in a volume drift velocity. Altogether, we conclude that the assumption of a vanishing volume-based drift velocity is justified. teNMRα is equal to a very good approximation of the volume-based transference numbers tvα. Hence, eqn (44) is indeed correct, and teNMRα can be interpreted as volume-based transference numbers with the boundary condition of vv = 0 in a standard eNMR set-up.
 | ||
| Fig. 4 Probing the assumption of vanishing volume drift velocity for various IL + Li-salt mixtures with common anion, see eqn (32). The horizontal line represents the analytical prediction. Data is based on mobilities from ref. 5, 6, 65 and 73 with partial molar volumes from ref. 65. Error bars result from measurement errors of the mobilities, conductivity and partial molar volumes. Chemical compositions are listed in Table S3 in the ESI† and teNMRα in Table S4 (ESI†). | ||
3.5 Comparison of reference frames
In this section, we investigate the influence of the reference frame on the sign and magnitude of the Li transference numbers. For this purpose, in Fig. 5, we compare three different cases based on the volume description, eqn (41), the mass-based description, eqn (42), and the species-based description with respect to the common anion, eqn (43). | ||
| Fig. 5 Comparison of sign and magnitude of Li transference numbers calculated with respect to the volume-based reference frame, eqn (41), the mass-based reference frame, eqn (42), and the anion-based reference frame, eqn (43). Chemical compositions are listed in Table S3 in the ESI.†. | ||
First, we discuss the Li transference numbers in the volume-based description. The orange circles in Fig. 5 show the transference numbers calculated from eqn (41). These quantities are negative for all electrolyte systems and their absolute magnitudes reside in the range between zero and roughly 0.15.
Next, we discuss the transference numbers tmLi of Li in the mass-based description, see the light blue squares in Fig. 5. We calculated the values from the mobilities viaeqn (42). Apparently, tmLi tends to be more positive than the transference numbers in the volume-based description tvLi. However, an actual sign switch does only occur for two systems here (EMIM FSI 2 and EMIM FSI 3) and is, thus, not a dominant effect. Although for two more systems, a possible switch of sign lies within the uncertainty when comparing the results of the volume- and the mass-based reference frame, the majority of transference numbers stays negative even within the error margins. Eqn (42) shows that the relation of volume- and mass-based transference number depends on the ratios of anion and cation mobilities to Li mobilities as well as the ratio of anion to cation density (see the expression in square brackets).
Finally, we discuss the Li transference numbers tsLi of the common anion reference frame shown by the purple diamonds in Fig. 5. tsLi is determined by the mobilities of Li and the common anions viaeqn (43). Most strikingly, the sign of the Li transference numbers for most of the investigated systems is positive, and only a few systems exhibit negative Li transference numbers in this reference frame. In addition, the absolute magnitudes spread over a relatively large range, when compared with the other two frames. We can rationalize the occurrence of positive Li transference numbers tsLi using eqn (43). Here, the mobilities uan and uLi are all negative, see ref. 6, 65 and 73. Thus, Li moves in the same direction as the anions, i.e. the drift velocity. Furthermore, both of the two species, and hence the drift velocity, move in the opposite direction than the electric current. This seems to be in conflict with the transference numbers in Fig. 5 being mostly positive (implying that Li moves in the same direction as the current). However, this seemingly contradictory behaviour can be resolved by the observation that the absolute magnitudes of the Li mobilities are in most cases smaller than the anion mobilities, see ref. 6, 65 and 73, resulting in positive transference numbers tsLi = FcLi(|uan| − |uLi|)/κ. Hence, for such systems where the anions move “faster” than Li, Li moves in the same direction as the electric current when viewed from the co-moving anion-fixed frame, resulting in positive transference numbers tsLi. Indeed, for electrolyte mixtures where the tsLi are negative, the experimental results show that the Li mobilities are larger in absolute magnitudes than the anion mobilities (|uLi| > |uan|).
4. Discussion
In this section, we complement our manuscript by a brief discussion of the relation between vehicular transport of Li and the sign of their transference numbers in the different frames of reference in IL + Li-salt electrolyte mixtures.Our discussion relates to an ongoing debate in the literature, regarding the interpretation of negative transference numbers and the occurrence of highly correlated motion of Li-ions with oppositely charged ion species. As argued by Schönhoff and co-workers,5,6,73 vehicular transport of Li-ions with strongly positive Li-anion correlations implies that the anion and Li mobilities have the same sign (as the Li-ions are “travelling together” with the anions).
In our description, the transference numbers of Li with respect to any frame of reference are completely determined by the species mobilities, see eqn (41)–(43). We make use of this description and investigate the influence of negative mobilities uan and uLi on the sign of the transference numbers in the three different frames of reference discussed above (the volume-based quantities tvLi, the mass-based quantities tmLi and the anion-based quantities tsLi).
For all electrolyte systems studied in this work, the anion mobilities obtained from the eNMR measurements are negative. In addition, for all electrolyte systems, the mobilities of Li are negative as well, which indeed suggests a correlated motion of the Li-ions with the anions.
First, we discuss the influence of negative mobilities uan and uLi on the sign of tvLi. As we have shown in Section 3.4, teNMRLi calculated from eqn (44) to a very good approximation tvLi since the volume drift velocity vanishes, i.e. teNMRLi ≈ tvLi. As a direct consequence of eqn (44), vehicular transport implies that the sign of tvLi equals the sign of uan. Hence, vehicular transport yields negative Li transference numbers in the volume frame. This is in accordance with our results shown in Fig. 5.
Furthermore, in the common-anion frame, we have sign(tsLi) = sign(uLi)·(1−|uan/uLi|) (see eqn (43)). Hence, depending on the relative magnitudes of |uLi| and |uan|, vehicular transport either implies that tsLi and tvLi have opposite sign (if |uan| > |uLi|) or the same sign (if |uan| < |uLi|). Here, in all systems, the mobilities of Li are negative, and the absolute magnitude of the anion mobility are mostly larger than that of Li. Hence, vehicular transport leads to positive transference numbers tsLi in the common anion frame. This finding is in accordance with the results for the majority of systems shown in Fig. 5.
Finally, in the mass-based frame of reference, it is harder to conclude from vehicular transport onto the sign of the Li transference numbers. As can be inferred from eqn (42), the relation between the sign of the Li transference number tmLi and the anion mobility depends on the species densities and on the mobilities of the anions and Li.
5. Conclusions
In this work, we supplement the discussion shown in ref. 65 and present a detailed discussion of transference numbers based on our novel transport theory. We applied our description to experimental results obtained from eNMR measurements and validated our model assumptions concerning the relevant boundary condition.Our discussion highlights the relevance of the reference frame for the interpretation of transport parameters. Furthermore, we present different definitions for the concept of transference numbers and use universal constraints to identify the number of independent parameters. In addition to the external frame of reference given by the resting laboratory, we focus on three different internal reference frames defined by the center-of-mass motion, by the volume-based velocity, and by the species-based reference frame. We derive the exact transformation rules for the flux densities and transport parameters between these reference frames.
We apply our description of eNMR measurement devices to pure ILs and to electrolytes based on IL-Li-salt mixtures with common anions, as discussed in ref. 65. Our analysis shows that, to a good approximation, the volume-based drift velocity can be neglected for such hardly compressible electrolytes. This highlights that for eNMR measurements the laboratory frame is best represented by the volume-based description. In contrast, assuming a vanishing momentum flux is a bad approximation.
It has to be noted though that it can be advantageous to state transference numbers in the mass-based description. In particular, it is straightforward to obtain the Li transference numbers from the species mobilities of the eNMR measurements because the molar masses are the only additional parameters needed, see eqn (42). In contrast to the partial molar volumes (which are usually not so easy to determine as they may vary with composition, pressure and temperature) needed for the volume-based description, see eqn (41), the molar masses are unambiguously defined.
Furthermore, we show that transforming from volume- to mass-based description does not commonly yield a switch of sign of the transference numbers, although in rare cases this can occur. This picture is different when transforming into the common-anion reference frame. Here, most Li transference numbers are positive due to the high mobility of the anion.
Our description rationalizes an ongoing debate in the literature regarding the sign and magnitude of transference numbers in ILs and highly concentrated electrolytes. Some apparent inconsistencies can be solved to a large extent when the boundary conditions are clearly stated and the choice of reference is clearly defined.
List of symbols
Indices
| +, cat | Subscripts referring to cation |
| −, an | Subscripts referring to anion |
| Li | Subscript referring to Li |
| α,β | Greek subscripts refer to ion constituents |
| ψ | Superscript referring to ψ-based reference frame |
| m | Superscript referring to a mass-based reference frame |
| s | Superscript referring to a species-based reference frame |
| v | Superscript referring to a volume-based reference frame |
Parameters
| D αβ | Diffusion coefficient (with respect to thermodynamic driving force) (m2 s−1) |
| F | Faraday constant (A s mol−1) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) αβ αβ | Onsager matrix (s mol2 kg−1 m−3) |
| M α | Molar mass (kg mol−1) |
| N | Number of species |
| t α | Transference number |
| u α | Mobility (A s−2 kg−1) |
| z α | Valence/charge number |
| β | Bruggemann coefficient |
| ε | Porosity/volume fraction of pore space |
| ε R | Relative permittivity |
| ε 0 | Vacuum permittivity (A s V−1 m−1) |
| κ | Conductivity (A2 s3 kg−1 m−3) |
| ν α | Partial molar volume (m3 mol) |
| τ α | Flux ratio/transference number weighted by charge number |
Variables
| c α | Species concentration/molarity (mol m−3) |
| E | Electric field (kg m A−1 s−3) |
| I | Electric current (A) |
| J | Electric current density (A m−2) |
| j | Electric current density in the laboratory frame (A m−2) |
| N α | Species flux density (mol m−2 s−1) |
| n α | Species flux density in the laboratory frame (mol m−2 s−1) |
| p | Pressure (kg m−1 s−2) |
| q | Electric charge density (A s m−3) |
| R | Entropy production rate (kg m−1 s−3) |
| r α | Species reaction rate (mol m−2 s−1) |
| v | Drift velocity (m s−1) |
| μ α | Chemical potential (kg m2 s−2 mol−1) |
| ρ | Mass density (kg m−3) |
| Φ | Electric potential (kg m2 A−1 s−3) |
| φ α | Electrochemical potential (kg m2 A−1 s−3) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union's Horizon 2020 research and innovation program via the “Si-DRIVE” project (grant agreement no. 814464).Notes and references
- J. Zheng, J. A. Lochala, A. Kwok, Z. D. Deng and J. Xiao, Adv. Sci., 2017, 4, 1700032 CrossRef PubMed.
- Y. Ma, M. Doyle, T. F. Fuller, M. M. Doeff, L. C. D. Jonghe and J. Newman, J. Electrochem. Soc., 1995, 142, 1859–1868 CrossRef CAS.
- A. Ferry, M. M. Doeff and L. C. DeJonghe, Electrochim. Acta, 1998, 43, 1387–1393 CrossRef CAS.
- D. M. Pesko, K. Timachova, R. Bhattacharya, M. C. Smith, I. Villaluenga, J. Newman and N. P. Balsara, J. Electrochem. Soc., 2017, 164, E3569–E3575 CrossRef CAS.
- M. Brinkkötter, G. A. Giffin, A. Moretti, S. Jeong, S. Passerini and M. Schönhoff, Chem. Commun., 2018, 54, 4278–4281 RSC.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470–7478 RSC.
- D. B. Shah, H. Q. Nguyen, L. S. Grundy, K. R. Olson, S. J. Mecham, J. M. DeSimone and N. P. Balsara, Phys. Chem. Chem. Phys., 2019, 21, 7857–7866 RSC.
- N. Molinari, J. P. Mailoa and B. Kozinsky, J. Phys. Chem. Lett., 2019, 10, 2313–2319 CrossRef CAS PubMed.
- N. Molinari, J. P. Mailoa, N. Craig, J. Christensen and B. Kozinsky, J. Power Sources, 2019, 428, 27–36 CrossRef CAS.
- E. A. Kaimakov and N. L. Varshavskaya, Russ. Chem. Rev., 1966, 35, 89–105 CrossRef.
- P. G. Bruce and C. A. Vincent, J. Electroanal. Chem. Interfacial Electrochem., 1987, 225, 1–17 CrossRef CAS.
- J. Evans, C. A. Vincent and P. G. Bruce, Polymer, 1987, 28, 2324–2328 CrossRef CAS.
- P. G. Bruce, M. T. Hardgrave and C. A. Vincent, Solid State Ionics, 1992, 53–56, 1087–1094 CrossRef CAS.
- J. Landesfeind, A. Ehrl, M. Graf, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A1254–A1264 CrossRef CAS.
- A. Ehrl, J. Landesfeind, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A826–A836 CrossRef CAS.
- A. Ehrl, J. Landesfeind, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A2716–A2731 CrossRef CAS.
- J. Landesfeind and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, A3079–A3097 CrossRef.
- F. Wohde, M. Balabajew and B. Roling, J. Electrochem. Soc., 2016, 163, A714–A721 CrossRef CAS.
- N. M. Vargas-Barbosa and B. Roling, ChemElectroChem, 2020, 7, 367–385 CrossRef CAS.
- F. Sälzer, L. Pateras Pescara, F. Franke, C. Müller, J. Winkler, M. Schwalm and B. Roling, Batteries Supercaps, 2020, 3, 117–125 CrossRef.
- J. S. Ho, O. A. Borodin, M. S. Ding, L. Ma, M. A. Schroeder, G. R. Pastel and K. Xu, Energy Environ. Mater., 2023, 6, e12302 CrossRef CAS.
- S. Zugmann, M. Fleischmann, M. Amereller, R. Gschwind, H. Wiemhöfer and H. Gores, Electrochim. Acta, 2011, 56, 3926–3933 CrossRef CAS.
- M. Gouverneur, J. Kopp, L. Van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680–30686 RSC.
- M. P. Rosenwinkel and M. Schönhoff, J. Electrochem. Soc., 2019, 166, A1977–A1983 CrossRef CAS.
- S. Pfeifer, F. Ackermann, F. Sälzer, M. Schönhoff and B. Roling, Phys. Chem. Chem. Phys., 2021, 23, 628–640 RSC.
- S. R. D. Groot and P. Mazur, Non-Equilibrium Thermodynamics, North-Holland Publishing Company, 1962 Search PubMed.
- H. J. V. Tyrrell and K. R. Harris, Diffusion in Liquids, Butterworths, 1984 Search PubMed.
- R. Haase, Thermodynamics of Irreversible Processes, Dover Publications Inc., 1990 Search PubMed.
- J. G. Kirkwood, R. L. Baldwin, P. J. Dunlop, L. J. Gosting and G. Kegeles, J. Chem. Phys., 1960, 33, 1505–1513 CrossRef CAS.
- D. G. Miller, J. Phys. Chem., 1966, 70, 2639–2659 CrossRef CAS.
- D. G. Miller, J. Phys. Chem., 1967, 71, 616–632 CrossRef CAS.
- D. G. Miller, J. Phys. Chem., 1967, 71, 3588–3592 CrossRef CAS.
- H. Schönert, J. Phys. Chem., 1984, 88, 3359–3363 CrossRef.
- A. Latz and J. Zausch, J. Power Sources, 2011, 196, 3296–3302 CrossRef CAS.
- J. Newman, D. Bennion and C. W. Tobias, Berichte der Bunsengesellschaft für physikalische Chemie, 1965, 69, 608–612 CrossRef CAS.
- J. Newman and K. E. Thomas-Alyea, Electrochemical systems, John Wiley & Sons, 2012 Search PubMed.
- J. Newman, Adv. Electrochem. Electrochem. Eng., 1967, 5, 87–136 CAS.
- A. Mistry, L. S. Grundy, D. M. Halat, J. Newman, N. P. Balsara and V. Srinivasan, J. Electrochem. Soc., 2022, 169, 040524 CrossRef CAS.
- J. Newman and T. W. Chapman, AIChE J., 1973, 19, 343–348 CrossRef CAS.
- H. Brenner, Phys. A, 2005, 349, 11–59 CrossRef.
- H. Brenner, Unsolved Problems in Chemical Engineering, Proceedings of the Ohio State University, Department of Chemical Engineering Centennial Symposium, 2003, pp. 31–39.
- P. Goyal and C. W. Monroe, J. Electrochem. Soc., 2017, 164, E3647–E3660 CrossRef CAS.
- J. Liu and C. W. Monroe, Electrochim. Acta, 2014, 135, 447–460 CrossRef CAS.
- A. A. Wang, A. B. Gunnarsdóttir, J. Fawdon, M. Pasta, C. P. Grey and C. W. Monroe, ACS Energy Lett., 2021, 6, 3086–3095 CrossRef CAS PubMed.
- M. Doyle, T. F. Fuller and J. Newman, Electrochim. Acta, 1994, 39, 2073–2081 CrossRef CAS.
- A. Nyman, M. Behm and G. Lindbergh, Electrochim. Acta, 2008, 53, 6356–6365 CrossRef CAS.
- T. Hou and C. W. Monroe, Electrochim. Acta, 2020, 332, 135085 CrossRef CAS.
- A. J. Ladd, Mol. Phys., 1984, 53, 459–463 CrossRef CAS.
- M. Schammer, B. Horstmann and A. Latz, J. Electrochem. Soc., 2021, 168, 026511 CrossRef CAS.
- Y. Shao, H. Gudla, D. Brandell and C. Zhang, J. Am. Chem. Soc., 2022, 144, 7583–7587 CrossRef CAS PubMed.
- D. R. Wheeler and J. Newman, J. Phys. Chem. B, 2004, 108, 18353–18361 CrossRef CAS.
- D. R. Wheeler and J. Newman, J. Phys. Chem. B, 2004, 108, 18362–18367 CrossRef CAS.
- W. Dreyer, C. Guhlke and R. Müller, Phys. Chem. Chem. Phys., 2013, 15, 7075 RSC.
- K. R. Harris, Phys. Chem. Chem. Phys., 2018, 20, 30041–30045 RSC.
- H. Schönert and C. Sinistri, Z. Elektrochem., 1962, 66, 413–423 Search PubMed.
- C. Sinistri, J. Phys. Chem., 1962, 66, 1600–1601 CrossRef CAS.
- A. Klemm, Molten Salt Chem., 1964, 535–606 CAS.
- A. Klemm, Z. Naturforsch., A: Phys. Sci., 1960, 15, 173–179 Search PubMed.
- R. Haase, Z. Naturforsch., A: Phys. Sci., 1973, 28, 1897–1905 CAS.
- C. L. Hussey and J. R. Sanders, J. Electrochem. Soc., 1987, 134, 1977–1980 CrossRef CAS.
- B. Sundheim, Fused Salts, McGraw-Hill Book Company, 1964 Search PubMed.
- B. R. Sundheim, J. Phys. Chem., 1956, 60, 1381–1383 CrossRef CAS.
- K. Kawamura and M. Okada, Electrochim. Acta, 1971, 16, 1151–1156 CrossRef CAS.
- F. R. Duke, R. W. Laity and B. Owens, J. Electrochem. Soc., 1957, 104, 299–300 CrossRef CAS.
- M. Lorenz, F. Kilchert, P. Nürnberg, M. Schammer, A. Latz, B. Horstmann and M. Schönhoff, J. Phys. Chem. Lett., 2022, 13, 8761–8767 CrossRef CAS PubMed.
- M. Schammer, A. Latz and B. Horstmann, J. Phys. Chem. B, 2022, 126, 2761–2776 CrossRef CAS PubMed.
- V. Hoffmann, G. Pulletikurthi, T. Carstens, A. Lahiri, A. Borodin, M. Schammer, B. Horstmann, A. Latz and F. Endres, Phys. Chem. Chem. Phys., 2018, 20, 4760–4771 RSC.
- H. Reiss, Methods of thermodynamics, Courier Corporation, 1996 Search PubMed.
- A. Latz and J. Zausch, Beilstein J. Nanotechnol., 2015, 6, 987–1007 CrossRef CAS PubMed.
- S. Matsunaga, T. Koishi and S. Tamaki, J. Mater. Sci. Eng. A, 2007, 449, 693–698 CrossRef.
- F. Schmidt, A. Pugliese, C. C. Santini, F. Castiglione and M. Schönhoff, Magn. Reson. Chem., 2020, 58, 271–279 CrossRef CAS PubMed.
- M. Schönhoff, C. Cramer and F. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 30046–30052 RSC.
- M. Brinkkötter, A. Mariani, S. Jeong, S. Passerini and M. Schönhoff, Adv. Energy Sustainability Res., 2021, 2, 2000078 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04423d |
| This journal is © the Owner Societies 2023 |
