 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nature of photoexcited states in ZnO-embedded graphene quantum dots†
Ivan
Shtepliuk
 *ab and
Rositsa
Yakimova
a
*ab and
Rositsa
Yakimova
a
aSemiconductor Materials Division, Department of Physics, Chemistry and Biology-IFM, Linkoping University, S-58183 Linkoping, Sweden. E-mail: ivan.shtepliuk@liu.se
bI.M. Frantsevich Institute for Problems of Materials Science, N.A.S. of Ukraine, 3, Krzhizhanovsky Str., UA-03142 Kyiv, Ukraine
First published on 16th March 2023
Abstract
The combination of wide-band gap semiconductors such as zinc oxide (ZnO) and graphene quantum dots (GQDs) is a promising strategy to tune the optoelectronic properties of GQDs and develop new functionalities. Here we report on a theoretical design of not-yet-synthesized hybrid materials composed of ZnO clusters surrounded by carbon moieties, hereinafter referred to as ZnO-embedded graphene quantum dots. Their structure and light absorption properties are presented, with an in-depth analysis of the nature of the photoexcited states. The stability of the (ZnO)nC96−2n system with n = 1, 3, 4, 7, 12 and 27 is investigated by performing vibrational mode analysis and estimating cohesive energy and zinc vacancy formation energy. A strong dependence of the structural and optoelectronic properties of the hybrid material on the amount of ZnO pairs is revealed and discussed. Strong light absorption and unexpected enhancement of Raman modes related to the vibrations in carbon moiety are observed for the highly symmetric (ZnO)27C42 system that makes it an ideal study subject. Complementary excited state analysis, charge density difference (CDD) analysis and interfragment charge transfer analysis present insights deep into the nature of the excited states. An equal contribution of doubly degenerate locally excited states and charge transfer states in broadband light absorption by (ZnO)27C42 is identified. The present results are helpful to elucidate the nature of the fundamental internal mechanisms underlying light absorption in ZnO-embedded graphene quantum dots, thereby providing a scientific background for future experimental study of low-dimensional metal–oxygen–carbon material family.
Introduction
Graphene quantum dots (GQDs) – nanosized graphene fragments – are currently considered as an exclusive organic material that brings together the beneficial properties of graphene (large surface area, high carrier mobility and conductivity) and the excellent light-emitting ability dictated by its semiconducting character. Possessing tuneable band gap, low toxicity, and good chemical stability, GQDs find applications in biomedicine, optoelectronics, energy, and sensing technologies. Further integration of zero-dimensional (0D) GQDs with inorganic compound semiconductors (ICS) is a winning strategy to create advanced organic–inorganic hybrid nanomaterials with novel functionalities. Among different ICS, zinc oxide (ZnO) is of special importance for many applications due its unique physical properties (direct bandgap of 3.3 eV at room temperature; strong radiation hardness; large exciton binding energy of 60 meV; antimicrobial activity etc.), relative growth/synthesis simplicity, and morphological diversity.1,2Over the recent years a great deal of progress has been made in synthesis, material characterization and conceptualization of ZnO-GQDs nanohybrids. More specifically, a combination of both materials enables designing high-performance sensors for the detection of different substances including H2O2,3 CO2,4 ammonia,5 ethanol,6 hydroquinone,7 zearalenone in mildewing cereal crops,8 acetone,9,10 H2S,11 acetic acid,12 chemo-therapeutic agent (6-mercaptopurine),13 and NO2.14,15 Apart from various sensing principles that have been applied for quantification of gas or liquid molecules, it should be emphasized that in most cases sensitive hybrid materials were constructed through functionalization or decoration of host ZnO matrix with undoped or doped GQDs. Another example of a beneficial synergy between GQDs and ZnO features concerns a high promise of related nanohybrids for design of next-generation ultraviolet (UV) photodetectors.16–29 On one hand, the presence of GQDs may favor separation and transport of the photogenerated carriers, thus reducing both the electron–hole recombination and the photoresponse time. Since GQDs have a good response to UV light, sensitization with GQDs may, on the other hand, enhance the overall UV absorption in ZnO and hence the photoconductivity of ZnO-based photodetector. The pronounced charge separation at the GQDs/ZnO interface also provides good prerequisites of using this hybrid material in perovskite-, dye sensitized-, quantum-dot-sensitized- and inverted polymer solar cells.30–43 ZnO–graphene quantum dots system is promising for designing optoelectronic devices (namely light-emitting diodes, LEDs),44–49 playing a role of either electron transport layer or active emissive component. Particularly, a brightness of 798 cd m−2 was achieved for white LEDs based on ZnO cores wrapped in a shell of GQDs.49
One more important application of ZnO–GQDs hybrid nanomaterials is related to their excellent photocatalytic properties. The enhanced light absorption in such combined systems and, consequently, increased number of photo-induced charge carriers make it possible to reach synthesis of tetrasubstituted propargylamines,50 improved solar-driven water splitting51 and photocatalytic H2 evolution under visible light,52 selective reduction of nitroarenes,53 and effective degradation of metronidazole (MNZ) antibiotic,54 colored pollutants (Rhodamine B, methylene blue (MB) and methylene orange (MO)),55–61 colorless pollutant (carbendazim (CZ) fungicide)62 and glyphosate herbicide contaminated in agricultural wastewater.63
Effective interfacial charge transfer between GQDs and ZnO under photoirradiation also facilitates the production of reactive oxygen species (ROS), which make it possible to use this material as an antibacterial agent.64–68 Indeed, the formation of ROS may activate the electrostatic attraction between ZnO–GQDs hybrid and target bacteria (Escherichia coli, Pseudomonas aeruginosa, Bacillus cereus and Staphylococcus aureus), thereby causing a damage of bacterial cell membrane and inhibiting the growth of bacterial colonies.
All mentioned here examples highlight the importance of a deep understanding of the fundamental nature of photoexcitation and charge transport in ZnO–GQDs hybrid materials. Reaching such an understanding will provide guidelines for application-specific designs of ZnO-GQDs nanohybrids. Although the fundamentals of the response of ZnO–GQDs to light upon photoexcitation have been described in detail in literature, the main focus of the existing investigations is on a physical combination of ZnO and GQDs, each of which remains its own functional characteristics. In this case, both materials interact in a way with each other, but no formation of a new substance is expected. But what if we combine two isolated components into one stable material platform? Intuitively, such an approach could be conducive to avoid poor inter-component adhesion, thereby addressing overall temporal stability problem. Inspired by an earlier work of Quang et al. which is dedicated to the formation of graphene-like monolayer ZnO membranes suspended in graphene pores,69 here we propose a new concept of organic–inorganic solid-state hybridization based on atomically thin graphene-like ZnO clusters embedded into GQDs. This can be referred to a monolithic integration between ZnO and GQDs. Since such a material system is still unexplored, we employ density-functional theory (DFT) and time-dependent DFT (TD-DFT) calculations to explore the nature of photoexcited states in (ZnO)nC96−2n system with n = 1, 3, 4, 7, 12 and 27.
Methodology
All quantum chemistry calculations were conducted by means of Gaussian 16 Rev. C.01 program package70 under gas-phase conditions. Closed-shell circumcircumcoronene molecule (C96H24) demonstrated in Fig. S1 (ESI†) was chosen as a representative of GQDs and a host organic molecule for ZnO clusters. Belonging to the neutral polycyclic aromatic hydrocarbons (PAHs) C96H24 molecule is commonly used model of GQDs,71–73 and it is a reasonable choice to investigate the local surface phenomena (adsorption, diffusion, nucleation, clustering, substitutional doping so on) at the graphene and to explore the optical properties of GQDs (absorption, fluorescence). Thus, the using of C96H24 as a core molecule to design ZnO-embedded GQDs is warranted. ZnO-embedded graphene quantum dots, hereinafter referred to as (ZnO)nC96−2n systems, were constructed through replacing carbon (C) atoms with zinc (Zn) and oxygen (O) atoms (see Fig. S2, ESI†) in a way that ensures balanced substitutional doping of the system of hexagonally arranged carbon atoms in C96H24. This is analogous to a symmetric doping of two sublattices of infinite graphene model. As a result, there were equal numbers of zinc and oxygen atoms, indicating that the stoichiometry of ZnO clusters embedded in graphene quantum dots is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. From the chemistry point of view, the incorporation of Zn into the carbon-based matrix is possible and already realized.74–76 Moreover, the bonding of the carbon atoms (including sp2-hybridized carbon atoms) to zinc is a basis of the formation of the different organozinc compounds.77 These examples suggest that (ZnO)nC96−2n systems can be experimentally synthesized. Geometry optimization of the (ZnO)nC96−2n systems was performed using Perdew–Burke–Ernzerhof exchange–correlation hybrid functional (PBE0, also called PBE1PBE),78 which combines 25% exact Hartree–Fock (HF) exchange with 75% of PBE exchange. PBE0 is a reasonable choice to correctly reproduce the experimentally observed electronic and optical properties of ZnO79 and GQDs.80–82 To validate the results obtained by PBE0, we performed additional calculations using B3LYP83 and long-range-corrected functionals like CAM-B3LYP84 and ωB97XD,85 respectively. 6-31G* basis sets86 were used for carbon, hydrogen, and oxygen atoms, while the SDD basis set developed by the Stuttgart-Dresden-Bonn group87 was used for zinc atom. Other basis sets like 6-31g(d)/LanL2DZ, 6-311++g(d,p)/LanL2DZ and cc-PVDZ/LanL2DZ were also tested to justify the use of computationally efficient 6-31G*/SDD. (ZnO)nC96−2n structures corresponding to the lowest energy minima were obtained by enabling a full relaxation of all coordinates using the default convergence criteria. Vibrational mode calculations were additionally carried out to make sure there are no imaginary frequencies and to confirm the equilibrium of the ground-state geometry. Finally, absorption spectra of the (ZnO)nC96−2n hybrid materials were predicted using the time-dependent density functional theory (TD-DFT) approach using CAM-B3LYP/6-31G(d) method, which is capable to adequately reproduce the experimental absorption spectra of GQDs88 and is an appropriate choice to study the charge-transfer excitations.89,90
1. From the chemistry point of view, the incorporation of Zn into the carbon-based matrix is possible and already realized.74–76 Moreover, the bonding of the carbon atoms (including sp2-hybridized carbon atoms) to zinc is a basis of the formation of the different organozinc compounds.77 These examples suggest that (ZnO)nC96−2n systems can be experimentally synthesized. Geometry optimization of the (ZnO)nC96−2n systems was performed using Perdew–Burke–Ernzerhof exchange–correlation hybrid functional (PBE0, also called PBE1PBE),78 which combines 25% exact Hartree–Fock (HF) exchange with 75% of PBE exchange. PBE0 is a reasonable choice to correctly reproduce the experimentally observed electronic and optical properties of ZnO79 and GQDs.80–82 To validate the results obtained by PBE0, we performed additional calculations using B3LYP83 and long-range-corrected functionals like CAM-B3LYP84 and ωB97XD,85 respectively. 6-31G* basis sets86 were used for carbon, hydrogen, and oxygen atoms, while the SDD basis set developed by the Stuttgart-Dresden-Bonn group87 was used for zinc atom. Other basis sets like 6-31g(d)/LanL2DZ, 6-311++g(d,p)/LanL2DZ and cc-PVDZ/LanL2DZ were also tested to justify the use of computationally efficient 6-31G*/SDD. (ZnO)nC96−2n structures corresponding to the lowest energy minima were obtained by enabling a full relaxation of all coordinates using the default convergence criteria. Vibrational mode calculations were additionally carried out to make sure there are no imaginary frequencies and to confirm the equilibrium of the ground-state geometry. Finally, absorption spectra of the (ZnO)nC96−2n hybrid materials were predicted using the time-dependent density functional theory (TD-DFT) approach using CAM-B3LYP/6-31G(d) method, which is capable to adequately reproduce the experimental absorption spectra of GQDs88 and is an appropriate choice to study the charge-transfer excitations.89,90
The lowest 100 excited states were considered. The analysis of excited states was performed using Multiwfn program.91 The VESTA program92 was employed to visualize the structures of (ZnO)nC96−2n.
The stability of (ZnO)nC96−2n structures at 0K was tested by estimating the cohesive energy per atom:93
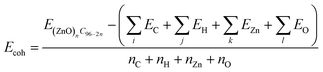 | (1) |
| EVZn = E(ZnO)nC96−2n − EZnn−1OnC96−2n − EZn | (2) |
To investigate the room temperature stability of the selected (ZnO)27C42 system we have performed ab initio molecular dynamic calculations at 300 K using atom density matrix propagation (ADMP) method95 implemented in Gaussian 16 Rev. C.01 program package. A time step (Δt) was chosen to be 0.1 fs.
Results and discussion
The optimized geometric structures of (ZnO)nC96−2n obtained by PBE0 method are illustrated in Fig. 1. Cohesive energies and selected structural parameters are reported in Table 1. First, it should be noted that all constructed hybrid structures are energetically stable (with quite high energy barriers for the decomposition of molecule into individual atoms), as evidenced by the negative cohesive energies. Such a predicted energetic stability implies the principal possibility of experimental design of (ZnO)nC96−2n quantum dots. However, the cohesive energy tends to become less negative with increasing the number of ZnO pairs embedded into the C96 matrix that entails a gradual decrease in the stability at 0 K (Fig. 2a). It is expected that under realistic conditions the stability of the considered systems can be more sensitive to the external factors. Despite pure GQDs have high corrosion resistance, excellent pH stability and photostability,96,97 the introduction of a certain number of impurities (zinc and oxygen atoms in our case) into the host matrix may influence the material stability and physicochemical properties. One of the possible consequences of ZnO incorporation is the increased likelihood of dissolution of hybrid quantum dots under wet conditions. This can be manifested as a release of zinc ions into the solution. One may anticipate that the zinc ions resulting from the dissolution of quantum dots may have a detrimental effect on their photoactivity. Thus, it is quite important to check whether the proposed materials are prone to dissolution. The formation of zinc vacancies through deliberate removal of zinc ions from the hybrid matrix is a possible chemical process that can be used to evaluate the dissolution tendency.94| Number of ZnO pairs, n | Cohesive energy, eV | Mean Zn–O bond length, Å | Mean C–C bond length, Å | Mean C–O bond length, Å | Mean C–Zn bond length, Å | Curvature parameter, Å |
|---|---|---|---|---|---|---|
| 0 | −8.2801 | — | 1.4302 | — | — | 0.0053 [0.0106] |
| 1 | −8.1190 | 2.0864 | 1.4167 | 1.3971 | 1.8748 | 2.0937 [3.1488] |
| 3 | −7.9128 | 2.1315 | 1.4197 | 1.2828 | 1.9416 | 2.4904 [3.4627] |
| 4 | −7.8183 | 1.9652 | 1.4178 | 1.3744 | 1.8949 | 3.4944 [5.2536] |
| 7 | −7.5421 | 2.0383 | 1.4198 | 1.3118 | 1.9439 | 3.4653 [5.1961] |
| 12 | −7.1017 | 1.9043 | 1.4211 | 1.3681 | 1.8909 | 3.8044 [5.8253] |
| 27 | −5.8035 | 1.9039 | 1.4091 | 1.3710 | 1.9396 | 3.7695 [6.8327] |
Fig. 2b demonstrates the relationship between zinc vacancy formation energy and chemical composition of hybrids. The structures with n = 1 and 3 exhibit positive values of the VZn formation energy, suggesting that the zinc vacancy formation in such hybrids is energetically favorable process. This makes them more prone to dissolution. Interestingly, with further increase in the number of ZnO pairs the formation energy becomes negative and reaches the largest value for the (ZnO)27C42 structure. This is indicative of a relatively high dissolution stability of ZnO-rich nanohybrids under operating conditions. The stability of the (ZnO)27C42 hybrid structure possessing the most negative zinc vacancy formation energy was additionally investigated through performing molecular dynamics (MD) calculations at room temperature (300 K).
Fig. 2c shows ADMP potential-energy profile at 300 K for the selected system. Ground state structure of (ZnO)27C42 obtained by DFT was chosen as a starting point of the MD simulation. Within the first 10 fs there is a small increase in the potential energy followed by trivial potential energy fluctuations. It is clear that Zn–C, Zn–O and C–O bonds are not broken down at room temperature and (ZnO)27C42 retains its semispherical shape. This highlights the thermal stability of this structure, which is a good prerequisite of a straightforward low-temperature synthesis of (ZnO)27C42. However, structural degradation at higher temperatures cannot be ruled out.
The accommodation of ZnO pairs in the GQDs is achieved not only through the formation of new bonds like Zn–O, Zn–C and C–O, but also through a pronounced curvature of initially flat GQDs (Fig. S4, ESI†). The curvature parameter is estimated as the difference between the average z-coordinate and the absolute highest z-coordinate in the (ZnO)nC96−2n. The results are listed in Table 1. The difference between minimum and maximum z-coordinates is included in square brackets as an additional curvature parameter (Table 1). It is apparent that both curvature parameters demonstrate a significant increase with increasing the amount of incorporated ZnO pairs, following the trend of decreasing stability. In the limit case (when 27 ZnO molecules are incorporated into C96 skeleton), i.e. (ZnO)27C42 system, to a large extend, resembles the hemisphere fullerene.98 Interestingly, the deviations from an ideally planar atomic arrangement decrease Zn–O, C–C and C–O bonds and, concomitantly, cause slight Zn–C bond length elongation. The structural properties of (ZnO)27C42 computed using PBE0/6-31g(d)/LanL2DZ, PBE0/6-311++g(d,p)/LanL2DZ and PBE0/cc-PVDZ/LanL2DZ are in broad agreement with those determined using PBE0/6-31g(d)/SDD (Fig. S5, ESI†). The relatively weak effect of the functional on the structure and the shape of the (ZnO)27C42 system was also observed (Fig. S6, ESI†). Therefore, our conclusion that (ZnO)27C42 has hemispherical shape is still unchanged. Fig. S7–S9 (ESI†) exhibit the optimized geometric structures of all considered systems calculated by CAM-B3LYP/6-31g(d)/SDD method, which are comparable to those predicted by PBE0/6-31g(d)/SDD.
The stability of (ZnO)nC96−2n systems has been further confirmed by performing frequency calculations by PBE0 and CAM-B3LYP methods. The absence of the appreciable imaginary frequencies suggests the good stability of (ZnO)nC96−2n hybrid materials. The most interesting part of predicted Raman spectra of the (ZnO)nC96−2n that is related to the vibrations of light C atoms is demonstrated in Fig. 3. It is clearly seen that the incorporation of ZnO into GQDs (up to n = 12) causes a reduction of the molecular symmetry that is manifested by the appearance of a large set of local vibrational modes instead of few Raman modes of pristine GQDs (including the most intensive ones at 1374 cm−1 and 1343 cm−1 predicted by PBE0 and CAM-B3LYP, respectively) within the spectral range from 1000 to 1800 cm−1. It is striking to note that, independently on the method, the (ZnO)27C42 structure has much stronger Raman activity than other considered structures including the reference pristine GQDs. The corresponding Raman spectrum predicted by PBE0 (CAM-B3LYP) is dominated by two bands at 1119 (1549) and 1384 (1561) cm−1, which are assigned to the atomic movements of carbon at the edges of (ZnO)27C42 structure (around the entire perimeter).
 | ||
| Fig. 3 Raman spectra of the (ZnO)nC96−2n structures computed by different methods: (a) PBE0/6-31G*/SDD and (b) CAM-B3LYP/6-31G*/SDD, respectively. | ||
Fig. S10 and S11 (ESI†) show (i) a moderate effect of the basis set on the Raman spectrum of (ZnO)27C42 and (ii) a pronounced effect of the functional on the Raman fingerprint of this hybrid structure. Noticeable, both long-range-corrected functionals – CAM-B3LYP and ωB97XD − give qualitatively similar results. We didn’t set a goal to investigate the red-shift of the modes, as this is out of scope of this article. However, we noticed the huge Raman enhancement of (ZnO)27C42 molecule, which could be originated from both plasmonic and nonplasmonic effects (like an improvement of molecular symmetry). The latter is further confirmed by the molecular orbital analysis, according to which the higher occupied molecular orbital (HOMO) and second unoccupied orbital are doubly degenerate. The incorporation of small amount of ZnO molecules reduces degeneracy of orbitals and causes an energy-level splitting, as was observed for the structures with n from 1 to 7. However, the fact that the lowest energy orbitals for both (ZnO)12C72 and (ZnO)27C42 systems remain degenerate with each other, like in the case of unperturbed C96 system, highlights the symmetric configuration of these two hybrid molecules. Much stronger Raman activity of (ZnO)27C42 compared to that of (ZnO)12C72 can be explained by the abundance of conduction electrons participating in collective oscillations of free charges and hence contributing to the plasmon resonance.
From Fig. S12a (ESI†), it is also seen that the HOMO–LUMO energy gap computed by PBE0 method decreases upon increasing the amount of ZnO molecules embedded into C96 matrix. The minimum energy gap of ∼1.24 eV is achieved for (ZnO)27C42 system (Fig. S12a, ESI†). The observed energy gap narrowing is mainly affected by the upward shift of the HOMO level, while the downward shift of LUMO acquires a less pronounced character. On the other hand, HOMO–LUMO energy gap evolution calculated at CAM-B3LYP/6-31g(d)/SDD level of theory is completely different (Fig. S12b, ESI†). In this case, the energy gap (ZnO)27C42 is approximately 3.26 eV. The possible reason of such difference is that PBE0 underestimates the HOMO–LUMO gap energy with respect to the CAM-B3LYP. Interestingly, the energy gap determined by B3LYP method is much underestimated compared to both PBE0 and CAM-B3LYP, while using of ωB97XD results in an increased HOMO–LUMO energy gap of (ZnO)27C42 up to 4.41 eV (Fig. S12c, ESI†). Considering the fundamental relationship between the HOMO–LUMO energy gap and the light absorption phenomena, a choice of the functional has an important effect on correctly interpreting results of the excited state analysis.
With (ZnO)27C42 molecule as an example, it becomes evident that electronic and photoexcitation properties of (ZnO)27C42 are strongly sensitive to the functional type (Fig. S13, ESI†). Although PBE0 and B3LYP give qualitatively similar results (the spectra are mostly overlapping), the absorption spectra computed using CAM-B3LYP and ωB97XD hybrid functionals are blue-shifted compared to PBE0 and B3LYP, which is the general trend (Fig. S14, ESI†). Meanwhile, we noticed that the extended basis sets cause slightly enhanced amplitude of the absorption band while keeping the overall spectrum shape intact (Fig. S15, ESI†). Taking the benefits of CAM-B3LYP for investigation of the charge-transfer excitations into account, we therefore focus only on a discussion of the absorption spectra predicted by CAM-B3LYP/6-31g(d)/SDD method.
Before discussion of the nature of the excited states with high oscillator strength, certain issues related to the first excited state should be addressed. This is due to the importance of S1 state in the emission process. Indeed, according to Kasha's rule, the lowest singlet S1 excited state is most probably fluorescent.99 Table S1 (ESI†) summarizes the properties of first excited state of (ZnO)nC96−2n. From this table, it can be seen that the S1 state of ZnO-free GQDs has zero oscillator strength and, hence, is optically forbidden. For this LE state, the equal contribution of H−1 → LUMO (47%) and HOMO → L+1 (47%) transitions to the excitation takes place. Upon increase of the ZnO pairs up to n = 4 LE character of the S1 state remains unchanged. Starting from (ZnO)7C82 structure, the S1 state first becomes a hybrid LE-CT state at n = 7 and then its character can be interpreted in terms of CT configuration. The results of analysis of the charge density difference for this state supports the above conclusion (Fig. S16, ESI†). Notably, despite S0 → S1 transition in (ZnO)7C82 structure is of LE-CT character, it is characterized by non-zero oscillator strength of 0.19. Therefore, it plays a non-negligible role in the overall light absorption process. In contrast, S1 state of highly symmetric molecules ((ZnO)12C72 and (ZnO)27C42) show strong CT characteristics. This finding can be helpful in developing an effective intermolecular charge-transfer transition emitter.
The results of electron excitation analysis also speak in favor of the supposition that the symmetry of the hybrid molecule affects its electronic properties. From Fig. 4 and Fig. S14b (ESI†) it is apparent that only highly symmetric molecules (C96, (ZnO)12C72 and (ZnO)27C42) exhibit doubly degenerate excited state configurations. The dominant spectral features observed at 243.83, 249.98, and 446.01 nm in the C96 spectrum are assigned to S81,82 ← S0, S69,70 ← S0, and S3,4 ← S0 transitions, respectively. Considering the electron–hole wave-function overlap integral (Sr), the distance between centroids of holes and electrons (D) and the degree of separation of holes and electrons (t) as descriptors of type of electron excitation,100–102 it is possible to draw some conclusions about the nature of these transitions. From Table 2 (see also Table S2 in ESI† summarizing the transitions with oscillator strength >0.1), it is clear that D of all aforementioned excited states is close to zero, while the S parameters are 0.95, 0.91 and 0.96 for S81,82 ← S0, S69,70 ← S0, and S3,4 ← S0, respectively. t indices are negative and are much less than 0, pointing out the absence of the charge separation. This suggests that the corresponding excitations are typical locally excited (LE) states. This finding is then corroborated by the analysis of the charge density difference (CDD) between ground state and excited state (Fig. S17, ESI†). Particularly, it was revealed that hole and electrons are delocalized over the entire area of pristine C96 system, and no charge separation occurs. Table 2 also summarizes the electronic transitions that are involved in these excited states.
| System | Excited state | Wavelength, nm | Oscillator strength, f | D, Å | S r | t, Å | Type | Major contribution |
|---|---|---|---|---|---|---|---|---|
| C96 | S3 | 446.01 | 1.98 | 0 | 0.96 | −1.90 | LE | H−1 → LUMO (23%), H−1 → L+1 (25%), HOMO → LUMO (25%), HOMO → L+1 (23%) |
| S69 | 249.98 | 0.75 | 0 | 0.91 | −3.96 | LE | H−3 → L+5 (21%), H−3 → L+12 (18%) | |
| S81 | 243.83 | 0.70 | 0 | 0.95 | −3.47 | LE | H−3 → L+12 (23%), H−1 → L+13 (12%), HOMO → L+14 (12%) | |
| ZnOC94 | S3 | 535.70 | 0.51 | 1.43 | 0.85 | −2.39 | LE-CT | H−1 → LUMO (26%), HOMO → L+1 (35%) |
| S4 | 513.68 | 0.43 | 0.87 | 0.84 | −2.29 | LE-CT | H−1 → L+1 (41%), HOMO → L+2 (22%) | |
| S11 | 412.31 | 0.38 | 1.07 | 0.89 | −3.13 | LE-CT | H−2 → L+1 (22%), H−1 → L+2 (13%), H−1 → L+3 (14%), HOMO → L+5 (16%) | |
| (ZnO)3C90 | S5 | 641.34 | 0.45 | 0.82 | 0.71 | −3.32 | LE | HOMO → L+1 (90%) |
| S8 | 560.20 | 0.52 | 1.03 | 0.82 | −2.39 | LE | H−5 → LUMO (12%), H−1 → L+1 (15%), HOMO → L+2 (52%) | |
| S9 | 554.26 | 0.69 | 0.47 | 0.82 | −3.29 | LE | H−3 → LUMO (75%), H−1 → L+2 (13%) | |
| (ZnO)4C88 | S10 | 428.72 | 1.25 | 0.85 | 0.87 | −3.46 | LE | H−3 → LUMO (12%), H−2 → L+1 (30%), HOMO → L+2 (16%), HOMO → L+3 (15%) |
| S26 | 351.83 | 0.49 | 0.60 | 0.90 | −3.67 | LE | H−5 → LUMO (20%), H−2 → L+2 (27%) | |
| S59 | 284.93 | 0.33 | 0.58 | 0.87 | −3.25 | LE | H−14 → LUMO (9%), H−12 → LUMO (6%), H−9 → LUMO (8%), H−7 → L+1 (7%), H−5 → L+1 (6%) | |
| (ZnO)7C82 | S16 | 396.11 | 0.52 | 1.89 | 0.83 | −2.72 | LE-CT | H−4 → L+1 (13%), HOMO → L+2 (43%) |
| S40 | 323.52 | 0.92 | 0.90 | 0.85 | −2.46 | LE-CT | H−5 → L+2 (10%), H−2 → L+3 (13%) | |
| S65 | 292.04 | 0.33 | 1.12 | 0.84 | −2.99 | LE-CT | H−3 → L+5 (16%), HOMO → L+8 (10%) | |
| (ZnO)12C72 | S21 | 341.35 | 0.78 | 0.55 | 0.84 | −2.20 | LE | H−5 → L+3 (13%) |
| S24 | 327.05 | 1.18 | 0.38 | 0.82 | −2.47 | LE | H−3 → L+6 (8%), H−3 → L+9 (9%), H−2 → L+5 (8%), H−1 → L+3 (5%), H−1 → L+8 (4%), H−1 → L+9 (9%), HOMO → L+4 (5%) | |
| S36 | 303.55 | 0.38 | 1.07 | 0.77 | −0.89 | LE-CT | H−3 → L+7 (14%) | |
| (ZnO)27C42 | S6 | 453.52 | 1.73 | 1.22 | 0.75 | −1.27 | LE-CT | H−1 → L+1 (13%), H−1 → L+3 (12%), HOMO → L+2 (13%), HOMO → L+4 (12%) |
| S8 | 446.87 | 0.72 | 2.79 | 0.54 | 0.057 | CT | H−1 → L + 1 (14%), H−1 → L+3 (12%), HOMO → L+2 (14%), HOMO → L+4 (12%) | |
| S66 | 277.94 | 0.25 | 1.65 | 0.61 | −0.87 | LE-CT | H−12 → LUMO (16%) |
The absorption spectrum of the ZnO-free pristine molecule undergoes substantial changes after ZnO incorporation (Fig. 4, Table 2 and Tables S3–S8, ESI†). A quick look at the evolution of the absorption spectra shows that the symmetry breaking leads to broadening of the main absorption bands of C96 and reduces the absorption intensity (the oscillator strength for the corresponding transitions), as can be clearly seen in the case of low-symmetry intermediate systems (from ZnOC94 to (ZnO)7C82).
However, a further increase of inserted ZnO molecules leads to a distinct increase of the oscillator strength and hence absorption intensity. Finally, highly symmetric (ZnO)27C42 molecule demonstrates a very strong absorbance spectrum extending from ultraviolet to visible, with oscillator strength that is comparable to that for the localized excitation in the case of pristine C96 system.
A more detailed consideration of each of the presented spectra shows that in the case of the ZnOC94 system, the most intense band extending from 225 nm to 700 nm is related to the S3, S4, and S11 excited states, respectively. The complementary analysis of the CDD (Fig. 5a, Fig. S18, ESI†), Sr, D, and t parameters (Table 2) shows that all three excitations are LE–CT hybrid states. Interestingly, the electrons and holes are more separated in the S3 and S11 states than in the S4 state (confirmed by larger D), indicating a dominant CT character for these excited states. For the (ZnO)3C90 system, the distance between the centroids of holes and the electrons for three most probable transitions is very low because they occupy the same space (Fig. 5b, Fig. S19, ESI†). Therefore, S5, S8, and S9 states are mostly local excitations (Fig. 5c and Fig. S20, ESI†). (ZnO)4C88 exhibits a relatively complex series of spectral features, with dominant contribution from S10, S26, and S59 excited states. All these states are characterized by the low D and rather negative t values, which are peculiar to the LE state with minimal charge separation. The absorption spectrum (ZnO)7C82 is dominated by a wide band peaked at 314 nm (with major contribution from S40 ← S0, and S65 ← S0 transitions), followed by the weak shoulder at ∼396 nm, which can be attributed to the S16 ← S0 transition. Based on analysis of the CDD (Fig. 5d, Fig. S21, ESI†), it is evident that all three excitations are the LE–CT hybrid states. The sharp spectral feature of the (ZnO)12C72 molecule at ∼327 nm is preferentially attributed to three doubly degenerate LE–CT hybrid states: S21,22, S24,25, and S36,37, respectively. Unexpectedly, all three transitions have completely different natures (see Table 2, Fig. 5e and Fig. S22, ESI†). S21,22 and S24,25 can be regarded as local excitations, while S36,37 has obvious LE–CT characteristics.
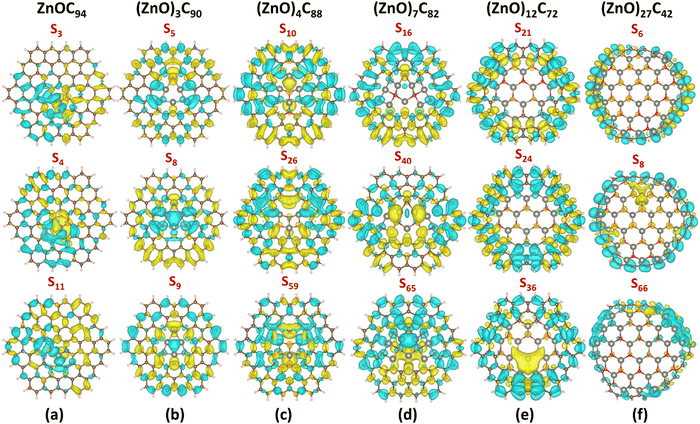 | ||
| Fig. 5 CDD for selected excited states (with the largest oscillator strength) in (a) ZnOC94, (b) (ZnO)3C90, (c) (ZnO)4C88, (d) (ZnO)7C82, (e) (ZnO)12C72, and (f) (ZnO)27C42, respectively. Herein, yellow denotes positive charge distribution and cyan means negative charge distribution. CDD was calculated as a difference between the corresponding excited state and the ground state of the considered system (ρexcited − ρground) using the CAM-B3LYP/6-31G*/SDD level of theory. The isosurface level is set to be 0.0003. See also Fig. S24–S26 (ESI†) demonstrating CDD maps obtained using PBE0, wB97XD, and B3LYP methods. | ||
Apparently, for (ZnO)27C42, the doubly degenerate S6,7 excited state possessing the largest oscillator strength of 1.73 is a typical LE-CT state, while the doubly degenerate S8,9 state demonstrates CT characteristics (Table 2, Fig. 5f; Fig. S23, ESI†). In this case, the S8,9 state is characterized by the largest D parameter (2.79 Å) and positive t index (0.06 Å). CDD analysis provides additional evidence of the origin of S8,9 states (Fig. 5f, Fig. S23, ESI†). In particular, we notice that the electron accumulation region is mainly located at the (ZnO)27 fragment, while the obvious charge depletion region is observed at the C42 moiety.
To shed more light on the nature of the absorption spectra of the (ZnO)nC96−2n structures, the nature of the dominating absorption bands is further scrutinized through the decomposition of the absorption spectrum into four different components. This method originally developed by Liu et al.103 enables distinguishing between intrafragment charge redistribution and interfragment charge transfer. In other words, by performing such an analysis, it is possible to conclude the contribution of the charge-transfer excited states to the total response of the system. In line with this, we selected two different fragments in (ZnO)nC96−2n – C96−2n and (ZnO)n – and then calculated the so-called charge-transfer spectra (CTS) of (ZnO)nC96−2n molecule (Fig. 4). The spectra are partitioned in a fixed fashion for all the structures. Even though the charge-transfer components (C96−2n → (ZnO)n and (ZnO)n → C96−2n, respectively) contribute to the total absorption spectra, it is seen that the main bands of the hybrid complexes with n ranging from 1 up to 7 mostly originate from the electron transitions within the C96−2n moiety, additionally pointing to the domineering role of local excitations. Therefore, it can be stated that zinc and oxygen atoms are minimally involved in the corresponding excitations since the electrons and holes are mostly localized at the peripheral carbon moieties. In contrast to this, the analysis of the absorption bands of (ZnO)12C72 and (ZnO)27C42 shows a significant role of charge transfer from the C72 and C42 moieties to the (ZnO)12 and (ZnO)27 parts in the corresponding excitations (see also the pie charts, Fig. 4). Notably, an equal contribution from the ICR and ICT components to the overall spectrum takes place at n = 27. A smaller contribution of charge-transfer components (C42 → (ZnO)27 and (ZnO)27 → C42, respectively) to the total spectrum is however observed for the spectra calculated by PBE0, B3LYP, and wB97XD methods (Fig. S27, ESI†).
Conclusion
By performing geometry optimization and frequency calculations using PBE0/6-31G*/SDD and CAM-B3LYP/6-31G*/SDD levels of DFT, stable (ZnO)nC96−2n hybrid systems with n = 1, 3, 4, 7, 12, and 27 were designed. The increase in the amount of ZnO pairs embedded in the C96 matrix caused the reduction of the cohesive energy of the system, which nonetheless remains negative, indicating a high possibility to synthesize these hybrid materials. By regulating the ZnO content, one can possible alter the symmetry and curvature of the ZnO-embedded graphene quantum dots, HOMO–LUMO energy gap, and hence light absorption properties including the dominant absorption wavelength, excitation type, and oscillator strength. A highly symmetric (ZnO)27C42 molecule was found to demonstrate the room-temperature stability, large VZn formation energy, and enhanced Raman signal mostly originating from the collective vibrations within the peripheral C42 moiety and the strong broad absorption band extending from the ultraviolet (UV)-C to visible region. These make such materials promising for designing both SERS-based sensors and cost-effective solar absorbers. The in-depth analysis of the prevailing excited states enabled us to shed light on their nature and to ascribe the strong absorption band in (ZnO)27C42 to the doubly degenerate locally excited and charge-transfer states. The current work provides rich insights into the nature of the photoexcited states in the ZnO-graphene hybrid materials and the guidelines for further experimental design of organic–inorganic frameworks with desired charge-transfer characteristics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. S. acknowledges the support from Ångpanneföreningens Forskningsstiftelse (Grant 21–112). The computations and data handling were enabled by resources provided by the National Supercomputer Centre (NSC), funded by Linköping University.References
- G. V. Lashkarev, V. A. Karpyna, V. I. Lazorenko, A. I. Ievtushenko, I. I. Shtepliuk and V. D. Khranovskyy, Low Temp. Phys., 2011, 37, 226 CrossRef CAS.
- G. V. Lashkarev, I. I. Shtepliuk, A. I. Ievtushenko, O. Y. Khyzhun, V. V. Kartuzov, L. I. Ovsiannikova, V. A. Karpyna, D. V. Myroniuk, V. V. Khomyak, V. N. Tkach, I. I. Timofeeva, V. I. Popovich, N. V. Dranchuk, V. D. Khranovskyy and P. V. Demydiuk, Low Temp. Phys., 2015, 41, 129 CrossRef CAS.
- C. Yang, L.-W. Hu, H.-Y. Zhu, Y. Ling, J.-H. Tao and C.-X. Xu, J. Mater. Chem. B, 2015, 3(13), 2651–2659 RSC.
- K. R. Nemade and S. A. Waghuley, Sci. Adv. Mater., 2014, 6(1), 128–134 CrossRef CAS.
- E. Wongrat, T. Nuengnit, R. Panyathip, N. Chanlek, N. Hongsith and S. Choopun, Sens. Actuators, B, 2021, 326, 128983 CrossRef CAS.
- K. Rahimi and A. Yazdani, Mater. Lett., 2018, 228, 65–67 CrossRef CAS.
- Y. Zhang and X. Bai, J. Electrochem. Soc., 2020, 167(2), 027541 CrossRef CAS.
- L. Luo, X. Liu, S. Ma, L. Li and T. You, Food Chem., 2020, 322, 126778 CrossRef CAS PubMed.
- W. Liu, X. Zhou, L. Xu, S. Zhu, S. Yang, X. Chen, B. Dong, X. Bai, G. Lu and H. Song, Nanoscale, 2019, 11(24), 11496–11504 RSC.
- D. Zhang, Z. Wu and X. Zong, Sens. Actuators, B, 2019, 288, 232–242 CrossRef CAS.
- S. Shao, X. Chen, Y. Chen, L. Zhang, H. W. Kim and S. S. Kim, ACS Appl. Nano Mater., 2020, 3(6), 5220–5230 CrossRef CAS.
- X. Chu, P. Dai, Y. Dong, W. Sun, L. Bai and W. Zhang, J. Mater. Sci.: Mater. Electron., 2017, 28(24), 19164–19173 CrossRef CAS.
- B. Hatamluyi and Z. Es’haghi, Electrochim. Acta, 2018, 283, 1170–1177 CrossRef CAS.
- K. S. Lee, J. Shim, J. S. Lee, J. Lee, H. G. Moon, Y. J. Park, D. Park and D. I. Son, J. Ind. Eng. Chem., 2022, 106, 279–286 CrossRef CAS.
- Y.-H. Zhang, C.-N. Wang, L.-J. Yue, J.-L. Chen, F.-L. Gong and S.-M. Fang, Physica E, 2021, 133, 114807 CrossRef CAS.
- M. Hoang Tran, T. Park and J. Hur, Appl. Surf. Sci., 2021, 539, 148222 CrossRef CAS.
- D. Ghosh, S. Kapri and B. Shattacharyya, ACS Appl. Mater. Interfaces, 2016, 8(51), 35496–35504 CrossRef CAS PubMed.
- S. Dhar, T. Majumder and S. P. Mondal, ACS Appl. Mater. Interfaces, 2016, 8(46), 31822–31831 CrossRef CAS PubMed.
- N. Fathima, N. Pradeep and J. Balakrishnan, Bull. Mater. Sci., 2021, 44(1), 33 CrossRef CAS.
- C. Yin, J. Wu, J. Zhou, D. Zhang, Z. Liu, X. Liu, L. Liu, Z. Zhan, S. Garner and Y. Fu, Sens. Actuators, A, 2021, 321, 112590 CrossRef CAS.
- L. Goswami, N. Aggarwal, R. Verma, S. Bishnoi, S. Husale, R. Pandey and G. Gupta, ACS Appl. Mater. Interfaces, 2020, 12(41), 47038–47047 CrossRef CAS PubMed.
- H. Wu, J. Ding, D. Yang, J. Li, Y. Shi and Y. Zhou, Ceram. Int., 2020, 46(11), 17800–17808 CrossRef CAS.
- K. S. Lee, Y. J. Park, J. Shim, H.-S. Chung, S.-Y. Yim, J. Y. Hwang, H. Cho, B. Lim and D. I. Son, Org. Electron., 2020, 77, 105489 CrossRef CAS.
- S. S. Mousavi, A. Kazempour, B. Efafi, M. H. M. Ara and B. Sajad, Appl. Surf. Sci., 2019, 493, 1187–1194 CrossRef CAS.
- K. B. Ko, B. D. Ryu, M. Han, C.-H. Hong, D. A. Dinh and T. V. Cuong, Appl. Surf. Sci., 2019, 481, 524–530 CrossRef CAS.
- S. S. Mousavi, B. Sajad and M. H. Majlesara, Mater. Des., 2019, 162, 249–255 CrossRef CAS.
- K. Rahimi, A. Yazdani and M. Ahmadirad, Mater. Des., 2018, 140, 222–230 CrossRef CAS.
- D. Liu, H.-J. Li, J. Gao, S. Zhao, Y. Zhu, P. Wang, D. Wang, A. Chen, X. Wang and J. Yang, Nanoscale Res. Lett., 2018, 13, 261 CrossRef PubMed.
- S. Dhar, T. Majumder and S. P. Mondal, Mater. Res. Bull., 2017, 95, 198–203 CrossRef CAS.
- M. M. Tavakoli, H. Aashuri, A. Simchi and Z. Fan, Phys. Chem. Chem. Phys., 2015, 17(37), 24412–24419 RSC.
- D. S. Ahmed, M. K. A. Mohammed and S. M. Majeed, ACS Appl. Energy Mater., 2020, 3(11), 10863–10871 CrossRef CAS.
- M. M. Tavakoli, R. Tavakoli, Z. Nourbakhsh, A. Waleed, U. S. Virk and Z. Fan, Adv. Mater. Interfaces, 2016, 3(11), 1500790 CrossRef.
- I. J. Peter, N. Rajamanickam, K. Ramachandran and P. Nithiananthi, AIP Conf. Proc., 1992, 040026 Search PubMed.
- G. Zamiri and S. Bagheri, J. Colloid Interface Sci., 2018, 511, 318–324 CrossRef CAS PubMed.
- T. Majumder, K. Debnath, S. Dhar, J. J. L. Hmar and S. P. Mondal, Energy Technol., 2016, 4(8), 950–958 CrossRef CAS.
- T. Majumder and S. P. Mondal, J. Electroanal. Chem., 2016, 769, 48–52 CrossRef CAS.
- T. Majumder, S. Dhar, P. Chakraborty, K. Debnath and S. P. Mondal, Nano, 2019, 14(1), 1950012 CrossRef CAS.
- M. Dutta, S. Sarkar, T. Ghosh and D. Basak, J. Phys. Chem. C, 2012, 116(38), 20127–20131 CrossRef CAS.
- B. J. Moon, K. S. Lee, J. Shim, S. Park, S. H. Kim, S. Bae, M. Park, C.-L. Lee, W. K. Choi, Y. Yi, J. Y. Hwang and D. I. Son, Nano Energy, 2016, 20, 221–232 CrossRef CAS.
- M. M. Tavakoli, Procedia Eng., 2016, 141, 38–46 CrossRef CAS.
- M. Ur Rahman, F. Xie, Y. Li and M. Wei, J. Electroanal. Chem., 2019, 840, 160–164 CrossRef.
- T. Majumder and S. P. Mondal, Bull. Mater. Sci., 2019, 42(2), 65 CrossRef.
- S. Tamandani and G. Darvish, Int. J. Mod. Phys. B, 2017, 31(2), 1650253 CrossRef CAS.
- M. Zubair, M. Mustafa, A. Ali, Y. H. Doh and K. H. Choi, J. Mater. Sci.: Mater. Electron., 2015, 26(5), 3344–3351 CrossRef CAS.
- S. Aaryashree Biswas, P. Sharma, V. Awasthi, B. S. Sengar, A. K. Das and S. Mukherjee, ChemistrySelect, 2016, 1(7), 1503–1509 CrossRef.
- S. Vempati, A. Celebioglu and T. Uyar, Nanoscale, 2015, 7(38), 16110–16118 RSC.
- Z. Shi, Y. He, J.-J. Cai, X.-N. Wang, C.-Q. He, X.-B. Tang and J.-A. Wang, J. Lumin., 2014, 35(2), 137–141 CrossRef CAS.
- Y. J. Park, K. B. Ko, K. S. Lee, T. H. Seo, C.-H. Hong, T. V. Cuong and D. I. Son, Appl. Surf. Sci., 2020, 510, 145407 CrossRef CAS.
- D. I. Son, B. W. Kwon, D. H. Park, W.-S. Seo, Y. Yi, B. Angadi, C.-L. Lee and W. K. Choi, Nat. Nanotechnol., 2012, 7(7), 465–471 CrossRef CAS PubMed.
- A. Kharkwal, G. Rahul Purohit and D. S. Rawat, Asian J. Org. Chem., 2020, 9(12), 2162–2169 CrossRef CAS.
- Z. Zeng, F.-X. Xiao, X. Gui, R. Wang, B. Liu and T. T. Yang Tan, J. Mater. Chem. A, 2016, 4(42), 16383–16393 RSC.
- H. Zhang, Y. Cao, L. Zhong, X. Cao, J. He, J. Sun and W. Lei, Appl. Surf. Sci., 2019, 485, 361–367 CrossRef CAS.
- D. Van Thuan, T. K. Nguyen, S.-W. Kim, J. S. Chung, S. H. Hur, E. J. Kim, S. H. Hahn and M. Wang, Catal. Commun., 2017, 101, 102–106 CrossRef CAS.
- M.-L. Hsieh, R.-S. Juang, Y. A. Gandomi, C.-C. Fu, C.-T. Hsieh and W.-R. Liu, J. Taiwan Inst. Chem. Eng., 2022, 131, 104180 CrossRef CAS.
- A. Cai, X. Wang, Y. Qi and Z. Ma, Appl. Surf. Sci., 2017, 391, 484–490 CrossRef CAS.
- J. Wang, Y. Li, J. Ge, B.-P. Zhang and W. Wan, Phys. Chem. Chem. Phys., 2015, 17(28), 18645–18652 RSC.
- Y. Li, L. Wang, J. Ge, J. Wang, Q. Li, W. Wan, B. Zhang, X. Liu and W. Xue, RSC Adv., 2016, 6(108), 106508–106515 RSC.
- K. Rahimi, A. Yazdani and M. Ahmadirad, Mater. Res. Bull., 2018, 98, 148–154 CrossRef CAS.
- M. Ebrahimi, M. Samadi, S. Yousefzadeh, M. Soltani, A. Rahimi, T.-C. Chou, L.-C. Chen, K.-H. Chen and A. Z. Moshfegh, ACS Sustainable Chem. Eng., 2017, 5(1), 367–375 CrossRef CAS.
- N. Elumalai, S. Prabhu, M. Selvaraj, S. Shanavas, M. Navaneethan, S. Harish, P. Ramu and R. Ramesh, J. Mater. Sci.: Mater. Electron., 2021, 32(24), 28633–28647 CrossRef CAS.
- M. Zhao, Y. Sun, J. Lv, L. Cao, Y. Jiang, G. He, M. Zhang, Z. Sun and X. Chen, J. Mater. Sci.: Mater. Electron., 2016, 27(9), 9131–9135 CrossRef CAS.
- S. Kumar, A. Dhiman, P. Sudhagar and V. Krishnan, Appl. Surf. Sci., 2018, 447, 802–815 CrossRef CAS.
- S. Phophayu, P. Pimpang, S. Wongrerkdee, S. Sujinnapram and S. Wongrerkdee, J. Reinf. Plast. Compos., 2020, 39(3–4), 81–94 CrossRef CAS.
- J. Liu, J. Shao, Y. Wang, J. Li, H. Liu, A. Wang, A. Hui and S. Chen, ACS Sustainable Chem. Eng., 2019, 7(19), 16264–16273 CrossRef CAS.
- J. Liu, M. D. Rojas-Andrade, G. Chata, Y. Peng, G. Roseman, J.-E. Lu, G. L. Millhauser, C. Saltikov and S. Chen, Nanoscale, 2018, 10(1), 158–166 RSC.
- M. Li, Q. Feng, H. Liu, Y. Wu and Z. Wang, Mater. Lett., 2021, 283, 128838 CrossRef CAS.
- S. Sheik Mydeen, R. Raj Kumar, R. Sivakumar, S. Sambathkumar, M. Kottaisamy and V. S. Vasantha, Chem. Phys. Lett., 2020, 761, 138009 CrossRef CAS.
- C. Tshangana, M. Chabalala, A. Muleja, E. Nxumalo and B. Mamba, J. Environ. Chem. Eng., 2020, 8(4), 103930 CrossRef CAS.
- H. T. Quang, A. Bachmatiuk, A. Dianat, F. Ortmann, J. Zhao, J. H. Warne, J. Eckert, G. Cunniberti and M. H. Rümmeli, ACS Nano, 2015, 9(11), 11408–11413 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Kuamit and V. Parasuk, Chem. Phys. Lett., 2022, 806, 140050 CrossRef CAS.
- P. Zhang, Q. Hu, X. Yang, X. Hou, J. Mi, L. Liu and M. Dong, RSC Adv., 2018, 8, 531 RSC.
- S. Sarkar, Phys. Chem. Chem. Phys., 2016, 18, 21278 RSC.
- Q. Xu, W. Cai, M. Zhang, R. Su, Y. Ye, Y. Li, L. Zhang, Y. Guo, Z. Yu, S. Li, X. Lin, Y. Chen, Y. Luo, J. Streetf and M. Xu, Photoluminescence mechanism and applications of Zn-doped carbon dots, RSC Adv., 2018, 8, 17254–17262 RSC.
- J. Cheng, C.-F. Wang, Y. Zhang, S. Yang and S. Chen, Zinc ion-doped carbon dots with strong yellow photoluminescence, RSC Adv., 2016, 6, 37189–37194 RSC.
- P. R. Kharangarh, V. Singh and G. Singh, AIP Conf. Proc., 2019, 2142, 060007 CrossRef CAS.
- J. T. B. H. Jastrzebski, J. Boersma and G. van Koten, Structural Organozinc Chemistry. In PATAI’S Chemistry of Functional Groups, ed. Z. Rappoport, 2009, DOI:10.1002/9780470682531.pat0365.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- M. Gerosa, C. E. Bottani, L. Caramella, G. Onida, C. Di Valentin and G. Pacchioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155201 CrossRef.
- Z. Qian, J. Ma, X. Shan, L. Shao, J. Zhou, J. Chena and H. Feng, RSC Adv., 2013, 3, 14571–14579 RSC.
- M. Zhao, F. Yang, Y. Xue, D. Xiao and Y. A. Guo, Chem. Phys. Chem., 2014, 15, 950–957 CrossRef CAS PubMed.
- I. Shtepliuk and R. Yakimova, Phys. Chem. Chem. Phys., 2018, 20(33), 21528–21543 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. J. Pople, Chem. Phys., 1980, 72, 650–654 CAS.
- J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420 CrossRef CAS.
- Y. Li, W. Zhang, X. Li and Y. Xu, Mater. Chem. Front., 2021, 5, 5814–5825 RSC.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- P. Wiggins, J. A. Gareth Williams and D. J. Tozer, J. Chem. Phys., 2009, 131, 091101 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- I. Shtepliuk, V. Khranovskyy and R. Yakimova, Phys. Chem. Chem. Phys., 2017, 19(45), 30445–30463 RSC.
- E. Fako, A. S. Dobrota, I. A. Pašti, N. López, S. V. Mentus and N. V. Skorodumovade, Phys. Chem. Chem. Phys., 2018, 20, 1524 RSC.
- H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763 CrossRef CAS.
- M. Kortel, B. D. Mansuriya, N. Vargas Santana and Z. Altintas, Micromachines, 2020, 11, 866 CrossRef PubMed.
- T. A. Tabish, C. J. Scotton, D. C. J. Ferguson, L. Lin, A. van der Veen, S. Lowry, M. Ali, F. Jabeen, M. Ali, P. G. Winyard and S. Zhang, Nanomedicine, 2018, 13(15), 1923–1937 CrossRef CAS PubMed.
- G. Centi, K. Barbera, S. Perathoner, N. K. Gupta, E. E. Ember and J. A. Lercher, ChemCatChem, 2015, 7, 3036 CrossRef CAS.
- M. Zhao, F. Yang, Y. Xue, D. Xiao and Y. Guo, Chem. Phys. Chem., 2014, 15, 950–957 CrossRef CAS PubMed.
- B. Moore, H. Sun, N. Govind, K. Kowalski and J. Autschbach, Charge-Transfer Versus Charge-Transfer-Like Excitations Revisited, J. Chem. Theory Comput., 2015, 11, 3305–3320 CrossRef CAS PubMed.
- W. Ding, Z. Xue, J. Li, M. Li, L. Bai, Q. Zhou, X. Zhou, Y. Peng and L. Miao, ECS J. Solid State Sci. Technol., 2022, 11, 016001 CrossRef.
- I. Shtepliuk and R. Yakimova, Materials, 2018, 11(7), 1217 CrossRef PubMed.
- Z. Liu, X. Wang, T. Lu, A. Yuan and X. Yan, Carbon, 2022, 187, 78–85 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04484f |
| This journal is © the Owner Societies 2023 |



