Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automated analysis of soft material microindentation†
Henry E.
Symons
 a,
Agostino
Galanti
a,
Agostino
Galanti
 ab,
Joseph C.
Surmon
c,
Richard S.
Trask
ab,
Joseph C.
Surmon
c,
Richard S.
Trask
 c,
Sebastien
Rochat
c,
Sebastien
Rochat
 d and
Pierangelo
Gobbo
d and
Pierangelo
Gobbo
 *ab
*ab
aSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK
bDepartment of Chemical and Pharmaceutical Sciences, University of Trieste, Via Giorgieri 1, 34127, Trieste, Italy. E-mail: pierangelo.gobbo@units.it
cDepartment of Aerospace Engineering and Bristol Composites Institute, School of Civil, Aerospace, and Mechanical Engineering, University of Bristol, Bristol, BS8 1TR, UK
dSchool of Chemistry, Department of Engineering Mathematics, and Bristol Composites Institute, University of Bristol, Bristol, BS8 1TS, UK
First published on 26th October 2022
Abstract
An understanding of the mechanical properties of soft hydrogel materials over multiple length scales is important for their application in many fields. Typical measurement methods provide either bulk mechanical properties (compression, tensile, rheology) or probing of nano or microscale properties and heterogeneity (nanoindentation, AFM). In this work we demonstrate the complementarity of instrumented microindentation to these techniques, as it provides representative Young's moduli for soft materials with minimal influence of the experimental parameters chosen, and allows mechanical property mapping across macroscopic areas. To enable automated analysis of the large quantities of data required for these measurements, we develop a new fitting algorithm to process indentation data. This method allows for the determination of Young's moduli from imperfect data by automatic selection of a region of the indentation curve which does not display inelastic deformation or substrate effects. We demonstrate the applicability of our approach with a range of hydrogels, including materials with patterns and gradients in stiffness, and expect the techniques described here to be useful developments for the mechanical analysis of a wide range of soft and biological systems.
Introduction
Hydrogels and related soft materials are highly studied for their use in tissue engineering, regenerative medicine and other biomedical applications such as use as cell culture media.1–6 Their biocompatibility, and flexible/stretchable nature also make hydrogels attractive candidates for use in soft robotics.7,8 For both these and many other applications, an understanding of the mechanical properties and their spatial relationships within these materials is crucial.9,10 For example, when considering biomedical applications, mechanical properties govern a plethora of biological processes including the regulation of stem cell fate and activity,11 cell locomotion and growth,12,13 and immune response modulation.14Hydrogel materials exhibit features spanning length scales from the macroscopic to the nanoscale.15 Recently, it has been recognised that in addition to their bulk mechanical properties, this heterogeneity is important to many of the aforementioned applications.16,17 Characterisation methods for hydrogels which examine both mechanical properties and their spatial relationships on multiple length scales will enable better understanding of these hierarchical and heterogeneous soft materials.
Bulk mechanical characterisation methods, such as compression or tensile tests and rheology, may provide representative properties for the entire material tested. Such methods, however, (i) are unable to provide spatial relationships of mechanical properties within materials; (ii) may be incompatible with hydrated soft material (including biological samples) which often require immersion in aqueous media throughout measurement; and (iii) require specific sample sizes and geometries which may be inaccessible or may damage many soft or biological materials.18
Conversely, indentation measurements probe localised mechanical properties, allowing a high degree of spatial information to be obtained. These techniques are also less limited in terms of sample geometry and require only small material quantities. Instrumented nanoindentation with a load cell and vertical probe setup allows for minimal analytical complexity, however, is traditionally applied predominantly to harder materials. As such, instruments typically use probe geometries (e.g. sharp Berkovich tips, which complicate analysis of soft materials)19 or analytical approaches (e.g. Oliver-Pharr analysis, which yields discrepancies for viscoelastic materials and does not account for adhesion effects)20,21 that are sub-optimal for softer materials. Alternatively, atomic force microscopes (AFMs) with cantilevers equipped with colloidal probes (typically <10 μm diameter) are frequently applied to study the mechanical properties of soft materials. These measurements may provide high resolutions nanoscale mapping of mechanical properties over localised areas (typically 100 × 100 μm or smaller).21–23 However, indentation measurements conducted with small probes and sub-micrometre indentation depths may be significantly influenced by highly localised or surface features.24 Furthermore, the small probes employed are more susceptible to significant changes in contact area due to adhesive fouling when measuring soft samples.25 This behaviour may result in significant discrepancies between the nanoscale and bulk mechanical properties.
Indentation with a microscale spherical probe (with diameter on the order of hundreds of micrometres) provides a complementary approach to both extremes, capable of determining spatial relationships in mechanical properties of material features with length scales between the nanoscale and the bulk. Measurements carried out on this length scale should be less affected by localised features, and may provide modulus values in greater agreement with bulk methodologies. Like nanoindentation, however, these measurements require careful experimental setup, and moduli determined may exhibit significant dependency on the indentation parameters chosen.26 Lastly, although automation of AFM nanoindentation is common and available in many commercial and open-source AFM software packages,27,28 comparable methods for microindentation are less widespread, limiting their large-scale application.
In this work, we investigate the general applicability of microindentation measurements to soft materials. We use an instrumented indenter with a capacitive microforce sensor utilising Micro-Electro-Mechanical System (MEMS) technology, with a transverse comb drive configuration.29 Compared with traditional load cells, this sensor class is compact but provides high sensitivity, a low noise level, and is unaffected by temperature.29 To better enable the acquisition and processing of large volumes of microindentation data, such as with macroscale mechanical property mapping, we developed an automated data analysis approach. We focus our study on hydrogels as readily accessible soft materials with many applications, however, given the similarities in their mechanical properties, findings should also be applicable to many soft biological or biomimetic systems.
Materials and methods
Indentation measurements
Indentation measurements were made used an FT-MTA03 “Micromechanical Testing and Assembly System” from FemtoTools AG. The instrument was equipped with an FT-S2000 Microforce Sensing Probe (with a force range of ± 2000 μN at a resolution of 0.005 μN). Spherical tips were obtained by attaching borosilicate glass microspheres (nominal diameter 250–300 μm, BSGMS-2.2 from Cospheric) to the silicon probe with Norland Optical Adhesive 81 and curing with a 365 nm UV LED (Thorlabs, Inc.).Hydrogel samples were prepared (as described below) in a bespoke aluminium sample holder, composed of a 4 × 4 array of circular sample wells (depth 8 mm, diameter 5 mm) with threaded walls to minimise sample movement. Unless otherwise specified, all measurements were carried out with a layer (approximately 1 mm thick) of aqueous medium covering the sample, with the spherical component of the probe fully submerged within the liquid medium for the entire measurement. During measurements a constant sample temperature of 25 °C was maintained using a bespoke environmental chamber equipped with a recirculating 600 W air heating system.
To obtain indentation data, the instrument was operated using the stick-slip actuator (29 mm vertical range, 1 nm positional resolution) in a stepped operating mode, with 0.5 μm increments. The hydrogel surface was found by applying a force threshold of between 5 and 30 μN, depending on the stiffness of the sample, before retracting the probe a distance of approximately 50 μm from the surface to allow the acquisition of baseline data. Unless otherwise specified, experimental parameters were selected such that a maximum indentation depth of approximately 50 μm was reached during each measurement, and movement speed and wait time were set to 10 μm s−1 and 0.1 s, respectively. Data were collected throughout the approach and indentation into the material (loading) and retraction back to the initial probe position (unloading). The sensor and probe were calibrated prior to each set of experiments on a stiff surface, and the integrated instrument software package used to correct acquired data accordingly.
Compression measurements
Hydrogel samples were tested using displacement control in quasi-static uniaxial compression (Shimadzu AGS-X, Japan) with a 500 N load cell. Samples were removed from solution shortly before testing, all tests were performed under atmospheric conditions. The cross-bar head was displaced at a speed of 0.2 mm min−1 for each sample, until a maximum compressive strain of 0.15 was reached. ‘Trapezium X’ software was connected to the Shimadzu to control displacement and acquire data. Two smooth and circular compressive plates were used to transfer compressive force from load cell to sample. The compressive plates were wiped down between each test to remove any residues. Stress-strain curves were obtained from the force and displacement data using the initial sample dimensions. Finally, the Young's modulus was calculated from the approximately linear region between 0–0.10 strain as described by Kingsley et al. for agarose hydrogels.30Theoretical models
Within our analysis application, we applied both the Hertz31 and the Johnson–Kendall–Roberts32 (JKR) contact mechanics models to fit indentation data. In the vast majority of hydrogel indentation data analysed, the JKR model provided a superior fit of the data, likely due to the presence of minor adhesive interactions between sample and probe even when sample were submerged in aqueous media. As such, all analysis in this work was carried out by fitting force-displacement data to the JKR model, described by eqn (1) and (2).32,33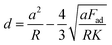 | (1) |
 | (2) |
 | (3) |
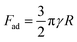 | (4) |
Hydrogel preparation
For compression testing samples, a heated 2% w/v solution of agarose in 1× PBS was poured into cylindrical moulds (diameter 20 mm) to heights of approximately 15 mm. Samples were allowed to cool for 60 minutes, then the resulting gels removed from their moulds and immersed in 1× PBS until testing.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio, pipetted into a sample holder well, then irradiated from above with a 365 nm, 76 mW cm−2, UV LED (Thorlabs) from a distance of 2.5 cm for 3 minutes.
1 volume ratio, pipetted into a sample holder well, then irradiated from above with a 365 nm, 76 mW cm−2, UV LED (Thorlabs) from a distance of 2.5 cm for 3 minutes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acrylamide
1 acrylamide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bisacrylamide molar ratio. This mixture was diluted two-fold with ultrapure water to give a 5% w/v solution. 7.5 μL of APS solution and 2.5 μL N,N,N′,N′-tetramethylethlyenediamine (TEMED, GE Healthcare) were added to 500 μL of each monomer solution, briefly mixed by vortex, then pipetted into sample holder wells. Samples were allowed to gelate for 1 hour prior to measurement.
bisacrylamide molar ratio. This mixture was diluted two-fold with ultrapure water to give a 5% w/v solution. 7.5 μL of APS solution and 2.5 μL N,N,N′,N′-tetramethylethlyenediamine (TEMED, GE Healthcare) were added to 500 μL of each monomer solution, briefly mixed by vortex, then pipetted into sample holder wells. Samples were allowed to gelate for 1 hour prior to measurement.
For thin-film samples, 50 μL of a 7.5% w/v monomer mixture (as described above) was added to a taut section of Parafilm, followed by 0.74 μL of APS solution (10% aq.). TEMED (0.74 μL) was added and the 3 solutions mixed briefly by pipetting. A glass coverslip (22 × 22 mm), treated with 3-(trimethoxysilyl)propyl methacrylate (Thermo Fisher),34 was placed over the droplet, and left for 30 minutes to allow gelation. Careful removal of the Parafilm left a thin film of hydrogel adhered to the glass coverslip, which was stored in ultrapure water until testing.
For compression testing samples, a 7.5% monomer solution (71.7 mL) was mixed with a 10% APS solution (1.07 mL) and TEMED (1.03 mL) and the mixture poured into cylindrical moulds (diameter 28 mm) to heights of approximately 25 mm. Samples were allowed to react for 60 minutes, then the resulting gels removed from their moulds and immersed in ultrapure water until testing.
Photolithographic masks were created by printing geometric designs on to acetate sheets with a commercial laser printer. A 2 mm thick poly(methyl methacryate) (PMMA) mould with a 5 × 5 mm square opening was positioned over the acetate mask. Each monomer solution was mixed in a 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio with the photoinitiator solution. 200 μL of the 15% w/v monomer/initiator solution was added to the mould, the solution carefully covered with a glass slide, and the apparatus sealed with binder clips. The apparatus was inverted then irradiated with a UV LED (365 nm, 76 mW cm−2) at a distance of 2.5 cm for 2 minutes. The acetate sheet was carefully removed. Excess monomer/initiator solution was removed with a medical tissue, and the cured hydrogel shape washed 3 times with ultrapure water then dried again with medical tissue. 200 μL of the 7.5% w/v monomer/initiator solution was added to the mould and carefully covered with a second glass slide. The sample was irradiated again for a further 2 minutes then removed from the mould prior to mechanical testing.
1 volume ratio with the photoinitiator solution. 200 μL of the 15% w/v monomer/initiator solution was added to the mould, the solution carefully covered with a glass slide, and the apparatus sealed with binder clips. The apparatus was inverted then irradiated with a UV LED (365 nm, 76 mW cm−2) at a distance of 2.5 cm for 2 minutes. The acetate sheet was carefully removed. Excess monomer/initiator solution was removed with a medical tissue, and the cured hydrogel shape washed 3 times with ultrapure water then dried again with medical tissue. 200 μL of the 7.5% w/v monomer/initiator solution was added to the mould and carefully covered with a second glass slide. The sample was irradiated again for a further 2 minutes then removed from the mould prior to mechanical testing.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio with the photoinitiator solution, then 50 μL of the mixture added to the mould. The solution was carefully covered with a glass slide, sealed with binder clips, then the apparatus was inverted then irradiated with a UV LED (365 nm, 76 mW cm−2) at a distance of 2.5 cm for 2 minutes. The transparency was carefully removed. Excess monomer/initiator solution was removed with a medical tissue, and the cured hydrogel shape washed 3 times with ultrapure water then dried with medical tissue. After removal from the mould, the gel was stored in water prior to and during indentation.
1 volume ratio with the photoinitiator solution, then 50 μL of the mixture added to the mould. The solution was carefully covered with a glass slide, sealed with binder clips, then the apparatus was inverted then irradiated with a UV LED (365 nm, 76 mW cm−2) at a distance of 2.5 cm for 2 minutes. The transparency was carefully removed. Excess monomer/initiator solution was removed with a medical tissue, and the cured hydrogel shape washed 3 times with ultrapure water then dried with medical tissue. After removal from the mould, the gel was stored in water prior to and during indentation.
Results and discussion
Data acquisition and analysis
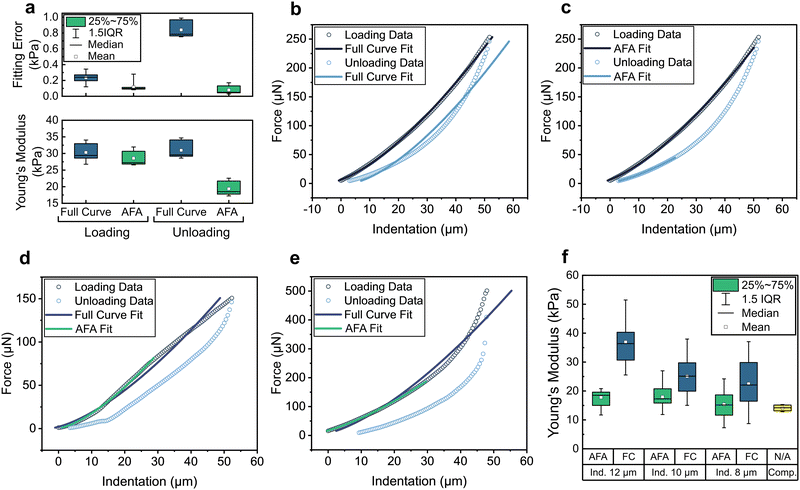
To develop our analysis approach, we investigated the mechanical properties of several model hydrogel systems, particularly the well-studied gels formed by agarose.35,36 We used a microindenter with a force sensor based on MEMS technology to acquire force-displacement curves from the materials tested.29 To minimise plastic deformation and penetration of the gels, we used large spherical probes with diameters of 250–300 μm.37,38 The raw indentation data obtained comprised time-indexed text data of recorded parameters including probe position and force.To process and analyse these data we developed a python-based application called “ALIAS”. The overall process applied by this application is summarised in Fig. 1a. A baseline is firstly determined by linear regression of a user-defined portion (typically 10% to 20%) of the loading data, then subtracted from both loading and unloading curves (Fig. 1b and c). The point of contact is then determined as the position at which the force measured differs from the baseline by the standard deviation of the baseline data multiplied by a user-defined factor (usually between 10–30). The corrected indentation data are then fit to an appropriate contact mechanics model, giving both material properties and accompanying fitting errors (presented as the RMSD, i.e. the standard deviation of residuals). Initially, the entire indentation curve is fit according to the chosen model (Fig. 1d), and with an input value of the Poisson's ratio for the sample (assumed here to be 0.5 for soft hydrogel materials), values for the Young's modulus (YFC) and associated fitting error (ErFC) are determined. An alternative fitting approach, termed the “automatic fitting algorithm” (AFA), is then applied to the same indentation data to minimise the fitting error in indentation curves that exhibit problems (sample fracture, plastic deformation etc.) by automatic selection of the data which best comply with the chosen model. With this AFA method, an indentation curve segment that starts from the point of contact and includes a user-defined number of datapoints is fit to the chosen model. Subsequently, the same number of user-defined datapoints is added to the first indentation curve segment and the new, longer segment is fit. This iterative fitting process continues until the entire indentation curve has been fitted (Fig. 1e). Each fitting process provides a value for the Young's modulus (Yn) and a fitting error (Ern). The algorithm then selects the indentation curve segment which results in the smallest fitting error (ErAFA), and provides the corresponding Young's modulus value (YAFA) (Fig. 1f). From each fitting method, a value for the Young's modulus, and other model dependent parameters including the adhesion force and interfacial energy, are output with their corresponding fitting errors.
It should be noted, however, that given only elastic contact mechanics models are incorporated within this application, this analysis method may only be applied to materials exhibiting predominantly elastic responses to applied strain. For example, hydrogels and other hydrated materials often display viscoelastic or poroelastic behaviour.39 These phenomena may result in a significant dependence of mechanical properties on the strain rate applied, unusual indentation curves, and other experimental irregularities.40,41 Reliable analysis of such materials via indentation measurements requires the use of appropriate viscoelastic models.42
Comparison of fitting methodologies
To test the suitability of our fitting algorithm for the automated analysis of microindentation data, we initially carried out measurements of 2% agarose hydrogels. Indentation data were obtained from this hydrogel system using experimental parameters which resulted in predominantly elastic deformation. Measurements were made in 25 different locations within a single hydrogel sample to enable comparison of the distribution of Young's moduli (Y) and fitting errors (Er) values obtained. Fig. 2a shows a summary of Y and corresponding Er obtained by applying either full curve or AFA fitting to these data. When comparing loading and unloading data, although fitting the entire curve results in similar Y values for each dataset, fitting errors obtained from unloading data are approximately 4-fold greater than those from the loading data. The cause of this discrepancy is clear when examining typical indentation curves, as shown in Fig. 2b; although the best fit for both sets of data is a curve of similar overall trajectory, unloading data deviate significantly from the model applied due to the inelastic response of the material, resulting in larger error values. Although smaller errors can be obtained from the unloading data by applying the AFA, this method results in only an unrepresentatively small portion of data being selected and consequently to much smaller Y values (Fig. 2c). Although fitting loading data is clearly preferable, it is worth noting that should this data be unusable, full curve fitting of the unloading data may provide a comparable modulus value.For modulus values determined from loading data, fitting both the entire curve, or the AFA-selected portion of data both yield similar modulus values. Examining typical curves obtained under optimal indentation conditions, as shown in Fig. 2c, reveals the algorithm selects almost the entirety of the data in most cases. This behaviour indicates data which largely comply with the chosen contact mechanics model, and therefore suitably selected experimental parameters (i.e., minimal non-elastic deformation of the sample). In these cases, the AFA gives modulus values that are not significantly different to those obtained from fitting the entire curve, albeit with lower fitting errors.
However, in cases where indentation data are imperfect, the AFA analysis approach appears to be advantageous. Two examples of this behaviour are shown in Fig. 2d and e. Fig. 2d shows a sample which displays plastic deformation in addition to elasticity, as evidenced by a transition from positive to negative curvature in the force displacement plot.43 In this case fitting the entire data gives an underestimate of the Y (YFC: 19.9 ± 0.3 kPa) but fitting with the AFA allows for the automatic selection of the elastic deformation regime (YAFA: 25.2 ± 0.2 kPa). Conversely, Fig. 2e shows the indentation of an agarose hydrogel with a thickness of approximately 500 μm tested on a glass substrate. In this case, a sharp increase in the force required to indent the gel is observed partway through indentation, a result of the influence of the substantially harder underlying substrate. The full curve fit results in an overestimate of the material's Young's modulus (YFC: 54.7 ± 1.3 kPa), whereas the AFA is able to automatically select the portion of data without significant effect from the substrate (YAFA: 40.9 ± 0.1 kPa).
To further demonstrate this substrate-dependent behaviour and the value of the fitting algorithm, we carried out measurements with systematic errors in the indentation parameters used, and compared both fitting methods. Specifically, Fig. 2f shows Y values from fitting curves obtained by indenting hydrogel (polyacrylamide 7.5%) thin films (150–200 μm thickness, covalently adhered to glass cover slips) to a range of depths, from approximately 8 to 12 μm. To enable meaningful comparison, 25 measurements at different locations were made at each indentation depth. Like the previous example (Fig. 2e), a significant influence of the underlying substrate is seen, with strong dependence of the obtained Y value on the depth of indentation when full indentation curves were analysed. Greater depth resulted in a larger contribution from the stiffer glass substrate and therefore a higher Y, with mean values ranging from 36–22 kPa. Conversely, when analysed using the AFA, comparable Y values of between 15–17 kPa were obtained regardless of indentation depth. Values obtained using the AFA were also notably more narrowly distributed than those from full curve fitting. To validate the obtained moduli from the algorithm, bulk samples with the same hydrogel composition were also analysed by uniaxial compression testing. Analysis of stress–strain curves from these samples (shown in Fig. S1, ESI†) resulted in a Y value (mean 14.1 kPa, yellow box) in excellent agreement with those generated by the fitting algorithm from thin-film sample data.
Overall, it appears the AFA approach offers several advantages over fitting the entirety of the data and should allow for a robust method to automatically analyse large volumes of indentation data, given such measurements often yield nonideal curves in practice. This algorithm is particularly advantageous when measuring heterogeneous materials where one set of experimental indentation parameters are often unsuitable for all mechanical domains.
Optimisation of experimental parameters for indentation of agarose hydrogels
In order to test the suitability of our experimental setup to analyse hydrogel materials, we carried out further optimisation studies with 2% w/v agarose hydrogels. In terms of experimental variables, we investigated: (1) the effects of measurements carried out either in liquid medium or air; (2) the predominant sources of error within these measurements; and (3) the effect of various indentation parameters on the Y values obtained. To avoid influencing data analysis with the fitting algorithm described, in this section we consider only the Y values obtained by fitting the entire indentation curves.Hydrogels are comprised largely of water and therefore should ideally be measured under equilibrium conditions (i.e., fully submerged in aqueous media). However, capillary forces between the liquid medium and probe may give rise to difficulties in detecting the contact point and other potential issues.44 These practicalities have led to a number of alternative approaches being explored, including measuring samples shortly after removal from aqueous media,45 or using hydrated foams or alternative means to maintain sample hydration state.46 Modulus values obtained by indenting 2% w/v agarose hydrogels either submerged in or directly after removal from an aqueous medium are shown in Fig. 3a, along with their corresponding fitting errors. The data show that measurements carried out in air result in substantially higher Y values and fitting errors than those acquired in aqueous media. This can be attributed to the fact that indentation curves acquired in air display a marked jump to contact feature compared to indentation curves acquired in aqueous media, which instead display a typical Hertzian trend (see Fig S2, ESI†). In particular, the jump to contact feature obscures the initial part of the indentation curve leading therefore to steeper fitted curves, higher moduli and greater fitting errors. Moreover, the broader moduli distribution observed for samples measured in air can be ascribed to different local hydration states of the hydrogel due to partial and inhomogeneous drying of the surface. Overall, it is clear that for these hydrogels, measurements conducted in aqueous media are highly preferable to measurements in air. All other measurements presented in this study are therefore carried out on hydrogels immersed in aqueous media.
To compare sources of error within microindentation measurements of hydrogels, two series of measurements were obtained from the same agarose sample; firstly, sets of 8 repeated measurements were carried out in 3 different locations within the sample, and secondly, single measurements were carried out in 24 different locations within the sample. Data from these experiments are shown in Fig. 3b, and allow comparison between three sources of error: (1) the fitting error from the chosen model (the standard deviation of residuals from the fit or RMSE, shown by the green error bars); (2) error caused by non-elastic deformation upon repeated measurements in one position (shown by the variation in grey datapoints); and (3) error due to inhomogeneity in the sample demonstrated by measurements in different positions (shown by the blue datapoints).
Mean modulus and error values for these comparisons are shown in Fig. 3c. Fitting errors are comparatively small with a mean value of ±0.2 kPa across all measurements of the agarose hydrogel tested. A monotonic increase and larger differences in modulus (Fig. 3b) are observed during repeated measurements in a single location, typically attributed to non-elastic deformation of the material, with a mean standard deviation of ±0.7 kPa for the 8 measurements conducted in each of 3 positions. Finally, error due to sample inhomogeneity is substantially larger, with a standard deviation of ±2.4 kPa determined for the 24 locations measured. Given that by far the greatest source of error within these measurements is the inhomogeneous nature of the sample, in order to achieve a reliable modulus value for hydrogel samples, microindentation measurement procedures should be designed to maximise the number of different locations tested within a sample.
The parameters chosen for indentation (depth, rate) have been often reported to have significant effects on modulus values obtained from both nanoscale and microscale indentation measurements.26,47 To investigate how these factors impacted modulus values obtained with the described experimental setup, we carried out further analysis of agarose hydrogels whilst systematically varying the depth and rate of indentation. Data from these investigations are shown in Fig. 3d–f. When considering the rate of indentation, we investigated both actuation methods possible with our instrument: a piezoscanner capable of continuous sample movement over short (<50 μm) distances, and a stick-slip actuator capable of stepped probe movement over greater distances (up to 7 mm). Indentation rate with the piezoscanner is controlled by a single variable (indentation speed), however with the stick-slip actuator it is also affected by an additional parameter (wait time) governing the delay between actuation increments.
With a fixed indentation rate, indentation depth had a considerable impact on the modulus values obtained, as shown in Fig. 3d. At the shallowest depth of 12.5 μm, significantly higher moduli (mean value of 25.5 kPa) were observed than at greater depths (mean values 18–20 kPa), accompanied by a broadening of the distribution of values and larger fitting errors. At the remaining indentation depths of between 25 and 100 μm, neither modulus values nor fitting errors change substantially. These observations likely indicate a difference in the hydrogel composition at the interface between liquid medium and gel, where effects such as surface roughness may lead to less consistent measurements. Given the apparent plateau at depths greater than 25 μm, measurements should be conducted with an indentation depth that is not below this value.
Data acquired using the piezoscanner operating at different indentation speeds are presented in Fig. 3e. Modulus values obtained in this mode show significant dependence on the indentation speed, with an increase of approximately 12 kPa from 2.5 to 40 μm s−1. Such behaviour is typical in indentation or AFM testing of hydrogels and is indicative of a viscoelastic material response,48–50 therefore necessitating careful selection and reporting of indentation parameters. By contrast, indentation measurements of the same sample to identical depth (30 μm) made using the stick-slip actuator (Fig. 3f) showed no dependence of Young's moduli on indentation speed, with values at all speeds comparable to those obtained at 2.5 μm s−1 with the piezoscanner. This apparent lack of viscoelastic behaviour is likely a consequence of the stepped actuation mode, where viscoelastic relaxation may occur between actuation increments. When using the stick-slip actuator, independent changes to the wait time parameter (Fig. S3, ESI†) resulted in no obvious trends in the mean moduli obtained. At the shortest wait time (0.02 s) a broader distribution was observed, which we attribute to an increase in experimental noise, however, using wait times greater than 0.08 s both moduli and fitting errors were almost identical.
To assess the generality of these findings, similar measurements were made on a synthetic PEGDA hydrogel (Fig. S4, ESI†). Comparable trends were observed, with a plateau in modulus observed at indentation depths greater than 50 μm, and indentation speed showing no clear effect on moduli. Overall, we therefore suggest that for this experimental setup, a depth of approximately 50 μm should be used as a guideline for indentation measurements. Utilising a stepped actuation mode, parameters affecting indentation speed have only limited effect on modulus values and should therefore be chosen largely on experimental practicalities: slower indentation yields data with less noise; however faster indentation may be preferable when many measurements are required.
Young's moduli of other hydrogel systems
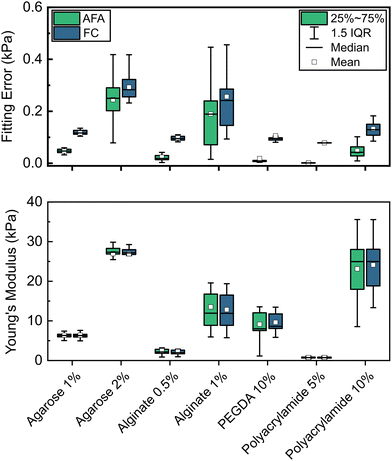
To explore the general applicability of the instrumental setup and analytical method described we further applied our approach to a broad range of common hydrogel systems. In all cases, we carried out indentation measurements following the optimised experimental protocol determined for agarose hydrogels (indentation depth of approximately 50 μm, using the stick-slip actuator at a speed of 10 μm s−1 with a 0.1 s wait time) and automatically analysed the raw data using the ALIAS application.Moduli and corresponding errors obtained by analysing loading data for each hydrogel using both fitting methods (full curve and AFA) are shown in Fig. 4. For all hydrogel systems studied, Y values obtained by both methods are highly comparable. This similarity indicates that force-displacement curves acquired are likely fitted well by the JKR model, with fitting of partial curves not significantly altering calculated moduli values. In all cases, fitting errors are reduced substantially with the AFA fit compared with the corresponding full curve fit. Typical indentation data for each hydrogel system, along with the corresponding fitting by both methods are presented in Fig. S5–S11 (ESI†).
To validate our experimental and analytical approach, we carried out additional uniaxial compression testing on bulk samples of 2% w/v agarose hydrogels. Data obtained from these tests are shown in Fig. S12 (ESI†), and show a reasonably good match between both measurement methods with mean (±SD) values of 27 ± 3 and 40 ± 5 kPa for indentation (AFA) and compression tests, respectively. We believe the modest discrepancies observed between methods are likely a result of different cooling rates during gel formation due to the notably different sample size and geometry in each method. Such thermal effects have been demonstrated have significantly impact the final properties of agarose hydrogels.51 For all materials studied, we also compare our modulus values to those reported in the literature for each hydrogel system.4,35,51–73 This comparison is summarised in Fig. 5. The literature values shown are collected using a wide range of techniques including both bulk measurements such as compression or tensile tests, rheology, macroscale indentation, and AFM indentation. Moreover, given differences in measurement geometry, analysis, and assumptions such as the Poisson's ratio of materials, no attempt is made to correct individual reported values, with values presented as originally reported. As such, reported modulus values vary significantly, in some cases spanning more than an order of magnitude for the same hydrogel system. Differences in materials (e.g., molecular weights, purity, etc., of polymers used), preparation methods, and hydration states of the hydrogels during measurement are also likely contributing factors to the wide range of moduli observed for this class of materials. Nevertheless, modulus values obtained by microindentation and analysed using the AFA approach are generally in strong agreement with literature values for comparable hydrogel systems. Importantly, the relationships between the moduli of different concentrations of hydrogels (e.g., 1 and 2% w/v agarose) are highly consistent with those reported elsewhere.
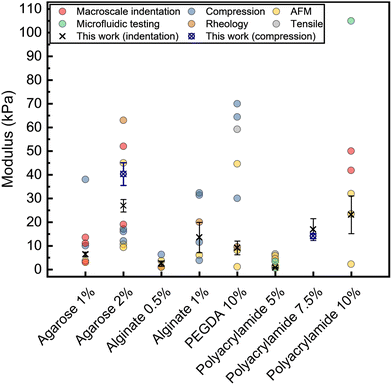 | ||
| Fig. 5 Comparison of the mean Young's modulus values obtained in this work (indentation with AFA, and uniaxial compression, error bars indicate standard deviation) for common hydrogels with moduli reported for comparable hydrogels in the literature. All values are presented as given in the original sources. A full list of the literature modulus values included, along with additional experimental details, is provided in Table S1 (ESI†). | ||
2D mapping of hydrogel mechanical properties
As demonstrated by the high degree of variability in modulus at different measurement locations, the mechanical properties of hydrogels are highly heterogeneous on multiple length scales. Quantification of this heterogeneity is crucial to aid our understanding of these materials, and is important when considering their behaviour at biological interfaces.17 Furthermore, techniques applicable to hydrogels are likely also able to map the mechanical properties of soft biological systems, and could, for example, be used to differentiate different cellular regions or to distinguish cancerous and normal cells.74 Although nanoscale mapping of soft material mechanical properties is commonplace through the use of AFM measurements,75–78 investigations of their heterogeneity on larger length scales remains uncommon. Boots et al. recently demonstrated the instrumented microindentation of patterned PDMS samples, thereby showing how the moduli varied over a range of approximately 2 to 16 MPa across mm-scale material features.79 Subsequent work by the same authors sought to deconvolute mechanical behaviour of individual domains within such measurements.80 However, mechanical mapping of soft hydrogel materials (with kPa range moduli) over macroscopic length scales remains challenging.To further test the capacity of our experimental setup and fitting algorithm to map large areas of soft materials and process large volumes of data, we carried out mapping indentation measurements covering macroscopic areas (up to 1 cm2) of hydrogel systems. Hydrogels with spatial patterns of mechanical properties were obtained by a multi-step photolithographic approach detailed in the Materials and methods section, and comprised of distinct regions of differing concentrations of polymerised PEGDA. Indentation data were acquired by automated array measurements of the hydrogels using the inbuilt indenter software package. Measurements were conducted with the gel immersed in water throughout, and an indentation depth of 50 μm or greater. However, given the negligible effects of indentation rate on the modulus values, measurements were conducted with a higher indentation speed (50 μm s−1) and a shorter wait time (0.05 s), allowing the acquisition of data at a rate of approximately 100 indentation curves per hour. Using the ALIAS application, data analysis was considerably faster, with a personal computer (3.2 GHz processor, 8 GB RAM) capable of analysing 2000+ curves per hour.
Data obtained by array measurements with different sampling intervals (10 × 10, 20 × 20, and 40 × 40) of the same patterned PEGDA hydrogel (with dimensions of 5 × 5 mm) are shown in Fig. 6a. In all cases, a core area with higher Y is clearly visible, corresponding to a triangular region of 15% w/v PEGDA, surrounded by a lower Young's modulus region of 7.5% w/v PEGDA. Data obtained from these measurements may be further analysed to determine the mechanical properties of individual constituents within a composite material. By this method Young's moduli of 3.8 and 41.9 kPa were determined for 7.5 and 15% w/v PEGDA, respectively, values consistent with the modulus of 9.1 kPa described for the equivalent 10% w/v hydrogel.
The spatial resolution attainable with these measurements is limited largely by the size of the spherical tip attached to the probe. For example, applying a common approximation for contact radius ( where a is the contact radius, d the indentation depth, and R the probe radius),81 a probe with a radius of 150 μm indented 50 μm into a sample results in a contact area with a radius of approximately 120 μm. Although a clear improvement in the resolution of the pattern is visible upon increasing the sampling coverage from 10 × 10 to 40 × 40, individual features smaller than the contact area are likely to be overlooked. The benefit of the larger contact area, however, is that the mechanical properties of materials can be reliably measured over macroscopic areas. Typical mechanical property mapping with an AFM is limited by the scan range of commercial instruments to regions smaller than 80 × 80 μm.22 Furthermore, the vertical movement range may be < 10 μm, leading to data acquisition issues for uneven biological samples.82 With the larger experimental setup and probe applied here, samples with lateral dimensions of multiple centimetres, and height fluctuations of hundreds of micrometres can be conveniently mapped.
where a is the contact radius, d the indentation depth, and R the probe radius),81 a probe with a radius of 150 μm indented 50 μm into a sample results in a contact area with a radius of approximately 120 μm. Although a clear improvement in the resolution of the pattern is visible upon increasing the sampling coverage from 10 × 10 to 40 × 40, individual features smaller than the contact area are likely to be overlooked. The benefit of the larger contact area, however, is that the mechanical properties of materials can be reliably measured over macroscopic areas. Typical mechanical property mapping with an AFM is limited by the scan range of commercial instruments to regions smaller than 80 × 80 μm.22 Furthermore, the vertical movement range may be < 10 μm, leading to data acquisition issues for uneven biological samples.82 With the larger experimental setup and probe applied here, samples with lateral dimensions of multiple centimetres, and height fluctuations of hundreds of micrometres can be conveniently mapped.
Finally, we investigated the minimum difference in Young's moduli that could be reliably differentiated with the experimental and analytical approach described. A hydrogel with a gradient in stiffness was prepared from a PEGDA precursor by irradiation through a mask with a gradient of translucency. From the entire array measurement of this gel (shown in Fig. S13, ESI†), a central region with a linear gradient in Y was selected. Y from this selection are presented in Fig. 6c, as a function of distance along the direction parallel with the stiffness gradient. At each distance along this axis, modulus values vary considerably, leading to substantial overlap in the distributions of adjacent datasets. By applying a linear fit to the entire data in this figure, the RMSE (standard deviation of the residuals) may be obtained, enabling quantification of variability in the modulus values. The fitted value ±3 SD should encompass 99.7% of any individual datapoints, and is indicated by the corresponding prediction bands in Fig. 6c. A difference of 6 SD between the moduli of two materials should therefore be sufficient to enable unequivocal differentiation.83 From the dataset studied, a difference of 3.6 kPa should be adequate to allow this distinction. Although this analysis does not provide a universal Y resolution limit, as such a property would depend on many factors including the heterogeneity and stiffness of the materials in question, it should enable a reasonable approximation for similar hydrogel materials.
Conclusions
We present a comprehensive study on the application of microindentation measurements with a MEMS-based force sensor to study hydrogel materials utilising a newly developed algorithm to enhance the data analysis process. This experimental technique appears to be well suited to the investigation of these soft materials and results in Young's modulus values which are highly comparable with both values determined by compression measurements of the same gels and those reported in the literature for a wide range of natural and synthetic hydrogel systems. Significantly, provided a sufficient indentation depth is reached, modulus values obtained appear to be largely unaffected by the rate of indentation, giving greater reliability to values determined. We attribute this behaviour to the stepped operating mode employed by the stick-slip actuator in our experimental setup, which minimises viscoelastic effects.The automatic fitting algorithm developed was found to be a valuable alternative to current fitting methodologies for elastic contact mechanics models. The stepwise nature of the fitting process applied by this algorithm is highly complementary to indentation measurements, with many typical issues in this class of experiments arising from indenting too far into a sample. Data from measurements exhibiting these complications (including influence of the underlying substrate, and non-elastic deformation of the sample) may be successfully analysed by applying the algorithm described, giving modulus values automatically determined from only the elastic section of each curve. For example, the AFA is demonstrated to extract Young's moduli in excellent agreement with independent compression measurements from hydrogel thin films, where full curve fitting gives substantial overestimates. Overall, this analysis approach facilitates both the acquisition of indentation data, by limiting the effect of imperfect experimental parameters on the modulus values obtained, and its analysis, by allowing a greater degree of automation.
We demonstrate the applicability of this methodology to process large volumes of indentation data by conducting and analysing mechanical property mapping of soft materials. Although inherently lower in spatial resolution than comparable AFM studies, these measurements allow the acquisition of data over far greater areas, spanning multiple centimetres in length and width, offering a unique perspective on the microscale and macroscale heterogeneity of the mechanical properties of soft materials. The methodologies described here will enable better understanding of macroscopic soft materials or biological and biomimetic systems, including tissues and organs, providing mechanical information not attainable from measuring smaller structures in isolation, or from bulk characterisation methods. High-throughput automation could also enable the collection of large datasets, providing opportunities for the implementation of artificial intelligence methods in micromechanical analysis.
Author contributions
Henry E. Symons: conceptualization, formal analysis, investigation, methodology, validation, visualization, writing – original draft, review and editing; Agostino Galanti: investigation, validation, writing – review and editing; Joseph C. Surmon: investigation, validation; Richard S. Trask: validation of compression data. Sebastien Rochat: project administration, writing – review and editing; Pierangelo Gobbo: conceptualization, funding acquisition, formal analysis, project administration, software, supervision, writing – original draft, review and editing.Code availability
The code that was developed to undertake the analysis presented in this work is provided in GitHub (“https://github.com/PierangeloGobbo1986/ALIAS”), along with documentation on installation and use, and an example dataset.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the EPSRC New Investigator Award (grant ref: EP/T01508X/1). Joseph C. Surmon acknowledges the support of the EPSRC (Grant No. EP/L0 16028/1). Agostino Galanti acknowledges the support of the European Commission (Marie Skłodowska Curie IF “SAPTiMeC; GAN: 101023978”). Additionally, the authors thank Dr Felix Beyeler and FemtoTools for advising on the collection and analysis of indentation data, and Prof. Orfeo Sbaizero (University of Trieste) for useful discussions.Notes and references
- J. L. Drury and D. J. Mooney, Biomaterials, 2003, 24, 4337–4351 CrossRef CAS PubMed.
- S. O. Ebhodaghe, Int. J. Polym. Mater., 2022, 71, 155–172 CrossRef CAS.
- K. Dey, E. Roca, G. Ramorino and L. Sartore, Biomater. Sci., 2020, 8, 7033–7081 RSC.
- L. M. Kock, J. Geraedts, K. Ito and C. C. van Donkelaar, Tissue Eng., Part A, 2013, 19, 1621–1631 CrossRef CAS PubMed.
- M. Zanon, A. Chiappone, N. Garino, M. Canta, F. Frascella, M. Hakkarainen, C. F. Pirri and M. Sangermano, Mater. Adv., 2022, 3, 514–525 RSC.
- L. J. Macdougall, M. M. Perez-Madrigal, J. E. Shaw, J. C. Worch, C. Sammon, S. M. Richardson and A. P. Dove, Angew. Chem., Int. Ed., 2021, 60, 25856–25864 CrossRef CAS PubMed.
- Y. Lee, W. J. Song and J. Y. Sun, Mater. Today Phys., 2020, 15, 100258 CrossRef.
- S. H. Kim, J. H. Jeong, H. Shim, H. C. Woo, K. B. C. Imani, J. Yoon, J. H. Jeong and M. H. Kim, Smart Mater. Struct., 2021, 30, 075014 CrossRef CAS.
- C. C. Li, L. L. Ouyang, J. P. Armstrong and M. M. Stevens, Trends Biotechnol., 2021, 39, 150–164 CrossRef CAS PubMed.
- C. Maiti, K. B. C. Imani and J. Yoon, ChemPlusChem, 2021, 86, 601–611 CrossRef CAS PubMed.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif, J. C. Weaver, N. Huebsch, H. P. Lee, E. Lippens, G. N. Duda and D. J. Mooney, Nat. Mater., 2016, 15, 326–334 CrossRef CAS PubMed.
- C. T. Mierke, Rep. Prog. Phys., 2019, 82, 064602 CrossRef CAS PubMed.
- Y. S. Hao, S. O. O. Cheng, Y. Tanaka, Y. Hosokawa, Y. Yalikun and M. Li, Biotechnol. Adv., 2020, 45, 107648 CrossRef CAS PubMed.
- W. H. Bu, Y. H. Wu, A. M. Ghaemmaghami, H. C. Sun and A. Mata, Regener. Biomater., 2022, 9, rbac009 CrossRef PubMed.
- J. L. Li, X. Jia and L. J. Yin, Food. Rev. Int., 2021, 37, 313–372 CrossRef CAS.
- S. L. Sridhar, M. C. Schneider, S. Chu, G. de Roucy, S. J. Bryant and F. J. Vernerey, Soft Matter, 2017, 13, 4841–4855 RSC.
- L. W. Zhang, L. Fu, X. Zhang, L. X. Chen, Q. Cai and X. P. Yang, Biomater. Sci., 2021, 9, 1547–1573 RSC.
- M. L. Oyen, Exp. Techniques, 2013, 37, 73–87 CrossRef.
- C. R. Jin and D. M. Ebenstein, J. Mater. Res., 2017, 32, 435–450 CrossRef CAS.
- S. V. Kontomaris and A. Malamou, Mater. Res. Express, 2020, 7, 033001 CrossRef CAS.
- L. Qian and H. W. Zhao, Micromachines, 2018, 9, 654 CrossRef PubMed.
- O. H. Olubowale, S. Biswas, G. Azom, B. L. Prather, S. D. Owoso, K. C. Rinee, K. Marroquin, K. A. Gates, M. B. Chambers, A. Xu and J. C. Garno, ACS Omega, 2021, 6, 25860–25875 CrossRef CAS PubMed.
- M. D. A. Norman, S. A. Ferreira, G. M. Jowett, L. Bozec and E. Gentleman, Nat. Protoc., 2021, 16, 2418–2449 CrossRef CAS PubMed.
- N. Guz, M. Dokukin, V. Kalaparthi and I. Sokolov, Biophys. J., 2014, 107, 564–575 CrossRef CAS PubMed.
- W. Megone, N. Roohpour and J. E. Gautrot, Sci. Rep., 2018, 8, 6780 CrossRef CAS PubMed.
- S. Huth, S. Sindt and C. Selhuber-Unkel, PLoS One, 2019, 14, e0220281 CrossRef CAS PubMed.
- D. C. Lin, E. K. Dimitriadis and F. Horkay, J. Biomech. Eng., 2007, 129, 430–440 CrossRef PubMed.
- M. Galluzzi, G. L. Tang, C. S. Biswas, J. L. Zhao, S. G. Chen and F. J. Stadler, Nat. Commun., 2018, 9, 3584 CrossRef PubMed.
- Y. Sun, S. N. Fry, D. P. Potasek, D. J. Bell and B. J. Nelson, J. Microelectromech. Syst., 2005, 14, 4–11 Search PubMed.
- D. M. Kingsley, C. H. McCleery, C. D. L. Johnson, M. T. K. Bramson, D. Rende, R. J. Gilbert and D. T. Corr, J. Mech. Behav. Biomed. Mater., 2019, 92, 152–161 CrossRef CAS PubMed.
- K. L. Johnson, Contact mechanics, Cambridge University Press, Cambridge [Cambridgeshire]; New York, 1987 Search PubMed.
- K. L. Johnson, K. Kendall, A. D. Roberts and D. Tabor, Proc. R. Soc. A., 1971, 324, 301–313 CAS.
- D. C. Lin, E. K. Dmitriadis and F. Horkay, J. Biomech. Eng., 2007, 129, 904–912 CrossRef PubMed.
- H. Garoff and W. Ansorge, Anal. Biochem., 1981, 115, 450–457 CrossRef CAS PubMed.
- C. T. Buckley, S. D. Thorpe, F. J. O'Brien, A. J. Robinson and D. J. Kelly, J. Mech. Behav. Biomed. Mater., 2009, 2, 512–521 CrossRef PubMed.
- P. Zarrintaj, S. Manouchehri, Z. Ahmadi, M. R. Saeb, A. M. Urbanska, D. L. Kaplan and M. Mozafari, Carbohydr. Polym., 2018, 187, 66–84 CrossRef CAS PubMed.
- M. L. Oyen, Philos. Mag., 2006, 86, 5625–5641 CrossRef CAS.
- N. Rodriguez-Florez, M. L. Oyen and S. J. Shefelbine, J. Mech. Behav. Biomed. Mater., 2013, 18, 90–99 CrossRef PubMed.
- Q. M. Wang, A. C. Mohan, M. L. Oyen and X. H. Zhao, Acta Mech. Solida Sin., 2014, 30, 20–27 CrossRef CAS.
- J. G. Sanchez, F. M. Espinosa, R. Miguez and R. Garcia, Nanoscale, 2021, 13, 16339–16348 RSC.
- A. Rubiano, C. Galitz and C. S. Simmons, Tissue Eng., Part C, 2019, 25, 619–629 CrossRef PubMed.
- Y. M. Efremov, W. H. Wang, S. D. Hardy, R. L. Geahlen and A. Raman, Sci. Rep., 2017, 7, 1541 CrossRef PubMed.
- Z. Song and K. Komvopoulos, Mech. Mater., 2013, 61, 91–100 CrossRef.
- D. M. Ebenstein, J. Mater. Res., 2011, 26, 1026–1035 CrossRef CAS.
- M. L. Oyen, Curr. Opin. Solid State Mater. Sci., 2015, 19, 317–323 CrossRef.
- D. M. Ebenstein and L. A. Pruitt, J. Biomed. Mater. Res., Part A, 2004, 69a, 222–232 CrossRef CAS PubMed.
- R. Long, M. S. Hall, M. M. Wu and C. Y. Hui, Biophys. J., 2011, 101, 643–650 CrossRef CAS PubMed.
- L. Cacopardo, N. Guazzelli, R. Nossa, G. Mattei and A. Ahluwalia, J. Mech. Behav. Biomed. Mater., 2019, 89, 162–167 CrossRef CAS PubMed.
- J. J. Roberts, A. Earnshaw, V. L. Ferguson and S. J. Bryant, J. Biomed. Mater. Res., Part B, 2011, 99b, 158–169 CrossRef CAS PubMed.
- Q. S. Chen, B. Suki and K. N. An, J. Biomech. Eng., 2004, 126, 666–671 CrossRef PubMed.
- P. Aymard, D. R. Martin, K. Plucknett, T. J. Foster, A. H. Clark and I. T. Norton, Biopolymers, 2001, 59, 131–144 CrossRef CAS PubMed.
- V. Normand, D. L. Lootens, E. Amici, K. P. Plucknett and P. Aymard, Biomacromolecules, 2000, 1, 730–738 CrossRef CAS PubMed.
- M. Ahearne, Y. Yang, A. J. El Haj, K. Y. Then and K. K. Liu, J. R. Soc., Interface, 2005, 2, 455–463 CrossRef CAS PubMed.
- D. G. T. Strange and M. L. Oyen, J. Mech. Behav. Biomed. Mater., 2012, 11, 16–26 CrossRef CAS PubMed.
- C. D. Markert, X. Y. Guo, A. Skardal, Z. Wang, S. Bharadwaj, Y. Y. Zhang, K. Bonin and M. Guthold, J. Mech. Behav. Biomed. Mater., 2013, 27, 115–127 CrossRef CAS PubMed.
- M. Salerno, S. Dante, N. Patra and A. Diaspro, Microsc. Res. Tech., 2010, 73, 982–990 CAS.
- S. Park, K. D. Costa, G. A. Ateshian and K. S. Hong, Proc. Inst. Mech. Eng. H, 2009, 223, 339–347 CrossRef CAS PubMed.
- R. L. Mauck, M. A. Soltz, C. C. B. Wang, D. D. Wong, P. H. G. Chao, W. B. Valhmu, C. T. Hung and G. A. Ateshian, J. Biomech. Eng., 2000, 122, 252–260 CrossRef CAS PubMed.
- J. Candiello, S. S. Singh, K. Task, P. N. Kumta and I. Banerjee, J. Biol. Eng., 2013, 7, 9 CrossRef CAS PubMed.
- M. O. Dalheim, L. A. Omtvedt, I. M. Bjorge, A. Akbarzadeh, J. F. Mano, F. L. Aachmann and B. L. Strand, Gels, 2019, 5, 23 CrossRef CAS PubMed.
- O. Aarstad, E. B. Heggset, I. S. Pedersen, S. H. Bjornoy, K. Syverud and B. L. Strand, Polymers, 2017, 9, 378 CrossRef PubMed.
- S. Lin, N. Sangaj, T. Razafiarison, C. Zhang and S. Varghese, Pharm. Res., 2011, 28, 1422–1430 CrossRef CAS PubMed.
- M. Parlato, S. Reichert, N. Barney and W. L. Murphy, Macromol. Biosci., 2014, 14, 687–698 CrossRef CAS PubMed.
- H. M. Liao, D. Munoz-Pinto, X. Qu, Y. P. Hu, M. A. Grunlan and M. S. Hahn, Acta Biomater., 2008, 4, 1161–1171 CrossRef CAS PubMed.
- S. Nemir, H. N. Hayenga and J. L. West, Biotechnol. Bioeng., 2010, 105, 636–644 CrossRef CAS PubMed.
- E. A. Corbin, L. J. Millet, J. H. Pikul, C. L. Johnson, J. G. Georgiadis, W. P. King and R. Bashir, Biomed. Microdevices, 2013, 15, 311–319 CrossRef CAS PubMed.
- K. W. Kolewe, S. Kalasin, M. Shave, J. D. Schiffman and M. M. Santore, ACS Appl. Mater. Interfaces, 2019, 11, 320–330 CrossRef CAS PubMed.
- A. Engler, L. Bacakova, C. Newman, A. Hategan, M. Griffin and D. Discher, Biophys. J., 2004, 86, 617–628 CrossRef CAS PubMed.
- J. R. Tse and A. J. Engler, Curr. Protoc. Cell Biol., 2010, 47, 10.16.11–10.16.16 Search PubMed.
- D. Ambrosi, A. Duperray, V. Peschetola and C. Verdier, J. Math. Biol., 2009, 58, 163–181 CrossRef CAS PubMed.
- J. H. Wen, L. G. Vincent, A. Fuhrmann, Y. S. Choi, K. C. Hribar, H. Taylor-Weiner, S. C. Chen and A. J. Engler, Nat. Mater., 2014, 13, 979–987 CrossRef CAS PubMed.
- L. B. Hazeltine, C. S. Simmons, M. R. Salick, X. Lian, M. G. Badur, W. Han, S. M. Delgado, T. Wakatsuki, W. C. Crone, B. L. Pruitt and S. P. Palecek, Int. J. Cell Biol., 2012, 2012, 508294 Search PubMed.
- H. M. Wyss, T. Franke, E. Mele and D. A. Weitz, Soft Matter, 2010, 6, 4550–4555 RSC.
- M. Lekka, Bionanoscience, 2016, 6, 65–80 CrossRef PubMed.
- B. Xue, D. Tang, X. Wu, Z. Xu, J. Gu, Y. Han, Z. Zhu, M. Qin, X. Zou, W. Wang and Y. Cao, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110961118 CrossRef CAS PubMed.
- A. Rigato, F. Rico, F. Eghiaian, M. Piel and S. Scheuring, ACS Nano, 2015, 9, 5846–5856 CrossRef CAS PubMed.
- Y. M. Efremov, A. I. Shpichka, S. L. Kotova and P. S. Timashev, Soft Matter, 2019, 15, 5455–5463 RSC.
- P. Schon, K. Bagdi, K. Molnar, P. Markus, B. Pukanszky and G. J. Vancso, Eur. Polym. J., 2011, 47, 692–698 CrossRef.
- J. N. M. Boots, R. Fokkink, J. van der Gucht and T. E. Kodgera, Rev. Sci. Instrum., 2019, 90, 015108 CrossRef CAS PubMed.
- J. N. M. Boots, R. Kooi, T. E. Kodger and J. van der Gucht, Front. Phys., 2021, 9, 723768 CrossRef.
- G. Mattei, G. Gruca, N. Rijnveld and A. Ahluwalia, J. Mech. Behav. Biomed. Mater., 2015, 50, 150–159 CrossRef CAS PubMed.
- M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, C. A. Schoenenberger and R. Y. H. Lim, Biophys. J., 2013, 104, 321a–321a CrossRef.
- G. L. Long and J. D. Winefordner, Anal. Chem., 1983, 55, 712A–724A CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00857b |
| This journal is © The Royal Society of Chemistry 2022 |