Shear-induced birefringence in an optically isotropic cubic liquid crystalline phase

Abstract

We report an unusually strong flow-induced birefringence in an optically isotropic cubic phase occurring below the isotropic chiral conglomerate phase formed by a low-molecular-weight polycatenar mesogen. The transition into the birefringent state occurs thresholdless and the induced birefringence is comparable with that observed in polymeric systems. We suggest that the flow-induced deformation of the cubic structure is responsible for the strong rheo-optical response.

---

1 Introduction

Liquid crystals (LCs) are one of the brightest manifestations of self-assembly in molecular and colloidal systems.¹ A series of symmetry-breaking instabilities lead from the isotropic fluid to the nematic, smectic and hexatic phases.¹ Chirality gives LCs new optical properties and response features, which find wide applications in technology. It can be introduced through the chiral structure of the molecules like in cholesterics or as spontaneous symmetry breaking. Spontaneous mirror-symmetry breaking was observed in various systems including phases of bent-shaped mesogens, twist-bend nematic phases (N_TB) formed by bent dimesogens,^2,3 in the optically isotropic dark-conglomerate (DC) phases, as well as in the fluid birefringent nematic (N) and SmC phases formed by bent-core molecules.^4–14 Although the fluid phases with short-range positional and orientational order types are isotropic, some liquid crystalline phases (mesophases) may also behave optically isotropic. Cubic (Cub) and blue phases (BP) are few examples.^15,16

Optical anisotropy and fluidity of the LCs find a broad range of applications in nature, technology and everyday life. Self-assembled liquid crystalline systems are also interesting for electronic semiconductor applications.¹⁷ In recent years, there has been significant progress in adapting columnar LCs as organic semiconductors and perspective applications for photovoltaics. Controlling the spatial organisation of π-conjugated molecules in soft systems is vital for designing new materials with application-relevant, optimised properties.

Swallow-tailed polycatenars are mesogens in which a slight modification of the terminal chains results in a wide variety of soft self-assembled π-stacked structures.^18,19 Among those are synclinic and anticlinic smectics, helical phases, bicontinuous cubic and even chiral isotropic phases. Optically isotropic liquid crystal phases, such as cubic phases, can be attractive in electro-optical device applications for high contrast and low dark levels. They are also interesting from the fundamental point of view since they can exhibit yet unexplored types of order such as tetrahedratic order. Bicontinuous cubic phases (Cub_bi) formed by nonsymmetric polycatenars appear totally dark between crossed polarisers.^19–21 On a slight rotation of one of the analysers from the crossed positions by a small angle, dark and bright areas could be observed only in the case of the chiral Cub_bi. The areas invert their brightness on reversing the direction of rotation of the analysers. This behaviour is compatible with the presence of the triple network Cub_bi phase with space group I23 (Cub_bi/I23^[*^]).^22,23 On the other hand, these chiral domains could not be observed in the case of the achiral gyroid double network cubic phase (Cub/Ia3̄d).^24,25

Cub_bi phases are very interesting for applications requiring fast charge transport due to their 3D network structures.^26–28 Another interesting phase which was also reported for nonsymmetric polycatenar is the chiral isotropic liquid phase assigned as 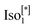phases.^19,21,29,30

In our paper, we study the rheo-optical effect in an optically isotropic bicontinuous cubic phase (Cub_bi) occurring below the metastable of a swallow-shaped polycatenar terminated with three alkoxy chains distributed in 2+1 fashion at both ends of the rod-like aromatic core (compound 1, Fig. 1) described in ref. 30. Shearing in the chiral isotropic phase 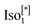triggers a transition to the Cub_bi phase, where a strong birefringence is observed under shearing conditions. The birefringence rapidly relaxes upon suspension of shearing. We attribute this behaviour to the reversible flow-induced deformation of the cubic lattice and the formation of the metastable smectic-like structures. This is a rare example of flow-induced birefringence in a low-molecular-weight system.

Fig. 1 Chemical structure and the mesophase behaviour of the investigated mesogen.

2 Experimental

The liquid crystalline material (1, Fig. 1) used for the current study was synthesized as described earlier.^19,30 Compound 1 exhibits the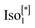 phase in addition to different types of mesophases including the achiral (Cub/Ia3̄d) phase along with the series of smectic phases including SmC, unknown SmC_x, the rare anticlinic smectic C (SmC_a) and the hexatic B phase (HexB) as the lower temperature mesophase.¹⁹

The rheo-optical measurements were done using AxioScope 40 polarising optical microscope (Zeiss GmbH) equipped with a CCD camera Hamamatsu ORCA (Fig. 2). The liquid crystal sample was placed between the two glass plates separated by 100 μm glass spacer. Shearing in this device was achieved by moving the top plate using an electric engine (OWIS GmbH). The shearing speed ranged from 2 μm s⁻¹ to 200 μm s⁻¹. The whole sample was placed in a heating stage INSTEC FS1 (INSTEC, USA). Birefringence was determined from the measurements of the optical transmittance T of the device filled with the LC using:

where d is the sample thickness and λ = 638 nm is the wavelength of the monochromatic light. Linear response of the CCD camera allowed to determine the light intensity from the images. The calibration was made by measuring the dark state and the transmission of the quarter-wave plate between crossed polarisers.

Fig. 2 Experimental setup for measuring the flow-induced birefringence. The sample is placed between a pair of glass slides in heating stage. The observations are made by polarising microscopy.

Freely-suspended films (FSF) in sizes from 1–5 mm were made over a custom-made glass frame placed into the Linkam heating stage LTS 450. Optical observations were made with a polarising microscope (AxioImager Pol, Carl Zeiss, GmbH) equipped with a high-resolution, cooled charge-coupled device camera(AxioCam HR, Carl Zeiss, GmbH) in both transmission and reflection.

3 Results and discussion

The high-temperature isotropic phase exhibits no static or flow-induced birefringence in the experimentally accessible range of shearing rates. A transition to the phase at T ≈ 181 °C is accompanied by an increase in the apparent viscosity. Continuous shearing of an LC droplet in the 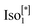phase triggers a transition into phase with a viscous isotropic phase with a slightly opaque appearance. From the comparison of the textural features with the low-temperature phases of the mesogen, we conclude that the 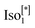transforms into a cubic-like phase (CubX), which is polymorphic to the Cub_bi. Further cooling to the Cub_bi phase of the non-sheared compound does not show any noticeable textural transformation.

A characteristic feature of the CubX phase is the development of birefringence on shearing (Fig. 3 and 4). The birefringence rapidly diminishes when shearing is ceased. No shear-induced birefringence could be observed upon the transition to the high-temperature isotropic phase.

Fig. 3 Flow-induced birefringent textures of a droplet between a pair of glass plates at T = 165 °C for different shear rates [small gamma, Greek, dot above]: (a) [small gamma, Greek, dot above] = 0 s⁻¹; (b) [small gamma, Greek, dot above] = 2 s⁻¹; (c) [small gamma, Greek, dot above] = 20 s⁻¹.

Fig. 4 Flow-induced birefringence Δn([small gamma, Greek, dot above]) measured on cooling at selected temperatures.

Flow-induced birefringence develops in the CubX phase. A simultaneous increase of the birefringence on increasing shear rate occurs without any apparent threshold. The optical transmission of the cell is maximal when the polarisers are at an angle of χ = 45° to the shearing direction, which is typical for the flow-aligning behaviour with the director aligned parallel to the shearing direction (Fig. 2). The transmission grows nearly linearly at low shearing rates at high temperatures and shows a saturation behaviour above 5 s⁻¹ (Fig. 4). As the temperature decreases, the saturation shifts to the lower values of the shear rate [small gamma, Greek, dot above], and the curve Δn([small gamma, Greek, dot above]) becomes steeper (Fig. 5a). The maximum birefringence, as well as the initial slope, are growing with the decreasing temperature (Fig. 5b). The birefringence values are much lower than in the conventional thermotropic nematics but about an order of magnitude higher than in the nematic phase of the worm-like micellular solutions.³¹

Fig. 5 (a) Rheo-optical response coefficient for low shear rate, (b) saturating birefringence as a function of the temperature.

As the temperature approaches the – Cub_bi transition in non-sheared samples (T = 139 °C), the rheo-optical behaviour changes quantitatively. A strong rise in Δn is followed by a slight decrease, manifesting an analogon of the shear-thinning behaviour (Fig. 4). The elastic contribution dominates the mechanical response. Small deformations applied to an LC droplet on a substrate relaxes back when external force is removed. The overall behaviour is similar to that of gels.^32,33

It is possible to draw small films with sizes up to 3 × 1 mm in the CubX phase. This is surprising since the stability of the freely suspended films requires some degree of smectic ordering. The films have a nonuniform thickness and no birefringence. They remain metastable on a time scale of a few minutes. Larger films rapidly collapse. In the Cub_bi phase, the material becomes gel-like, exhibiting an elastic response to the deformation breaking in when the deformation is sufficiently large. Further cooling leads to a transition to a smectic phase.

X-Ray studies indicate the presence of several tilted smectic phase SmC with a synclinic order, anticlinic SmC_a, and not-identified SmC_x phase at temperatures below .¹⁹ Resonant X-ray scattering (RSoXS) demonstrated a double-layer periodicity in the SmC_a phase suggesting an anticlinic tilt order equivalent to a double-layer periodicity.¹⁹ The double-layer periodicity disappears upon the transition to the SmC_x phase. At the same time, the POM studies show no optical tilt as would be expected in the synclinic SmC phase. This can be explained by the helical superstructure of the SmC_x or randomised tilt as in the de-Vries-type SmA phases. However, RSoXS did not indicate the helical structure on the length scale up to 40 nm.

Freely-suspended films can be prepared in any of those smectic phases. The films have a very low birefringence which complicates the characterisation (Fig. 6). The birefringence decreases both towards the Cub phase and towards the HexB phase.

Fig. 6 A microscopic texture of a freely suspended film in the SmC phase (T = 107 °C) recorded in reflection. The image is taken in reflection mode with slightly uncrossed polarisers to improve the brightness.

Pronounced flow-induced birefringence usually occurs in the polymeric systems, such as polymeric melts and side-chain polymeric liquid crystals.^31,34–36 In low-molecular-weight isotropic fluids, it is much less common. In colloidal systems, the flow birefringence was found in dispersions of anisometric particles, magnetic fluids and emulsions.^37–40 In polymer-based liquid crystals, the shear-induced isotropic-nematic transition was reported.³⁵ In contrast, our system does not show any threshold behaviour. The birefringence develops continuously under shearing conditions. The formation of these Cub_bi phase is the result of increasing interface curvature between the aromatic cores and the aliphatic chains. The cubic structure is formed by the two helical networks with opposite handedness.^19,30 We can assume that the CubX structure has short-range correlations between helixes on the submicrometre scale resulting in light scattering, opaque appearance of the liquid, and low yield stress. Under shearing, such a soft structure easily deforms into clusters with tetragonal or orthorhombic symmetry. At low temperatures, percolation between the clusters drives the transition into the Cub_bi phase with gel-like rheological properties.

The flow-induced birefringence may result from the deformation of the percolated network and the alignment of the clusters with the deformed structure. Another possible effect is the enhancement of the smectic fluctuations and nucleation of the tilted smectic. The tendency to form smectic-like clusters (cybotaxis) is supported by the fact that we can observe metastable freely suspended films. The surface-stabilised smectic order is required to stabilise the FSFs. In fact, the smectic phases occur in the whole homologue series of this compound.¹⁹ As the terminal chain length decreases, the high-temperature Cub phase transforms into the smectic (SmA) phase resulting in direct → SmA transition. The disappears in the shortest-chain homologue with n = 4.

Another possible mechanism for the flow-induced birefringence is the presence of the tetrahedratic order in the and the CubX phases. The theory of the liquid crystal tetrahedratic phases was developed in the pioneering works by Fel,⁴¹ Brandt, Pleiner and Cladis,^42–45 and also developed by Lubensky and Radzihovski⁴⁶ to describe the isotropic – tetrahedratic phase transition. The pure tetrahedratic phase has octopolar symmetry and is optically anisotropic. In the mean-field approximation, the transition from the pure isotropic to the tetrahedratic phase is of second order. However, the fluctuations are predicted to render this phase transition to the first-order transition. In our experiment, however, the 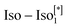transition is continuous, in contrast to the predictions of the theory. Cross-coupling terms between the order parameters and the behaviour in external fields were investigated in the theoretical works by Brand Cladis and Pleiner.⁴⁴ Tetrahedratic order was thought to explain the behaviour of some liquid crystals formed by bent-core mesogens.⁴³ The coupling between the orientational, octopolar order parameters and the flow results in a reduction of the symmetry to C₁ upon the extensional flow. Although in our experiments, we cannot directly establish the symmetry of the flow-induced state or the presence of the octopolar order.

4 Conclusions

We suggest that the cluster structure together with the flow-induced deformation of the cubic structure and the formation of the oblique smectic clusters can be responsible for the high rheo-optical response.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft (Projects ER 467/18-1 and AL2378/1-1, 424355983).

Notes and references

1. P. G. d Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, 1995.
2. R. J. Mandle, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2017, 23, 14554–14562.
3. J. P. Abberley, R. Killah, R. Walker, J. M. D. Storey, C. T. Imrie, M. Salamonczyk, C. Zhu, E. Gorecka and D. Pociecha, Nat. Commun., 2018, 9, 228.
4. T. Niori, T. Sekine, J. Watanabe, T. Furukawa and H. Takezoe, J. Mater. Chem., 1996, 6, 1231–1233.
5. L. Hough, M. Spannuth, M. Nakata and D. Coleman, Science, 2009, 325, 452–456.
6. C. Zhang, N. Diorio, O. D. Lavrentovich and A. Jákli, Nat. Commun., 2014, 5, 3302.
7. F. Araoka, M. Isoda, D. Miyajima, I. Seo, M. Oh-e, T. Aida and H. Takezoe, Adv. Electron. Mater., 2017, 3, 1600503.
8. M. Alaasar, M. Prehm, M. Brautzsch and C. Tschierske, J. Mater. Chem. C, 2014, 2, 5487–5501.
9. M. Alaasar, M. Prehm and C. Tschierske, Chem. – Eur. J., 2016, 22, 6583–6597.
10. A. Lehmann, M. Alaasar, M. Poppe, S. Poppe, M. Prehm, M. Nagaraj, S. P. Sreenilayam, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. – Eur. J., 2020, 26, 4714–4733.
11. M. Poppe, M. Alaasar, A. Lehmann, S. Poppe, M.-G. Tamba, M. Kurachkina, A. Eremin, M. Nagaraj, J. K. Vij, X. Cai, F. Liu and C. Tschierske, J. Mater. Chem. C, 2020, 8, 3316–3336.
12. M. Alaasar, M. Prehm, M. Nagaraj, J. K. Vij and C. Tschierske, Adv. Mater., 2013, 25, 2186–2191.
13. M. Alaasar, M. Prehm, S. Belau, N. Sebastián, M. Kurachkina, A. Eremin, C. Chen, F. Liu and C. Tschierske, Chem. – Eur. J., 2019, 25, 6362–6377.
14. M. Nagaraj, Liq. Cryst., 2016, 43, 1–10.
15. H. J. Coles and M. N. Pivnenko, Nature, 2005, 436, 997–1000.
16. J. Martínez-Perdiguero, I. Alonso, C. L. Folcia, J. Etxebarria and J. Ortega, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031702.
17. T. Yasuda, H. Ooi, J. Morita, Y. Akama, K. Minoura, M. Funahashi, T. Shimomura and T. Kato, Adv. Funct. Mater., 2009, 19, 411–419.
18. T. Reppe, C. Dressel, S. Poppe, A. Eremin and C. Tschierske, Adv. Opt. Mater., 2021, 9, 2001572.
19. M. Alaasar, S. Poppe, Y. Cao, C. Chen, F. Liu, C. Zhu and C. Tschierske, J. Mater. Chem. C, 2020, 8, 12902–12916.
20. C. Dressel, F. Liu, M. Prehm, X. Zeng, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2014, 53, 13115–13120.
21. C. Dressel, T. Reppe, M. Prehm, M. Brautzsch and C. Tschierske, Nat. Chem., 2014, 6, 971–977.
22. M. Alaasar, Y. Cao, Y. Liu, F. Liu and C. Tschierske, Chem. – Eur. J., 2022, e202201857.
23. X. Zeng and G. Ungar, J. Mater. Chem. C, 2020, 8, 5389–5398.
24. Y. Cao, M. Alaasar, A. Nallapaneni, M. Salamonczyk, P. Marinko, E. Gorecka, C. Tschierske, F. Liu, N. Vaupotic and C. Zhu, Phys. Rev. Lett., 2020, 125, 027801.
25. M. Alaasar, X. Cai, Y. Cao and F. Liu, New J. Chem., 2022, 46, 15871–15881.
26. T. Kato, M. Yoshio, T. Ichikawa, B. Soberats, H. Ohno and M. Funahashi, Nat. Rev. Mater., 2017, 2, 17001.
27. S. Kutsumizu, Isr. J. Chem., 2012, 52, 844–853.
28. O. Kwon, X. Cai, W. Qu, F. Liu, J. Szylowska, E. Gorecka, M. J. Han, D. K. Yoon, S. Poppe and C. Tschierske, Adv. Funct. Mater., 2021, 31, 2102271.
29. M. Alaasar, M. Prehm, Y. Cao, F. Liu and C. Tschierske, Angew. Chem., 2016, 128, 320–324.
30. M. Alaasar, S. Poppe, Q. Dong, F. Liu and C. Tschierske, Angew. Chem., 2017, 129, 10941–10945.
31. J. F. Berret, D. C. Roux, G. Porte and P. Lindner, EPL, 1994, 25, 521–526.
32. R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, 1999.
33. F. Castles, S. M. Morris, J. M. C. Hung, M. M. Qasim, A. D. Wright, S. Nosheen, S. S. Choi, B. I. Outram, S. J. Elston, C. Burgess, L. Hill, T. D. Wilkinson and H. J. Coles, Nat. Mater., 2014, 13, 817–821.
34. C. Pujolle-Robic and L. Noirez, Nature, 2001, 409, 167–171.
35. V. Schmitt, F. Lequeux, A. Pousse and D. Roux, Langmuir, 1994, 10, 955–961.
36. V. Reys, Y. Dormoy, J. L. Gallani, P. Martinoty, P. L. Barny and J. C. Dubois, Phys. Rev. Lett., 1988, 61, 2340–2343.
37. P. Salamon, Y. Geng, A. Eremin, R. Stannarius, S. Klein and T. Börzsönyi, J. Mol. Liq., 2020, 313, 113401.
38. E. K. Hobbie, J. Chem. Phys., 2004, 121, 1029–1037.
39. R. Marchessault, F. Morehead and M. Koch, J. Colloid Sci., 1961, 16, 327–344.
40. R. Marchessault, M. Koch and J. Yang, J. Colloid Sci., 1961, 16, 345–360.
41. L. Fel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 702–717.
42. H. Brand, H. Pleiner and P. Cladis, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 7, 163.
43. H. R. Brand, P. E. Cladis and H. Pleiner, Ferroelectrics, 2005, 315, 165–172.
44. H. R. Brand, H. Pleiner and P. Cladis, Physica A, 2005, 351, 189–197.
45. P. E. Cladis, H. Pleiner and H. R. Brand, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 283–291.
46. L. Radzihovsky and T. C. Lubensky, Europhys. Lett., 2007, 54, 206–212.

---

Footnote

† These authors contributed equally to this work.

---