Formation of kinetically trapped small clusters of PEGylated gold nanoparticles revealed by the combination of small-angle X-ray scattering and visible light spectroscopy

Abstract

Gold nanoparticles coated with polyethylene glycol (PEG) are able to form clusters due to the collapse of the surface-grafted polymer chains when the temperature and ion concentration of the aqueous medium are increased. The chain collapse reduces the steric repulsion, leading to particle aggregation. In this work, we combine small angle X-ray scattering (SAXS) and visible light spectroscopy to elucidate the structure of the developing clusters. The structure derived from the SAXS measurements reveals a decrease in interparticle distance and drastic narrowing of its distribution in the cluster, indicating restricted particle mobility and displacement within the cluster. Surprisingly, instead of forming a large crystalline phase, the evolving clusters are composed of about a dozen particles. The experimental optical extinction spectra measured during cluster formation can be very well reproduced by optical simulations based on the SAXS-derived structural data.

---

Introduction

The interest in the localized plasmon resonance supported by metallic nanoparticles fostered intensive research not only related to the fundamental aspects of nanoparticle plasmons, but also regarding possible applications that derive from the plasmonic properties.¹ Near-field effects and plasmon coupling upon particle aggregation are of special interest, as these are widely used in simple particle aggregation and plasmonic hot-spot based analyte detection schemes.² The attractivity of the simple, ensemble-based optoplasmonic sensing approach lies in its simplicity compared to more advanced techniques, which can undoubtedly provide more detailed information, but require a rather complex infrastructure.³ It has to be emphasized, however, that the underlying particle aggregation or clustering requires the (partial) loss of colloidal stability and the resulting cluster structure will depend on the strength of the attractive colloidal interactions.^4,5 One straightforward way to tune the aggregation is by controlled reduction of solvent quality in surface-grafted polymer-stabilized nanoparticle systems.^6,7 On the other hand, depending on the structure of the cluster and on the distance between the particles within the clusters, the resulting optical spectrum can have markedly different characteristics. When only a few particles participate in forming the clusters and/or their structure is well defined, the resulting optical changes can be well interpreted with the help of optical calculations.^8–10 For larger and 3D aggregates, or when the structure is less defined, the interpretation of the spectra is difficult due to the usually broad peak emerging in the NIR region of the spectrum as a result of a multitude of overlapping optically dominant coupled plasmon modes.^11,12

We have shown earlier that the bulk phase clustering of PEG covered gold nanoparticles can be triggered by raising the temperature at elevated background ion concentration, leading to the formation of large and compact nanoparticle clusters with ordered internal structure.⁵ The driving force of the process is the developing soft-sphere type colloidal pair interaction energy profile as a result of surface grafted polymer chain collapse,¹³ and has been shown theoretically to be critical in the preparation of ordered nanoparticle clusters.¹⁴ Kinetic control of the clustering process can be also realized by controlling the concentration and temperature levels, leading to particle aggregates with different sizes.¹⁵ Our concept has been confirmed by others, preparing 2D and 3D aggregates of PEGylated gold nanoparticles, indicating a hexagonal (FCC) arrangement of the particles in the nanoparticle solid.^4,16–18 It is important to note that this clustering approach differs substantially from creating ab ovo unstable systems or aggregation schemes relying on (macro)molecular linkers,^8,19 but belongs to the broader family of solvent quality tuning based aggregation approaches.^6,7,20

In this work, we aimed to investigate the development of nanoparticle clusters, where the driving force for clustering is rather moderate, favoring the formation of smaller particle aggregates. We investigated the assembly of PEGylated nanoparticles by a combined SAXS and visible light spectroscopy approach in order to consistently link these independent measurement results to the structural changes. The measurements were interpreted by theoretical calculations both of the structure factor and of the extinction spectra. We showed that SAXS provides a detailed picture of the cluster structure and can capture subtle structural changes as a function of temperature. By full-curve fitting the measured SAXS data, we found compact clusters composed of only a moderate number of particles, instead of the formation of a large crystalline nanoparticle solid phase. Optical extinction measurements to follow the clustering process of gold nanoparticles are far easier to perform, but they are less sensitive to fine details of the cluster structure as aggregation-related plasmon coupling dominates the observed spectral changes. Realistic agreement between simulated and measured optical spectra can be obtained, however, if the SAXS derived structural data is used as input for the simulations and the surface damping of the localized nanoparticle surface plasmons is also taken into account. Besides demonstrating the advantages in combining SAXS and spectroscopy approaches for the study of particle clustering, the results also underline that special care is required when only simple ensemble optical measurements are employed to monitor the clustering of gold nanoparticles – an approach that is broadly applied in various detection schemes.

Experimental

For nanoparticle synthesis, surface modification and clustering hydrogen tetrachloroaurate trihydrate (99,9%), sodium citrate tribasic dihydrate (99%), potassium sulfate (99%) were obtained from Sigma-Aldrich and thiolated polyethylene glycol (mPEG-SH, 750 Da) was purchased from Rapp Polymere GmbH. All chemicals were used as received. For all experiments, ultrapure water with a resistivity of 18.2 MΩ cm was used. The glassware was cleaned using aqua regia.

The spherical nanoparticles were prepared by the traditional Turkevich method,²¹ while their PEGylation was carried out as reported earlier.⁵ Visible light extinction spectroscopy was realized using a fiber coupled stabilized tungsten halogen light source (Thorlabs SL201L) and spectrometer (Thorlabs CCS200) at different temperatures in a cuvette holder (Thorlabs CVH100) with laboratory built external temperature control. Three different temperature values (35 °C, 45 °C and 55 °C) and two different potassium sulfate concentrations (0.125 M and 0.25 M) were considered. The gold concentration is always 7.2 nM, corresponding to a volume fraction φ_P = 10⁻⁵.

For recording the optical extinction spectra, a custom written Labview software was used. Before recording the spectra, the temperature of both the nanoparticle sol and the salt solution was set to the desired value and the dilution of the salt solution upon injection was taken into account. The temperature was kept constant during the measurement. Optical simulations of the nanoparticles’ and nanoparticle clusters’ extinction spectra were performed by the MNPBEM MATLAB module,²² using the dielectric function of gold given by Olmon et al.²³ This dielectric function was modified to include an interfacial damping term, which accounts for surface scattering of the conduction electrons and for chemical interface damping.²⁴ The simulation algorithm accounts for retardation and the effective refractive index of the embedding medium was set to 1.467 due to the presence of PEG. The particles and the particle assemblies were illuminated along the x, y and z principal axes each with two perpendicular polarizations and the extinction spectrum was obtained by averaging over these 6 excitations. Ten different, randomized nanoparticle cluster structures were simulated and averaged in each case, generated in the same way as for the SAXS evaluation (see ESI†).

SAXS experiments were carried out using the SWING beamline at SOLEIL synchrotron facility, at an energy of 16 keV. The sample-detector distance was set to 6.223 m. The scattered intensity as a function of q vector modulus was obtained by radially averaging the measured scattering pattern using the FOXTROT software developed at the beamline. This SAXS signal (I(q)) can be written in the form of I(q) = nV²Δρ²P(q)S(q), where V is the volume of the particle and Δρ is the difference in scattering length density between the particle and the surrounding medium. The form factor, denoted by P(q), normalized such that P(q → 0) = 1, is due to the size and the shape of the particles, while the structure factor S(q) provides information on their configuration. To determine the experimental structure factor, the SAXS signal of assembled nanospheres was divided by a polydisperse sphere model fit to the initial (well-dispersed) sample: I₀(q) S(q) = I(q)/I_model(q). As shown in the ESI,†I_model(q) is very close to I₀(q), confirming that interparticle interactions can be neglected at room temperature. Note also that, due to this polydispersity, S(q) is strictly speaking an effective structure factor and is only equal to the true structure factor in the decoupling approximation: 〈V²P(q)S(q)〉 = 〈V²P(q)〉〈S(q)〉: considering the low relative polydispersity (about 10%), we neglect this distinction in the following.

Results and discussion

The SAXS measurements of the as-prepared particle sample yielded a core diameter of 14.2 ± 1.3 nm (mean ± SD, see ESI,† Fig. S1).

Combined with the gold concentration, this parameter yields a number concentration of particles n_P = 6.5 × 10⁻⁹ nm⁻³. The prepared samples are kinetically stable, as in addition to the electric double layer repulsion the end-grafted polymer chains also counteracts the van der Waals attraction. When the PEGylated particles are placed in a salt solution, however, their aggregation can be induced at elevated temperature due to the collapse of the surface-grafted polymer chains and the decrease of the associated steric repulsion between particles (Scheme 1).^5,18 Depending on the resulting colloidal interaction profile, destabilization can lead either to relatively slow nanoparticle cluster formation, or to rapid aggregation,²⁵ similar to the results obtained on ‘hairy’ and plain silica nanoparticles.²⁶ When a soft-sphere type interaction curve is present due to a strong short range repulsion (due to PEG in the present case) with only a small (few kT) attractive potential minimum, the particles will assemble into fairly ordered colloidal clusters.¹⁴ Larger attractive potentials on the other hand results in fast aggregation rates and the diffusion limited growth produces fractal-like aggregates.^5,27

Scheme 1 PEGylated gold nanoparticles can form nanoparticle clusters when the temperature and ion concentration in the system is increased. The clustering leads to a pronounced change of the small-angle X-ray scattering and visible light extinction spectra. Scale bars: 100 nm.

For the PEGylated particles used in the present study, the decreasing stability of the particles with increasing temperature can be clearly detected in their time-dependent visible extinction spectra (Fig. 1). At the lowest investigated salt concentration and temperature (0.125 M; 35 °C) the sample remains stable and no change in the extinction maximum nor in the width of the peak can be observed. As the temperature is increased to 45 or 55 °C, however, a small redshift is observed and the extinction measured in the visible wavelength range decreases continuously. As the extinction value around 400 nm is dominated by interband transition instead of the localized plasmon resonance, its value correlates with the amount of Au⁰ in the light path.²⁸ Hence, this observed decrease already indicates that some particles leave the detection volume, that is, the samples sediment to some extent. The effect of sedimentation can be separated from the changes induced by plasmon coupling by performing a renormalization of the extinction spectra at 400 nm. The renormalized spectra (for details see ESI,† Fig. S2) at 0.125 M for the 45 and 55 °C case show a small redshift and (especially for the 55 °C case) peak broadening can be observed, with slightly increasing extinction in the near infrared region. This plasmon-coupling-related effect confirms that the nanoparticles approach each other. On the other hand, the extent of the near-field coupling is small, indicating a rather large coordination distance. More pronounced spectral changes can be observed at higher, 0.25 M salt concentration. There is already a clear indication of cluster formation at 35 °C and the NIR extinction becomes dominant at higher temperature. At 55 °C a qualitatively different behavior is observed, with the appearance of a broad extinction peak in the NIR wavelength region, typical for the case of aggregation due to stronger interparticle attraction.^5,11 It appears that, even though clustering takes place at different concentration/temperature combinations, there is a fundamental difference in the extent of clustering and/or in the resulting structure for the 0.25 M; 55 °C case. This is also indicated by SEM images taken from drop-casted samples after 60 minutes, which show that smaller clusters are formed at lower temperatures and ion concentrations (Fig. 2). Note, however, that the structure of dried-in SEM samples might differ from that of the as-formed cluster structure in the liquid phase. The spectroscopy measurements also indicate that after 60 minutes the clustering process comes to a hold, and no further aggregation related spectral shifts can be anticipated, except for sedimentation of large aggregates.

Fig. 1 Time evolution of the ensemble optical extinction spectra recorded at different ion concentrations and temperatures after addition of the salt solution. The extinction peak around 520 nm corresponding to the dipolar localized plasmon resonance redshifts upon clustering (a)–(e), while additional extreme broadening due to a multitude of coupled modes is observed upon rapid aggregation (f).

Fig. 2 Scanning electron microscopy images of drop-casted samples taken after 60 minutes clustering time at 45 °C and 0.125 M (a) and 55 °C 0.25 M (b).

SAXS investigation of the same systems was carried out to obtain more direct information about the structure of the evolving nanoparticle clusters. A locally compact nanosphere arrangement was assumed when evaluating the SAXS data,²⁹ locally similar to the FCC structure of the extended nanoparticle aggregates obtained with large (6 kDa) PEG grafted nanoparticles.¹⁶ Cluster configurations are generated starting from an initial arrangement with equal interparticle distances, by adding along the three space directions random position fluctuations drawn from a Gaussian distribution with a given standard deviation. The structure factor of these objects is computed using the Debye equation.³⁰ Our approach is similar to Hansen's Monte Carlo method.³¹

The structure factor depends sensitively on the average separation distance between the particles, its distribution, the number of spheres in the cluster as well as on the fraction of free vs. clustered nanoparticles (see ESI,† Fig. S3 for details). It is noteworthy that the calculated structure factors show the average of 1000 individual configurations, the corresponding particle–particle separation distribution functions are shown as insets in Fig. 3. The main parameters obtained from the SAXS measurements are listed in Table 1; particle surface separation refers to gold particle surface-to-surface distance, α is the ratio of clustered to all particles. The time evolution of the SAXS measurements (ESI,† S4 and S5.) corresponds to the spectral changes observed using visible light spectroscopy, that is, cluster formation proceeds rather slowly on the hour scale, and the clusters do not completely disintegrate when the system is cooled back to 25 °C.

Fig. 3 Measured and calculated structure factors for the nanoparticle clusters obtained at different ion concentration and temperature: (a) 0.125 M, 45 °C; (b) 0.125 M, 55 °C; (c) 0.25 M, 45 °C; (d) 0.25 M, 55 °C. The insets show the particle separation distribution (counts vs. gap size).

Table 1 Structural parameters obtained from SAXS measurements at different salt concentrations and temperatures

	Particle surface separation (Å)	Fraction of clustered particles – α
0.125 M; 45 °C	27.9 ± 13.3	0.63
0.125 M; 55 °C	27.5 ± 13.8	0.78
0.25 M; 45 °C	26.0 ± 12.4	0.83
0.25 M; 55 °C	18.0 ± 1.7	0.96

---

The structure factor calculations provide good agreement with the measurements in Fig. 3(a)–(c), whereas for the sample measured at 0.25 M and 55 °C there is a clear difference at the peak around q = 0.09. The experimental spectrum exhibits additional features around q = 0.04 and q = 0.08, not captured by the calculation. They might originate from the presence of more complex cluster structures. It is important to emphasize that the best agreement with the experimental data was obtained assuming N = 13 particles in the cluster, regardless of salt concentration and temperature (ESI,† Fig. S6 and S7 for the demonstration). This also suggests that, in spite of the obvious nanoparticle association, the system is kinetically trapped in the few-particle cluster state, without developing huge particle aggregates. This conclusion is coherent with the results of the time-dependent spectroscopy measurements shown above. Even for the highest investigated salt concentration and temperature (0.25 M and 55 °C), the loose coordination of the smaller clusters can be anticipated, without leading to very large, compact aggregates. This is in agreement with the spectroscopic data (Fig. 1) and the SEM images. The average gap between the particles in the clusters shows generally a decreasing trend as the ion concentration and the temperature increase (Table 1). This is in qualitative agreement with recent results involving gold nanoparticles grafted with larger polymer chains.¹⁷ More importantly, there is a fundamental difference in the particle separation distribution. While for (a)–(c) the gap between the particles covers a fairly broad range, in the case of (d) there is a clear reduction of the particle separation and a pronounced narrowing of the gap distribution (also see ESI,† Fig. S8). We attribute this difference to the collapse of the surface-grafted PEG chains, which results in a deeper potential well in terms of colloidal interactions due to reduction of the steric repulsion range,^5,15 and the attractive forces effectively lock the particles in place as the cluster is formed. This also explains the trend observed during the visible light extinction measurements: as long as the PEG only shrinks, the particles experience only moderate attraction and are separated from each other due to the still effective steric repulsion, so both the particle coordination within the cluster and the plasmon coupling will be rather weak. When PEG collapses, on the other hand, it leads to aggregation with small interparticle separations and hence to pronounced plasmon coupling. This conclusion is also supported by the calculated nanoparticle pair interaction potentials (ESI,† Fig. S9). An initial PEG brush thickness of 1.85 nm can be inferred from dynamic light scattering experiments.⁵ As a rough estimate, the SAXS-based surface separation values listed in Table 1 divided by a factor of 2 indicate ca. 25% smaller values (ca. 50% in the 0.25 M; 55 °C case); the separation data in Table 1 were used as input to obtain the steric interaction contribution. As expected, at these high ion concentrations the electric double layer interaction is basically absent with Debye lengths well below 1 nm (ESI,† Fig. S9), the interaction is dominated by the balance of the attractive dispersion and repulsive steric interactions.⁵

While there is a steady decrease of the interaction energy minimum, for the 0.25 M; 55 °C sample its depth drops well below −5 kT. This also means that while the particle separation is reduced, the strong interparticle attraction impedes reorganization of the particles within the clusters, enabling the growth of non-centrosymmetric clusters.¹⁴ The observed trend of α is also in line with the derived structural data and the colloidal interaction calculations. It indicates that the fraction of nanoparticles incorporated in a cluster gradually increases with ion concentration and temperature.

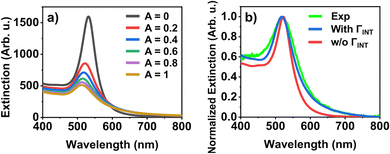
To confirm this scenario, data derived from the SAXS measurements was used as input for optical simulations and the clusters’ optical extinction spectra were compared with the experimental ones. As the particles used in this study are well below the mean free electron path length (ca. 37.7 nm for gold),³² the conduction electrons will scatter at the particle surface. Additionally, PEG is attached to the particles’ surface via a thiol moiety, resulting in an additional chemical surface damping (CID) of the plasmons. For spherical particles, the combined effect of surface scattering and chemical interface damping can be given as the interfacial damping Γ_int = Av_F/R, where v_F is the Fermi velocity (1.4 nm fs⁻¹)³³ and R is the particle radius in nanometers. A is the combined surface and CID – or interfacial – parameter, which is of order unity and can be taken into account in simulations by modifying the bulk dielectric function of gold.²⁴ As shown in Fig. 4(a), the increase of the interfacial damping contribution results in a blueshift and broadening of the individual particle's resonance. While in theory the size of the nanoparticles as well as the polydispersity can affect both the position and width of the dipole resonance, for the given particle size their influence is negligible (ESI,† Fig. S10). As a consequence, the measured ensemble optical extinction spectrum can be compared to a particle's calculated spectrum. Following the approach of Berciaud et al.,³⁴ setting the interfacial (combined surface and CID) parameter to A = 0.35 yields very good agreement with the experimental spectrum (Fig. 4(b)). Our A parameter is somewhat larger than the previously reported value (A = 0.25) for similarly sized gold nanospheres,³⁴ which is the result of chemical linkage between the gold surface and the thiolated PEG in the present case, leading to a larger CID contribution,³⁵ close to the value obtained for CTAB-capped gold nanoparticles (A ≈ 0.35).^36,37

Fig. 4 (a) Simulated extinction spectra of 14.2 nm diameter gold nanospheres without (A = 0) and with increasing interfacial damping contribution. (b) Comparison of the experimental spectrum with the calculated ones without (A = 0) and with interfacial damping term (A = 0.35).

The good agreement of the measured and calculated spectra allows the calculation of the nanoparticle clusters’ spectra, with clusters constructed based on the SAXS-derived data. The cluster extinction spectrum simulation not only includes the separation distance and distribution values, but the fraction of particles incorporated in the clusters as well. This latter is done by dividing first the calculated cluster spectrum with the corresponding number of particles, yielding the average spectral contribution of a single clustered particle. The final simulated spectrum is then calculated as the sum of the spectral contributions from clustered and free particles with weighting factors α and 1 − α for the clustered and free particles, respectively, where the value of α is taken from the corresponding SAXS evaluation (Table 1). The comparison of the starting and final (after 60 minutes) measurement with the optical calculations is shown in Fig. 5. It is noteworthy that we achieve excellent agreement for (a)–(c), implying that the optical calculation based on the SAXS-derived structure effectively captures the small changes occurring during clustering.

Fig. 5 Experimental and simulated optical extinction spectra of the PEGylated gold nanosphere sols at different ion concentrations and temperatures at the beginning of the clustering process (t₀) and after 60 minutes (t_F) – spectra are vertically shifted for better visibility. The dashed vertical lines show the original position of the extinction maxima.

A similar spectral evolution for clustered gold nanoparticles was observed earlier for 3-mercatopropionate-induced clustering in the presence of PEG.¹⁹ Note, however, that for the system indicating PEG collapse (0.25 M; 55 °C – Fig. 5(d)), the calculation fails to reproduce the experimental data: the emerging peak in the NIR wavelength region and the extreme broadening are not reproduced in the optical simulation. The measured spectrum for (d) indicates that, as a result of strong interparticle attraction, elongated structures (e.g. chain-like aggregates) are also present, and extinction from these optically dominant modes determines the measured spectra.^4,11 Note that when the nanoparticle design limits the growth of the clusters (e.g. when Janus-type gold nanospheres are used where the clustering is self-limited due to anisotropic particle structure or encapsulation of the small clusters in a polymer shell), the optical spectrum does not show this extreme broadening.^9,38

Conclusions

The combined small angle X-ray scattering and optical spectroscopy investigation of the clustering process for PEGylated gold nanospheres (ca. 14 nm; 750 Da PEG) indicated that it is possible to form ordered nanoparticle clusters that are composed of only a moderate number of particles. It was found that with increasing salt concentration and temperature the coordination of the nanospheres in the developing compact ordered clusters becomes stronger. It was found that before the pronounced PEG chain collapse the coordinated particles are still separated by ca. 2.5–3 nm, meaning that steric repulsion between the polymer chains is still active. The optical measurements are consistent with the SAXS-derived data: although particle clustering takes place, the rapid aggregation cannot be observed, as indicated by only a redshift and broadening of the localized plasmon resonance peak. Optical simulation of the clusters corroborates these assumptions and leads to excellent agreement with the measured spectra. When the solvent conditions induce the collapse of the PEG chains, the average distance between the particles in the cluster strongly decreases. At the same time, the separation distance distribution is drastically narrowed, indicating a strong attraction and low mobility of the particles within the clusters. This is also reflected in the measured optical spectra, which – together with the optical simulations – indicate that more complex structures are also produced during clustering. Hence, when functionalized nanoparticles are employed as signal transducers (e.g. in plasmonic nanoparticle aggregation based sensing applications), cluster-structure related optical effects should be also considered carefully.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the French–Hungarian bilateral agreements Balaton Program – 41878TK and National Research, Development and Innovation Office – NKFIH, 2018-2.1.13-TÉT-FR-2018-00002 and NKFIH FK128327. We acknowledge SOLEIL for the provision of synchrotron radiation facilities, and thank Thomas Bizien for assistance in using beamline SWING.

Notes and references

1. L. Wang, M. Hasanzadeh Kafshgari and M. Meunier, Adv. Funct. Mater., 2020, 30, 2005400.
2. D. Vilela, M. C. González and A. Escarpa, Anal. Chim. Acta, 2012, 751, 24–43.
3. J. Xavier, S. Vincent, F. Meder and F. Vollmer, Nanophotonics, 2018, 7, 1–38.
4. N. K. Kwon, T. K. Lee, S. K. Kwak and S. Y. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 39688–39698.
5. D. Zámbó, G. Z. Radnóczi and A. Deák, Langmuir, 2015, 31, 2662–2668.
6. R. M. Choueiri, A. Klinkova, H. Thérien-Aubin, M. Rubinstein and E. Kumacheva, J. Am. Chem. Soc., 2013, 135, 10262–10265.
7. S. Izor, A. Schantz, A. Jawaid, C. Grabowski, T. Dagher, H. Koerner, K. Park and R. Vaia, Macromolecules, 2021, 54, 10435–10446.
8. L. Guo, Y. Xu, A. R. Ferhan, G. Chen and D.-H. Kim, J. Am. Chem. Soc., 2013, 135, 12338–12345.
9. N. Castro, D. Constantin, P. Davidson and B. Abécassis, Soft Matter, 2016, 12, 9666–9673.
10. J. Lyu, D. Alloyeau, C. Hamon and D. Constantin, J. Mater. Chem. C, 2021, 9, 1730–1739.
11. R. W. Taylor, R. Esteban, S. Mahajan, R. Coulston, O. A. Scherman, J. Aizpurua and J. J. Baumberg, J. Phys. Chem. C, 2012, 116, 25044–25051.
12. D. Zámbó and A. Deák, Period. Polytech., Chem. Eng., 2016, 60, 244–251.
13. N. Backmann, N. Kappeler, T. Braun, F. Huber, H.-P. Lang, C. Gerber and R. Y. H. Lim, Beilstein J. Nanotechnol., 2010, 1, 3–13.
14. D. Klotsa and R. L. Jack, Soft Matter, 2011, 7, 6294.
15. D. Zámbó, S. Pothorszky, D. F. Brougham and A. Deák, RSC Adv., 2016, 6, 27151–27157.
16. H. Zhang, W. Wang, M. Akinc, S. Mallapragada, A. Travesset and D. Vaknin, Nanoscale, 2017, 9, 8710–8715.
17. H. J. Kim, W. Wang, S. Mallapragada, A. Travesset and D. Vaknin, J. Phys. Chem. C, 2021, 125, 10090–10095.
18. H. J. Kim, W. Wang, H. Zhang, G. Freychet, B. M. Ocko, A. Travesset, S. K. Mallapragada and D. Vaknin, Langmuir, 2021, 37, 10143–10149.
19. D. Van Haute, J. M. Longmate and J. M. Berlin, Adv. Mater., 2015, 27, 5158–5164.
20. H. Tao, E. Galati and E. Kumacheva, Macromolecules, 2018, 51, 6021–6027.
21. J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55.
22. J. Waxenegger, A. Trügler and U. Hohenester, Comput. Phys. Commun., 2015, 193, 138–150.
23. R. L. Olmon, B. Slovick, T. W. Johnson, D. Shelton, S.-H. Oh, G. D. Boreman and M. B. Raschke, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(23), 235147.
24. H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 18178–18188.
25. T. Gisler and M. Borkovec, Langmuir, 1993, 9, 2247–2249.
26. M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Langmuir, 2005, 21, 5761–5769.
27. S. H. Behrens, D. I. Christl, R. Emmerzael, P. Schurtenberger and M. Borkovec, Langmuir, 2000, 16, 2566–2575.
28. W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221.
29. A. Burke, M. Chevreuil, A. Paris, V. de La Grange, C. Goldmann, J. Pérez, D. Constantin and G. Tresset, Phys. Rev. Appl., 2018, 10, 054065.
30. Small angle x-ray scattering, ed. O. Glatter and O. Kratky, Academic Press, London,New York, 1982.
31. S. Hansen, J. Appl. Crystallogr., 1990, 23, 344–346.
32. D. Gall, J. Appl. Phys., 2016, 119, 085101.
33. G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887.
34. S. Berciaud, L. Cognet, P. Tamarat and B. Lounis, Nano Lett., 2005, 5, 515–518.
35. B. Foerster, A. Joplin, K. Kaefer, S. Celiksoy, S. Link and C. Sönnichsen, ACS Nano, 2017, 11, 2886–2893.
36. C. Novo, D. Gomez, J. Perez-Juste, Z. Zhang, H. Petrova, M. Reismann, P. Mulvaney and G. V. Hartland, Phys. Chem. Chem. Phys., 2006, 8, 3540.
37. K. Slyusarenko, B. Abécassis, P. Davidson and D. Constantin, Nanoscale, 2014, 6, 13527–13534.
38. A. S. Urban, X. Shen, Y. Wang, N. Large, H. Wang, M. W. Knight, P. Nordlander, H. Chen and N. J. Halas, Nano Lett., 2013, 13, 4399–4403.

---

Footnote

† Electronic supplementary information (ESI) available: SAXS measurement evaluation details, uncorrected experimental optical extinction spectra, scanning electron microscopy images of drop-casted samples, calculated structure factors and derived particle separation distributions, time evolution of the experimental structure factors (PDF). See DOI: https://doi.org/10.1039/d2sm01257j

---