Interplay between substrate rigidity and tissue fluidity regulates cell monolayer spreading†
Michael F.
Staddon
abc,
Michael P.
Murrell
 df and
Shiladitya
Banerjee
df and
Shiladitya
Banerjee
 *e
*e
aCenter for Systems Biology Dresden, Dresden, Germany
bMax Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
cMax Planck Institute for the Physics of Complex Systems, Dresden, Germany
dDepartment of Biomedical Engineering and Department of Physics, Yale University, New Haven, CT, USA
eDepartment of Physics, Carnegie Mellon University, Pittsburgh, PA, USA. E-mail: shiladtb@andrew.cmu.edu
fSystems Biology Institute, Yale University, West Haven, CT, USA
First published on 7th October 2022
Abstract
Coordinated and cooperative motion of cells is essential for embryonic development, tissue morphogenesis, wound healing and cancer invasion. A predictive understanding of the emergent mechanical behaviors in collective cell motion is challenging due to the complex interplay between cell–cell interactions, cell–matrix adhesions and active cell behaviors. To overcome this challenge, we develop a predictive cellular vertex model that can delineate the relative roles of substrate rigidity, tissue mechanics and active cell properties on the movement of cell collectives. We apply the model to the specific case of collective motion in cell aggregates as they spread into a two-dimensional cell monolayer adherent to a soft elastic matrix. Consistent with recent experiments, we find that substrate stiffness regulates the driving forces for the spreading of cellular monolayer, which can be pressure-driven or crawling-based depending on substrate rigidity. On soft substrates, cell monolayer spreading is driven by an active pressure due to the influx of cells coming from the aggregate, whereas on stiff substrates, cell spreading is driven primarily by active crawling forces. Our model predicts that cooperation of cell crawling and tissue pressure drives faster spreading, while the spreading rate is sensitive to the mechanical properties of the tissue. We find that solid tissues spread faster on stiff substrates, with spreading rate increasing with tissue tension. By contrast, the spreading of fluid tissues is independent of substrate stiffness and is slower than solid tissues. We compare our theoretical results with experimental results on traction force generation and spreading kinetics of cell monolayers, and provide new predictions on the role of tissue fluidity and substrate rigidity on collective cell motion.
Tissue spreading is a fundamental biological process underlying collective cell movement during development,1–4 cancer invasion,5–8 and wound healing.9–12 The collective motion of cells during tissue spreading is regulated by the interplay between cell–cell and cell–matrix adhesions,13–15 as well as by active processes such as lamellipodial cell crawling and actomyosin contractility that control the dynamic mechanical properties of individual cells and tissues.16,17 Many of the active mechanical components of cells are mechanosensitive and interact with each other via complex feedback networks,18–22 making it experimentally challenging to decipher the key regulators of cellular mechanical behaviors.23,24
A common model system for studying the mechanics of collective cell migration is the spreading of a three-dimensional cell aggregate over a soft elastic substrate.25–30 When placed onto an adhesive substrate, the aggregate spreads out in a process similar to the wetting of liquid droplets, in which differences in adhesion between cell–cell and cell–substrate contacts drives the spreading of the fluid aggregate.26,27,31,32 However, the spreading dynamics of a living tissue is more complex than the wetting of passive liquid droplets. Recent work has demonstrated the importance of cellular mechanics and intercellular adhesions in regulating the spreading dynamics of tissues, whose mechanical properties can range from fluids to glassy jammed solids.12,33–35 Both tissue viscosity and cell–cell adhesion strengths are regulated by E-cadherins.20,36,37 Upon reduction in E-cadherin expression, the spreading rate of the cell aggregate is elevated,25 while increasing E-cadherin expression28 or substrate stiffness can induce dewetting of already spread aggregates.38
The active, non-equilibrium behavior of cells is another key regulator of collective cell spreading not accounted for in the wetting model and remains poorly understood. However, recent experiments have begun to uncover how cellular aggregates adapt to the mechanics of the extracellular matrix in order to drive robust collective motion.29 Depending on matrix rigidity, cells may polarize, generating active traction stresses to crawl outwards. The stiffness of the substrate is important not only for providing passive friction to cell motion, but can also induce cell polarization.24,39 A recent study showed that cellular aggregates can tune their mechanics and migratory behaviors depending on matrix rigidity.29 On stiff substrates, traction stresses are elevated at the tissue boundary, driving rapid outward motion of cells. By contrast, on soft substrates, traction stresses are attenuated and cell spreading in driven by an outward active pressure.
In this paper, we develop a cell-based active vertex model for cellular monolayers to investigate the role of substrate stiffness and tissue mechanics in monolayer spreading. A variety of theoretical models and methods have been developed in recent years to describe the collective motility of cells, including continuum models,40–45 particle-based models,46,47 lattice-based models,48,49 as well as vertex-based50–52 and voronoi models.53 While continuum models of tissue spreading have been successful in predicting traction force organization,45 wave-like dynamics41 and wetting transitions,25,28,44 these models assume fixed constitutive relations for tissue materials properties, and thus do not account for dynamic changes in tissue mechanical properties due to single-cell level active mechanical behaviors. On the other hand, discrete cell-based models for tissues have not yet been implemented to study how cellular aggregates adapt to substrate mechanical properties in order to drive collective cell motion. We bridge this gap by developing an active vertex model for cell aggregate spreading that allow us to study the interplay between tissue mechanics, substrate mechanics, as well as the role of active single-cell behaviors in the collective motility of cell monolayers.
We model the collective motion of cells in a three-dimensional aggregate as they spread into a two-dimensional monolayer adherent to a flat substrate (Fig. 1a). The aggregate acts as a reservoir of cells, feeding cells into the spreading monolayer by a process called permeation26 (Fig. 1a). By developing an active vertex model for the monolayer, we study how changes in substrate stiffness affects the speed and the modes of monolayer spreading. Our model successfully captures the experimental behaviour initially reported by ref. 29. We find that monolayer spreading on soft substrates is driven by an active pressure due to the influx of cells coming from the aggregate. By contrast, on stiff substrates, monolayer spreading is driven by active crawling of cells that generate elevated traction forces at the monolayer boundary. To conceptually understand the role of substrate stiffness in collective cell motion, we develop a simple mechanical model of the monolayer as a viscoelastic material that spreads by active crawling as well as due to growth in the preferred area of the material. This model captures the key results from the vertex model, and predicts that tissue stiffness governs the long term spreading rate of the tissue. To test this prediction, we vary both monolayer tension and substrate stiffness in the vertex model, and find that tissues with increased tension display increased sensitivity to substrate stiffness. Moreover, we find that solid-like tissues spread faster than fluid-like tissues due to a reduced bulk modulus of the tissue overall. These results provide a theoretical understanding for the role of both tissue fluidity and substrate rigidity, and their interplay, on the spreading dynamics of multicellular aggregates.
1 Active vertex model for collective cell spreading
To describe the dynamics of cell monolayer spreading, we model the cell monolayer underneath the aggregate as a two-dimensional tissue using the framework of the vertex model.54–57 The aggregate generates a continuous flux of cells into the monolayer uniformly within a central region that marks the contact area of the aggregate (Fig. 1a). Cells in the monolayer are able to actively crawl out into the free space during spreading, while the cell influx from the aggregate, modeled by stochastic insertion of new cells, increases the number of cells in the monolayer over time (Fig. 1a and b). Each cell in the monolayer is modeled by a two-dimensional polygon, with edges representing the cell–cell junctions and the vertices representing tri-cellular junctions (Fig. 1b and c). The mechanical energy E of the monolayer is given by | (1) |
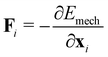 | (2) |
 and length scales by
and length scales by  so that our non-dimensional energy Ẽ becomes
so that our non-dimensional energy Ẽ becomes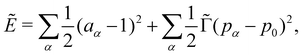 | (3) |
 , and
, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) = Γ/KA0.
= Γ/KA0.
To model active cell crawling, each cell is assigned a unit polarity vector pα that defines the direction of cell crawling or self-propulsion. Self-propulsion models for cell motility have been extensively studied in the active matter literature, including in particle-based models,58–60 active gel models,41,42,61 vertex models,51,52,62,63 and self-propelled voronoi models for cell layers.53 These models implement various different rules for cell polarity dynamics including random rotation,53,62 alignment with the polarity of cell neighbors,51,52,59,63 cell migration direction51,58,60 or the total force acting on each cell.61 Here we assume that cells on the boundary attempt to crawl into free space, setting the polarity vector to be a unit vector perpendicular to their free edge pointing outwards. Cells within the monolayer then align their polarity vector with their neighbours
 | (4) |
 | (5) |
 .
.
For computational efficiency, we do not explicitly model the substrate but assume an effective model that the cell–substrate friction μ increases monotonically with substrate elastic modulus E, such that μ = μ0E, where μ0 is a constant. This result follows from our previous work11,52 where we had shown that cell–substrate friction increases with substrate stiffness by explicitly modeling the substrate as an elastic network adherent to a migrating cell collective. Furthermore, the linear relationship between friction and substrate stiffness also follows from a kinetic model of focal adhesion complexes,64 which predicts that cell–substrate adhesive interactions provide a frictional drag that increases with the elastic modulus of the substrate. At high elastic modulus, the friction is likely to saturate. Cell polarity and migration speeds are also substrate stiffness-dependent. Experimentally it was observed that actin stress fiber organization and directionality of cell movement is substrate stiffness dependent, such that cell polarization increases monotonically with substrate elastic modulus.23,29,65–67 While single-cell migration speeds show biphasic stiffness dependence,68,69 the speed of collective cell migration increases monotonically with substrate stiffness.70 Based on these observations, we assume for simplicity that cell crawling speed in a tissue increases linearly with substrate elastic modulus, v0 = c0E, where c0 is a proportionality constant, although typically the crawl speed would saturate at high rigidity.
The influx of cells from the aggregate into the monolayer is modelled by stochastically inserting new cells into the 2D monolayer, within a region that the aggregate occupies above the monolayer29 (Fig. 1). When a new cell is added, an existing cell within the aggregate area is randomly selected and subdivided into two, with the new cell initialized to have zero polarity. The cell influx, or rate of cell additions, increases with monolayer area, as the aggregate has more contact area to add cells in, until the monolayer spreads outside of the aggregate area. This results in a time-dependent cell flux J(t) = Gmin(A(t),Aag)/a*, where G is the maximum flux, A(t) is the area of the monolayer at time t, Aag is the contact area of the aggregate at 90° contact angle, and a* is the area of a single cell at the mechanical equilibrium. Thus, without cell crawling, the monolayer area grows exponentially until it is larger than the aggregate area, after which grows linearly. Without the addition of cells from the aggregate, the monolayer exhibits Kelvin–Voigt type viscoelasticity, in which the aggregate increases in area up to a maximum value. However, at longer timescales cells in the monolayer adapt their shape to stretch and get thinner, or divide, giving a more fluid like behaviour of the tissue which is often used to model monolayers.
The model is implemented in Surface Evolver71 and solved numerically using the forward Euler method, with a timestep dt = 0.05 min. At each time step, we update the vertex position and then perform T1 transitions, or neighbour swaps, for edges that become lower than a length threshold L* = 0.05. To implement cell influx from the aggregate we calculate the rate of cell additions, J(t) = Gmin(A(t),Aag)/a*, where a* is the mean area of a single cell at equilibrium. Then, with probability Jdt, a random cell from the monolayer within the aggregate area is subdivided into two cells by splitting the cell with a new edge. The tissue mechanical parameters are taken from a previous study on MDCK monolayers,11 while the cell flux rate and crawling speeds are chosen to reproduce experimentally measured spreading rates of the monolayer29 (Table 1). To simulate monolayer spreading, we begin with a monolayer of half the contact area of the aggregate, located at the center of the aggregate and beginning from a state of mechanical equilibrium. The aggregate remains fixed in position as the monolayer spreads out, injecting cells into the monolayer over a maximum contact area Aag.30 We then simulate cell spreading including cell flux and crawling for 400 minutes, tracking the monolayer area and traction forces at each cell vertex of the tissue.
| Parameter | Symbol | Value |
|---|---|---|
| Contractility |
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif)
|
0.166 |
| Shape index | p 0 | 1.5 |
| Crawl speed coefficient | c 0 = v0/E | 1 |
| Friction coefficient | μ 0 = μ/E | 0.1 min |
| Polarity alignment rate | k p | 1 min |
| Aggregate flux rate | G | 22.5% hour−1 |
| Aggregate area | A ag | 100 |
2 Substrate rigidity regulates the driving forces for collective spreading
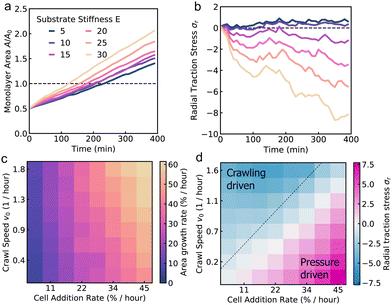
To understand how substrate rigidity regulates collective cell spreading, we simulated the active vertex model of a spreading monolayer at different values of substrate stiffness, E. Our simulations reveal two distinct mechanisms of cell monolayer spreading which are dependent on the substrate stiffness. On soft substrates, cell spreading is driven by an active pressure arising from the influx of cells from the aggregate into the center of the monolayer (Fig. 2a, b and Movies 1, 2, ESI†). As cells are added into the monolayer, pressure builds from the newly incorporated compressed cells, producing radially outward traction stresses localized around the center of the monolayer that increase in magnitude over time (Fig. 2b and Movie 2, ESI†). By contrast, monolayer spreading on stiff substrates is driven primarily by cell crawling. This results in faster spreading rates on stiff substrates as compared to soft (Fig. 2c and Movie 3, ESI†), and radially inward traction stresses accumulate on the border of the monolayer (Fig. 2d and Movie 4, ESI†). While peripherally localized traction stresses have been observed in experiments of spreading tissues before,28,33,42 and reproduced in theoretical models,28,41–43 pressure-driven traction stresses at the center of the tissue have been recently reported in experiments on cell aggregates spreading on soft substrates.29The dynamics of monolayer area depend on the mechanism driving monolayer spreading. When cell monolayer spreading is driven by the influx of cells from the aggregate, the monolayer area initially increases exponentially, as the cell influx rate is proportional to the monolayer area (Fig. 3a). Once the monolayer spread area is larger than the contact area of the aggregate, cells are added at a constant rate, resulting in a constant rate of monolayer area increase. On a soft substrate, the radial traction stress (σr) takes positive values due to the accumulation of compressed cells near the center of the monolayer, before plateauing (Fig. 3b). As substrate stiffness increases, there is a transition to crawling-driven spreading resulting in negative (inward) traction stresses. At high substrate stiffness, the monolayer area initially increases rapidly due to border crawling forces until the cells are strained, creating large inward traction stresses (Fig. 3a). The monolayer area then increases linearly in time, at a faster rate than on soft gels, with a gradual increase in the magnitude of traction stresses (Fig. 3b).
Next, we investigate how the speed of cell crawling and the rate of cell additions control the spreading rate and the pattern of traction forces generated by the cell monolayer. At high cell addition rate, cell motion is pressure-driven (outward traction stresses), whereas at high crawling speeds, cell motion is crawling-driven (inward traction stresses). The interplay between pressure-driven and crawling-driven motion is regulated by substrate stiffness, as discussed previously (Fig. 3a and b). At a fixed (intermediate) value of substrate stiffness, we find that the area growth rate, measured by the rate of area increase as the monolayer doubles in size, increases with crawl speed, but is limited by the rate of cell addition (Fig. 3c). When the crawling speed is high but the cell addition rate is low, the monolayer is unable to effectively spread. When we compute the traction forces, we find large outward tractions when the cell addition rate is high (compared to cell crawling speeds), indicating pressure-driven spreading. In the limit where cells are unable to crawl but the cell addition rate is high, spreading rates still remain high, with crawling forces providing a small boost to the overall spreading rate while reducing the magnitude of traction stresses (Fig. 3d). By contrast, large inward traction forces are generated as cells stretch during spreading driven primarily by crawling forces (Fig. 3d). In this case, spreading rates are limited by the lower rate of stress relaxation stemming from newly added cells.
3 Continuum model for collective cell spreading reveals the relative roles of substrate rigidity and tissue mechanics
While the vertex model simulations describe the role of substrate rigidity and cell influx on traction force generation and monolayer spreading rate, it does not immediately reveal an intuitive understanding of the relative roles of substrate rigidity and tissue mechanics on cell monolayer spreading. To this end, we develop a continuum mean-field model for the spreading of an elastic monolayer, neglecting spatial variations in dynamics for simplicity. We consider a monolayer of N(t) cells of area ai(t) each, where 1 ≤ i ≤ N(t). Each cell is self-propelled along their polarity vector at a speed v0, and K is the area compressibility modulus or a 2D bulk modulus of each cell. Total mechanical energy of the cells in the monolayer is given by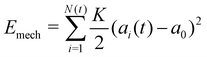 | (6) |
 | (7) |
 | (8) |
 , given by the sum of the rate of energy dissipated
, given by the sum of the rate of energy dissipated  , rate of change in free energy of the system (Ėmech) and the rate of work done by active forces (Ẇa):
, rate of change in free energy of the system (Ėmech) and the rate of work done by active forces (Ẇa): | (9) |
 with respect to ȧi:
with respect to ȧi:| μȧi = μhv0cos(θi) − K(ai − a0)h2. | (10) |
 as the total spread area of the monolayer, and A0(t) = a0N(t) as the total target area. Net self-propulsion speed is given by
as the total spread area of the monolayer, and A0(t) = a0N(t) as the total target area. Net self-propulsion speed is given by  where we made a simple mean-field assumption that cells are polarized in the direction of spreading, θi≈0, thereby neglecting spatial variations in cell polarity in the spreading monolayer. Defining V0 = hv0/a0, we get the following simple equation describing the dynamics of the spread area of the monolayer:
where we made a simple mean-field assumption that cells are polarized in the direction of spreading, θi≈0, thereby neglecting spatial variations in cell polarity in the spreading monolayer. Defining V0 = hv0/a0, we get the following simple equation describing the dynamics of the spread area of the monolayer:| Ȧ = V0A0(t) − k(A(t) − A0(t)), | (11) |
| Ȧ0 = gA0. | (12) |
The time-dependent solution for monolayer area is given by:
 | (13) |
If instead, the monolayer reference area expands at a constant rate due to a constant flux of cells from the aggregate, as reported experimentally,29 we have
| Ȧ0 = gA(0). | (14) |
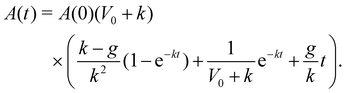 | (15) |
 . Thus, at long times the monolayer spread rate increases with the growth rate or crawl speed, but decreases with tissue stiffness. Setting the cell crawl speed and friction to increase with substrate stiffness, V0 ∝ E and k ∝ 1/E, and fitting the remaining parameters to vertex model simulations, we are able to recapitulate the trends in spread rate and traction stress as substrate stiffness is varied (Fig. 4a and b). On soft substrates, spreading is driven by pressure from cell influx. Growth of newly added cells causes an increases in the rest area of the monolayer, A0, resulting in an exponential growth in monolayer area and positive traction stress. As substrate stiffness increases, cell crawling regulates tissue spreading with monolayer area increasing linearly, outpacing the influx of cells and generating negative traction stresses. At long times, we observe a constant rate of area increase that increases with substrate stiffness, consistent with experimental data.29
. Thus, at long times the monolayer spread rate increases with the growth rate or crawl speed, but decreases with tissue stiffness. Setting the cell crawl speed and friction to increase with substrate stiffness, V0 ∝ E and k ∝ 1/E, and fitting the remaining parameters to vertex model simulations, we are able to recapitulate the trends in spread rate and traction stress as substrate stiffness is varied (Fig. 4a and b). On soft substrates, spreading is driven by pressure from cell influx. Growth of newly added cells causes an increases in the rest area of the monolayer, A0, resulting in an exponential growth in monolayer area and positive traction stress. As substrate stiffness increases, cell crawling regulates tissue spreading with monolayer area increasing linearly, outpacing the influx of cells and generating negative traction stresses. At long times, we observe a constant rate of area increase that increases with substrate stiffness, consistent with experimental data.29
4 Tissue fluidity impedes collective cell spreading independent of substrate rigidity
The continuum model for monolayer spreading predicts a simple relationship between spreading rate, substrate rigidity and tissue elasticity. This is evident from eqn (15), which leads to the relation A(t) ≈ A(0)g(1 + V0/k)t as t ≫ k−1. As the tissue stress relaxation rate k (or equivalently tissue bulk modulus K) is reduced or if substrate rigidity E is increased, the model predicts a faster rate of monolayer spreading (Fig. 4c). However, this spreading rate also depends on the speed of cell crawling, which in turn is regulated by substrate rigidity. If the crawling speeds are low, as on soft substrates, then the monolayer spreading is driven by cell influx and spreading rate is not affected by the tissue elasticity (Fig. 4d). By contrast, if the tissue has a higher relaxation rate k, then the spreading rate is less sensitive to tissue and substrate mechanical properties, as the effect of increase in crawl speed is counteracted by the higher tissue bulk modulus (Fig. 4d).To validate the predictions of our continuum model, we sought to investigate how the mechanical properties of the cells influence aggregate spreading, on soft to stiff substrates, using our active vertex model. We vary the target shape index of the cells, p0, to control tissue material properties. When p0 is low, cells are under high tension and the tissue behaves like a jammed solid. When p0 is above a critical value, p0 > 3.81 (in the absence of activity), cells are under no tension and the tissue is in a fluid state, in which the tissue has zero shear modulus.78 In this state, the cells are able to flow around each other and rearrange with no energy cost. We note that the critical target shape index for rigidity transition depends on the procedure used to generate polygonal tiling. In recent work79,80 it has been shown that the critical p0 can be larger than 3.81 in the presence of vertices with coordination number greater than or equal to four and with cells having five or less neighbors. When we vary both the target shape index and the substrate stiffness, we find that on soft substrates, changing p0 has little impact on monolayer spreading rate (Fig. 5a). On soft substrates, tissue spreading is pressure-driven (Fig. 5b), with the aggregate adding the same area of cells per unit time. Thus monolayer spreading can only be slowed down by modulating the friction with the substrate. Changing the fluidity or tension of the tissue has little effect on the isotropic bulk pressure driving monolayer spreading. However, when spreading occurs on stiff substrates, we find that cells with a lower p0, and thus higher tension, spread faster, with the monolayer spreading twice as fast at p0 = 0.5 compared to p0 = 4.5 (Fig. 5c). Moreover, the mechanosensitivity of monolayer spreading reduces as p0 increases. At high p0, changes in substrate stiffness have less effect on the rate of spreading than for low p0.
Why do fluid tissues spread slower than solid tissues (Fig. 5c)? While it is expected that cells in a fluidized tissue move faster as they can rearrange more easily,12 monolayer spreading is driven by a radially outward stress arising from active cell crawling or isotropic pressure from cell influx, where tissue shear modulus does not play a role. Fluid tissues have a zero shear modulus,78 but can still maintain a finite bulk modulus that can resist isotropic expansion of the tissue. To determine the relationship between tissue fluidity and bulk modulus, we computed cell area strain during spreading for a range of p0 values. We find that cells are much more strained at low p0, with cells area increasing by around 60% for p0 = 0.5, compared to cells area maintained at p0 = 4.5 (Fig. 5d). When we compute the energy cost per unit area for such bulk deformations in the vertex model with perfectly hexagonal cells, cells with a lower p0 require much less energy for deformation than cells with a higher p0, despite low p0 cells being under higher tension (Fig. 5e). These data suggest a counterintuitive result that tissue bulk modulus increases with increasing p0 or increasing tissue fluidity. Thus, on stiff gels where we have high forces generated by active cell crawling, decreasing tissue fluidity also reduces the bulk modulus, allows for a faster rate of monolayer spreading.
To quantify the relationship between tissue bulk modulus and target shape index, we calculate the bulk modulus K as the second derivative of energy density with respect to the area strain ε, K = (1/a*)∂2Ẽ/∂ε2, where a* is the area of the cell at equilibrium, and Ẽ is given by eqn (3). We find that the bulk modulus increases monotonically with p0 for p0 < phex ≈ 3.722, where phex is the perimeter of a hexagon of unit area (Fig. 5f). Interestingly, there is a discontinuity in bulk modulus for p0 > phex, beyond which the bulk modulus stays constant. To gain a mechanistic understanding of these results, we note that the cell area and perimeter can be written as a = a*(1 + ε) and p = p*(1 + ε)1/2. As previously shown by Staple et al.,56 taking the second derivative of Emech with respect to ε and evaluating the energy at ε = 0 one obtains K = a* + Γp*p0/4a*. For p0 < phex, a* ∝ p0 and p* ∝ a*1/2. The second term in K thus scales like a*1/2, resulting in an increase in bulk modulus with increasing cell area, which in turn increases with p0 (Fig. 5f). Since low p0 cells are under higher tension they are also smaller in size, resulting in a lower bulk modulus (Fig. 5f). Having a low p0, high tension cell corresponds to two springs in series that are softer than a single spring: while the energy cost per unit area is similar, the deformation is spread between more cells and so we have a lower overall energy cost. However, for p0 > phex, cells adapt their perimeters to the target perimeter. As a result, the perimeter term doesn't contribute to energy in eqn (3), resulting in a discontinuity in the bulk modulus. Taken together, our theory and simulations reveal the interdependence between cell shape, tissue elasticity and substrate rigidity in the spreading of cell monolayers on compliant substrates.
5 Discussion
In this study, we investigated how tissue mechanics and substrate stiffness, and their interplay, regulate the dynamics of a spreading cellular aggregate, using a combination of computational simulations and mathematical modeling. In particular, we developed an active vertex model to simulate the spreading of a cellular monolayer emanating from a three-dimensional aggregate, which is undergoing active growth as well as driven forward by cell crawling. Our simulations reveal two distinct modes of cell monolayer spreading depending on substrate rigidity. On soft substrates, cell monolayer spreading is pressure-driven, exhibiting radially outward traction stresses that originate from the influx of cells into the monolayer from the aggregate. By contrast, on stiff substrates, cell crawling forces drive monolayer expansion, generating inward traction forces localized to the periphery of the cell monolayer. Despite the different mechanisms for spreading, our simulation reveals comparable spreading rates on substrates of varying rigidity, consistent with experimental data.29 The rigidity-dependent transition from pressure-based to traction-based spreading arises in the model because of the cell–substrate coupling that increases cell polarisation, crawl speed, and traction forces with increased substrate rigidity.23,29,65–67The modes of collective cell motion and the rate of spreading is not only dependent on substrate rigidity but can also be tuned by varying the rate of cell influx from the aggregate and the speed of cell crawling. When the cell crawling speed is high relative to the cell influx rate, crawling-driven spreading dominates, with inward traction forces localized to the tissue periphery. By contrast, when crawling speeds are lower compared to cell influx rate, pressure-driven spreading drives monolayer expansion with outward traction forces distributed throughout the monolayer. However, we find that the cell addition rate is the main regulator of spreading rates, with crawling speeds only able to increase spread rates by 50%, suggesting that the influx of new cells is the limiting factor for spreading.
To further understand the cellular mechanisms controlling spreading rates, we develop a simple continuum model of the spreading tissue as an elastic medium with active growth and cell crawling. We identify the tissue bulk modulus as another important mechanical property governing the dynamics of spreading. When the cells are very stiff with a high bulk elastic modulus, our model predicts little variation of spread rates with a change in substrate stiffness or crawl speed, with the rate of cell addition governing the spreading rates. However, when the cells are soft, traction forces generated by crawling cells may produce larger strains on cells. This results in spreading rates that are very sensitive to the mechanical stiffness of the underlying substrate. To tests this prediction, we used our active vertex model to simulate monolayer spreading by varying cell stiffness through changes in the target shape index p0. When the target shape index is low, cells are under high tension but have a reduced bulk modulus. By contrast, cells with a higher target shape index result in a fluid tissue that has a high bulk modulus. As a result, cell monolayers with a lower target shape index (and consequently lower bulk modulus) spread faster on stiff substrates than on soft substrates.
Overall, these results capture previously reported data on the spreading of cellular aggregates with increased spreading rates on stiff substrates, and also explain the spatiotemporal patterns in traction stresses on soft substrates driven by active pressure, and on stiff substrates driven by active cell crawling. Moreover, our theory and simulations provide new predictions on the role of tissue mechanics on cell spreading, with fluid tissues being less sensitive to substrate rigidity and spread slower than solid tissues.
Author contributions
Michael F. Staddon: conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing. Michael P. Murrell: conceptualization, supervision, writing – review & editing. Shiladitya Banerjee: conceptualization, investigation, methodology, project administration, supervision, validation, visualization, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. B. acknowledges funding from HFSP RGY0073/2018 and NIH R35 GM143042. MPM acknowledges funding from ARO MURI W911NF-14-1-0403, NIH RO1 GM126256, NIH U54 CA209992 and HFSP RGY0073/2018.Notes and references
- P. Friedl and D. Gilmour, Nat. Rev. Mol. Cell Biol., 2009, 10, 445–457 CrossRef CAS PubMed.
- M. Behrndt, G. Salbreux, P. Campinho, R. Hauschild, F. Oswald, J. Roensch, S. W. Grill and C.-P. Heisenberg, Science, 2012, 338, 257–260 CrossRef CAS PubMed.
- F. Jülicher and S. Eaton, Seminars in cell & developmental biology, 2017, pp. 103–112 Search PubMed.
- E. Maniou, M. F. Staddon, A. R. Marshall, N. D. Greene, A. J. Copp, S. Banerjee and G. L. Galea, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(19), e2023163118 CrossRef CAS PubMed.
- M. F. Leber and T. Efferth, Int. J. Oncol., 2009, 34, 881–895 CAS.
- S. P. Carey, T. M. D’Alfonso, S. J. Shin and C. A. Reinhart-King, Critical Rev. Oncology/Hematology, 2012, 83, 170–183 CrossRef PubMed.
- P. Friedl, J. Locker, E. Sahai and J. E. Segall, Nat. Cell Biol., 2012, 14, 777–783 CrossRef PubMed.
- A. Labernadie, T. Kato, A. Brugués, X. Serra-Picamal, S. Derzsi, E. Arwert, A. Weston, V. González-Tarragó, A. Elosegui-Artola and L. Albertazzi, et al. , Nat. Cell Biol., 2017, 19, 224–237 CrossRef CAS PubMed.
- P. Martin and S. M. Parkhurst, Development, 2004, 131, 3021–3034 CrossRef CAS PubMed.
- A. Brugués, E. Anon, V. Conte, J. H. Veldhuis, M. Gupta, J. Colombelli, J. J. Muñoz, G. W. Brodland, B. Ladoux and X. Trepat, Nat. Phys., 2014, 10, 683–690 Search PubMed.
- V. Ajeti, A. P. Tabatabai, A. J. Fleszar, M. F. Staddon, D. S. Seara, C. Suarez, M. S. Yousafzai, D. Bi, D. R. Kovar and S. Banerjee, et al. , Nat. Phys., 2019, 15, 696–705 Search PubMed.
- R. J. Tetley, M. F. Staddon, D. Heller, A. Hoppe, S. Banerjee and Y. Mao, Nat. Phys., 2019, 15, 1195–1203 Search PubMed.
- C. Collins and W. J. Nelson, Curr. Opin. Cell Biol., 2015, 36, 62–70 CrossRef CAS PubMed.
- P. Friedl and R. Mayor, Cold Spring Harbor Perspect. Biol., 2017, 9, a029199 CrossRef PubMed.
- C. De Pascalis and S. Etienne-Manneville, Mol. Biol. Cell, 2017, 28, 1833–1846 CrossRef CAS PubMed.
- G. Salbreux, G. Charras and E. Paluch, Trends Cell Biol., 2012, 22, 536–545 CrossRef CAS PubMed.
- B. Ladoux and R.-M. Mège, Nat. Rev. Mol. Cell Biol., 2017, 18, 743–757 CrossRef CAS PubMed.
- S. Huveneers and J. de Rooij, J. Cell Sci., 2013, 126, 403–413 CrossRef CAS PubMed.
- L. B. Case and C. M. Waterman, Nat. Cell Biol., 2015, 17, 955–963 CrossRef CAS PubMed.
- K. V. Iyer, R. Piscitello-Gómez, J. Paijmans, F. Jülicher and S. Eaton, Curr. Biol., 2019, 29, 578–591 CrossRef CAS PubMed.
- K. E. Cavanaugh, M. F. Staddon, S. Banerjee and M. L. Gardel, Curr. Opin. Genet. Dev., 2020, 63, 86–94 CrossRef CAS PubMed.
- S. Banerjee, M. L. Gardel and U. S. Schwarz, Annu. Rev. Condens. Matter Phys., 2020, 11, 421–439 CrossRef PubMed.
- D. E. Discher, P. Janmey and Y.-L. Wang, Science, 2005, 310, 1139–1143 CrossRef CAS PubMed.
- B. Ladoux, R.-M. Mège and X. Trepat, Trends Cell Biol., 2016, 26, 420–433 CrossRef PubMed.
- S. Douezan, K. Guevorkian, R. Naouar, S. Dufour, D. Cuvelier and F. Brochard-Wyart, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7315–7320 CrossRef CAS PubMed.
- G. Beaune, T. V. Stirbat, N. Khalifat, O. Cochet-Escartin, S. Garcia, V. V. Gurchenkov, M. P. Murrell, S. Dufour, D. Cuvelier and F. Brochard-Wyart, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8055–8060 CrossRef CAS PubMed.
- G. Beaune, G. Duclos, N. Khalifat, T. V. Stirbat, D. M. Vignjevic and F. Brochard-Wyart, Soft Matter, 2017, 13, 8474–8482 RSC.
- C. Pérez-González, R. Alert, C. Blanch-Mercader, M. Gómez-González, T. Kolodziej, E. Bazellieres, J. Casademunt and X. Trepat, Nat. Phys., 2019, 15, 79–88 Search PubMed.
- M. S. Yousafzai, V. Yadav, S. Amiri, M. F. Staddon, Y. Errami, G. Jaspard, S. Banerjee and M. Murrell, Phys. Rev. X, 2022, 12, 031027 Search PubMed.
- M. Yousafzai, V. Yadav, S. Amiri, Y. Errami and M. Murrell, Phys. Rev. Lett., 2022, 128, 048103 CrossRef CAS PubMed.
- P. L. Ryan, R. A. Foty, J. Kohn and M. S. Steinberg, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 4323–4327 CrossRef CAS PubMed.
- D. Gonzalez-Rodriguez, K. Guevorkian, S. Douezan and F. Brochard-Wyart, Science, 2012, 338, 910–917 CrossRef CAS PubMed.
- X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler and J. J. Fredberg, Nat. Phys., 2009, 5, 426–430 Search PubMed.
- T. E. Angelini, E. Hannezo, X. Trepat, M. Marquez, J. J. Fredberg and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4714–4719 CrossRef CAS PubMed.
- J.-A. Park, J. H. Kim, D. Bi, J. A. Mitchel, N. T. Qazvini, K. Tantisira, C. Y. Park, M. McGill, S.-H. Kim and B. Gweon, et al. , Nat. Mater., 2015, 14, 1040–1048 CrossRef CAS PubMed.
- F. Van Roy and G. Berx, Cell. Mol. Life Sci., 2008, 65, 3756–3788 CrossRef CAS PubMed.
- T. Lecuit and A. S. Yap, Nat. Cell Biol., 2015, 17, 533–539 CrossRef CAS PubMed.
- G. Beaune, C. Blanch-Mercader, S. Douezan, J. Dumond, D. Gonzalez-Rodriguez, D. Cuvelier, T. Ondarçuhu, P. Sens, S. Dufour and M. P. Murrell, et al. , Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12926–12931 CrossRef CAS PubMed.
- M. Gupta, B. L. Doss, L. Kocgozlu, M. Pan, R.-M. Mège, A. Callan-Jones, R. Voituriez and B. Ladoux, Phys. Rev. E, 2019, 99, 012412 CrossRef CAS PubMed.
- M. H. Köpf and L. M. Pismen, Soft Matter, 2013, 9, 3727–3734 RSC.
- S. Banerjee, K. J. Utuje and M. C. Marchetti, Phys. Rev. Lett., 2015, 114, 228101 CrossRef PubMed.
- J. Notbohm, S. Banerjee, K. J. Utuje, B. Gweon, H. Jang, Y. Park, J. Shin, J. P. Butler, J. J. Fredberg and M. C. Marchetti, Biophys. J., 2016, 110, 2729–2738 CrossRef CAS PubMed.
- C. Blanch-Mercader, R. Vincent, E. Bazellières, X. Serra-Picamal, X. Trepat and J. Casademunt, Soft Matter, 2017, 13, 1235–1243 RSC.
- R. Alert and J. Casademunt, Langmuir, 2018, 35, 7571–7577 CrossRef PubMed.
- S. Banerjee and M. C. Marchetti, Cell Migrations: Causes and Functions, 2019, 45–66 CAS.
- B. A. Camley, J. Zimmermann, H. Levine and W.-J. Rappel, Phys. Rev. Lett., 2016, 116, 098101 CrossRef PubMed.
- J. Zimmermann, B. A. Camley, W.-J. Rappel and H. Levine, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2660–2665 CrossRef CAS PubMed.
- A. Szabó, R. Ünnep, E. Méhes, W. Twal, W. Argraves, Y. Cao and A. Czirók, Phys. Biol., 2010, 7, 046007 CrossRef PubMed.
- M. H. Swat, G. L. Thomas, J. M. Belmonte, A. Shirinifard, D. Hmeljak and J. A. Glazier, Methods Cell Biol., 2012, 110, 325–366 Search PubMed.
- A. G. Fletcher, M. Osterfield, R. E. Baker and S. Y. Shvartsman, Biophys. J., 2014, 106, 2291–2304 CrossRef CAS PubMed.
- D. L. Barton, S. Henkes, C. J. Weijer and R. Sknepnek, PLoS Comput. Biol., 2017, 13, e1005569 CrossRef PubMed.
- M. F. Staddon, D. Bi, A. P. Tabatabai, V. Ajeti, M. P. Murrell and S. Banerjee, PLoS Comput. Biol., 2018, 14, e1006502 CrossRef PubMed.
- D. Bi, X. Yang, M. C. Marchetti and M. L. Manning, Phys. Rev. X, 2016, 6, 021011 Search PubMed.
- T. Nagai and H. Honda, Philos. Mag. B, 2001, 81, 699–719 CrossRef CAS.
- R. Farhadifar, J.-C. Röper, B. Aigouy, S. Eaton and F. Jülicher, Curr. Biol., 2007, 17, 2095–2104 CrossRef CAS PubMed.
- D. B. Staple, R. Farhadifar, J.-C. Röper, B. Aigouy, S. Eaton and F. Jülicher, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 117–127 CrossRef CAS PubMed.
- S. Alt, P. Ganguly and G. Salbreux, Philos. Trans. R. Soc., B, 2017, 372, 20150520 CrossRef PubMed.
- B. Szabo, G. Szöllösi, B. Gönci, Z. Jurányi, D. Selmeczi and T. Vicsek, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061908 CrossRef CAS PubMed.
- H. Chaté, F. Ginelli, G. Grégoire, F. Peruani and F. Raynaud, Eur. Phys. J. B, 2008, 64, 451–456 CrossRef.
- S. Henkes, Y. Fily and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 040301 CrossRef PubMed.
- G. Peyret, R. Mueller, J. d’Alessandro, S. Begnaud, P. Marcq, R.-M. Mège, J. M. Yeomans, A. Doostmohammadi and B. Ladoux, Biophys. J., 2019, 117, 464–478 CrossRef CAS PubMed.
- D. M. Sussman, Comput. Phys. Commun., 2017, 219, 400–406 CrossRef CAS.
- E. N. Schaumann, M. F. Staddon, M. L. Gardel and S. Banerjee, Mol. Biol. Cell, 2018, 29, 2835–2847 CrossRef CAS PubMed.
- S. Walcott and S. X. Sun, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7757–7762 CrossRef CAS PubMed.
- A. Zemel, F. Rehfeldt, A. Brown, D. Discher and S. Safran, Nat. Phys., 2010, 6, 468–473 Search PubMed.
- L. Trichet, J. Le Digabel, R. J. Hawkins, S. R. K. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933–6938 CrossRef CAS PubMed.
- P. W. Oakes, S. Banerjee, M. C. Marchetti and M. L. Gardel, Biophys. J., 2014, 107, 825–833 CrossRef CAS PubMed.
- A. Pathak and S. Kumar, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10334–10339 CrossRef CAS PubMed.
- B. L. Bangasser, G. A. Shamsan, C. E. Chan, K. N. Opoku, E. Tüzel, B. W. Schlichtmann, J. A. Kasim, B. J. Fuller, B. R. McCullough and S. S. Rosenfeld, et al. , Nat. Commun., 2017, 8, 1–10 CrossRef PubMed.
- M. R. Ng, A. Besser, G. Danuser and J. S. Brugge, J. Cell Biol., 2012, 199, 545–563 CrossRef CAS PubMed.
- K. A. Brakke, Exper. Math., 1992, 1, 141–165 CrossRef.
- L. Onsager, Phys. Rev., 1931, 37, 405 CrossRef CAS.
- M. Doi, S. F. Edwards and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988, vol. 73 Search PubMed.
- M. Doi, J. Phys.: Condens. Matter, 2011, 23, 284118 CrossRef PubMed.
- S. Banerjee, N. F. Scherer and A. R. Dinner, Soft Matter, 2016, 12, 3442–3450 RSC.
- Y.-H. Zhang, M. Deserno and Z.-C. Tu, et al. , Phys. Rev. E, 2020, 102, 012607 CrossRef CAS PubMed.
- H. Wang, T. Qian and X. Xu, Soft Matter, 2021, 17, 3634–3653 RSC.
- D. Bi, J. Lopez, J. M. Schwarz and M. L. Manning, Nat. Phys., 2015, 11, 1074–1079 Search PubMed.
- M. Merkel, K. Baumgarten, B. P. Tighe and M. L. Manning, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6560–6568 CrossRef CAS PubMed.
- S. Tong, N. K. Singh, R. Sknepnek and A. Košmrlj, PLoS Comput. Biol., 2022, 18, e1010135 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00757f |
| This journal is © The Royal Society of Chemistry 2022 |