Development of a transferable coarse-grained model of polydimethylsiloxane

Abstract

Polydimethylsiloxane (PDMS) is a popular silicon-based polymer with advanced applications in microfluidics and nanocomposites. The slow dynamics of polymer chains in such complex systems hinders molecular dynamics investigations based on all atom force fields. This limitation can be overcome by exploiting finely tuned coarse-grained (CG) models. This paper develops a transferable CG model of PDMS, compatible with the recent Martini 3 force field, using structural and thermodynamic properties as targets in the parametrization, including a vast set of experimental free energies of transfer. We validate the model transferability by reproducing the correct scaling laws for the PDMS gyration radius in the melt and good and bad solvents. We successfully test the model by reproducing the wetting behavior of water and acetonitrile on PDMS and the phase behavior of a PDMS–peptide triblock copolymer system. This work sets the stage for computational studies involving the interaction between PDMS and many synthetic and biological molecules modeled within the Martini framework.

---

Introduction

Silicones are polymers constituted by a flexible silicon–oxygen chain and two organic functional groups bonded to each silicon atom. The two functional groups in polydimethylsiloxane (PDMS) are methyls (see Fig. 1(a)).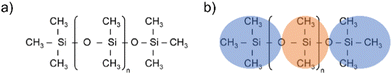

Fig. 1 (a) PDMS chemical structure, (b) Atomistic and CG representations of PDMS. Orange areas represent the core beads (), blue areas represent the end beads ().

PDMS is widely used in both everyday and highly technological applications. Some of the most relevant physical properties of PDMS are optical transparency, biocompatibility, low surface energy, and flexibility provided by the siloxane bonds of its chain.¹ Furthermore, PDMS is thermally and electrically insulating and has high gas permeability. Since it is inert and non-toxic, PDMS applications include contact lenses, anti-foaming agents for food, shampoos, and lubricants. PDMS is also one of the polymers with the lowest glass transition temperatures (T_g ≈ −125 °C).^2,3

At standard temperature and pressure conditions, non-crosslinked PDMS may be a viscous liquid or semi-solid, depending on the length of the chains. Therefore, PDMS is often used in the form of a silicone elastomer obtained by curing: in this form, it is one of the most common materials used to mold microfluidic devices.^4–7

In its unmodified form, PDMS is very hydrophobic (for example, too hydrophobic to be filled with capillary forces⁸); it can be subject to fouling or too permeable to small hydrophobic molecules that can cause unwanted swelling and solvent diffusion.⁹ Tailoring PDMS modifications with specific requirements is a highly exploited strategy to fix these limitations and enhance the material properties.² Surface and bulk modifications expand PDMS usability, particularly in lab-on-a-chip devices, microfluidics, biomedical devices, and soft lithography.^10,11 PDMS can also be combined with polypeptides to build block copolymers materials.¹² In this context, molecular simulations can be a fundamental tool to predict the behavior of modified PDMS, allowing for high-resolution investigations of its structure, dynamics, and interactions. Computer simulations can thus contribute to the knowledge-based design of PDMS-based materials.

The design of PDMS nanocomposites is another area of growing scientific interest. Both structural and conductivity properties of PDMS can be tailored by adding different kinds of nanofillers to the polymer matrix.^13,14 However, the characterization of PDMS nanocomposites, both from the structural and dynamical points of view, can be experimentally daunting. Most often, the experiments do not allow the study of the PDMS–nanofiller interaction with the required spatial resolution to investigate, for instance, the molecular mechanisms that determine the filler retention and release. Once again, computer simulations can be a valuable tool to complement experimental studies with high spatial and time resolution insights.

The main limitation of molecular dynamics (MD) simulations based on atomistic models is their computational cost: the space and time scales sampled within a single simulation are limited to a few tens of nm and 10–20 microseconds. This limit is critical in the case of simulations involving polymers with long chains, which have very slow dynamics. A practical solution to this problem is coarse-grained (CG) modeling, which consists of lowering the resolution of the models reducing the degrees of freedom of the systems to reach for longer space and time scales.

To the best of our knowledge, only two coarse-grained PDMS models are present in the literature. A Martini 2¹⁵ model for PDMS is provided by Johnson et al.,¹² who focused on the study of poly(γ-benzyl-L-glutamate)-b-polydimethylsiloxane-b-poly(γ-benzyl-L-glutamate) (GSG) triblock copolymers systems. While developed within the framework of Martini 2, the transferability of the model had not been tested. Indeed, the PDMS non-bonded parameters were validated only for the PDMS self-interaction, while the interactions with the polypeptide had been artificially reduced to simulate the strong segregation limit. A more recent coarse-grained model of PDMS has been developed by Huang et al.,¹⁶ who focused on the structural, thermal, and mechanical properties of the PDMS melt. The Huang model uses polynomial expansions up to the fourth-order for bonded interactions and temperature-dependent non-bonded terms, adjusted to correctly reproduce the temperature dependence of the polymer density, its surface tension, vaporization enthalpy, and glass transition temperature. While ideally suited to study melts or cured PDMS matrixes, this is a standalone model since no validated PDMS interactions with the rest of the chemical space exist. Therefore, the main shortcomings of both existing CG models of PDMS lie in their very limited transferability.

To build a transferable PDMS CG model, we chose to rely on the latest version of the widely used Martini force field, Martini 3.¹⁷ Initially designed for lipids and biomolecular systems, the Martini force field has recently found many applications in materials science.¹⁸ It has been used to simulate polymeric systems, with several Martini 2 polymer models available in the literature (a non-exhaustive list includes ref. 19–25). Martini 3 is expected to improve the force field applicability in soft matter science. More specifically, the introduction of a new bead size, the tiny size, and the use of the center of geometry in the parametrization stage should improve the description of molecular packing, positively affecting the structural properties of polymer melts. Moreover, a rebalancing of all non-bonded interaction terms, including new bead types, interaction levels, and labels, allows the parametrization of many systems with more precise chemical specificity.

In this work, we develop a transferable PDMS model, fully compatible with the Martini 3 force field. We show that our model correctly reproduces structural and thermodynamic properties of PDMS in the melt and dilute conditions, both in good and bad solvents, while being suited for studying the interaction of PDMS with a large variety of molecules, covering most of the chemical space that can be described within the Martini framework. As a test application, we reproduce the phase behavior of the PDMS/peptide GSG triblock copolymer system.¹²

Methods

Atomistic model

Our PDMS atomistic parameters relied on some previous all-atom classical force fields obtained from quantum chemistry calculations and validated against experimental data. To describe non-bonded interactions, Smith et al.²⁶ used a Coulomb term for the electrostatic part and a Buckingham potential for the van der Waals interactions. The Buckingham potential describes the repulsive term of the VDW interactions more accurately than a Lennard Jones (LJ) potential,²⁷ but it is computationally more expensive. Therefore, we adopted a classic 12-6 LJ potential for our model, and we derived its parameters to reproduce the original Buckingham potential at best. In particular, we took the parameters of the self-interactions from Shi et al.,²⁸ while we obtained those of the mixed interactions (C–H, C–O, O–H, Si–O, and Si–C) from the fit of Fig. SI1 (ESI†). The Si–H interaction was calculated with the Lorentz–Berthelot combination rule. We choose the partial atomic charges according to Smith. We slightly adjusted the partial charges for the terminal groups of the chains to keep the polymer charge neutrality. In Tables SI1 and SI2 (ESI†), we report all the non-bonded parameters.

Smith included cubic and quartic terms for the bond and angle contributions to describe bonded interactions. However, we used harmonic potentials for bonds and angles for better computational efficiency, following Sok et al.²⁹ Since Sok developed a united atom model for PDMS, we could use only the bond and angle parameters of the interactions not involving H atoms. From ref. 26, we used the quadratic terms for the remaining bond or angle interactions and the periodic potential parameters for proper dihedrals. Table SI3 and Fig. SI2a (ESI†) show our final set of bonded parameters.

Once we set the bonded and non-bonded interactions, we verified that our PDMS atomistic model could reproduce some of the structural properties of the polymer melt. Specifically, we took melt density (ρ) and gyration radius (R_g) as targets from reference atomistic simulations and experiments. Both ρ and R_g were computed from 200 ns MD runs and the results are reported in the ESI† (Fig. SI2b, c and Table SI4). The density values are a bit smaller than the one obtained in the benchmark atomistic model²⁸ but in excellent agreement with the experimental value obtained by Arrighi et al.³⁰ We computed the scaling of the gyration radius vs. the molecular weight (M_w) and compared the model prediction to the experimental scaling coefficient obtained by Arrighi³⁰ with SANS measurements on low molecular weight PDMS (M_w < 15 000), finding again an excellent agreement.

Atomistic unbiased simulation set up

Simulations were performed with a time step of 1 fs in the NPT ensemble, using the velocity-rescale thermostat³¹ (t = 1 ps) and the Berendsen barostat³² (P = 1 bar, t = 1 ps). The intramolecular non-bonded interactions for atoms separated by less than three bonds were excluded, while the 1–4 non-bonded interactions were scaled by 0.5. We used a Verlet cutoff scheme with a radius of 12 Å for calculating the Lennard-Jones interactions with a switch function and the Fast Smooth Particle-mesh Ewald (PME) method for computing electrostatic interactions.

The parametrization of CG bonded interactions relied on atomistic simulations of a PDMS melt. A simulation box containing 300 PDMS chains composed of 17 monomers (PDMS17) was first equilibrated in the NVT ensemble at T = 300 K for 50 ps. We chose such a short chain to obtain an equilibrated all atom melt and to be consistent with the reference atomistic simulations of Shi et al.²⁸ The target properties, namely the melt density and radius of gyration, were calculated from a production run of 200 ns at T = 300 K.

Coarse-grained unbiased simulation set up

We ran CG MD simulations with a time step of 20 fs. We used a Verlet cutoff to update the neighbor list in combination with a straight cutoff of 1.1 nm and a potential shift to zero at the cutoff distance.³³ For the simulations in the NPT ensemble, we used the velocity-rescale thermostat³¹ (t = 1 ps) and the Parrinello–Rahman barostat³⁴ (P = 1 bar, t = 12 ps). The temperature and pressure of the CG simulations were the same as the atomistic ones.

Coarse-grained free energy calculations set up

To tune the non-bonded interactions, we computed the partition free energy of small molecules between PDMS and Martini water (standard size) through Thermodynamic Integration³⁵ (TI). TI involves the integration of the average derivative Hamiltonian with respect to a coupling parameter λ. In TI the coupling parameter array controls the decoupling of the LJ interactions. In our simulations, this array consisted of ten values of λ equally spaced between 0.0 and 1.0. We followed the thermodynamic cycle shown in Fig. 2(a).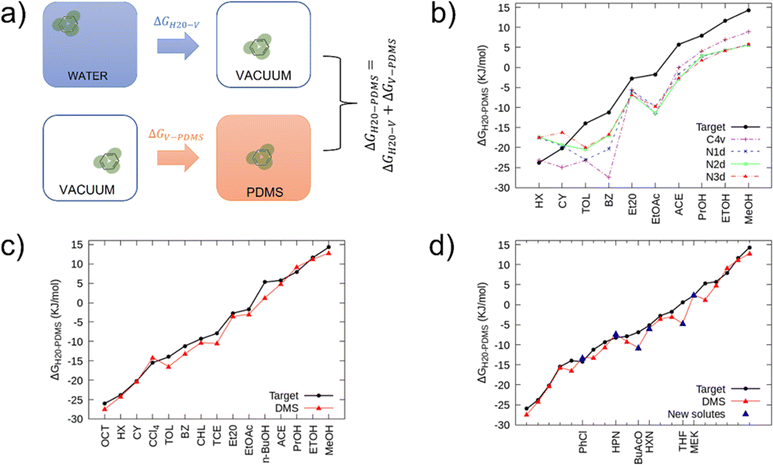

Fig. 2 (a) Graphical representation of the Thermodynamic Integration procedure used to obtain the free energy of transfer between water and PDMS, which consists of merging the results from two independent simulations. With the first, one can compute the free energy of transfer of a small molecule from water to vacuum (ΔG_H20-V), and with the second the free energy of transfer from vacuum to PDMS (ΔG_V-PDMS). Summing the two free energies, one obtains the desired result: ΔG_H20-PDMS. (b) Free energies of transfer of several small molecules between water and PDMS oil. The thick black line represents the experimental target,³⁹ while the dashed and dotted lines are the free energies of transfer obtained with TI calculations using different Martini 3 beads to describe PDMS. The abbreviations used for the solutes are reported in Table 2. (c) Comparison between the experimental target³⁹ (thick black line) and the free energies of transfer obtained with TI (thin red line) using the new set of energy levels between the DMS bead and the already existing Martini 3 beads that compose the solutes. (d) New DMS bead validation: comparison between the experimental data,³⁹ the set of solutes used during the targeting stage, and six new solutes (blue triangles) including different Martini 3 beads. In figures (b), (c), and (d) the error bars are smaller than data symbols.

The GROMACS²⁷ bar module performed the integration through the Bennet acceptance ratio (BAR) method.³⁶ During the creation or annihilation of particles, TI can suffer from instabilities, due to possible particle overlapping. This problem is usually addressed by using soft core potential functions that keep pairwise interactions finite at short distances. We used the following softcore potential V_sc(r):

where V^A and V^B are the normal hard-core LJ potentials in state A (λ = 0) and state B (λ = 1) respectively.²⁷ In our simulations, the soft-core parameter α was set to 0.5 and the soft-core λ power p was set to 1 to specify that the change in the interaction is linear in λ. σ is the radius of the interaction.

The simulated system consisted of a molecule of solute inserted in either a box of 80 PDMS25 chains or a box of 1280 water molecules. Solvent models are all part of the latest Martini 3 release.^17,37

Calculation of the radius of gyration

The target property we chose for the CG model validation was the gyration radius of PDMS in different solvents and the melt. We used water, cyclohexane, hexane, and PDMS as solvents and made various simulations using different degrees of polymerization, namely PDMS chains made of 10, 50, 100, 150, and 250 monomers. We inserted one PDMS chain in a big solvent box for each length. After the minimization and equilibration steps, we performed an MD run of 5 μs. Then, the GROMACS tool polystat calculated R_g(t) from the trajectory data. Once convergence was achieved, we used the rest of the run to compute the average value and the standard error. In the case of the PDMS melt, where convergence was longer to achieve, we increased the duration of the simulation run to 30 μs.

List of simulations

Table SI5 (ESI†) reports the details of all the atomistic and CG simulations described above. We used the GROMACS 20 MD package to perform all the simulations. Starting configurations of atomistic and CG melts were generated with the python suite Polyply.³⁸

Results

We followed the standard workflow to develop the coarse-grained model:

• Mapping coarse-grained beads on top of the atomistic structure

• Tuning bonded interactions based on atomistic data

• Tuning non bonded interactions based on experimental thermodynamic data

• Validation based on reproduction of atomistic data

Choice of PDMS mapping

The first step of the CG model development procedure is mapping the PDMS atomistic structure into its coarse-grained analog, obtained by grouping atoms into CG beads. The usual choice for Martini models is a four-to-one mapping scheme, in which a single interaction center represents four heavy atoms and their associated hydrogen atoms. The most trivial choice for PDMS would be grouping one monomer into one bead. In this way, however, an asymmetric configuration is obtained since it would be necessary to introduce two other beads to map the closures of the chain. Instead, we decided to split the oxygen atoms between neighboring beads (see Fig. 1(b)), as already done by Huang.¹⁶ In this case, only two kinds of beads are necessary to map the molecule: one for the end groups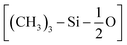 and one for the core groups 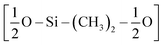. The obtained CG configuration of PDMS is therefore more symmetric with this mapping choice.

Derivation of bonded interactions – targeting atomistic distributions

As first suggested by Rossi et al.,²⁰ the Martini philosophy for developing a polymer model consists of matching bond and angle distributions from atomistic reference simulations while tuning the non-bonded interactions against free energies of transfer and long-range structural properties. To set the bonded parameters, we used as targets the distributions of bonds, angles, and dihedrals obtained at the atomistic level. We converted a 200 ns atomistic PDMS melt trajectory into the corresponding CG one, obtaining the trajectory of the centers of geometry of the groups of PDMS atoms that constitute a bead. From the latter, we extracted the target distributions.

In the CG model we used the GROMACS harmonic function for bonds and angles distributions and the periodic-type function for proper dihedrals.²⁷ We set up a coarse-grained melt with the same size and composition of the atomistic target. With an iterative procedure, we changed the parameters of the bonded potentials (force constants and equilibrium lengths, angles, and dihedral angles) until we reached a satisfactory agreement between CG and atomistic distributions on the position of the peaks and the width of distributions.

Table 1 shows the optimized parameters. The final CG bond distributions, in Fig. SI3 (ESI†), show excellent agreement with the atomistic target. The angle and dihedral distributions show a good agreement, keeping in mind the structural simplification of the coarse-grained model (four heavy atoms in one bead). The deviations from the atomistic distribution are however comparable with the ones obtained in previous Martini polymer models.^19,20,23

Table 1 CG PDMS bonded parameters. E and C indicate the end beads and the core beads, respectively. The functional forms of the potential for bonds, angles, and dihedrals are the same as those used for the atomistic model. The parameters b₀ (nm) and k_b (kJ mol⁻¹ nm⁻²) are the equilibrium bond length and the elastic constant of the harmonic bond potential. θ₀ (deg) and k_θ (kJ mol⁻¹) are the equilibrium angle and the harmonic angle potential elastic constant. k_φ and φ₀ are the dihedral force constant and the equilibrium angle between the ijk and jkl planes; n is the multiplicity

Bonds	k b (kJ mol^−1 nm^−2)	b 0 (nm)
E–C	11 000	0.446
C–C	11 500	0.448
C–E	11 000	0.446

---

Angles	k θ (kJ mol^−1)	θ 0 (deg)
E–C–C	78	87
C–C–C	45.89	86
C–C–E	78	87

---

Dihedrals	k φ (kJ mol^−1)	φ 0 (deg)	n
E–C–C–C	1.2	1.85	1
C–C–C–C	1.4	1.18	1
C–C–C–E	1.2	1.85	1

---

Derivation of non bonded interactions

The core of our PDMS model development is the tuning of non-bonded interactions. We used the experimental partition coefficient of small molecules between PDMS oil and water as a target. The partition coefficient (P) is related to the free energy of transfer (ΔG) as follows:

ΔG_H20-PDMS = ΔG_H20-V + ΔG_V-PDMS = RT ln P, (2)

where ΔG_H20-V is the free energy of transfer between water and vacuum and ΔG_V-PDMS is the free energy of transfer between vacuum and PDMS. Fig. 2(a) shows a scheme of the TI procedure used to obtain ΔG_H20-PDMS. Thanks to a large set of experimental data of partition coefficients of small molecules,³⁹ many of which were already parametrized in Martini 3, we tuned the interactions between PDMS and almost all P, N, and C bead types with high precision. Table 2 reports all the small molecules used for the simulations and their corresponding Martini 3 bead types.

Table 2 Partition coefficients of small molecules between water and PDMS-oil. Experimental data for different solutes and the Martini 3 beads that constitute them. Solutes in bold were not used at the stage of model development, but only during model validation. H/P is the ratio between air/water Henry's constant (H) and the partition coefficient between air and silicon oil (P_air); it corresponds to the partition coefficient between water and silicon oil

Solutes	Martini beads	H/Pair	ΔG (kJ mol^−1)
Octane (OCT)	C1	33 422	−25.98
n-Hexane (HX)	SC2	13 791	−23.8
Cyclohexane (CY)	SC3	3336	−20.2
Tetrachloromethane (CCl4)	X1	490	−15.4
Toluene (TOL)	SC4, TC5	274	−14
Chlorobenzene (PhCl)	SX3, TC5	298	−14.21
Benzene (BZ)	TC5	90	−11.2
Chloroform (CHL)	X2	43	−9.38
Hepta-2-one (HPN)	C2, N6a	27	−8.22
Trichloroethene (TCE)	X3h	24	−7.9
n-Butyl acetate (BuAcO)	C2, SN4a	16	−6.91
Hexa-2-one (HXN)	C2, SN6a	8	−5.19
Diethyl ether (Et2O)	N2	3	−2.74
Ethyl acetate (EtOAc)	TC3, SN4a	2	−1.73
Tetrahydrofuran (THF)	TN4a, SC3	0.8	0.56
Butanone (MEK)	N4ah	0.4	2.28
Butanol (n-BuOH)	TC2, SP1	0.12	5.28
Acetone (ACE)	N5a	0.1	5.74
1-Propanol (PrOH)	N6	4.1 × 10^−2	7.97
Ethanol (EtOH)	SP1	9.7 × 10^−3	11.6
Methanol (MeOH)	SP2r	3.3 × 10^−3	14.3

---

At first, we employed already existing Martini beads to represent PDMS and compared the partition coefficients of ten small molecules with their experimental targets. Fig. 2(b) shows the TI results obtained with various Martini 3 beads (N1d, N2d, N3d, C4v) modeling PDMS.

As one can notice, only a few free energies are reproduced satisfactorily, namely within the typical accuracy of the Martini force field (3–5 kJ mol⁻¹). None of the selected beads can reproduce the correct trend and changing the bead types improves only some of the interactions at the expense of some others.

We thus addressed the new goal to create a Martini 3 compatible bead modeling the PDMS monomer while still using the energy levels already defined in the force field.

The first step of parametrizing the new bead was the refinement of the self-interactions: we fixed σ at 0.51 nm and reduced ε to 3.07 kJ mol⁻¹ to reproduce the density and gyration radius (Fig. SI4, ESI†) of the melt at best. Then, we tuned the interactions between PDMS and the other beads until we found a satisfactory agreement, reported in Fig. 2(c), between our results and the experimental target. We obtained a final average discrepancy between the target and the calculated data of only 1.3 kJ mol⁻¹ (∼0.5 k_BT). In this way, we obtained the correct set of non-bonded interaction parameters between the new bead, called DMS, and the bead types that constitute the solutes listed in Fig. 2(c).

Validation of the DMS bead – partitioning of new molecules

So far, through the targeting procedure explained above, we obtained the correct interaction levels for a certain number of Martini 3 beads, corresponding to the fifteen solutes of Fig. 2(c) Now, we wanted to verify the reliability of the targeting procedure by checking the partition coefficients of some new solutes that were not in the target set. Table 2 shows the experimental data relative to six new solutes (solutes in bold) described in the Martini force field by the same bead types of the previous solvents, but with different sizes and labels. Then, starting from the set of parameters we fixed before, we applied the Martini 3 rules to obtain the correct interactions with the new solutes. Finally, we computed the partition coefficients using the TI procedure. Fig. 2(d) shows the free energies obtained with the DMS bead for both the solutes employed for the targeting (red line) and the test procedure (blue triangles). The average discrepancy between the target and the new data is 1.9 kJ mol⁻¹, while the larger discrepancy is about 5 kJ mol⁻¹, which is comparable to the typical errors of the Martini force field.

Validation of the PDMS chain – scaling of gyration radius in different solvents

We performed a second model validation against a structural property, namely the gyration radius. At first, to qualitatively test the transferability of the model, we checked if the PDMS molecule took different structures while solvated into different kinds of solvents, from good to bad solvents. As expected, Fig. 3(a) and (b) show that PDMS stretches out in hexane, which is a good solvent, and contracts in water, which is a bad solvent. Then, to be more quantitative, we tested the scaling law that links R_g to the degree of polymerization (N) for PDMS chains in various solvents. The gyration radius increases exponentially with N, according to

R_g ∝ N^ν, (3)

where the exponent ν takes different values depending on the type of solvent: 1/3 for bad solvents, 1/2 for theta solvents, and 3/5 for good solvents. According to the experimental measurements of Arrighi,³⁰ν = 0.53 ± 0.03 for the PDMS melt.

Fig. 3 (a) Snapshot of the simulation of a hexane box containing one PDMS chain composed of 250 monomers. (b) Snapshot of the simulation of a water box containing one PDMS chain composed of 250 monomers. Since water is a bad solvent for PDMS, the molecule takes a globular conformation, while the PDMS chain swells in hexane. (c) Scaling law of the gyration radius (R_g) with the degree of polymerization (N) in logarithmic scale for a PDMS chain in hexane. (d) Validation results summary that shows the exponent (ν) values of the scaling law of PDMS gyration radius in different solvents. The targets result from the theoretical scaling law (2) in the case of hexane (HEX), cyclohexane (CY), and water (WAT), and the experimental data for PDMS. In figures (c), and (d) the error bars for the calculated data are smaller than the data symbols.

We computed the gyration radii from 5 μs production runs, except for the PDMS melt, for which we needed to increase the simulation duration to 30 μs to achieve convergence. To test the scaling law, we fitted the R_g data in Table SI6 (ESI†) with a logarithmic function (ln(R_g) = C + ν ln(N)), where C is the proportionality constant, and ν is the factor distinctive of the type of solvent.

Fig. 3(c) and Fig. SI5 (ESI†) show the fits relative to hexane, cyclohexane, water, and PDMS. Fig. 3(d) and Table SI7 (ESI†) report the results obtained for ν, which are in satisfactory agreement with the theoretical prevision of the scaling law. Furthermore, when excluding the values of R_g at low molecular weight from the fit of ν in the PDMS melt, we obtained ν ∼ 0.5, in agreement with the ideal chain model. The result obtained in cyclohexane showed a slightly worse agreement. However, the magnitude of the discrepancy is comparable with those obtained in previous Martini polymer works.^20,23 Therefore, we considered our PDMS model fully validated. Example topologies of PDMS chains and interaction parameters can be downloaded from our open repository.⁴⁰ We remark that interactions between the DMS bead and charged Martini beads were not tuned and thus are not present in the parameter file.

We now move to a more complex test application of the PDMS model.

Test application

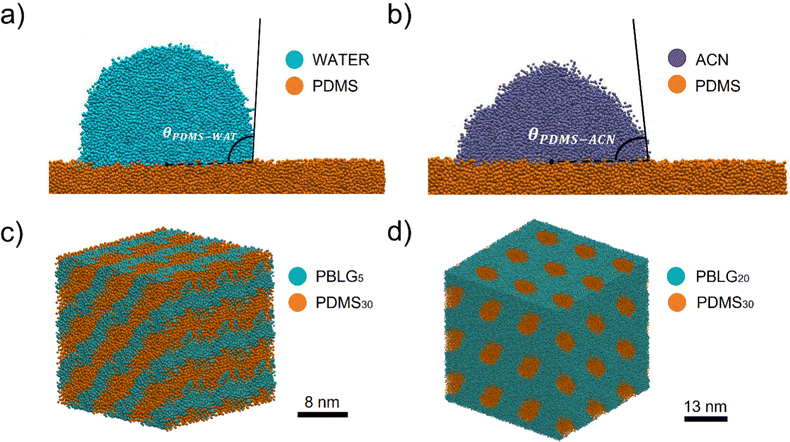
We tested our system on two different applications. First, we investigated the wettability of a PDMS surface, through contact angle calculations. Then, we reproduced the phase behavior of a PDMS-based copolymer.

Contact angle calculations. We computed the contact angles of water and acetonitrile on PDMS. Given the importance of water–PDMS interaction in microfluidics systems, several data can be found in literature regarding the contact angle of water on PDMS. Experimental^41–45 and computational^46,47 studies give values in the range of 100–115° for water–PDMS contact angle. He et al.⁴⁵ report a contact angle of 90° ± 5° for acetonitrile, a conventional solvent for DNA synthesis.

For each solvent we performed a set of five independent simulations in the NVT ensemble at 298 K. The system consisted of an equilibrated PDMS slab and a cylindrical solvent droplet. Fig. 4(a) and (b) show a section of the system perpendicular to the cylinder axis. To compute the contact angle, we did a circular cap fit to the isodensity contour of the solvent–vacuum interface. More information on the system set-up and contact angle calculations can be found in the ESI.†

Fig. 4 PDMS model test applications. Representative configuration of (a) water and (b) acetonitrile cylindrical droplets on a PDMS substrate, taken from the simulations used to compute the contact angle of the two solvents on PDMS. (c) Final configuration (with periodic representations of the original box) of the G₅S₃₀G₅ triblock with the formation of lamellar domains. (d) Final configuration with periodic representations (three boxes in each direction) of the G₂₀S₃₀G₂₀ triblock with hexagonally packed PDMS cylinders. The box side length matches that of the bar.

We obtained the following values for the contact angles:

• θ_w = 110° ± 2° for water

• θ_acn = 83° ± 3° for acetonitrile,

in good agreement with experimental references.

Triblock copolymer phase behavior. The second system we chose to test our new PDMS model is a poly(γ-benzyl-L-glutamate)-b-polydimethylsiloxane-b-poly(γ-benzyl-L-glutamate) (GSG) triblock copolymer. The GSG triblock in Fig. SI6 (ESI†) comprises two rigid rod-like liquid crystal blocks formed by polypeptides poly(γ-benzyl-L-glutamate), called PBLG, and a soft, central PDMS block.⁴⁸ The copolymer self-assembly behavior depends on the peptide-PDMS ratio.

In particular, experimental⁴⁸ and computational¹² data suggest that, at fixed PDMS content, copolymers with short peptide chains (e.g. G₅S₃₀G₅) self-assemble in lamellar structures, while copolymers with longer peptide chains (e.g. G₂₀S₃₀G₂₀) self-assemble into hexagonal patterns. SAXS measurements by Ibarboure et al.⁴⁸ suggest domain spacing of about 7 nm for the lamellar structure and 10 nm for the hexagonally packed PDMS cylinders.

After adapting and validating Johnson's PBLG Martini 2 model to Martini 3 (details in the ESI†), we tested the phase behavior of G₅S₃₀G₅ and G₂₀S₃₀G₂₀, built with the new DMS bead.

Fig. 4(c) and (d) show the final configuration of the GSG triblock with the formation of lamellae and hexagonally packed PDMS cylinders, respectively. We obtained a domain spacing of 7 nm for the lamellae and a domain spacing of about 13 nm for the cylinders, both in agreement with the experimental ref. 48.

We can conclude that our PDMS model correctly reproduces the different phase separation between the polymer and the peptide blocks when varying the peptide block length.

Conclusions

In this work, we developed, validated, and tested a transferable coarse-grained model for PDMS based on the most recent update of the Martini force field. We built the model by means of atomistic reference simulations to tune the bonded interactions, and by using large experimental partitioning data to tune the non-bonded interactions. Since Martini 3 did not include a bead able to represent the chemical specificity of the PDMS monomer (containing a Si atom), we created a new one, called DMS, which obeys the Martini rules and makes the PDMS model transferable to virtually any environment. Indeed, our model correctly reproduces the density and radius of gyration of PDMS in its melt while satisfactorily reproducing the gyration radius scaling laws in bad (water) and good (hexane, cyclohexane) solvents. As final test applications, proving once again the model transferability, we verified that our PDMS model correctly reproduces the water/acetonitrile contact angles on PDMS and the phase behavior of GSG triblock copolymers.

This work sets the stage for various future investigations. The subsequent developments will include an automated procedure to simulate the crosslinking procedure, allowing for studying a cured PDMS matrix.^49,50 The transferability of the model will allow studies involving the PDMS used as a solvent,⁵¹ as a matrix containing nano-particles of different kinds (nano-composites),⁵² or, by specific functionalizations, as a basis to obtain materials with tunable surface properties. Furthermore, since the Martini 3 force field includes a DNA model, our PDMS model opens up the possibility to complement experimental microfluidic studies involving PDMS and DNA with sub-molecular resolution simulations of their interaction.⁷

Furthermore, it is worth recalling that silicon compounds were not included in the set of molecules used to tune the interactions between Martini 3 beads.¹⁷ The new DMS bead is the first Martini bead suited to reproduce the chemical specificity of a Si-containing group and thus provide a starting point to develop a new block of beads designed to describe silicon compounds. This addition to the Martini 3 force field will pave the way to the simulation of systems of great interest to material sciences,^53,54 like engineered mesoporous silica nanoparticles, together with the possibility to investigate their interaction with the biological environment.

Author contributions

We strongly encourage authors to include author contributions and recommend using CRediT for standardised contribution descriptions. Please refer to our general author guidelines for more information about authorship.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

SC, GR and DB acknowledge MUR for funding computational resources (DIFI – Dipartimento di eccellenza 2018-2021). SC, GR and DB acknowledge funding from the SUNSHINE project (H2020, grant number 952924). The authors thank Fabian Grünewald from the University of Groningen for useful discussions.

Notes and references

1. J. E. Mark, Some interesting things about polysiloxanes, Acc. Chem. Res., 2004, 37(12), 946–953,  DOI:10.1021/ar030279z.
2. M. P. Wolf, G. B. Salieb-Beugelaar and P. Hunziker, PDMS with designer functionalities—properties, modifications strategies, and applications, Prog. Polym. Sci., 2018, 83, 97–134,  DOI:10.1016/j.progpolymsci.2018.06.001.
3. E. Yilgör and I. Yilgör, Silicone containing copolymers: Synthesis, properties and applications, Prog. Polym. Sci., 2014, 39(6), 1165–1195,  DOI:10.1016/j.progpolymsci.2013.11.003.
4. E. K. Sackmann, A. L. Fulton and D. J. Beebe, The present and future role of microfluidics in biomedical research, Nature, 2014, 507(7491), 181–189,  DOI:10.1038/nature13118.
5. P. Fanzio, C. Manneschi, E. Angeli, V. Mussi, G. Firpo, L. Ceseracciu, L. Repetto and U. Valbusa, Modulating DNA translocation by a controlled deformation of a PDMS nanochannel device, Sci. Rep., 2012, 2, 1–6,  DOI:10.1038/srep00791.
6. J. C. Mcdonald, D. C. Duffy, J. R. Anderson and D. T. Chiu, Fabrication of microfluidic systems in PDMS, Electrophoresis, 2000, 21(1), 27–40.
7. J. M. Sidorova, N. Li, D. C. Schwartz, A. Folch and R. J. Monnat, Microfluidic-assisted analysis of replicating dna molecules, Nat. Protoc., 2009, 4(6), 849–861,  DOI:10.1038/nprot.2009.54.
8. D. Bodas and C. Khan-Malek, Hydrophilization and hydrophobic recovery of PDMS by oxygen plasma and chemical treatment-an SEM investigation, Sens. Actuators, B, 2007, 123(1), 368–373,  DOI:10.1016/j.snb.2006.08.037.
9. J. N. Lee, C. Park and G. M. Whitesides, Solvent compatibility of poly(dimethylsiloxane)-based microfluidic devices, Anal. Chem., 2003, 75(23), 6544–6554,  DOI:10.1021/ac0346712.
10. A. Shakeri, S. Khan and T. F. Didar, Conventional and emerging strategies for the fabrication and functionalization of PDMS-based microfluidic devices, Lab Chip, 2021, 21(16), 3053–3075,  10.1039/d1lc00288k.
11. K. Raj M and S. Chakraborty, PDMS microfluidics: A mini review, J. Appl. Polym. Sci., 2020, 137(27), 1–14,  DOI:10.1002/app.48958.
12. J. C. Johnson, L. T. J. Korley and M. Tsige, Coarse-grained modeling of peptidic/PDMS triblock morphology, J. Phys. Chem. B, 2014, 118(47), 13718–13728,  DOI:10.1021/jp506553v.
13. A. Kausar, Polydimethylsiloxane-based nanocomposite: Present research scenario and emergent future trends, Polym. Technol. Mater., 2020, 59(11), 1148–1166,  DOI:10.1080/25740881.2020.1719149.
14. L. W. Jang, J. Lee, M. E. Razu, E. C. Jensen and J. Kim, Fabrication of PDMS nanocomposite materials and nanostructures for biomedical nanosystems, IEEE Trans Nanobioscience, 2015, 14(8), 841–849,  DOI:10.1109/TNB.2015.2509602.
15. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI force field: Coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111(27), 7812–7824,  DOI:10.1021/jp071097f.
16. H. Huang, F. Cao, L. Wu and H. Sun, All-atom and coarse-grained force fields for polydimethylsiloxane, Mol. Simul., 2017, 43(18), 1513–1522,  DOI:10.1080/08927022.2017.1328597.
17. P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: A general purpose force field for coarse-grained molecular dynamics, Nat. Methods, 2021, 18(4), 382–388,  DOI:10.1038/s41592-021-01098-3.
18. R. Alessandri, F. Grünewald and S. J. Marrink, The martini model in materials science, Adv. Mater., 2021, 33(24), 1–25,  DOI:10.1002/adma.202008635.
19. F. Grunewald, G. Rossi, A. H. De Vries, S. J. Marrink and L. Monticelli, Transferable MARTINI model of poly(ethylene oxide), J. Phys. Chem. B, 2018, 122(29), 7436–7449,  DOI:10.1021/acs.jpcb.8b04760.
20. G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Coarse-graining polymers with the MARTINI force-field: Polystyrene as a benchmark case, Soft Matter, 2011, 7(2), 698–708,  10.1039/C0SM00481B.
21. R. Alessandri, J. J. Uusitalo, A. H. De Vries, R. W. A. Havenith and S. J. Marrink, Bulk heterojunction morphologies with atomistic resolution from coarse-grain solvent evaporation simulations, J. Am. Chem. Soc., 2017, 139(10), 3697–3705,  DOI:10.1021/jacs.6b11717.
22. M. Vögele, C. Holm and J. Smiatek, Coarse-grained simulations of polyelectrolyte complexes: MARTINI models for poly(styrene sulfonate) and poly(diallyldimethylammonium), J. Chem. Phys., 2015, 143(24), 243151,  DOI:10.1063/1.4937805.
23. E. Panizon, D. Bochicchio, L. Monticelli and G. Rossi, MARTINI coarse-grained models of polyethylene and polypropylene, J. Phys. Chem. B, 2015, 119(25), 8209–8216,  DOI:10.1021/acs.jpcb.5b03611.
24. H. Lee, A. H. De Vries, S. J. Marrink and R. W. Pastor, A coarse-grained model for polyethylene oxide and polyethylene glycol: Conformation and hydrodynamics, J. Phys. Chem. B, 2009, 113(40), 13186–13194,  DOI:10.1021/jp9058966.
25. H. Lee and R. G. Larson, Coarse-grained molecular dynamics studies of the concentration and size dependence of fifth- and seventh-generation PAMAM dendrimers on pore formation in DMPC bilayer, J. Phys. Chem. B, 2008, 112(26), 7778–7784,  DOI:10.1021/jp802606y.
26. J. S. Smith, O. Borodin and G. D. Smith, A Quantum chemistry based force field for poly(dimethylsiloxane, J. Phys. Chem. B, 2004, 108(52), 20340–20350,  DOI:10.1021/jp047434r.
27. GROMACS development team. GROMACS Documentation Release 2020. 2020.
28. W. Shi, N. S. Siefert and B. D. Morreale, Molecular simulations of CO₂, H₂, H₂O, and H₂S gas absorption into hydrophobic poly(dimethylsiloxane) (PDMS) solvent: Solubility and surface tension, J. Phys. Chem. C, 2015, 119(33), 19253–19265,  DOI:10.1021/acs.jpcc.5b05806.
29. R. M. Sok, H. J. C. Berendsen and W. F. Van Gunsteren, Molecular dynamics simulation of the transport of small molecules across a polymer membrane, J. Chem. Phys., 1992, 96(6), 4699–4704,  DOI:10.1063/1.462806.
30. V. Arrighi, S. Gagliardi, A. C. Dagger, J. A. Semlyen, J. S. Higgins and M. J. Shenton, Conformation of cyclics and linear chain polymers in bulk by SANS, Macromolecules, 2004, 37(21), 8057–8065,  DOI:10.1021/ma049565w.
31. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101,  DOI:10.1063/1.2408420.
32. H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81(8), 3684–3690,  DOI:10.1063/1.448118.
33. D. H. De Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Martini straight: Boosting performance using a shorter cutoff and GPUs, Comput. Phys. Commun., 2016, 199, 1–7,  DOI:10.1016/j.cpc.2015.09.014.
34. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A New molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190,  DOI:10.1063/1.328693.
35. D. Frenkel and B. Smith, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, USA, 2nd edn, 2001.
36. C. H. Bennett, Efficient estimation of free energy differences from monte carlo data, J. Comput. Phys., 1976, 22(2), 245–268,  DOI:10.1016/0021-9991(76)90078-4.
37. R. Alessandri, J. Barnoud, A. S. Gertsen, I. Patmanidis, A. H. de Vries, P. C. T. Souza and S. J. Marrink, Martini 3 coarse-grained force field: Small molecules, Adv. Theory Simul., 2022, 5(1), 1–19,  DOI:10.1002/adts.202100391.
38. F. Grünewald, R. Alessandri, P. C. Kroon, L. Monticelli, P. C. T. Souza and S. J. Marrink, Polyply: A python suite for facilitating simulations of (bio-)macromolecules and nanomaterials, 2021, 27–30.
39. M. J. Patel, S. C. Popat and M. A. Deshusses, Determination and correlation of the partition coefficients of 48 volatile organic and environmentally relevant compounds between air and silicone oil, Chem. Eng. J., 2017, 310, 72–78,  DOI:10.1016/j.cej.2016.10.086.
40. Open repository of the Nanobiocomp group. Nanobiocomp repo https://bitbucket.org/biomembnp/biomembnp.
41. A. Mata, A. J. Fleischman and S. Roy, Characterization of polydimethylsiloxane (PDMS) properties for biomedical micro/nanosystems, Biomed. Microdevices, 2005, 7(4), 281–293,  DOI:10.1007/s10544-005-6070-2.
42. A. A. G. Santiago, J. G. S. Gondim, R. L. Tranquilin, F. S. Silva, F. F. Fernandez, M. C. B. Costa, F. V. Motta and M. R. D. Bomio, Development of ZnO/PDMS Nanocomposite with photocatalytic/hydrophobic multifunction, Chem. Phys. Lett., 2020, 740(October 2019), 137051,  DOI:10.1016/j.cplett.2019.137051.
43. S. Park, J. Sung and H. So, Three-dimensional printing-assisted all-in-one surfaces inspired by peristome structures for water–oil separation, Surf. Interfaces, 2022, 29, 101721,  DOI:10.1016/j.surfin.2022.101721.
44. M. Kanungo, S. Mettu, K. Y. Law and S. Daniel, Effect of roughness geometry on wetting and dewetting of rough PDMS surfaces, Langmuir, 2014, 30(25), 7358–7368,  DOI:10.1021/la404343n.
45. Q. He, Z. Liu, P. Xiao, R. Liang, N. He and Z. Lu, Preparation of hydrophilic poly(dimethylsiloxane) stamps by plasma-induced grafting, Langmuir, 2003, 19(17), 6982–6986,  DOI:10.1021/la020785h.
46. A. Boudaghi and M. Foroutan, Investigation of the wettability of chemically heterogeneous smooth and rough surfaces using molecular dynamics simulation, J. Mol. Liq., 2022, 348, 118017,  DOI:10.1016/j.molliq.2021.118017.
47. A. E. Ismail, G. S. Grest, D. R. Heine, M. J. Stevens and M. Tsige, Interfacial structure and dynamics of siloxane systems: Pdms-vapor and Pdms-water, Macromolecules, 2009, 42(8), 3186–3194,  DOI:10.1021/ma802805y.
48. E. Ibarboure, E. Papon and J. Rodríguez-Hernández, Nanostructured Thermotropic PBLG-PDMS-PBLG Block Copolymers, Polymer, 2007, 48(13), 3717–3725,  DOI:10.1016/j.polymer.2007.04.046.
49. S. J. Lue, C. L. Tsai, D. T. Lee, K. P. O. Mahesh, M. Y. Hua, C. C. Hu, Y. C. Jean, K. R. Lee and J. Y. Lai, Sorption, diffusion, and perm-selectivity of toluene vapor/nitrogen mixtures through polydimethylsiloxane membranes with two cross-linker densities, J. Membr. Sci., 2010, 349(1–2), 321–332,  DOI:10.1016/j.memsci.2009.11.064.
50. G. Liu, W. S. Hung, J. Shen, Q. Li, Y. H. Huang, W. Jin, K. R. Lee and J. Y. Lai, Mixed matrix membranes with molecular-interaction-driven tunable free volumes for efficient bio-fuel recovery, J. Mater. Chem. A, 2015, 3(8), 4510–4521,  10.1039/c4ta05881j.
51. G. Darracq, A. Couvert, C. Couriol, A. Amrane, D. Thomas, E. Dumont, Y. Andres and P. Le Cloirec, Silicone oil: An effective absorbent for the removal of hydrophobic volatile organic compounds, J. Chem. Technol. Biotechnol., 2010, 85(3), 309–313,  DOI:10.1002/jctb.2331.
52. S. Chovau, A. Dobrak, A. Figoli, F. Galiano, S. Simone, E. Drioli, S. K. Sikdar and B. Van der Bruggen, Pervaporation performance of unfilled and filled PDMS membranes and novel SBS membranes for the removal of toluene from diluted aqueous solutions, Chem. Eng. J., 2010, 159(1–3), 37–46,  DOI:10.1016/j.cej.2010.02.020.
53. J. G. Croissant, K. S. Butler, J. I. Zink and C. J. Brinker, Synthetic amorphous silica nanoparticles: Toxicity, biomedical and environmental implications, Nat. Rev. Mater., 2020, 5(12), 886–909,  DOI:10.1038/s41578-020-0230-0.
54. R. K. Kankala, Y. H. Han, J. Na, C. H. Lee, Z. Sun, S. B. Wang, T. Kimura, Y. S. Ok, Y. Yamauchi, A. Z. Chen and K. C. W. Wu, Nanoarchitectured structure and surface biofunctionality of mesoporous silica nanoparticles, Adv. Mater., 2020, 32(23), 1907035,  DOI:10.1002/adma.201907035.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00939k

---