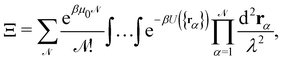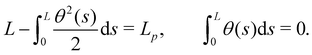DOI:
10.1039/D1SM01765A
(Paper)
Soft Matter, 2022,
18, 3891-3901
Frame tension governs the thermal fluctuations of a fluid membrane: new evidence
Received
12th December 2021
, Accepted 20th April 2022
First published on 22nd April 2022
Abstract
Two different tensions can be defined for a fluid membrane: the internal tension, γ, conjugated to the real membrane area in the Hamiltonian, and the frame tension, τ, conjugated to the projected (or frame) area. According to the standard statistical description of a membrane, the fluctuation spectrum is governed by γ. However, using rotational invariance arguments, several studies argued that the fluctuation spectrum must be governed by the frame tension τ instead. These studies disagree on the origin of the result obtained with the standard description yet: either a miscounting of configurations, quantified with the integration measure, or the use of a quadratic approximation of the Helfrich Hamiltonian. Analyzing the simplest case of a one-dimensional membrane, for which the arc length offers a natural parametrization, we give a new proof that the fluctuations are driven by τ, and show that the origin of the issue with the standard description is a miscounting of membrane configurations. The origin itself of this miscounting depends on the thermodynamic ensemble in which calculations are made.
1 Introduction
Bilayer membranes are quasi-two-dimensional fluid sheets formed by spontaneous self-assembly of lipid molecules in water. They are of utmost importance for the proper functioning of living cells, as they spatially separate intracellular compartments and present a boundary to the extracellular environment. Their mechanical properties play a key role in many cellular processes like motility, proliferation and endocytosis. Hence, a physical understanding of the bilayer membrane and its mechanics is necessary for the proper understanding of biological cells, and has motivated a long series of investigations. In particular, a number of questions have been raised regarding the definition of the tension of a fluid membrane, stirring up much debate among physicists.
The elasticity of a fluid membrane is traditionally studied in the framework of the Helfrich effective Hamiltonian:1,2
| | 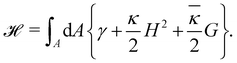 | (1) |
Here the integral runs over the surface area
A of the membrane,
H and
G are the mean and Gaussian curvatures, while
κ and
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif)
are the bending rigidity and the Gaussian rigidity, respectively. According to the Gauss–Bonnet theorem, the surface integral over the Gaussian curvature
G can be written as a constant plus a boundary term which, for larger membranes, is negligible in comparison with the
γA term.
It must be noted that eqn (1) applies to a fluid membrane with fluctuating area A: either the membrane is incompressible but exchanges lipid molecules with a reservoir, and then the intrinsic (or internal) tension γ is essentially the chemical potential of the reservoir of molecules;3 or the membrane is compressible but contains a fixed number of molecules, and then γ is the mechanical tension associated with the departure of the lipid surface concentration from the equilibrium configuration.4
The intrinsic tension γ must not be confused with the frame tension τ, which corresponds to the force per unit length that the interface would exert on a surrounding frame whose area Ap is kept fixed, and which is the actual mechanically accessible quantity. Intrinsic and frame tensions are clearly different for a fluctuating membrane: γ is the conjugate variable to its surface area A, while τ is the conjugate variable to its area projected on the frame Ap = Lp × Lp. The latter is then a thermodynamic quantity which depends on the entropy of the membrane, and can be seen as the renormalized version of the former.
When the membrane fluctuates only weakly about a plane, its statistical properties are treated analytically, based on the following set of assumptions:
1. Monge parametrization: the membrane position is described in terms of its height h(x, y) above the underlying reference plane as a function of the orthogonal coordinates x and y, thereby excluding conformations in which the surface forms overhangs. The area of the membrane is then 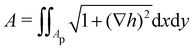 .
.
2. Assuming small fluctuations, the energy of the membrane is described with the quadratic approximation of the Helfrich Hamiltonian eqn (1) (omitting the contribution of the Gaussian curvature):
| | 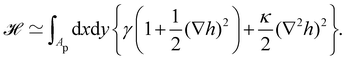 | (2) |
3. Monge integration measure: the membrane partition function Ξ is obtained by summing over all interface configurations, which mathematically expresses as a functional integral:
| | 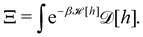 | (3) |
Defining an integration measure
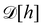
requires discretization of the interface.
5 Here, the membrane is discretized in
Np ×
Np patches with constant dimension
ap (with
Np =
Lp/
ap ≫ 1) on the reference frame, and the integration measure is
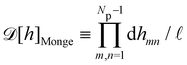
where
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
, the
quantum of height fluctuation, is a characteristic length introduced to render the integration measure properly dimensionless.
In the rest of the present paper, we will refer to this set of assumptions as the Monge model (although this is more than just the Monge parametrization, obviously).
A third tension has been introduced in the literature, named fluctuation tension r, and defined as the q2-coefficient in the membrane fluctuation spectrum:
| | 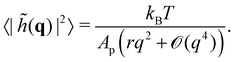 | (4) |
Using very general arguments based on the rotational invariance of the free energy of an incompressible membrane, Cai
et al.3 came to the conclusion that the fluctuation tension must coincide with the frame tension:
r =
τ. This result was then extended to the case of a compressible membrane by Farago.
4 Yet, evaluation of the height fluctuations based on the Monge model yields
r =
γ instead (see Section 2). The reason advanced to explain this discrepancy differs with authors: Farago,
4 then Schmid,
6 attributed this issue to the use of the approximated Hamiltonian
eqn (2) in the Monge model, which does not satisfy rotational invariance. For Cai
et al.3 on the other hand, the issue comes from the non-rotational invariance of the integration measure
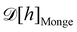
. Hence, for Farago and Schmid, if one uses the exact Helfrich Hamiltonian but keeps the Monge measure in the calculations, one should recover
r =
τ, while for Cai
et al., the integration measure must be modified. In their study,
3 the latter derives the corrective terms to the integration measure in order to recover
r =
τ, while still using the approximated Hamiltonian
eqn (2). In spite of the results presented in these different studies, expressions of
eqn (4) with both
r =
τ3,6–12 and
r =
γ13–16 are still commonly found in the devoted literature, and still nowadays the exact relation between the different membrane tensions is the object of numerical investigations.
17,18 Elucidating whether the fluctuation tension
r matches the frame tension
τ, or the intrinsic tension
γ, or none of them, is not just a purely academic question: it is also crucial for experimental
19–21 and particle-based numerical
13,22–25 investigations dealing with membrane fluctuations. The intrinsic tension, introduced within the Helfrich Hamiltonian, is not a quantity which is directly measurable; its determination relies on the accurate theoretical relationship with the frame or fluctuation tension.
In the present paper, focusing on the simpler case of a one-dimensional (1D) membrane embedded in the plane (or equivalently, a two-dimensional membrane which fluctuates along one direction only), we provide a new demonstration that the membrane fluctuations are governed by the frame tension. This demonstration enforces previous arguments advanced to justify that r = τ, and then increases our confidence in the final result. Moreover, our analysis allows clearly pointing out the inconsistencies in the Monge model: in agreement with Cai et al., we show that they are caused by an inaccurate integration measure, rather than the use of the approximated Hamiltonian. Nonetheless, restoring rotational invariance of the integration measure is not mandatory to recover r = τ from calculations: a consistent expansion of the Hamiltonian and the measure leads to the correct result.
The outline of the paper is as follows: in Section 2, we give one more evidence than the Monge model has some consistency issues: analyzing the fluctuations of a 1D incompressible membrane either with fluctuating physical length L but fixed projected length on the frame Lp, or with fixed L but fluctuating Lp, we show that the Monge model does not satisfy equivalence of thermodynamic ensembles, in contradiction with the fundamentals of statistical physics. Specifically, we obtain r = γ in the first ensemble, while r = τ in the second ensemble. In Section 3 we discuss the coarse-graining procedure based on which the Monge model is built, highlighting the origin of the troubles with this model: the choices made for the expression of the coarse-grained Hamiltonian (or its quadratic approximation) and that of the integration measure are not compatible choices to build a free energy that satisfies rotational invariance. In Section 4 we develop a coarse-grained model for a 1D membrane, for which a rotationally invariant integration measure is built from first principles. Using a consistent expansion of this measure and the Hamiltonian, we obtain r = τ for a membrane with fluctuating length and then recover ensemble equivalence. In Section 5 we show that to obtain this result, the only correction needed for the Monge model is to take into account the fluctuating character of the number of patches in the integration measure. We then discuss the situation of a compressible membrane with a fixed number of molecules. We show that here again, the Monge integration measure must be modified to recover r = τ. We also discuss the case of an interface between two fluids, which has no bending rigidity and so is stabilized by surface tension only. In that case the intrinsic tension and frame tension cannot be distinguished for small fluctuations.
2 One more evidence of Monge model inconsistency: non-equivalence of ensembles
We start our analysis by calculating the average square height and average length of a 1D incompressible membrane within two different statistical ensembles using the Monge model, and show that the expressions are different in the thermodynamic limit, in contradiction with the fundamentals of statistical physics.
2.1 (T, Lp, γ) ensemble
We first consider an incompressible membrane in the ensemble (T, Lp, γ) where temperature T, projected length Lp and intrinsic tension γ are fixed (see Fig. 1a). The 1D version of Helfrich Hamiltonian eqn (1) is| | 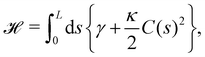 | (5) |
(where C(s) is the local curvature along arc length s, and L is the length of the membrane), and its quadratic approximation is written as| | 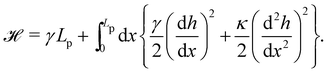 | (6) |
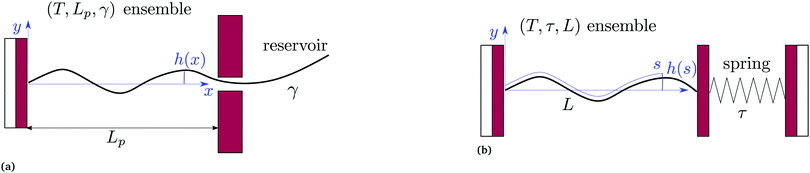 |
| | Fig. 1 Two different thermodynamic ensembles used to calculate the height and length fluctuations of an incompressible membrane: (a) (T, Lp,γ) ensemble; and (b) (T, τ, L) ensemble. | |
In agreement with the Monge model, we consider a discretized version of the membrane made of Np ≫ 1 patches whose x coordinates are distributed evenly, with projected distance ap = Lp/Np. Assuming fixed boundary conditions h (x = 0) = h (x = Lp) = 0, we expand h(x) as a sine Fourier series:
| | 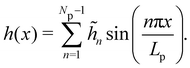 | (7) |
The Hamiltonian
eqn (6) can be rewritten in terms of the
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n
n as:
| | 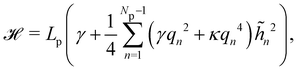 | (8) |
where
qn =
nπ/
Lp.
We then evaluate the partition function of the membrane 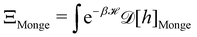 , with
, with 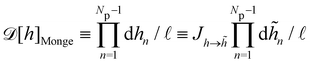 . We introduced in the last equality Jh→
. We introduced in the last equality Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) , the Jacobian associated with the change of variables from the real to reciprocal space. Because of the linear relationship between the two sets of variables (eqn (7)), we know that Jh→
, the Jacobian associated with the change of variables from the real to reciprocal space. Because of the linear relationship between the two sets of variables (eqn (7)), we know that Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) is constant. Its value can be obtained, e.g., by calculating a simple Gaussian integral in both direct and reciprocal spaces. We show in Appendix A that, with our choice for normalization of Fourier coefficients, one has Jh→
is constant. Its value can be obtained, e.g., by calculating a simple Gaussian integral in both direct and reciprocal spaces. We show in Appendix A that, with our choice for normalization of Fourier coefficients, one has Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = ((Np − 1)/2)Np/2. Summing over all Fourier components
= ((Np − 1)/2)Np/2. Summing over all Fourier components ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n finally yields
n finally yields
| | 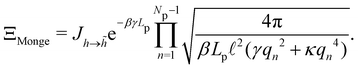 | (9) |
Let us emphasize again that the number of molecules that compose the interface fluctuates, so
ΞMonge is really a grand-canonical partition function. Assuming the moderate tension and/or thermodynamic limit
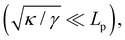
and using a continuous description of Fourier modes, we get
| | 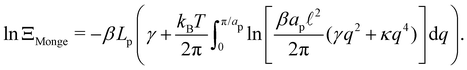 | (10) |
Note that the introduction of the Jacobian
Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif)
ensures that ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΞMonge
ΞMonge is extensive at the thermodynamic limit: ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΞMonge
ΞMonge ∝
Lp. It will also affect the expression of the frame tension
τ.
We then obtain the average squared amplitude of height straightforwardly:
| | 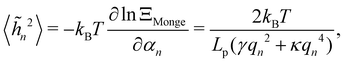 | (11) |
where
αn =
Lp (
γqn2 +
κqn4)/4. Actually, defining the fluctuation tension from the mean square amplitude of the Fourier mode is not very convenient when it comes to comparing between different thermodynamic ensembles, because the wavenumber does not necessarily follow the same discretization in different ensembles (
e.g., multiples of π/
Lp in the ensemble where
Lp is fixed, and multiples of π/
L in the ensemble where
L is fixed). As a consequence, the variable
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n
n does not correspond to the same wavenumber value in different ensembles. To avoid this complication, we express the average of real variables such as the average squared height 〈
h2〉 or equivalently, the average membrane length 〈
L〉 =
Lp(1 +〈
h′
2〉/2), which can be deduced directly from the partition function as:
| | 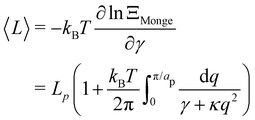 | (12) |
| | 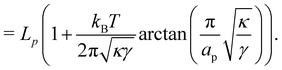 | (13) |
Eqn (11) and (13) are the 1D versions of the expressions of 〈
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n2
n2〉 and 〈
A〉 derived for a 2D membrane with the Monge model.
3,26 As mentioned above, within this description the fluctuation tension matches the intrinsic tension:
r =
γ. In ref.
6, the expression of
L has been derived assuming
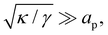
whereas
eqn (13) assumes
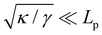
. Hence, both expressions converge to the same following formula within the range
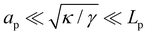
:
| | 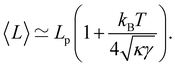 | (14) |
The frame tension is given by
| | 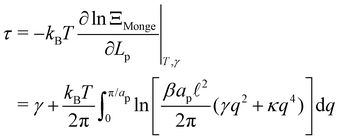 | (15) |
| | 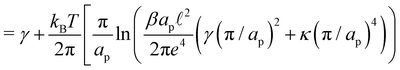 | (16) |
| | 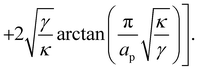 | (17) |
In the range
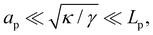
verified by most membranes, this expression simplifies to:
| | 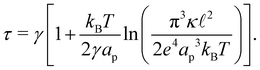 | (18) |
Although the condition 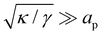 is not required for our purpose, it is easy to see in this regime that γ differs from τ: According to eqn (14), the small fluctuation approximation is satisfied whenever
is not required for our purpose, it is easy to see in this regime that γ differs from τ: According to eqn (14), the small fluctuation approximation is satisfied whenever 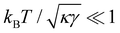 . Since
. Since 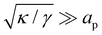 , kBT/apγ can have any finite value. According to eqn (18), one then has τ ≠ γ in general (anticipating that
, kBT/apγ can have any finite value. According to eqn (18), one then has τ ≠ γ in general (anticipating that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ ap, as we will argue in Section 4, the argument of the ln function is ≫1, and so τ > γ). The specific case of an interface between two immiscible fluids, for which κ = 0, will be discussed in Section 5.3.
∼ ap, as we will argue in Section 4, the argument of the ln function is ≫1, and so τ > γ). The specific case of an interface between two immiscible fluids, for which κ = 0, will be discussed in Section 5.3.
Note that including quartic terms in the expansion of the Helfrich Hamiltonian would lead to corrective terms into the fluctuation spectrum and thus in the expression of r. Using Wick's theorem, it is found that 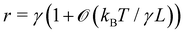 .3,27 Clearly, these corrective terms cannot yield r = τ, as this was already emphasized by Cai et al. In the rest of the manuscript we will not consider these corrections coming from the quartic terms in
.3,27 Clearly, these corrective terms cannot yield r = τ, as this was already emphasized by Cai et al. In the rest of the manuscript we will not consider these corrections coming from the quartic terms in 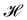 .
.
2.2 (T, τ, L) ensemble
The same incompressible membrane is now treated within the (T, τ, L) ensemble, in which the frame tension τ and the membrane length L are fixed, while the projected length Lp fluctuates. The effective Hamiltonian associated with this ensemble is derived from 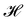 using a double Legendre transform:
using a double Legendre transform:| | 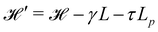 | (19) |
| | 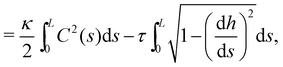 | (20) |
and its quadratic approximation can be written as:| | 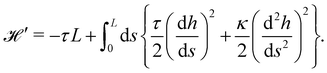 | (21) |
Note that we have parametrized the height with the arc length s rather than x, because L – and not Lp – is fixed here. Still using fixed boundary conditions h (s = 0) = h (s = L) = 0, we expand the membrane height as 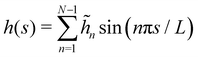 . The approximated Hamiltonian can then be rewritten as:
. The approximated Hamiltonian can then be rewritten as:| | 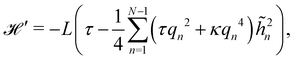 | (22) |
where qn = nπ/L. After integrating the canonical partition function 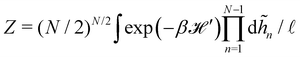 over the variables
over the variables ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n, and still assuming moderate tension or thermodynamic limit
n, and still assuming moderate tension or thermodynamic limit 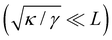 , we obtain
, we obtain| | 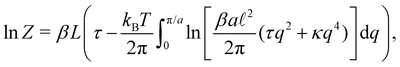 | (23) |
where a = L/N is the patch length. It comes straightforwardly| | 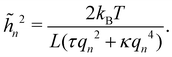 | (24) |
Note that this expression is identical to eqn (11) with the substitution γ → τ and Lp→ L. From this observation, ref. 6 (see footnote 5 herein) argued that the fluctuation tension should be renormalized as r= (Lp/L)τ. However, as we already emphasized above, we compared the square amplitudes of height for two different wavenumbers in the two ensembles, since here qn = nπ/L ≠ nπ/Lp. Hence, 〈![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n2〉 does not correspond to the same quantity in both ensembles. Instead, we compare the relation between the membrane and frame length in both ensembles:
n2〉 does not correspond to the same quantity in both ensembles. Instead, we compare the relation between the membrane and frame length in both ensembles:| | 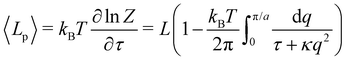 | (25) |
| | 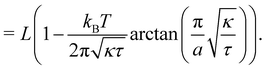 | (26) |
which can be inverted, in the regime of small fluctuations (L − Lp)/Lp ≪ 1, as:| | 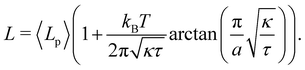 | (27) |
The internal tension γ = kBT∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z/∂L|T,τ can be expressed here as
Z/∂L|T,τ can be expressed here as| | 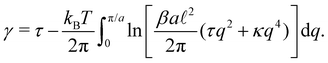 | (28) |
Eqn (27) then implies that here r = τ! Moreover, following the same arguments as in Section 2.1, one can easily realize from eqn (28) that γ ≠ τ for finite values of kBT/aτ.
Note that we took care to distinguish the patch length (named ap and a, respectively) in the two ensembles. It could be argued that the difference between these two cutoffs exactly compensates for the apparent difference in the expression of the average squared height or average length obtained in the two ensembles. A relation between a and ap can be set by imposing ensemble equivalence for the average energy 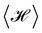 : according to the equipartition theorem, each quadratic term in eqn (8) and (22) contributes kBT/2 to the average energy. Thus, the equivalence of the ensemble requires that the numbers of modes in both ensembles, respectively Np = Lp/ap and N = L/a, are equal. Clearly, with this relation eqn (24) and (27) do not match eqn (11) and (13). Therefore, the ensemble equivalence is not satisfied for the average squared height or average length, in the thermodynamic limit (L, Lp → ∞), in contradiction with the fundamentals of statistical physics.
: according to the equipartition theorem, each quadratic term in eqn (8) and (22) contributes kBT/2 to the average energy. Thus, the equivalence of the ensemble requires that the numbers of modes in both ensembles, respectively Np = Lp/ap and N = L/a, are equal. Clearly, with this relation eqn (24) and (27) do not match eqn (11) and (13). Therefore, the ensemble equivalence is not satisfied for the average squared height or average length, in the thermodynamic limit (L, Lp → ∞), in contradiction with the fundamentals of statistical physics.
Let us emphasize that we assumed 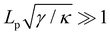 in the calculations, so we are not in the vanishing tension regime, and the equivalence of ensembles is not questionable here.6 Indeed, eqn (27) (or 13) shows that in this regime, L and Lp are extensive variables which are linearly related for a fixed tension. In the next two sections we identify the origins of the paradox we pointed out, and show that r = τ is the correct result.
in the calculations, so we are not in the vanishing tension regime, and the equivalence of ensembles is not questionable here.6 Indeed, eqn (27) (or 13) shows that in this regime, L and Lp are extensive variables which are linearly related for a fixed tension. In the next two sections we identify the origins of the paradox we pointed out, and show that r = τ is the correct result.
3 Tracking the Monge model inconsistencies
The description of a membrane at the mesoscopic scale – where it appears as a continuous sheet – relies on a coarse-graining construction from its description at the atomic level. To understand the origin of the issue pointed above, it is useful to come back to the coarse-graining construction at the roots of the Monge model. As before, we consider a 1D incompressible membrane with a fluctuating number of molecules. Our starting point is then the classical grand-canonical partition function of the lipid molecules that form the membrane. After integrating over the molecules' momenta, it can be written as:
where 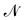 is the (fluctuating) number of molecules, rα = (xα,yα) are their position vectors, μ0 is the chemical potential of the reservoir of molecules, U ({rα }) is the intermolecular potential, and λ is the thermal de Broglie length.
is the (fluctuating) number of molecules, rα = (xα,yα) are their position vectors, μ0 is the chemical potential of the reservoir of molecules, U ({rα }) is the intermolecular potential, and λ is the thermal de Broglie length.
We now want to sum over all microstates corresponding to the same membrane shape. In a first step, we define a discrete interface by introducing 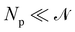 points (but Np ≫ 1), whose locations are the coarse-grained degrees of freedom (dof) that define the membrane shape. In the Monge model, these points are distributed evenly on the reference axis x, with fixed projected distance ap, and the height hn of point n (1 ≤ n ≤ Np) is defined as the height of the center of mass of the molecules whose x coordinate lies within [nap,(n + 1) ap[. Note that this is not the only coarse-grained model we could build, e.g., rather than points evenly distributed along the reference frame, we could have chosen them evenly distributed along the membrane geometric support. Grouping all microscopic configurations with the same heights {hn}, the partition function can be rewritten as:
points (but Np ≫ 1), whose locations are the coarse-grained degrees of freedom (dof) that define the membrane shape. In the Monge model, these points are distributed evenly on the reference axis x, with fixed projected distance ap, and the height hn of point n (1 ≤ n ≤ Np) is defined as the height of the center of mass of the molecules whose x coordinate lies within [nap,(n + 1) ap[. Note that this is not the only coarse-grained model we could build, e.g., rather than points evenly distributed along the reference frame, we could have chosen them evenly distributed along the membrane geometric support. Grouping all microscopic configurations with the same heights {hn}, the partition function can be rewritten as:
| | 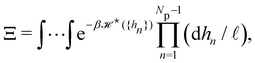 | (29) |
where
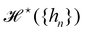
is defined through:
| | 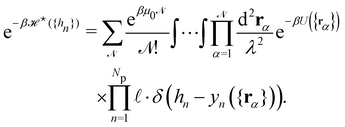 | (30) |
In this equation
yn ({
rα}) is the height of the center of mass of the patch
n, expressed in terms of the molecule coordinates
rα:
| | 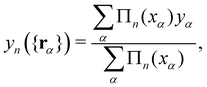 | (31) |
where
Πn is the boxcar function, defined as
| | 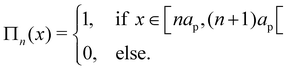 | (32) |
Within the context of a continuum model, the quantum of height fluctuations
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
introduced in
eqn (29) may be thought of as an arbitrary coarse-graining length for vertical displacements, so that the height of a patch center must be increased or decreased by an amount
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
or greater before its new height is treated as distinct from its old one in the sum over membrane configurations.
28 At the microscopic level,
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
is actually related to the range of the interaction potential
U({
rα}) between molecules.
In the continuous limit (Np → ∞, ap → 0), Ξ is expressed as a functional integral
| | 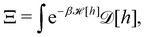 | (33) |
where
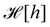
is the Helfrich Hamiltonian (
eqn (5)) and
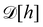
is the measure for functional integration, which should physically correspond to an integration over all interface configurations, not counting any configuration twice. Comparing
eqn (29) and (33), it is tempting to identify
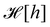
with
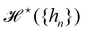
, and the integration measure
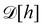
with
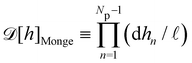
. This is actually the identification made in the Monge model. However, other choices are possible: we can introduce any function
f ({
hn}) and make the identification
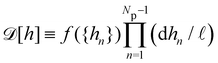
,
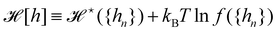
. At this point, it may seem artificial or useless to introduce such a function, as the two terms cancel each other. However, the expression of
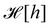
(
eqn (5)) is obtained from an independent reasoning, based on symmetry and invariance properties, and not through the identification with the microscopic description above.
1 Therefore, the
f function appears in the measure only, and it is important to have the correct one to evaluate
Ξ correctly. Both
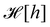
and
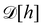
are quantities that should depend solely on the interface shape, and not on the way the surface is parametrized. They should also be invariant under translation and rotation, as
Ξ. These properties restrain the possible expressions for
f. Actually, there is something wrong with the choice made within the Monge model (
f ≡ 1): the Hamiltonian
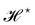
does not satisfy rotational invariance, because of the Delta Dirac terms in
eqn (30), and thus should not be identified with the (rotationally invariant) Helfrich Hamiltonian
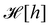
. Likewise, the measure
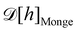
does not satisfy rotational invariance, as pointed out by Cai
et al.3 Hence, there is a clear inconsistency in the Monge model: in one hand, the model uses the rotationally invariant Helfrich Hamiltonian for the continuous description of the interface, implying a non-trivial function
f to ensure that
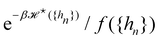
is rotationally invariant. On the other hand, the naive integration measure is used in the model sets
f ({
hn}) = 1. Stated differently, identifying
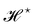
with the Helfrich Hamiltonian (or its quadratic approximation) and using
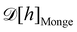
as integration measure are incompatible choices to make
Ξ rotationally invariant. It is also clear that replacing the Helfrich Hamiltonian with its quadratic approximation cannot be the (only) cause of the rotational non-invariance of
Ξ, contrary to what has been argued in previous studies:
4,6 the
f function that makes
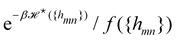
is still different from 1.
To restore the rotational invariance of Ξ, Cai et al.3 introduced two corrective terms to the Monge measure. The first one, named the Faddeev-Popov term, corrects the fact that the Monge measure 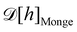 induces over-counting of configurations of a fluid membrane. Indeed, the infinitesimal vertical displacement dhn of point n has a component which is locally tangent to the bilayer. At first order, this locally tangent displacement does not change the shape of the membrane, and then should be disregarded to avoid multiple counting of the same configuration.29 The Faddeev-Popov term regularizes this overcounting by removing the locally tangential component from the measure. However, Cai et al. acknowledged that this term is still not sufficient to restore the rotational invariance of Ξ. They introduced a second term, named the Liouville term, to meet this requirement. The interpretation of this term is less obvious, but the above derivation of the coarse-graining procedure helps us to gain insight on its origin: we passed from a fined-grained description where the number of molecules fluctuates, to a coarse-grained description, where the number Np of membrane patches is fixed (while their masses fluctuate). But Np – or equivalently the projected distance ap = Lp/Np – has been chosen arbitrarily. Its value should be related to the average of the fluctuating number of molecules that form the interface. An alternative approach, which we will develop in the next section, is to let this number of patches fluctuate by grouping a fixed number of molecules on every patch.
induces over-counting of configurations of a fluid membrane. Indeed, the infinitesimal vertical displacement dhn of point n has a component which is locally tangent to the bilayer. At first order, this locally tangent displacement does not change the shape of the membrane, and then should be disregarded to avoid multiple counting of the same configuration.29 The Faddeev-Popov term regularizes this overcounting by removing the locally tangential component from the measure. However, Cai et al. acknowledged that this term is still not sufficient to restore the rotational invariance of Ξ. They introduced a second term, named the Liouville term, to meet this requirement. The interpretation of this term is less obvious, but the above derivation of the coarse-graining procedure helps us to gain insight on its origin: we passed from a fined-grained description where the number of molecules fluctuates, to a coarse-grained description, where the number Np of membrane patches is fixed (while their masses fluctuate). But Np – or equivalently the projected distance ap = Lp/Np – has been chosen arbitrarily. Its value should be related to the average of the fluctuating number of molecules that form the interface. An alternative approach, which we will develop in the next section, is to let this number of patches fluctuate by grouping a fixed number of molecules on every patch.
Note that Cai et al. determined the expression of the Liouville term by imposing r = τ, which is required by the rotational invariance of Ξ. Hence, the equality r = τ is not an outcome of the correction, but a requisite instead. In the next Sections we show that a consistent expansion of the Hamiltonian and the measure – what requires to take the fluctuating character of the number of patches into account – allows us to obtain r = τ.
 |
| | Fig. 2 Coarse-grained models of an incompressible lipid bilayer in the (T, Lp,γ) ensemble. (a) Monge model, in which every patch has a fixed projected length ap, and contains a fluctuating number of molecules; and (b) self-similar coarse-grained description, in which every patch has a fixed length a and contains a fixed number of molecules. | |
4 Fixing Monge model: a self-similar coarse-graining
The previous section showed that the Monge model is built on the passage from a fined-grained description in which the number of molecules (with fixed masses) fluctuates to a coarse-grained description in which the number of patches (with fluctuating masses) is fixed. No relation is set on the number of such patches and the average number of molecules in the membrane. We develop here an alternate coarse-graining in which each patch contains a fixed number of molecules (see Fig. 2). The number of patches N is then a fluctuating variable, and considering that the membrane is incompressible, the average number of patches is here trivially related to the average number of molecules in the membrane. This “self-similar” coarse-graining does not alter the system description: like in the fine-grained description, the membrane is made of a fluctuating number of particles (the patches) with fixed masses, and distributed evenly along the membrane physical length. Furthermore, since patches are all identical, a chemical potential of the patches μ can be defined unambiguously, and is related to the chemical potential of molecules μ0 through μ =μ0Γa, where a is the size of a patch and Γ is the linear density of molecules. The definition of a unique chemical potential is less obvious within the Monge model, where patches do not have constant sizes. The intrinsic tension γ of the membrane is defined as γ = −μ/a.
For a 1D incompressible membrane, patches can only rotate and translate. This is why the 1D case is much simpler than its two-dimensional counterpart, whose patches also deform from one configuration to another, as changes in the membrane conformation are generally not isometric. A coarse-grained configuration of the 1D membrane is then specified by the number of patches it contains N, and the orientation θn of each one of them. However, the variables θn cannot vary independently as the projected membrane length of the x and y axes are fixed. Each coarse-grained conformation of the membrane is counted only once in the evaluation of the grand-canonical partition function by summing uniformly over the patch orientations which are compatible with these constraints. Grouping all fine-grained configurations corresponding to a given value of the variables θn, the grand-canonical partition function becomes:
| | 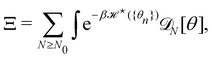 | (34) |
where
N0 =
Lp/
a is the minimal number of patches, and
| | 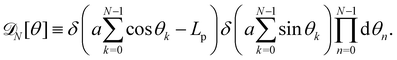 | (35) |
In the continuous limit (N → ∞, a → 0, with Na = L), the membrane is parametrized by the local tangent angle θ (s) along the curvilinear coordinate s (s ∈ [0, L]). Clearly, the measure 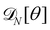 is invariant by rotation of the reference frame. Subsequently the coarse-grained Hamiltonian
is invariant by rotation of the reference frame. Subsequently the coarse-grained Hamiltonian 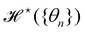 is also rotationally invariant and can be identified with the Helfrich Hamiltonian eqn (5), which can be rewritten in terms of θ (s) as
is also rotationally invariant and can be identified with the Helfrich Hamiltonian eqn (5), which can be rewritten in terms of θ (s) as
| | 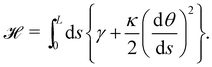 | (36) |
In order to evaluate Ξ, we now assume small fluctuations: cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk ≃ 1 − θk2/2. In the continuous limit, the two constraints can be rewritten as
θk ≃ 1 − θk2/2. In the continuous limit, the two constraints can be rewritten as
Note that this expansion breaks the rotational invariance of the measure
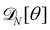
, but is consistent with the expression of the Helfrich Hamiltonian
eqn (36), which is limited to quadratic terms in
θ (
s). Expressing the first constraint with the help of the identity
| |  | (37) |
the partition function can be rewritten as:
| | 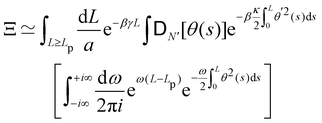 | (38) |
where
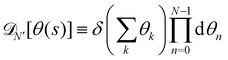
. Introducing the Fourier expansion
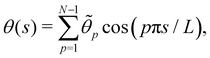
in which the zeroth order term has been eliminated to satisfy the second constraint, we get:
| | 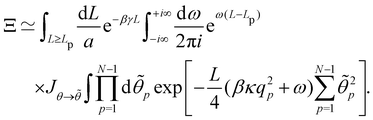 | (39) |
We show in Appendix B that the Jacobian associated with the change of variables is still
Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif)
≃ (
N/2)
N/2 when
N =
L/
a ≫ 1. Here again, taking the Jacobian into account ensures that ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ξ
Ξ is an extensive quantity for large membranes, and will also affect the expression of the frame tension
τ. After integrating over the
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p
p variables, we get:
| | 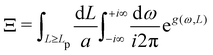 | (40) |
where
g (
ω,
L) = −
βγL +
ω (
L −
Lp) −
Lu (
ω), with
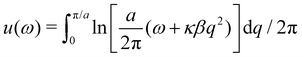
. Here again, we assumed
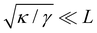
so that the lower bound in the integral is ≃0.
This double integral can be evaluated in the thermodynamic limit (L, Lp → ∞) thanks to the saddle point approximation: 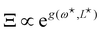 where
where 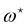 and
and 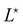 , the values of ω and L that extremize g (ω, L), are given implicitly by:
, the values of ω and L that extremize g (ω, L), are given implicitly by:
| | 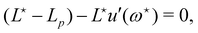 | (41) |
and
| | 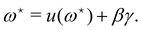 | (42) |
Using this last equation, we get:
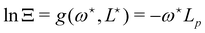
. From
eqn (42), we also see that
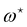
is independent of
Lp, so the frame tension is
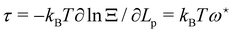
. Substituting this relation into
eqn (42) finally yields:
| | 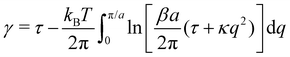 | (43) |
and
| | 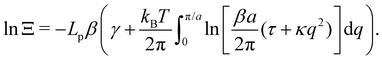 | (44) |
Eqn (44) is identical to
eqn (10) derived with the Monge model, just by replacing
γ with
τ and taking
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
=
ea/π. The quantum of height fluctuations is then of the order of magnitude of a patch size (which is a few molecule sizes), while Morse
et al.3,30 argued it should be of the order of the de Broglie length (which is smaller than the molecule size). However, if we had introduced a
quantum of angle fluctuations Θ in the integration measure,
i.e.:
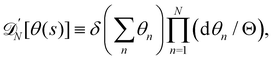
we then would end up with
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
=
Θea/π.
Eqn (43) can be inverted for small fluctuations 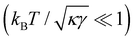 . The frame tension is thus
. The frame tension is thus
| | 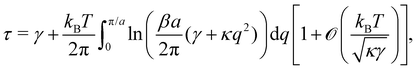 | (45) |
in agreement with previous studies.
3,4,7,31
The average length is 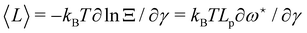 . Deriving eqn (42) with respect to γ gives:
. Deriving eqn (42) with respect to γ gives: 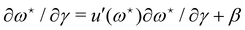 . Together with eqn (41) yields
. Together with eqn (41) yields 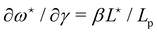 , and thus
, and thus 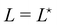 : the average and most probable values coincide, as expected. eqn (41) can then be rewritten as
: the average and most probable values coincide, as expected. eqn (41) can then be rewritten as
| | 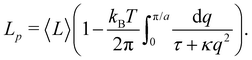 | (46) |
This equation is identical to
eqn (26) derived in the (
T,
τ,
L) ensemble. Assuming small fluctuations, the relation is inverted as
| | 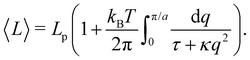 | (47) |
Eqn (47) is then identical to
eqn (12) with the substitution
γ →
τ (and the undetermined length
ap replaced with the physical patch length
a). Using the same substitution in
eqn (11), the height fluctuations are characterized by:
| | 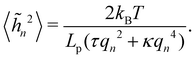 | (48) |
These results prove that the fluctuation tension r does coincide with the frame tension τ, in agreement with those of Cai et al. It is also worth noticing that eqn (46) suggests a linear scaling of 〈L − Lp〉 with 〈L〉 rather than Lp when departing from the regime of small fluctuations, in agreement with the numerical findings of ref. 6.
5 Discussion
5.1 Varying patch number is mandatory to recover r = τ
Starting from a coarse-grained description in which both the Hamiltonian and the measure are rotationally invariant, we were able to recover r = τ for an incompressible membrane within the (T, Lp, γ) ensemble. However, let us emphasize again that to obtain this result, we used a quadratic expansion of the measure 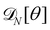 , thereby breaking its rotational invariance. Moreover, the approximation sin
, thereby breaking its rotational invariance. Moreover, the approximation sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (s) ≃ θ (s), cos
θ (s) ≃ θ (s), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (s) ≃ 1 − θ (s)2/2 used in the measure is equivalent to assume that θ (s) and h (s) are linearly related: θ (s) ≃ dh/ds. Therefore, the associated measures are also linearly related:
θ (s) ≃ 1 − θ (s)2/2 used in the measure is equivalent to assume that θ (s) and h (s) are linearly related: θ (s) ≃ dh/ds. Therefore, the associated measures are also linearly related: 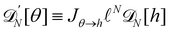 (the factor
(the factor ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) N has been introduced to make the measure dimensionless), with Jθ→h = 1/aN (the derivation of this Jacobian is reported in Appendix C). Accordingly, the Faddeev–Popov corrective term, which is a correction to the linear relationship between the two measures, and whose expression is derived in Appendix C, is a second order correction to the expression of τ, in agreement with Cai et al.3 Moreover, inserting θ (s) ≃ dh/ds in eqn (36) breaks the rotational invariance of the Hamiltonian. Yet, substituting θ (s) → dh/ds (and using
N has been introduced to make the measure dimensionless), with Jθ→h = 1/aN (the derivation of this Jacobian is reported in Appendix C). Accordingly, the Faddeev–Popov corrective term, which is a correction to the linear relationship between the two measures, and whose expression is derived in Appendix C, is a second order correction to the expression of τ, in agreement with Cai et al.3 Moreover, inserting θ (s) ≃ dh/ds in eqn (36) breaks the rotational invariance of the Hamiltonian. Yet, substituting θ (s) → dh/ds (and using ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = ea/π) in the grand-canonical partition function (eqn (38)) will not change its final expression (eqn (44)). Hence, the use of an approximated Hamiltonian cannot explain the Monge model inaccuracies and the non-equivalence of ensembles discussed in Section 2 either. This should come as no surprise: ensemble equivalence is a very general feature of standard statistical physics and does not makes any assumption on the realism of the Hamiltonian. It can also be noticed that in the ensemble (T, τ, L), we obtained (Section 2.2) r = τ while using both an approximated measure and an approximated Hamiltonian.
= ea/π) in the grand-canonical partition function (eqn (38)) will not change its final expression (eqn (44)). Hence, the use of an approximated Hamiltonian cannot explain the Monge model inaccuracies and the non-equivalence of ensembles discussed in Section 2 either. This should come as no surprise: ensemble equivalence is a very general feature of standard statistical physics and does not makes any assumption on the realism of the Hamiltonian. It can also be noticed that in the ensemble (T, τ, L), we obtained (Section 2.2) r = τ while using both an approximated measure and an approximated Hamiltonian.
Therefore, the only remaining reason why the Monge model in the (T, Lp, γ) does not give the right value for r is because it disregards the inherent fluctuation of the number of patches. This correction can be identified with the Liouville corrective term introduced in ref. 3. Note that the saddle point approximation we used in our derivation allows us to replace the sum over the patch number with a fixed ad-hoc patch number 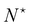 , and can be interpreted as a correction (so-called Liouville correction) to the Monge measure. However, for calculating accurately other quantities, such as 〈h4〉, the other corrections to the Monge model (expansion of
, and can be interpreted as a correction (so-called Liouville correction) to the Monge measure. However, for calculating accurately other quantities, such as 〈h4〉, the other corrections to the Monge model (expansion of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) to higher terms, and Faddeev-Popov term) might be mandatory.
to higher terms, and Faddeev-Popov term) might be mandatory.
5.2 The case of a compressible membrane
At this point, one question still remains: we mentioned in the introduction that the same Helfrich Hamiltonian also applies to compressible membranes with fluctuating surface area but a fixed number of molecules; the term γA then corresponds to a stretching energy.32 This is the point of view adopted by Farago and Pincus.4,26 For a 1D membrane, the relevant thermodynamic ensemble is the ensemble of fixed temperature, number of patches and projected length, (T, N, Lp). How can we then explain that the result obtained with the Monge model (r = γ) is still not correct in this ensemble? Clearly, the issue cannot be associated with a fluctuating number of patches as in the ensemble. Farago,4 then Schmid,6 invoked the lack of rotational invariance of the approximated Hamiltonian to explain the inaccuracies in the Monge model. Yet, we obtained r = τ in the (T, L, τ) and (T, Lp, γ) ensembles while using the very same approximated Hamiltonian, and all three ensembles should be equivalent in the thermodynamic limit. More likely, the issue originates from the measure 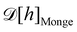 that still does not properly enumerate the membrane configurations: because the allowed displacements of the patches are those which keep uniform patch length, we should consider all the possible membrane conformations for a given patch length a, and sum over all possible values of a. The partition function can then be written as:
that still does not properly enumerate the membrane configurations: because the allowed displacements of the patches are those which keep uniform patch length, we should consider all the possible membrane conformations for a given patch length a, and sum over all possible values of a. The partition function can then be written as:| | 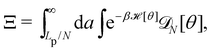 | (49) |
where 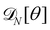 and
and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) [θ] are given by eqn (35) and (36), respectively. Taking the fluctuating character of the patch size a is thus essential to get the correct result, in the same way as the fluctuation of the patch number is essential to recover r = τ in the (T, Lp, γ). Indeed, in both cases this boils down to sum over membrane length L, and the partition function (49) is in fact identical to eqn (38).
[θ] are given by eqn (35) and (36), respectively. Taking the fluctuating character of the patch size a is thus essential to get the correct result, in the same way as the fluctuation of the patch number is essential to recover r = τ in the (T, Lp, γ). Indeed, in both cases this boils down to sum over membrane length L, and the partition function (49) is in fact identical to eqn (38).
5.3 The case of a fluid interface
We finally focus our attention on the case of an interface between two immiscible fluids, and ask ourselves whether internal and frame tensions should be distinguished. With the difference of a membrane, an interface between two immiscible fluids has no bending rigidity (κ = 0).2 The interface is stabilized by the surface tension only, whose origin comes from a non-affinity between the molecules of the two bulk phases,33 and therefore is very different from – and usually much larger than – a typical tension value in a membrane. The high tension criterion kBT/τa ≪ 1, which is required to be in the small fluctuation regime (eqn (27)) when κ → 0, is then satisfied. According to eqn (45), τ and γ are then equal up to 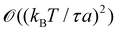 and so can be used indifferently in the expressions of the height and length fluctuations of a fluid interface.
and so can be used indifferently in the expressions of the height and length fluctuations of a fluid interface.
6 Conclusions
In summary, starting from the description of a membrane at the molecular level, we first revealed the inconsistencies lying in the foundations of the Monge model to describe the statistics of an incompressible membrane: the choices made for the expression of the coarse-grained Hamiltonian (or its quadratic approximation) and that of the integration measure are not compatible choices to build a free energy that satisfies rotational invariance. By analyzing the simpler case of a 1D membrane, for which an integration measure that satisfies rotational invariance can be built from first principles, we found in agreement with previous studies that the lack of rotational invariance of the measure used in the Monge model has two origins itself: first, it assumes a fixed number of patches, while for an incompressible membrane with fluctuating length the number of patches must fluctuate; and second, for a given number of membrane patches, there is an over-counting of membrane configurations because the size of a patch is allowed to vary with this linear measure. Finally, using a consistent expansion of the measure and the Hamiltonian, we were able to prove that the frame tension τ drives the thermal fluctuations of a membrane. Our analysis then shows that to obtain this result, the rotational invariance of the Hamiltonian is not necessary, and one can use its quadratic approximation. Only the measure used in the Monge model must be amended, in agreement with Cai et al., although its rotational invariance is not required either. In fact, the only correction that must be taken into account is the fluctuating character of the membrane length. We believe that the multiplicity of the arguments advanced to justify that r = τ will reinforce the conviction in these results, and hence will encourage the use of the correct expressions in future studies. As a final note, let us emphasize that the Helfrich model represents a simplified version of a real membrane; in particular it is described as an infinitely thin sheet, and energy does not depend on the local lipid concentration along the membrane. All the discussion about whether r = τ or not is restricted in the context of this specific theoretical framework. But real membranes are more complex, and recent particle-based numerical simulations taking into account the fluctuations of lipid concentration and membrane thickness have been performed in recent years.22,23 These simulations have shown that for membranes under very strong stretching, the fluctuation tension deviates from the frame tension. A possible explanation for this result is the existence of a coupling term between the membrane height and membrane thickness.
Conflicts of interest
There are no conflicts to declare.
Appendix
A Expression of Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0068_0303.gif)
The integration measure in the Monge model is 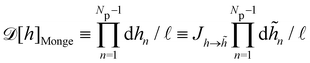 , where Jh→
, where Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) is the constant Jacobian associated with the linear change of variables eqn (7). Its value can be obtained e.g., by calculating a simple Gaussian integral
is the constant Jacobian associated with the linear change of variables eqn (7). Its value can be obtained e.g., by calculating a simple Gaussian integral 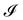 in both direct and reciprocal spaces. Using the identity
in both direct and reciprocal spaces. Using the identity 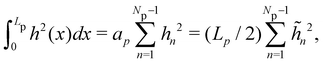 the integral can be written as
the integral can be written as| | 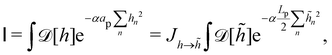 | (50) |
where α is any constant with a positive real part. The first expression gives 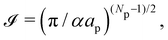 and the second one
and the second one 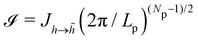 . Therefore, Jh→
. Therefore, Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = (Np/2)(Np−1)/2.
= (Np/2)(Np−1)/2.
B Expression of Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e123.gif)
We evaluate the Jacobian Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) associated with the linear change of variables {θn} → {
associated with the linear change of variables {θn} → {![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p}, with
p}, with 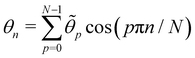 , n ∈ {0,…, N − 1}. As in Appendix A, Jθ→
, n ∈ {0,…, N − 1}. As in Appendix A, Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) is obtained by evaluating a simple integral expressed with both sets of variables. Note however that here the N variables θn are not independent, but are constrained by
is obtained by evaluating a simple integral expressed with both sets of variables. Note however that here the N variables θn are not independent, but are constrained by 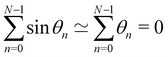 . This constraint is properly taken into account by introducing a Dirac delta in the integration. For the variables {
. This constraint is properly taken into account by introducing a Dirac delta in the integration. For the variables {![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p} on the other hand, this constraint simply reads
p} on the other hand, this constraint simply reads ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) 0 = 0. The second constraint of fixed projected length
0 = 0. The second constraint of fixed projected length 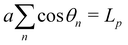 does not need to be considered to evaluate Jθ→
does not need to be considered to evaluate Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) , since its value does not depend on the choice of the integral to evaluate. Let us then evaluate the integral
, since its value does not depend on the choice of the integral to evaluate. Let us then evaluate the integral| | 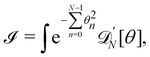 | (51) |
with 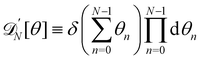 . Using the identities
. Using the identities 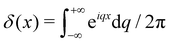 , and
, and 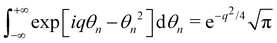 , we get:
, we get:| | 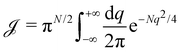 | (52) |
| | 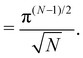 | (53) |
The integral 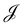 can be rewritten with variables
can be rewritten with variables ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p as
p as| | 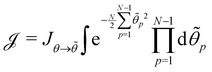 | (54) |
| | 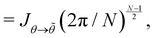 | (55) |
where we used the equality 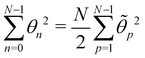 . Comparing both expressions eqn (53) and (55) finally yields
. Comparing both expressions eqn (53) and (55) finally yields| | 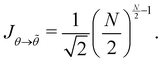 | (56) |
Hence, for N ≫ 1, 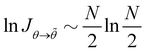 .
.
C Expression of Jθ→h
The two sets of variables are related through θn= arcsin((hn+1 − hn)/a). Since h0 = hN = 0, and 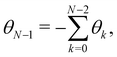 there are N − 1 independent variables for each set. The Jacobian matrix associated with the change of variables θn → hn is
there are N − 1 independent variables for each set. The Jacobian matrix associated with the change of variables θn → hn is| | 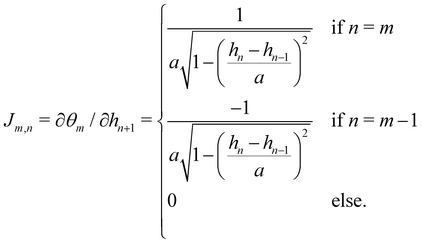 | (57) |
and thus its determinant is| | 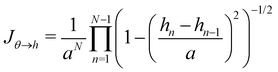 | (58) |
| | 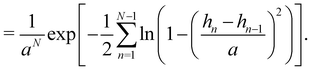 | (59) |
At first order, θ (s) ≃ dh/ds, and then:Note that expanding the logarithm at next order yields, in the continuous limit:| | 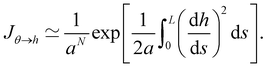 | (61) |
in which we recognize the Faddeev–Popov corrective term.3
Acknowledgements
I thank J. B. Fournier for bringing this problem to my attention and for the careful reading of the manuscript.
Notes and references
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CrossRef CAS PubMed.
-
S. Safran, Statistical Thermodynamics Of Surfaces, Interfaces, And Membranes, CRC Press, 2018 Search PubMed.
- W. Cai, T. C. Lubensky, P. Nelson and T. Powers, J. Phys. II, 1994, 4, 931–949 CrossRef CAS.
- O. Farago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051914 CrossRef PubMed.
- U. Seifert, Z. Naturforsch., B: Condens. Matter, 1995, 97, 299–309 CAS.
- F. Schmid, EPL, 2011, 95, 28008 CrossRef.
- M. E. S. Borelli, H. Kleinert and A. M. Schakel, Phys. Lett. A, 1999, 253, 239–246 CrossRef CAS.
- O. Farago and P. Pincus, J. Chem. Phys., 2004, 120, 2934–2950 CrossRef CAS PubMed.
- E. Lindahl and O. Edholm, J. Chem. Phys., 2000, 113, 3882–3893 CrossRef CAS.
- S. Marrink and A. Mark, J. Phys. Chem. B, 2001, 105, 6122–6127 CrossRef CAS.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef PubMed.
- Z.-J. Wang and D. Frenkel, J. Chem. Phys., 2005, 122, 234711 CrossRef PubMed.
- J. Stecki, J. Chem. Phys., 2006, 125, 154902 CrossRef CAS PubMed.
- A. Imparato, J. Chem. Phys., 2006, 124, 154714 CrossRef PubMed.
- J.-B. Fournier and C. Barbetta, Phys. Rev. Lett., 2008, 100, 078103 CrossRef PubMed.
-
H. Turlier and T. Betz, Physics of Biological Membranes, Springer, 2018, pp. 581–619 Search PubMed.
- H. Shiba, H. Noguchi and J.-B. Fournier, Soft Matter, 2016, 12, 2373–2380 RSC.
- G. Gueguen, N. Destainville and M. Manghi, Soft Matter, 2017, 13, 6100–6117 RSC.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097 CrossRef CAS PubMed.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- T. Betz and C. Sykes, Soft Matter, 2012, 8, 5317–5326 RSC.
- J. Neder, B. West, P. Nielaba and F. Schmid, J. Chem. Phys., 2010, 132, 115101 CrossRef PubMed.
- F. Schmid, Biophys. Rev. Lett., 2013, 08, 1–20 CrossRef CAS.
- E. Chacón, P. Tarazona and F. Bresme, J. Chem. Phys., 2015, 143, 034706 CrossRef PubMed.
- M. M. Terzi, M. Deserno and J. F. Nagle, Soft Matter, 2019, 15, 9085–9092 RSC.
- O. Farago and P. Pincus, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 399–408 CrossRef CAS PubMed.
- J. Meunier, J. de Physique, 1987, 48, 1819–1831 CrossRef CAS.
- Any free energy contributions arising from vertical displacements of the membrane over distances less than
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are, like the contributions of undulation modes of wavelength less than ap, implicitly included within the values of the phenomenological parameters of the model, i.e.: the surface tension γ and the bending rigidities κ and
are, like the contributions of undulation modes of wavelength less than ap, implicitly included within the values of the phenomenological parameters of the model, i.e.: the surface tension γ and the bending rigidities κ and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) .
.
- Hence, the density of points in the phase space of membrane configurations, whose axes are the Fourier mode amplitudes
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n, is not uniform.
n, is not uniform.
- D. Morse and S. T. Milner, EPL, 1994, 26, 565 CrossRef CAS.
- F. David and S. Leibler, J. Phys. II, 1991, 1, 959–976 CrossRef CAS.
- The membrane is under tension (γ > 0) when the area A is larger than the relaxed area A0. We assume that molecules diffuse rapidly along the membrane,
so that the surface concentration remains uniform. The stretching energy then writes for small area departure from A0: Es = K(A − A0)2/2, where K is the 2D compressive modulus of the membrane. Expanding this relation around A = Ap, one obtains Es ≃ γA + cst with γ = K(Ap − A0).
- M. Durand, Am. J. Phys., 2021, 89, 261–266 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
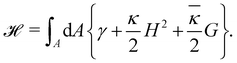
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) are the bending rigidity and the Gaussian rigidity, respectively. According to the Gauss–Bonnet theorem, the surface integral over the Gaussian curvature G can be written as a constant plus a boundary term which, for larger membranes, is negligible in comparison with the γA term.
are the bending rigidity and the Gaussian rigidity, respectively. According to the Gauss–Bonnet theorem, the surface integral over the Gaussian curvature G can be written as a constant plus a boundary term which, for larger membranes, is negligible in comparison with the γA term.
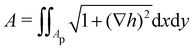 .
.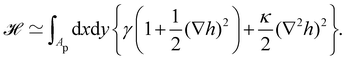
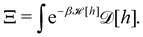
 requires discretization of the interface.5 Here, the membrane is discretized in Np × Np patches with constant dimension ap (with Np = Lp/ap ≫ 1) on the reference frame, and the integration measure is
requires discretization of the interface.5 Here, the membrane is discretized in Np × Np patches with constant dimension ap (with Np = Lp/ap ≫ 1) on the reference frame, and the integration measure is 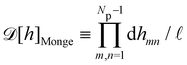 where
where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the quantum of height fluctuation, is a characteristic length introduced to render the integration measure properly dimensionless.
, the quantum of height fluctuation, is a characteristic length introduced to render the integration measure properly dimensionless.
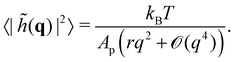
 . Hence, for Farago and Schmid, if one uses the exact Helfrich Hamiltonian but keeps the Monge measure in the calculations, one should recover r = τ, while for Cai et al., the integration measure must be modified. In their study,3 the latter derives the corrective terms to the integration measure in order to recover r = τ, while still using the approximated Hamiltonian eqn (2). In spite of the results presented in these different studies, expressions of eqn (4) with both r = τ3,6–12 and r = γ13–16 are still commonly found in the devoted literature, and still nowadays the exact relation between the different membrane tensions is the object of numerical investigations.17,18 Elucidating whether the fluctuation tension r matches the frame tension τ, or the intrinsic tension γ, or none of them, is not just a purely academic question: it is also crucial for experimental19–21 and particle-based numerical13,22–25 investigations dealing with membrane fluctuations. The intrinsic tension, introduced within the Helfrich Hamiltonian, is not a quantity which is directly measurable; its determination relies on the accurate theoretical relationship with the frame or fluctuation tension.
. Hence, for Farago and Schmid, if one uses the exact Helfrich Hamiltonian but keeps the Monge measure in the calculations, one should recover r = τ, while for Cai et al., the integration measure must be modified. In their study,3 the latter derives the corrective terms to the integration measure in order to recover r = τ, while still using the approximated Hamiltonian eqn (2). In spite of the results presented in these different studies, expressions of eqn (4) with both r = τ3,6–12 and r = γ13–16 are still commonly found in the devoted literature, and still nowadays the exact relation between the different membrane tensions is the object of numerical investigations.17,18 Elucidating whether the fluctuation tension r matches the frame tension τ, or the intrinsic tension γ, or none of them, is not just a purely academic question: it is also crucial for experimental19–21 and particle-based numerical13,22–25 investigations dealing with membrane fluctuations. The intrinsic tension, introduced within the Helfrich Hamiltonian, is not a quantity which is directly measurable; its determination relies on the accurate theoretical relationship with the frame or fluctuation tension.
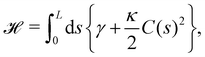
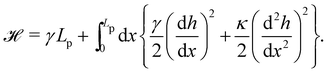

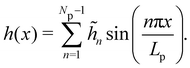
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n as:
n as: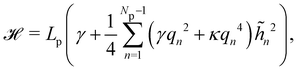
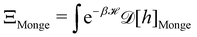 , with
, with 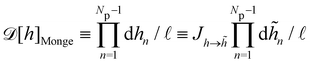 . We introduced in the last equality Jh→
. We introduced in the last equality Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) , the Jacobian associated with the change of variables from the real to reciprocal space. Because of the linear relationship between the two sets of variables (eqn (7)), we know that Jh→
, the Jacobian associated with the change of variables from the real to reciprocal space. Because of the linear relationship between the two sets of variables (eqn (7)), we know that Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) is constant. Its value can be obtained, e.g., by calculating a simple Gaussian integral in both direct and reciprocal spaces. We show in Appendix A that, with our choice for normalization of Fourier coefficients, one has Jh→
is constant. Its value can be obtained, e.g., by calculating a simple Gaussian integral in both direct and reciprocal spaces. We show in Appendix A that, with our choice for normalization of Fourier coefficients, one has Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = ((Np − 1)/2)Np/2. Summing over all Fourier components
= ((Np − 1)/2)Np/2. Summing over all Fourier components ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n finally yields
n finally yields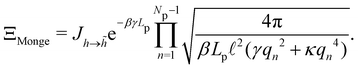
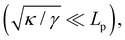 and using a continuous description of Fourier modes, we get
and using a continuous description of Fourier modes, we get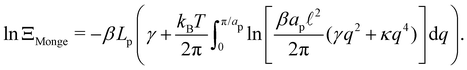
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ensures that ln
ensures that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΞMonge is extensive at the thermodynamic limit: ln
ΞMonge is extensive at the thermodynamic limit: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΞMonge ∝ Lp. It will also affect the expression of the frame tension τ.
ΞMonge ∝ Lp. It will also affect the expression of the frame tension τ.
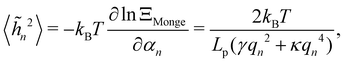
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n does not correspond to the same wavenumber value in different ensembles. To avoid this complication, we express the average of real variables such as the average squared height 〈h2〉 or equivalently, the average membrane length 〈L〉 = Lp(1 +〈h′2〉/2), which can be deduced directly from the partition function as:
n does not correspond to the same wavenumber value in different ensembles. To avoid this complication, we express the average of real variables such as the average squared height 〈h2〉 or equivalently, the average membrane length 〈L〉 = Lp(1 +〈h′2〉/2), which can be deduced directly from the partition function as: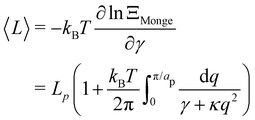
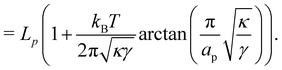
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n2〉 and 〈A〉 derived for a 2D membrane with the Monge model.3,26 As mentioned above, within this description the fluctuation tension matches the intrinsic tension: r = γ. In ref. 6, the expression of L has been derived assuming
n2〉 and 〈A〉 derived for a 2D membrane with the Monge model.3,26 As mentioned above, within this description the fluctuation tension matches the intrinsic tension: r = γ. In ref. 6, the expression of L has been derived assuming 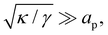 whereas eqn (13) assumes
whereas eqn (13) assumes 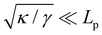 . Hence, both expressions converge to the same following formula within the range
. Hence, both expressions converge to the same following formula within the range 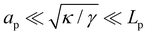 :
: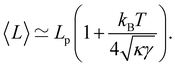

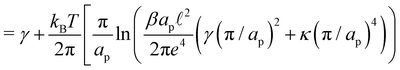

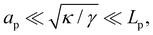 verified by most membranes, this expression simplifies to:
verified by most membranes, this expression simplifies to: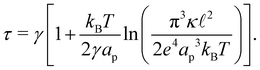
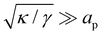 is not required for our purpose, it is easy to see in this regime that γ differs from τ: According to eqn (14), the small fluctuation approximation is satisfied whenever
is not required for our purpose, it is easy to see in this regime that γ differs from τ: According to eqn (14), the small fluctuation approximation is satisfied whenever 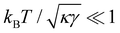 . Since
. Since 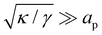 , kBT/apγ can have any finite value. According to eqn (18), one then has τ ≠ γ in general (anticipating that
, kBT/apγ can have any finite value. According to eqn (18), one then has τ ≠ γ in general (anticipating that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ ap, as we will argue in Section 4, the argument of the ln function is ≫1, and so τ > γ). The specific case of an interface between two immiscible fluids, for which κ = 0, will be discussed in Section 5.3.
∼ ap, as we will argue in Section 4, the argument of the ln function is ≫1, and so τ > γ). The specific case of an interface between two immiscible fluids, for which κ = 0, will be discussed in Section 5.3.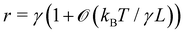 .3,27 Clearly, these corrective terms cannot yield r = τ, as this was already emphasized by Cai et al. In the rest of the manuscript we will not consider these corrections coming from the quartic terms in
.3,27 Clearly, these corrective terms cannot yield r = τ, as this was already emphasized by Cai et al. In the rest of the manuscript we will not consider these corrections coming from the quartic terms in  .
. using a double Legendre transform:
using a double Legendre transform: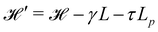
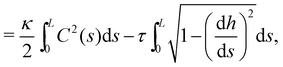
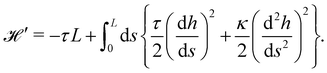
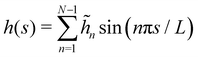 . The approximated Hamiltonian can then be rewritten as:
. The approximated Hamiltonian can then be rewritten as: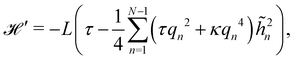
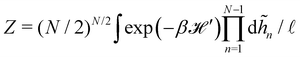 over the variables
over the variables ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n, and still assuming moderate tension or thermodynamic limit
n, and still assuming moderate tension or thermodynamic limit 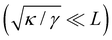 , we obtain
, we obtain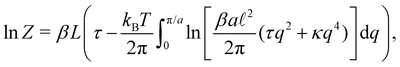
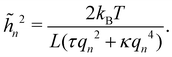
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n2〉 does not correspond to the same quantity in both ensembles. Instead, we compare the relation between the membrane and frame length in both ensembles:
n2〉 does not correspond to the same quantity in both ensembles. Instead, we compare the relation between the membrane and frame length in both ensembles: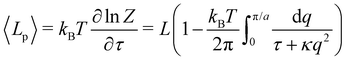
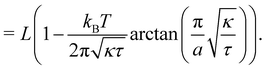
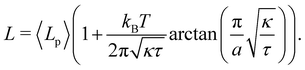
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z/∂L|T,τ can be expressed here as
Z/∂L|T,τ can be expressed here as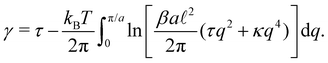
 : according to the equipartition theorem, each quadratic term in eqn (8) and (22) contributes kBT/2 to the average energy. Thus, the equivalence of the ensemble requires that the numbers of modes in both ensembles, respectively Np = Lp/ap and N = L/a, are equal. Clearly, with this relation eqn (24) and (27) do not match eqn (11) and (13). Therefore, the ensemble equivalence is not satisfied for the average squared height or average length, in the thermodynamic limit (L, Lp → ∞), in contradiction with the fundamentals of statistical physics.
: according to the equipartition theorem, each quadratic term in eqn (8) and (22) contributes kBT/2 to the average energy. Thus, the equivalence of the ensemble requires that the numbers of modes in both ensembles, respectively Np = Lp/ap and N = L/a, are equal. Clearly, with this relation eqn (24) and (27) do not match eqn (11) and (13). Therefore, the ensemble equivalence is not satisfied for the average squared height or average length, in the thermodynamic limit (L, Lp → ∞), in contradiction with the fundamentals of statistical physics. in the calculations, so we are not in the vanishing tension regime, and the equivalence of ensembles is not questionable here.6 Indeed, eqn (27) (or 13) shows that in this regime, L and Lp are extensive variables which are linearly related for a fixed tension. In the next two sections we identify the origins of the paradox we pointed out, and show that r = τ is the correct result.
in the calculations, so we are not in the vanishing tension regime, and the equivalence of ensembles is not questionable here.6 Indeed, eqn (27) (or 13) shows that in this regime, L and Lp are extensive variables which are linearly related for a fixed tension. In the next two sections we identify the origins of the paradox we pointed out, and show that r = τ is the correct result. is the (fluctuating) number of molecules, rα = (xα,yα) are their position vectors, μ0 is the chemical potential of the reservoir of molecules, U ({rα }) is the intermolecular potential, and λ is the thermal de Broglie length.
is the (fluctuating) number of molecules, rα = (xα,yα) are their position vectors, μ0 is the chemical potential of the reservoir of molecules, U ({rα }) is the intermolecular potential, and λ is the thermal de Broglie length.
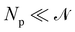 points (but Np ≫ 1), whose locations are the coarse-grained degrees of freedom (dof) that define the membrane shape. In the Monge model, these points are distributed evenly on the reference axis x, with fixed projected distance ap, and the height hn of point n (1 ≤ n ≤ Np) is defined as the height of the center of mass of the molecules whose x coordinate lies within [nap,(n + 1) ap[. Note that this is not the only coarse-grained model we could build, e.g., rather than points evenly distributed along the reference frame, we could have chosen them evenly distributed along the membrane geometric support. Grouping all microscopic configurations with the same heights {hn}, the partition function can be rewritten as:
points (but Np ≫ 1), whose locations are the coarse-grained degrees of freedom (dof) that define the membrane shape. In the Monge model, these points are distributed evenly on the reference axis x, with fixed projected distance ap, and the height hn of point n (1 ≤ n ≤ Np) is defined as the height of the center of mass of the molecules whose x coordinate lies within [nap,(n + 1) ap[. Note that this is not the only coarse-grained model we could build, e.g., rather than points evenly distributed along the reference frame, we could have chosen them evenly distributed along the membrane geometric support. Grouping all microscopic configurations with the same heights {hn}, the partition function can be rewritten as: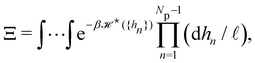
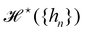 is defined through:
is defined through: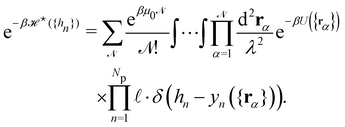
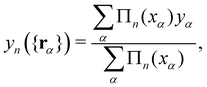
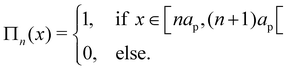
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) introduced in eqn (29) may be thought of as an arbitrary coarse-graining length for vertical displacements, so that the height of a patch center must be increased or decreased by an amount
introduced in eqn (29) may be thought of as an arbitrary coarse-graining length for vertical displacements, so that the height of a patch center must be increased or decreased by an amount ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) or greater before its new height is treated as distinct from its old one in the sum over membrane configurations.28 At the microscopic level,
or greater before its new height is treated as distinct from its old one in the sum over membrane configurations.28 At the microscopic level, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is actually related to the range of the interaction potential U({rα}) between molecules.
is actually related to the range of the interaction potential U({rα}) between molecules.
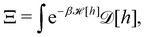
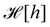 is the Helfrich Hamiltonian (eqn (5)) and
is the Helfrich Hamiltonian (eqn (5)) and 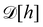 is the measure for functional integration, which should physically correspond to an integration over all interface configurations, not counting any configuration twice. Comparing eqn (29) and (33), it is tempting to identify
is the measure for functional integration, which should physically correspond to an integration over all interface configurations, not counting any configuration twice. Comparing eqn (29) and (33), it is tempting to identify 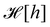 with
with 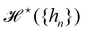 , and the integration measure
, and the integration measure 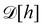 with
with 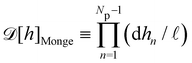 . This is actually the identification made in the Monge model. However, other choices are possible: we can introduce any function f ({hn}) and make the identification
. This is actually the identification made in the Monge model. However, other choices are possible: we can introduce any function f ({hn}) and make the identification 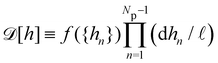 ,
, 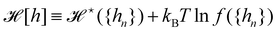 . At this point, it may seem artificial or useless to introduce such a function, as the two terms cancel each other. However, the expression of
. At this point, it may seem artificial or useless to introduce such a function, as the two terms cancel each other. However, the expression of 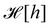 (eqn (5)) is obtained from an independent reasoning, based on symmetry and invariance properties, and not through the identification with the microscopic description above.1 Therefore, the f function appears in the measure only, and it is important to have the correct one to evaluate Ξ correctly. Both
(eqn (5)) is obtained from an independent reasoning, based on symmetry and invariance properties, and not through the identification with the microscopic description above.1 Therefore, the f function appears in the measure only, and it is important to have the correct one to evaluate Ξ correctly. Both 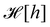 and
and 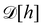 are quantities that should depend solely on the interface shape, and not on the way the surface is parametrized. They should also be invariant under translation and rotation, as Ξ. These properties restrain the possible expressions for f. Actually, there is something wrong with the choice made within the Monge model (f ≡ 1): the Hamiltonian
are quantities that should depend solely on the interface shape, and not on the way the surface is parametrized. They should also be invariant under translation and rotation, as Ξ. These properties restrain the possible expressions for f. Actually, there is something wrong with the choice made within the Monge model (f ≡ 1): the Hamiltonian 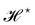 does not satisfy rotational invariance, because of the Delta Dirac terms in eqn (30), and thus should not be identified with the (rotationally invariant) Helfrich Hamiltonian
does not satisfy rotational invariance, because of the Delta Dirac terms in eqn (30), and thus should not be identified with the (rotationally invariant) Helfrich Hamiltonian 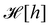 . Likewise, the measure
. Likewise, the measure 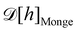 does not satisfy rotational invariance, as pointed out by Cai et al.3 Hence, there is a clear inconsistency in the Monge model: in one hand, the model uses the rotationally invariant Helfrich Hamiltonian for the continuous description of the interface, implying a non-trivial function f to ensure that
does not satisfy rotational invariance, as pointed out by Cai et al.3 Hence, there is a clear inconsistency in the Monge model: in one hand, the model uses the rotationally invariant Helfrich Hamiltonian for the continuous description of the interface, implying a non-trivial function f to ensure that 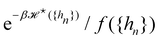 is rotationally invariant. On the other hand, the naive integration measure is used in the model sets f ({hn}) = 1. Stated differently, identifying
is rotationally invariant. On the other hand, the naive integration measure is used in the model sets f ({hn}) = 1. Stated differently, identifying 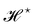 with the Helfrich Hamiltonian (or its quadratic approximation) and using
with the Helfrich Hamiltonian (or its quadratic approximation) and using 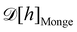 as integration measure are incompatible choices to make Ξ rotationally invariant. It is also clear that replacing the Helfrich Hamiltonian with its quadratic approximation cannot be the (only) cause of the rotational non-invariance of Ξ, contrary to what has been argued in previous studies:4,6 the f function that makes
as integration measure are incompatible choices to make Ξ rotationally invariant. It is also clear that replacing the Helfrich Hamiltonian with its quadratic approximation cannot be the (only) cause of the rotational non-invariance of Ξ, contrary to what has been argued in previous studies:4,6 the f function that makes 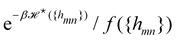 is still different from 1.
is still different from 1.
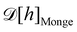 induces over-counting of configurations of a fluid membrane. Indeed, the infinitesimal vertical displacement dhn of point n has a component which is locally tangent to the bilayer. At first order, this locally tangent displacement does not change the shape of the membrane, and then should be disregarded to avoid multiple counting of the same configuration.29 The Faddeev-Popov term regularizes this overcounting by removing the locally tangential component from the measure. However, Cai et al. acknowledged that this term is still not sufficient to restore the rotational invariance of Ξ. They introduced a second term, named the Liouville term, to meet this requirement. The interpretation of this term is less obvious, but the above derivation of the coarse-graining procedure helps us to gain insight on its origin: we passed from a fined-grained description where the number of molecules fluctuates, to a coarse-grained description, where the number Np of membrane patches is fixed (while their masses fluctuate). But Np – or equivalently the projected distance ap = Lp/Np – has been chosen arbitrarily. Its value should be related to the average of the fluctuating number of molecules that form the interface. An alternative approach, which we will develop in the next section, is to let this number of patches fluctuate by grouping a fixed number of molecules on every patch.
induces over-counting of configurations of a fluid membrane. Indeed, the infinitesimal vertical displacement dhn of point n has a component which is locally tangent to the bilayer. At first order, this locally tangent displacement does not change the shape of the membrane, and then should be disregarded to avoid multiple counting of the same configuration.29 The Faddeev-Popov term regularizes this overcounting by removing the locally tangential component from the measure. However, Cai et al. acknowledged that this term is still not sufficient to restore the rotational invariance of Ξ. They introduced a second term, named the Liouville term, to meet this requirement. The interpretation of this term is less obvious, but the above derivation of the coarse-graining procedure helps us to gain insight on its origin: we passed from a fined-grained description where the number of molecules fluctuates, to a coarse-grained description, where the number Np of membrane patches is fixed (while their masses fluctuate). But Np – or equivalently the projected distance ap = Lp/Np – has been chosen arbitrarily. Its value should be related to the average of the fluctuating number of molecules that form the interface. An alternative approach, which we will develop in the next section, is to let this number of patches fluctuate by grouping a fixed number of molecules on every patch.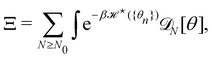
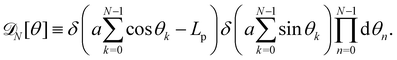
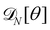 is invariant by rotation of the reference frame. Subsequently the coarse-grained Hamiltonian
is invariant by rotation of the reference frame. Subsequently the coarse-grained Hamiltonian 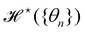 is also rotationally invariant and can be identified with the Helfrich Hamiltonian eqn (5), which can be rewritten in terms of θ (s) as
is also rotationally invariant and can be identified with the Helfrich Hamiltonian eqn (5), which can be rewritten in terms of θ (s) as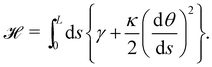
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk ≃ 1 − θk2/2. In the continuous limit, the two constraints can be rewritten as
θk ≃ 1 − θk2/2. In the continuous limit, the two constraints can be rewritten as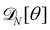 , but is consistent with the expression of the Helfrich Hamiltonian eqn (36), which is limited to quadratic terms in θ (s). Expressing the first constraint with the help of the identity
, but is consistent with the expression of the Helfrich Hamiltonian eqn (36), which is limited to quadratic terms in θ (s). Expressing the first constraint with the help of the identity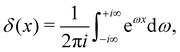
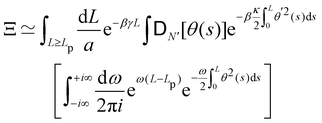
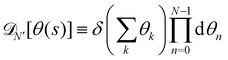 . Introducing the Fourier expansion
. Introducing the Fourier expansion 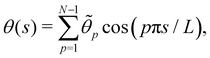 in which the zeroth order term has been eliminated to satisfy the second constraint, we get:
in which the zeroth order term has been eliminated to satisfy the second constraint, we get: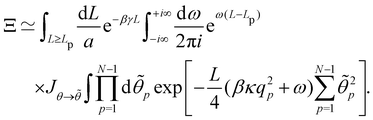
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ≃ (N/2)N/2 when N = L/a ≫ 1. Here again, taking the Jacobian into account ensures that ln
≃ (N/2)N/2 when N = L/a ≫ 1. Here again, taking the Jacobian into account ensures that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ξ is an extensive quantity for large membranes, and will also affect the expression of the frame tension τ. After integrating over the
Ξ is an extensive quantity for large membranes, and will also affect the expression of the frame tension τ. After integrating over the ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p variables, we get:
p variables, we get: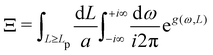
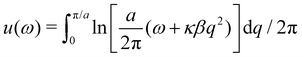 . Here again, we assumed
. Here again, we assumed 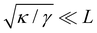 so that the lower bound in the integral is ≃0.
so that the lower bound in the integral is ≃0.
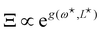 where
where 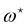 and
and 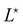 , the values of ω and L that extremize g (ω, L), are given implicitly by:
, the values of ω and L that extremize g (ω, L), are given implicitly by: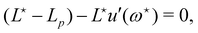
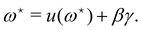
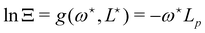 . From eqn (42), we also see that
. From eqn (42), we also see that 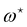 is independent of Lp, so the frame tension is
is independent of Lp, so the frame tension is 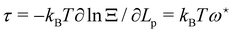 . Substituting this relation into eqn (42) finally yields:
. Substituting this relation into eqn (42) finally yields: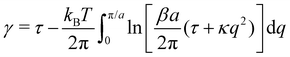
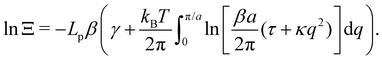
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = ea/π. The quantum of height fluctuations is then of the order of magnitude of a patch size (which is a few molecule sizes), while Morse et al.3,30 argued it should be of the order of the de Broglie length (which is smaller than the molecule size). However, if we had introduced a quantum of angle fluctuations Θ in the integration measure, i.e.:
= ea/π. The quantum of height fluctuations is then of the order of magnitude of a patch size (which is a few molecule sizes), while Morse et al.3,30 argued it should be of the order of the de Broglie length (which is smaller than the molecule size). However, if we had introduced a quantum of angle fluctuations Θ in the integration measure, i.e.: 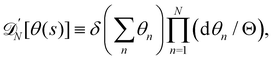 we then would end up with
we then would end up with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =Θea/π.
=Θea/π.
 . The frame tension is thus
. The frame tension is thus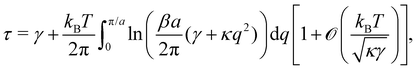
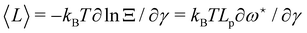 . Deriving eqn (42) with respect to γ gives:
. Deriving eqn (42) with respect to γ gives: 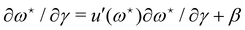 . Together with eqn (41) yields
. Together with eqn (41) yields 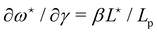 , and thus
, and thus 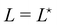 : the average and most probable values coincide, as expected. eqn (41) can then be rewritten as
: the average and most probable values coincide, as expected. eqn (41) can then be rewritten as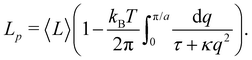
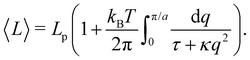
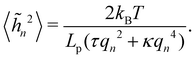
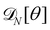 , thereby breaking its rotational invariance. Moreover, the approximation sin
, thereby breaking its rotational invariance. Moreover, the approximation sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (s) ≃ θ (s), cos
θ (s) ≃ θ (s), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (s) ≃ 1 − θ (s)2/2 used in the measure is equivalent to assume that θ (s) and h (s) are linearly related: θ (s) ≃ dh/ds. Therefore, the associated measures are also linearly related:
θ (s) ≃ 1 − θ (s)2/2 used in the measure is equivalent to assume that θ (s) and h (s) are linearly related: θ (s) ≃ dh/ds. Therefore, the associated measures are also linearly related: 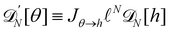 (the factor
(the factor ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) N has been introduced to make the measure dimensionless), with Jθ→h = 1/aN (the derivation of this Jacobian is reported in Appendix C). Accordingly, the Faddeev–Popov corrective term, which is a correction to the linear relationship between the two measures, and whose expression is derived in Appendix C, is a second order correction to the expression of τ, in agreement with Cai et al.3 Moreover, inserting θ (s) ≃ dh/ds in eqn (36) breaks the rotational invariance of the Hamiltonian. Yet, substituting θ (s) → dh/ds (and using
N has been introduced to make the measure dimensionless), with Jθ→h = 1/aN (the derivation of this Jacobian is reported in Appendix C). Accordingly, the Faddeev–Popov corrective term, which is a correction to the linear relationship between the two measures, and whose expression is derived in Appendix C, is a second order correction to the expression of τ, in agreement with Cai et al.3 Moreover, inserting θ (s) ≃ dh/ds in eqn (36) breaks the rotational invariance of the Hamiltonian. Yet, substituting θ (s) → dh/ds (and using ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = ea/π) in the grand-canonical partition function (eqn (38)) will not change its final expression (eqn (44)). Hence, the use of an approximated Hamiltonian cannot explain the Monge model inaccuracies and the non-equivalence of ensembles discussed in Section 2 either. This should come as no surprise: ensemble equivalence is a very general feature of standard statistical physics and does not makes any assumption on the realism of the Hamiltonian. It can also be noticed that in the ensemble (T, τ, L), we obtained (Section 2.2) r = τ while using both an approximated measure and an approximated Hamiltonian.
= ea/π) in the grand-canonical partition function (eqn (38)) will not change its final expression (eqn (44)). Hence, the use of an approximated Hamiltonian cannot explain the Monge model inaccuracies and the non-equivalence of ensembles discussed in Section 2 either. This should come as no surprise: ensemble equivalence is a very general feature of standard statistical physics and does not makes any assumption on the realism of the Hamiltonian. It can also be noticed that in the ensemble (T, τ, L), we obtained (Section 2.2) r = τ while using both an approximated measure and an approximated Hamiltonian.
 , and can be interpreted as a correction (so-called Liouville correction) to the Monge measure. However, for calculating accurately other quantities, such as 〈h4〉, the other corrections to the Monge model (expansion of
, and can be interpreted as a correction (so-called Liouville correction) to the Monge measure. However, for calculating accurately other quantities, such as 〈h4〉, the other corrections to the Monge model (expansion of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) to higher terms, and Faddeev-Popov term) might be mandatory.
to higher terms, and Faddeev-Popov term) might be mandatory.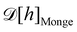 that still does not properly enumerate the membrane configurations: because the allowed displacements of the patches are those which keep uniform patch length, we should consider all the possible membrane conformations for a given patch length a, and sum over all possible values of a. The partition function can then be written as:
that still does not properly enumerate the membrane configurations: because the allowed displacements of the patches are those which keep uniform patch length, we should consider all the possible membrane conformations for a given patch length a, and sum over all possible values of a. The partition function can then be written as: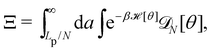
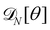 and
and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) [θ] are given by eqn (35) and (36), respectively. Taking the fluctuating character of the patch size a is thus essential to get the correct result, in the same way as the fluctuation of the patch number is essential to recover r = τ in the (T, Lp, γ). Indeed, in both cases this boils down to sum over membrane length L, and the partition function (49) is in fact identical to eqn (38).
[θ] are given by eqn (35) and (36), respectively. Taking the fluctuating character of the patch size a is thus essential to get the correct result, in the same way as the fluctuation of the patch number is essential to recover r = τ in the (T, Lp, γ). Indeed, in both cases this boils down to sum over membrane length L, and the partition function (49) is in fact identical to eqn (38).
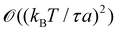 and so can be used indifferently in the expressions of the height and length fluctuations of a fluid interface.
and so can be used indifferently in the expressions of the height and length fluctuations of a fluid interface.
![[h with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0068_0303.gif)
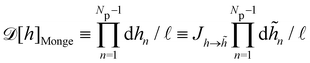 , where Jh→
, where Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) is the constant Jacobian associated with the linear change of variables eqn (7). Its value can be obtained e.g., by calculating a simple Gaussian integral
is the constant Jacobian associated with the linear change of variables eqn (7). Its value can be obtained e.g., by calculating a simple Gaussian integral  in both direct and reciprocal spaces. Using the identity
in both direct and reciprocal spaces. Using the identity 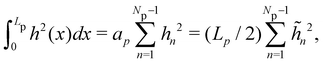 the integral can be written as
the integral can be written as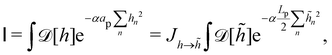
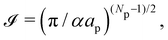 and the second one
and the second one 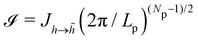 . Therefore, Jh→
. Therefore, Jh→![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = (Np/2)(Np−1)/2.
= (Np/2)(Np−1)/2.
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/h3_i_char_e123.gif)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) associated with the linear change of variables {θn} → {
associated with the linear change of variables {θn} → {![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p}, with
p}, with 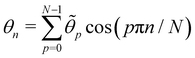 , n ∈ {0,…, N − 1}. As in Appendix A, Jθ→
, n ∈ {0,…, N − 1}. As in Appendix A, Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) is obtained by evaluating a simple integral expressed with both sets of variables. Note however that here the N variables θn are not independent, but are constrained by
is obtained by evaluating a simple integral expressed with both sets of variables. Note however that here the N variables θn are not independent, but are constrained by 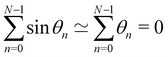 . This constraint is properly taken into account by introducing a Dirac delta in the integration. For the variables {
. This constraint is properly taken into account by introducing a Dirac delta in the integration. For the variables {![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p} on the other hand, this constraint simply reads
p} on the other hand, this constraint simply reads ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) 0 = 0. The second constraint of fixed projected length
0 = 0. The second constraint of fixed projected length 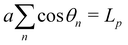 does not need to be considered to evaluate Jθ→
does not need to be considered to evaluate Jθ→![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) , since its value does not depend on the choice of the integral to evaluate. Let us then evaluate the integral
, since its value does not depend on the choice of the integral to evaluate. Let us then evaluate the integral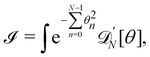
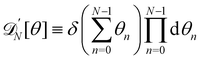 . Using the identities
. Using the identities 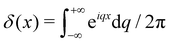 , and
, and 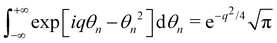 , we get:
, we get: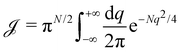
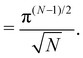
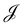 can be rewritten with variables
can be rewritten with variables ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) p as
p as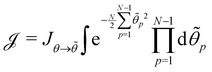
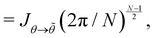
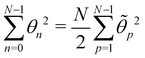 . Comparing both expressions eqn (53) and (55) finally yields
. Comparing both expressions eqn (53) and (55) finally yields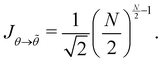
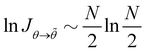 .
.
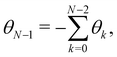 there are N − 1 independent variables for each set. The Jacobian matrix associated with the change of variables θn → hn is
there are N − 1 independent variables for each set. The Jacobian matrix associated with the change of variables θn → hn is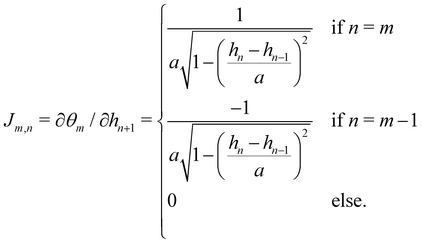
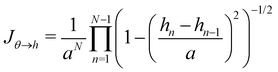
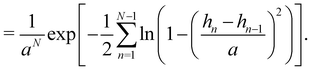
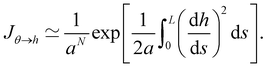
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are, like the contributions of undulation modes of wavelength less than ap, implicitly included within the values of the phenomenological parameters of the model, i.e.: the surface tension γ and the bending rigidities κ and
are, like the contributions of undulation modes of wavelength less than ap, implicitly included within the values of the phenomenological parameters of the model, i.e.: the surface tension γ and the bending rigidities κ and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) .
.![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) n, is not uniform.
n, is not uniform.