Dynamic effect of polymers at the surfactant–water interface: an ultrafast study

Abstract

Interfaces play a role in controlling the rates and outcomes of chemical processes. Characterizing the interactions at heterogeneous interfaces is critical to developing a comprehensive model of the role of interfaces and confinement in modulating chemical reactions. Reverse micelles are an ideal model system for exploring the effect of encapsulated species on interfacial environments. Here, we use a combination of ultrafast two-dimensional infrared (2D IR) spectroscopy and molecular dynamics (MD) simulations to characterize the picosecond interfacial dynamics in reverse micelles (RMs) containing acrylamide monomers and polyacrylamide polymers within the aqueous phase. The ester carbonyl vibrations of the sorbitan monostearate surfactants are examined to extract interfacial hydrogen-bonding populations and dynamics. Hydrogen bond populations at the ester carbonyl positions remain unchanged with the inclusion of either polymer or monomer species. Hydrogen-bond dynamics are not altered with the addition of monomer but are slowed down twofold in the presence of encapsulated polyacrylamide polymer species as a result of polymer chains partially localizing to the interface. These findings imply that kinetics of reactions that occur at interfaces or in confined environments could be modulated by interfacial localization of the different components.

---

Introduction

Reverse micelles (RMs) are a class of thermodynamically-stable emulsions formed by dispersing water and surfactants in a continuous nonpolar phase.^1–3 The RM interface is heterogeneous, providing a range of microenvironments that can be exploited to control chemical processes.^4–9 While in bulk solution the rate of chemical reactions is determined by diffusion rates and activation barriers.^10–15 Confinement produces a range of solvation environments where reactants or products can remain in bulk or become localized near interfaces, and thereby the thermodynamics of different components can be altered by the interface, therefore this nanometer-scale “reaction vessel” can substantially modulate the free energy landscapes of chemical processes through complex interactions.^14,16–19 These environments can be not only be exploited to control reaction rates, but also to affect the outcome chemical processes.²⁰

Radical polymerization reactions represent an important example of chemical processes commonly carried out in microemulsions.²¹ Surfactant compositions are designed to modulate polymer length and polydispersity.^22,23 Understanding the equilibrium dynamics of encapsulated reactants (monomers) and products (polymers) with the interface is therefore the first step towards obtaining a quantitative description of the interfacial effects within these processes.

Ultrafast infrared spectroscopy is a powerful tool to probe interfacial dynamics and extract a molecular-level description of the interface between water in the RM and the hydrophobic environment of the hydrocarbon solvent.^24,25 In this study we examine nonionic sorbitan monostearate surfactants (Fig. 1A), containing ester carbonyls precisely located within the 1-nanometer interface between the hydrophilic and hydrophobic environments, and therefore these carbonyl groups report on local water environments.^26,27 Specifically, in this study two-dimensional infrared (2D IR) spectroscopy is used to measure the effects of acrylamide (AM) monomers and polyacrylamide (PAM) polymers (Fig. 1B and C) on the sub-picosecond frequency fluctuations of the carbonyls.^28–30 Measurements are then interpreted through molecular dynamics (MD) simulations of the same systems. Direct, one-to-one comparison between simulations and experiments provides an atomistic view of the H-bond networks and H-bond dynamics at the interface.

Fig. 1 (A) Structure of sorbitan monostearate. The non-polar acyl chain is shown in red and polar headgroup shown in blue. The ester carbonyl at the interface of the two regions, which serves as the vibrational probe, is shown in black. (B) Acrylamide and (C) polyacrylamide. Each unit has an amide group. (D) Ester carbonyl IR absorption spectra of Span-60 reverse micelles containing acrylamide monomers or polymers as indicated in the inset. The shaded peaks represent Gaussian fits to a representative FTIR spectrum used to extract the H-bond populations. The three peaks correspond to 0, 1, and 2 H-bond ensembles in order of decreasing center frequency.

Methods

Sample preparation

RM were prepared with a water loading ratio (w_o, water/surfactant mole ratio) of 20 with a concentration of 0.07 M solution of sorbitan monostearate (Span-60) using D₂O, and n-octane as the hydrophobic medium. AM or PAM was dissolved in D₂O at 5% by weight (wt%). Before sample preparation, the surfactants were lyophilized overnight to remove residual water, then in dissolved n-octane, and the resulting surfactant/octane mixture was dried under molecular sieves for 12 hours to remove any additional water. The AM or PAM in D₂O solution was then added to the surfactant/octane mixture heated to 45 °C and sonicated at this temperature for 15 minutes. Sorbitan monostearate, AM, PAM, and D₂O were purchased from Sigma-Aldrich, and n-octane was purchased from Alfa Aesar. RMs with monomer and polymer were characterized using dynamic light scattering (DLS) measurements (Section S1, ESI†). Bulk solution measurements were performed on ethyl acetate/PAM in D₂O solutions. These were prepared by dissolving PAM in D₂O at 5 wt% and ethyl acetate at a concentration of 20 mg mL⁻¹.

IR absorption spectroscopy

IR absorption spectra were measured in the ester carbonyl stretch of the RMs and ethyl acetate samples at 45 °C (Sections S2–S4, ESI†) using a custom-machined temperature-controlled brass sample cell. Samples were held between two 1 mm-thick CaF₂ windows with a 50 μm PTFE spacer. Spectra were collected with a 1 cm⁻¹ resolution using Bruker Vertex 70 FTIR spectrometer equipped with a DTGS detector. MATLAB R2021b was used to plot and analyze the FTIR and 2D IR spectra. Ester carbonyl H-bond populations were extracted using a previously-reported peak fitting technique.³¹ H-bond enthalpies were extracted from temperature-dependent IR absorption spectra using a van’t Hoff analysis described previously.³² To summarize, the natural log of the non-H-bond population over the H-bonded populations is plotted as a function of inverse temperature (1/K). The slope of the resulting line is .³²

2D IR spectroscopy

Ultrafast 2D IR spectra were measured using a custom-built spectrometer described previously.³³ In brief, 100 fs mid-IR pulses, centered at 5.7 μm, generated using an OPA/DFG, were split into excitation (pump), and detection (probe) pulses. The coherence time (t₁) was scanned using a mid-IR pulse shaper (QuickShape, PhaseTech Inc) and was numerically Fourier transformed to generate the excitation frequency (ω₁). The t₁ time was scanned to 3 ps in 15 fs steps, and spectra were measured in a 1500 cm⁻¹ rotating frame. The probe pulse was measured through a grating spectrometer in a 128–128 pixel MCT array, to generate the detection frequency (ω₃). Spectra were measured at selected waiting times from 150 fs to 3 ps as indicated in Fig. S8–S12 (ESI†). All spectra were measured using a perpendicular pump–probe polarization condition to minimize the scattered light at the detector. The 1745 cm⁻¹ region was analyzed via center-line slope (CLS) analysis.³⁴ The CLS relaxation as a function of waiting time was fit to a monoexponential function, and error bounds were computed using a statistical bootstrapping method described previously.³⁵ Previous analysis have established that the CLS decay time constant is unaffected by contamination from neighboring 2D peaks, but the CLS offset can vary depending on the frequency region used for generating the CLS, as a result, the offset values can be unreliable and are not further analyzed as part of this study.³⁵

MD simulations

Sorbitan monostearate, n-octane, AM, and PAM initial structures and topologies were generated using the CHARMM36 force field as implemented in CHARMM-GUI.³⁶ Packmol was then used to generate initial configurations.³⁷ The number of surfactants added to the MD box was adjusted to produce an initial area-per-surfactant of 35 Ų.³⁸ While the sorbitan monostearate product contains a small distribution of tail lengths, simulations only included surfactants with an 18-carbon fully saturated tail.³⁹ Each box is composed of 92 surfactant molecules, 2000 TIP3P water molecules, 420 octane molecules, and PAM corresponding to the wt% used in the experiments. Each simulation was performed using the following steps: steepest-descent energy minimization; 500 ps NVT equilibration; 20 ns NPT equilibration; and 20 ns NPT production. Simulations were run with a 2 fs time step and snapshots were stored every 1 ps for H-bond population analysis (Table 1), tetrahedral order parameters (Fig. S19, ESI†), water mean-squared displacement (Fig. S20, ESI†). In addition, a 500p ps subset of the NPT production trajectory saved every 20 fs for generating FFCFs and computing exponential relaxation lifetimes (Table 1). The V-rescale thermostat and a Parrinello–Rahman barostat were used for the NPT ensemble. All simulations were performed using the GROMACS 2019.4 package.

Table 1 Experimental and simulated H-bond populations and frequency-frequency correlation functions of the experimental three ensembles corresponding to RMs without encapsulated monomer or polymer, or RMs with 5 wt% of either AM or PAM

System	Measured H-bond populations (%)			Simulated populations (%)			Experimental FFCF dynamics (ps)	Simulated FFCF dynamics (ps)
	0HB	1HB	2HB	0HB	1HB	2HB
Reverse micelle (RM)	44 ± 2	31 ± 1	24 ± 3	55	41	4	1.5 ± 0.2	0.60
RM with acrylamide (5 wt%)	46 ± 1	31 ± 1	23 ± 1	47	46	6	1.6 ± 0.1	0.36
RM with polyacrylamide (5 wt%)	47 ± 2	31 ± 1	22 ± 1	52	43	5	3.3 ± 0.4	0.65

---

MD trajectory analysis

Comparison between experiments and simulations provides insight into interfacial H-bond ensemble structures and carbonyl H-bond lifetimes. Surfactant carbonyl H-bond populations were extracted from the MD trajectories using a geometric criterion based on a donor–acceptor cutoff length of 3.5 Å and the donor–hydrogen–acceptor angle of 35° as previously established in the literature.⁴⁰ All H-bond donors, including water, AM or PAM hydroxyls, and surfactant headgroup hydroxyls, were included in the population analysis.

The fluctuating electric fields at the ester carbonyl positions were used as the basis for computing frequency–frequency correlation functions (FFCFs) using a previously-described electrostatic frequency map.²⁷ The computed FFCF is then fit to a sum of three exponentials. The three decays constants represent different contributions to the FFCF: a fast (∼50 fs) contribution from inertial motions, an intermediate (∼1 ps) contribution from H-bond dynamics, and a slow (>10 ps) contribution from reorganization of the surfactant headgroups.⁴¹ The picosecond component is directly compared to the experimental relaxation extracted from the lifetime of the CLS relaxation as a function of waiting time.

Results

H-bond populations

The ester carbonyl absorption band is composed of three peaks centered around 1750, 1730, and 1712 cm⁻¹ representing the 0, 1, and 2 H-bond ensembles respectively as shown by the Gaussian peaks in Fig. 1D. The H-bond populations are extracted from areas of the Gaussian functions, weighted by the oscillator strengths, as shown in Fig. 1 and described in Section S2. The addition of both AM monomer and polymer leads to a small decrease in solvation at the interface. The 0 H-bond population undergoes a 5% increase when polymer species are incorporated, in comparison with the RM with no encapsulated species (Table 1). The dehydration effect of polymer addition is more pronounced at higher temperatures, indicating that the H-bond enthalpy is altered by the presence of the polymer. Experimentally, the populations include contributions from water, polymer, as well as hydroxyl groups of neighboring surfactant headgroups, all H-bonds in this system produce a similar frequency shift, given the similarity in the induced electric field along the carbonyl bond, for this reason, it is not possible to distinguish between different H-bond donor types without more advanced modeling.42 In brief, the observed shifts are indistinguishable from one another due to the similar H-bond strength of the (poly)acrylamide –NH and Span-60 –OH moieties to be of similar H-bonding strength to that of water.⁴³ After benchmarking against the experimental populations, the comparison between MD models and experiments offers a route to separate the contributions from H-bond donors to the overall populations.

Temperature-dependent FTIR spectra were used to extract H-bond formation enthalpies, ΔH_f as shown in Fig. S1–S6 (ESI†). RMs with no encapsulated species show enthalpies of 2.7 ± 0.1 kJ mol⁻¹, RMs with encapsulated monomer ΔH_f of 3.1 ± 0.1 kJ mol⁻¹, RMs with encapsulated polymer has a ΔH_f of 3.8 ± 0.1 kJ mol⁻¹ at a concentration of 5 wt%. For perspective, fully solvated ethyl acetate produces a ΔH_f of 4.8 kJ mol⁻¹ (Fig. S14, ESI†). The difference in H-bond enthalpies as a result of AM and PAM in the RM could have two origins: 1. an indirect effect, where the interface could be perturbed by the presence of the polymer, for example, the balance between surfactant–surfactant interactions surfactant–water interactions, could be altered by the presence of polymer in the interfacial environment. 2. Direct interactions where the monomer or polymer form H-bonds with the surfactant headgroups. In the next section we analyze the MD trajectories to elucidate the effects of AM and PAM on the interfacial H-bond populations and dynamics.

Ultrafast 2D IR spectroscopy provides a sub-picosecond measurement of the local solvation dynamics at the interface. Fig. 2 shows the ester carbonyl of Span-60, with three H-bond peaks centered around 1750, 1730, and 1712 cm⁻¹, respectively. The ω₁ axis represents excitation and ω₃ detection frequencies respectively. Peaks appear as a positive and negative doublet. The positive (red) peak corresponds to a ground state bleach and the negative (blue) represents the excited-state absorption.²⁹

Fig. 2 (A) Sample ester carbonyl 2D IR spectra of RMs without added monomer or polymer and RMs containing 5 wt% AM or 5 wt% PAM as indicated in each panel. Red and blue contours represent the ground state and excited states transitions, respectively. Along the diagonal there are three peaks with no off-diagonal features. Fitted to the highest intensity 0 H-bond peak is the CLS. (b) CLS decays of all the reverse micelles as a funcion of waiting time. The addition of AM monomer does not affect the measured dynamics, however, the PAM polymer does cause a twofold slow down in dynamics.

The interfacial dynamics were extracted through CLS analysis of the highest-frequency peak as described previously.³⁹ The CLS analysis reports on the overall timescale for H-bond fluctuations of the water present at the surfactant ester carybonyl, as measured in terms of fluctuations of the carbonyl frequencies. In the RMs without added solute species, the relaxation decay time is 1.6 ± 0.2 ps. The addition of monomers did not affect the dynamics as indicated by a nearly identical CLS relaxation time, however, the polymer addition slowed dynamics approximately by a twofold increase to the CLS relaxation time to 3.3 ± 0.4 ps (Table 1). These observations indicate that PAM interacts preferentially with the interface over the same mass of monomer in the RM. To ensure that the observed water H-bond fluctuations at the surfactant interface results from direct interactions of polymers with the interface and not through overall slowing of the entire water ensemble in the RMs, control experiments of ethyl acetate with varying polymer concentrations were performed. Ethyl acetate was selected as a bulk vibrational probe for its excellent solubility in water and its lack of ability to H-bond to itself, preventing aggregation.⁴⁴ The 2D IR with the accompanying CLS decays of ethyl acetate with no polymer and of 5 wt% PAM are shown in Fig. 3. The values of the CLS decays (Fig. 3) demonstrate that the slow down of H-bond fluctuations seen in the RM is not replicated in bulk solution. Each ethyl acetate spectrum does not show a significant change to the CLS decay time comparable to the RM sample. This shows that the RM interfacial dynamics slowdown is due to direct perturbation of the interface by the polymers and not a simple increase in the bulk viscosity.

Fig. 3 Sample 2D IR spectra (A) of ethyl acetate in D₂O without added polymer and ethyl acetate in 5 wt% polyacrylamide in D₂O solution. The red and blue peaks represent the ground state and excited states transitions, respectively. The CLS fit (B) along with the decays of the ethyl acetate spectra. The inclusion of the polymer does not display a significant change in the bulk water dynamics.

The experimental frequency fluctuations are interpreted in terms of H-bond fluctuations in MD simulations by comparing the picosecond-component of the computed FFCF relaxation and the experimental CLS decay time. The FFCF was calculated as described in Section S5 (ESI†). In brief, an electrostatic map was used to convert the local electric fields of each surfactant ester carbonyl into an instantaneous frequency. The numerical FFCF is then fit to the sum of a tri-exponential decay. The second exponential is directly comparable to the experimental H-bond fluctuations as its timescale is on the same order as those measured by the CLS analysis. Section S5 (ESI†) describes the computation of FFCF from MD simulations using a vibrational map. The computed ester carbonyl relaxation constants for the AM and PAM inside the RM are 0.60 ps and 0.65 ps, respectively.

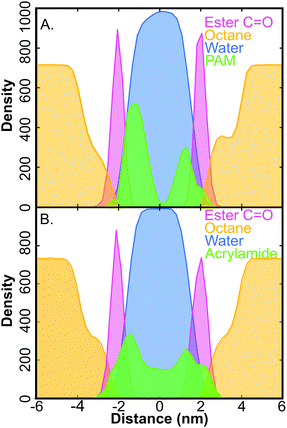
Compared to the relaxation constant of the same simulation parameters with no encapsulated species the relaxation time is 8% slower for the PAM system and the AM system is 40% faster. The absolute value of the MD FFCF relaxation times lacks quantitative agreement with the experiment possibly suggesting that simulations underestimate the surfactant–polymer interactions, however, simulations do reproduce the experimental H-bond populations, as discussed in the next section. In general, the experimental result shows that the inclusion of polymer perturbs the interfacial environment more significantly compared to equivalent quantity of monomer units. This is furthered by the evidence displayed in Fig. 4. The AM monomer is more uniformly distributed across the interior of the membrane with a partial localization at the surfactant interface, in contrast, the polymer becomes significantly more localized to the interface. Thus this evidence strongly suggests that polymer localization is the primary cause of the slowdown in H-bond fluctutations at the RM interface.

Fig. 4 Representative mass distributions of octane, water, surfactant, and encapsulated species in the simulated MD box, in units of kg m⁻³. The surfactant ester C=O is shown in pink and is located at the interface between the water (blue) and the octane (orange). The encapsulated polymer is localized at near the surfactant carbonyls (a) and the acrylamide is distributed across the entire micelle. The surfactant C=O, monomer, and polymer density values were scaled by a factor of 10 for better illustration.

Discussion

The enthalpy of H-bond formation remains unchanged by the presence of AM monomers and agree with previous measurements of the pure RMs (Section S2, ESI†).^35,39 RMs with PAM display ∼20% larger H-bond enthalpies of formation (Section S1, ESI†). This comparison suggests that monomers do not perturb the interface, whereas the polymer may interact directly with the surfactants or indirectly affects the packing or hydration. Interfacial water H-bond frequency fluctuations measured using 2D IR spectroscopy, show that the encapsulated monomer species do not differ from the pure RMs (Table 1). The solvation dynamics of the RMs containing the polymer are approximately two-fold slower in relation to the other systems studied (Fig. 2), suggesting, once again, that the slowdown is a result of interactions with the interface. Interestingly, bulk solution H-bond frequency fluctuations, as measured by ethyl acetate, a fully soluble probe, indicate that PAM does not change significantly at the 5 wt% concentrations used in the RM experiments, suggesting that the polymer slowdown is a purely interfacial phenomenon, without an accompanying slowdown of the bulk.

Since the polymers interact with the interface, it is important to characterize any alterations to the overall structure of the RM such as changes in the diameter or heterogeneity, which have been observed in analogous systems.^39,45,46 DLS RM size measurements were performed on the RMs with 5 wt% polymer and monomer concentrations (Table S1, ESI†). The DLS measurements show no significant changes across samples, and in addition, the sizes are comparable to previous measurements of these RM systems.^35,39 This demonstrates that AM or PAM maintain the global RM structure relatively intact, suggesting that the change in both H-bond enthalpy and interfacial H-bond frequency fluctuations is due to the interaction of the polymer and the interface, not due to a significant change in the surfactant packing or global surfactant–water interactions that would alter the RM size.

Next, to understand the molecular interactions resulting in the observed slowdown at the interface, we analyze the MD trajectories. The C=O frequency fluctuation timescales extracted from simulations are in good overall agreement with the experimental CLS decay time constants shown in Table 1. Although the MD dynamics are ∼50% faster compared to the experiment. Table 1 also shows that the MD dynamics speed up with the addition of monomer, while the dynamics become slower with the addition of polymer, this suggests that perhaps MD overestimates surfactant–monomer interactions compared to experiments.

Fig. 4 illustrates the polymer localization at the surfactant interface, in the MD box, whereas the monomer is more evenly distributed through the surfactant and water regions. AM's structure (Fig. 1B) displays both H-bond accepting and donating sites. This allows for AM monomer to insert itself into the H-bond network in water in a less perturbative way. Furthermore, the small size of the water layer, chosen to reproduce the water-to-surfactant ratio of 20 used for the experiments, may not provide sufficient “bulk” water, which could overestimate the surfactant–monomer or surfactant–polymer interactions.

Understanding the effect of surfactant interactions with polymer or monomer affect the interface requires characterizing the ordering of water molecules as the interface using a tetrahedral order parameter.⁴⁷ In brief, the order parameter describes the ordering of H-bonds within the network and has a value of one in a perfectly tetrahedral “ice-like” structure, and a value of zero for a completely random “ideal gas” structure. The tetrahedral order parameter (Section S7 and Fig. S19, ESI†) indicates that the interfacial water with 5 wt% AM monomer is more ordered than either of the two other systems. This indicated that the dynamics would be increased as a result of the more ordered H-bond structure. More ordered H-bond networks maintain proper angle and distance requirements for H-bond exchange, resulting in faster dynamics. The opposite effect is observed with PAM where the interfacial water becomes more disordered, leading to slower dynamics. These MD results give insight into the underlying physical picture that results in the computed H-bond dynamics (Table 1). This also explains why the polymer does not have the same order-of-magnitude effect in the simulated FFCF when compared to the experimental CLS decays. The polymers used in the MD simulations, which have a molecular mass of 569 Da, are significantly smaller than those used in the experiments, which have an average molecular mass of 40 000 Da. The overall aim of the MD simulations, to elucidate the effect of the polymer was accomplished through the tetrahedral order parameter analysis and mean squared displacement (Section S7, ESI†). More advanced simulations on larger systems are likely necessary to quantitatively reproduce the experimental results.

Conclusion

Here we demonstrated the non-ionic AM monomers and PAM polymers interact differently with a surfactant interface, as probed at the surfactant headgroup location. The polymers induce a significant effect on the H-bond dynamics whereas the monomers appear to be largely non-perturbative. The H-bond populations of the three systems remained largely unchanged between experiment and simulation, but the H-bond enthalpies are altered only by the presence of polymer suggesting that polymer may alter the surfactant–surfactant or surfactant–water interactions. Simulations predict that the monomer system would speed up the solvation dynamics, however, this is not reflected in the experimental findings. This may be due to the simulation overestimating the interactions of AM monomer with the interface, as a result of the force field or the size of the simulation system. Simulations elucidated the origin of the polymer effects, showing that the water H-bond network is disrupted by the presence of the polymer. Even though AM can donate and accept H-bonds, the restricted degrees of freedom of a polymer (when compared to a monomer unit) does not allow for minimal disruption of the H-bond network.

The study showed that the non-charged but polar interface interacts with a polar monomer and polymer in different degrees; showing a preferential interaction with the polymer species when compared to the monomer. The preferential interaction the polymer has with the interface has implications in modulating kinetics as a function of reaction coordinate in polymer synthesis in RMs. As monomers react and form short-chain polymers and continue to react to form longer polymer chains the thermodynamics and water dynamics at the interface also change. The interface has a unique dynamic role in the formation of products not seen in bulk reactions.

Conflicts of interest

The authors state there are no conflicts to declare.

Acknowledgements

Simulations were carried out at the Texas Advanced Computing Center (TACC). We gratefully acknowledge Research Corporation for Science Advancement (RCSA) for a Cottrell Scholars Award to CRB and the Welch Foundation (F-1891) for supporting this project. We thank Christopher P. Baryiames for their insightful discussions.

References

1. K. T. De and A. Maitra, Solution Behaviour of Aerosol OT in Non-Polar Solvents, Adv. Colloid Interface Sci., 1995, 59(31), 95–193.
2. K. Shinoda and Y. Shibata, Principles for the Attainment of Minimum Oil-Water Interfacial Tension by Surfactants: The Characteristics of Organized Surfactant Phase, Colloids Surf., 1986, 19(2–3), 185–196,  DOI:10.1016/0166-6622(86)80335-3.
3. L. Sepulveda, E. Lissi and F. Quina, Interactions of Neutral Molecules with Ionic Micelles, Adv. Colloid Interfaces Sci., 1986, 25, 1–57.
4. P. L. Luisi, M. Giomini, M. P. Pileni and B. H. Robinson, Reverse Micelles as Hosts for Proteins and Small Molecules, Biochim. Biophys. Acta, 1988, 947(1), 209–246,  DOI:10.1016/0304-4157(88)90025-1.
5. K. Vos, C. Laane and A. J. W. G. Visser, Spectroscopy of Reveresed Micelles, Photochem. Photobiol., 1987, 45(6), 863–878.
6. V. Uskoković and M. Drofenik, Synthesis of Materials within Reverse Micelles, Surf. Rev. Lett., 2005, 12(2), 239–277,  DOI:10.1142/S0218625X05007001.
7. K. Kumar, D. Dhachinamoorthi, R. Saravanan, U. Gopal and V. Shanmugam, Microemulsions as Carrier for Novel Drug Delivery: A Review, J. Pharm. Sci., 2011, 37-45, 10.
8. J. Jiang, Y. He, L. Wan, Z. Cui, Z. Cui and G. P. Jessop, Synthesis of CdS Nanoparticles in Switchable Surfactant Reverse Micelles, Chem. Commun., 2013, 49, 1912–1914,  10.1039/C2CC38202D.
9. Y. Chen, Y. Liu, Y. Yao, S. Zhang and Z. Gu, Reverse Micelle-Based Water-Soluble Nanoparticles for Simultaneous Bioimaging and Drug Delivery, Org. Biomol. Chem., 2017, 15, 3232–3238,  10.1039/C7OB00169J.
10. K. Takashima and M. J. Riveros, Gas-Phase Solvaed Negative Ions, Mass Spectom. Rev., 1998, 17, 409–430.
11. S. F. Nelsen, A. Konradsson, L. T. Jentzsch, J. J. O’Konek and R. J. Pladziewicz, Comparison of Gas and Solution Phase Intrinsic Rate Constants for Electron Transfer of Tetraalkylhydrazines, J. Chem. Soc., Perkin Trans. 2, 2001, 1552–1556,  10.1039/B103361C.
12. A. A. Viggiano, T. S. Arnold, A. R. Morris, A. F. Ahrens and M. P. Hierl, Temperature Dependences of the Rate Constants and Branching Ratios for the Reactions of OH-(H₂O)_0–4 + CH₃Br, J. Phys. Chem., 1996, 100, 14397–14402,  DOI:10.1021/jp961250y.
13. V. J. Seely, A. R. Morris and A. A. Viggiano, Temperature Dependences of the Rate Constants and Branching Ratios for the Reactions of F-(H₂O)_0–5 with CH₃Br, J. Phys. Chem., 1997, 101(25), 4598–4601,  DOI:10.1021/jp970492a.
14. J. Faeder and M. B. Ladanyi, Solvation Dynamics in Reverse Micelles: The Role of Headgroup-Solute Interactions, J. Phys. Chem. B, 2005, 109(14), 6732–6740,  DOI:10.1021/jp045202m.
15. H. Shirota, Y. Tamoto and H. Segawa, Dynamic Fluorescence Probing of the Microenviroment of Sodium Dodcyl Sulfate Micelle Solutions: Surfactant Concentration Dependence and Solvent Isotope Effect, J. Phys. Chem. A, 2004, 108(16), 3244–3252,  DOI:10.1021/jp035861j.
16. K. R. Mitchell-Koch and W. H. Thompson, How Important Is Entropy in Determining the Position Dependent Free Energy of a Solute in a Nanoconfined Solvent?, J. Phys. Chem., 2007, 111(32), 11991–12001,  DOI:10.1021/jp072580t.
17. J. Chowdhary and B. Ladanyi, Molecular Dynamics Simulation of Aerosol-OT Reverse Micelles, J. Phys. Chem. B, 2009, 113(45), 15029–15039,  DOI:10.1021/jp906915q.
18. J. Huang and F. V. Bright, Microheterogeneity of Sodium Dodecylsulfate Micelles Probed by Frequency-Domain Fluorometetry, Appl. Spectrosc., 1992, 46(2), 329–339,  DOI:10.1366/0003702924125663.
19. C. A. Munson, A. G. Baker, N. S. Baker and V. F. Bright, Effects of Subzero Temperatures on Fluorescent Probes Sequestered within Aerosol-OT Reverese Micelles, Langmuir, 2004, 20(5), 1551–1557,  DOI:10.1021/la0302753.
20. W. H. Thompson, Solvation Dynamics and Proton Transfer in Nanoconfined Liquids, Annu. Rev. Phys. Chem., 2011, 62, 599–619,  DOI:10.1146/annurev-physchem-032210-103330.
21. L. Garcia-Uriostegui, G. Pineda-Torres, S. López-Ramírez, J. Barragán-Aroche and C. Durán-Valencia, Inverse Emulsion Free-Radical Polymerization of Acrylamide Terpolymer for Enhanced Oil Recovery Application in Harsh Reservoir Conditions, Polym. Eng. Sci., 2017, 57(11), 1214–1223,  DOI:10.1002/pen.24499.
22. A. Finne-Wistrand and A.-C. Alberston, The Use of Polymer Design in Resorbable Colloids, Annu. Rev. Mater. Res., 2006, 36, 369–395,  DOI:10.1146/annurev.matsci.36.032905.091005.
23. M. M. Fryd and T. G. Mason, Advanced Nanoemulsion, Annu. Rev. Phys. Chem., 2012, 63, 493–518,  DOI:10.1146/annurev-physchem-032210-103436.
24. M. K. Petti, J. P. Lomont, M. Maj and M. T. Zanni, Two-Dimensional Spectroscopy Is Being Used to Address Core Scientific Questions in Biology and Materials Science, J. Phys. Chem. B, 2018, 122(6), 1771–1780,  DOI:10.1021/acs.jpcb.7b11370.
25. A. L. Le Sueur, R. E. Horness and M. C. Thielges, Applications of Two-Dimensional Infrared Spectroscopy, Analyst, 2015, 140, 4336–4359,  10.1039/C5AN00558B.
26. S. D. Fried, S. Bagchi and S. G. Boxer, Measuring Electrostatic Fields in Both Hydrogen-Bonding and Non-Hydrogen-Bonding Environments Using Carbonyl Vibrational Probes, J. Am. Chem. Soc., 2013, 135(30), 11181–11192,  DOI:10.1021/ja403917z.
27. S. C. Edington, J. C. Flanagan and C. R. Baiz, An Empirical IR Frequency Map for Ester C=O Stretching Vibrations, J. Phys. Chem. A, 2016, 120(22), 3888–3896,  DOI:10.1021/acs.jpca.6b02887.
28. A. Ghosh, J. S. Ostrander and M. T. Zanni, Watching Proteins Wiggle: Mapping Structures with Two-Dimensional Infrared Spectroscopy, Chem. Rev., 2017, 117(16), 10726–10759,  DOI:10.1021/acs.chemrev.6b00582.
29. P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, 2011.
30. M. Cho, Coherent Two-Dimensional Optical Spectroscopy, Chem. Rev., 2008, 108(4), 1331–1418,  DOI:10.1021/cr078377b.
31. X. You, E. Lee, C. Xu and C. R. Baiz, Molecular Mechanism of Cell Membrane Protection by Sugars: A Study of Interfacial H-Bond Networks, J. Phys. Chem. Lett., 2021, 12(39), 9602–9607,  DOI:10.1021/acs.jpclett.1c02451.
32. A. C. Guerin, K. Riley, K. Rupnik and D. G. Kuroda, Determining the Energetics of the Hydrogen Bond through FTIR: A Hands-On Physical Chemistry Lab Experiment, J. Chem. Educ., 2016, 93(6), 1124–1129,  DOI:10.1021/acs.jchemed.5b01014.
33. S. C. Edington, A. Gonzalez, T. R. Middendorf, D. B. Halling, R. W. Aldrich and C. R. Baiz, Coordination to Lanthanide Ions Distorts Binding Site Conformation in Calmodulin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(14), E3126–E3134,  DOI:10.1073/pnas.1722042115.
34. S. T. Roberts, J. J. Loparo and A. Tokmakoff, Characterization of Spectral Diffusion from Two-Dimensional Line Shapes, J. Chem. Phys., 2006, 125(8), 84502,  DOI:10.1063/1.2232271.
35. C. P. Baryiames and C. R. Baiz, Slow Oil, Slow Water: Long-Range Dynamic Coupling across a Liquid-Liquid Interface, J. Am. Chem. Soc., 2020, 142(18), 8063–8067,  DOI:10.1021/jacs.0c00817.
36. B. R. Brooks, C. L. Brooks, A. D. MacKerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, CHARMM: The Biomolecular Simulation Program, J. Comput. Chem., 2009, 30(10), 1545–1614,  DOI:10.1002/jcc.21287.
37. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations, J. Comput. Chem., 2009, 30(13), 2157–2164,  DOI:10.1002/jcc.21224.
38. L. Peltonen, J. Hirvonen and J. Yliruusi, The Behavior of Sorbitan Surfactants at the Water–Oil Interface: Straight-Chained Hydrocarbons from Pentane to Dodecane as an Oil Phase, J. Colloid Interface Sci., 2001, 240(1), 272–276,  DOI:10.1006/jcis.2001.7612.
39. C. P. Baryiames, M. Teel and C. R. Baiz, Interfacial H-Bond Dynamics in Reverse Micelles: The Role of Surfactant Heterogeneity, Langmuir, 2019, 35(35), 11463–11470,  DOI:10.1021/acs.langmuir.9b01693.
40. D. van der Spoel, P. J. van Maaren, P. Larsson and N. Timneanu, Thermodynamics of Hydrogen Bonding in Hydrophilic and Hydrophobic Media, J. Phys. Chem. B, 2006, 110(9), 4393–4398,  DOI:10.1021/jp0572535.
41. D. E. Moilanen, E. E. Fenn, D. Wong and M. D. Fayer, Water Dynamics in Large and Small Reverse Micelles: From Two Ensembles to Collective Behavior, J. Chem. Phys., 2009, 131(1), 014704,  DOI:10.1063/1.3159779.
42. I. M. Pazos, A. Ghosh and M. J. Tucker, Ester Carbonyl Vibration as a Sensitive Probe of Protein Local Electric Field, Angew. Chem., Int. Ed., 2014, 53(24), 6080–6084.
43. S. A. Roget, Z. A. Piskulich, W. H. Thompson and M. D. Fayer, Identical Water Dynamics in Acrylamide Hydrogels, Polymers, and Monomers in Solution: Ultrafast IR Spectroscopy and Molecular Dynamics Simulations, J. Am. Chem. Soc., 2021, 143(46), 14855–14868.
44. L. De Marco, M. Thämer, M. Reppert and A. Tokmakoff, Direct Observation of Intermolecular Interactions Mediated by Hydrogen Bonding, J. Chem. Phys., 2014, 141, 034502.
45. B. P. Wiebenga-Sanford, J. B. Washington, B. Cosgrove, E. Palmoares, D. A. Vasquez, C. D. Rithner and N. E. Levinger, Sweet Confinement: Glucose and Carbohydrate Osmolytes in Reverse Micelles, J. Phys. Chem. B, 2018, 122(41), 9555–9566.
46. A. A. Bakulin, D. Cringus, P. A. Pieniazek, J. L. Skinner, T. L. C. Jansen and M. S. Pshenichnikov, Dynamics of Water Confined in Reversed Micelles: Multidimensional Vibrational Spectroscopy Study, J. Phys. Chem. B, 2013, 117(49), 15545–15558,  DOI:10.1021/jp405853j.
47. J. R. Errington and P. G. Debenedetti, Relationship between Structural Order and the Anomalies of Liquid Water, Nature, 2001, 409, 318–321,  DOI:10.1038/35053024.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01651b

---