Coarse-grained molecular models of the surface of hair

Abstract

We present a coarse-grained molecular model of the surface of human hair, which consists of a supported lipid monolayer, in the MARTINI framework. Using coarse-grained molecular dynamics (MD) simulations, we identify a lipid grafting distance that yields a monolayer thickness consistent with both atomistic MD simulations and experimental measurements of the hair surface. Coarse-grained models for fully-functionalised, partially damaged, and fully damaged hair surfaces are created by randomly replacing neutral thioesters with anionic sulfonate groups. This mimics the progressive removal of fatty acids from the hair surface by bleaching and leads to chemically heterogeneous surfaces. Using molecular dynamics (MD) simulations, we study the island structures formed by the lipid monolayers at different degrees of damage in vacuum and in the presence of polar (water) and non-polar (n-hexadecane) solvents. We also use MD simulations to compare the wetting behaviour of water and n-hexadecane droplets on the model surfaces through contact angle measurements, which are compared to experiments using virgin and bleached hair. The model surfaces capture the experimentally-observed transition of the hair surface from hydrophobic (and oleophilic) to hydrophilic (and oleophobic) as the level of bleaching damage increases. By selecting surfaces with specific damage ratios, we obtain contact angles from the MD simulations that are in good agreement with experiments for both solvents on virgin and bleached human hairs. To negate the possible effects of microscale curvature and roughness of real hairs on wetting, we also conduct additional experiments using biomimetic surfaces that are co-functionalised with fatty acids and sulfonate groups. In both the MD simulations and experiments, the cosine of the water contact angle increases linearly with the sulfonate group surface coverage with a similar slope. We expect that the proposed systems will be useful for future molecular dynamics simulations of the adsorption and tribological behaviour of hair, as well as other chemically heterogeneous surfaces.

---

1 Introduction

A detailed understanding of the chemical composition and structure of the surface of human hair is important for the development of more effective and sustainable hair care products.¹ The human hair consists of a keratin core, the cortex, and a medulla in thicker hair.² The keratin core is covered by thin (∼0.5 μm) cuticle layers, which are arranged in an overlapping structure from the root to the tip of the hair.³ The cuticles themselves are constituent of another set of characteristic layers, which are described in detail elsewhere.^2,4 In virgin hair, a fatty acid monolayer (F-layer) covers the cuticles and governs their surface properties.^5,6 18-Methyleicosanoic acid (18-MEA) has been identified as the dominant lipid species within the F-layer.^7,8 18-MEA is covalently bonded to the protein layers below,⁹ mostly via thioester bonds to cysteine groups (Cys-18-MEA).¹⁰ However, chemical or mechanical damage can lead to partial or complete removal of the F-layer.^1,8 Even a single bleach treatment can cause significant damage to the F-layer, mostly through oxidation of the thioester groups in Cys-18-MEA to form cysteic acid.¹¹ Previous experiments have shown that the amount of 18-MEA decreases from the root of the hair to the tip.¹² There are also higher 18-MEA concentrations in the cuticle centre than at its edges, which are more prone to mechanical damage.¹³ Moreover, hair from older individuals contains lower 18-MEA levels than younger ones.¹⁴

The outer layers of hair are of particular interest since the adsorption of cosmetic formulation components, as well as the lubrication between hair fibres, will largely depend on its surface properties.¹ Experimental surface characterization of virgin and damaged human hair has included the measurement of wetting by means of liquid contact angles,^15–22 surface charge density^23–25 as well as surface topography and friction using the atomic force microscope (AFM)^8,22,26,27 and high-load nanotribometers.²⁸ These studies have shown that compared to virgin hair, damaged hair usually displays increased surface charge density, hydrophilicity, and friction. These effects can be attributed to removal of the 18-MEA monolayer and formation of anionic cysteic acid (sulfonate) islands on the surface.^29,30

In addition to experiments, a range of molecular modelling techniques have been used to study the mechanical and surface properties of hair. Akkermans and Warren³¹ developed a multiscale modelling approach to the mechanics of human hair fibre. They used molecular dynamics (MD) simulations with different levels of coarse-graining to study the mechanics of keratin dimers and filaments.³¹ All-atom (AA) models of keratin dimers have also been developed and applied to study the effect of disulfide cross-linker on mechanical properties.³² This atomistic model was used to parameterise a coarse-grained model with a bottom-up approach.³³ This enabled the mechanical properties of keratin fibrils to be modelled at larger scales, approaching the size of entire hairs.³³

McMullen and Kelty³⁴ used MD simulations with a united-atom (UA) force field to study the conformational and dynamical properties of 18-MEA and eicosanoic acid (EA) monolayers at the air–water interface. Natarajan and Robbins³⁵ used MD simulations to estimate the thickness of the 18-MEA layer on an ultra-high-sulfur protein surface. Their results suggested that the monolayer thickness was ∼1 nm,³⁵ which agreed well with previous X-ray photoelectron spectroscopy (XPS) experiments.³⁶ Cheong et al.³⁷ used MD simulations with an AA force field to investigate the optimum separation distance between 18-MEA chains grafted on a graphene surface, which was found to be in the range of d_graft = 0.49–0.65 nm. These results were consistent with the epicuticle model proposed by Negri et al.,³⁸ but their optimal separation distance was much smaller than the frequently cited value of 0.94 nm.³⁹ At the optimal molecular separation distance, the monolayer thickness was between 2.0–2.6 nm, which was consistent with experimental measurements using transmission electron microscopy (TEM),⁴⁰ but much thicker than previous results from MD simulations³⁵ and XPS experiments.³⁶

As well as structural and mechanical investigations, density functional theory calculations have been used to study the adsorption of explosive compounds onto 18-MEA monolayers.⁴¹ Coarse-grained simulations have been employed to study the adsorption of surfactants and polymers on model hair surfaces.^42–44 A recent study by Morozova et al.⁴⁵ used coarse-grained MD simulations to investigate the adsorption of polymers onto heterogeneous surfaces obtained from the mapping of experimental AFM data of damaged hair surfaces. The authors investigated the polymer adsorption as a function of chain length and concentration. They also probed the stability of the adsorbed structures under shear flow.⁴⁵

Here, we present new coarse-grained molecular models for the F-layer found on the outer layer of the hair cuticle in the fully-functionalised state and at several different degrees of damage. The coarse-grained MARTINI force field^46,47 is used throughout. The level of coarse-graining provided by the MARTINI force field allows for significant system upscaling compared to AA force fields.³⁷ Importantly, local three-dimensional structural details, thermodynamic properties, and certain phase transitions can still be resolved,^47,55 all of which are particularly relevant for the hair surfaces studied here. This enables distinct advantages over mean field approximations, such as the self-consistent field (SCF) theory, which have been used to study surfactant and polymer adsorption on model hair surfaces.^43,44 For fully-functionalised hair, we construct a three-dimensional surface model of fatty acids grafted to a graphene substrate in a hexagonal arrangement. This model is validated against previous AA-MD simulations.³⁷ To represent damaged hair, we randomly replace an increasing proportion (0–100%) of the neutral fatty acid molecules with anionic sulfonate groups. We study how the surface structure changes with increased damage in vacuum, aqueous, and non-aqueous environments. Using contact angle measurements, we confirm that the MARTINI model can capture the wetting behaviour of fully-functionalised and damaged hair in both polar (water) and non-polar (n-hexadecane) solvents. We anticipate that the proposed models will facilitate MD simulations of the adsorption of surfactants and polymers found in hair care formulations onto the surface of hair. The significant reduction in computational cost compared to AA force fields will enable the simulation of large macromolecules that are used to improve the feel and appearance of hair.¹ The coarse-grained models proposed here will also enable non-equilibrium MD simulations of hair friction in dry and aqueous environments. Due to the similar surface chemistries involved, we also anticipate that the characteristic wetting behavior of the hair surfaces developed in this work will be relevant in other biological surfaces such as textiles (e.g. wool)⁹ and skin.¹ More generally, the proposed methodology can be used to improve understanding of the wetting behaviour of chemically heterogeneous surfaces functionalised with hydrophobic and/or hydrophilic groups^56,57 using MD simulations with the MARTINI force field.⁵⁵

2 Methodology

2.1 Coarse-grained hair model

Coarse-grained MD simulations are used to study both fully-functionalised and damaged hair surfaces. The MARTINI force field (version 2.0)^46,47 was selected for this purpose. The MARTINI model generally represents groups of four atoms into a single coarse-grained bead (4 : 1 mapping), although smaller bead sizes have also been developed.^58,59 This model has been used extensively to study lipids in aqueous environments.⁴⁷ It is also now increasingly being used for materials science applications.⁵⁵ Of particular relevance to the current study, the MARTINI model has been successfully employed in MD simulations of supported lipid monolayers⁶⁰ and bilayers.^49,61

Schematics of the model structures for fully-functionalised and damaged hair are depicted in Fig. 1. The fully-functionalised hair surface model includes a complete monolayer of 18-MEA groups, which are covalently bound to cysteine amino acids that are grafted to a rigid graphene substrate. This approach is similar to that used in the AA-MD study by Cheong et al.³⁷ The 18-MEA molecules consist of C₂₀ chains with a methyl branch on the eighteenth C atom and are modeled here as a chain of five C₁ (alkyl) beads. In a subset of MD simulations, a chain of four C₁ beads and a terminal C₂ bead are used to represent stronger alkyl-water interactions.⁶² This could be expected for 18-MEA (compared to EA) due to the conformational disorder⁶³ caused by the methyl branch-containing alkyl group⁶⁴ (see Fig. S1 in the ESI†). The C₁ beads are connected to a C₅ and P₅ bead, which are representative of the thioester and amine/carboxyl groups in cysteine, respectively. This structure is an extension of the palmitoyl cysteine (C₁₆ chain) MARTINI parametrisation suggested by Atsmon-Raz and Tieleman⁴⁸ by one additional C₁/C₂ bead. The P₅ beads, which represent parts of the outer protein layer of the epicuticle, are grafted to the graphene layer below using a bonded potential. The graphene sheets are represented by a 4 : 1 coarse-grained mapping^52–54 Unlike 3 : 1⁶⁵ and 2 : 1⁶⁶ mapping, this retains a hexagonal lattice of atomistic graphene.

Fig. 1 Schematics of the coarse-grained MARTINI model^46,47 of the hair surface. (a) Coarse-grained mapping of the Cys-18-MEA, EA and cysteic acid molecules. The fully-functionalised 18-MEA molecules are represented by P₅, C₅, C₁, and C₂ beads.⁴⁸ The EA molecule is represented by C₁ and N_a beads.⁴⁹ The sulfonate groups are represented by negatively charged Q_a beads.⁵⁰ (b) Coarse-grained 4 : 1 mapping of the polarisable water beads,⁵¹n-hexadecane (C₁) and sodium cations with first hydration shell (Q_d).⁴⁷ (c) Nominal grafting distances relative to CG graphene. The graphene layer, as employed in previous atomistic MD studies of the hair surface,³⁷ is represented by a 4 : 1 mapping to C₁ beads.^52–54 Ghost bead positions overlap with graphene beads on the hexagonal lattice where positions coincide. (d) Different degrees of damage (0–100% fatty acids removed) are considered.

This graphene layer prevents solvent molecules from escaping through the monolayer surface and can also be used to control pressure and sliding in future non-equilibrium MD simulations. The hexagonal structure of the graphene sheet is somewhat different from the proteinaceous structure below the 18-MEA on real hair.³⁵ However, it effectively represents an atomically-smooth, impermeable surface to support the lipid monolayer.³⁷ We expect the effect of this simplification on the monolayer structure and wettability to be small. The graphene beads only directly interact with the other beads through Lennard-Jones (LJ) interactions, which are relatively short ranged. The additional P₅ beads provide sufficient separation from the graphene beads to ensure that direct interactions with the lipid and solvent beads are negligible.

The lipids are positioned in a hexagonal arrangement on top of the graphene layer, which is supported by experimental observations.^39,67 The grafting positions are independent from the graphene bead positions to allow for intermediate grafting distances, similar to those used in the AA-MD simulations by Cheong et al.³⁷ These intermediate values would otherwise not be possible using the 4 : 1 mapping for the graphene. Therefore, ghost beads were introduced in the plane of the graphene sheet and solely interact with the P₅ bead of the lipid chain through a bonded potential. For the comparisons with the AA-MD simulations by Cheong et al.,³⁷ lipid grafting distances of 0.49, 0.65, and 0.85 nm were considered, which correspond to surface coverages of 4.2, 2.7, and 1.6 molecules nm⁻², respectively. From these comparisons, the intermediate grafting distance of 0.65 nm was selected for the MD simulations to calculate the contact angle.

In the case of damaged hair, the 18-MEA molecules are randomly removed by breaking the thioester bond (C₅ to P₅) and replacing the neutral P₅ bead with an anionic Q_a bead to represent a sulfonate group.⁵⁰ This is representative of the oxidation of Cys-18-MEA to cysteic acid, which has been observed in several experimental studies of bleached hair.^8,11,30 Charge neutrality is maintained by adding the appropriate number of non-polarisable sodium cation (Na⁺) beads Q_d,⁴⁶ which also represent the first hydration shell in the MARTINI model.⁴⁷ Since they are expected to be easily removed through washing, free fatty acid molecules are not considered in the current MD simulations. We randomly remove chains at a number corresponding to the desired damage ratio,

χ_N = N_rem/N_FF, (1)

where N_rem is the number of fatty acid chains to be removed and N_FF is the number of grafted chains in the fully-functionalised system. Discrete damage ratios of χ_N = 0 (fully-functionalised), χ_N = 0.25, 0.5, 0.75, 0.85, 0.92 (partially damaged) and χ_N = 1 (fully damaged) are considered here. Previous experiments have suggested that the surface of bleached hair mostly consists of negatively charged sulfonate groups, with a mean surface coverage of approximately 2.2 molecules nm⁻² (2.8 molecules nm⁻² in the damaged regions).³⁰ For the chosen grafting distance (0.65 nm), this coverage of sulfonate groups is approximately reproduced by using χ_N = 0.85.

The projected surface area ratio between lipid coverage and exposed charged groups,

χ_S = (S_total − S_MEA)/S_total, (2)

is used as an additional measure for quantifying monolayer damage. Macroscopic wetting theories such as the Cassie–Baxter model⁶⁸ rely on the exposed surface area. Here, S_MEA and S_total are the projected area occupied by the Cys-18-MEA chains and the total projected surface area respectively. The Cys-18-MEA surface area S_MEA is obtained from projecting all remaining Cys-18-MEA beads with an assumed radius of r_b = 0.235 nm onto the xy plane of the periodic simulation box. This approach accounts for the effects of collapsing Cys-18-MEA chains onto the charged layers below.

2.2 Coarse-grained liquid-phase model

The original MARTINI water model was single-site and non-polarisable.⁴⁶ Previous CG-MD simulations of supported lipid bilayers have suggested that the polarisable MARTINI water model gives more accurate results.⁶¹ In this study, we employ the original polarisable MARTINI water model developed by Yesylevskyy et al.⁵¹ Other polarisable water models compatible with the MARTINI framework, such as the refPol,⁶⁹ BMW-MARTINI,⁷⁰ and refined BMW-MARTINI⁷¹ models were also tested in slab geometry simulations of the water–vapor and n-hexadecane–water interfaces.⁷² The underestimation of the water–vapour surface tension is a well known limitation of MARTINI water models.⁴⁷ The refPol model gives significantly lower water–vapor and water–hexadecane surface tensions than both the original polarisable model and particularly experiments. It was therefore discarded after preliminary analysis. The BMW-MARTINI model was originally optimised to reproduce a range of properties, including the water–vapor surface tension. However, both investigated versions suffer from freezing artefacts when moving from a slab geometry of the water–vapor interface to a water droplet deposited on a surface. Moreover, previous studies^62,71 found that the water–alkane surface tension was significantly over-estimated with the original BMW-MARTINI model. This is an unfavourable side-effect of the stronger LJ interactions used to increase the surface tension of water. The BMW-MARTINI model was therefore deemed unsuitable for the current study because the systems contain both water and alkane components. We selected the original polarisable MARTINI water model by Yesylevskyy et al.⁵¹ for the remainder of the CG-MD simulations. Although the water–vapor surface tension is underestimated by more than 50% with this model⁵¹ (similar to the non-polarisable MARTINI model⁴⁶), the n-hexadecane–water and n-hexadecane–water surface tensions are within 15% and 30% of the experimental values, respectively (Table S1 in the ESI†).^71,73 Further details on the comparisons between the water models can be found in the ESI.† The n-hexadecane molecules are represented by a chain of four C₁ beads.

2.3 MD simulation details

The MD simulations are performed in LAMMPS^74,75 using the velocity-Verlet⁷⁶ integration scheme with a timestep of 5 fs.⁴⁶ Non-bonded interactions between beads are represented by the 12-6 LJ potential for the uncharged beads and the LJ and Coulomb potentials for the charged beads. LJ interactions between beads are shifted to zero between the cut-off radius r_LJ,cut = 0.9 and r_LJ,shift = 1.2 nm.⁴⁶ Bonds and angles are treated using weak harmonic potentials as in the original MARTINI framework.⁴⁶ The bond lengths in the water units are constrained using the SHAKE⁷⁷ algorithm. The full set of force field parameters used in this study can be found in the ESI.† Long-range electrostatic interactions are treated using a slab implementation⁷⁸ of the particle–particle particle-mesh (PPPM) method⁷⁹ with a Fourier grid spacing of at least Δx = 0.2 nm, a Coulombic switching radius of r_C,cut = 0.12 nm, and a relative energy tolerance of 10⁻⁵.

All systems were constructed using the Moltemplate software.⁸⁰ The systems are periodic in the lateral (x and y) directions. A reflective boundary condition is imposed at the top of the simulation cell in the z direction to prevent water molecules from escaping the simulation cell. Interactions of the vapor phase water beads with these boundaries are rare due to sufficient separation distance of surfaces and droplets from the surface. A nominal box size for the water droplet wetting systems of [script L]_x = 35.7 nm, [script L]_y = 30.9 nm and [script L]_z = 25.0 nm was found to be sufficient to prevent interactions between the droplets and their periodic images. For n-hexadecane, which has lower contact angles at moderate damage levels, the system size in x and y was increased to [script L]_x = 71.5 nm, [script L]_y = 61.9 nm, respectively.

The thickness of a human hair is typically 50–100 μm and each cuticle cell is approximately 5–10 μm long.²⁹ This is much larger than can be directly simulated in the MARTINI framework. The surfaces used in the current CG-MD simulations are therefore representative of a small region of the epicuticle surface. For the damaged surfaces, the outer F-layer is partially removed, which occurs during a single bleach treatment.¹¹ More severe damage, such as that caused by repeated bleaching,⁸¹ can lead to cuticle removal. This can change the microscale topography⁸² and porosity⁸³ of the hair surface, which cannot be accounted for in the current CG-MD simulation framework.

The initial conditions for the monolayer-vacuum configurations consist of fully extended lipid chains normal to the graphene sheet and Q_d counter-ions placed at random positions above the monolayer (Δz = 0.4 nm) for the damaged hair surfaces. Other initial configurations for the counter-ions were also tested but led to similar distributions after equilibration. Energy minimization is performed for the monolayer surfaces in vacuum. The model surfaces are then equilibrated for 10 ns in the canonical (NVT) ensemble using a Nosé–Hoover thermostat^84,85 set at T = 298 K. A production run was then performed for a further 10 ns. The graphene layer and corresponding ghost beads are excluded from the thermostatting. Convergence to equilibrium values was monitored by means of the global kinetic and potential energies, monolayer thickness and tilt angles as well as first and second moments of the monolayer bead positions.

Coarse-grained droplet wetting MD simulations were run in the NVT ensemble for at least 20 ns. The data shown below were extracted over the final 10 ns of these simulations. The initial hemispherical droplet configuration is obtained from bulk simulations in the isoenthalpic–isobaric (NPT) ensemble at atmospheric pressure and T = 298 K.⁸⁶ The total number of polarisable water units in the base configuration is N = 18 121, leading to an initial droplet radius, r≈10 nm. For n-hexadecane, N = 4036 molecules are used for the initial droplets, which resulted in a similar initial droplet radius. The hemispherical droplets are placed at the centre of the equilibrated monolayer surfaces and simulated in the NVT ensemble along with the lipid molecules.

The possible effect of the water droplet size on the equilibrium contact angle was investigated by testing droplets with approximately half (N = 8994), two times (N = 36  464), and four times (N = 73 268) the number of beads in the initial hemisphere at t₀.⁵⁸ All damage ratios where χ_N < 1 were considered for this comparison (see Fig. S2 in the ESI†). A significant increase in contact angle with droplet size is observed between N = 8994 and N = 18 121, indicating that the former droplet size is too small to be representative of macroscale contact angles.⁸⁷ The contact angle is more sensitive to the droplet size on surfaces with a larger damage ratio. Above this droplet size (N ≥ 18 121), the contact angle increase is sufficiently small (within the statistical uncertainty intervals) to be considered representative of experimental measurements.⁵⁸ The change in contact angle with droplet size can be fit using the modified Cassie–Baxter approach for fuzzy interfaces (see Fig. 2 in the ESI†).⁸⁸ However, using this equation for accurate extrapolation to microscale droplet sizes, as used in the accompanying experiments, would require further simulations at larger droplet sizes, which are beyond the scope of this current study.

Equilibrium contact angles for water and n-hexadecane are obtained based on the procedure described by de Ruijter et al.⁸⁹ and Werder et al.⁹⁰ and successfully applied to MARTINI water droplets on graphene surfaces by Sergi et al.⁵⁸ Discretization sizes of Δz = 0.05 nm and Δz = 0.025 nm in the surface-normal direction are used for high contact angle droplets (χ_N ≤ 0.75) and low contact angles (χ_N > 0.75) respectively. Circular fits are obtained from averaging over five individual snapshots within a bin of Δt_bin = 0.25 ns each. One LJ cut-off length normal to the hair surface is excluded at both the base and top of the droplet. As noted in de Ruijter et al.,⁸⁹ the droplet base is prone to deviations from the spherical shape as non-bonded interactions with the surface are strongest in that region. This is expected particularly for the heterogeneous damaged surfaces. We also exclude the top of the droplet due to the high angular offset with respect to the droplet surface, which leads to poor fitting results for the density profiles in the Cartesian coordinates. The vertical position of measurement for the contact angle is determined as the surface-normal position z corresponding to a threshold of 99% of the cumulative monolayer mass distribution function,

The heterogeneous nature of the damaged surfaces and nanoscale droplet sizes mean that pinning is possible in the wetting simulations.⁹¹ To account for this variability, two different initial water droplet positions shifted diagonally across the periodic box (Δx = ±138 nm, Δy = ±90 nm) and two different random monolayer damage seeds with a water droplet at the centre position are considered. This leads to five trials per damage level, which are used to obtain the equilibrium contact angles shown below. Similar position and random seed investigations were omitted for n-hexadecane because these results show less variability.

Further MD simulations with AA force fields were also conducted to validate the structure of the fully-functionalised CG hair model. For this purpose, we used the optimised potentials for liquid simulations (OPLS)^92,93 force field for the 18-MEA monolayers and the extended simple point charge (SPC/E)⁹⁴ force field for water. Two lipid grafting distances were considered (d_graft = 0.49 nm, 0.65 nm). The simulation protocol of fully-functionalised monolayers in vacuum follows the approach by Cheong et al.³⁷ All bonds containing H atoms were constrained using the SHAKE algorithm.⁷⁷ A water droplet consisting of 14 642 molecules (droplet radius ∼ 5 nm) was introduced on the equilibrated surface and contact angles were obtained following the same procedure as for the CG model.⁸⁷ The surface tension of the water–vapour and n-decane–vapour interfaces was recently evaluated for several force fields, including SPC/E and OPLS.⁹⁵ The authors found good agreement with experimental data for both the water–vapour (underestimated by 15%) and n-decane–vapour (underestimated by 5%) interfaces,⁹⁵ which underlines the suitability of the AA-MD as reference cases for comparison with the corresponding CG-MD configurations.

3 Experimental setup

3.1 Hair contact angle

Dynamic contact angle measurements on hair surfaces were conducted using the Wilhelmy force balance method.⁹⁷ We chose the dynamic approach over pseudo-static contact angle measurements on single hair fibres for practical reasons. Nanoscale water droplets have been found to quickly evaporate from or penetrate into the hair surface.¹⁸ While nanoscale droplets of non-polar solvents (e.g. squalane) are more stable,^18,19 they tend to be perturbed by both the hair curvature and the overlapping cuticle edges. Pseudo-static contact angle measurements of water have been successfully measured using larger droplets on multiple aligned hairs, and these were found to be in good agreement with the advancing contact angle from dynamic measurements with single hairs.²⁰

Our experimental procedure closely follows the approach described in the literature for dynamic contact angle measurements of single hairs.^15,17 A ∼2 cm segment of single fibre hair is mounted on a Kruss mount (Hamburg, Germany – Part number: SH0801) with double sided sticky tape tabs. A straight 1.5 cm segment is extended from the mount parallel to the axis of the mount to ensure perpendicular hair contact with the solvent. The diameter of the hair was measured optically. A bath of 99+% n-hexadecane or distilled water is raised at 6 mm min⁻¹ until the lower end of the fibre is wetted. The segment is then immersed 0.2 mm to avoid the cut tip. The hair is further immersed at 3 mm min⁻¹, stopping every 0.2 mm for one second to measure the wetting force on the hair. This is continued until 6 mm length of hair is measured.

To validate the coarse-grained hair models at different levels of damage, we investigate two types of hair samples experimentally: virgin (pristine) and medium bleached (single bleach treatment) hair. During the bleach treatment, the hair swatches were soaked for 35 minutes in 6% hydrogen peroxide solution (also containing 2% ammonium hydroxide, 0.5% acetic acid, and 0.2% EDTA). The hairs were then washed for 20 minutes using tap water, with excess water being removed by squeezing with a towel before dying with a commercial blow drier and comb for 3 minutes. Five hairs from 120 virgin and 80 medium bleached hair swatches were analysed at the tip, middle and root positions. The results given below correspond to the mean, minimum, and maximum of these experimentally measured values.

3.2 Biomimetic surface contact angle

Biomimetic hair surfaces were produced by functionalising atomically-smooth silicon wafers with eicosanoic acid (C₁₈) and/or sulfonate (SO₃⁻) groups. Virgin hair was represented by a pristine C₁₈-terminated monolayer, while complete damage was represented by a SO₃⁻-terminated monolayer. Intermediate levels of damage (e.g. medium bleached and heavily bleached) are represented by co-functionalised surfaces. The use of biomimetic surfaces eliminates any damage-induced change in microscale surface topography⁸² or porosity,⁸³ from the experimental contact angle measurements. They therefore facilitate a more direct comparison to our CG-MD simulation results.

We apply the ASTM D7490-13 Standard⁹⁸ test method for measurement of the surface tension of solid coating, substrates and pigments using contact angle measurements which utilizes a traditional sessile drop approach.^99–101 Both temperature (23.1 ± 0.3 °C) and humidity (50 ± 1%) were controlled. Approximately 3 mL DI water droplets were deposited on horizontally positioned silicon wafers by dangling a drop about 200 μm from the surface and slowly growing the drop at 0.5 mL s⁻¹ until it detached from the needle. Profiles of the droplets wetting and equilibrating on the surface were captured at 50 frames per second for 10 s. The First Ten Angstroms (Portsmouth, USA) software (Version 2.1, Build 381) was used to extract contact angles from the resultant movie. Equilibrium contact angles were determined and measurements were repeated five times for each sample.

4 Results and discussion

4.1 Monolayer properties

Fig. 2 depicts the variation in film thickness and tilt angle of the equilibrated fully-functionalised lipid monolayers at increasing nominal grafting distance. Comparisons to the AA-MD reference data by Cheong et al.³⁷ are also shown. A simplified CG model equivalent to their AA model of EA has been included to facilitate more direct comparison to our CG-MD results. This simplified CG EA model only differs from our final model (Cys-18-MEA) by means of the P₅ bead being omitted and a change in bead type from C₅ (thioester) to N_a (ester) for the first bead in the lipid chain. The monolayer thickness is evaluated as the mean of the distance in the surface-normal direction z between the P₅ bead (N_a for EA) and the bead with the highest position in z. The length of a fully extended EA and Cys-18-MEA chain in the MARTINI framework is ∼3 nm. Note that the definition for the tilt angle used by Cheong et al.³⁷ is based on the difference in centre of mass between the top and bottom C atoms in the lipid chain within a finite set of regions. Such a definition effectively captures regional anisotropic lipid tilt, which is not relevant for our CG-MD simulations. Instead, the tilt angle in our CG-MD simulations is computed as an average over all individual lipid chain tilt angles between the P₅ (N_a for EA) and the terminal C₁ beads.

Fig. 2 Snapshots of Cys-18-MEA lipid monolayers at different grafting distances rendered using VMD⁹⁶ (a). C₁ beads are shown in black, C₅ in blue, and P₅ in green. EA and Cys-18-MEA monolayer (b) film thickness and (c) tilt angles compared to AA-MD reference data for EA and 18-MEA from Cheong et al.³⁷ Lines are guides for the eye. The thickness and tilt angles are measured from the centre of mass of the N_a bead to the terminal C₁ bead for EA and the P₅ bead to the terminal C₁/C₂ bead for Cys-18-MEA.

All of the molecules and models in Fig. 2 show a general collapse of fatty acids with increasing grafting distance, as indicated by the decreasing monolayer thickness and increasing tilt angles. As the grafting distance increases, the molecules move from being aligned mostly perpendicular to the surface (tilt angle ≈0°) to aligning more parallel to the surface (≈90°). This is due to a reduction in inter-chain van der Waals interactions as the distance between them increases and a concurrent increase in van der Waals interactions between the chains and the graphene layer as more of the surface is exposed.¹⁰² There is excellent agreement between the AA-MD³⁷ and CG-MD results for the thickness and tilt angle of the EA monolayer at the three chosen grafting distances. In general, the CG monolayers are thicker than the AA ones, although the difference is always less than the van der Waals radius of a single CG bead (∼0.5 nm). The thickness of the Cys-18-MEA decreases faster than EA due to the presence of the P₅ bead, which enables the chains to align more parallel with the surface to maximise the van der Waals interactions with the damaged regions of the surface.

The estimate of the optimum separation distance of the 18-MEA molecules of d_graft = 0.49 nm to d_graft = 0.65 nm presented by Cheong et al.³⁷ from their AA-MD simulations is supported by our CG-MD results. This grafting distance yields a thickness that is consistent with previous TEM experiments of virgin hair.⁴⁰ Moreover, the cysteic acid molecular density presented by Korte et al.³⁰ for bleached hair closely agrees with a grafting distance of 0.65 nm. In the remainder of this study, we only consider a nominal d_graft = 0.65 nm for both fully-functionalised and damaged hair.

We also investigated the effects of random damage to the lipid monolayer. Several methods for quantifying the degree of damage on the hair surface can be applied within our CG-MD simulation framework. The simplest approach is to directly use the damage ratios by means of the number of randomly removed fatty acids, χ_N, and surface coverage, χ_S, introduced in eqn (1) and (2) respectively. The area damage ratio, χ_S, is selected as the damage quantification parameter in the remainder of this study, since it is most representative of the degree of damage that can be measured experimentally (e.g. from AFM scans^30,45). The relationship between the various damage ratios, both in vacuum and in the presence of wetting fluids, is shown in Fig. 4. The morphology of the damaged hair surfaces will depend on the external influences causing such damage. Random removal of lipid chains is likely from chemical treatments such as bleaching. Other authors have observed roughly circular⁴⁵ and striped³⁰ damage patterns on hair surfaces. However, the size of these regions is comparable to the size of the surfaces employed in our CG-MD simulations.

Fig. 3 shows the variation in the film thickness and tilt angle of the monolayers at a nominal grafting distance of 0.65 nm with an increasing degree of damage (χ_S) in vacuum and in the presence of water and n-hexadecane. In vacuum, a collapse of the lipid chains is observed with an increasing degree of damage, similar to that observed with increasing grafting distance.

Fig. 3 Snapshots of monolayers in vacuum from χ_S = 0 (top) to χ_S = 1 (bottom) rendered using VMD⁹⁶ (a). C₁ beads are shown in black, C₅ in blue, and P₅ in green. Monolayer thickness (b) and tilt angle (c) at a nominal grafting distance of d_graft = 0.65 nm and various degrees of random damage in vacuum environment and with water and n-hexadecane. Lines are guides for the eye.

Introducing wetting fluids to the surface leads to intermolecular interactions with the solvent beads as well as between the chains and the surface. The addition of n-hexadecane molecules on top of the monolayer surfaces does not have any significant effect on the thickness and tilt angles compared to those obtained in vacuum. This is because the van der Waals interactions between the n-hexadecane molecules and the grafted chains are similar in strength to those between proximal grafted chains. On the other hand, swelling is observed for the damaged surfaces as water penetrates into the monolayer. In polymer brushes, such swelling behavior is observed when the interactions between solvent molecules (i.e. water hydrogen bonding) are strong compared to the interactions between solvent and polymer (i.e. van der Waals).¹⁰³ This leads to a slight increase of the monolayer thickness with higher degrees of damage in water. The degree of swelling increases with increasing damage because a reduced number of lipid chains result in weaker inter-chain interactions and allow increased water penetration into the monolayer. This is consistent with experimental measurements that have shown an increase in swelling in less densely packed monolayers.¹⁰⁴ The maximum degree of swelling relative to the vacuum case (∼0.5 nm) is also in good agreement with previous experimental measurements of ionic surfactant monolayers adsorbed on mica surfaces from water.¹⁰⁴ Swelling is further confirmed by increased area damage ratios with water as opposed to the vacuum cases (see Fig. 4).

Fig. 4 Surface coverage ratio, χ_S, as a function of the number damage ratio, χ_N, for the CG hair surfaces in vacuum, water, and n-hexadecane. Snapshots show the projected lipid coverage for the partially damaged surfaces in vacuum. Details of the calculation of χ_S and examples of the projected lipid coverage for water and n-hexadecane are shown in Fig. 3 in the ESI.†

Fig. 4 shows the evolution of the surface coverage of the hair monolayer (χ_S) for different degrees of damage (χ_N) in vacuum, water, and n-hexadecane environments. For all of the partially damaged systems, χ_S is lower than χ_N. This is because the flexible lipid molecules rearrange to cover the surface, increase the surface-molecule van der Waals interactions, and reduce the surface energy. The reduction in χ_S compared to χ_N is less for water than for the vacuum and n-hexadecane environments. This is due to the swelling behaviour observed in Fig. 3 for water. Water penetrates into the lipid layer and reduces agglomeration of the lipid chains, which means that less of the surface is covered.

Projected surface coverage maps are shown for water in Fig. 4 (vacuum and n-hexadecane cases shown in Fig. S3 in the ESI†). The coverage maps were obtained by projecting individual beads using their van der Waals radius onto a continuous planar surface. For the vacuum case at χ_N = 0.25, negatively-charged islands are observed within an otherwise dense monolayer surface. When χ_N = 0.50, the size of the damaged islands increases and they begin to merge. As a result of lipid reorganisation to maximise the chain-surface van der Waals interactions, less than half of the underlying charged surface is exposed. The surfaces at higher damage ratios then show a transition from charged damaged islands to isolated lipid islands. These islands of agglomerated lipid chains shrink in size as the damage ratio is increased further. At χ_N = 0.92, some islands constituent of single lipids are observed due to the mean distance to neighboring lipids being too large to be bridged, even when fully collapsed onto the charged surface below. The shape of the damage patterns is qualitatively similar to that observed in previous AFM experiments at lower resolutions.^25,30,45

Similar coverage surface coverage projections are also observed for water and n-hexadecane (Fig. S3 in the ESI†). For water, more of the charged surface is exposed at each damage ratio due to swelling of the monolayer (Fig. 3). For n-hexadecane, the surface coverage is essentially identical to the vacuum case. This is because of the similar interaction strength between the grafted chains and the solvent in this case, which means that swelling is negligible (Fig. 3). As a result of these similar interactions, there is some coarsening of the coverage pattern underneath the n-hexadecane droplet (Fig. S3 in the ESI†), but this does not affect χ_S (Fig. 4).

4.2 Liquid droplet wetting

The CG hair surface models are further evaluated by measuring the equilibrium contact angle of nanoscopic water and n-hexadecane droplets placed on top of the surfaces. Examples of the fits to the density profiles of water from the CG-MD simulations are shown for the fully-functionalised and partially damaged surfaces in Fig. 5. Contact angle fits for CG-MD n-hexadecane and AA-MD water are also provided (Fig. S4 and S5 in the ESI†). For the fully-functionalised system shown in Fig. 5a), there is negligible penetration of water into the closely-packed lipid layer and the lipid–water interface is easily defined. The water penetration distance into the fully-functionalised monolayer is consistent between the AA-MD (1.29 nm) and CG-MD (0.85 nm) simulations (see Table S2 in the ESI†). For the damaged systems shown in Fig. 5(b) and (c), water molecules penetrate into the lipid monolayer and form layers in the z-direction (see Fig. S6 in the ESI†). The penetration distance and solvent layering increase with increasing damage level for water. For n-hexadecane, the opposite trend is observed (see Fig. S7 in the ESI†); the solvent molecules penetrate into the lipid monolayer for the fully-functionalised system but the solvent and monolayer form separate layers for the damaged systems. These observations are consistent with previous experiments.¹⁰⁵ The penetration of both fluids into the monolayers and layering justifies the exclusion of the region close to the interface from the density fitting for the contact angle determination. There is also good agreement between the mass density profiles from the AA-MD and CG-MD simulations for the fully-functionalised surfaces (see Fig. S8 in the ESI†).

Fig. 5 Circular surface fits of a water droplets on the (a) fully-functionalised, χ_N = 0, and partially damaged, (b) χ_N = 0.5, (c) χ_N = 0.85, monolayers from the CG-MD simulations. Four temporal bin fits for the droplet surface (solid circles) are shown. Averaged contact angles (solely from the shown four temporal bins) are indicated by bold red lines. The surface-normal position for the contact angle measurement is shown (dashed red line). Individual surface density fits in the radial direction are omitted for the sake of clarity. Note that the CG-MD simulation domain is larger than the radial section shown here.

The nominal contact angle data from the CG-MD model, AA-MD, and experimental data of dynamic contact angle measurements for water and n-hexadecane on virgin hair are given in Table 1. Experimental values for advancing and receding contact angles for medium bleached hair are given in Table 2. Water shows much larger hysteresis between the advancing and receding contact angles, which is partially due to the swelling effects described above.¹⁰⁶ The advancing contact angles are used for comparison with the MD simulations because the receding contact angles are particularly sensitive to microscale roughness effects (e.g. cuticle edge trapping¹⁷), which cannot be captured in the current simulations. The preferential use of the advancing contact angle from dynamic measurements is common practice.¹⁰⁶ Moreover, previous experiments have suggested that the pseudo-static water contact angle (as quantified in the MD simulations) is similar to the advancing contact angle on both virgin hair (both 103°) and medium bleached hair (86° vs. 79°).²⁰ Good agreement is obtained between the contact angles obtained from the AA-MD and CG-MD simulations of the fully-functionalised hair surface. In both the experiments and CG-MD simulations, the fully-functionalised/virgin hair surfaces are hydrophobic (water contact angle >90°) and oleophilic (n-hexadecane contact angle <90°). The experimental advancing contact angles for virgin hair are slightly overestimated by both of the molecular modeling approaches. One potential cause of the differences between the experiments (106°) and the CG-MD simulations (120°) for the water contact angle is the underestimated water-vapor surface tension (∼50%) with the polarisable MARTINI water model.^46,51 However, even the AA-MD simulations (116°), which use an atomistic water model (SPC/E⁹⁴) that has a water–vapour (∼15%) much closer to the experimental value,⁹⁵ overestimates the water contact angle compared to experiments using virgin hair. This suggests that the virgin hair surfaces in the experiments are not completely covered by a lipid surface and are, in fact, partially damaged.

Table 1 Contact angle data (in degrees) on fully-functionalised hair from CG-MD (MARTINI) and reference AA-MD (OPLS-AA, SPC/E) and experimental advancing and receding contact angle data for virgin hair. Ranges shown are maximum and minimum values measured

	Water	n-Hexadecane
CG-MD (C1)	120	28
	−10	−10
	+3	+7
CG-MD (C2)	112	26
	−3	−14
	+2	+9
AA-MD	116	n/a
	−2
	+3
Experiments (advancing)	106	36
	−2	−7
	+4	+7
Experiments (receding)	44	22
	−12	−9
	+11	+9

---

Table 2 Experimental advancing and receding contact angle data (in degrees) for medium bleached hair. Ranges shown are maximum and minimum values measured

	Water	n-Hexadecane
Exp. (advancing)	72	72
	−14	−8
	+8	+7
Exp. (receding)	17	70
	−6	−6
	+14	+6

---

The effect of terminal bead type (C₁ or C₂) on water and n-hexadecane contact angle for the different damage levels was investigated in further CG-MD simulations (see Fig. S1 in the ESI†). As expected, the use of the C₂ bead, which has stronger LJ interactions, resulted in a lower contact angle for both water and n-hexadecane on the fully-functionalised surface.⁶² Use of the terminal C₂ bead improves the agreement with experimental results for the water contact angle on virgin hair compared to C₁, but leads to poorer agreement for n-hexadecane (Table 1). Therefore, for the remainder of this study, we employ a C₁ terminal bead.

Fig. 6 shows the change in the contact angles of the water and n-hexadecane droplets on the hair surfaces as the level of damage is increased (data in Table S3 in the ESI†). The vertical bars consider contributions from temporal fluctuations, different initial droplet positions on the hair surface, different random damage seeds, and uncertainties of the droplet surface fit. A detailed description of the uncertainty quantification process for the MD simulations of the equilibrium contact angles is given in Appendix A.

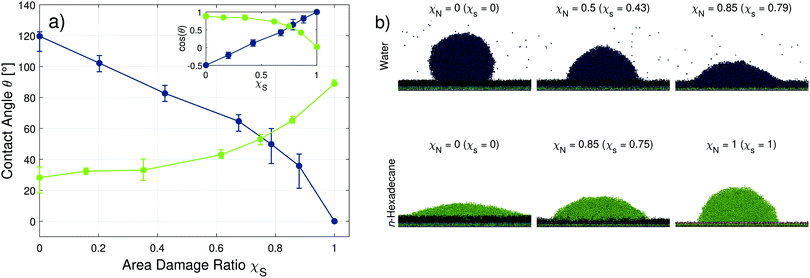Fig. 6 Change in the water and n-hexadecane contact angles on model hair surfaces with an increasing degree of random damage (a). Points show mean values from three different initial droplet positions and three different initial random damage seeds. Vertical bars show the minimum and maximum values observed across the temporal binning of the different position and seed trials. Solid lines are guides for the eye. Snapshots of water (blue) and n-hexadecane (green) droplets at low, medium, and high levels of damage rendered using VMD⁹⁶ (b). Surface coverage ratios χ_S are computed independently for monolayers with water and n-hexadecane. The inset shows the change in the cosine of the angle, rather than the angle.

The fully-functionalised hair surface is characterised by large water droplet contact angles, which is indicative of a hydrophobic surface. The droplet shape in this case is well defined because the hair surface is homogeneous and there is clear separation between the water and lipid monolayer layers. This is reflected in relatively small uncertainties in the water contact angle at low damage ratios. Increasing the damage ratio leads to the formation of chemically heterogeneous surfaces.^56,57 Islands of charged SO₃⁻ groups become exposed, which reduces the water contact angles, indicating that the hair surfaces become more hydrophilic. These observations are consistent with previous experiments of bleached hair.^16,17,20 For moderate damage (χ_S < 0.7), an approximately linear reduction of the water contact angle with increasing damage ratio is observed. Complete wetting by water occurs when the lipid F-layer is completely removed and replaced by anionic cysteic acid groups. Previous experiments have measured contact angles as low as 48° for heavily bleached hair,²⁰ which suggests that around 85% of the lipid molecules have been removed (see Fig. S9 in the ESI†). An increase in the uncertainty in the contact angle is observed at higher damage ratios due to both the larger droplet radius and the increasing heterogeneity of the surface. The transition from strongly hydrophobic to increasingly hydrophilic surfaces agrees with the experimental contact angle measurements of water on virgin and bleached hair, as shown in Tables 1 and 2, respectively. To match the experimental advancing contact angle of virgin hair (106 ± 3°), a lipid surface coverage ratio, χ_S ≈ 0.2 is required in the CG-MD simulations (χ_N = 0.25, Fig. S9 in the ESI†). A damage ratio larger than zero seems reasonable for virgin hair, since they will have been subjected to weathering effects and are therefore unlikely to be completely covered by a pristine 18-MEA monolayer.¹¹ The experimental advancing contact angle of medium bleached hair (72 ± 11°) is approximately reproduced at χ_S ≈ 0.8 (χ_N = 0.85, Fig. S9 in the ESI†).

For n-hexadecane, consistently low contact angles (<50°) are sustained over a wide range of area damage ratios (χ_S < 0.7). Unlike water, electrostatic interactions between the wetting fluid and the surface are not relevant due to the uncharged, non-polar nature of the coarse-grained n-hexadecane molecules. The hair surface becomes less oleophilic as the damage ratio increases above χ_S > 0.7, as indicated by an increase in n-hexadecane contact angles. This transition is consistent with the experimental measurements of the advancing contact angle of n-hexadecane on virgin (36 ± 7°) and medium bleached (72 ± 8°) hair. These experimental contact angles can also be approximately matched in the CG-MD simulations by using χ_S ≈ 0.2 (χ_N = 0.25, Fig. S9 in the ESI†) for virgin hair and χ_S ≈ 0.8 (χ_N = 0.85, Fig. S9 in the ESI†) for medium bleached hair. Reassuringly, these values are the same as those required to match the experimental water contact angles (Fig. S9 in the ESI†). The contact angles at intermediate damage are in good agreement with static nanoscale droplet experiments on hair samples with non-covalently bound lipids removed using another non-polar wetting fluid, squalane (45°),¹⁹ which has a comparable surface tension to n-hexadecane. The observed χ_N values for both water and n-hexadecane are also consistent with chromatography measurements of the content of the 18-MEA on virgin hair (25% reduced compared to the root content) and single-bleached hair (80% content removed compared to the root).¹¹

The dynamic contact angle experiments are further complemented by static contact angle measurements on biomimetic silicon wafer surfaces with different degrees of functionalisation with eicosanoic acid (C₁₈) and sulfonate (SO₃⁻) groups. The experiments on these model surfaces are not perturbed by hysteresis, curvature effects, or microscale cuticle effects. The Cassie–Baxter⁶⁸ model is applied to the experimental contact angle data to estimate the surface area coverage of C₁₈ and SO₃⁻ groups respectively.

Fig. 7 compares the cosines of contact angles of water from the CG-MD simulations with the corresponding experimental values. A good agreement in the slope of the contact angle as a function of damage is found between the experimental and numerical values for water at moderate damage (χ_S < 0.7). The offset in absolute water contact angle values is a result of the underestimated water–vapor surface tension of the polarizable MARTINI water model^46,51 (and consequent overestimation of the contact angle⁵⁸). Lines of best fit corresponding to the linear Cassie–Baxter⁶⁸ model have been included for the experimental and simulation data. The Cassie–Baxter line of best fit for the simulations lies within the uncertainty bounds for all of the data points. The CG-MD data can also be fit using the extension of this equation proposed by Israelachvili and Gee for chemically heterogeneous surfaces,⁵⁶ although the agreement with the data is poorer than the standard Cassie–Baxter⁶⁸ model. Reasonable agreement between the slopes of the experimental and simulation data fits is obtained suggesting that the Cassie–Baxter model (or its extensions^56,88) can serve as a simple approach to describe the hydrophobic–hydrophilic transition of the idealised surface of the epicuticle of virgin and bleached hair.

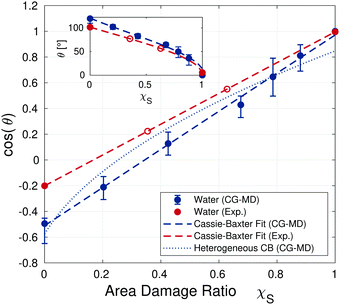Fig. 7 Cosine of the water contact angle from the CG-MD simulations at different degrees of damage and experiments using silicon wafer surfaces (Exp.) at various degrees of C₁₈/SO₃⁻ functionalisation. Simulation points show mean values from three different initial droplet positions, vertical bars represent minimum and maximum values observed across the temporal binning of the different position and seed trials. Dashed lines are Cassie–Baxter⁶⁸ fits (cos(θ) = χ_S cos(θ_d) + (1 − χ_S)cos(θ_ff)) predict contact angles for fully-functionalised and fully damaged monolayers of θ_CG,ff = 121° (θ_exp,ff = 102°) and θ_CG,d = 14° (θ_exp,d = 5°) respectively. The blue dotted line indicates the Cassie–Baxter fit for chemically heterogeneous surfaces.⁵⁶ Open symbols represent points where the surface coverage has been obtained from the Cassie–Baxter relation based on experimental contact angles. The inset shows the change in the angle, rather than the cosine of the angle.

5 Conclusions

We have developed a coarse-grained molecular model within the MARTINI framework of the lipid monolayer that protects the surface of the hair epicuticle. The 3D models presented accurately reproduce the experimental surface properties of virgin and medium bleached human hair in MD simulations.

The surface coverage of lipids grafted to the underlying protein (graphene) layer is determined from comparisons to atomistic MD simulations and previous TEM experiments. We replicate the effects of bleaching by randomly removing different fractions of fatty acid molecules from the surface and replacing them with anionic sulfonate groups. This leads to nanoscale heterogeneities due to the clustering of the remaining lipid chains to form damaged islands. The size of these islands increases with an increasing degree of damage.

The wetting characteristics of the models show good agreement with the trends observed in experiments and atomistic MD simulations. The highly hydrophobic surface in the fully-functionalised state becomes increasingly hydrophilic as the degree of damage increases, up to complete wetting when all of the fatty acids are removed. Conversely, the surfaces become less oleophilic as the level of damage increases. Accounting for the uncertainties from the two methods, we can define number damage ratios (fatty acid/sulfonate) in the MD simulations that replicate the experimental contact angles for water and n-hexadecane on both virgin hair (χ_N = 0.25) and medium bleached hair (χ_N = 0.85). The cosine of the water contact angle increases linearly with the area damage ratio, as predicted by the Cassie–Baxter equation. The slope of this increase is similar to that obtained with biomimetic hair surfaces functionalised with different fatty acid/sulfonate ratios.

These results pave way for further MD simulations of adsorption on the hair surface and non-equilibrium MD simulations of the tribological behavior of hair. These could facilitate the virtual screening of surfactants and polymers for the development of improved hair care formulations. Additionally, this work may contribute to the development of new bioinspired surfaces with tunable oleophilicity and hydrophilicity. Such chemically heterogeneous surfaces are commonplace in nature and could be of interest in many other areas of research, for example skin and textiles.

Data availability statement

The LAMMPS input files and initial configuration data files have been made available through a designated GitHub repository, which can be found on Zenodo (https://doi.org/10.5281/zenodo.5897232).

Author contributions

E. W. performed all of the simulations, Y. R. and S. H. P. performed the contact angle experiments. J. P. E., P. H. K., S. A. U., and D. D. conceptualised the study and supervised the project. E. W. wrote the first draft of the paper, which was reviewed and edited by all authors.

Conflicts of interest

There are no conflicts to declare.

Appendix

Uncertainty quantification

Uncertainties are obtained from temporal binning of contact angles obtained from five individual snapshots within bins of Δt_bin= 0.25 ns each. Fluctuations of the droplet surface are considered. Further uncertainties from the fluctuation of the droplet base were found to be negligible after sufficient equilibration time. The entirety of datasets for each degree of damage (apart from the fully-functionalised and fully damaged cases) is obtained from all different initial droplet position and random damage seed trials, leading to a total number of five trials per configuration. The nominal contact angle for each damage ratio is evaluated as the ensemble average of the union of all five individual temporal datasets from binning.

The minimum and maximum limits are obtained by means of the extreme values observed among all data points from binning with additional consideration of uncertainties of the individual binned droplet surface circle fits. These two extreme values resemble the error bars shown for the data points in Fig. 6. The one-sided 95% confidence intervals for both the droplet radius and centre position along the surface-normal direction are evaluated to obtain the two extreme slopes of the circle fits at the intersection with the monolayer surface.

Acknowledgements

E. W. thanks the Engineering and Physical Sciences Research Council (EPSRC) and Procter and Gamble for PhD funding through an iCASE studentship (EP/T517690/1). J. P. E. was supported by the Royal Academy of Engineering through the Research Fellowships scheme. D. D. thanks the EPSRC for funding through an Established Career Fellowship (EP/N025954/1). We acknowledge the use of Imperial College London Research Computing Service (https://www.doi.org/10.14469/hpc/2232) and the UK Materials and Molecular Modelling Hub, which is partially funded by the EPSRC (EP/P020194/1 and EP/T022213/1). We also thank Sumanth Jamadagni, Andrei Bureiko, and Francisco Rodriguez-Ropero (Procter and Gamble) for useful discussions.

References

1. G. S. Luengo, A.-L. Fameau, F. Léonforte and A. J. Greaves, Adv. Colloid Interface Sci., 2021, 290, 102383.
2. L. J. Wolfram, J. Am. Acad. Dermatol., 2003, 48, S106–S114.
3. S. P. Gurden, V. F. Monteiro, E. Longo and M. M. C. Ferreira, J. Microsc., 2004, 215, 13–23.
4. J. A. Swift and J. R. Smith, J. Microsc., 2001, 204, 203–211.
5. M. Sadaie, N. Nishikawa, S. Ohnishi, K. Tamada, K. Yase and M. Hara, Colloids Surf., B, 2006, 51, 120–129.
6. F. J. Wortmann, G. Wortmann and E. Schulze Zur Wiesche, Langmuir, 2010, 26, 7365–7369.
7. L. N. Jones and D. E. Rivett, Micron, 1997, 28, 469–485.
8. S. Breakspear, J. R. Smith and G. S. Luengo, J. Struct. Biol., 2005, 149, 235–242.
9. D. J. Evans and M. Lanczki, Text. Res. J., 1997, 67, 435–444.
10. M. Okamoto, K. Ishikawa, N. Tanji and S. Aoyagi, Surf. Interface Anal., 2012, 44, 736–739.
11. Y. Masukawa, H. Tsujimura, H. Tanamachi, H. Narita and G. Imokawa, Exog. Dermatol., 2004, 3, 273–281.
12. S. Thibaut, E. De Becker, B. A. Bernard, M. Huart, F. Fiat, N. Baghdadli, G. S. Luengo, F. Leroy, P. Angevin, A. M. Kermoal, S. Muller, M. Peron, G. Provot, S. Kravtchenko, D. Saint-Leger, G. Desbois, L. Gauchet, K. Nowbuth, A. Galliano, J. Y. Kempf and I. Silberzan, Int. J. Cosmet. Sci., 2010, 32, 422–434.
13. A. P. Fellows, M. T. L. Casford and P. B. Davies, Appl. Spectrosc., 2020, 74, 1540–1550.
14. T. Takahashi, A. Mamada, S. Breakspear, T. Itou and N. Tanji, J. Cosmet., Dermatol. Sci. Appl., 2015, 14, 2–8.
15. Y. K. Kamath, C. J. Dansizer and H.-D. Weigmann, J. Appl. Polym. Sci., 1978, 22, 2295–2306.
16. R. Molina, F. Comelles, M. R. Juliá and P. Erra, J. Colloid Interface Sci., 2001, 237, 40–46.
17. R. A. Lodge and B. Bhushan, J. Appl. Polym. Sci., 2006, 102, 5255–5265.
18. V. Dupres, T. Camesano, D. Langevin, A. Checco and P. Guenoun, J. Colloid Interface Sci., 2004, 269, 329–335.
19. V. Dupres, D. Langevin, P. Guenoun, A. Checco, G. S. Luengo and F. Leroy, J. Colloid Interface Sci., 2007, 306, 34–40.
20. E. Schulze Zur Wiesche, A. Körner, K. Schäfer and F.-J. Wortmann, J. Cosmet. Sci., 2011, 62, 237–249.
21. T. Gao, Y. He, P. Landa and J.-M. Tien, J. Cosmet. Sci., 2011, 62, 127–137.
22. S. Tokunaga, H. Tanamachi and K. Ishikawa, Cosmetics, 2019, 6, 31.
23. V. M. Longo, V. F. Monteiro, A. S. Pinheiro, D. Terci, J. S. Vasconcelos, C. A. Paskocimas, E. R. Leite, E. Longo and J. A. Varela, Int. J. Cosmet. Sci., 2006, 28, 95–101.
24. R. A. Lodge and B. Bhushan, J. Vac. Sci. Technol., A, 2007, 25, 893–902.
25. F. M. Maddar, D. Perry, R. Brooks, A. Page and P. R. Unwin, Anal. Chem., 2019, 91, 4632–4639.
26. C. LaTorre and B. Bhushan, J. Vac. Sci. Technol., A, 2005, 23, 1034–1045.
27. H. Mizuno, G. S. Luengo and M. W. Rutland, Langmuir, 2010, 26, 18909–18915.
28. J. Bowen, S. A. Johnson, A. R. Avery and M. J. Adams, Surf. Topogr.: Metrol. Prop., 2016, 4, 024008.
29. B. Bhushan, Prog. Mater. Sci., 2008, 53, 585–710.
30. M. Korte, S. Akari, H. Kühn, N. Baghdadli, H. Möhwald and G. S. Luengo, Langmuir, 2014, 30, 12124–12129.
31. R. L. Akkermans and P. B. Warren, Philos. Trans. R. Soc., A, 2004, 362, 1783–1793.
32. C.-C. Chou and M. J. Buehler, Biomacromolecules, 2012, 13, 3522–3532.
33. C.-C. Chou, E. Lepore, P. Antonaci, N. Pugno and M. J. Buehler, J. Mater. Res., 2014, 30, 26–35.
34. R. L. McMullen and S. P. Kelty, J. Phys. Chem. B, 2007, 111, 10849–10852.
35. U. Natarajan and C. Robbins, J. Cosmet. Sci., 2010, 61, 467–477.
36. R. J. Ward, H. A. Willis, G. A. George, G. B. Guise, R. J. Denning, D. J. Evans and R. D. Short, Text. Res. J., 1993, 63, 362–368.
37. D. W. Cheong, F. C. Lim and L. Zhang, Langmuir, 2012, 28, 13008–13017.
38. A. P. Negri, H. J. Cornell and D. E. Rivett, Text. Res. J., 1993, 63, 109–115.
39. J. A. Swift, J. Cosmet. Sci., 1999, 50, 23–47.
40. J. A. Swift and A. W. Holmes, Text. Res. J., 1965, 35, 1014–1019.
41. I. Efremenko, R. Zach and Y. Zeiri, J. Phys. Chem. C, 2007, 111, 11903–11911.
42. E. Antunes, C. F. Cruz, N. G. Azoia and A. Cavaco-Paulo, RSC Adv., 2015, 5, 12365–12371.
43. S. Banerjee, C. Cazeneuve, N. Baghdadli, S. Ringeissen, F. Léonforte, F. A. M. Leermakers and G. S. Luengo, J. Phys. Chem. B, 2017, 121, 8638–8651.
44. F. A. M. Leermakers, G. S. Luengo, N. Baghdadli, C. Mazilier, A. Potter and F. Léonforte, Soft Matter, 2020, 16, 4823–4839.
45. T. I. Morozova, N. A. García, J.-L. Barrat, G. S. Luengo and F. Léonforte, ACS Appl. Mater. Interfaces, 2021, 13, 30086–30097.
46. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
47. S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822.
48. Y. Atsmon-Raz and D. P. Tieleman, J. Phys. Chem. B, 2017, 121, 11132–11143.
49. S. Wang and R. G. Larson, Soft Matter, 2013, 9, 480–486.
50. M. Vögele, C. Holm and J. Smiatek, J. Chem. Phys., 2015, 143, 243151.
51. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810.
52. D. Wu and X. Yang, J. Phys. Chem. B, 2012, 116, 12048–12056.
53. E. J. Wallace and M. S. Sansom, Nano Lett., 2007, 7, 1923–1928.
54. E. J. Wallace and M. S. Sansom, Nano Lett., 2008, 8, 2751–2756.
55. R. Alessandri, F. Grünewald and S. J. Marrink, Adv. Mater., 2021, 33, 2008635.
56. J. N. Israelachvili and M. L. Gee, Langmuir, 1989, 5, 288–289.
57. J. Wang, D. Bratko and A. Luzar, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6374–6379.
58. D. Sergi, G. Scocchi and A. Ortona, J. Chem. Phys., 2012, 137, 094904.
59. F. Grunewald, G. Rossi, A. H. De Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449.
60. C. Xing and R. Faller, Soft Matter, 2009, 5, 4526–4530.
61. A. Lamberg and T. Taniguchi, J. Phys. Chem. B, 2014, 118, 10643–10652.
62. A. Ramazani, T. Mandal and R. G. Larson, Langmuir, 2016, 32, 13084–13094.
63. J. Chen, B. Chang, S. Oyola-Reynoso, Z. Wang and M. Thuo, ACS Omega, 2017, 2, 2072–2084.
64. J. F. Liljeblad, E. Tyrode, E. Thormann, A. C. Dublanchet, G. Luengo, C. Magnus Johnson and M. W. Rutland, Phys. Chem. Chem. Phys., 2014, 16, 17869–17882.
65. A. V. Titov, P. Král and R. Pearson, ACS Nano, 2010, 4, 229–234.
66. C. Gobbo, I. Beurroies, D. D. Ridder, R. Eelkema, S. J. Marrink, S. D. Feyter, J. H. V. Esch and A. H. D. Vries, J. Phys. Chem. C, 2013, 117, 15623–15631.
67. L. Coderch, M. A. Oliver, V. Martínez, A. M. Manich, L. Rubio and M. Martí, Skin Res. Technol., 2017, 23, 479–485.
68. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551.
69. J. Michalowsky, L. V. Schäfer, C. Holm and J. Smiatek, J. Chem. Phys., 2017, 146, 054501.
70. Z. Wu, Q. Cui and A. Yethiraj, J. Chem. Theory Comput., 2011, 7, 3793–3802.
71. V. Miguel, M. A. Perillo and M. A. Villarreal, Biochim. Biophys. Acta, 2016, 1858, 2903–2910.
72. F. Goujon, A. Dequidt, A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2018, 14, 2644–2651.
73. M. Ndao, J. Devémy, A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2015, 11, 3818–3828.
74. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
75. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
76. L. Verlet, Phys. Rev., 1967, 159, 98.
77. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
78. I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162.
79. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, New York, 1989.
80. A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J. E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841.
81. A. J. Grosvenor, S. Deb-Choudhury, P. G. Middlewood, A. Thomas, E. Lee, J. A. Vernon, J. L. Woods, C. Taylor, F. I. Bell and S. Clerens, Int. J. Cosmet. Sci., 2018, 40, 536–548.
82. N. Wang, R. Barfoot, M. Butler and C. Durkan, ACS Biomater. Sci. Eng., 2018, 4, 3063–3071.
83. Y. Z. Hessefort, B. T. Holland and R. W. Cloud, J. Cosmet. Sci., 2008, 59, 303–315.
84. S. Nosé, Mol. Phys., 1984, 52, 255–268.
85. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
86. W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103.
87. G. Scocchi, D. Sergi, C. D'Angelo and A. Ortona, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061602.
88. P. Letellier, A. Mayaffre and M. Turmine, J. Colloid Interface Sci., 2007, 314, 604–614.
89. M. J. de Ruijter, T. D. Blake and J. D. Coninck, Langmuir, 1999, 15, 7836–7847.
90. T. Werder, J. H. Walther, R. L. Jaffe, T. Halicioglu and P. Koumoutsakos, J. Phys. Chem. B, 2003, 107, 1345–1352.
91. H. G. Ozcelik, E. Satiroglu and M. Barisik, Nanoscale, 2020, 12, 21376–21391.
92. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
93. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
94. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
95. T. R. Underwood and H. C. Greenwell, Sci. Rep., 2018, 8, 352.
96. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
97. L. Wilhelmy, Ann. Phys., 1863, 195, 177–217.
98. ASTM D7490-13, Standard Test Method for Measurement of the Surface Tension of Solid Coatings, Substrates and Pigments using Contact Angle Measurements, ASTM International, 2013.
99. N. M. Dingle and M. T. Harris, J. Colloid Interface Sci., 2005, 286, 670–680.
100. M. Hoorfar and A. W. Neumann, Adv. Colloid Interface Sci., 2006, 121, 25–49.
101. A. F. Stalder, T. Melchior, M. Müller, D. Sage, T. Blu and M. Unser, Colloids Surf., A, 2010, 364, 72–81.
102. J. P. Ewen, C. Gattinoni, N. Morgan, H. A. Spikes and D. Dini, Langmuir, 2016, 32, 4450–4463.
103. M. Biesalski and J. Rühe, Langmuir, 2000, 16, 1943–1950.
104. Y.-L. Chen and J. N. Israelachvili, J. Phys. Chem., 1992, 96, 7752–7760.
105. M. Chu, M. Miller and P. Dutta, Langmuir, 2020, 36, 906–910.
106. C. Lam, N. Kim, D. Hui, D. Kwok, M. Hair and A. Neumann, Colloids Surf., A, 2001, 189, 265–278.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01720a

---