 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of hydrodynamic interactions on the aggregation kinetics of sedimenting colloidal particles†
Lorenzo
Turetta
and
Marco
Lattuada
 *
*
Department of Chemistry, University of Fribourg, Chemin du Musée 9, 1700 Fribourg, Switzerland. E-mail: lorenzo.turetta@unifr.ch; marco.lattuada@unifr.ch
First published on 25th January 2022
Abstract
The aggregation kinetics of sedimenting colloidal particles under fully destabilized conditions has been investigated over a wide range of particle volume fractions (Φ) and Péclet numbers (Pe) using the recent PSE algorithm implementing the Rotne–Prager–Yamakawa (RPY) approximation for long-range Hydrodynamic Interactions (HI). Fast Lubrication Dynamics (FLD) and simple Brownian Dynamics (BD) methods have also been employed to assess the importance of long range hydrodynamic interactions on the resulting dynamics. It has been observed that long-range hydrodynamic interactions are essential to capture the fast aggregation rates induced by the increase in sedimentation rate of clusters with increasing mass, which manifests with an explosive-like cluster growth after a given induction time. On the contrary, simulations employing only short-range hydrodynamic interactions (such as FLD) and BD (which neglects completely hydrodynamic interactions) are incapable of predicting this very rapid kinetics, because sedimentation simply leads to all particles and clusters moving vertically with identical velocity. It has been observed that at high volume fractions and low Pe values, a gel point can be formed and a phase diagram predicting when gelation is reached has been obtained. It was also observed that, as Pe increases, the anisotropy of the resulting clusters decreases, suggesting that denser clusters with spherical-like morphology are formed due to cluster breakage and restructuring. We can conclude that long-range hydrodynamic effects are of crucial importance in understanding the aggregation dynamics of settling clusters, revealing important features of the complex interplay between sedimentation, and colloidal interactions.
Introduction
The dynamics of colloidal aggregation is of fundamental importance in materials science and in a wide range of industrial applications, including paint preparation, wastewater treatment, formulation of pharmaceutical products, and food processing.1 Therefore, it has been the subject of a large body of experimental and theoretical studies.2–6 Most of the work to date has been concerned with the fundamental understanding of the physical mechanism governing aggregation kinetics in aqueous suspensions under both the diffusion-limited cluster aggregation (DLCA) regime, where particles stick immediately as they encounter each other and the aggregation rate is solely governed by diffusion, and reaction-limited cluster aggregation (RLCA) conditions,7 which is a regime governed by interparticle repulsive interactions.Extensive experimental and theoretical studies pioneered by the Weitz group7,8 showed that the fractal dimension df, which describes the internal structure of the aggregates, depends on the mechanism of aggregation, but is independent of the chemical and physical properties of the system (i.e., the colloidal particle type). This suggested a universal nature of the aggregation processes for clusters formed in both the DCLA and RCLA regimes. Colloidal clusters generated by the two aforementioned mechanisms exhibit a “fractal” structure, meaning that their mass (m) scales with the radius of gyration (Rg) as m ∝ (Rg/Rp)df, with Rp being the radius of the constituent particles and df the fractal dimension of the clusters, which quantifies the spatial organization of the particles embedded in these aggregates, and therefore their compactness. In particular, aggregates formed in the DLCA regime are rather open with fractal dimensions df of about 1.8,9,10 while denser clusters with df values close to 2.1 are typically observed under RLCA conditions.8
Although aggregation of particles in water under stagnant conditions is relevant in many circumstances, cluster aggregation driven by sedimentation plays an essential role in many industrial processes, such as separation of particles in suspensions and wastewater treatment, and has motivated numerous studies in the literature.2,4,5,11–13
Allain and co-workers2 observed that in calcium carbonate colloidal suspensions sedimenting in high cylindrical cells at concentrations low enough to prevent gelation, the fractal dimension of the resulting clusters increased from 1.8 (typical of DLCA regimes) to 2.2–2.3, due to the flow-induced restructuring and rearrangement of the aggregates. They also reported a limiting size above which aggregates did not grow anymore and observed a power-law relationship between settling velocity and cluster radius.11 Gonzalez and coworkers4 employed Monte Carlo simulations to study the effect of particle volume fraction and Péclet number on the aggregation mechanics of colloidal particles that sediment in a confined prism,14–16 showing that both parameters can influence the aggregation process and the fractal dimension of the formed aggregates. They also identified a “sweeping” regime of aggregation, characterized by higher values of the fractal dimension, similar to the ones found experimentally (2.2–2.3). Under such conditions, larger clusters sediment faster and can therefore encounter and easily aggregate individual particles and smaller aggregates.
So far, Monte Carlo (MC) techniques have proved to be an especially viable modeling approach to study the aggregation process under various conditions, providing remarkable flexibility in terms of ease of implementation, low computational cost, and accuracy. However, these techniques show some limitations, such as the inability to include hydrodynamic interactions and the fact that the investigation of real-time dynamics is not immediate. An alternative approach is based on the Brownian Dynamics (BD) technique, which allows for the simultaneous implementation of real colloidal forces, thermal motion, and Hydrodynamic Interactions (HI) in the same model. BD simulations have been successfully used to explore the effect of colloidal interactions and particle volume fraction on the structure of aggregates and sediments,12 study the structure of percolating networks in concentrated suspensions of particles,17 and investigate the aggregation process under various conditions.18–21
When colloidal aggregates are exposed to high shear rates or external gravitational fields, i.e., under intense stirring or sedimentation, hydrodynamics effects become essential. In fact, when a particle moves in a fluid, it perturbs the fluid around it and induces a flow field in the solvent that affects the motion of other particles. These hydrodynamic disturbances are very long-ranged and, in a quiescent, unbounded fluid, decay with the inverse of the center-to-center interparticle distance. In this complex dynamical process, an accurate description of the flow-induced clustering, as well as breakage events, requires more sophisticated models to account for the interplay between hydrodynamics, colloidal interactions, and gravitational forces.
In this context, Brady and Bossis22 developed the well-known Stokesian Dynamics (SD) method, a discrete numerical technique that accurately accounts for both the far-field hydrodynamic and short-range lubrication interactions. This method, coupled with colloidal interactions, thermal motion, and contact mechanics, has been successfully employed to shed light on the rheological behavior of many shear-driven processes, especially shear-thickening.23–26
One major problem with SD techniques is their high computational cost, as the building and inversion of the far-field mobility matrix require O(Np2) and O(Np3) calculations, respectively (with Np being the total number of particles in the system). For this reason, in general, only small-size systems containing a limited number of particles or single clusters can be dealt with. Other approaches, such as the Accelerated Stokesian Dynamics (ASD)27 and the more recent Fast Stokesian dynamics (FSD)28 methods, could maintain the same level of accuracy as conventional SD with a lower computational cost that scales as O(Np![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Np) and O(Np), respectively. However, these operations are still prohibitive for large systems containing thousands of particles. Nevertheless, depending on the specific needs, different approximations of the SD method can be adopted. Recently, advances in technology and the use of faster approximate iterative methods allowed scientists to successfully model very large systems of particles and reproduce experimental results by including only a specific contribution to the hydrodynamic interactions. For dense colloidal suspensions, where many particle–particle surfaces are in close proximity (0.1 ≤ Φ ≤ 0.5), the so-called Fast Lubrication Dynamics method (FLD)29–31 has been successfully applied for the study of suspension dynamics and rheology over a wide range of different operating conditions and physical parameters. In the FLD algorithm, the overall resistance tensor R, which mathematically describes the many-body HI, is split into an isotropic diagonal matrix, that attempts to approximate long-range HI via the use of self-diffusivity values obtained from SD in equilibrium conditions, and a lubrication matrix, which includes the pairwise summation of the short-range interactions.
Np) and O(Np), respectively. However, these operations are still prohibitive for large systems containing thousands of particles. Nevertheless, depending on the specific needs, different approximations of the SD method can be adopted. Recently, advances in technology and the use of faster approximate iterative methods allowed scientists to successfully model very large systems of particles and reproduce experimental results by including only a specific contribution to the hydrodynamic interactions. For dense colloidal suspensions, where many particle–particle surfaces are in close proximity (0.1 ≤ Φ ≤ 0.5), the so-called Fast Lubrication Dynamics method (FLD)29–31 has been successfully applied for the study of suspension dynamics and rheology over a wide range of different operating conditions and physical parameters. In the FLD algorithm, the overall resistance tensor R, which mathematically describes the many-body HI, is split into an isotropic diagonal matrix, that attempts to approximate long-range HI via the use of self-diffusivity values obtained from SD in equilibrium conditions, and a lubrication matrix, which includes the pairwise summation of the short-range interactions.
Another possibility consists in neglecting the lubrication effects, which result from relative motion between particles, and include only long-range hydrodynamic interactions using Brownian Dynamics Simulations with the Rotne Prager Yamakawa tensor (RPY),32 as originally developed by Ermak and McCammon.33
One of the most accepted frameworks in this context is the one proposed by Fiore and Swan,34 who recently developed a fast and highly efficient GPU implementation of the Positively Split Ewald (PSE) algorithm, capable of computing both the RPY mobility tensor and the stochastic thermal contribution with a much shorter calculation time than the one required by standard methods designed to run on CPUs.
Different studies in the literature have performed simulations using Brownian Dynamics coupled with hydrodynamic interactions. Moncho-Jordà and co-workers,35 employed BD with HI to investigate microstructure and transient cluster aggregation in steady-state sedimentation and observed that the fractal dimension and the probability of finding larger aggregates decrease with increasing the Pe number, as clusters undergo simultaneous restructuring and breakup. Varga and co-workers36 showed that in the process of aggregation, and eventually gelation, BD simulations with RPY are capable of accurately modeling hydrodynamic interactions between larger aggregates, like those generated during sedimentation, and that long-range HI play a predominant role if compared to the purely dissipative effect given by short-range lubrication forces.6
From experiments and theoretical studies, there is also evidence that attractive forces between sedimenting particles always lead to faster settling processes, however, the effect of the Péclet number and particle concentration on the evolution of cluster mass and aggregation kinetics is still a matter of discussion.37,38 From an experimental point of view, Wu and coworkers5 investigated the kinetics of aggregation of polystyrene particles dispersed in water under sedimentation, which was induced by tuning the density difference between particles and solvent. They measured experimentally the time evolution of the average radius of gyration for clusters generated under different conditions by using a small-angle light scattering (SALS) instrument and provided a comparative study with the data obtained using Population Balance Equations (PBE). They observed that in the case of small density differences, the fractal dimensions remained almost identical, but the aggregation kinetics changed, resulting in an increase in the growth rate of the average cluster mass and radius of gyration at the final stage of the process, which were found to be dependent on the density differences between the colloidal particles and the suspension medium. Conversely, larger density differences have been observed to lead to an increase of the fractal dimension, and more compact structures are generally produced, as shown by several experimental and theoretical studies in the literature.2,39,40 However, a direct comparison between experimental and modeling results is not always possible, especially under sedimentation when a direct measurement of the number of clusters in time is rather difficult to be determined experimentally.
In the presence of shear flows, the rate of aggregation of colloids depends upon the frequency of collisions and the probability of two particles sticking together to form a stable bond. The presence of a shear flow promotes the aggregation of colloidal particles in two main ways. First, for kinetically-stabilized colloidal suspensions with a sufficiently high energy barrier to prevent aggregation, the convective energy imparted by the fluid may be sufficient for the particles to cross the repulsive barrier and aggregate. In the second scenario, for fully destabilized suspensions, the collision rate entirely depends on the intensity of the flow field, resulting in a substantial enhancement of the aggregation kinetics compared to a purely diffusion process (a mechanism called “perikinetic aggregation”).41
Numerous theoretical studies have been carried out to ascertain the effect of thermal motion, interparticle colloidal forces, and hydrodynamic interactions on the shear-induced aggregation of colloidal particles. A delicate balance among them determines the final microstructure of the formed clusters and the kinetics of the process.42 For example, during the application of steady-shear flow at high Péclet, it has been observed that the microstructure tends to reorganize in order to accommodate the hydrodynamic and the applied colloidal forces. Under such conditions, simulations with the Stokesian Dynamics algorithm can accurately model the shear thickening transition occurring at such high Pe,43 providing a much higher accuracy when compared to a BD algorithm not including hydrodynamic interactions.
Chen and Doi,44 studied the dynamical behavior and microstructural properties of colloidal aggregates produced under strong shear flows at low volume fractions, using numerical simulations; they investigated the disaggregation and aggregation process, reporting a dependence of the viscosity on both the shear rate and concentration (fraction area), and a cluster coordination number dependent only on the shear rate. Zaccone et al.45 investigated the reaction-limited kinetics of aggregation in concentrated sheared suspensions of Brownian particles (Φ ≥ 0.1) by comparing experimental results and theoretical predictions based on the solution of the Smoluchowski equations. The study shows that the characteristic aggregation time decreases with increasing colloid concentration as a result of the increase in the effective Péclet number and the collision rate between particles.
The purpose of our work is to reproduce the conditions that a suspension of colloids is exposed to in the presence of sedimentation and highlight the role of hydrodynamics on the sedimentation behavior under various flow conditions and particle concentrations. The target conditions for the current study are typically found in the bulk of a suspension, where a constant particle concentration can be assumed to persist. Two types of simulations have been performed in our work. In the first group of simulations, the PSE algorithm for RPY hydrodynamics has been employed to study aggregation kinetics at different particle volume fractions and Péclet numbers. In the second set of simulations, a comparison between different methods based on FLD, BD, and PSE algorithms has been performed with the aim of revealing the effect of near-field and far-field hydrodynamic contribution on the aggregation process and the structural properties of the clusters.
Simulation method
The main set of simulations employing the Positively Split Ewald (PSE)34 algorithm, available as a plugin for the GPU molecular dynamics suite HOOMD-blue,46 were performed starting from a population of Np = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polystyrene particles dispersed in water at room temperature with a primary radius Rp = 50 nm, small enough to experience Brownian motion. The physical constants of these particles (such as the Hamaker constant, density and Young's modulus) are chosen in order to represent those of bulk polystyrene. The study covers a wide spectrum of particle volume fractions Φ, ranging from 0.005 up to 0.2. Before starting the simulations, an algorithm randomly generates the x, y, z coordinates of each particle for a given Φ, ensuring that there is no overlap with the others. Periodic boundary conditions in conjunction with the minimum image convention have been also applied. This random configuration is then allowed to equilibrate in the absence of sedimentation under diffusion regime with an energy barrier to prevent aggregation. Once the system reaches an equilibration state, a gravitational field along the z-direction is applied, attractive van der Waals interactions are introduced, and the repulsive barrier among the particles is removed. Simulations have been carried out over a range of Péclet numbers spanning two orders of magnitude (i.e., ranging between 0.1 and 10). A change in Péclet is physically related to the change in the acceleration that the particles are exposed to, as it would happen in a centrifugal field by increasing the revolution rate of the samples. Once the number of aggregates falls below a threshold value, which depends on the specific operating conditions, simulations are stopped. All the information about aggregation kinetics and clusters morphology has been extracted from the simulated particle trajectories, stored at specific time intervals during each run. The trajectories of the particles have been further analyzed using molecular visualization programs which are designed for displaying and animating large and complex systems. The animated movies provided in the ESI† are indicated in the text with the letter M and consecutively numbered with Arabic numerals in the order of their appearance. These animations show the temporal evolution of the colloidal system under various conditions and can therefore help the reader to interpret graphs and better visualize the structure and morphology of the formed clusters. This analysis can ultimately reveal unique features of the system and shed light on the more intrinsic aspects of the aggregation dynamics under sedimentation. In this work, the majority of the post-processing work has been carried out using the software packages Ovito®,47 Python®, and Matlab® (The MathWorks).
000 polystyrene particles dispersed in water at room temperature with a primary radius Rp = 50 nm, small enough to experience Brownian motion. The physical constants of these particles (such as the Hamaker constant, density and Young's modulus) are chosen in order to represent those of bulk polystyrene. The study covers a wide spectrum of particle volume fractions Φ, ranging from 0.005 up to 0.2. Before starting the simulations, an algorithm randomly generates the x, y, z coordinates of each particle for a given Φ, ensuring that there is no overlap with the others. Periodic boundary conditions in conjunction with the minimum image convention have been also applied. This random configuration is then allowed to equilibrate in the absence of sedimentation under diffusion regime with an energy barrier to prevent aggregation. Once the system reaches an equilibration state, a gravitational field along the z-direction is applied, attractive van der Waals interactions are introduced, and the repulsive barrier among the particles is removed. Simulations have been carried out over a range of Péclet numbers spanning two orders of magnitude (i.e., ranging between 0.1 and 10). A change in Péclet is physically related to the change in the acceleration that the particles are exposed to, as it would happen in a centrifugal field by increasing the revolution rate of the samples. Once the number of aggregates falls below a threshold value, which depends on the specific operating conditions, simulations are stopped. All the information about aggregation kinetics and clusters morphology has been extracted from the simulated particle trajectories, stored at specific time intervals during each run. The trajectories of the particles have been further analyzed using molecular visualization programs which are designed for displaying and animating large and complex systems. The animated movies provided in the ESI† are indicated in the text with the letter M and consecutively numbered with Arabic numerals in the order of their appearance. These animations show the temporal evolution of the colloidal system under various conditions and can therefore help the reader to interpret graphs and better visualize the structure and morphology of the formed clusters. This analysis can ultimately reveal unique features of the system and shed light on the more intrinsic aspects of the aggregation dynamics under sedimentation. In this work, the majority of the post-processing work has been carried out using the software packages Ovito®,47 Python®, and Matlab® (The MathWorks).
If inertia is neglected, the discrete equation of motion that models the trajectories of a system of Np equal-sized Brownian particles of radius Rp suspended in an incompressible Newtonian fluid at low Reynolds numbers, is given by:48
| x(t + Δt) = x(t) + M·FCΔt + FBΔt + kBT∇·MΔt | (1) |
 accounts for the stochastic thermal force, and X is a normally distributed vector with zero mean and unit variance. The last term requires the calculation of the divergence of the mobility tensor kBT∇∙M, which can be avoided by adopting a mid-point scheme.49
accounts for the stochastic thermal force, and X is a normally distributed vector with zero mean and unit variance. The last term requires the calculation of the divergence of the mobility tensor kBT∇∙M, which can be avoided by adopting a mid-point scheme.49
Assuming only the coupling between particles’ translational velocity and forces, the arrays x, X, FC and FB are 3Np-dimensional vectors, while the mobility matrix M has dimension 3Np × 3Np (which means 3 degrees of freedom for each particle). If hydrodynamic interactions are neglected, M is a diagonal matrix whose elements are given by the Stokes–Einstein 1/(6πηRp) (if only the translational motion without rotation is considered).
In reality, as stated above, the hydrodynamic disturbances induced by the motion of a particle in a fluid make it more challenging to determine the coupling between particle velocity and colloidal forces.
These long-range hydrodynamic interactions have been taken into account by the Rotne–Prager–Yamakawa hydrodynamic tensor MRPY, which is a function of the particles configuration and couples the non-hydrodynamic forces on particle j to the motion of particle i with inter-particles distance r and radius Rp immersed in a fluid of viscosity η:
 | (2) |
In the first set of simulations, short-range HI interactions (i.e., the lubrication effects) have been neglected. The Brownian dynamics simulations employing the PSE algorithm were run on a Multi-core CPUs computer powered with Nvidia graphic card and provided by the University of Fribourg, Switzerland. In the present study, particles are only subjected to attractive colloidal interactions to reproduce fully destabilized conditions.
The van der Waals attractive potential between two particles of radius Rp with a center-to-center separation distance r is given by the Hamaker equation:50
 | (3) |
The van der Waals force FvdW is the gradient of the van der Waals interaction energy VvdW:
| FvdW(r) = −∇VvdW(r) | (4) |
 | (5) |
 | (6) |
In addition, to ensure that the van der Waals energy in eqn (3) has a finite value and avoid numerical instability at contact, the minimum of the potential has been shifted using a cut-off separation distance equal to D0.
The expressions for the elastic normal restoring force FN and the radius of the contact region rc can be written as follows:51,53,54
 | (7) |
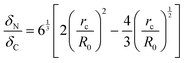 | (8) |
 indicates the maximum particle adhesive force.
indicates the maximum particle adhesive force.
In our simulations, the value of FN was adjusted to have the smallest possible overlap by monitoring the peak at distance zero of the pair–pair correlation function. A plot of the interparticle potential resulting from the attractive and repulsive normal contributions coming from contact mechanics is presented in the ESI† (Fig. S6).
According to the JKR theory, as particles are pulled apart from the equilibrium configuration, they form a small neck which maintains contact even for positive values of δN. Particles surfaces will eventually detach at δN = δC > 0 if the applied force exceeds the value of the pull-off force FAD. The adhesive forces arising from the mechanical contact can also provide sliding and twisting resistance to the relative motion of two touching particles. Following the equations shown in Marshall and co-workers,53 we implemented a granular package in HOOMD which works along with the PSE algorithm to reproduce such behavior and investigate the effect of tangential interactions during the aggregation process. Our plugin does not include “history” effects that account for the tangential displacement between particles for the whole duration of the time they are in contact, and it is, therefore, less efficient to counteract the Brownian motion of particles in small aggregates, so that they can eventually slide on top of each other in the absence of lubrication effects. This approach is the equivalent of the “quasi-static” treatment,54 where the deformation of the touching particles is assumed to be restricted to the contact zone and governed only by instantaneous forces, thus ignoring the history (i.e., accumulated tangential displacements).
In order to evaluate the effect of the box size (i.e., the number of primary particles Np) on the aggregation kinetics, we carried out some runs by increasing the number of particles up to 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, finding no significant changes in our results. The simulation timestep Δt has been chosen in order to minimize the particle–particle overlaps. In our simulations with the PSE algorithm, Δt ≈ 1 ns and a refinement of this time value had no significant effect on the results.
000, finding no significant changes in our results. The simulation timestep Δt has been chosen in order to minimize the particle–particle overlaps. In our simulations with the PSE algorithm, Δt ≈ 1 ns and a refinement of this time value had no significant effect on the results.
The second set of simulations has been performed using the Fast Lubrication Dynamics (FLD) algorithm provided by the LAMMPS55 software in the lubricateU pair style. The objective is to understand the effect of short-range hydrodynamic interactions, which becomes relevant at high volume fractions and low Péclet values. The same colloidal interactions among particles have been implemented in these simulations along with a full contact model which supports accumulated tangential displacement (i.e., contact history). This method is included in the granular style package provided by LAMMPS and follows the spring-dashpot-slider scheme proposed by Cundall and Strack56 for the sliding resistance and will be briefly explained below.
Assuming two connected particles i and j, with surface velocities at the contact point equal to vSi = vi + ωi × rcpi and vSj = vj + ωj × rcpj, the resulting tangential projection vt of their relative velocity vR = vSi − vSj is given by:
| vt = vR − (vR·n)n | (9) |
The relative tangential velocity at the point of contact vt acts along the tangential direction t, which can be expressed as follows:
 | (10) |
 | (11) |
| FT = −ktξ·t + Ft,damp·t | (12) |
| Parameter | Numerical value | Units |
|---|---|---|
| Particle radius – Rp | 50 | nm |
| Hamaker constant – AH | 1.33 × 10−20 | J |
| Boltzmann constant – kB | 1.38 × 10−23 | J K−1 |
| Temperature – T | 25 | °C |
| Viscosity of water – η | 8.9 × 10−4 | Pa s |
| Density of water – ρs | 997 | kg m−3 |
| Density of particles – ρp | 1050 | kg m−3 |
| Particle surface energy – γs | 6.5 × 10−3 | J m−2 |
| Young modulus – E | 3 × 109 | Pa |
| Poisson ratio – v | 0.33 | — |
| Tangential stiffness – kt | 1.7 × 10−4 | N m−1 |
| Cut-off separation distance – D0 | 0.165 | nm |
The structural parameters of clusters
In our work, two particles belong to the same cluster if the distance between their centres is lower than 2.001Rp. The parameters used to characterize the structure and morphology of the clusters include the radius of gyration Rg, the mass m (which is equivalent to the number of particles in the cluster) and the relative shape anisotropy parameter κ2. The radius of gyration of the ith cluster composed of nP primary particles Rg,i has been derived based on its geometrical structure as follows: | (13) |
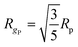 indicates the radius of gyration of the primary particles. We decided to compute a zeta-average gyration radius Rg for a given population of Ncl clusters, as measured in a Static-Light Scattering experiment, which is given by:59
indicates the radius of gyration of the primary particles. We decided to compute a zeta-average gyration radius Rg for a given population of Ncl clusters, as measured in a Static-Light Scattering experiment, which is given by:59 | (14) |
The gyration R tensor can be defined as follows:
 | (15) |
The average mass 〈mav〉 of the cluster population can be computed as:
 | (16) |
To quantify the structural anisotropy of the aggregates, the relative shape anisotropy parameter κ2 has been used, which depends on the eigenvalues λ1, λ2 and λ3 of the gyration tensor R and can be defined as follows:
 | (17) |
The numerical values and the corresponding units of the parameters employed in our simulations are presented in Table 1.
Results and discussion
The effect of the Péclet number (Pe) and particle volume fraction Φ on the kinetics of aggregation
The kinetics of aggregation as a function of the particle volume fraction Φ for a given Pe number can be investigated from the evolution of the dimensionless number concentration of clusters X in eqn (18) plotted against the dimensionless time τ, reported in eqn (19): | (18) |
 | (19) |
 is the primary particle aggregation rate constant for DLCA as derived by Smoluchowski,60t is the simulation time in seconds, and W ≈ 1 the Fuchs stability ratio (without including the effect of lubrication and of van der Waals interactions).
is the primary particle aggregation rate constant for DLCA as derived by Smoluchowski,60t is the simulation time in seconds, and W ≈ 1 the Fuchs stability ratio (without including the effect of lubrication and of van der Waals interactions).
The physical time t has been made dimensionless in eqn (19) using the initial number concentration of primary particles N0, which depends on the initial particle volume fraction Φ. As a result, if curves computed at different Φ collapse onto a single curve, one can assume an aggregation mechanism following classical DLCA.3 On the contrary, if the simulated data deviate from a mastercurve, the aggregation process follows a more complex dynamics, which is governed by the interplay between sedimentation and long-range hydrodynamics. The Péclet number (Pe) characterizes the strength of sedimentation to that of diffusion and can be defined as follows:
 | (20) |
 | ||
Fig. 1 Log–log plot of the dimensionless number concentration of clusters X against the dimensionless time τ as a function of the Péclet number and particle volume fractions for Np = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 obtained from simulations employing the RPY approximation of HI with the PSE algorithm. Fig. 1a shows the effect of the Péclet number for a specific particle volume fraction. Fig. 1b reports the effect of particle volume fraction for a given Péclet number. 000 obtained from simulations employing the RPY approximation of HI with the PSE algorithm. Fig. 1a shows the effect of the Péclet number for a specific particle volume fraction. Fig. 1b reports the effect of particle volume fraction for a given Péclet number. | ||
In particular, Fig. 1a reports the effect of an increasing Péclet number Pe on the aggregation kinetics measured at a specific value of the particle volume fraction Φ. One can observe that, for particle volume fractions Φ ≤ 0.1, increasing the Péclet number always leads to an increase in the aggregation rate, which is evident from the slope obtained from the corresponding graphs. This is not surprising since an increase of the Pe number implies higher sedimentation velocity, which has a strong impact on the collision rate and, therefore, on the resulting aggregation kinetics. However, at the highest particle volume fraction (Φ = 0.2), the aggregation is almost Pe independent, and the effect of sedimentation becomes negligible, as seen in the last graph of Fig. 1a where the curves fall on a single mastercurve for all Pe values. Under such conditions, in the range of Pe numbers investigated in this work, the size of the clusters does not have the time to reach a sufficiently high value for sedimentation to kick in, because the system reaches a gel point very early on, and also because the long-range hydrodynamic interactions are strongly screened at such high concentrations, thus reducing the sedimentation velocity.
From the temporal evolution of the number of clusters X computed at different values of the particle volume fraction Φ for a given Péclet number shown in Fig. 1b, it can be seen that, for Pe = 0 (i.e., in the absence of sedimentation), the number of clusters reduction as a function of time deviates from a single mastercurve and becomes faster as the particle volume fraction increases. This is a result of the progressive increase in the aggregation rate for high volume fractions compared to what was predicted by Smoluchowski's theory,60 as pointed out several times in the literature.3,61 When considering the data obtained at Pe > 0, an increase in the particle volume fraction always leads to an increase in the aggregation rate. However, our findings reveal that this effect is less pronounced for Φ ≤ 0.05, where curves tend to collapse onto a single curve, suggesting a similar aggregation mechanism. In general, the fact that, for all Pe numbers, the curves plotted as a function of the dimensionless time do not fall on a single mastercurve is a manifestation of high concentration-enhanced aggregation rate.
Fig. 2 reports the dimensionless time evolution of the average radius of gyration Rg normalized by the radius of the primary particles Rp computed at different particle volume fractions for a given Péclet number. A common feature of all the curves is that they all show an increase in size up to a certain time. Afterward, depending on the relative importance of sedimentation and the particle volume fraction, different scenarios are possible. In the first case, hydrodynamic forces and viscous stresses induced by the sedimentation are strong enough to break the bonds among particles, leading to progressive breakage, reaggregation, and restructuring of the clusters and resulting in a rapid fluctuation of the radius of gyration, as shown at Pe = 10 and 0.01 ≤ Φ ≤ 0.1. In the second case, the curve describing the temporal evolution of Rg experiences a rapid increase after a specific time, as shown at Pe = 1 and Φ ≤ 0.05, which corresponds to the time at which clusters grow over a critical dimension, and a sharp acceleration of the aggregation kinetics is observed (see Fig. 1). The explosive-like clusters growth after a given time has also been reported for the shear-induced clustering of DLVO colloids.61 Furthermore, a third scenario is possible, where at sufficiently high concentrations the radius of gyration reaches a plateau value, indicating that the colloidal system reached a gel point, which is evident for example at Pe = 0.1 and Φ ≥ 0.05. As before, overlapping curves suggest a volume fraction independent aggregation mechanism.
 | ||
| Fig. 2 Dimensionless time evolution of the average radius of gyration Rg normalized by the radius of the primary particles plotted as a function of the particle volume fraction for a given Pe number. | ||
Our findings reveal a complex interplay between the intensity of the flow field and particle concentration, thereby confirming that these parameters constitute the essential factors affecting the aggregation mechanism. In order to better understand how the presence of long-range hydrodynamic interactions influences the aggregation process and the shape and structure of settling clusters under various conditions, it is useful to compare the snapshots taken from the animated movies, created from particles’ trajectories and showing the temporal evolution of the aggregates, with the corresponding structural parameters mentioned in the previous section.
From Fig. 3a and 4a, it can be seen that for Φ = 0.01 and Pe = 0.1, the aggregation process leads to large, open structures with df ∼ 1.8 (typical value for a DLCA aggregate). The time evolution of the fractal dimension in Fig. 4a provides a more comprehensive view of the aggregation dynamics, showing that rather compact clusters form in the early stages of the aggregation process, which then assemble into larger and more branched structures (with lower fractal dimension). In addition, although only instantaneous tangential interactions have been accounted for, the animation movie M1 provided in the ESI† shows that the increased number of bonds among the constituent particles leads to denser clusters and also appears to impart increased rigidity to the formed aggregates, as soon as the particles arrange into subclusters that, at a first qualitative analysis, seem to be capable of supporting bending moments. It can also be seen that the cluster fractal dimension has profound implications on the aggregation behavior during sedimentation: the larger and more ramified clusters occupy a larger amount of space and can easily incorporate smaller aggregates and single particles, thus favoring the aggregation process.
 | ||
| Fig. 3 Representative structures of clusters produced as a result of sedimenting-induced aggregation at Φ = 0.01 and different Pe numbers, taken from the animation movies (M1, M2, and M3) (ESI†) of the time evolution of the system configuration provided in the ESI.† At Pe = 0.1 (a), clusters exhibit very open structures characterized by low fractal dimension df around 1.8 (Fig. 4a and movie M1, ESI†). At Pe = 1 (b), clusters tend to align with the flow and then rearrange in more compact structures, which is also evident from the time evolution of the fractal dimension in Fig. 4a and from the movie M2 (ESI†). At the highest Pe (c), more compact structures with spherical-like shapes and higher fractal dimensions are observed (movie M3 (ESI†) and Fig. 4a), which correspond to lower values of the relative shape anisotropy parameter k2 in Fig. 4b. The blue arrows provide a schematic representation of the convective motions induced by large clusters settling at intermediate and high Pe. The red arrows in Fig. 3a indicate that at low values of the Pe number, clusters settle slower along the direction of sedimentation. Under such conditions, at a first glance, they show a certain degree of rigidity which enables them to withstand the restructuring effects induced by the flow field, thus resulting in more open structures, as shown in the movie M1 in the ESI.† | ||
In the case of colloids sedimenting at low particle volume fraction (Φ = 0.01) and Pe ≥ 1 presented in Fig. 3b and c, animation movies M2 and M3 (in the ESI†) show that larger aggregates, which sediment more rapidly than smaller ones, generate high convective motions in the fluid, with a strong impact on the global aggregation rate and cluster morphology. In particular, the resulting velocity flow field enhances the mobility of the aggregates and can be accurately described only if long-range HI are included in the model. As a result, at the highest Pe, the aggregation process is accompanied by restructuring, leading to a dramatic change in the cluster morphology.
In fact, the stronger the effect of sedimentation, the larger is the fractal dimension, reaching values close to 2.4 (Fig. 4a). This suggests that particles can slide over each other at the contact point under the effect of the viscous stresses induced by the flow field, leading to more spherically-shaped conformations if compared to those obtained at lower Pe values, accompanied by a substantial decrease of the shape anisotropy parameter κ2, as shown in Fig. 4b. More specifically, clusters can rotate and reorient with the “lowest-resistance” side exposed to the directions of the flow field that constantly changes. This phenomenon is enhanced by the convective motions generated in the fluid by the sedimentation of larger clusters at high Péclet numbers.
Moreover, as aggregates are more compact, the suspension exhibits the presence of large void regions (clearly noticeable in Fig. 3c and Movie M3, ESI†) which lead to a lower collision rate between clusters. The average minimum surface-to-surface distance for the system of clusters presented in Fig. 3c has been calculated and is approximately 27 radius units. As a consequence, the aggregation rate decreases at the later stage of the process, as shown in Fig. 1, and the slope of the curve representing the dimensionless number of clusters over time is expected to reach a plateau value at long times. From Fig. 3b at Pe = 1, it can also be seen that most of the larger clusters exhibit elongated structures with preferential orientation along the direction of the flow field. However, at the latest stages of the process, these aggregates tend to become more compact upon rearrangements of the particles as a result of the restructuring effects induced by the flow field, which is evident from time evolutions of the fractal dimension and the shape anisotropy parameter k2 reported in Fig. 4. Similar results have been obtained at Φ = 0.005.
Fig. 5 shows the time evolution of the average radius of gyration Rg and the average cluster mass mav as a function of the Péclet number at Φ = 0.01. It is evident that both parameters increase with time, however, depending on the intensity of the flow field and particle concentration, curves show a different behavior. First of all, at a low or zero Péclet number, specifically Pe ≤ 0.1, it can be seen that the curves almost overlap throughout the whole simulation time, indicating an aggregation process independent of the Péclet number and structures of the obtained aggregates very similar to each other. For Pe = 1, the time evolution of both quantities shows a rapid growth after a given time, corresponding to a sharp decrease in the dimensionless number concentration in Fig. 1, as already observed in the case of shear-induced clustering.61 This is due to the effect caused by sedimentation-induced aggregation, which becomes more prominent as clusters grow in size, as revealed from Fig. 5b. A different behavior is observed for Pe values equal to 10, where the curves describing the time evolution of both quantities reach a plateau value after a given time, corresponding to a dynamic equilibrium between breakage and sedimentation-induced formation of clusters.
At intermediate concentrations (Φ = 0.05) and low Péclet numbers (Pe = 0.1), clusters exhibit very open branched structures with a fractal dimension value around 1.8, as illustrated by the snapshots taken from simulations presented in Fig. S1 (ESI†) and from the corresponding curves describing the temporal evolution of the fractal dimension in Fig. 6a. Under the influence of long-range HI, which promote their mobility, these clusters merge to form a gel-like spanning network, and the average cluster mass reaches a plateau value corresponding to the total number of particles in the system, which is evident from the snapshots of the colloidal system at the end of the simulation presented in Fig. 7a and from the curves describing the temporal evolution of the average mass in Fig. S2 (ESI†). Further increasing the Pe number leads to breakage and restructuring phenomena, thereby resulting in a lowered plateau and rapid fluctuation of the average radius of gyration Rg value, as shown in Fig. 6b for Pe ≥ 1. As a consequence, the fractal dimension values of the resulting clusters (Fig. 6a) increases from 1.8 to 2.2–2.4, consistently with the experimental observations previously outlined and theoretical predictions.
 | ||
| Fig. 7 Snapshots taken at the end of simulations performed at Φ = 0.05 (a), Φ = 0.1 (b) and Φ = 0.2 (c) at different Pe numbers. | ||
Further increasing particle concentrations up to Φ = 0.2 is generally a factor that can lead to gelation, as shown by the snapshots presented in Fig. 7b and c (and from the movies M4, M5, and M6, ESI†) for Pe ≤ 1. However, at the highest Pe equal to 10, the gel structure can either collapse in on itself or result in a net preferential orientation along the direction of the flow, as shown in Fig. 7b and c at Pe = 10 and movies M7 and M8 (ESI†), for Φ = 0.1 and Φ = 0.2, respectively. In the former case, snapshots of the system clearly show that clusters undergo simultaneous breakup and restructuring at Φ = 0.1, which is also evident from the fluctuations of the average cluster mass mav reported in Fig. 8.
 | ||
| Fig. 8 Time evolution of the average cluster mass mav for different particle volume fractions at Pe = 10. For Φ ≤ 0.1, the curves exhibit fluctuations around an equilibrium value, suggesting that aggregates undergo substantial restructuring until balance between clusters formation and breakage occurs. At the highest volume fraction (Φ = 0.2), the curve rapidly increases until it reaches a plateau value corresponding to the total number of particles Np. As a result, the system percolates and forms a stable gel-like network, as shown in Fig. 7c at Pe = 10. | ||
Our findings reveal that a colloidal system exposed to sedimentation can either reach a percolated gel-like network structure or not, depending on the combined effect of particle volume fraction Φ and Péclet number Pe.
In order to better visualize the relationship between these two parameters and comprehend their influence on the final state of the system, the K-Nearest-Neighbors (KNN) classification method with Neighborhood Components Analysis (NCA) provided by the open-source library Scikit-learn62 has been employed. KNN is a supervised machine learning algorithm that relies on a set of labeled input data (given by the combination of features x and the corresponding labels y) to learn a function h(x) able to predict the output labels when new unlabeled data are given.
In our case, given an unseen set of features Pe and Φ, the function h(Pe, Φ) should be able to capture the relationship between them and predict the corresponding status of the system, indicated with the label 0 or 1 depending on whether the system gels or not. To do so, an extended labeled dataset consisting of 100 observed combinations of Φ and Pe and the corresponding label outputs has been built. The hyperparameter K, which indicates the number of the nearest neighbors, can be used to control the learning process and has been tuned during the training and validated using the k-fold cross-validation technique,63 which iteratively takes a different kth part of the dataset to train the model and the remaining one to evaluate it.
The resulting decision boundary plot is shown in Fig. 9. Based on the classification obtained from the given dataset, the graph separates the two classes (percolated gel-like network structure or no-gel) and allows to easily classify a new couple of Φ and Pe. In order to evaluate the classification model, we adopted the accuracy metrics, defined as the number of correct predictions divided by the total number of predictions. From our findings, the accuracy metrics equal 0.924 with a standard deviation of 0.056, computed as the average of the recorded scores obtained during cross-validation.
Long-range vs. short-range hydrodynamics
In the second set of simulations, the role of different hydrodynamics contributions on the aggregation dynamics and cluster morphology has been investigated using three different modeling approaches. The first model is based on RPY simulations with long-range hydrodynamics computed using the PSE algorithm and already employed in the previous section; the second method neglects the far-field part and accounts only for near-field lubrication terms via the FLD algorithm. The last one employs a BD method without HI under the same set of conditions. As lubrication forces become more effective in dense suspensions where a large number of particle–particle surfaces are in proximity, we tested the three different methods for a system of Np = 8000 particles for volume fractions ranging from 0.05 to 0.2 at Pe = 1 and 10.The dimensionless number concentration of clusters X plotted against the dimensionless time τ for the three different methods under various flow conditions, and particle concentrations is shown in Fig. 10. It is immediately apparent that in the early stages of the process when aggregation occurs mostly between primary particles, simulations neglecting HI and employing a pure BD algorithm lead to faster kinetics, whereas simulations incorporating only lubrication forces show a slower decay of the number of clusters with time if compared to the method which includes the long-range hydrodynamics contributions. The effect is due to the increased resistance induced by lubrication effects, arising when particles are approaching each other, and their relative velocity goes to zero. The effect of lubrication forces is typically to slow down the dynamics by roughly a factor of two.64 In the subsequent stages, the process is dominated by particle–cluster and cluster–cluster interactions, and the long-range hydrodynamics term becomes predominant, resulting in a rapid increase of the aggregation rate and radius of gyration after a given time, as shown in Fig. 10 and Fig. S3 (ESI†), respectively. Conversely, model approaches based on short-range lubrication and simple BD fail to describe the hydrodynamic interactions between the particles forming the large settling clusters, which are responsible for the sedimentation rate of a cluster made of np particles scaling as  , and lead to the consequence that all particles and clusters are dragged vertically by sedimentation at the same rate with a substantial underestimation of the aggregation rate. This makes the effect of the Péclet number on the aggregation kinetics null because the collision mechanism depends only on the difference in sedimentation velocity of the involved clusters. Thus, neglecting the long-range contributions to HI produces an underestimation of the aggregation dynamics and can only provide a partial picture of the phenomenon. This was found to be valid only for particle volume fractions Φ < 0.2. In fact, for more dense suspensions (Φ = 0.2), lubrication effects can significantly slow down the aggregation rate with a dramatic impact on the resulting kinetics. This suggests that, under such conditions, long-range HI are screened, and the resulting aggregation dynamics is prevalently controlled by the short-range lubrication forces, thus making the FLD algorithm more accurate in describing the phenomenon. This observation is also supported by the fact that RPY and BD methods are nearly equivalent, showing the same trend and just differing by a numerical factor, which is evident in Fig. 10 at Φ = 0.2. Furthermore, the strong friction forces introduced by lubrication interactions are capable of slowing down the relative motion of nearly touching particles and providing them with strong forces to counteract Brownian motion. This allows to evaluate the effect of tangential contact forces on the cluster structure via the modeling approach previously reported. The results of the simulations including lubrication and tangential forces are shown in Fig. S4 and S5 (ESI†).
, and lead to the consequence that all particles and clusters are dragged vertically by sedimentation at the same rate with a substantial underestimation of the aggregation rate. This makes the effect of the Péclet number on the aggregation kinetics null because the collision mechanism depends only on the difference in sedimentation velocity of the involved clusters. Thus, neglecting the long-range contributions to HI produces an underestimation of the aggregation dynamics and can only provide a partial picture of the phenomenon. This was found to be valid only for particle volume fractions Φ < 0.2. In fact, for more dense suspensions (Φ = 0.2), lubrication effects can significantly slow down the aggregation rate with a dramatic impact on the resulting kinetics. This suggests that, under such conditions, long-range HI are screened, and the resulting aggregation dynamics is prevalently controlled by the short-range lubrication forces, thus making the FLD algorithm more accurate in describing the phenomenon. This observation is also supported by the fact that RPY and BD methods are nearly equivalent, showing the same trend and just differing by a numerical factor, which is evident in Fig. 10 at Φ = 0.2. Furthermore, the strong friction forces introduced by lubrication interactions are capable of slowing down the relative motion of nearly touching particles and providing them with strong forces to counteract Brownian motion. This allows to evaluate the effect of tangential contact forces on the cluster structure via the modeling approach previously reported. The results of the simulations including lubrication and tangential forces are shown in Fig. S4 and S5 (ESI†).
More specifically, it can be seen that the inclusion of tangential inter-particle interactions has a strong impact on the resulting cluster morphology (Fig. S4, ESI†), leading to the formation of highly branched clusters that have a more open structure (Fig. S5a and b, ESI†) and lower values of the mean coordination number (Fig. S5c, ESI†), if compared to the case where these forces were neglected, and more compact aggregates are formed. In the presence of tangential forces, the cluster show highly ramified branches and a very porous structure, where the relative positions of particles and bond orientations remain unaltered over time due to the strong friction forces acting at the contact surface that prevent rearrangement of particles into denser structures, resulting in fractal dimension values between 1.6 and 1.8, as shown in Fig. S5a and b (ESI†). These clusters are generally referred to as “isostatic”, characterized by a coordination number of about 2, which scales with the number of constituent particles np as 2(np − 1)/np. As particles aggregate to form rigid bonds, the randomness of each collision event driven by thermal motion leads to the formation of a wide variety of different conformations and morphologies (Fig. S4a, ESI†), in contrast to what is observed in the absence of tangential contact forces, where the structures are more compact and show a very similar initial shape, as evident from Fig. S4b (ESI†). In the absence of tangential forces, particles interacting only via normal contact forces can slide and roll at contact due to Brownian motion, causing densification of the aggregates during their growth and leading to the formation of highly connected structures with average coordination number close to 6 (Fig. S4b and S5c, ESI†).
In this case, the aggregation mechanism follows a different path, similar to that already presented for the clusters produced in Fig. 3a and Fig. S1 (ESI†) using the PSE algorithm: in the early stages of the aggregation process, particles aggregate to form dense and compact clusters with spheroidal shape. In the subsequent stages, these clusters slowly move, and self-assemble, forming more open structures characterized by high coordination number and a fractal dimension comparable to that observed when tangential forces are included (Fig. S5b (ESI†) for Φ = 0.05). In the dilute limit, (Φ = 0.01) we expect to observe the same process at very long timescales (as suggested by Fig. 5a where the curve describing the temporal evolution of the fractal dimension computed without tangential forces start to decrease), however the FLD algorithm is not as efficient as the PSE algorithm in accounting for the increased mobility of large clusters, resulting in very slow aggregation rates. In fact, as stated above, in the presence of long-range HI, the self-assembly process of particles and clusters is dramatically enhanced, resulting in fractal structures larger than those formed including only lubrication forces, as evident from a comparison between clusters presented in Figure S4b and Figure S1; here a wide range of shapes and conformations can be observed, quite similar to what has already been noticed for the clusters formed in the presence of lubrication interactions and tangential forces with a history effect shown in Fig. S4a (ESI†). At sufficiently high particle concentrations and specific Péclet numbers, these aggregates grow into a system spanning network that fills the whole space. Our findings also reveal that instantaneous tangential forces employed along with the PSE algorithm are able to provide a certain degree of bending resistance to the cluster structure only when particles are closely packed together, while fail to counteract Brownian motion and restructuring effects. This can be prevented by introducing lubrication forces along with long-range multibody interactions and will be the object of future work.
In view of this, lubrication forces, in conjunction with tangential contact interactions, can safely be neglected to study the kinetics of aggregation and the evolution of the cluster structure and morphology (even in the dilute limit), as their main effect is to contribute to the formation of isostatic clusters characterized by low values of the coordination number close to 2, but that possess a fractal dimension very similar to that of the clusters produced when these interactions are neglected. Moreover, the inclusion of long-range HI has been proven to be an essential factor to fully capture the multi-body interactions among large aggregates and the resulting self-assembly process.
Concluding remarks
In this paper, we performed large-scale BD-HI simulations with the PSE algorithm to study the effect of short-range attractive forces and hydrodynamic interactions on the aggregation process of sedimenting clusters. Simulations were conducted under various concentrations and flow conditions, to provide an exhaustive quantitative description of the sedimentation-induced aggregation phenomenon and the structure of the resulting clusters.In general, the aggregation rate increases with increasing both particle volume fraction and Péclet number. However, depending on the specific conditions, different behaviors have been observed. Simulations predict that at lower concentrations, the settling of larger aggregates at moderate and high Péclet numbers induces high convective motions in the fluid, which have a strong impact on the collision rate, the aggregation dynamics, and the resulting cluster morphology. Results indicate that as the Péclet number increases, denser clusters are generally formed with a substantial increase in the value of the fractal dimension df and a decrease of the relative shape anisotropy parameter k2. Depending on the flow intensity, the resulting clusters span a wide range of fractal dimension values generally encountered in applications (1.8 < df < 2.5).
Moreover, for concentrations low enough to prevent gelation, it has been observed that after a given time, the slope of the curve describing the dimensionless number concentration of clusters over time rapidly increases, leading to a fast increase in the radius of gyration and cluster mass, consistently with experimental observations and theoretical predictions. It has been also found that at the highest concentrations and Pe numbers, the aforementioned curve in normalized form is roughly independent of these parameters, suggesting a similar aggregation mechanism.
It was also observed that, for high concentrations and low Péclet numbers, the colloidal system evolves into what appears to be a rigid gel structure capable of supporting bending moments. However, at the highest Pe, aggregates undergo substantial restructuring until equilibrium between the breakage and sedimentation-induced aggregation of clusters has been reached. However, at the highest concentrations, particles aggregate to form a stable gel like network even at high Pe, showing a preferential net orientation along the direction of sedimentation.
As a result of our comparison of selected modeling approaches for multi-particle systems, PSE with long-range HI is revealed to be a more effective technique over FLD and BD methods, especially in accounting for the effect of an increase in the Pe number on the dynamics of aggregation and in capturing the very fast dynamics of evolution of the cluster morphology under sedimentation.
In our system, the inclusion of short-range hydrodynamic forces, except for some quantitative differences in the prediction of the aggregation kinetics of dense suspensions (Φ = 0.2), produces, in all the other cases, results similar to those obtained using BD simulations, as both of them fail to capture the sharp increase in the average cluster mass and radius of gyration after a given time observed when the long-range contribution to the hydrodynamics is included. This leads to a substantial underestimation of the aggregation rate at high Pe numbers, with the clusters passively dragged by the fluid along linear trajectories. However, lubrication is of crucial importance for assessing the effects of tangential inter-particle interactions on the clusters’ morphology and the mean coordination number.
In fact, in the presence of lubrication forces, two approaching particles experience an increased resistance to the relative motion induced by thermal fluctuations, thereby allowing to include tangential displacement along the contact surface for the whole duration of the time they are in contact, without encountering numerical instabilities. Furthermore, rolling and twisting angles are also tracked for the entire duration of the contact. The accumulated tangential displacement characterizes the contact history and is therefore referred to as the “history effect”, which is responsible for the dramatic change of the mean coordination number and fractal dimension of the formed aggregates. In absence of lubrication, for example when the PSE algorithm is employed, tangential forces are only instantaneous and unable to effectively counteract the relative motion of the particles along the contact surface, leading to internal restructuring and densification of the aggregates.
Moreover, our findings provide evidence that the gelation process is much more rapid and efficient if long-range HI are included.
The performed comparison suggests that a model which includes only long-range HI represents a valid alternative to the more computationally expensive full Stokesian Dynamics technique for understanding the behavior of colloidal systems under sedimentation.
Our simulations unravel the complex interplay existing between sedimentation and hydrodynamics, revealing unique features of the aggregation phenomenon, and providing a quantitative description of the time evolution of the structural properties of the formed clusters. We present a wide range of different scenarios where the effect of the individual parameters on the aggregation kinetics and cluster morphology can be easily and qualitatively analyzed, thus providing a useful tool to design real experiments and interpret data.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
Financial support from the University of Fribourg is kindly acknowledged.Notes and references
- J. C. Berg, An introduction to interfaces & colloids: the bridge to nanoscience, World Scientific, Singapore; Hackensack, NJ, 2010 Search PubMed.
- C. Allain, M. Cloitre and M. Wafra, Phys. Rev. Lett., 1995, 74, 1478–1481 CrossRef CAS PubMed.
- M. Lattuada, P. Sandkühler, H. Wu, J. Sefcik and M. Morbidelli, Adv. Colloid Interface Sci., 2003, 103, 33–56 CrossRef CAS PubMed.
- A. E. González, G. Odriozola and R. Leone, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 165–178 CrossRef PubMed.
- H. Wu, M. Lattuada, P. Sandkühler, J. Sefcik and M. Morbidelli, Langmuir, 2003, 19, 10710–10718 CrossRef CAS.
- Z. Varga, G. Wang and J. Swan, Soft Matter, 2015, 11, 9009–9019 RSC.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Nature, 1989, 339, 360–362 CrossRef CAS.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. Klein, R. C. Ball and P. Meakin, J. Phys.: Condens. Matter, 1990, 2, 5283 CrossRef.
- D. A. Weitz, J. S. Huang, M. Y. Lin and J. Sung, Phys. Rev. Lett., 1984, 53, 1657–1660 CrossRef CAS.
- D. A. Weitz and M. Oliveria, Phys. Rev. Lett., 1984, 52, 1433–1436 CrossRef CAS.
- C. Allain, M. Cloitre and F. Parisse, J. Colloid Interface Sci., 1996, 178, 411–416 CrossRef CAS.
- G. C. Ansell and E. Dickinson, Faraday Discuss. Chem. Soc., 1987, 83, 167–177 RSC.
- J. K. Whitmer and E. Luijten, J. Chem. Phys., 2011, 134, 034510 CrossRef PubMed.
- A. E. González, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061403 CrossRef PubMed.
- A. E. González, J. Phys.: Condens. Matter, 2002, 14, 2335–2345 CrossRef.
- A. E. González, F. Martínez-López, A. Moncho-Jordá and R. Hidalgo-Álvarez, Phys. A, 2002, 314, 235–245 CrossRef.
- M. Hütter, J. Colloid Interface Sci., 2000, 231, 337–350 CrossRef PubMed.
- M. Lattuada, J. Phys. Chem. B, 2012, 116, 120 CrossRef CAS PubMed.
- A. A. Rzepiela, J. H. J. van Opheusden and T. van Vliet, J. Colloid Interface Sci., 2001, 244, 43–50 CrossRef CAS.
- A. M. Puertas, A. Fernández-Barbero and F. J. de las Nieves, Phys. A, 2002, 304, 340–354 CrossRef CAS.
- A. M. Puertas, A. Fernández-Barbero and F. J. de las Nieves, J. Chem. Phys., 2001, 115, 5662–5668 CrossRef CAS.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- Y. M. Harshe and M. Lattuada, J. Phys. Chem. B, 2016, 120, 7244–7252 CrossRef CAS PubMed.
- G. Frungieri and M. Vanni, Can. J. Chem. Eng., 2017, 95, 1768–1780 CrossRef CAS.
- T. N. Phung, J. F. Brady and G. Bossis, J. Fluid Mech., 1996, 313, 181–207 CrossRef CAS.
- J. W. Swan, J. F. Brady, R. S. Moore and ChE 174, Phys. Fluids, 2011, 23, 071901 CrossRef.
- A. Sierou and J. F. Brady, J. Fluid Mech., 2001, 448, 115–146 CrossRef CAS.
- A. Fiore and J. Swan, J. Fluid Mech., 2019, 878, 544–597 CrossRef.
- M. D. Bybee, PhD Thesis, University of Illinois at Urbana-Champaign, 2009.
- A. Kumar, Microscale dynamics in suspensions of non-spherical particles, University of Illinois at Urbana-Champaign, 2010 Search PubMed.
- A. Kumar and J. J. Higdon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051401 CrossRef PubMed.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- A. M. Fiore, F. B. Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 2017, 146, 124116 CrossRef PubMed.
- A. Moncho-Jordá, A. A. Louis and J. T. Padding, J. Chem. Phys., 2012, 136, 064517 CrossRef PubMed.
- Z. Varga and J. Swan, Soft Matter, 2016, 12, 7670–7681 RSC.
- A. M. Fiore, G. Wang and J. W. Swan, Phys. Rev. Fluids, 2018, 3, 063302 CrossRef.
- E. Lattuada, S. Buzzaccaro and R. Piazza, Phys. Rev. Lett., 2016, 116, 038301 CrossRef PubMed.
- A. E. González, Phys. Rev. Lett., 2001, 86, 1243–1246 CrossRef PubMed.
- R. Leone, G. Odriozola, L. Mussio, A. Schmitt and R. Hidalgo-Álvarez, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 7, 153–161 CAS.
- W. B. Russel, W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal dispersions, Cambridge university press, 1991 Search PubMed.
- J. Vermant and M. J. Solomon, J. Phys.: Condens. Matter, 2005, 17, R187 CrossRef CAS.
- J. F. Brady, Chem. Eng. Sci., 2001, 56, 2921–2926 CrossRef CAS.
- D. Chen and M. Doi, J. Colloid Interface Sci., 1999, 212, 286–292 CrossRef CAS PubMed.
- A. Zaccone, D. Gentili, H. Wu and M. Morbidelli, J. Chem. Phys., 2010, 132, 134903 CrossRef PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- A. J. Banchio and J. F. Brady, J. Chem. Phys., 2003, 118, 10323–10332 CrossRef CAS.
- P. S. Grassia, E. J. Hinch and L. C. Nitsche, J. Fluid Mech., 1995, 282, 373–403 CrossRef CAS.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- K. L. Johnson, K. Kendall, A. D. Roberts and D. Tabor, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2015 Search PubMed.
- J. S. Marshall, J. Comput. Phys., 2009, 228, 1541–1561 CrossRef.
- A. Chokshi, A. G. G. M. Tielens and D. Hollenbach, Astrophys. J., 1993, 407, 806 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- P. A. Cundall and O. D. L. Strack, Géotechnique, 1979, 29, 47–65 CrossRef.
- J. P. Pantina and E. M. Furst, Phys. Rev. Lett., 2005, 94, 138301 CrossRef PubMed.
- Y. Tsuji, T. Tanaka and T. Ishida, Powder Technol., 1992, 71, 239–250 CrossRef CAS.
- C. S. Johnson and D. A. Gabriel, Laser light scattering, Dover New York, 1994 Search PubMed.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- M. Lattuada, A. Zaccone, H. Wu and M. Morbidelli, Soft Matter, 2016, 12, 5313–5324 RSC.
- L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, V. Niculae, P. Prettenhofer, A. Gramfort and J. Grobler, J. Mach. Learn. Res., 2013, 12, 2825–2830 Search PubMed.
- J. Friedman, T. Hastie and R. Tibshirani, The elements of statistical learning, Springer series in statistics New York, 2001, vol. 1 Search PubMed.
- E. Kim, K. Stratford, P. J. Camp and M. E. Cates, J. Phys. Chem. B, 2009, 113, 3681–3693 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01637g |
| This journal is © The Royal Society of Chemistry 2022 |





