Formation and growth of lithium phosphate chemical gardens

Abstract

We show that a chemical garden can be developed from an alkaline metal precipitate using a flow-driven setup. By injecting sodium phosphate solution into lithium chloride solution from below, a liquid jet appears, on which a precipitate grows forming a structure resembling a hydrothermal vent. The precipitate column continuously builds upward until a maximum height is reached. The vertical growth then significantly slows down while the tube diameter still increases. The analysis of the growth profiles has revealed a linear dependence of volume growth rate on the injection rate, hence yielding a universal growth profile. The expansion in diameter, localized at the tip of the structure, scales with a power law suggesting that the phenomenon is controlled by both diffusion and convection.

---

1 Introduction

Chemical gardens, the inanimate plant-like formations discovered by Johann Glauber in 1646, result upon placing transition metal salt crystals in water glass.¹ Researchers over the ages have been fascinated with these chemical structures, and numerous studies have been conducted in order to seek an explanation for their evolution (for a review see Barge et al.²) and to explain their possible connection to the origin of life here on Earth.^3–5 One of these attempts has been made by mimicking the conditions of a soda-type ocean found on Enceladus (Saturn's moon) in the laboratory.⁶ This chemical garden phenomenon has been discovered to occur in nature as hydrothermal vents or chimneys^7–10 and rusts on metals.^11,12 Scientists are now focusing on the formation mechanism,¹³ growth behavior,¹⁴ periodic membrane rupture,¹⁵ surface instabilities¹⁶ or even pattern formation^17,18 and its dynamics in thin solution layer.^19,20

The fascination with chemical gardens has not stopped within the Earth's ground gravity. Buoyancy-aided growth coupled with osmosis occurs for the chemical garden grown under the influence of Earth's gravitational field, leading to the formation of upward growing structures.² In microgravity, on the other hand, the presence of buoyancy is eliminated resulting in the development of randomly oriented chemical garden structures through the action of forced convection and osmosis instead.^21,22

As part of its applications, chemical garden tubes have considerable electrochemical potential differences across them and could be harnessed for electric current generation.^23,24 A sufficient amount of energy can be obtained when an alkaline solution of sodium sulfide, sodium hydroxide and methanol was injected into an acidic solution of iron (II) and (III) chloride and sodium nitrate, and linking several cells in series. The electric current generated from this setup is sufficient to light an LED.²⁵ Chemical garden structures can also serve as a flow-through reactor.²⁶ By forging a chemical garden structure from a catalytic material, it could offer a surface for the reactants to adsorb and be transformed in the process. This method might not be easy to handle due to the lack of rigidity of the tubes retrieved, but its application could open a vast universe into the study of catalysis.²⁷ In this chemobrionic approach, the growing chemical structures also provide an opportunity for the fabrication of functional materials²⁸ such as gradient composites^29,30 or quantum dots,³¹ to name a few.

The preparation of a macroscopic self-assembled chemical structure stems from the appearance of a reasonable chemical gradient, which continuously induces precipitation, its dissolution, osmosis, diffusion and other transport processes. One method to achieve the growth of a chemical garden is the solid-in-liquid method consisting of a pellet or solid salt seeds from one of the ions placed in the solution of the other ion.^6,32 The other method involves a liquid-in-liquid system, where a solution of one of the ions is injected into the solution of the other ion, leading to the formation of a concentration gradient generated by flow, and the evolution of a chemical structure.^16,33–35 The advantage of the latter is the possibility of precise characterization of the structural development. Recently, an extension of this technique has utilized an interface of a liquid in contact with a gel containing one of the reactants, which can lead to thin precipitate tubes.^36,37

In our study, we will demonstrate that chemical gardens can evolve from an alkaline metal precipitate and will characterize their growth.

2 Experimental

We prepared a solution of 6 mol dm⁻³ LiCl and poured 6 mL into a cuvette of 1 cm × 1 cm × 10 cm dimension. Using a syringe pump (KD Scientific), 0.6 mol dm⁻³ Na₃PO₄ solution was pumped into the LiCl solution through a 0.4 mm internal diameter needle with the injection rate set in the range of 0.01–0.05 mL min⁻¹. Several tests involved a larger square container with 3 cm width, or the reverse configuration where LiCl solution was pumped into the stagnant Na₃PO₄ solution. The changes inside the cuvette were monitored with a digital camera (see Fig. 1), saving side-view images every 5 s for a period of 750 s. Each experiment was repeated about 8–10 times. The density and the viscosity of the solutions were measured using a digital density meter (Anton Paar DMA500) with 10⁻⁴ g cm⁻³ precision and a rotational viscometer (Anton Paar ViscoQC 300) with 1.0% precision, respectively.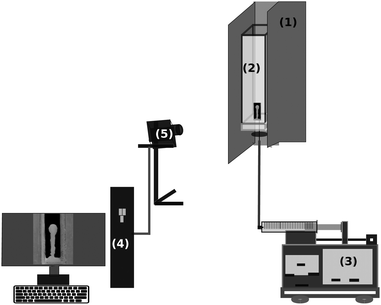

Fig. 1 Experimental setup: support jacket and dark background (1), reactor with size of 1 × 1 × 10 cm3 (2), injection pump (3), processing unit (4), digital camera (5).

The images were then analyzed using a specially designed macro³⁸ of ImageJ and other in-house programs to construct the growth profile in height and volume, and the diameter of the tube at the tip of the precipitate structure. To determine the volume of the tube, we first converted the images into binary form, and then found the centroid, i.e., the center of mass. We divided the image vertically through its center of mass and measured the radius of rotation at the height of the centroid (R_s). Because the structure can be approximated by a symmetric solid of revolution,³⁹ the volume was calculated following Pappus 2nd centroid theorem

V = 2πR_sA (1)

with A being the half cross section of the structure divided through its centroid.

For the microscopic analyses, the lithium phosphate tubes were carefully collected, washed several times with deionized water and dried at room temperature. A scanning electron microscope (Hitachi S4700) was used to visualize both the inner and the outer structure, after sputtering a double layer of gold to achieve an appropriately conductive surface.

3 Results and discussion

Upon the injection of LiCl solution into the stagnant solution of Na₃PO₄ from below, corresponding to the classical chemical garden scenario, a thin vertical jet reaching the liquid surface arises. The momentum of the injected liquid dominates the fluid motion at these flow rates because buoyant forces remain weak due to the small density difference between the two solutions (ρ_LiCl = 1.1283 g cm⁻³ and ρ_Na3PO4 = 1.1041 g cm⁻³). The small precipitate particles forming around the perimeter of the jet make it clearly visible; however, they travel with the flow and no contiguous structure is being built. Instead, close to the upper liquid surface, larger flakes of lithium phosphate appear that later sink to the bottom due to their greater density.

In the reverse configuration, when the solution of sodium phosphate is injected into the LiCl solution, the previously described processes are significantly less pronounced. Here, following the formation of the jet, the steady growth of a precipitate structure around it is observed, which creates a vertical column (see Fig. 2(a)). The architecture initially continuously builds upward until a maximum height is reached when the vertical only growth almost stops, while the diameter of the tubular structure further increases, especially in the vicinity of the tip.

Fig. 2 Image sequence of the lithium phosphate chemical garden obtained by injecting 0.6 mol dm⁻³ Na₃PO₄ solution into 6.0 mol dm⁻³ LiCl solution (a), SEM image of the outer surface of the tube (b and c), and the inner one (d and e).

The resultant precipitate tube is sufficiently rigid so that it can easily be removed from the solution, then dried and used for further analysis. The tubes consist of lithium phosphate; the carbonate concentration due to impurities in the basic solution does not reach the level required for the formation of lithium carbonate because of its greater solubility.³⁸ The microstructures of the inner and the outer surfaces of the tube are shown in Fig. 2(b–e). The outer parts of the structure comprise nanospherical crystals with rough surfaces (Fig. 2(b and c)), while the inner surface has filled spheres with hairy crystals (Fig. 2(d and e)). The observed difference in morphology is a result of the presence of concentration gradients that maintain a distinct chemical environment on the opposite sides, common characteristics of tubular precipitate assemblies in chemical gardens.^28,40

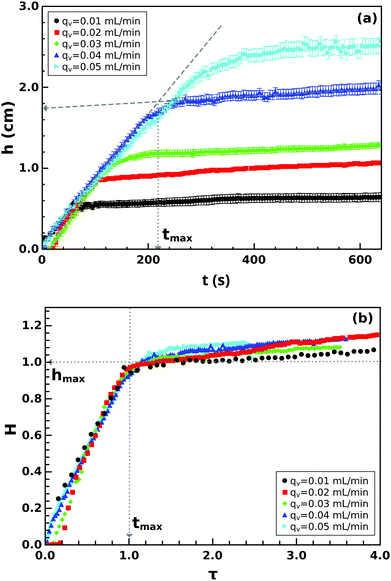
The tube dimensions can be generally characterized by the height and diameter, and from the temporal evolution of these data, the linear and volume growth rate can be determined. The tube height increases linearly as time progresses up to a certain height as illustrated in Fig. 3(a) for several flow rates. The initial steady growth is found to be independent of the injection rate. The linear growth rate, determined from the slope of the vertical growth before attaining maximum height, is u₁ = 74.0 ± 0.6 μm s⁻¹, which is significantly smaller than the fluid jet velocity that is in the range of 200–1000 μm s⁻¹. The vertical growth rate suddenly drops significantly, and hence, the maximum height h_max reached by the initial evolution at t_max is defined by the intersection of the two growth regimes.

Fig. 3 Growth profile of the precipitate structure at different flow rates (a) and dimensionless height, H as a function of dimensionless time, τ (b). The dashed lines correspond to the fitted lines while the dotted lines aid the eye.

With our selected injection rates, the height reached during the first stage is independent of the width of the container, i.e., the return bulk flow has a negligible contribution. In addition, the solution height of the originally stagnant fluid has to be sufficiently large so that the tip does not come into the vicinity of the liquid surface.

The growth rate in the second stage is also found to be independent of the injection rate with u₂ = 2.86 ± 0.33 μm s⁻¹, and therefore a universal growth profile can be constructed for all the measurements where height is scaled to the maximum height reached by the precipitate structure during the first stage. By plotting the dimensionless height, defined as H = h/h_max, as a function of the dimensionless time, τ = t/t_max, the data collapse onto a single curve (Fig. 3(b)) with

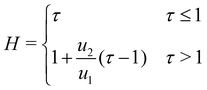for all the investigated injection rates, where u₂/u₁ is the ratio of the linear growth rates in the two regimes. Furthermore, there is a linear relationship between the injection rate q_v and both the maximum height h_max and the time required to reach that height t_max, as illustrated in Fig. 4.

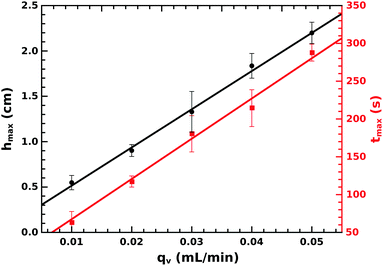Fig. 4 The maximum height h_max and the corresponding time t_max as a function of injection rate with their corresponding fitting.

There is a gradual diffusive change in lithium concentration and pH as the liquid jet advances. Because of the critical lithium concentration and pH beyond which precipitation stops, it leads to saturation in the height of the precipitate structure.^40–42 The ratio of the slopes from Fig. 4 highlights the inherent linear growth rate of 75 ± 8 μm s⁻¹ matching u₁ determined according to Fig. 3(a).

In the same vein, from the area of the half structure and R_s, we calculated the volume using eqn (1). The obtained volume increases with time in the manner depicted in Fig. 5(a). The volume growth rate depends on the injection rate but in a single experiment, it remains constant even when the growth characteristics change at t = t_max. Upon comparing it with the injection rate (see Fig. 5(b)), a linear relation is revealed with a slope of 0.55 ± 0.05. This implies that the precipitate tube does not form a closed structure, and the injected solution leaks through the porous membrane into the external solution or through any opening, mostly at the tip of the tube.

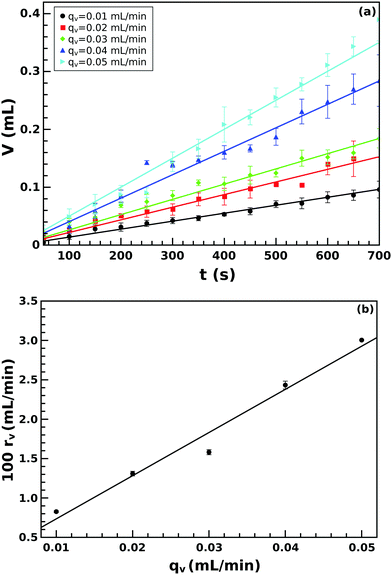Fig. 5 Temporal evolution of the precipitate volume for various injection rates (a), and volume growth rate r_v as a function of injection rate q_v (b).

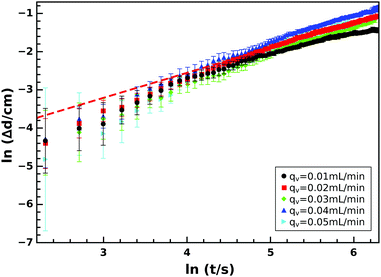
Once this growing precipitate structure reaches a maximum height, the diameter at the tip (Fig. 6) begins to increase. This expansion follows a simple power law function

Δd = (d − d₀) = k(t − t₀)ⁿ (3)

where d is the diameter at any time t, d₀ is the initial diameter at the time t₀ = t_max, k is a proportionality constant, and n is the growth order. By fitting the curves in Fig. 6 to eqn (3), we obtain n = 0.75 ± 0.01, with k = (3.12 ± 0.03) × 10⁻³ cm s⁻ⁿ. Since the exponent is greater than 0.5, convection plays a role in the structure formation besides diffusion.

Fig. 6 Temporal change in the tip diameter of the precipitate after h_max was reached.

The flow characteristics are determined from the Reynolds number defined as

where q_v is the injection rate, ν_i = 0.0322 cm² s⁻¹ is the injected solution's kinematic viscosity, and d = 0.04 cm is the inlet diameter. In our experiments, the flow is laminar with 0.08 < Re < 0.4, which can maintain the steady elongation of the tubular structure in the first growth regime driven by convective transport.

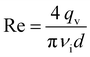4 Conclusions

In the recovery of lithium ions from spent batteries, the ions are converted into hydroxides and carbonates, and subsequently to phosphates, which can then be used for battery production. Understanding the mechanisms underlying the formation of lithium phosphate enables the simplification of recycling procedures of the lithium ions from used batteries. We have described the conversion of lithium ions into chemical gardens for the first time to the best of our knowledge, whose principle of formation could be harnessed for the conversion of used lithium ions. Furthermore, we have demonstrated the possibility of growing hollow-tubed lithium phosphate hydrothermal vent-like precipitate structures. Because of their catalytic applications, like in the isomerization of propylene oxide to allyl alcohol,⁴³ the hollow-tubed structures offer an opportunity for catalyzing reactions in flow-through reactors.

Author contributions

Conceptualization D. H., Á. T.; data curation and investigation M. E.; formal analysis M. E., E. L.; visualization M. E.; resources D. H., Á. T.; software D. H.; supervision D. H., Á. T.; validation Á. T.; funding acquisition Á. T.; writing – original draft M. E.; writing – review and editing D. H., Á. T.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office (NN125746 and K138844) and the University of Szeged Open Access Fund (5648).

Notes and references

1. P. Cintas, Chasing synthetic life: A tale of forms, chemical fossils, and biomorphs, Angew. Chem., Int. Ed., 2020, 59, 7296–7304.
2. L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein and F. Haudin, et al., From chemical gardens to chemobrionics, Chem. Rev., 2015, 115, 8652–8703.
3. M. J. Russell and A. J. Hall, The emergence of life from iron monosulphide bubbles at a submarine hydrothermal redox and pH front, J. Geol. Soc., 1997, 154, 377–402.
4. W. Martin, J. Baross, D. Kelley and M. J. Russell, Hydrothermal vents and the origin of life, Nat. Rev. Microbiol., 2008, 6, 805–814.
5. J. H. E. Cartwright and M. J. Russell, The origin of life: the submarine alkaline vent theory at 30, Interface Focus, 2019, 9, 20190104.
6. S. S. S. Cardoso, J. H. E. Cartwright and C. I. Sainz-Daz, Carbonate-hydroxide chemical-garden tubes in the soda ocean of Enceladus: Abiotic membranes and microtubular forms of calcium carbonate, Icarus, 2019, 319, 337–348.
7. G. L. Früh-Green, D. S. Kelley, S. M. Bernasconi, J. A. Karson, K. A. Ludwig, D. A. Butterfield, C. Boschi and G. Proskurowski, 30,000 years of hydrothermal activity at the Lost City vent field, Science, 2003, 301, 495–498.
8. M. Russell, First life: Billions of years ago, deep under the ocean, the pores and pockets inminerals that surrounded warm, alkaline springs catalyzed the beginning of life, Am. Sci., 2006, 94, 32–39.
9. R. E. Mielke, K. J. Robinson, L. M. White, S. E. McGlynn, K. McEachern, R. Bhartia, I. Kanik and M. J. Russell, Iron-sulfide-bearing chimneys as potential catalytic energy traps at life's emergence, Astrobiology, 2011, 11, 933–950.
10. L. M. Barge, J.-P. Jones, J. J. Pagano, E. Martinez and J. Bescup, Three-dimensional analysis of a simulated prebiotic hydrothermal chimney, ACS Earth Space Chem., 2020, 4, 1663–1669.
11. B. C. Batista and O. Steinbock, Chemical gardens without silica: The formation of pure metal hydroxide tubes, Chem. Commun., 2015, 51, 12962–12965.
12. F. Brau, F. Haudin, S. Thouvenel-Romans, A. De Wit, O. Steinbock, S. S. S. Cardoso and J. H. E. Cartwright, Filament dynamics in confined chemical gardens and in filiform corrosion, Phys. Chem. Chem. Phys., 2018, 20, 784–793.
13. O. Steinbock, J. H. E. Cartwright and L. M. Barge, The fertile physics of chemical gardens, Phys. Today, 2016, 69, 44–51.
14. D. Spanoudaki, F. Brau and A. De Wit, Oscillatory budding dynamics of a chemical garden within a co-flow of reactants, Phys. Chem. Chem. Phys., 2021, 23, 1684–1693.
15. Y. Ding, C. M. Gutiérrez-Ariza, I. C. Sainz-Daz, J. H. E. Cartwright and S. S. S. Cardoso, Exploding chemical gardens: A phase-change clock reaction, Angew. Chem., Int. Ed., 2019, 58, 6207–6213.
16. P. Kumar, C. Hajdu, Á. Tóth and D. Horváth, Flow-driven surface instabilities of tubular chitosan hydrogel, ChemPhysChem, 2021, 22, 488–492.
17. F. Haudin, J. H. E. Cartwright, F. Brau and A. De, Wit, Spiral precipitation patterns in confined chemical gardens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17363–17367.
18. E. Balog, P. Papp, Á. Tóth, D. Horváth and G. Schuszter, The impact of reaction rate on the formation of flow-driven confined precipitate patterns, Phys. Chem. Chem. Phys., 2020, 22, 13390–13397.
19. F. Haudin, V. Brasiliense, J. H. E. Cartwright, F. Brau and A. De Wit, Genericity of confined chemical garden patterns with regard to changes in the reactants, Phys. Chem. Chem. Phys., 2015, 17, 12804–12811.
20. L. A. M. Rocha, J. H. E. Cartwright and S. S. S. Cardoso, Filament dynamics in planar chemical gardens, Phys. Chem. Chem. Phys., 2021, 23, 5222–5235.
21. D. E. H. Jones and U. Walter, The silicate garden reaction in microgravity: A fluid interfacial instability, J. Colloid Interface Sci., 1998, 203, 286–293.
22. J. H. E. Cartwright, B. Escribano, C. I. Sainz-Daz and L. S. Stodieck, Chemical-garden formation, morphology, and composition. II. Chemical gardens in microgravity, Langmuir, 2011, 27, 3294–3300.
23. F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. Garca-Ruiz, Formation and evolution of chemical gradients and potential differences across self-assembling inorganic membranes, Angew. Chem., Int. Ed., 2012, 51, 4317–4321.
24. F. Glaab, J. Rieder, J. M. Garca-Ruiz, W. Kunz and M. Kellermeier, Diffusion and precipitation processes in iron-based silica gardens, Phys. Chem. Chem. Phys., 2016, 18, 24850–24858.
25. L. M. Barge, Y. Abedian, M. J. Russell, I. J. Doloboff, J. H. E. Cartwright, R. D. Kidd and I. Kanik, From chemical gardens to fuel cells: Generation of electrical potential and current across self-assembling iron mineral membranes, Angew. Chem., Int. Ed., 2015, 54, 8184–8187.
26. S. E. McGlynn, I. Kanik and M. J. Russell, Peptide and RNA contributions to iron-sulphur chemical gardens as life's first inorganic compartments, catalysts, capacitors and condensers, Philos. Trans. R. Soc., A, 2012, 370, 3007–3022.
27. S. S. S. Cardoso, J. H. E. Cartwright, J. Cejková, L. Cronin, A. De Wit, S. Giannerini, D. Horváth, A. Rodrigues, M. J. Russel, C. I. Sainz-Daz and Á. Tóth, Chemobrionics: From self-assembled material architectures to the origin of life, Artif. Life, 2020, 26, 315–326.
28. Q. Wang and O. Steinbock, Materials synthesis and catalysis in microfluidic devices: Prebiotic chemistry in mineral membranes, ChemCatChem, 2020, 12, e1901495.
29. W. Zhao and K. Sakurai, Realtime observation of diffusing elements in a chemical garden, ACS Omega, 2017, 2, 4363–4369.
30. E. A. B. Hughes, T. E. Robinson, R. J. A. Moakes, M. Chipara and L. M. Grover, Controlled self-assembly of chemical gardens enables fabrication of heterogeneous chemobrionic materials, Commun. Chem., 2021, 4, 145.
31. R. Makki, X. Ji, H. Mattoussi and O. Steinbock, Self-organized tubular structures as platforms for quantum dots, J. Am. Chem. Soc., 2014, 136, 6463–6469.
32. J. H. E. Cartwright, B. Escribano and C. I. Sainz-Daz, Chemical-garden formation, morphology, and composition. I. Effect of the nature of the cations, Langmuir, 2011, 27, 3286–3293.
33. S. Thouvenel-Romans and O. Steinbock, Oscillatory growth of silica tubes in chemical gardens, J. Am. Chem. Soc., 2003, 125, 4338–4341.
34. B. Bohner, G. Schuszter, O. Berkesi, D. Horváth and Á. Tóth, Self-organization of calcium oxalate by flow-driven precipitation, Chem. Commun., 2014, 50, 4289–4291.
35. F. Haudin, J. H. E. Cartwright and A. De Wit, Direct and reverse chemical garden patterns grown upon injection in confined geometries, J. Phys. Chem. C, 2015, 119, 15067–15076.
36. E. A. B. Hughes, M. Chipara, T. J. Hall, R. L. Williams and L. M. Grover, Chemobrionic structures in tissue engineering: self-assembling calcium phosphate tubes as cellular scaffolds, Biomater. Sci., 2020, 8, 812–822.
37. A. Fogde, S. Qudsia, T.-A. Le, T. Sandberg and T.-P. Huynh, (Calcium-phosphate)/carrageenan gardens grown from the gel/liquid interface, ChemSystemsChem, 2021, 3, e2000064.
38. M. Emmanuel, D. Horváth and Á. Tóth, Flow-driven crystal growth of lithium phosphate in microchannels, CrystEngComm, 2020, 22, 4887–4893.
39. S. Thouvenel-Romans and O. Steinbock, Silica tubes in chemical gardens: Radius selection and its hydrodynamic origin, Europhys. Lett., 2004, 67, 42–48.
40. E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Osmotic contribution to the flow-driven tube formation of copper-phosphate and copper-silicate chemical gardens, Phys. Chem. Chem. Phys., 2018, 20, 5766–5770.
41. D. A. Stone, B. Lewellyn, J. C. Baygents and R. E. Goldstein, Precipitative growth templated by a fluid jet, Langmuir, 2005, 21, 10916–10919.
42. V. Kaminker, J. Maselko and J. Pantaleone, The dynamics of open precipitation tubes, J. Chem. Phys., 2014, 140, 244901.
43. W. Ma, W. Si, W. Wu and Q. Zhong, Structures and catalytic properties of lithium phosphates, Catal. Lett., 2011, 141, 1032–1036.

---