Elastocapillary interaction between a long rectangular membrane and a liquid drop
R. A.
Samy
 ,
N. S.
Satpathi
and
A. K.
Sen
,
N. S.
Satpathi
and
A. K.
Sen
 *
*
Fluid Systems Lab, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai, India. E-mail: ashis@iitm.ac.in
First published on 23rd November 2021
Abstract
We report elastocapillary interaction between a long rectangular membrane fixed along its central axis and a liquid drop dispensed at one of its ends. The introduction of the drop results in the elastocapillary-driven wrapping of the membrane along its width and a concomitant flow in the resulting conduit along its length. Depending upon the drop size (d) and capillary length scale (Lc), we identified general criteria for achieving complete wrapping of the membrane in the dry state from energy considerations. For small droplets satisfying d ≲ Lc, we find that the critical membrane length (Wc) required for complete wrapping is proportional to the elastocapillary length scale (Lec). In the case of large droplets with d > Lc, the wrapping behavior depends on the ratio of membrane width to elastocapillary length scale (W/Lec) and the ratio of capillary length scale to the elastocapillary length scale (Lc/Lec). Our study suggests that the critical membrane width for complete wrapping is smaller in the wet state compared to that in the dry state, which can be attributed to the existence of a transmembrane pressure in the wet state. The effect of membrane thickness and width and drop volume on the length and cross-section of the wrapped conduit and attached width of the wrapped membrane is studied. For small droplets, the resulting elastocapillary flow exhibits an inertial regime at small times, followed by a Washburn regime at intermediate times, and finally an inertial regime, and for large droplets, only an inertial regime is observed throughout.
Introduction
Surface tension-induced phenomena are widely observed in nature. Such phenomena are responsible for the spherical shape of droplets,1 liquid rise or flow through capillaries,2 prey transport in sea birds,3 walking of strider insects on water,4 nectar transport in hummingbirds,5 the collapse of lung airways,6 and so on. Surface tension force plays a significant role relative to bulk forces when the length scales associated with the systems are small. This is attributed to the linear scaling of surface forces with length scale in comparison to the bulk forces that scale as the cubic power of length. Consequently, surface tension can drive liquids in narrow confinements such as capillaries, and microchannels,7 and open surfaces.8Recent advancements in microfabrication technology involving soft materials have motivated fundamental studies of the coupling between surface tension and elasticity that has led to a topic called “elastocapillarity”. In this context, surface tension has been exploited to achieve the reconfiguration of microstructures in microelectromechanical systems.9 The reconfiguration is mainly achieved by self-assembly in which the parts are deformed and assembled into three-dimensional structures with the aid of surface tension force. The elastocapillary interaction of interfacial forces with soft substrates has been studied extensively.10–12 For substrates that are either soft or thin, the capillary force can overcome the elastic force to bring out interesting phenomena. Such events can be observed in the form of ridge formation at the contact line of droplets on soft substrates,13–15 capillary flow in flexible microchannels,16–19 coalescence of bristles of a brush when removed from a liquid bath,20 self-assembly of an array of slender structures21 and capillary origami.22–24
In a seminal work, the concept of capillary origami was used to demonstrate the wrapping of a liquid droplet by a thin polymer membrane into three-dimensional self-assembled structures.22 This work has motivated several subsequent studies involving the variation of capillary origami by imparting the system with an external electric field24 and magnetic field,25 non-zero droplet impact velocity,26 and different membrane materials including superhydrophobic surfaces27 and thin atomic membranes.28 It is evident that most of the above studies aimed at studying the origami effects of elastocapillarity. Nevertheless, elastocapillarity with a long membrane can also be used for transporting liquid in the concomitant flow conduit formed. Directional liquid transport with a polymeric membrane comprising a Janus bilayer material was demonstrated by using the concept of capillary origami.29 The membrane is observed to sway to either side after the introduction of a liquid droplet and the stability of the flow configuration is not ensured. Stable elastocapillary flow is achieved by bonding a long rectangular membrane to the edge of a rigid substrate forming a soft wedge and a planar substrate along its central axis.30,31 Despite the above developments in elastocapillarity, it is evident that a fundamental understanding of the interaction between a droplet and a long rectangular membrane is not available. The interplay between surface tension and elastic energies can give rise to the wrapping of the liquid by the membrane resulting in the formation of a close conduit and consequently an elastocapillary flow, which needs to be investigated. A thorough understanding of such a system could help in the fabrication of self-folded closed conduit structures30 from membranes and the design of a lab on a membrane31 device for biochemical assays.
Here, we study the elastocapillary interaction between a long rectangular membrane fixed along its central axis and a liquid drop dispensed at one of its ends. The wrapping behavior of the membrane is studied for two different limits of drop size (d) compared to the capillary length scale (Lc): for small droplets satisfying d ≲ Lc, and large droplets with d > Lc. The contrasting wrapping behavior just after the introduction of the liquid, i.e. wet state, and after complete evaporation of the liquid, i.e. dry state, are studied. The effect of membrane thickness and width and drop volume on the length and cross-section of the wrapped conduit and attached width of the wrapped membrane is investigated. The meniscus dynamics for small and large droplets are studied in terms of the meniscus position with time.
Experimental
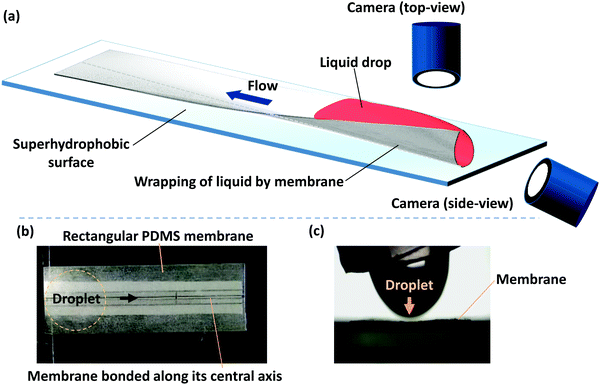
Our experiments are performed with polydimethylsiloxane (PDMS) membranes of varying thickness and width and a fixed length. PDMS monomer and curing agent (Dow Corning, Sylgard 184) were mixed at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and degassed in a desiccator. The mixture was spin-coated onto an acrylic sheet at rotation rates of 700 to 1500 rpm. After the PDMS layer was cured, it resulted in thin membranes with a thickness (h) in the range of 90 to 35 μm. Membrane thickness was measured by observing the cross-section of a membrane with the help of a microscope (Olympus IX73) and a high-resolution camera (FASTCAM SA3 model, Photron USA, Inc.), and taking averages of measurements at three different points. PDMS is normally hydrophobic and hence for a droplet dispensed on a PDMS membrane, the capillary force will be negligible. In order to facilitate the wrapping of the liquid droplet by the membrane and the consequent capillary flow, hydrophilic PDMS membranes are used. PDMS membranes of a fixed length (L) of 50 mm and width (W) in the range of 2 to 10 mm were exposed to oxygen plasma (Harrick Plasma, USA) to render hydrophilic surfaces. The contact angle of the hydrophilic PDMS surfaces with DI water was measured using a Goniometer (DSA25, KRÜSS GmbH) and was found to be 20° ± 1°, up to 1 h after plasma exposure. All the experiments were conducted within 1 h of the plasma exposure so that the effect of contact angle recovery on the membrane dynamics is negligible. A schematic of the experimental setup and photograph of the membrane and a liquid drop getting dispensed from a micropipette tip is shown in Fig. 1. One of our objectives is to study the elastocapillary flow along the membrane length that emerges from the wrapping of a liquid droplet by a PDMS membrane. Therefore, the membrane is fixed along its central line to avoid folding of the membrane along the length, toppling of the membrane during elastocapillary folding, and provide a predefined path for the elastocapillary flow. During a typical experiment, membranes of desired width and length were cut out and placed on a superhydrophobic surface with the bottom surface of the membrane glued with the superhydrophobic surface longitudinally along its central axis, indicated by a dotted line in Fig. 1, over a width of <1 mm. A drop of dyed DI water of volume 30 to 110 μl is deposited on the PDMS membrane at one of its ends. DI water is mixed with red color dye to improve visualization. However, the concentration of the dye is kept small so the contact angle and surface tension of dyed DI water are the same as that of pure DI water. The elastocapillary wrapping of the membrane along its width and length and the concomitant capillary flow are captured using two USB cameras (Dinolite Edge Digital Microscope). The water is then allowed to evaporate completely and the time-lapse images of the membrane profile are captured.
1 ratio and degassed in a desiccator. The mixture was spin-coated onto an acrylic sheet at rotation rates of 700 to 1500 rpm. After the PDMS layer was cured, it resulted in thin membranes with a thickness (h) in the range of 90 to 35 μm. Membrane thickness was measured by observing the cross-section of a membrane with the help of a microscope (Olympus IX73) and a high-resolution camera (FASTCAM SA3 model, Photron USA, Inc.), and taking averages of measurements at three different points. PDMS is normally hydrophobic and hence for a droplet dispensed on a PDMS membrane, the capillary force will be negligible. In order to facilitate the wrapping of the liquid droplet by the membrane and the consequent capillary flow, hydrophilic PDMS membranes are used. PDMS membranes of a fixed length (L) of 50 mm and width (W) in the range of 2 to 10 mm were exposed to oxygen plasma (Harrick Plasma, USA) to render hydrophilic surfaces. The contact angle of the hydrophilic PDMS surfaces with DI water was measured using a Goniometer (DSA25, KRÜSS GmbH) and was found to be 20° ± 1°, up to 1 h after plasma exposure. All the experiments were conducted within 1 h of the plasma exposure so that the effect of contact angle recovery on the membrane dynamics is negligible. A schematic of the experimental setup and photograph of the membrane and a liquid drop getting dispensed from a micropipette tip is shown in Fig. 1. One of our objectives is to study the elastocapillary flow along the membrane length that emerges from the wrapping of a liquid droplet by a PDMS membrane. Therefore, the membrane is fixed along its central line to avoid folding of the membrane along the length, toppling of the membrane during elastocapillary folding, and provide a predefined path for the elastocapillary flow. During a typical experiment, membranes of desired width and length were cut out and placed on a superhydrophobic surface with the bottom surface of the membrane glued with the superhydrophobic surface longitudinally along its central axis, indicated by a dotted line in Fig. 1, over a width of <1 mm. A drop of dyed DI water of volume 30 to 110 μl is deposited on the PDMS membrane at one of its ends. DI water is mixed with red color dye to improve visualization. However, the concentration of the dye is kept small so the contact angle and surface tension of dyed DI water are the same as that of pure DI water. The elastocapillary wrapping of the membrane along its width and length and the concomitant capillary flow are captured using two USB cameras (Dinolite Edge Digital Microscope). The water is then allowed to evaporate completely and the time-lapse images of the membrane profile are captured.
Results and discussion
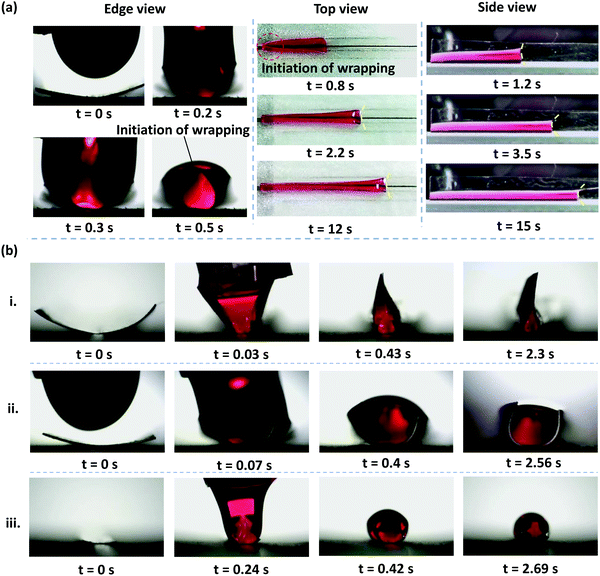
When we deposited a drop of DI water at one end of a rectangular PDMS membrane, we observed that the membrane bends along its width, wrapping the liquid. The time-lapse top and edge view images of elastocapillary phenomena when a drop of DI water of volume V = 70 μl is deposited at one of the ends of a rectangular PDMS membrane of thickness h = 70 μm, width W = 5 mm, and length L = 50 mm is shown in Fig. 2a. As observed from the top, side, and edge views, the wrapping of the membrane is initiated from the nearest edge in the length direction, offering a conduit that facilitates the advancement of the liquid meniscus along the membrane length. As the meniscus advances, the wrapping of the membrane also proceeds downstream. For a thinner and wider membrane with h = 35 μm, and width W = 8 mm, the membrane closes in the width direction for the entire length of the membrane and the edges come closer to each other forming a straight contact region and a liquid cross-section akin to a rose flower bud, as shown in Fig. 2b(i). Depending on the membrane width and thickness, the membrane may partially or completely wrap the liquid forming a fully or partially closed conduit, as shown in Fig. 2b. We observe that while membranes of larger width and smaller thickness can completely wrap the liquid for the entire membrane length, those of smaller width and higher thickness will only partially wrap the liquid or completely wrap the liquid only over a short length of the membrane, as shown in Fig. 2. For example, in the case of a membrane of h = 70 μm, and width W = 5 mm completely wrapping the liquid is observed only over a part of the membrane length (see Fig. 2a), whereas in the case of a membrane of h = 90 μm, and width W = 8 mm, and membrane of h = 35 μm, and width W = 2 mm, only partial wrapping of the liquid is observed.Please note the initial curvature of the membrane before the droplet is dispensed is because the membrane is glued to the substrate along the central axis, as indicated by the dotted line in Fig. 1a. Once the glue gets cured due to the compressive stress developed in the glue it pulls the membrane downward and as a result, the membrane lifts from both sides giving rise to the initial curvature.
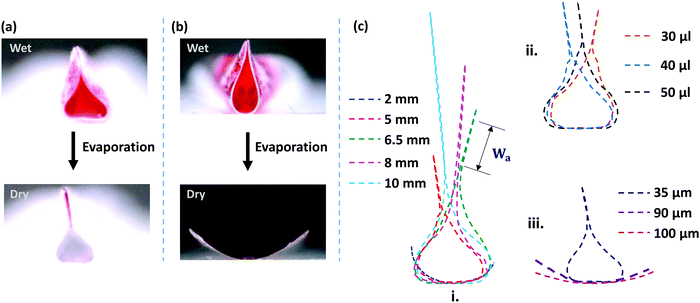
However, as the initial curvature is very large compared to the curvature of a completely wrapped membrane, it will have an insignificant impact on the wrapping dynamics, which is mainly driven by the interplay of the different energies, i.e., bending, potential and capillary energies, as discussed later. The wrapped liquid is then allowed to evaporate completely giving rise to a final configuration of the membrane in its dry state, which is presented in Fig. 3. The images of the final wrapped configuration of a membrane of thickness 35 μm and width 5 mm are shown Fig. 3a and the open configuration of a membrane of thickness 90 μm and width 5 mm is shown in Fig. 3b. The final configurations of the membranes of different thicknesses and widths and different liquid volumes are presented in Fig. 3c. By comparing the experimental images of the membrane profiles in the wet state in Fig. 3a and b, for membranes of thickness 35 μm and 90 μm, respectively, we find that the membrane of smaller thickness has a larger base area compared to the thicker membrane that has a negligible base area. Furthermore, from the profiles shown in Fig. 3c-ii, we see that the base area is larger for higher droplet volumes which suggests that the flat base area at the bottom of the membrane is influenced by the weight of the liquid and membrane thickness. We see that the membranes of smaller thickness and larger width result in completely wrapped structures whereas membranes of larger thickness and smaller width yield open structures. Please note that here the liquid volumes are small as droplets of large volumes will exhibit a markedly different wrapping behavior due to the contribution of gravitational energy in addition to the capillary and bending energies. We now proceed to analyze the final configuration of the wrapped membranes in the dry state after complete drying of the liquid, depending on the relative magnitudes of the droplet size (d) compared to the capillary length scale of the liquid 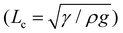 .
.
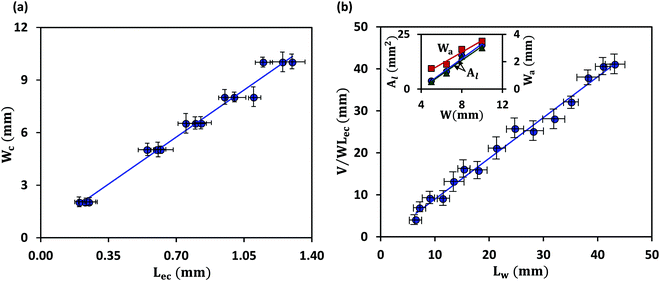
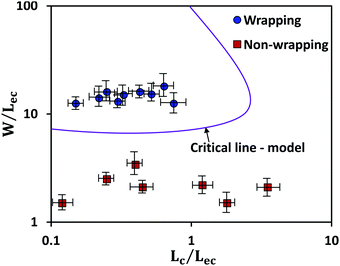
We first discuss the limit when the d ≲ Lc, when the effect of gravitational energy can be neglected, and in that case, the balance between the surface energy and elastic energy becomes important. Upon introduction of the liquid droplet, the membrane deforms to reduce the surface energy at the expense of elastic energy. For a membrane of width W and liquid of surface tension γ, the surface energy scales as S ∼ γW2 and the bending energy of a membrane of thickness h, Young's modulus E and Poisson's ratio ν, is given by, D = Eh3/12(1 − ν2). By comparing the surface energy and bending energy, one can obtain an elastocapillary length scale,23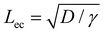 . From our experiments with different membrane thickness and droplet volumes, we found out the critical membrane width, Wc required for complete wrapping of the membrane. Interestingly, we find that even for long membranes, Wc is found to be proportional to Lec, as shown in Fig. 4a, in agreement with capillary origami studies reported in the literature,23–25 and in the present case, Wc = 7.5Lec.
. From our experiments with different membrane thickness and droplet volumes, we found out the critical membrane width, Wc required for complete wrapping of the membrane. Interestingly, we find that even for long membranes, Wc is found to be proportional to Lec, as shown in Fig. 4a, in agreement with capillary origami studies reported in the literature,23–25 and in the present case, Wc = 7.5Lec.
It is observed that the width over which the two sides of the membranes along the width direction get attached (Wa) increases with an increase in the membrane width (W), as shown in the inset of Fig. 4b. As the membrane width increases, the capillary energy requirement towards bending of the membrane is smaller, and therefore the higher remainder capillary energy can lead to the attachment of the sides of the membrane over a longer width. Also, we find that the cross-sectional area of the membrane (Al) is higher in the case of a membrane of higher width (see Fig. 3c-i). For a larger membrane width, a smaller amount of capillary energy is used for wrapping the membrane, and hence the surface area corresponding to the remaining energy is higher giving rise to a larger membrane cross-sectional area. It is also observed that in the limit of d ≲ Lc, the liquid volume has a negligible effect on the conduit cross-section (see Fig. 3c-ii).
We find that in the wet state, wrapping of the membrane can take place even at a higher thickness or smaller critical membrane width, as shown in Fig. 3a. Due to the presence of capillary force and the transmembrane pressure in the wet state, which are absent in the dry state, it is observed that even thicker or smaller width membranes can wrap the liquid in the wet state, but the membrane will open up once the liquid evaporates, as shown in Fig. 3a. We see that the meniscus curvatures across all the three planes, x–y, y–z, and x–z planes, are of a concave shape, as indicated in Fig. 2a by the yellow dotted lines, suggesting a sub-atmospheric pressure inside the liquid, and hence in the inner side of the membrane. The initial transmembrane pressure can be scaled as, p = γ/r, where r is the meniscus radius. We find that the curvature in the y–z plane is much smaller compared to those in the other two planes and in addition to the capillary energy, the transmembrane pressure arising from this interfacial curvature helps in wrapping the membrane. Our calculation shows that the scaled values of the capillary force and the force due to the transmembrane pressure are of the same order of magnitude (∼10 μN). The curvatures in the x–y and x–z planes are also concave which are responsible for the advancement of the capillary flow along the x-direction.
The length up to which a membrane is completely wrapped (Lw) is found to be related to elastocapillary length (Lec), membrane width (W) and droplet volume (V). The curvature of the wrapped membrane is inversely related to the elastocapillary length, κ ∼ (1/Lec). The cross-sectional area of the conduit formed due to the wrapping of the membrane increases with an increase in the membrane width (see inset in Fig. 4b) and hence Lw ∼ (1/W). As the cross-sectional area of the conduit is independent of droplet volume (see inset in Fig. 4b) in the limit d ≲ Lc with negligible gravity, it suggests that Lw increases with droplet volume. So, we scale Lw ∼ (V/WLec), which compares well with the experimental results, as shown in Fig. 4b. From curve fitting, we find that Lw ≈ (V/WLec), which offers a condition required for the liquid to cover the entire length of a membrane, and this condition along with the critical wrapping condition can be used for fabricating closed conduit structures from membranes using elastocapillary phenomena.
We now discuss the limit when d ≥ Lc, and in that case, in addition to the surface energy and elastic energy, the contribution of gravitational energy will also become important. The bending energy can be scaled as
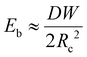 | (1) |
| Eg ≈ ρghAl | (2) |
| Ec ≈ γW | (3) |
In the limit, when the membrane completely wraps the liquid, the free surface does not exist except that at the advancing meniscus which can be neglected and therefore, Ec ≈ 0. For a completely wrapped membrane, h = Rc, W = 2πRc, and Al = W2/4π. Therefore, the total energy in the completely wrapped condition can be written as
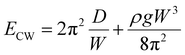 | (4) |
In the other limit, when the membrane does not wrap the liquid, the bending energy will be negligible, Eb ≈ 0. In that case, the sessile droplet will simply form a spherical cap with the radius of curvature rl and arc angle θ. From geometry, we obtain the position of the center of mass of the liquid such that C = (h/W) ≈ 0.01. Therefore, the total energy of the system in the open condition is given as
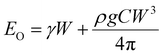 | (5) |
The membrane will completely wrap the liquid if the total energy in the wrapped state is less than that in the open state, ECW < EO. By using two characteristic length scales of the system: capillary length scale, 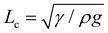 and elastocapillary length scale,
and elastocapillary length scale, 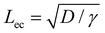 , the wrapping condition is represented by the following dimensionless equation,
, the wrapping condition is represented by the following dimensionless equation,
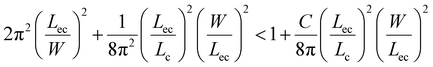 | (6) |
The above equation is plotted for a range of values of (W/Lec) and (Lc/Lec), as shown by the solid line in Fig. 5. It is observed that complete wrapping of the liquid is observed for a large (W/Lec) and small (Lc/Lec), which indicates that the membrane width is adequate so the capillary energy overcomes the elastic energy while ensuring the flattening of the membrane due to negligible gravitational energy. Experimental data obtained with membranes of different widths, thicknesses, and drop volumes are presented in Fig. 5. We see that the above model, which is represented by the solid line in Fig. 5, can predict the wrapping and non-wrapping conditions and is in good agreement with the experimental data.
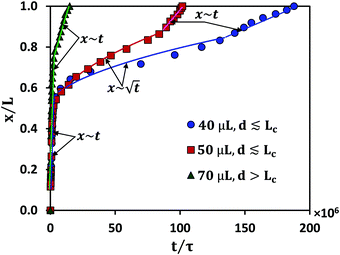
Experimental conditions satisfying the wrapping criterion give rise to elastocapillary flow along the membrane length. The meniscus dynamics of elastocapillary flow is characterized in terms of the meniscus position (x) with time (t), as shown in Fig. 6. We find that the meniscus dynamics depends on the relative magnitudes of the droplet size (d) and capillary length scale of the liquid (Lc). For d ≲ Lc, initially, the meniscus position changes linearly with time, x∼t indicating the inertial regime34 and at later times the meniscus dynamics follows the typical Washburn regime,17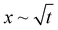 . At small times, the viscous effects are negligible since the membrane is not completely wrapped and the flow is mainly governed by the balance between capillary and inertial forces. At later times, the viscous effects become significant and the flow dynamics is governed by the interplay of viscous and capillary forces, giving rise to the Washburn regime. At very large times, for cases where Lw = L, a sudden increase in the velocity is observed with a linear variation of the meniscus position with time. When the capillary meniscus approaches the end of the membrane along its length, the ends of the membrane get wrapped well ahead of the meniscus. This provides a smaller radius of curvature of the meniscus and higher driving capillary pressure resulting in the inertial regime observed. For large volumes, with d > Lc, the effect of gravity becomes more pronounced and the flow dynamics is governed by the gravitational, capillary, and viscous forces, and a linear increase in the meniscus position with time is observed throughout. Due to the contribution of gravitational energy, in addition to the capillary energy, the driving energy is higher than the viscous energy which results in the inertial regime.32
. At small times, the viscous effects are negligible since the membrane is not completely wrapped and the flow is mainly governed by the balance between capillary and inertial forces. At later times, the viscous effects become significant and the flow dynamics is governed by the interplay of viscous and capillary forces, giving rise to the Washburn regime. At very large times, for cases where Lw = L, a sudden increase in the velocity is observed with a linear variation of the meniscus position with time. When the capillary meniscus approaches the end of the membrane along its length, the ends of the membrane get wrapped well ahead of the meniscus. This provides a smaller radius of curvature of the meniscus and higher driving capillary pressure resulting in the inertial regime observed. For large volumes, with d > Lc, the effect of gravity becomes more pronounced and the flow dynamics is governed by the gravitational, capillary, and viscous forces, and a linear increase in the meniscus position with time is observed throughout. Due to the contribution of gravitational energy, in addition to the capillary energy, the driving energy is higher than the viscous energy which results in the inertial regime.32
Conclusions
We studied elastocapillary interaction between a long rectangular membrane fixed along its central axis and a liquid drop dispensed at one of its ends. We found that introduction of the drop gives rise to the elastocapillary driven wrapping of the membrane along its width and a concomitant flow along its length. By considering the capillary energy, elastic energy, and gravitational energy, we identified general criteria for achieving complete wrapping depending upon the droplet size (d) and capillary length scale (Lc). Our study showed that in the case of small droplets satisfying d ≲ Lc, the critical membrane length (Wc) required for complete wrapping is related to the elastocapillary length scale (Lec) following, Wc = 7.5Lec. For large droplets with d > Lc, the wrapping behavior is represented in terms of the ratio of membrane width to elastocapillary length scale, (W/Lec) and the ratio of capillary length scale to the elastocapillary length scale, (Lc/Lec). We find that a smaller value of (Lc/Lec) < 1 and a large value of (W/Lec) > 10 are favorable for complete wrapping. Our study shows that the critical membrane width for complete wrapping is smaller in the wet state compared to that in the dry state, which is attributed to the existence of the transmembrane pressure force originating from the curved liquid meniscus in the wet state. Effects of membrane thickness and width and drop volume on the cross-section of the wrapped conduit and attached width of the membrane are studied. It is found that the conduit cross-section and the attached length increase linearly with an increase in membrane width but are independent of drop volume. Our study showed that the wrapped length of the membrane (Lw) is proportional to the droplet volume (V) and inversely related to the membrane width (W) and elastocapillary length scale (Lec). The elastocapillary flow is characterized by studying the meniscus position (x) with time (t). We find that for small droplets with d ≲ Lc, we observe an inertial regime, x ∼ t, at small times, followed by a Washburn regime,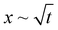 , at intermediate times, and finally an inertial regime at large times, and for large droplets with d > Lc, we only observed an inertial regime throughout. Our study could help in the fabrication of self-folded closed conduit structures and the design of lab on membrane devices for biochemical assays.
, at intermediate times, and finally an inertial regime at large times, and for large droplets with d > Lc, we only observed an inertial regime throughout. Our study could help in the fabrication of self-folded closed conduit structures and the design of lab on membrane devices for biochemical assays.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by IIT Madras via project no. MEE1718860RFIRASHS, and by the Ministry of Human Resources and Development, Government of India, through the Institute of Eminence (IoE) scheme via grant no. 11/9/2019-U.3(A).References
- P. G. de Gennes and F. Q. D. Brochard-Wyart, Capillarity and wetting phenomena- drops, bubbles, pearls, waves, Springer, New York, 2004 Search PubMed.
- J. Jurin, An Account of Some Experiments Shown before the Royal Society; With an Enquiry into the Cause of the Ascent and Suspension of Water in Capillary Tubes. By James Jurin, M. D. and R. Soc. S, Philos. Trans. R. Soc. London, 1717, 30(351–363), 739–747 Search PubMed.
- M. Prakash, D. Quéré and J. W. M. Bush, Surface tension transport of prey by feeding shorebirds: the capillary ratchet, Science, 2008, 320, 931–934 CrossRef CAS PubMed.
- D. L. Hu, B. Chan and J. W. M. Bush, The hydrodynamics of water strider locomotion, Nature, 2003, 424(6949), 663–666 CrossRef CAS PubMed.
- W. Kim, F. Peaudecerf, M. W. Baldwin and J. W. M. Bush, The hummingbird's tongue: a self-assembling capillary syphon, Philos. Trans. R. Soc., B, 2012, 279(1749), 4990–4996 Search PubMed.
- M. Heil, A. L. Hazel and J. A. Smith, The mechanics of airway closure, Respir. Physiol. Neurobiol., 2008, 163, 214–221 CrossRef PubMed.
- A. Olanrewaju, M. Beaugrand, M. Yafia and D. Juncker, Capillary microfluidics in microchannels: From microfluidic networks to capillaric circuits, Lab Chip, 2018, 18(16), 2323–2347 RSC.
- A. W. Martinez, S. T. Phillips, G. M. Whitesides and E. Carrilho, Diagnostics for the developing world: Microfluidic paper-based analytical devices, Anal. Chem., 2010, 82(1), 3–10 CrossRef CAS PubMed.
- R. R. A. Syms, E. M. Yeatman, V. M. Bright and G. M. Whitesides, Surface tension-powered self-assembly of microstructures – The state-of-the-art, J. Microelectromech. Syst., 2003, 12, 387–417 CrossRef.
- R. W. Style, A. Jagota, C.-Y. Hui and E. R. Dufresne, Elastocapillarity: Surface Tension and the Mechanics of Soft Solids, Annu. Rev. Condens. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- J. Bico, É. Reyssat and B. Roman, Elastocapillarity: When Surface Tension Deforms Elastic Solids, Annu. Rev. Fluid Mech., 2018, 50(1), 629–659 CrossRef.
- R. A. Samy, P. P. A. Suthanthiraraj, D. George, R. Iqbal and A. K. Sen, Elastocapillarity-based transport of liquids in flexible confinements and over soft substrates, Microfluid. Nanofluid., 2019, 23(8), 1–32 CrossRef CAS.
- R. W. Style, R. Boltyanskiy, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses, Phys. Rev. Lett., 2013, 110(6), 1–5 CrossRef PubMed.
- R. W. Style and E. R. Dufresne, Static wetting on deformable substrates, from liquids to soft solids, Soft Matter, 2012, 8(27), 7177–7184 RSC.
- B. Andreotti, O. Bä Umchen, F. Boulogne, K. E. Daniels, E. R. Dufresne and H. Perrin, et al., Solid capillarity: when and how does surface tension deform soft solids?, Soft Matter, 2016, 12(12), 2993–2996 RSC.
- R. Anoop and A. K. Sen, Capillary flow enhancement in rectangular polymer microchannels with a deformable wall, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(1), 013024 CrossRef CAS PubMed.
- D. George, R. Anoop and A. K. Sen, Elastocapillary powered manipulation of liquid plug in microchannels, Appl. Phys. Lett., 2015, 107, 261601 CrossRef.
- S. P. Reddy, R. A. Samy and A. K. Sen, Interaction of elastocapillary flows in parallel microchannels across a thin membrane Role of shear induced diffusion in acoustophoretic focusing of dense suspensions Capillary flow of blood in a microchannel with differential wetting for blood plasma sep, Appl. Phys. Lett., 2016, 109(10), 141601 CrossRef.
- J. W. Van Honschoten, M. Escalante, N. R. Tas, H. V. Jansen and M. Elwenspoek, Elastocapillary filling of deformable nanochannels, J. Appl. Phys., 2007, 101, 094310 CrossRef.
- H. Y. Kim and L. Mahadevan, Capillary rise between elastic sheets, J. Fluid Mech., 2006, 548, 141–150 CrossRef.
- B. Pokroy, S. H. Kang, L. Mahadevan and J. Aizenberg, Self-Organization of a Mesoscale Bristle into Ordered, Hierarchical Helical Assemblies, Science, 2009, 323(5911), 237–240 CrossRef CAS PubMed.
- C. Py, P. Reverdy, L. Doppler, J. Bico, B. Roman and C. N. Baroud, Capillary origami: Spontaneous wrapping of a droplet with an elastic sheet, Phys. Rev. Lett., 2007, 98, 156103 CrossRef PubMed.
- N. D. Brubaker and J. Lega, Two-dimensional capillary origami, Phys. Lett. A, 2016, 380, 83 CrossRef CAS.
- M. Piñeirua, J. Bico and B. Roman, Capillary origami controlled by an electric field, Soft Matter, 2010, 6, 4491–4496 RSC.
- T. Jamin, C. Py and E. Falcon, Instability of the origami of a ferrofluid drop in a magnetic field, Phys. Rev. Lett., 2011, 107(20), 1–5 CrossRef PubMed.
- A. Antkowiak, B. Audoly, C. Josserand, S. Neukirch and M. Rivetti, Instant fabrication and selection of folded structures using drop impact, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(26), 10400–10404 CrossRef CAS PubMed.
- N. R. Geraldi, F. F. Ouali, R. H. Morris, G. McHale and M. I. Newton, Capillary origami and superhydrophobic membrane surfaces, Appl. Phys. Lett., 2013, 102(21), 214104 CrossRef.
- M. F. Reynolds, K. L. McGill, M. A. Wang, H. Gao, F. Mujid and K. Kang, et al., Capillary Origami with Atomically Thin Membranes, Nano Lett., 2019, 19(9), 6221–6226 CrossRef CAS PubMed.
- W. S. Y. Wong, M. Li, D. R. Nisbet, V. S. J. Craig, Z. Wang and A. Tricoli, Mimosa Origami: A nanostructure-enabled directional self-organization regime of materials, Sci. Adv., 2016, 2, e1600417 CrossRef PubMed.
- R. A. Samy, D. George and A. K. Sen, Bio-inspired liquid transport via elastocapillary interaction of a thin membrane with a liquid meniscus, Soft Matter, 2017, 13, 6858–6869 RSC.
- R. A. Samy and A. K. Sen, Elastocapillary flow driven lab-on-a-membrane device based on differential wetting and sedimentation effect for blood plasma separation, J. Micromech. Microeng., 2019, 29(6), 065001 CrossRef CAS.
- S. Das, P. R. Waghmare and S. K. Mitra, Early regimes of capillary filling, Phys. Rev. E, 2012, 86, 067301 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2022 |