Open Access Article
Open Access ArticleCharacterising different molecular landscapes in dynamic covalent networks†
Filip
Van Lijsebetten
a,
Kevin
De Bruycker
a,
Evelyne
Van Ruymbeke
 *b,
Johan M.
Winne
*b,
Johan M.
Winne
 *a and
Filip E.
Du Prez
*a and
Filip E.
Du Prez
 *a
*a
aPolymer Chemistry Research Group, Centre of Macromolecular Chemistry (CMaC) and Laboratory of Organic Synthesis, Department of Organic and Macromolecular Chemistry, Faculty of Sciences, Ghent University, Krijgslaan 281-S4, Ghent, 9000, Belgium. E-mail: Filip.DuPrez@UGent.be; Johan.Winne@UGent.be
bBio and Soft Matter, Institute of Condensed Matter and Nanosciences, Université Catholique de Louvain, Croix du Sud 1, Louvain-la-Neuve, 1348, Belgium. E-mail: Evelyne.Vanruymbeke@uclouvain.be
First published on 21st October 2022
Abstract
Dynamic covalent networks present a unique opportunity to exert molecular-level control on macroscopic material properties, by linking their thermal behaviour to the thermodynamics and kinetics of the underlying chemistry. Yet, existing methods do not allow for the extraction and analysis of the influence of local differences in chemical reactivity caused by available reactants, catalysts, or additives. In this context, we present a rheological paradigm that allows us to correlate the composition of a reactive polymer segment to a faster or slower rate of network rearrangement. We discovered that a generalised Maxwell model could separate and quantify the dynamic behaviour of each type of reactive segment individually, which was crucial to fully comprehend the mechanics of the final material. More specifically, Eyring and Van 't Hoff analysis were used to relate possible bond catalysis and dissociation to structural changes by combining statistical modelling with rheology measurements. As a result, precise viscosity changes could be measured, allowing for accurate comparison of various dynamic covalent network materials, including vitrimers and dissociative networks. The herein reported method therefore facilitated the successful analysis of virtually any type of rate-enhancing effect and will allow for the design of functional and fast (re)processable materials, as well as improve our ability to predict and engineer their properties for future applications.
Introduction
Dynamic and reversible covalently cross-linked polymers such as vitrimers or dissociative covalent adaptable networks (CANs) hold great promise in the context of the design of innovative polymer materials with programmed properties and performance.1–4 Unlike classical thermosets, the covalent topology of such cross-linked networks is not permanent and can change in response to a trigger (e.g. elevated temperature), allowing material flow. While providing opportunities for polymer processing and recycling, this distinct behaviour also renders these materials chemically less inert, putting long-term structural integrity at risk, and balancing the two can be particularly difficult.5–7 A good molecular understanding of how, and under which conditions chemical reactivity is activated, is therefore critical for controlling and predicting material properties.8–12Over the last two decades, a great deal of research has gone into determining on which time scale and to what extent a dynamic covalent network will start to show significant flow.5,7,13–19 To accurately address this question, one should investigate both the kinetics and thermodynamics of the underlying bond formation, cleavage, reformation or rearrangement within the viscoelastic material. This is for example quite relevant if advanced processing options such as extrusion and additive manufacturing are targeted for such dynamic materials.20–24 However, because many characterisation techniques commonly used to monitor the chemical structure and reactivity of small organic molecules are incompatible with the viscoelastic state of polymer networks, this can become very challenging.4,6,25 Furthermore, because other factors are involved, a direct causal chain connecting chemical reactivity properties to macroscopic material properties cannot always be established. Nonetheless, by treating a polymer network as a single chemical system, rheology studies can be used to extract molecular information about the underlying rearrangement reactions.6,26
To precisely predict and engineer material properties, data analysis and evaluation are critical. In this regard, stress-relaxation experiments have undeniably been the method of choice for characterising polymer dynamics of reversible networks that show macroscopic flow within a reasonable time frame.27–35 The viscoelastic parameters are typically calculated by fitting the experimental data to a mathematical model. A reasonable starting point is to assume that each segment of the polymer network relaxes stress at the same rate, following a single Maxwell behaviour and thus fitting to a single exponential decay. Many systems, however, exhibit a more complex rheological behaviour, especially when studied near the glass transition temperature (Tg),36,37 or when observing structuration of different network architectures,38–42 but also in seemingly homogeneous systems.43–49 As a result, a growing number of studies show that a stretched single exponential function produces a much better fit to experimental data, which can lead to small but significant changes in the derived viscoelastic parameters.48,50,51 Nonetheless, using empirical fitting functions such as stretched exponentials does not provide insight into the rheological phenomena or contributing factors and also makes it quite difficult to compare the outcome of different studies.52 In fact, even when such studies are done on essentially the same system, different interpretations can arise from similar data.45
To better capture the wealth of information provided by linear rheology experiments, such as stress-relaxation data, a more realistic assumption is that the macroscopic deformation response of a polymer network is the result of additive contributions of different parts or segments of the network (Fig. 1).53–55 Apart from the dynamic cross-link itself, also its topological location and surrounding backbone chemistry will impact its dynamic and mechanical behaviour. When applied to stress-relaxation experiments, the generalised Maxwell model can be used to consider each of these contributions separately as distinct Maxwell elements (adhering to a specific single exponential decay).56 Thus, when two or more significantly distinct segment types contribute to the overall stress-relaxation in such dynamic systems, a generalised Maxwell model – using only a limited amount of elements – should provide a powerful analysis tool to associate a specific chemistry, or type of exchanging chain segment, to a specific relaxation time. As a result, we hypothesised that the contribution of each component can be assessed, and a relationship between viscoelastic parameters and fundamental chemical parameters could be more straightforward to address.25
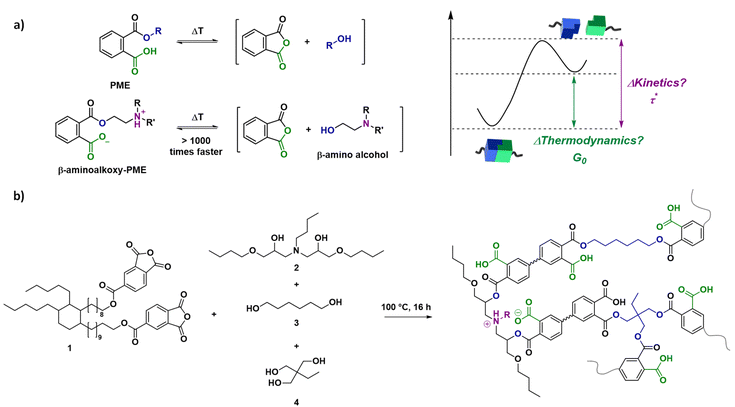
In this combined experimental, analytical and theoretical study, we aimed to develop a step-by-step method for relating changes in reactivity of molecular components to temperature-dependent properties of dynamic covalent networks. As a first suitable model polymer network system to link experiments to theory and demonstrate the validity of the approach, a known catalyst-free transesterification system based on phthalate monoesters (PMEs) has been selected.20,57 More specifically, PME networks, consisting of two drastically different dynamic cross-links have been prepared for this study, resulting in both fast and slow relaxing segments with clear deviation from the single Maxwell behaviour (Scheme 1a). For this purpose, we relied on the concept of internal catalysis or ‘neighbouring group effects’ in which built-in tertiary amines significantly accelerate the exchange of PME cross-links directly bound to them, and not (or to a much lesser extent) more remote ones. We have previously shown this effect both on small molecule models, as well as in heteropolymer networks made up from both types of cross-links.20
 | ||
| Scheme 1 Schematic representation of the model system used, highlighting the transesterification of phthalate monoesters (PMEs) with two cross-links of varying reactivity.20 (a) Scheme for dissociation reaction of a phthalate monoester with and without substituents on the β-carbon. (b) Network synthesis by mixing a dianhydride and polyol mixture. | ||
As a result, it was expected that stress-relaxation curves deviate significantly from a single exponential decay and that a generalised Maxwell model, rather than a single (stretched) model, allows a straightforward correlation of the deviations in the stress-relaxation data to the known differences in exchange rate (reaction kinetics). Critically, the original model system has been specifically chosen to be dissociative in order to capture the effect of temperature-related elasticity changes. To this end, statistical modelling was used to investigate and quantify the effect of bond dissociation on network connectivity (thermodynamics), as well as to validate our assumptions. Furthermore, to emphasize the general utility of the method, overall viscosity changes will be assessed and compared to an associative dynamic covalent network (vitrimer) by taking into account each aspect of chemical reactivity.
Finally, in order to simplify numerical evaluation of rheology data, an open-access Python program for automated curve fitting and relaxation parameter read-out was developed, which could become a useful tool for future studies in this research field.
Results and discussion
Synthesis of model covalent adaptable networks
A first objective within this work was to obtain a range of model dissociative dynamic networks with complex but relatively predictable viscoelastic properties, based on our insights from previous research on PME-type CANs.20 A flexible dianhydride (1) was chosen as the main building block for these polymer networks and was synthesised as previously reported.57 Dynamic PME networks could then be obtained by mixing with a diol mixture (0.4 eq.) and triol (0.4 eq.) to yield equimolar amounts of anhydride and alcohol functional groups (Scheme 1b). The diol mixture contained varying amounts of the faster exchanging β-amino diol (2), which was made by the reaction of butylamine and butyl glycidyl ether (see ESI†), and the slower exchanging 1,6-hexanediol (3). After combination with the cross-linker trimethylolpropane (4) and heating at 100 °C for 16 hours, cured networks were obtained as confirmed by ATR-FTIR analysis (Fig. S1†). As a result, model networks N-1%, N-5%, N-10%, and N-20% were obtained, in which x% represents the percentage of β-amino diol in the diol mixture.The addition of the β-amino diol resulted not only in the formation of a more activated ester, but can also initiate strong hydrogen bonding or even ionic interactions after proton transfer between the tertiary amine and the dangling carboxylic acid of the phthalate monoester (Scheme 1).20 However, as shown in Table S1,† from DSC analysis similar Tg values were obtained for the different networks, with a small decrease from N-1% (14 °C) to N-5% (5 °C) as a result of the introduction of the more flexible β-amino diol compared to 1,6-hexanediol (Fig. S2†). In line with our previous observations, this was quickly overcome again by additional ionic interactions, resulting in a slight increase in Tg for N-20%.20 Furthermore, good thermal stability (i.e. Td5% > 275 °C) and network integrity (i.e. soluble fraction between 5 and 7%) could be concluded from TGA analysis and swelling experiments (Fig. S3 and S4†).
Viscoelasticity of the dynamic polymer networks was assessed using stress-relaxation measurements from 160 °C to 110 °C (Fig. S5†). The absolute values of the relaxation data could be used to extract information about changes in cross-linking density. Higher temperatures caused a decrease in the initial relaxation modulus G0, which can be attributed to an increased bond dissociation at those temperatures (Fig. S6†). As a result, also more reactive chain ends are formed, which are required for exchange or, on a macroscopic level, for stress-relaxation. Since both bond dissociation (G[T]) and exchange (τ[T]) can be expected to have an important effect on the rheology of the networks (η[T]), each contribution will be discussed separately within the remainder of the manuscript.
Bond exchange – stress-relaxation (kinetics)
Increasing the tertiary amine-content from N-1% to N-20% resulted in an increase in relaxation rate and the introduction of visible shoulders in the relaxation curves (Fig. 2). A generalised Maxwell model (two elements) was fitted to quantitatively analyse the effect of this two-step relaxation, with one Maxwell element representing the fast exchanging segments and the other representing slower exchanging segments (eqn (1)). For comparison, the relaxation data of all model networks were additionally fitted to a single (stretched) exponential (eqn (S1) and (S2)†), with representative fits for N-20% shown in Fig. 2 and S7.† It is clear from the overlap of the mathematical fit and the experimental data that using two Maxwell elements yielded a much better fit than using just one. Furthermore, the contribution of the fast mode (G0,fast) is significantly lower than that of the slow mode (G0,slow), due to the insufficient amount of fast segments (only up to N-20%) to overtake the macroscopic stress-relaxation process (see Table S2†). | (1) |
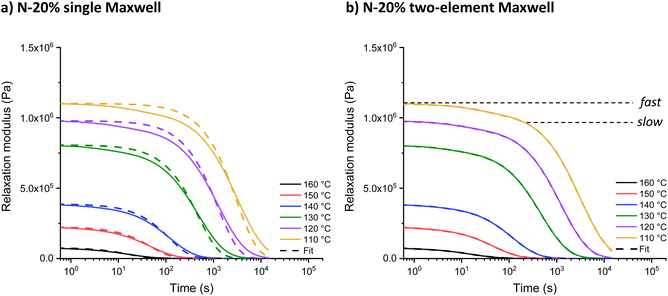 | ||
| Fig. 2 (a) Single and (b) double exponential fit to the stress-relaxation data of N-20% from 160 °C to 110 °C. | ||
Characteristic relaxation times (τ*) were calculated from all fitted functions (i.e. single, stretched and double exponential) and were related to the reaction rate of dynamic bond exchange (Fig. S8†). The overall effect of relaxation dynamics (τ[T]) (obtained from the double exponential fit) on network viscosity (η[T]) can then be estimated by taking the sum of τfast and τslow, which is the time required to fully relax all polymer segments. For example, when switching from N-1% to N-20% at 160 °C, relaxation times decreased from 134 to 34 s. Before describing the kinetic data in more detail, it is worthwhile to consider how to establish a link between chemical reactivity changes and absolute relaxation values.
When characterising dissociative CANs and vitrimers, the empirical Arrhenius equation (eqn (S3)†) is commonly used to determine the effect of temperature on the rate of material flow, yielding a flow activation energy (Ea,flow). However, using Ea,flow values as a quantification of dynamic bond exchange rates is a gross oversimplification.6,45,46 In fact, this parameter only shows the temperature dependence of a reaction rate and not its absolute rate. Macroscopic rate-enhancing effects are thus not necessarily related to a change in Ea,flow, but are more commonly the result of a different reaction pathway or availability of reactants and catalysts for a specific pathway. This often neglected part of the reaction rate is related to the so-called ‘pre-exponential factor’ of the Arrhenius theory (collision factor and reaction order of reagents and catalysts). Using Eyring's description, an absolute rate theory, allows one to relate this pre-exponential factor to the entropy of activation (ΔS‡), which is the difference in standard entropy between the transition state and reactants.58 More specifically, reactions will proceed faster when the ΔS‡ term becomes more favourable due to a relative increase in thermal probability between the transition and initial state.
The concept of neighbouring group participation (NGP), as applied here for PME networks, is an interesting example of a catalysed chemical reaction with a relatively high activation enthalpy (ΔH‡ or barrier to form/break a bond in the transition state) but favourable ΔS‡. Moreover, the statistical likelihood that the reaction is successful at a given temperature increases with the proximity of reactive (catalytic) functions such as e.g. tertiary amines. Thus, our current analysis now allows us to translate the observed changes in relaxation rate to parameters that are easier to interpret in terms of chemical reactivity. We can use the adjusted Eyring equation (eqn (2)) to explicitly address the effect of ΔH‡ and ΔS‡ when going from N-1% to N-20% and study the minimal energy required for reaction in the model networks.59,60
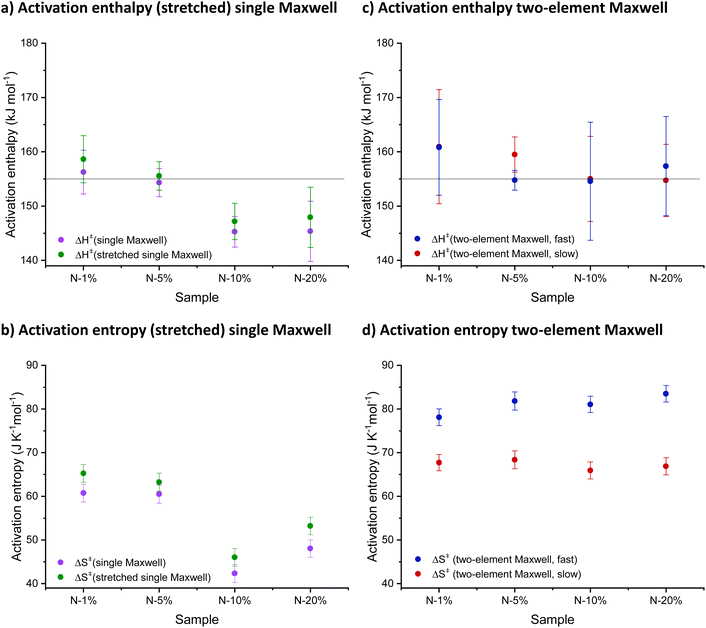
Eyring plots were generated from the obtained τ* values, an approach that was previously used in reversible network research by Bowman and co-workers for furan-maleimides and Tibbitt and co-workers for boronic esters.8,26 The apparent activation parameters could be calculated by plotting ln(1/Tτ*) against 1000/T (Fig. S9†) and taking the slope and intercept. Fig. 3 shows a summary of the obtained values for ΔH‡ and ΔS‡ for each fitting function.
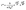 | (2) |
The use of τ* obtained by fitting the relaxation data to a single and stretched exponential decay revealed a significant trend of decrease in both apparent ΔH‡ and ΔS‡ with increased N% content, which was difficult to chemically interpret and rationalise (Fig. 3a and b). This (apparent) lowering of the activation parameters could be interpreted as a change in exchange mechanism, or could lead to the wrong interpretation that our assumptions for NGP network rearrangements are unwarranted. However, we found that these discrepancies disappeared when moving from a single (stretched) Maxwell model to a more realistic one that takes into account the contributions of fast and slow segments separately for the networks with increasing N% content. Indeed, a drastically different analysis of the same rheology data was possible when the activation parameters for the fast and slow processes were obtained separately from a double exponential fit to the relaxation data (Fig. 3c and d). The fitted double exponential decay function revealed a chemically interpretable trend in the apparent ΔH‡ values, indicating that the rate-enhancing effect does not change the high activation barriers for exchange, which remain around 155 kJ mol−1.
Similarly, no downward trend in apparent ΔS‡ for either process (fast or slow) was observed, although a significant difference between the two apparent activation entropies can be noted (∼70 J K−1 mol−1 for the slow process and ∼80 J K−1 mol−1 for the fast process). This indicates that the faster process is entropically more preferred over the slower process, although both processes have the same enthalpic barrier. This is nicely in line with the fact that the ‘fixed proximity’ of the amine catalyst facilitates the fast reaction (Scheme S1†). Moreover, the sign of ΔS‡, next to its magnitude, highlights the smaller entropic penalty for the dissociative process compared to an associative one.61 As a reference, the data of the N-0% network was added to the ESI (Fig. S10 and S11†). This material does not contain fast exchanging segments and, as a result, the respective relaxation data could not be accurately fit to eqn (1). However, fitting to a single exponential decay (eqn (S1)†) and subsequent kinetic analysis allowed to determine very similar ΔH‡ and ΔS‡ values, compared to the slow exchanging segments of N-1% to N-20%.
Importantly, the proposed kinetic analysis is applicable to both dissociative CANs and vitrimers (vide infra), but it neglects the effect of depolymerisation on overall exchange rates. Nonetheless, decross-linking of a PME cross-link to an anhydride and alcohol pendant chain should indeed not influence for the rate of the network rearrangement, although it does make the network less elastic. This approximation holds as long as the system does not actually cross the gel point and starts to relax stress like a thermoplastic (i.e. liquid-like physical flow).6
From the obtained kinetic data, it became clear that choosing the correct model to fit relaxation data is important to obtain accurate molecular parameters, in particular if it is of interest to relate the observed energy of viscous flow activation back to the underlying activation energies for the network rearrangement reaction. This is particularly valid when attempting to determine the effect of nearby substituents, catalysts, or additives on the reactivity in polymer networks. Moreover, it may also aid in the analysis of polymer networks that combine more than one dynamic (covalent) chemistry, which is an increasingly recurrent feature in recent literature.62 Despite the fact that the proposed fitting method was quite informative, data analysis when using our approach can become more complex. Therefore, we created a Python package that can import raw data and automatically generate (normalised) relaxation plots to make the evaluation of multiple relaxation spectra more straightforward (see ESI†). In fact, by simply selecting the desired fitting model, the user can obtain the associated relaxation parameters, such as G0 and τ*, thus significantly reducing the analysis time.
Bond dissociation (thermodynamics)
The evolution of G0 as a function of temperature was used to assess the degree of decross-linking when heating the materials (ranging from N-1% to N-20%). To analyse the rheology data in relation to the two-step relaxation process, a theoretical plateau modulus (G0,N) for each dynamic covalent network was calculated by taking into account the attainable cross-linking density at a given conversion level. A full description of the approach, calculations and output of the used Python script can be found in the ESI.†63 As a result, statistical network compositions were calculated by considering that a network segment can be a trapped segment (i.e. ended by two cross-linking points), a free linear chain (i.e. ended by two chain ends) or a dangling chain (i.e. ended by cross-linking point on one side and chain end on the other), based on the probability of each alcohol monomer to react with a dianhydride compound (pass,slow and pass,fast, Fig. 4).64,65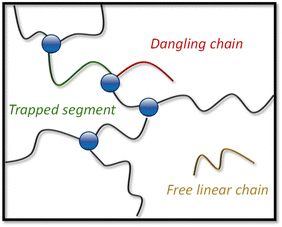 | ||
| Fig. 4 Depiction of a hypothetical network composition showing network segments (which can be composed of several building blocks) and defects, without considering e.g. loop formation. | ||
To simplify calculations and only have one unknown parameter, we assumed pass = pass,slow = pass,fast (Fig. S12–S14†). This assumption implies that the β-amino alcohols did not form a stronger PME cross-link, an assumption which seems warranted as essentially the same bonds are formed and broken for both reversible equilibria. From the generated data, the average molar mass of the trapped polymer segments between each cross-link, Mw,trapped, as well as the weight fraction of trapped segments, φtrapped, were determined and related to G0,N as a function of the pass-value using eqn (3) (eqn (S7)†).
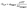 | (3) |
Knowing the relationship between the plateau modulus G0,N and association probability pass (see Fig. S15†), the value of the parameter pass could be obtained from the experimental plateau modulus G0 at various temperatures (Fig. S16 and S17†), with representative data shown in Fig. 5a for N-1% and N-20%. The plateau followed by a non-linear decrease in pass with temperature, which is observed for both systems, indicates that there is only limited bond dissociation below 130 °C (viscoelastic regime I) and a relatively sharply increasing decross-linking above 130 °C (viscoelastic regime II). Interestingly, even at high levels of dissociation (at short timescales), we assumed that the polymer segments are strongly associated (i.e. short lifetime of dissociation) and that the dynamics of the individual polymer chains are not sufficient to introduce liquid-like physical flow (Fig. 5b).10,12 In other words, while a significant build-up of free chain-ends does reduce the elasticity of the network, diffusion over a large distance is limited due to a high interaction energy.66 To detect macroscopic relaxation or flow, a dissociated intermediate must first find a new partner, which takes time and has its own thermal barrier.
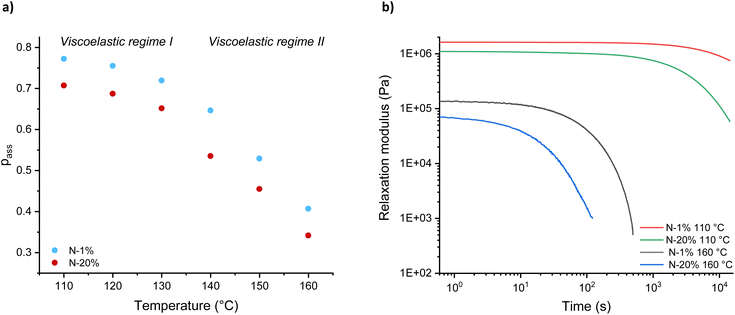 | ||
| Fig. 5 Temperature dependence of (a) association probability (pass) and (b) stress-relaxation data at 160 °C and 110 °C for N-1% and N-20%. | ||
In order to describe and predict the shift in equilibrium towards dissociation as a function of temperature, we hypothesised that pass could be related to the dissociation constant (Kdiss) according to eqn (S14) and (S15).† Interestingly, this K-value closely matched previously determined equilibrium constant values for ester formation, indicating that the moduli of the network can in fact surprisingly be used as a macroscopic observable to directly monitor a dissociation equilibrium in these systems.67 Furthermore, Van 't Hoff plots were constructed by plotting −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdiss against 1000/T (Fig. S18†), with the linear part of the curve used to characterise changes in dissociation enthalpy (ΔrH) and entropy (ΔrS) (eqn (4)). Fig. 6 shows a summary of both thermodynamic parameters for N-1% to N-20%.
Kdiss against 1000/T (Fig. S18†), with the linear part of the curve used to characterise changes in dissociation enthalpy (ΔrH) and entropy (ΔrS) (eqn (4)). Fig. 6 shows a summary of both thermodynamic parameters for N-1% to N-20%.
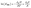 | (4) |
 | ||
| Fig. 6 Overview of obtained (a) dissociation enthalpy (ΔrH) and (b) entropy (ΔrS) values after modelling of rheology data and temperature-modulated differential scanning calorimetry (mDSC) analysis. | ||
When comparing ΔrH values, one can conclude that the dissociation enthalpy increases with decreasing tertiary amine-content with a shift of roughly 20 kJ mol−1 (Fig. 6a, blue). Moreover, bond scission was characterised by a large gain in ΔrS confirming the fact that the decross-linked intermediate state is entropically preferred (Fig. 6b, blue), resulting in a significant shift in the bonding equilibrium at high temperatures.4 Finally, to validate our results, we investigated whether similar thermodynamic data could be obtained using calorimetry measurements. To that end, temperature-modulated DSC analysis was carried out between 80 °C and 160 °C (Fig. S19†), where an increase in molar heat capacity (Cp) could be related to the thermodynamic functions of dissociation using eqn (S18) and (S20),† respectively.68,69 A good agreement was found between the thermodynamic values obtained by modelling and mDSC measurements, as indicated in red in Fig. 6a and b, supporting our findings. Moreover, the obtained values were in the same order of magnitude to the ones obtained by Rowan and co-workers on the dissociation of hindered urea bonds.70
Impact on network viscosity
The preceding discussion was critical in determining the precise molecular origin of a viscosity change (i.e. “the chemist's point of view”). Furthermore, with all of the viscoelastic parameters listed above, accurate apparent viscosity (ηapparent) values could now be calculated using the Maxwell relation (η = Gτ). Specifically, heating from 120 to 160 °C reduced the viscosity drastically from 109–108 to 106–105 Pa s for N-1% to N-20%. Surprisingly, a quasi-linear Arrhenius plot with identical Ea,flow of ∼250 kJ mol−1 for N-1% and N-20% was obtained by plotting ln(ηapparent) against 1000/T (Fig. 7). This highlighted again that important data can be “hidden” and care should be taken when relating macroscopic parameters of dynamic covalent networks to the underlying rich molecular landscape.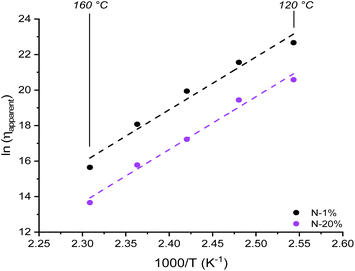 | ||
| Fig. 7 Viscosity plot showing the effect of increasing amounts of tertiary amine content from N-1% to N-20% close to the dynamic ester bond. | ||
Potential of the rheological method
Until now, the presented rheological method has only been used to investigate viscosity changes in a dissociative model system that affected both G[T] and τ[T]. However, vitrimers being associative dynamic covalent networks are generally distinguished by a constant cross-linking density, implying that the ηapparent is frequently solely controlled by the kinetics of a bond exchange reaction τ[T], greatly simplifying the analysis. Nonetheless, from a (re)processing viewpoint, attaining equally sharp changes in viscosity within a reasonable temperature interval can be quite challenging. To this end, our research group recently demonstrated that the use of acidic additives can greatly accelerate material flow of vinylogous urethane (VU) vitrimers.21,71 As a result, external catalysis of VU vitrimers was chosen as a second model system in this study to demonstrate the approach's broad applicability beyond a single chemotype, cross-linking mode or rate-enhancing effect.For this, a reference material was prepared according to a previously reported procedure by reacting 1,1,1-trimethylpropane trisacetoacetate (5) and Priamine 1074 (6) in a stoichiometric ratio of 15 mol% excess primary amine groups (VU-ref, Fig. 8a). Subsequently, an acid-catalysed VU network was synthesised by adding 10 mol% of para-toluenesulfonic acid (pTsOH) to the same formulation (VU–pTsOH). A summary of the thermomechanical properties of both networks was added to the ESI (Table S3†). After reprocessing the samples using compression moulding at 150 °C for 1–5 min, depending on the acid content, viscoelastic properties could be assessed via stress-relaxation experiments.
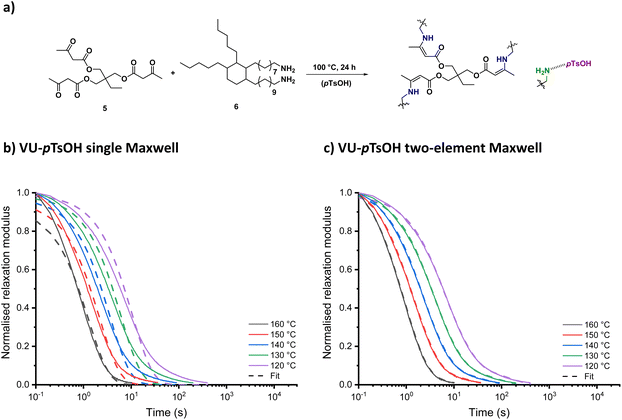 | ||
| Fig. 8 (a) Vinylogous urethane network formation with and without acid catalyst. (b) Single and (c) double exponential fit to the stress-relaxation data of VU-pTsOH from 160 °C to 120 °C. | ||
When looking at the normalised stress-relaxation measurements from 160 to 120 °C (Fig. 8b and c and S20†), also in this case a clear deviation from the single Maxwell model could be identified as a result of ‘acid-rich’ and ‘acid-poor’ polymer segments with different exchange kinetics. The corresponding viscoelastic parameters (Fig. S21†) could be calculated by fitting the data to the double exponential function in eqn (1). Unlike the PME system described above, which relied on favourable ΔS‡ values to increase relaxation, acid catalysis in VU transamination resulted in a substantial decrease in apparent ΔH‡ values, effectively lowering the energy barrier for exchange by around 50 kJ mol−1.
Following that, the obtained viscoelastic parameters were again used to calculate apparent viscosity values and draw an Arrhenius plot, yielding Ea,flow values ranging from 100 to 150 kJ mol−1 (Fig. 9). Moreover, because the same approach was applied for both an associative and dissociative system (by accounting for the contribution of kinetics and/or thermodynamics), the attainable network viscosities for both systems could be compared. As a result, it became clear that less favourable viscosity values in the range of 107 to 106 Pa s were obtained when heating from 120 to 160 °C for the externally catalysed VU vitrimer system.
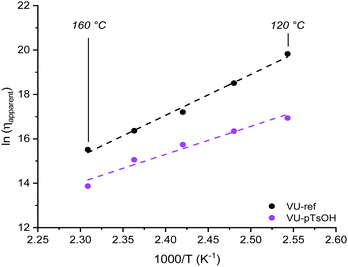 | ||
| Fig. 9 Viscosity plot indicating the effect of introducing an acid catalyst in a vinylogous urethane vitrimer. | ||
Conclusions
This study covered a detailed analysis of the kinetics and thermodynamics of bond exchange in both dissociative and associative dynamic covalent networks. On the one hand, dissociative phthalate monoester based networks with explicit differences in chemical reactivity of the constituting bonds were prepared, resulting in a two-step deformation response. On the other hand, an externally catalysed vitrimer has been selected as an associative counterpart in this general study. Stress-relaxation experiments were performed and analysed by three different ways to fit relaxation, indicating that the data could be best described by a generalised Maxwell model using two elements for both types of dynamic networks. The obtained relaxation times (τ*) were used to determine the activation parameters of bond exchange for each response separately. The separate Arrhenius plots showed that the origin of the faster relaxation process was not enthalpic in nature for the PME-networks, as the activation enthalpies for both processes are very similar, but lies in the pre-exponential part. In Eyring's formalism, this can be related to a lower entropic cost of activation for the fast process, despite its high energy barrier (∼155 kJ mol−1).An Eyring analysis thus seems to be a good way to dissect distinct stress-relaxation phenomena. Statistical modelling was subsequently used to relate the evolution of cross-linking density or relaxation modulus (G0) with temperature to the thermodynamics of bond dissociation using a Van 't Hoff analysis. In addition, by combining this method with simple network viscosity calculations, our approach can be generally applied as a characterisation and comparison tool for both associative and dissociative systems in terms of (re)processability.
While the reported method was validated for two specific types of dynamic covalent networks, an identical approach is generally applicable to several other types of dynamic network systems. In fact, because they only differ in the timescale of interest, the same approach could be extended to non-covalent systems such as supramolecular networks. Furthermore, we believe that the reported approach could become useful in the development and characterisation of so-called hybrid materials, which combine multiple dynamic (covalent) chemistries with different temperature responses.
Although the results in this manuscript focused on thermally controlled reactivity, we believe that the same rheological framework could be extended to study photochemical reactivity in dynamic polymer networks. For example, local differences in irradiation, photocuring and/or photodynamics, could be investigated in greater detail based on similarities or differences in molar extinction coefficients of the network components. Ideally, this could provide information about the optimal activation wavelength for a specific photochemical process.72,73 However, remaining challenges that would have to be resolved in the latter systems are limited light penetration and homogeneity in the number of absorbed photons across the irradiated volume.
In general, we are strongly convinced that performing detailed rheological analysis using the generalised Maxwell approach, and focusing on variations in relaxation time and cross-linking density with temperature (or light) will improve our ability to engineer, predict, and use the unique properties of dynamic covalent networks for basic and more advanced applications.
Data availability
The raw and reprocessed data needed to replicate these results are available upon request from the corresponding author. The code for rheological analysis can be found at https://pypi.org/project/aprheology/.Author contributions
F. V. L. conducted the majority of all syntheses and the rheological experiments. K. D. B. assisted with the syntheses as well as optimised data analysis and developed the essential pyhton tools. E. V. R. conceptualised and wrote the statistical model. J. M. W. and F. E. D. P. supervised the project and were responsible for writing the grants on which the study is based. All authors discussed the data and co-edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. D. P. and J. W. thank BOF-UGent for GOA-funding. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (CiMaC project – grant agreement No. 101021081). E. V. R. is Senior Research Associate of the F.R.S.-F.N.R.S. F. V. L. acknowledges the Research Foundation-Flanders (FWO) for a PhD (Application 1S49122N) fellowship. We would like to thank Bernhard De Meyer for technical support and Dr Chiel Mertens and Dr Nezha Badi for fruitful discussions.Notes and references
- M. Podgórski, B. D. Fairbanks, B. E. Kirkpatrick, M. McBride, A. Martinez, A. Dobson, N. J. Bongiardina and C. N. Bowman, Adv. Mater., 2020, 32, 1906876 CrossRef PubMed.
- G. M. Scheutz, J. J. Lessard, M. B. Sims and B. S. Sumerlin, J. Am. Chem. Soc., 2019, 141, 16181–16196 CrossRef CAS PubMed.
- C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173 RSC.
- J. M. Winne, L. Leibler and F. E. Du Prez, Polym. Chem., 2019, 10, 6091–6108 RSC.
- M. Capelot, M. M. Unterlass, F. Tournilhac and L. Leibler, ACS Macro Lett., 2012, 1, 789–792 CrossRef CAS PubMed.
- A. Jourdain, R. Asbai, O. Anaya, M. M. Chehimi, E. Drockenmuller and D. Montarnal, Macromolecules, 2020, 53, 1884–1900 CrossRef CAS.
- M. M. Obadia, A. Jourdain, P. Cassagnau, D. Montarnal and E. Drockenmuller, Adv. Funct. Mater., 2017, 27, 1703258 CrossRef.
- R. J. Sheridan and C. N. Bowman, Macromolecules, 2012, 45, 7634–7641 CrossRef CAS.
- W. C. Yount, D. M. Loveless and S. L. Craig, J. Am. Chem. Soc., 2005, 127, 14488–14496 CrossRef CAS PubMed.
- J. Brassinne, A. Cadix, J. Wilson and E. van Ruymbeke, J. Rheol., 2017, 61, 1123 CrossRef CAS.
- A. N. Semenov and M. Rubinstein, Macromolecules, 1998, 31, 1373–1385 CrossRef CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 1998, 31, 1386–1397 CrossRef CAS.
- F. Van Lijsebetten, J. O. Holloway, J. M. Winne and F. E. Du Prez, Chem. Soc. Rev., 2020, 49, 8425–8438 RSC.
- L. Li, X. Chen, K. Jin, M. Bin Rusayyis and J. M. Torkelson, Macromolecules, 2021, 54, 1452–1464 CrossRef CAS.
- O. Anaya, A. Jourdain, I. Antoniuk, H. Ben Romdhane, D. Montarnal and E. Drockenmuller, Macromolecules, 2021, 54, 3281–3292 CrossRef CAS.
- D. Reisinger, S. Kaiser, E. Rossegger, W. Alabiso, B. Rieger and S. Schlögl, Angew. Chem. Int. Ed., 2021, 60, 14302–14306 CrossRef CAS PubMed.
- L. Li, X. Chen, K. Jin and J. M. Torkelson, Macromolecules, 2018, 51, 5537–5546 CrossRef CAS.
- F. Van Lijsebetten, K. De Bruycker, J. M. Winne and F. E. Du Prez, ACS Macro Lett., 2022, 11, 919–924 CrossRef CAS PubMed.
- F. Van Lijsebetten, T. Debsharma, J. M. Winne and F. E. Du Prez, Angew. Chem. Int. Ed., 2022, 202210405 Search PubMed.
- M. Delahaye, F. Tanini, J. O. Holloway, J. M. Winne and F. E. Du Prez, Polym. Chem., 2020, 11, 5207–5215 RSC.
- C. Taplan, M. Guerre, J. M. Winne and F. E. Du Prez, Mater. Horizons, 2020, 7, 104–110 RSC.
- L. Yue, H. Guo, A. Kennedy, A. Patel, X. Gong, T. Ju, T. Gray and I. Manas-Zloczower, ACS Macro Lett., 2020, 11, 836–842 CrossRef PubMed.
- D. T. Sheppard, K. Jin, L. S. Hamachi, W. Dean, D. J. Fortman, C. J. Ellison and W. R. Dichtel, ACS Cent. Sci., 2020, 6, 921–927 CrossRef CAS PubMed.
- M. Röttger, T. Domenech, R. van der Weegen, A. Breuillac, R. Nicolaÿ and L. Leibler, Science, 2017, 356, 62–65 CrossRef PubMed.
- S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson, Y. Hu, D. J. Lundberg, G. Stoychev, S. L. Craig, J. A. Johnson, J. A. Kalow, B. D. Olsen and M. Rubinstein, Chem. Rev., 2021, 121, 5042–5092 CrossRef CAS PubMed.
- B. Marco-Dufort, R. Iten and M. W. Tibbitt, J. Am. Chem. Soc., 2020, 142, 15371–15385 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- W. Denissen, G. Rivero, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. Du Prez, Adv. Funct. Mater., 2015, 25, 2451–2457 CrossRef CAS.
- J. S. A. Ishibashi and J. A. Kalow, ACS Macro Lett., 2018, 7, 482–486 CrossRef CAS PubMed.
- F. Van Lijsebetten, Y. Spiesschaert, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2021, 143, 15834–15844 CrossRef CAS PubMed.
- F. Van Lijsebetten, K. De Bruycker, Y. Spiesschaert, J. M. Winne and F. E. Du Prez, Angew. Chem. Int. Ed., 2022, 61(9) DOI:10.1002/anie.202113872.
- A. Rekondo, R. Martin, A. Ruiz de Luzuriaga, G. Cabañero, H. J. Grande and I. Odriozola, Mater. Horiz., 2014, 1, 237–240 RSC.
- M. M. Obadia, B. P. Mudraboyina, A. Serghei, D. Montarnal and E. Drockenmuller, J. Am. Chem. Soc., 2015, 137, 6078–6083 CrossRef CAS PubMed.
- P. Chakma, C. N. Morley, J. L. Sparks and D. Konkolewicz, Macromolecules, 2020, 53, 1233–1244 CrossRef CAS.
- D. J. Fortman, J. P. Brutman, C. J. Cramer, M. A. Hillmyer and W. R. Dichtel, J. Am. Chem. Soc., 2015, 137, 14019–14022 CrossRef CAS PubMed.
- Y. Nishimura, J. Chung, H. Muradyan and Z. Guan, J. Am. Chem. Soc., 2017, 139, 14881–14884 CrossRef CAS PubMed.
- S. Wu, H. Yang, S. Huang and Q. Chen, Macromolecules, 2020, 53, 1180–1190 CrossRef CAS.
- A. Breuillac, A. Kassalias and R. Nicolaÿ, Macromolecules, 2019, 52, 7102–7113 CrossRef CAS.
- Z. Song, Z. Wang and S. Cai, Mech. Mater., 2021, 153, 103687 CrossRef.
- R. G. Ricarte, F. Tournilhac and L. Leibler, Macromolecules, 2019, 52, 432–443 CrossRef CAS.
- S. Wu, Z. Yang, S. Fang, Z. Tang, F. Liu and B. Guo, J. Mater. Chem. A, 2019, 7, 1459–1467 RSC.
- S. Ge, S. Samanta, B. Li, G. P. Carden, P.-F. Cao and A. P. Sokolov, ACS Nano, 2022, 16, 4746–4755 CrossRef CAS PubMed.
- R. L. Snyder, D. J. Fortman, G. X. De Hoe, M. A. Hillmyer and W. R. Dichtel, Macromolecules, 2018, 51, 389–397 CrossRef CAS.
- J. J. Lessard, G. M. Scheutz, R. W. Hughes and B. S. Sumerlin, ACS Appl. Polym. Mater., 2020, 2, 3044–3048 CrossRef CAS.
- L. E. Porath and C. M. Evans, Macromolecules, 2021, 54, 4782–4791 CrossRef CAS.
- M. Guerre, C. Taplan, R. Nicolaÿ, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2018, 140, 13272–13284 CrossRef CAS PubMed.
- Q.-A. Poutrel, J. J. Blaker, C. Soutis, F. Tournilhac and M. Gresil, Polym. Chem., 2020, 11, 5327–5338 RSC.
- H. Zhang, S. Majumdar, R. A. T. M. van Benthem, R. P. Sijbesma and J. P. A. Heuts, ACS Macro Lett., 2020, 9, 272–277 CrossRef CAS PubMed.
- F. Van Lijsebetten, S. Engelen, E. Bauters, W. Van Vooren, M. M. J. Smulders and F. E. Du Prez, Eur. Polym. J., 2022, 176, 111426 CrossRef CAS.
- D. C. Johnston, Phys. Rev. B, 2006, 74, 184430 CrossRef.
- M. A. Bin Rusayyis and J. M. Torkelson, Polym. Chem., 2021, 12, 2760–2771 RSC.
- D. Apitz and P. M. Johansen, J. Appl. Phys., 2005, 97, 063507 CrossRef.
- J. Bergström, in Mechanics of Solid Polymers, Elsevier, 2015, pp. 309–351 Search PubMed.
- R. G. Ricarte, F. Tournilhac, M. Cloître and L. Leibler, Macromolecules, 2020, 53, 1852–1866 CrossRef CAS.
- L. Porath, J. Huang, N. Ramlawi, M. Derkaloustian, R. H. Ewoldt and C. M. Evans, Macromolecules, 2022, 55, 4450–4458 CrossRef CAS.
- J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 1980, p. 672 Search PubMed.
- M. Delahaye, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2019, 141, 15277–15287 CrossRef CAS PubMed.
- L. L. Schaleger and F. A. Long, Adv. Phys. Org. Chem., 1963, 1, 1–33 CrossRef CAS.
- S. Aime, N. D. Eisenmenger and T. A. P. Engels, J. Rheol., 2017, 61, 1329 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1936, 4, 283 CrossRef CAS.
- A. Pross, in Theoretical and physical principles of organic reactivity, John Wiley and Sons, 1995 Search PubMed.
- M. Guerre, C. Taplan, J. M. Winne and F. E. Du Prez, Chem. Sci., 2020, 11, 4855–4870 RSC.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- L. G. D. Hawke, M. Ahmadi, H. Goldansaz and E. van Ruymbeke, J. Rheol., 2016, 60, 297 CrossRef CAS.
- E. Van Ruymbeke, J. J. M. Slot, M. Kapnistos and P. A. M. Steeman, Soft Matter, 2013, 9, 6921–6935 RSC.
- B. J. Gold, C. H. Hövelmann, N. Lühmann, N. K. Székely, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, ACS Macro Lett., 2017, 6, 73–77 CrossRef CAS PubMed.
- S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem. Int. Ed., 2002, 41, 898–952 CrossRef PubMed.
- G. W. H. Höhne, Thermochim. Acta, 1991, 187, 283–292 CrossRef.
- X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698–1702 CrossRef CAS PubMed.
- L. Zhang and S. J. Rowan, Macromolecules, 2017, 50, 5051–5060 CrossRef CAS.
- W. Denissen, M. Droesbeke, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. Du Prez, Nat. Commun., 2017, 8, 14857 CrossRef CAS PubMed.
- I. M. Irshadeen, S. L. Walden, M. Wegener, V. X. Truong, H. Frisch, J. P. Blinco and C. Barner-Kowollik, J. Am. Chem. Soc., 2021, 143, 21113–21126 CrossRef CAS PubMed.
- N. Sowan, H. B. Song, L. M. Cox, J. R. Patton, B. D. Fairbanks, Y. Ding and C. N. Bowman, Adv. Mater., 2021, 33, 2007221 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05528g |
| This journal is © The Royal Society of Chemistry 2022 |