Intermolecular noncovalent interactions with carbon in solution

Abstract

One of the most familiar carbon-centered noncovalent interactions (NCIs) involving an antibonding π*-orbital situated at the Bürgi–Dunitz angle from the electron donor, mostly lone pairs of electrons, is known as n → π* interactions, and if it involves a σ* orbital in a linear fashion, then it is known as the carbon bond. These NCIs can be intra- or inter-molecular and are usually weak in strength but have a paramount effect on the structure and function of small-molecular crystals and proteins. Surprisingly, the experimental evidence of such interactions in the solution phase is scarce. It is even difficult to determine the interaction energy in the solution. Using NMR spectroscopy aided with molecular dynamics (MD) simulation and high-level quantum mechanical calculations, herein we provide the experimental evidence of intermolecular carbon-centered NCIs in solution. The challenge was to find appropriate heterodimers that could sustain room temperature thermal energy and collisions from the solvent molecules. However, after several trial model compounds, the pyridine-N-oxide:dimethyltetracyanocyclopropane (PNO–DMTCCP) complex was found to be a good candidate for the investigation. NBO analyses show that the PNO:DMTCCP complex is stabilized mainly by intermolecular n → π* interaction when a weaker carbon bond gives extra stability to the complex. From the NMR study, it is observed that the NCIs between DMTCCP and PNO are enthalpy driven with an enthalpy change of −28.12 kJ mol⁻¹ and dimerization energy of ∼−38 kJ mol⁻¹ is comparable to the binding energies of a conventional hydrogen-bonded dimer. This study opens up a new strategy to investigate weak intermolecular interactions such as n → π* interaction and carbon bonds in the solution phase.

---

Introduction

In the province of noncovalent interactions (NCIs), the hydrogen bond (H-bond) is the most celebrated one.^1,2 Other interactions also play a paramount role in stabilizing small-molecule crystals to macromolecules such as proteins and nucleic acids.^3–7 Apart from H atoms, other elements can act as electron acceptors and form several NCIs.⁸ For example, carbon can use both an antibonding σ*-orbital and π*-orbitals as electron acceptors giving rise to the formation of carbon bonds and n → π* interactions, respectively. Carbon bonds are σ-hole driven noncovalent interactions.⁹ The σ-hole is the positive or electron-deficient region formed along the extension of the Y–X covalent σ-bond (Y = electron-rich atom or group, X = atom of groups 14–17; 14: tetrel, 15: pnictogen, 16: chalcogen, and 17: halogen groups). It arises due to the anisotropic distribution of electron density on the atom of groups 14–17 when covalently bonded to electron-withdrawing groups. These σ-holes are suitable for NCIs with electron-rich moieties, provided they approach each other in a favorable geometrical fashion.¹⁰ Similarly, suppose the nonbonding electrons (n) of the donor go to the π*-orbital of the acceptor in a Bürgi and Dunitz fashion (vide infra), it is called an n → π* interaction. Since their inception, n → π* interactions have been widely explored by researchers across the globe. In several cases, both the carbon bond and n → π* interaction are responsible for biomolecular structures and function.^{4–7,11–16} There are plenty of organic/inorganic reactions where a nucleophilic attack occurs in a Bürgi–Dunitz fashion. Wallis and co-workers observed the very first nucleophilic approach in such a manner.¹⁷ They proposed that the lone pair of pyridine N atoms approaches the adjacent nitrile group present in the same molecule through an angle of 108°. In 2017, Shang et al. proposed a mechanism for the α-arylation of alkyl nitriles, where they reported a simultaneous process of attaching the triflyl anion to the nitrile and the addition of the nitrogen atom to the sulfur atom of the sulfoxide;¹⁸ the former process involves an intermolecular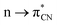 interaction. Similarly, Bauzá et al. provided computational evidence for the carbon bonds that enable these small cycloalkanes to be good supramolecular synthons.¹⁹ Frontera and co-workers reported that carbon bonds are responsible in many cases for stabilizing the structures of acylhydrazones.²⁰ Sarma and coworkers showed the same effect in diacylhydrazines.²¹ With the help of X-ray diffraction and DFT study, Mooibroek and co-workers showed the applications of carbon bonds in crystal engineering.²² Wang et al., by using NMR spectroscopy, provided ample evidence of the importance of carbon bonds in catalysis.²³

Bürgi and Dunitz were the first to report the n → π* interaction.²⁴ They revealed that the lone pair of electrons of the nucleophile approaches the empty π*-orbital of the electrophile at a 150–300 pm distance and an angle of 107°. The approaching angle of the nucleophile to the electrophile is known as the Bürgi–Dunitz trajectory. Later on, Allen found such interaction in carbonyls with a strength similar to H bonds.²⁵ For a given O⋯C=O interaction, the distance between O and C (d_O⋯C) should be within the sum of their van der Waals' radii, and ∠O⋯C=O (θ) within the range of 109 ± 10° to have the Bürgi–Dunitz trajectory (Fig. 1a). It is reported that the donor carbonyl distorts the acceptor carbonyl from its planarity due to the n → π* interaction, which is a signature of the said interaction.²⁶ The distortion can be measured by using the angle of deviation from the plane (φ) and the degree of pyramidization (Δ). However, Raines and co-workers' seminal contributions to investigating the n → π* interaction in biomolecules are worth mentioning here. Since then, the interaction has been observed in other proteins, polypeptides, peptoids, thiopeptoids, and model compounds.^7,11,27–29 Using nuclear magnetic resonance (NMR) experiments, X-ray crystallography, and ab initio calculations, Raines and co-workers explained the nature and the role of n → π* interaction in proline derivatives, collagen triple helix structures, and different conformations of peptoids and thiopeptoids.^6,30–32 Later on, Alonso and co-workers unveiled the n → π* interaction in dipeptides with the help of rotational spectroscopy and computational calculations.³³ But the n → π* interaction lacked direct spectroscopic evidence until Aloke Das and co-workers provided it in gas and solution phases.^34,35 They used one color two-photon ionization and UV–UV hole burning spectroscopy and additional computational calculations to assign the vibrational bands of the cis and trans conformers of phenyl formate, and they inferred that the intramolecular 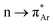interaction is responsible for the stabilization of the cis-conformer of phenyl formate.³⁴ In a successive study of the same system in the solution phase, they found intramolecular interaction competing with the H bond between phenyl formate and water by incorporating 2D-IR spectroscopy.³⁵ Recently, Sarma and co-workers provided evidence of intramolecular interaction using NMR and IR spectroscopy.^29,36 Concisely, direct and indirect experimental evidence has been produced for the intramolecular n → π* interaction in both gas and solution phases to date. Recently, López and co-workers^37,38 and Gou and co-workers³⁹ produced evidence for intermolecular n → π* interactions using rotational spectroscopy in the gas phase.³

Fig. 1 (a) Geometrical parameters of an n → π* interaction. (b) Geometrical parameters of the carbon bond. The molecular electrostatic potential surface (isovalue: 0.001 a.u.) of DMTCCP calculated at the MP2/def2TZVPP level of theory shows the positive electrostatic potential region at (c) the face of the C₁–C₃ bond of the cyclopropane ring and at (d) the face of two methyl groups including the C₂ atom of the ring.

The other NCI involving carbon is known as the C bond. Arunan and co-workers were the first to discover it in small molecular systems.⁹ The concept of the C bond was extended to protein–ligand systems⁴⁰ and between the residues¹⁶ by Frontera and Biswal groups, respectively. The geometrical features of the carbon bond mentioned by Mundlapati et al.¹⁶ state that the carbon bond donor–acceptor distance should be within the sum of their van der Waals radii, and it should be highly directional, i.e., the θ₁ and θ₂ should be within the range of 160° to 180° (Fig. 1b). Later on, Frontera and coworkers explored the potential implications of the carbon bonds in crystal engineering and catalysis.⁴¹ It is worth mentioning that these studies are computational. Using X-ray charge density analysis, Guru Row and Frontera groups provided experimental evidence of carbon bonds in the solid state.^42,43 Bauzá et al. reported the presence of highly directional noncovalent carbon bond donors in small cycloalkanes.⁴⁴ After that, with the help of X-ray crystallography aided by rotational spectroscopy Mooibroek and co-workers showed the presence of the carbon bond in the crystal structure of 3,3-dimethyltetracyanocyclopropane and tetrahydrofuran.⁴⁵ Southern et al. used solid-state NMR spectroscopy to probe the carbon bonding in caffeine and theophylline based co-crystals.⁴⁶ Recently, Wang et al. used supramolecular carbon-bonding catalysis for tail-to-head terpene cyclization in the solution phase.²³

The above-cited literature and the references thereby suggest that the intramolecular n → π* interaction is well studied in the gas and solution phases, whereas only gas phase studies are reported for the intermolecular n → π* interactions. On the other side, there are very few molecular-level investigations on intermolecular and intramolecular carbon bonds in the solution state. However, the noticeable point is that no such experimental studies report intermolecular n → π* interaction in the solution phase. We did not find any report that describes the experimental methodologies to determine the strength of the n → π* interaction or the carbon bond experimentally in the solution phase. The gap in this area impelled us to do the present study and find suitable molecular systems and experimental conditions to provide evidence of intermolecular n → π* interaction in solution and determine its strength. Herein, we present the first experimental report on the strength of intermolecular n → π* interaction co-existing with the carbon bond in the solution phase. The experimental results are supported by molecular dynamics (MD) simulations and high-level quantum mechanical (QM) calculations at the CCSD(T) level.

Results and discussion

Experimental criteria and the system

The first and foremost challenge was to choose the model compounds very wisely, considering a few factors: (i) they must not alter the polarity, density, and viscosity of the solvent used in the experiment, (ii) they should sustain room temperature thermal energy and collisions from the solvent molecules, and (iii) they should possess high interaction energy so that we can probe the NCI in solution. After several trial and error experiments, we chose 3,3-dimethyltetracyanocyclopropane (DMTCCP) as our model compound. This compound possesses different types of carbon atoms (ring carbon, methyl carbon, and nitrile carbon), which can make the carbon bond and n → π* interactions feasible at the same time. The nitrile (CN) group is a good probe to monitor through spectroscopy. The molecular electrostatic potential surface of DMTCCP, provided in Fig. 1c and d, shows the positive blue region at the face of the C₁–C₃ bond and at the face of the methyl groups, which can give rise to the formation of carbon bonds. Similar tetrel-bonded molecular complexes have been reported by Scheiner et al.⁴⁷ If the nucleophile approaches the nitrile carbon atoms through the Bürgi–Dunitz trajectory, it can give rise to n → π* interaction. We chose pyridine-N-oxide (PNO) as the nucleophile to meet the experimental criteria.

Molecular dynamics (MD) studies for the solvated structure of the complex

MD simulations were used to unravel the solvation structure of PNO molecules around DMTCCP (Fig. 2a). The general AMBER force field (GAFF)^48,49 was chosen for MD simulation. GAFF is known to predict thermodynamic properties very accurately.⁵⁰ The DMTCCP–PNO system contained 1 DMTCCP, 40 PNO, and 512 chloroform molecules. A production trajectory of 40 ns post equilibrium was used for analysis. The possibility of the formation of heterodimers of DMTCCP and PNO was diagnosed through various distribution functions. The radial distribution function (RDF) of the oxygen atom of PNO molecules with respect to the center of the ring (COR) of DMTCCP shows a sharp peak at 358 pm (Fig. S1a, ESI†), indicating a possible ordering of PNO molecules when present close to DMTCCP. This prompted us to find the number of PNO molecules close to DMTCCP. Fig. 2b shows the RDFs of the oxygen atoms of the nearest, second-nearest and third nearest PNO molecules with respect to the COR of DMTCCP. The peaks for the nearest and the second-nearest PNO molecules are centered at 353 and 374 pm, respectively. It is worth mentioning that no such peak is found for the third nearest PNO molecule. However, the intensity of the peak corresponding to the nearest PNO molecule is ∼4 times more than that of the second-nearest PNO molecule. This significant difference between the RDFs shows that DMTCCP predominantly interacts with only one molecule of PNO.

Fig. 2 (a) A representative complex between DMTCCP and PNO obtained at t = 1 ns from an MD trajectory of 40 ns. The distance, d_O⋯C and angle ∠O⋯C≡N are 320 pm and 107°, respectively, indicative of an n → π* interaction. (b) Radial distribution function (RDF) between the oxygen atom of PNO molecules and COR of DMTCCP for the nearest (black), second-nearest (red), and third-nearest (blue) neighboring PNO molecules around DMTCCP. (c) Spatial distribution function (SDF) of the oxygen of the PNO molecule (red isosurface) around DMTCCP. (d) Combined distribution function (CDF) between d_O⋯C and ∠O⋯C≡N, and (e) Angular distribution function (ADF) of ∠O⋯C≡N for the nearest neighboring PNO molecules of DMTCCP.

We also looked into the spatial distribution functions (SDFs) to find the three-dimensional density distribution of the oxygen atom of PNO molecules around DMTCCP. The SDF given in Fig. 2c shows that the maximum probability of finding PNO near DMTCCP (large spherical region) is in the pocket flanked by the four nitrile groups. Apart from this region, there is a small probability of finding PNO near the other two sides of the cyclopropane ring (small spheres on two sides of the cyclopropane ring). This outcome corroborates the RDFs on the observation that DMTCCP primarily interacts with one PNO at any given time. Additional angular distribution functions (ADFs) supporting the RDFs and the SDFs are given in the ESI (Fig. S1b–d†).

To further elucidate the interaction between DMTCCP and PNO, we observed the combined distribution function (CDF) of the RDF of the distance between the oxygen of PNO and the nitrile carbon (d_O⋯C) and ADF of the angle formed by the approaching oxygen with the nitrile bond at the nitrile carbon (∠O⋯C≡N). As noncovalent interactions are usually defined by distance and angle criteria, CDFs have been used to observe them.⁵¹ The CDF in Fig. 2d shows a peak between 310 and 330 pm for d_O⋯C and a peak between 100 and 110° for ∠O⋯C≡N. This deep basin in the CDF (magenta region) suggested a possible attractive interaction between DMTCCP and PNO. Also, a significant region of the peak corresponding to d_O⋯C falls within the sum of the van der Waals' radii of carbon and oxygen atoms (i.e., 322 pm), indicative of noncovalent interaction between the oxygen of PNO and the nitrile carbon of DMTCCP. The upper limit of the peak for d_O⋯C (330 pm) is overestimated compared to the sum of van der Waals' radii (322 pm) due to the poor representation of electron donation in the existing force fields.²⁷ We further observed the ADF of ∠O⋯C≡N (Fig. 2e), where the peak is centered at ∼107°. This observation implies that the oxygen of PNO approaches the nitrile group of DMTCCP following a Bürgi–Dunitz trajectory. Hence, there is a high probability of n → π* interaction between the oxygen of PNO and the nitrile of DMTCCP. As classical molecular dynamics cannot fully capture the quantum mechanical nature of n → π* interaction, we further carried out various quantum mechanical calculations to establish this interaction.

Structure and energetics

After optimizing the PNO:DMTCCP complex and its respective monomers in chloroform at the RI-B97D3/def2-TZVPP level of theory, we found that the structures are at energy minima (no imaginary vibrational frequency found). The RI-B97D3 functional is useful in predicting noncovalent interactions fairly well. It faithfully reproduces the experimental spectra and has recently been practiced by several researchers.^52–55 The geometrical analysis of the PNO:DMTCCP complex (Fig. 3a) revealed that two (O⋯C_4/10) of the four d_O⋯C and ∠O⋯C≡N are 293 pm and 107°, respectively, whereas the other two (O⋯C_6/8) d_O⋯C and ∠O⋯C≡N are 312 pm and 114°, respectively. We also found that the ∠C–C≡N in DMTCCP deviates from linearity (180° → 177°) in the complex. These observations are the signatures of n → π* interaction. On the other hand, the distance between the PNO–O and the C₁/C₃ atoms is 291 pm but the ∠O⋯C₁₍₃₎–C₂ is 133°, which does not satisfy the geometrical features of a carbon bond. Then we calculated the single point energy of the optimized structures at the gold standard CCSD(T)/def2-TZVPP level of theory in chloroform.^56,57 The binding energy of the PNO:DMTCCP complex in chloroform was estimated to be −37.60 kJ mol⁻¹, which is comparable to the hydrogen bond energies.⁵⁸ The binding energy is much higher than that of the homodimers of DMTCCP (−19.72 kJ mol⁻¹) and homodimers of PNO (−15.70 kJ mol⁻¹). Again, we did not observe any spectral features of homodimers in our experimental conditions (vide infra). Thus the intermolecular complex with high binding energy is a suitable model system to carry out experiments to detect the n → π* or n → σ* interactions in solution.

Fig. 3 (a) Fully optimized structure of the PNO:DMTCCP complex at the RI-B97D3/def2-TZVPP level of theory. The binding energy at the CCSD(T) level is −37.6 kJ mol⁻¹. (b) The energy decomposition analysis shows that the interaction is dominated by electrostatic and dispersion. (c) Natural bond orbital (NBO) overlaps between the lone pairs of electrons of PNO–oxygen and the π*-orbital of the nitrile bond of DMTCCP: n → π* interaction. (d) NBO overlap between the lone pairs of electrons of PNO–oxygen and the σ*-orbital of the C₁–C₂ bond of DMTCCP: n → σ* interaction.

We performed an energy decomposition analysis to determine the major contributor to the high binding energy. The second-order symmetry-adapted perturbation theory (SAPT2) methodology was used to decompose the total binding energy to electrostatic (EL), exchange (EX), dispersion (DISP), and induction (IND). The energy distribution is shown in Fig. 3b. From Fig. 3b, it is clear that the electrostatic and dispersion are the major contributors to the interaction energy. The obtained result is in accordance with a recent study on intermolecular n → π* interaction.³⁸ To get insight into orbital involvement for this intermolecular complex, we performed NBO analysis in chloroform at the MP2/def2-TZVPP level of theory.⁵⁹ The donor–acceptor interaction energy was calculated under the framework of second-order perturbation theory. The lone pairs of oxygen in PNO delocalized into the π*-orbitals of C≡N (Fig. 3c), providing a total donor–acceptor interaction energy of 17.97 kJ mol⁻¹ (details are provided in the ESI, Table S1†). The donor–acceptor interaction energy for each interaction is higher than the lower limit (1.13 kJ mol⁻¹) for any type of n → π* interaction¹⁵ and comparable to the donor–acceptor energy found for an intermolecular interaction.³ We also observed overlaps between the lone pair of electrons of PNO–oxygen and σ*-orbital of the C₁–C₂ bond and C₂–C₃ bond of the cyclopropane ring in DMTCCP (n → σ*, carbon bond) (Fig. 3d), and the total donor–acceptor energy of the carbon bond interaction is 5.16 kJ mol⁻¹ which is ∼3.5 times lower than that of the n → π* interaction. Hence, in the PNO:DMTCCP complex, the primary interaction is n → π* interaction, while the n → σ* interaction or carbon bonding is the auxiliary interaction providing extra stability to the complex. It is worth mentioning that the PNO forms an intermolecular complex with DMTCCP through the n → π* interaction (major) and the n → σ* interaction (minor), which results in high binding energy. This type of enhancement in binding energy due to multiple binding is known as the avidity effect.⁶⁰ We also analyzed the electron density with Bader's quantum theory of atoms in molecules.⁶¹ The positive mutual penetration values (Table S2†) confirm the presence of noncovalent interactions⁹ between the PNO–O and the C atoms of the DMTCCP molecule through n → π* interaction and carbon bonds. A detailed analysis is provided in the ESI.†

Spectroscopic tools

The theoretical observations persuaded us to find out the strength of the interactions experimentally in the solution. DMTCCP possesses nitrile (cyano, C≡N) functional groups, which can be probed through IR and NMR spectroscopy. IR and NMR spectroscopy are quite useful techniques to probe any NCI experimentally.^62–66 Thus, the strength of the interactions can be determined in two ways: (i) by monitoring the vibrational stretching frequency of the C≡N bond (ν_C≡N) in DMTCCP and (ii) by monitoring the chemical shift of the nitrile carbon (δ_CN) of DMTCCP.

We carried out the theoretical vibrational frequency and NMR analyses to have an initial idea about the change in the C≡N stretching frequency and the chemical shift of the nitrile carbon upon complex formation. It was observed that the C≡N stretching frequency (ν_C≡N) in DMTCCP redshifts by 1.2 cm⁻¹ (from 2255.8 cm⁻¹ to 2254.6 cm⁻¹, Fig. 4a) upon complex formation with PNO. In general, the experimental IR spectra are broad. On the other hand, the ¹³C-NMR spectra of the nitrile carbon show a downfield chemical shift of ∼0.9 ppm (from 107.9 ppm to 108.8 ppm, Fig. 4b) upon complex formation with PNO. The experimental ¹³C-NMR peaks are sharp, and the NMR spectra are narrower in comparison to the IR spectra in solution. Hence, we adopted NMR spectroscopy over IR spectroscopy to quantify the strength of the interaction experimentally.

Fig. 4 (a) Theoretical IR spectra in the nitrile (ν_C≡N) stretching region for the monomer (black line) and PNO:DMTCCP complex (red line) in CHCl₃. The spectra are fitted with the experimental FWHM and scaled by a factor of 0.95. (b) Theoretical ¹³C-NMR chemical shifts for nitrile carbon atoms in the monomer and the complex, scaled with the experimental data by a factor of 0.93.

Quantitative NMR spectroscopy is regularly practiced to study the non-covalent interactions and reaction mechanisms.^63,67–69 We carried out ¹³C-NMR titrations in two ways. The chemical shift of nitrile carbon of DMTCCP was monitored: (i) by fixing [DMTCCP] and varying [PNO] (concentration-dependent NMR), and (ii) by varying the temperature at a fixed concentration (0.03 M DMTCCP + 1.5 M PNO) of DMTCCP and PNO (temperature-dependent NMR), because it is well known that the dimer yielding from an NCI is favorable at high concentrations and low temperatures. The concentration-dependent NMR study provides the association constant or equilibrium constant (K_a) of the reaction: PNO + DMTCCP ⇌ PNO–DMTCCP. We observed a downfield chemical shift in δ_CN upon increasing the PNO concentration. The downfield chemical shift of δ_CN is due to the complex formation⁷⁰ (more explanation is provided in the ESI†). A saturation of chemical shift of δ_CN after a particular concentration of PNO (Fig. S6, ESI†) was noticed. The downfield chemical shift of δ_CN is about 0.7 ppm, which is in line with the computationally predicted downfield shift. The fitting of the chemical shifts against the concentration of PNO in a 1 : 1 binding isotherm (eqn (S4), ESI†) yielded an association constant (K_a) of 2.32 ± 0.18 M⁻¹. The Gibbs free energy change (ΔG) calculated from K_a is −2.09 ± 0.39 kJ mol⁻¹ (Fig. 5a). The temperature-dependent NMR study in the temperature range of 233–313 K reveals the enthalpy change (ΔH) of the interaction. We observed an upfield shift of δ_CN with increasing temperature due to the weakening of the noncovalent interactions at high temperature (Fig. S7, ESI†), indicating the dissociation of the complex at the higher temperature. The chemical shift values were plotted against the temperature and fitted to the 1 : 1 binding isotherm (eqn (S5), ESI†). The fitting yielded a ΔH of −28.12 ± 3.42 kJ mol⁻¹ (Fig. 5b). This experimentally obtained ΔH is comparable to the calculated ΔH of −35.88 kJ mol⁻¹ at the CCSD(T) level of theory. The change in entropy (ΔS) calculated from the ΔG and ΔH values is −0.09 kJ mol⁻¹ K⁻¹. From the values of ΔG, ΔH, and ΔS, one can infer that the high negative value of enthalpy change is the stabilizing factor for complexation. To ensure that the downfield chemical shift upon addition of PNO is due to the complex formation between DMTCCP and PNO, we performed the conventional diffused ordered spectroscopy (DOSY) experiment.^71,72 The natural logarithmic normalized signal strength [ln(I/I₀)] against the squared gradient pulse power was fitted with the Stejskal–Tanner equation to calculate the translational diffusion coefficients (D) of the DMTCCP and PNO–DMTCCP mixture (Fig. 5c).^63,73

Fig. 5 (a) Concentration-dependent NMR experiment shows the shift of δ_CN (downfield) upon addition of PNO providing the ΔG-value. (b) Temperature-dependent shifts of δ_CN of 0.03 M DMTCCP-1.5 M PNO solution provides the ΔH-value. (c) Calculation of the diffusion co-efficient by fitting the data obtained from DOSY experiments of DMTCCP (hollow dots and blue line) and PNO–DMTCCP (solid dots and red line) into the Stejskal–Tanner equation. (d) Calculation of the diffusion coefficients of DMTCCP in CHCl₃ (black) and DMTCCP in PNO and CHCl₃ (red) by using the mean squared displacement (MSD)–time plot from the MD trajectories.

The D_DMTCCP is 2.085 × 10⁻⁹ m² s⁻¹, and D_PNO–DMTCCP is 1.412 × 10⁻⁹ m² s⁻¹. The ratio of the translational diffusion coefficient between the monomer and the complex is 1.476. The Stoke–Einstein (SE) equation: D = k_BT/6πηR, k_B is the Boltzmann constant, T is the absolute temperature, η is the shear viscosity coefficient of the solution, and R is the hydrodynamic radius of the molecule, is usually used to predict the molecular weight of the complex, assuming that the molecule is spherical and does not change the viscosity, the density and the temperature of the solvent. However, there are reports where the Stoke–Einstein equation fails to explain the diffusion coefficient for small molecules.^74–76 Nevertheless, the ratio of translational diffusion coefficients of monomer to complex calculated from the MD trajectories by the mean squared displacement method (see the ESI† for details)⁷⁷ was 1.40 (Fig. 5d), close to the experimental value. Again, as we saw that the DMTCCP molecule has only one neighboring PNO molecule from the MD simulation data (vide supra), the downfield chemical shift of the nitrile carbon atom of DMTCCP upon adding PNO is due to the dimer formation between the said molecules. Therefore, the NMR experiments provided experimental evidence of dimer formation between DMTCCP and PNO along with the strength of the noncovalent interactions i.e., intermolecular n → π* interactions assisted by intermolecular carbon bonds in solution, which were confirmed through the quantum mechanical and MD simulation studies. As mentioned earlier, finding appropriate model systems and experimental conditions and choosing suitable spectroscopic tools are challenging. To our fortune, all these choices are befitting to provide ample evidence and the strength of those intermolecular carbon-centered noncovalent interactions in the solution.

Conclusions

Although there are plenty of experimental reports on intramolecular n → π* interactions in solution, only gas phase studies were carried out to evidence the presence of intermolecular n → π* interactions. Concisely, there was no report on the experimental evidence of the intermolecular n → π* interaction and its strength in solution to date. Herein, we have provided evidence of the existence and strength of the intermolecular carbon-centered noncovalent interactions, i.e., n → π* and n → σ* interactions, in solution through a combined study of NMR spectroscopy and quantum mechanical calculations aided with MD simulations. The CCSD(T) binding energy for the dimer formation is ∼38 kJ mol⁻¹. The NBO anlyses suggest that the overall binding energy is due to the combined contributions from the n → π* (major) and the n → σ* (minor) interaction. The ΔH-value of −28.12 kJ mol⁻¹ obtained from concentration- and temperature-dependent NMR experiments suggests that the interaction between DMTCCP and PNO is enthalpy driven. Therefore, it can be said that the co-existence of the two moderately strong (n → π*) and weak (n → σ*) interactions provided great stability to the PNO:DMTCCP heterodimer structure. The experimental and computational methodologies adopted in this work will be useful in rationally designing experimental protocols to investigate weak noncovalent interactions in the condensed phase. We hope that the work presented here will be helpful to scientists in crystal engineering, chemical biology, and organic chemistry in designing new molecules and reactions, explaining the conformational stability of various biomolecules, and deducing and illustrating the mechanism of the reactions involving n → π* interaction and carbon bonds.

Author contributions

The manuscript was written through the contributions of all authors. H. S. B. conceived the idea. J. D. performed all the experiments and electronic structure calculations. C. R. carried out MD simulations. S. P. helped in DOSY measurements. All authors have given approval to the final version of the manuscript.

Data availability

The data supporting this work is uploaded as a part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The manuscript is dedicated in memory of Prof. Jack D. Dunitz, who is famous for the Bürgi–Dunitz angle. J. D., C. R., S. P., and H. S. B. acknowledge the financial support from the Department of Atomic Energy, Govt. of India. Financial support (Project File No. CRG/20l8/000892) from the Department of Science and Technology, Govt. of India, is duly acknowledged.

Notes and references

1. A. Chand, D. K. Sahoo, A. Rana, S. Jena and H. S. Biswal, Acc. Chem. Res., 2020, 53, 1580–1592.
2. S. Scheiner, J. Indian Inst. Sci., 2020, 100, 61–76.
3. S. K. Singh, S. Kumar and A. Das, Phys. Chem. Chem. Phys., 2014, 16, 8819–8827.
4. S. Sarkhel, A. Rich and M. Egli, J. Am. Chem. Soc., 2003, 125, 8998–8999.
5. M. Egli and R. V. Gessner, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 180–184.
6. G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620.
7. W. G. Scott, J. T. Finch and A. Klug, Cell, 1995, 81, 991–1002.
8. S. Jena, J. Dutta, K. D. Tulsiyan, A. K. Sahu, S. S. Choudhury and H. S. Biswal, Chem. Soc. Rev., 2022, 51, 4261–4286.
9. D. Mani and E. Arunan, Phys. Chem. Chem. Phys., 2013, 15, 14377–14383.
10. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
11. M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197–205.
12. T. K. Pal and R. Sankararamakrishnan, J. Phys. Chem. B, 2010, 114, 1038–1049.
13. H. R. Kilgore and R. T. Raines, J. Am. Chem. Soc., 2018, 140, 17606–17611.
14. H. R. Kilgore, C. R. Olsson, K. A. D'Angelo, M. Movassaghi and R. T. Raines, J. Am. Chem. Soc., 2020, 142, 15107–15115.
15. R. W. Newberry, B. VanVeller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135, 7843–7846.
16. V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Angew. Chem., Int. Ed., 2018, 57, 16496–16500.
17. P. N. W. Baxter, J. A. Connor, D. C. Povey and J. D. Wallis, J. Chem. Soc., Chem. Commun., 1991, 1135–1137,  10.1039/c39910001135.
18. L. Shang, Y. Chang, F. Luo, J.-N. He, X. Huang, L. Zhang, L. Kong, K. Li and B. Peng, J. Am. Chem. Soc., 2017, 139, 4211–4217.
19. A. Bauzá, A. Frontera and T. J. Mooibroek, Phys. Chem. Chem. Phys., 2016, 18, 1693–1698.
20. M. M. Naseer, M. Hussain, A. Bauzá, K. M. Lo and A. Frontera, ChemPlusChem, 2018, 83, 881–885.
21. J. K. R. Deka, B. Sahariah, K. Baruah, A. K. Bar and B. K. Sarma, Chem. Commun., 2020, 56, 4874–4877.
22. J. J. Roeleveld, S. J. Lekanne Deprez, A. Verhoofstad, A. Frontera, J. I. van der Vlugt and T. J. Mooibroek, Chem.–Eur. J., 2020, 26, 10126–10132.
23. W. Wang, X. Li, P.-P. Zhou and Y. Wang, Angew. Chem., Int. Ed., 2021, 60, 22717–22721.
24. H. B. Burgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067.
25. F. H. Allen, C. A. Baalham, J. P. M. Lommerse and P. R. Raithby, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 320–329.
26. A. Choudhary, R. W. Newberry and R. T. Raines, Org. Lett., 2014, 16, 3421–3423.
27. R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846.
28. S. K. Singh and A. Das, Phys. Chem. Chem. Phys., 2015, 17, 9596–9612.
29. B. Sahariah and B. K. Sarma, Phys. Chem. Chem. Phys., 2020, 22, 26669–26681.
30. M. L. DeRider, S. J. Wilkens, M. J. Waddell, L. E. Bretscher, F. Weinhold, R. T. Raines and J. L. Markley, J. Am. Chem. Soc., 2002, 124, 2497–2505.
31. A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 7244–7246.
32. A. Choudhary and R. T. Raines, ChemBioChem, 2011, 12, 1801–1807.
33. I. León, E. R. Alonso, C. Cabezas, S. Mata and J. L. Alonso, Commun. Chem., 2019, 2, 3.
34. S. K. Singh, K. K. Mishra, N. Sharma and A. Das, Angew. Chem., Int. Ed., 2016, 55, 7801–7805.
35. P. Deb, G. Y. Jin, S. K. Singh, J. Moon, H. Kwon, A. Das, S. Bagchi and Y. S. Kim, J. Phys. Chem. Lett., 2018, 9, 5425–5429.
36. J. K. R. Deka, B. Sahariah, S. S. Sakpal, A. K. Bar, S. Bagchi and B. K. Sarma, Org. Lett., 2021, 23, 7003–7007.
37. S. Blanco and J. C. López, J. Phys. Chem. Lett., 2018, 9, 4632–4637.
38. J. C. López, I. Alkorta, A. Macario and S. Blanco, Phys. Chem. Chem. Phys., 2022, 24, 15484–15493.
39. H. Wang, J. Wang, J. Chen, S. Herbers, H. Zheng and Q. Gou, Phys. Chem. Chem. Phys., 2021, 23, 8778–8783.
40. A. Bauzá and A. Frontera, Crystals, 2016, 6, 26.
41. A. Frontera, C, 2020, 6, 60.
42. S. P. Thomas, M. S. Pavan and T. N. Guru Row, Chem. Commun., 2014, 50, 49–51.
43. E. C. Escudero-Adán, A. Bauzá, A. Frontera and P. Ballester, ChemPhysChem, 2015, 16, 2530–2533.
44. A. Bauzá, T. J. Mooibroek and A. Frontera, Chem.–Eur. J., 2014, 20, 10245–10248.
45. T. J. Mooibroek, Molecules, 2019, 24, 3370.
46. S. A. Southern, M. S. West, M. J. Z. Bradshaw and D. L. Bryce, J. Phys. Chem. C, 2021, 125, 2111–2123.
47. S. Scheiner, Molecules, 2020, 25, 4495.
48. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
49. G. A. Özpınar, W. Peukert and T. Clark, J. Mol. Model., 2010, 16, 1427–1440.
50. K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882–5895.
51. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023.
52. V. R. Mundlapati, Z. Imani, V. C. D'Mello, V. Brenner, E. Gloaguen, J.-P. Baltaze, S. Robin, M. Mons and D. J. Aitken, Chem. Sci., 2021, 12, 14826–14832.
53. Z. Imani, V. R. Mundlapati, G. Goldsztejn, V. Brenner, E. Gloaguen, R. Guillot, J.-P. Baltaze, K. Le Barbu-Debus, S. Robin, A. Zehnacker, M. Mons and D. J. Aitken, Chem. Sci., 2020, 11, 9191–9197.
54. G. Goldsztejn, V. R. Mundlapati, V. Brenner, E. Gloaguen and M. Mons, Molecules, 2022, 27, 3163.
55. J. Donon, J.-X. Bardaud, V. Brenner, S.-I. Ishiuchi, M. Fujii and E. Gloaguen, Phys. Chem. Chem. Phys., 2022, 24, 12121–12125.
56. A. R. Neves, P. A. Fernandes and M. J. Ramos, J. Chem. Theory Comput., 2011, 7, 2059–2067.
57. P. Hobza, Acc. Chem. Res., 2012, 45, 663–672.
58. H. A. Gebbie, W. J. Burroughs, J. Chamberlain, J. E. Harries and R. G. Jones, Nature, 1969, 221, 143–145.
59. J. N. Sharley, arXiv preprint arXiv:1512.04171, 2015.
60. P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271–16284.
61. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15.
62. L. Nisius and S. Grzesiek, Nat. Chem., 2012, 4, 711–717.
63. V. R. Mundlapati, S. Gautam, D. K. Sahoo, A. Ghosh and H. S. Biswal, J. Phys. Chem. Lett., 2017, 8, 4573–4579.
64. M. R. Panman, B. H. Bakker, D. den Uyl, E. R. Kay, D. A. Leigh, W. J. Buma, A. M. Brouwer, J. A. J. Geenevasen and S. Woutersen, Nat. Chem., 2013, 5, 929–934.
65. B. Auer, R. Kumar, J. R. Schmidt and J. L. Skinner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14215–14220.
66. N. Nagels, D. Hauchecorne and W. A. Herrebout, Molecules, 2013, 18, 6829–6851.
67. S. S. Choudhury, S. Mahapatra and H. S. Biswal, Green Chem., 2022, 24, 4981–4990.
68. G. N. M. Reddy, A. Marsh, J. T. Davis, S. Masiero and S. P. Brown, Cryst. Growth Des., 2015, 15, 5945–5954.
69. Y. Chae, S. Min, E. Park, C. Lim, C.-H. Cheon, K. Jeong, K. Kwak and M. Cho, Anal. Chem., 2021, 93, 2106–2113.
70. S. Jena, C. Routray, J. Dutta and H. S. Biswal, Angew. Chem., Int. Ed., 2022, 61, e202207521.
71. C. S. Johnson, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203–256.
72. Y. Cohen, L. Avram and L. Frish, Angew. Chem., Int. Ed., 2005, 44, 520–554.
73. E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292.
74. J. T. Edward, J. Chem. Educ., 1970, 47, 261.
75. R. Evans, Z. Deng, A. K. Rogerson, A. S. McLachlan, J. J. Richards, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2013, 52, 3199–3202.
76. A. Polson, J. Phys. Colloid Chem., 1950, 54, 649–652.
77. J. Wang and T. Hou, J. Comput. Chem., 2011, 32, 3505–3519.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05431k

---