ChemSims: using simulations and screencasts to help students develop particle-level understanding of equilibrium in an online environment before and during COVID

Abstract

Equilibrium is a challenging concept for many, largely because developing a deep conceptual understanding of equilibrium requires someone to be able to connect the motions and interactions of particles that cannot be physically observed with macroscopic observations. Particle level chemistry animations and simulations can support student connections of particle motion with macroscopic observations, but for topics such as equilibrium additional visuals such as graphs are typically present which add additional complexity. Helping students make sense of such visuals requires careful scaffolding to draw their attention to important features and help them make connections between representations (e.g., particle motion and graphical representations). Further, as students enter our classrooms with varying levels of background understanding, they may require more or less time working with such simulations or animations to develop the desired level of conceptual understanding. This paper describes the development and testing of activities that use the PhET simulation “Reactions and Rates” to introduce the concept of equilibrium as a student preclass activity either in the form of directly using the simulation or guided by an instructor through a screencast. The pre-post analysis of the two most recent implementations of these activities indicates that students show improved understanding of the core ideas underlying equilibrium regardless of instructor, institution, or type of instructional environment (face to face or remote). We also observed that students were more readily able to provide particle level explanations of changes in equilibrium systems as they respond to stresses (such as changes to concentration and temperature) if they have had prior course instruction on collision theory. Lastly, we observed that student answers to explain how an equilibrium will respond to an applied stress more often focus on either initial responses or longer-term stability of concentrations, not on both key aspects.

---

Introduction

Students enter our introductory college science classes with a variety of background experiences and abilities. For some students, introductory science courses are largely a review from high school while for others it is the first time they are encountering the material. Further, some students may require more or less time to process material. This is one of the rationale for “flipped” classrooms where students engage in some kind of activity on their own prior to class (readings, watching videos, etc.) and then spend class time working through homework problems (Abeysekera and Dawson, 2015). The popularity of the flipped classroom has grown substantially in the last decade as evidenced by fewer than 20 articles focused on flipped classroom published in science education journals in 2010, to over 100 in 2018, and over 200 for the years 2020 and 2021. Of those published in 2020–2021, 31 focused specifically on chemistry education (Eichler, 2022). Unfortunately, the traditional version of the flipped classroom, where students watch lecture videos outside of class and do homework type problems in class, suffers from the same issues as the traditional lecture (Bancroft et al., 2021). In a recent commentary on the future of the flipped classroom, Eichler encourages the chemistry education community to, “transition the focus from probing the general efficacy of the flipped classroom to investigating how the preclass learning and in-person instruction can be optimized to address chemistry-specific learning objectives.” Determining the key features of effective preclass learning activities is critical given that although the stated impetus for implementing a flipped classroom is often the incorporation of more active learning during the in-class instruction, research studies have shown that improved student outcomes depend largely on the preclass activities (Eichler and Peeples, 2016; Rau et al., 2017; Bancroft et al., 2021). Passive lectures, whether in class or outside of class via video, have been repeatedly shown to have very little impact on student learning (Koedinger et al., 2015). However, incentivizing students’ active engagement in activities that support their development of conceptual understanding have been found to increase student achievement (Chi and Wylie, 2014; Bancroft et al., 2021). The use of such activities in college classes have sometimes been shown to result in lower student perceptions of learning and enjoyment (Deslauriers et al., 2019), but in the recent emergency shift to remote teaching caused by the COVID-19 pandemic, it was these types of activities that resulted in increased student perceptions of enjoyment and learning (Nguyen et al., 2021).

This paper focuses on the development and evaluation of activities designed to actively engage students in the construction of a conceptual understanding of equilibrium systems and to be completed by students outside of the classroom prior to any formal in-class instruction. These activities are designed to provide students with an introduction to dynamic equilibrium systems by scaffolding their interactions with a particle-level simulation. Equilibrium is typically a challenging concept in chemistry (Bergquist and Heikkinen, 1990; Cheung, 2009) and providing students an opportunity to engage with this concept outside of the classroom allows them to work through the material at their own pace as well as provides a common experience that instructors can build on during in class instruction. However, appropriate scaffolding is critical as students interacting with complex simulations on their own can result in them missing or misinterpreting key elements of the simulation (Hegarty, 2004). Thus, an alternative to students’ independent interactions with the simulation is students viewing a screencast in which an instructor manipulates the simulation and provides some narration to highlight key elements of the simulation for students (Herrington et al., 2017; Martinez et al., 2021). As there are potential benefits and challenges to both independent simulation manipulation and watching of a screencast (Mayer and Moreno, 2003; Hegarty, 2004; Keehner et al., 2008), we aim to identify the key challenges that students have in using these activities outside of class to develop a particle-level understanding of equilibrium, as well as any differences that exist between students who use the simulation compared with those who watch the screencast. Further, as we were in the middle of this study when the COVID-19 hit, we were able to compare student learning gains using these materials to support a face-to-face class as compared to their use in a class that had transitioned to emergency remote instruction, and to determine how the necessary modifications of some questions when switching to a fully online delivery impacted information obtained from student responses.

Background

Student understanding of equilibrium

Equilibrium is a challenging concept for students because of its abstract nature; though students may be able to solve algorithmic equilibrium problems, they often struggle to be able to provide correct reasoning about equilibrium systems (Quílez-Pardo and Solaz-Portolés, 1995; Karpudewan et al., 2015). In teaching equilibrium, there are several common, non-productive ideas that students have been found to consistently hold. These include ideas that: reactions stop at equilibrium or that concentrations of products and reactants are equal at equilibrium (Demircioğlu et al., 2013); the forward and reverse reactions are oscillatory rather than occurring simultaneously (van Driel et al., 1998); there is a difference between reaction rate and extent of reaction (Erdemir et al., 2000); and reactions must go to completion before the reversing (Al-Balushi et al., 2012). One key factor that may contribute to the difficulty students have in understanding the concept of equilibrium is their inability to physically see what is happening to the particles so they can connect particle motion to the macroscopic observations (Lekhavat and Jones, 2009; Ganasen and Shamuganathan, 2017).

One way to help students visualize abstract chemical concepts at the particulate level is through the use of animations and simulations (Nakhleh, 1992; Sanger et al., 2000; Kelly and Jones, 2007). Viewing particle motion and interactions involved in chemical phenomena have been successful in helping students develop a better understanding of chemical equilibrium (Akaygun and Jones, 2014; Ganasen and Shamuganathan, 2017), and are most useful when they are short, visually appealing, and cover material at the desired specificity and context (Burke et al., 1998; Suits and Sanger, 2013). As chemical equilibrium is one of the more difficult concepts to master and has applications in several other chemistry concepts (Bergquist and Heikkinen, 1990), it is critical that students develop scientifically accurate mental models, and simulations may be a powerful pedagogical tool in supporting this development.

Something else that may contribute to students’ and instructors’ difficulty with equilibrium is the overreliance on Le Chatelier's principle (LCP) to explain changes in equilibrium systems (Cheung, 2009). Using LCP to predict or justify shifts in an equilibrium system resulting from external stresses (such as changes to concentration and temperature), without an underlying understanding of how such stresses affect the concentrations and interactions of the particles, is akin to applying an algorithm to solve a problem without understanding why. Many curricula rely heavily on Le Chatelier's principle to explain how an equilibrium system responds to stresses, as opposed to collision theory or the reaction quotient, the basis for particle interactions and concentration (Cheung, 2009).

Use of simulations and screencast in online learning

The constructivist theory of learning posits that learning occurs as individuals use experience to build new knowledge structures or integrate experiences into existing knowledge structures (Bodner, 1986). As Seery (2015) notes in his evaluation of flipped learning in college chemistry courses, “teaching under the umbrella of constructivism would therefore mean that teachers don't just tell students what they need to know, but provide structured activities so that students can develop their knowledge within the parameters of their own prior understanding.” In chemistry, coherent conceptual knowledge requires understanding phenomena at three different levels, the macroscopic (what we can observe with our eyes), the symbolic (chemical equations), and the particle (atoms, molecules, ions) levels (Johnstone, 1991; Liu and Lesniak, 2005; Adbo and Taber, 2009; Taber, 2013). This is often particularly challenging for students as atoms, ions, and molecules are far too small to be seen with our eyes, even with very powerful microscopes. Thus, a particle-level understanding of phenomena requires students to be able to imagine in their heads how particles are moving and interacting to develop a mental model. Using animations or simulations in the classroom have been shown to help students develop such mental models of chemical processes at the particle level (Williamson and Abraham, 1995). Typically, when used in class, an instructor will help students to focus on and understand the aspects of the simulation that can assist in the creation of productive mental models (Mayer and Anderson, 1991). In the ChemSims project (ChemSims, 2020), we have built on these ideas by developing outside-of-class activities where students engage with such simulations using carefully scaffolded instructions or by watching a screencast, a video recording of an expert using the simulation. In both cases, students simultaneously answer supporting questions. The scaffolded instructions and supporting questions are designed to ensure that the students are actively engaging in the learning task (Chi and Wylie, 2014) and focus students on identifying patterns in the data or observing how the particles interact to support them in developing an understanding of the underlying concepts. The use of scaffolding and embedded assignment questions to support students’ use of simulations or screencasts is supported by Mayer's cognitive load theory of multimedia learning (Mayer, 2011). By providing scaffolding and questions to focus students on the most germane elements of the simulation and helping them identify the patterns and/or make the connections required to build a conceptual understanding of a concept, we can reduce the cognitive load of the learning. Further, a recent study indicates that videos with embedded questions support learning better than reading from a textbook (Pulukuri and Abrams, 2021).

When simulations or animations are used in class it is possible for the instructor to direct student attention to the more salient aspects of the animation or simulation. However, in such cases, students are limited in the amount of time they can spend observing the particle interactions and identifying patterns that can help them construct a coherent particle level understanding of a concept. As students enter our classrooms with very different backgrounds, it is reasonable to assume that they may require differing amounts of time watching or interacting with an animation or simulation to develop the desired mental model. When using such materials outside of class, students can spend as much time as they need interacting with the simulation or re-watching parts of the screencast (Keengwe and Kidd, 2010).

We have previously reported that similar activities addressing other content areas where strong conceptual understanding requires accurate particle level models have resulted in significant learning gains with the screencast typically showing equal (Sweeder et al., 2019) or better results (Herrington et al., 2017; Martinez et al., 2021; VandenPlas et al., 2021). Since these activities are completed outside of class by the students, they also provide a common learning experience that the instructor can build upon in the classroom.

Learning during COVID emergency remote instruction

The concern about learning loss as a result of COVID has been widespread. A recent study from the Netherlands suggests that the learning loss they saw was the equivalent of about one-fifth of a school year, with losses being up to 60% greater for students from less-educated homes (Engzell et al., 2021). Given the accessibility, physical, and emotional challenges that accompanied the disruption to education as instructors worldwide scrambled to learn new technologies and figure out how to move the teaching of classes and, in the case of chemistry, labs online, this learning loss is perhaps not surprising (DeKorver et al., 2020). However, materials used during what many hoped would be a temporary move to remote instruction, frequently focused on “moving content online.” The most frequently used strategies were recorded lectures (asynchronous) or synchronous online lectures using platforms such as Zoom, with some courses using small group breakout rooms, individual worksheets, and drop-in virtual office hours (Gillis and Krull, 2020). Students generally reported a decrease in instructional quality and learning as a result of the shift to remote instruction, though they also reported preferring synchronous over asynchronous and classes that incorporated active learning over just passive (Usher et al., 2021). As the materials we describe in this paper were specifically designed to support learning outside of a standard classroom setting, we felt it was important to compare results from students who completed these activities during a regular academic year to those from students who completed them during the spring 2021 semester when the course was taught online to determine whether differences existed in those two instructional environments.

Research questions

Given the many challenges students have with the concept of equilibrium, combined with the challenges and affordances of the use of simulations and screencasts to support student learning of core chemistry concepts outside of the classroom, this study was guided by the following research questions:

(1) What differences exist between students who use the simulation on their own as compared to those who view a narrated screencast of the simulation being used to investigate the concept of equilibrium?

(2) What are the major challenges students have in developing a particle level understanding of equilibrium?

(3) What learning differences are seen in the use of the developed simulation or screencast equilibrium materials to support in-person versus remote instruction?

Methods

Overview

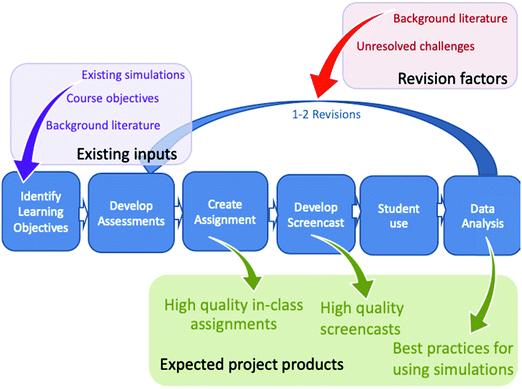
The overall design and evaluation process used for this activity is outlined in Fig. 1 and has been explained in detail for several other topics previously (Herrington et al., 2017; Sweeder et al., 2019; Martinez et al., 2021; VandenPlas et al., 2021). A key element in this Backwards Design (Wiggins and McTighe, 2005) model is the use of student data to revise the assessments and activities. The following sections outline details of the activity design and evaluation process.

Fig. 1 Outline of activity design and evaluation process.

Assignment design process

All activities for the ChemSims project are designed to be introductory activities that focus on core chemistry concepts requiring an understanding of particle motion and interactions. Thus, it is important that we find a high-quality simulation to help students visualize the key particle motions and interactions and identify core course learning objectives that can be supported by interactions with and targeted observations of the simulations. We look for a simulation that:

(1) accurately represents aspects of particle-level interactions (a challenge for many students);

(2) focuses on common general chemistry learning objectives; and

(3) provides a connection between the particle-level and some additional level of representation (e.g., graphical or macroscopic).

Making connections between representational levels is very important in developing a deep conceptual knowledge (Talanquer, 2011; Taber, 2013); however, this additional level of complexity makes it more difficult for students to make important connections on their own, thus necessitating quality scaffolding (Vygotsky, 1980). The identified PhET simulation (Reactions & Rates, 2013) not only met these criteria, but was particularly attractive as it was used for the development of a related kinetics activity (Sweeder et al., 2019), which meant that many students had previously used this simulation to explore a different concept.

For equilibrium, the following learning objectives were identified.

Students should be able to:

(1) Identify when a reaction reaches equilibrium by finding the point when the concentration of reactants and products remain relatively constant.

(2) Explain that equilibrium is a dynamic process. That the forward and reverse reactions are constantly occurring, but that equilibrium occurs when those two rates are equal.

(3) Predict and explain how adding or removing reactants or products will influence the equilibrium system to achieve a new equilibrium state by altering the rate of the forward or reverse reactions.

(4) Describe how and why temperature affects the equilibrium position of endo- and exothermic reactions differently.

Before designing the activities, we identified suitable assessments that would allow students to demonstrate if they had achieved the learning objective. These questions were used to create a pretest and an analogous set of follow-up questions for the purpose of measuring student learning gains (Table 1). These assessment questions guided how we would want students to interact with the simulations and the observations that students would need to make to construct the desired understanding. This provided the foundation for developing the scaffolded instructions and questions embedded in the simulation assignment. We then used the simulation assignment as a script for the screencast in which an instructor provided narrated interactions with the simulation that students used to answer the same embedded assignment questions as the students who interacted with the simulation on their own. Although the instructor helped to focus student attention through their actions, they strove to avoid interpreting what the students were observing, instead leaving students to do this as they answered the questions.

Table 1 Pre and posttest questions

Question #		Scoring	Learning Objective
1 Each graph below represents a reaction that involves the conversion of reactants to products and shows the concentration of each over time. Many reactions reach a state of equilibrium where there are some reactants and some products present in the reaction mixture		1 point total, ⅓ point for each part a–c	1
(a) Circle all of the graphs that represent a system that comes to equilibrium
(b) What features of the graphs indicated that the system was at equilibrium?
(c) For any graph that you circled above (meaning it reaches equilibrium), put a vertical line on the graph indicating the time point at which equilibrium was achieved
2 Your friends are discussing what they think they learned about why the concentrations of the reactants and products remain constant when a reaction reaches equilibrium		1 pt each for explain why Bob and Betty were wrong	2
Betty: Because the concentration of the reactants is equal to the concentration of the products
Bob: Because the reaction stops before it reacts completely
Beth: Because the rate of reactants going to products is equal to the rate of products going back to reactants
(a) Which friend do you think is correct?
(b) Explain why you think your other two friends are incorrect:
3 The following reaction will reach an equilibrium		Original 1 pt for correct drawing	3
2SO2 + O2 ⇌ 2SO3		Revised: 1 pt for correct selection and correct reasoning
If, while this system was at equilibrium, more SO2(g) were added to the system, the concentration of SO2 would initially increase as illustrated on the graph below
Original: Extend the concentration lines for each of the 3 compounds to timepoint x to illustrate how the concentrations of each would change as the reaction progressed
Revised:
(a) Which graph correctly shows what the concentration lines for each of the 3 compounds will look like as the reaction proceeds to time point x?
(b) Explain why you chose the answer you did to the question above
4 This reaction of N2 + 3H2 ⇌ 2NH3 is exothermic. What would you expect to happen to the amount of each compound present if, once at equilibrium, the temperature was decreased?		1 point if all changes were correct	4
N2	Increase/decrease/remain unchanged/impossible to determine
H2	Increase/decrease/remain unchanged/impossible to determine
NH3	Increase/decrease/remain unchanged/impossible to determine

---

Data collection

This study was reviewed and approved as exempt by the Institutional Review Boards (GVSU ref. No. 16-012-H; MSU x15-799e). All the participants voluntarily agreed to be in the study and consented through electronic forms to share their solutions and written thinking process on the assignments. During the 2021 data collect, one of the researchers was also one of several instructors simultaneously teaching the course. The activity was used as part of the standard course instruction for all instructors and the researcher did not have access to information about consent until after the completion of the course. Data were collected from students enrolled in second-semester introductory chemistry courses at two separate large public universities. At Institution 1, equilibrium is discussed after a focus on kinetics including collision theory, reaction coordinate diagrams, rates of reactions and mechanisms. The introduction to kinetics used a similar assignment based on the same PhET simulation, thus these students were already familiar with the simulation. At Institution 2, equilibrium was discussed after acid and base chemistry and prior to kinetics and collision theory. Hence, to equip these students with appropriate background knowledge, prior to completing the assignment, they all watched an additional 2 minute video that used the PhET simulation to introduce them to collision theory. Unlike the screencast assignment, this video did not require students to answer questions concurrent with their viewing and the narrator provided more interpretation of what was observed.

Data were collected through several implementations. For all data collections, students completed a pretest and then their assignment outside of class prior to formal in-class discussion of the topic of equilibrium. However, the broad idea of equilibrium had been mentioned in previous relevant topics such as vapor pressure of liquids and colligative properties in solutions. For the initial data collection round (N ≈ 50), analysis of student responses resulted in reworking some questions to better align the pretest and follow-up questions and ensure that the assignment prompts were effectively supporting students in their learning following the revision process outlined in Fig. 1. The revised pretest and assignments were used in two subsequent semesters at the two different institutions (N = 243 students), which again led to some additional minor revisions to address student learning challenges. This third version provides the basis for the pre-COVID data analysis used in this study and was deployed in five classes at the two institutions (Table 2). This data collection was completed just before the institutions halted in-person classes as a result of the COVID-19 pandemic. All students completed the pretest in class and then completed the assignment (screencast or simulation) including the embedded assignment and follow-up questions outside of class (for full assignment see Appendix A).

Table 2 Summary of implementations

Version	Semester	Implementation	N (institutions/classes/students^a)
a For students the number represents those who provided consent for use of their data for research purposes and fully completed both the pretest and assignment activities.
3	Spring 2020	Pencil and paper; Simulation and Screencast	2/5/337
4	Spring 2021	Online data collection via Google Forms; Screencast only; Revised Question 3 (Table 1)	1/3/215

---

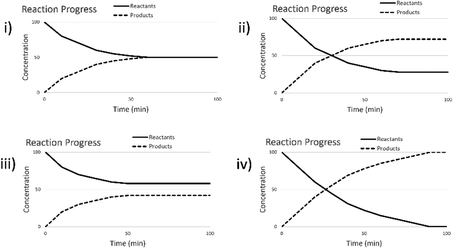
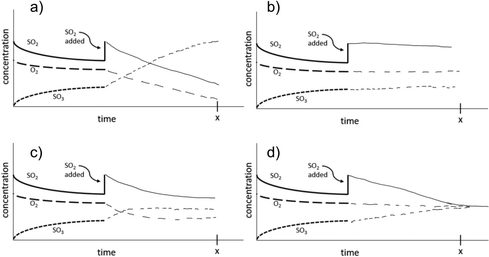
The change to remote instruction for Spring 2021 provided an opportunity to directly compare the use of these materials to support in-person versus remote instruction. To do this, the screencast assignment was converted to an online-only format (Version 4) using Google Forms (2018). Although we could keep most of the questions nearly identical in this different format, one of the pretest and follow-up questions (Question 3 in Table 1) had to be modified. Since collecting images of drawings online had resulted in lower levels of participation in other studies (Sweeder and Herrington, 2020), we modified the question to have students select which graph illustrated how the concentrations of species would change over time, and then provide an explanation as to why they chose that graph. The multiple-choice options were derived from the most commonly drawn student responses for the paper and pencil version of the assessment. This implementation happened at a single institution across three classes (Table 2). Pre and posttest questions, along with how they were scored for pre-post analysis, are shown in Table 1. Full details of the scoring rubric can be found in Appendix B.

Data analysis

Student learning gains. Student learning gains, as measured by pre and posttest questions, were determined using SPSS (IBM SPSS Statistics 25, 2017) to perform several statistical analyses. For the pre-COVID comparison of student performance using the screencast vs. the simulation assignment, a mixed 2-way ANOVA, with treatment (screencast or simulation assignment) as the between subjects variable and time (pre to post) as the within subjects variable, was used to compare overall changes in scores as well as to examine performance on each individual question. To measure learning gains for the COVID administration, we used paired sample t-tests, as there was only one treatment, the screencast. Finally, comparison of student gains between the pre-COVID and COVID administrations of the screencast assignment was done using a 2-way mixed ANOVA with year as the between subjects and time as the within subjects variables.

Student particulate level understanding of equilibrium. A major intent for the development of these activities was to help students construct a particle level understanding of equilibrium systems. We investigated student understanding by qualitatively analyzing student responses to particle level assignment questions that were separate from the pre and post assessment questions. The specific set of questions we analyzed for our qualitative analysis were:

(I) Starting the simulation reaction with the numbers of reactant and product particles shown below (specific starting number of particles for each reactant and product species provided):

(a) At the beginning of the experiment, is the rate of the forward reaction (forming products) faster/slower/the same as (circle one) the rate of the reverse reaction (forming reactants)? What evidence from the simulation supports your conclusion?

(b) Use particle collisions (collision theory) to explain why the rates of the forward and reverse reaction would initially be different.

(c) In general, after the reaction has occurred for a while, is the rate of the forward reaction faster than/slower than/the same as (circle one) the rate of reverse reaction?

(d) Explain why this relationship between the forward and reverse reactions would make sense based on the idea of Collision Theory and concentrations of products and reactants.

For this set of questions, we first looked at whether students could correctly answer part a, which in all cases was at least 70% of the students. If correct, we then coded their responses to the subsequent questions. Open qualitative coding of these responses indicated answers fell into one of three general categories: (i) correct use of particle collisions to explain relative rates; (ii) used particle collisions, but did not explain relative rates; (iii) did not use particle collisions to explain relative rates.

Additionally, several questions were asked where students had to observe or predict what would happen to the concentrations of reactants and products (increase/decrease/stay the same) in an equilibrium system when a stress such as adding/removing a substance or changing temperature was applied. For these questions we identified if students provided answer sets that were internally consistent with reactions at a particulate level. For example, if students have a particle level understanding of a chemical equilibrium, then they should understand that it is impossible for the concentrations of both the reactants and products to increase if the temperature changes. For both the 2020 and 2021 data we looked at consistency for responses to question 4 on the pre/post-test (Table 1) and three of the assignment questions that required similar reasoning. Additionally, in moving to the all online administration of the assignment in 2021, we revised the question shown below from one that was more open (which side of the reaction will show an increase in the number of molecules when we decrease the temperature? – and students write in an answer) to one that forced student choices to (increased/decreased/stayed the same). This gave us an additional two questions for comparisons of consistency in the 2021 data (shown below as question II).

(II) Based on your observations from the simulation, after lowering the temperature and allowing the molecules to reach a relatively stable distribution again, note what happens to the concentration of the reactants and products:

(a) For an endothermic reaction?

(i) Reactant concentrations (increased/decreased/stayed the same)

(ii) Product concentrations (increased/decreased/stayed the same)

(b) For an exothermic reaction?

(i) Reactant concentrations (increased/decreased/stayed the same)

(ii) Product concentrations (increased/decreased/stayed the same)

(c) How does Collision Theory help explain your answers to parts a and b?

As part c to question II above also asked student for a particle level explanation, we initially tried to qualitatively code student responses to this question as we had above with question I; however, few students made the connection to activation energy and instead most attempted explanations focusing on temperature impacting the kinetic energy of the particles or the connection of energy associated with bond breaking and forming.

Results

Student learning gains

2020 simulation vs. screencast analysis (pre-COVID). An initial analysis for Institution 1 showed no differences based on instructor, so we were able to group students by treatment. Looking at overall student gains for each institution separately, for Institution 1 we see a main effect for time (pre to post) with an increase from 1.31 to 2.81 on a 5-point scale and a large effect size (p < 0.001, F₁₂₄₅ = 375.353, η_p² = 0.605) as well as an interaction effect between time and treatment, albeit it with a small effect size (p = 0.008, F₁₂₄₅ = 7.187, η_p² = 0.028). Fig. 2 shows in this case the simulation students make slightly larger gains than the screencast students even though they started at a lower level. For institution 2 we see a main effect for time with an increase from 1.09 to 2.83 with a large effect size (p < 0.001, F₁₈₀ = 133.385, η_p² = 0.625), but no interaction effect. As shown in Fig. 2, in this case the screencast students make slightly larger gains than the simulation students, but the differences are not statistically significant. When all students from both institutions are combined, we found a significant main effect with respect to time for all students with a 1.55 point increase from 1.26 to 2.81 and a large effect size (p < 0.001, F₁₃₂₈ = 506.171, η_p² = 0.607). However, there was no main effect for treatment or an interaction effect between treatment and time. Fig. 2 also illustrates that the treatment resulted in a narrowing of the variance in scores between treatment groups, suggesting that students are as a whole at a more consistent level of understanding after completing the assignment, an effect that we have noted for another content topic (VandenPlas et al., 2021).

Fig. 2 Pre to posttest change for each institution and treatment.

2020 vs. 2021 screencast comparison. Obviously, many changes occurred during the shift to remote instruction that go well beyond this assignment; however, the comparison between these implementations provides insight into the functioning of these assignments as instructional support tools in different learning environments. As this activity was only used at one of the institutions and it was only the screencast version that was used, the 2020 data used for comparison were the screencasts students from Institution 1. Further, because Question 3 had to be modified for the online administration and we were reluctant to use the score from this question to compare between years, we created a new total score, combining the results across Questions 1, 2, and 4 (out of a total of four points), for comparison purposes. Using a mixed 2-way ANOVA with year as the between subject variable, we saw an overall improvement from 1.27 to 2.36 with a large effect size (F₁₃₂₇ = 214.859, p = <0.001, η_p² = 0.397) for the main effect of time. There was also a significant, but small interaction effect for the year (F₁₃₂₇ = 10.194, p = 0.002, η_p² = 0.030) with the 2020 students showing a greater improvement from 1.12 to 2.54 compared to the 2021 students improving from 1.35 to 2.27.

2021 revised question 3 analysis. Question 3 required significant changes in format as described above. In 2021, students were asked to select the correct graph that depicted how concentrations would change after the addition of a reactant to a system already in equilibrium and then explain their reasoning. Table 3 shows the distribution of graphical selections for students for each the pre- and posttest versions. The students’ reasoning for selection of the graph was determined to be correct if they selected the correct graph and gave a reason that correctly invoked either correct initial changes to the concentrations or the reestablishment of a constant concentrations.

Table 3 2021 student responses to revised question three

Graph selected	Pretest % selected (correct reasoning)	Posttest % selected (correct reasoning)
a	20	22
b	14	14
c (correct)	34 (17)	44 (28)
d	32	20

---

Student particle level understanding of equilibrium

Student responses to several assignment questions were qualitatively coded to determine if the student used particulate level reasoning. For question I in the Data Analysis section, we looked at student explanations/evidence in parts a, b, and/or d because different students used particle collisions to answer different parts. Answers in part a or b indicating that initially there are more particles of reactants able to collide which makes the forward reaction faster, or in part d that after a while as products are formed they will collide and react so the rates will be equal were considered to have a correct use of collisions. If students wrote an answer like “particles will collide more” or “particles need to collide to react” in their explanations but did not connect it to the relative rates in any of the parts, then they were classified as used particle collisions, but that they did not use the collisions to explain rates. The students that were classified as not using particle collisions most frequently gave answers that tried to use energy, talked about concentration in general but not about numbers of particles or collisions, or said that collisions had to occur with proper orientation and energy (basically just a statement of collision theory) but did not go any further. The frequency counts for each type of explanation for the different groups of students in this study are found in Table 4. Although we found all of these types of answers in all the different groups of students, the students from Institution 1 had a larger percentage of students in each case (simulation and screencast treatment and 2021 administration) who correctly used collisions to explain relative rates and had fewer students who did not use collisions at all.

Table 4 Student responses to question I

Institution – treatment	1 – sim	1 – screencast	2 – sim	2 – screencast	1 – 2021
Total number of students	62	94	46	45	214
Correct answer to part a (%)	89	70	78	71	81
(i) Correct use of collisions	54	68	36	44	54
(ii) Use of collisions	20	6	17	19	31
(iii) No use of collisions	25	26	47	38	15

---

To determine if student answers maintained internal consistency at a particulate level when considering the response of an equilibrium system to stress we examined six different questions. Each question required the students to observe or predict what would happen to the concentrations of reactants and products (increase/decrease/stay the same) in a given equilibrium system when a stress such as adding/removing a substance or changing temperature was applied. If students have a particle level understanding of chemical processes, their answers should always reflect that if reactants are consumed by a reaction, that the quantity of products should increase or vice versa. Any answer where students claim both the reactants and products increase is not possible. For each of the (up to) six different question sets of this predictive format that the students encountered across the pretest, assignment, and follow up questions, we checked the set of student response for internal consistency. In any case where the question indicated that one specific compound was changed, we excluded the student response about that specific compound. For example, if compound A was removed from an equilibrium system, we ignored any response about the concentration of A. This is because it may not be clear if the students were considering the final equilibrium relative to the initial state or if the students is considering the final equilibrium relative to the moment immediately after the A was removed from the system. This meant that for some questions, students had to provide consistent answers across three question parts, whereas some questions looked at reactants or products as a set, so only two question parts were required to be consistent. These data are summarized below in Table 5.

Table 5 Consistency across questions

Question (# of question parts to be consistent)	Provided chemical viable answer
	2020 (all students) N = 149	2021 N = 214
a Questions were not asked with forced responses so data is inconsistent.
Pretest 4 – endothermic rxn (3)	68%	57%
Assignment – predict (add product) (3)	78%	68%
Assignment – predict (remove reactant) (3)	68%	60%
Assignment – observe (cool endothermic rxn) (2)		90%
Assignment – observe (cool exothermic rxn) (2)		85%
Posttest 4 – exothermic rxn (3)	83%	77%

---

Discussion

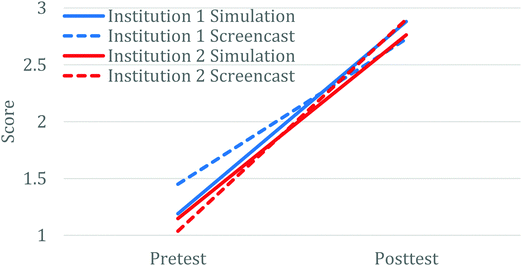
Research question one: comparison of student outcomes with simulation vs. screencast

Research question one seeks to better understand any differences in learning that result between student use of the screencast as compared with the simulation to complete the out-of-class activity. The comparisons above in the Results section (Fig. 2) highlight that regardless of institution or treatment, students generally made very similar learning gains with large effect size, and that the variance in scores at the class level was smaller with the posttest measurement than with the pretest. Further, the small effect size that was observed for differences between treatments (screencast vs. simulation) at Institution 1 during the 2020 year, appears to have arisen primarily due to the initial differences on the pretest scores, as the pretest scores between the two treatment groups were statistically different while the posttest scores were equivalent between the two different treatment groups. These result are consistent with a previous study using similar types of activities to introduce students to the topic of atomic interactions, which also showed that the posttest learning outcomes were consistent across multiple classes, regardless of differences in their pretest scores (VandenPlas et al., 2021). Further, though we have seen interaction effects with one treatment (simulation or screencast) making larger gains, the effect sizes for these have always been small (Herrington et al., 2017; VandenPlas et al., 2021). Finally, comparing the scores on the three nearly identical questions between the in-person and online versions of the course also showed fairly consistent results. Together, these provide relatively good evidence that these learning activities can act as a solid preclass introduction to equilibrium across a variety of class designs. Also, in general, having the students manipulate the simulation themselves or watch a narrated screencast will yield the same overall outcomes. However, though not leveraged in this case, screencasts can provide an opportunity for instructors to enhance the simulation experience, for example by allowing students to see side by side representations of two different conditions or by adding additional non-simulation-based content, which may enhance student conceptual understanding (VandenPlas et al., 2021). Further, the use of screencasts may circumvent student technology issues for simulations that require software such as Java.

Research question two: challenges in developing a particle level understanding of equilibrium

In many ways, research question two is the more interesting question. Although, pre-post comparisons show learning gains, to determine how this activity affects students’ particle level understanding of equilibrium requires a qualitative look at student responses to questions that offered them an opportunity to demonstrate particle level reasoning. From this, we gathered three interesting takeaways.

First, instructional content order can influence student learning. Our data suggest that meaningfully learning about collision theory prior to engaging with the activity notably increased students’ ability to explain shifts in equilibrium using particle level reasoning. Student responses to question I (Table 4), show that many of the students were able to correctly use Collision Theory and the number of collisions to explain the relative rates of the forward and reverse reactions with 36–68% of any class giving a correct explanation. However, what is striking about these data is the disparity in the rates between the two different institutions. Here there is a statistically significant difference between the two groups (58% vs. 40% correct, z = 1.74, p = 0.041). We hypothesize that this difference arises from a difference in the order of content between the courses at the two institutions. At Institution 1, kinetics and collision theory are introduced prior to this activity involving equilibrium. However, at Institution 2, kinetics and collision theory are encountered in more depth after equilibrium. Recognizing this difference and the need for students to use collision theory to explain equilibrium at the particle level, when the activity was administered at Institution 2 we included a short introductory video and a few related questions on collision theory, focusing on the fact that reactions occur as a result of particle collisions. Unsurprisingly, we see statistically higher rates of the correct use of collisions in explanations by students at Institution 1 who (presumably) had more comfort with that content having learned and used it previously in the context of explaining kinetics concepts. Ensuring that collision theory is deeply addressed prior to equilibrium may be key in addressing a reliance on Le Chatelier's Principle for explaining equilibrium (Cheung, 2009) by ensuring that they have the potential to construct a particle level explanation.

The second takeaway was that many 2nd semester general chemistry students do not inherently consider the consistency of sets of related answers when it comes to mass balance and chemical reactions. A particle level understanding of chemical reactions and the Law of Conservation of Mass necessitates that as an equilibrium system responds to a stress, either reactants are increased and products decreased, or vice versa. Yet, as is evidenced by our data, internal consistency of their answers is not yet an automatic consideration for all second semester general chemistry students. In looking at their answers to a number of different questions that involved disturbing systems at equilibrium and predicting or observing the changes to all the species present (Table 5), 10–40% of students provided chemically impossible answers such as suggesting that when one reactant was removed from a system, the concentration of one of the products increased and the other decreased (a mass balance impossibility). In general, when asked to describe what happened to reactants or products as a whole when a stress was applied (e.g., what happened to the concentration of the reactants when the temperature was increased), students provided a chemically viable answer 85–90% of the time, meaning they recognized that as one went up the other had to go down. However, when asked to predict what would happen to individual reactant and product species when a given stress was applied, this number dropped to 60–80% of students providing chemically viable answers. It should also be noted that the 2021 students performed somewhat lower than the 2020 students on all of these questions (Table 5).

The last takeaway was that it was extremely challenging for students to make the jump to use Collision Theory and particle motion to understand why a change in temperature would differentially impact rates of forward and reverse reactions (question II part c). To correctly apply Collision Theory to this phenomenon, students would have to recall and connect to previous learning about activation energy and how that differs for exo vs. endothermic reactions. Though this is something that is depicted graphically in the simulation, the activation of these prior mental resources when learning a new topic is very challenging, even with suitable prompts. Though we tried to qualitatively code the student responses to this question, too few of them gave answers that could be meaningfully grouped together. However, even if students are not yet able to make this connection on their own, the asking of the question can help students realize there should be a connection and help them identify where there might be a gap in their understanding so that instructors can more thoroughly engage with the topic during the follow-up class discussion.

Research question three: supporting student learning for in-person vs. online instruction

As mentioned previously, the COVID-19 pandemic provided us with an opportunity to compare student outcomes when completing this activity as a supplement to an in-person, face-to-face class, as compared with those completing it as an activity that was part of a class offered online. Both classes regularly engaged students in group active learning activities during synchronous class meetings, with the online class using Zoom breakout rooms for group activities. Additionally, in both cases equilibrium screencast activities were completed by students outside of class as an introduction to the topic of equilibrium. One key difference between the two class formats was that the online class students were expected to complete a preclass activity on their own outside of class before attending each synchronous session. In the in-person class, these preclass activities were the exception as opposed to the norm.

As reported in the Results section under 2020 vs. 2021 Screencast Comparison we saw both groups make significant gains from pre to post with a large effect size. Though we saw a small interaction effect for year with the 2020 students making slightly larger gains, given all of the additional challenges that many students faced during the 2020–2021 academic year, similar gains could definitely be considered a success. Perhaps the largest take away from this comparative analysis is the importance of question format on what can be gleaned from student responses. Of particular note was Question 3 (Table 1). This question had to be substantially revised for use as an online assessment question. Further, although we were able to generally classify student drawing from the 2020 data into four main categories (represented by the four answer choices shown in Table 1), coding individual student graphs was often quite challenging with respect to determining which of two categories it should fit into. This may not be surprising as the ability to draw and interpret graphs is an additional significant barrier for many students (Potgieter et al., 2008). With the initial question, the implicit assumption was that if students could correctly complete the lines on the graph that indicated they had a strong understanding of equilibrium as a dynamic system and the underlying basis for Le Chatalier's Principle. In just asking students to choose the correct graph, we felt we needed to ask students to explain their choice to determine how their understanding of equilibrium was involved in their choice. Requiring this explanation was fortuitous as student responses provided some additional insights into how students may have been approaching their drawings in 2020.

A complete explanation of the correct answer would include both how the concentrations will initially change after the addition of a reactant and that a new set of stable concentrations would be formed. However, only 10% of the 2021 students on the post assessment included both of these aspects in their explanation. More tended to provide an explanation that focused on only the immediate change after the addition of the excess reactant, or on the fact that the concentrations reached a “steady state”; however, each of these reasonings individually are consistent with two different graph options. Interestingly, students who provided a pretest answer that focused on the end state (stable concentrations) were more likely on the posttest to give an answer that focused only on the changes immediately after the addition of the new compound than to add this aspect to their already solid answer. This may suggest that the assignment focuses students more on the initial changes, and not as much on the long-term equilibrium state. This might also be explained by students’ tendency to use one-reason decision making (Talanquer, 2014), or it may be the case that the prompt did not provide enough structure to help students understand that a complete explanation required addressing the initial change as well as the final state (Cooper et al., 2016).

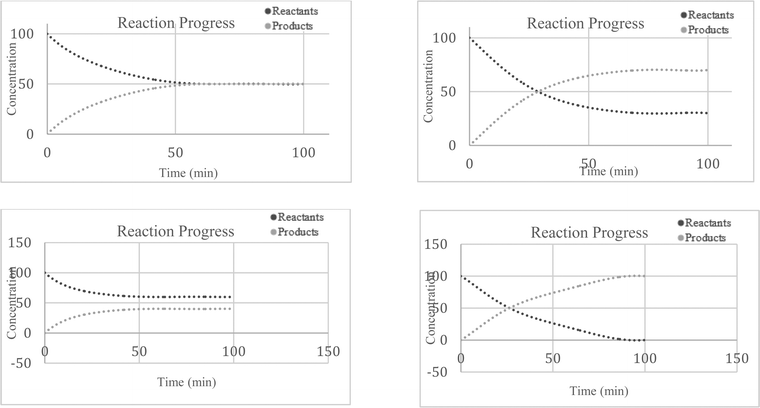
The incorrect explanations were also quite illuminating. Students who selected Graph (a) (Table 3) correctly identified how the concentrations of compounds would shift after the disruption of the equilibrium but lacked the recognition that a new equilibrium would be reestablished. About a third of the explanations from these students suggested the students were simply applying Le Chatelier's Principle as an algorithm. Students selecting Graph (b) believed that the system at equilibrium would just remain at equilibrium or that no change would occur. This selection was generally accompanied by explanations that indicated students thought that no more reaction would occur after equilibrium was reached or that they were just focusing on the constant concentration part of the graph. Students selecting Graph (d) primarily justified their selection with the idea that the concentrations of the compounds had to be equal to be in equilibrium. However, there were a few responses which seemed to indicate a misinterpretation of the graph such as “The rates of each reaction whether forward or backward, became equal resulting in a conversion of each line.” or “all lines reach equilibrium as the concentrations and rxn rates are equivalent. This means rate of rxn for fwd and rev rxns are =”. These students seem to recognize the importance of the forward and reverse reaction rates being equal at equilibrium, but do not fully understand equal rates does not necessarily mean equal concentrations. In this case they may be applying the and associative-activation heuristic where same means identical, rather than recognizing the same rates imply not equality with respect to concentrations, but rather unchanging (Talanquer, 2014).

Limitations

There are several limitations that should be noted when considering the results from this study. First, although we have seen equivalent results across institutions and instructors at two separate institutions, both institutions recruit students from similar backgrounds, and introductory chemistry courses at both institutions have course learning objectives that require students to provide particulate level explanations for chemical principles. Thus, differences may arise if these interventions were used with different student populations or in courses without an emphasis on particle level explanations. Second, though one of the benefits of students completing these activities outside of the classroom is that they are able to spend as much time engaging with the content as they need to, students must still choose to engage with the materials meaningfully. Requiring students to answer questions that focus them in on key aspects of the simulation, note patterns, and test their understanding throughout the activity helps support this meaningful engagement; however, it is likely that there are students who do not put in the time that they need, do not complete the activity in one sitting, or are distracted by other things while completing the activities. Lastly, the comparisons between the 2020 (in-person, pre COVID) and 2021 (remote instruction) should be interpreted through the lens of the fact that the overall structure of the course and student experience changed dramatically. The online version employed far more preclass learning activities and a much greater role for group work and peer instruction during the class, at the same time many students were experiencing a great deal of fatigue with learning online.

Conclusions and implications for instruction

Equilibrium is a challenging topic for students; therefore, providing students with time to engage with the concept in a meaningful way on their own can serve as a productive common experience on which subsequent instruction can build. We have shown that both assignment formats (screencast or simulation) can serve as effective preclass experiences. Further, the detailed analysis of student responses to these assignments provides several insights that can help improve our instruction of equilibrium. First, the simulation appears to be most effective at helping students develop an appreciation of the dynamic nature of equilibrium, as the simulation allows them to see and understand that the reaction itself proceeds in both a forward and reverse direction. Second, the ability to develop a meaningful understanding of how dynamic equilibrium relates to the direct interaction of particles, appears to be notably enhanced by the students having meaningful prior experience with collision theory. This understanding is central to explaining how equilibrium systems work and why they respond in a way that can be predicted using Le Chatelier's Principle. As such, if we wish to move away from students overly relying on Le Chatelier's Principle, then it would behoove us to ensure that the course content is structured such that they have previously learned collision theory and thus have this as a foundation for understanding equilibrium. Lastly, the student explanations for why they selected different graphs highlights the need to focus instruction on both how the equilibrium responds to the initial stress and the reestablishment of the equilibrium condition.

The results from this study also provide some broader implications. The first is that this intervention led to similar learning gains in similar populations of students regardless of instructor, institution, or course modality. The consistency of the learning gains suggest that the approach can be an effective initial introduction across a range of settings. However, as Eichler (2022) suggests, this preclass activity should not be viewed as the entirety of instruction, but rather just a foundation. If used effectively, such preclass activities can be used to inform instruction and elicit student buy-in. Student responses can provide valuable insight into the challenges that students are still having with the content so that in-class instruction can be short and targeted so as to provide ample time for students to practice applying their understanding. This is consistent with findings by Bancroft et al. (2021) showing that in addition to pre and in-class activities with accountability, another required component for flipped instruction that resulted in significant gains in course GPA was the inclusion of responsive mini-lectures. Further, we have observed that sharing a summary of the students’ responses to preclass activities at the start of class not only provides this targeted review of the content but also demonstrates to students the importance of the preclass activities for their learning and greatly increased their buy-in regarding the value of completing preclass activities.

Author contributions

Sweeder and Herrington were involved in all aspects of study development and authorship of this manuscript. Hilborn was involved with the formal analysis and the writing of the initial draft of the manuscript. Sielaff was involved in the methodology and creating the initial assignment and early revisions.

Conflicts of interest

There are no conflicts to declare.

Appendix A: screencast assignment (2020)

(1) Go to the YouTube link https://www.youtube.com/watch?v=cOZkwm3Es2s, watch the introduction to reactions and rates and answer the following questions:

(2) What is the current clock time?

(3) Using the reaction where the A atom is yellow and the following initial conditions

A = 20 BC = 15

AB = 1 C = 0

(a) How do the concentrations of reactants and products change initially?

(b) How do they change after the reaction has occurred for a while?

(c) The forward reaction and reverse reactions for this system are:

Forward: A + BC → AB + C

Reverse: AB + C → A + BC

At the beginning of the experiment, is the rate of the forward reaction (forming products) faster/slower/the same as (circle one) the rate of the reverse reaction (forming reactants)? What evidence from the simulation supports your conclusion?

(d) Use particle collisions (collision theory) to explain why the rates of the forward and reverse reaction would initially be different?

(e) In general, after the reaction has occurred for a while, is the rate of the forward reaction faster than/slower than/the same as (circle one) the rate of reverse reaction.

(f) Explain why this relationship between the forward and reverse reactions would make sense based on the idea of Collision Theory and concentrations of products and reactants.

(4) When 20 additional atoms of C are added:

(a) In the table, predict what you think will happen to the number of each type of particle when the simulation is restarted and equilibrium is reestablished. Use Collision Theory and rates of the forward and reverse reaction to justify your predictions.

Particle	Predict: increase/decrease	Justification of your predictions based on rates of forward and reverse reactions
A
BC
AB
C

(b) Was your prediction correct? Yes/No (circle one)

(c) If your prediction was not correct, explain what actually happened.

Try it Yourself

Go to the PhET simulation Reactions & Rates: https://phet.colorado.edu/en/simulation/legacy/reactions-and-rates. Note: You will need Java installed (see separate Java instructions). To start: Microsoft edge – click the image of the simulation; Chrome or other browsers you may have to download the simulation, then open it.

Set up the experiment as in the screencast with the following initial conditions:

A = 20 BC = 15

AB = 1 C = 0

• Bring up the strip chart. Zoom out on the strip chart so that you can see 20 molecules on the y axis.

• Adjust the initial temperature so that the total average energy line is halfway between the potential energy of the products and peak of the reaction coordinate diagram.

• Begin the experiment and allow it to run for a while and then pause the simulation

(d) What do you anticipate will happen to the number of each kind of particle if you decrease the number of one of the types of particles? Circle the type of particle you want to decrease the number of, and then as before, complete the table below.

Particle	Predict: increase/decrease	Justification of your predictions based on rates of forward and reverse reactions
A
BC
AB
C

(e) Adjust the amount of the particle you circled above, and test your prediction. Was your prediction correct? Yes/No (circle one)

(f) If your prediction was not correct, explain what actually happened.

Going further: impact of temperature

(5) Click End Experiment. When you click Begin Experiment, it should reset with the conditions from part 3.

Begin the experiment with the same settings and wait for the simulation to reach a relatively consistent number of each particle. Note the number of each particle type:

A =  AB =

BC =  C =

(a) Lower the temperature considerably. What happens to the total average energy as this happens?

(b) Allow the molecules to reach a relatively stable distribution again. Once this happens, are there more reactants, more products, or have each remained unchanged?

(6) Switch the exothermic reaction (4th reaction with red atom of A). Begin the Experiment using the same setting used in part 5. (Note, the Total Average Energy line may not move when you do this.) As before, allow the number of molecules to stabilized and record the numbers.

A =  AB =

BC =  C =

(a) Lower the temperature considerably. What do you notice about the change in reactant and product molecules?

(7) Looking at your results from parts 5 and 6, which side of the reaction will show an increase in the number of molecules when we decrease the temperature?

(a) Part 5 – endothermic?

(b) Part 6 – exothermic?

(c) How does Collision Theory help explain your answers to parts a and b?

Follow Up – Using your findings

(8) (a) Circle all of the graphs below that represent a system that comes to equilibrium

(b) What features of the graphs indicated that the system was at equilibrium?

(c) For any graph that you circled above (meaning it reaches equilibrium), put a vertical line on the graph indicating the time point at which equilibrium was achieved.

(d) Your friend Bob says a reaction reaches equilibrium because the reaction stops. You know this is not correct. How would you explain to Bob why the concentrations remain constant at equilibrium?

(e) Your friend Betty says that at equilibrium means that the concentration of the reactants and products are equal. You know that is not correct. What would you tell Betty is actually equal at equilibrium?

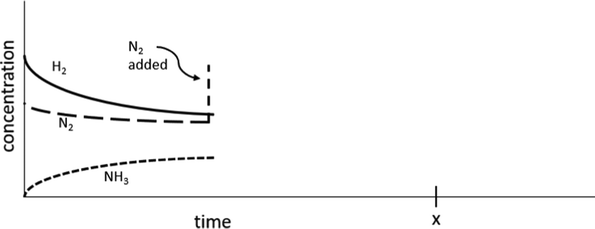
(9) The following reaction will reach an equilibrium.

N₂(g) + 3H₂(g) ⇌ 2NH₃(g)

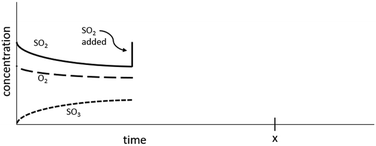
If, while this system was at equilibrium, more N₂(g) were added to the system, the concentration of N₂ would initially increase as illustrated on the graph below. Extend the concentration lines for each of the 3 compounds to timepoint x to illustrate how the concentrations of each would change as the reaction progressed.

(10) The reaction of 2SO₂ + O₂ ⇌ 2SO₃ is exothermic. What would you expect to happen to the amount of each compound present if, once at equilibrium, the temperature was decreased?

SO2(g)	Increase/decrease/remain unchanged/impossible to determine
O2(g)	Increase/decrease/remain unchanged/impossible to determine
SO3(g)	Increase/decrease/remain unchanged/impossible to determine

Appendix B: coding and scoring scheme used

Question	Coding scheme	Value
(1a) Selecting systems at equilibrium (pre and posttest)	¼ credit for each correctly indicate(i, ii, and iii selected, iv not selected)	0.3333 total
(1b) Why were 1a selected? (pre and posttest)	1 = concentrations constant/reactants and products are constant OR rates equal/constant OR graphs level out/straight parallel lines (correct)	0.3333
	2 = reactants and products are equal/have equal concentrations OR Graph lines meet or end at the same place	0
	3 = meet at a point OR conc of reactants and products are equal at some point OR lines cross or meet	0
	4 = approach an intermediate value OR curves approach one another	0
	5 = other	0
(1c) When is equilibrium established? (pre and posttest)	1 = consistently selected where curves start to flatten out (correct) [this was still possible if iv was also selected in part 1a]	0.3333
	2 = consistently selected where curves cross/meet	0
	3 = inconsistent or other	0
2 Who was correct (not scored for points) (pretest only)	1 = Beth
	2 = Betty
	3 = Bob
	4 = Other (e.g., circled more than one)
2 Why was Bob wrong? (pretest and posttest)	1 = something about reactions continuing but rates being equal	1
	2 = reaction doesn’t stop	0
	3 = concentration remains constant	0
	4 = something about the reaction not being at equilibrium if it goes to completion or reactant is used up	0
	5 = misc	0
	6 = reaction goes to completion	0
2 Why was Betty wrong? (pretest and posttest)	1 = something about it is the rates that are the same, not the concentrations OR that the concentrations remain constant but don’t have to be equal	1
	2 = concentrations don’t have to be equal to reach equilibrium	0
	3 = misc	0
2 Why was Betty wrong? (pretest only)	1 = it is the rates that are the same, not the concentrations OR that the concentrations remain constant but don’t have to be equal	Not scored
	2 = concentrations don’t have to be equal to reach equilibrium	Not scored
	3 = misc	Not scored
3 Selection (Pre and Post)	Coded by selection
3 Reasoning (pre and post)	1 = indicates that initially SO2 and O2 should decrease while SO3 increases AND indicates that constant concentrations will be reestablished	1 point if correct graph selected
	2 = indicates that constant concentrations will be reestablished (focus only on ending state)	0.75 point if correct graph selected
	3 = indicates that initially SO2 and O2 should decrease while SO3 increases or other Le Chatelier’ Principle inspired statement (focus only on initial change after addition of SO2)	0.75 point if correct graph selected
	4 = just “reaches equilibrium” without indicating what that means or supporting w prod/reactants	0
	5 = other responses	0
4 (Pre and Post)	Coded by selections for N2/H2/NH3
	Decrease/decrease/increase	1 (consistent)
	Increase/increase/decrease	0 (consistent)
	No change/No change/no change	0 (consistent)
	All other combinations	0 (inconsistent)

Acknowledgements

The authors would like to thank Lauren Miling and Jessica VandenPlas for their assistance with some of the early work on this study. Hilborn would like to thank Lyman Briggs College for financial support. This material is based upon work supported by the National Science Foundation under Grant No. 1705365 and 1702592.

References

1. Abeysekera L. and Dawson P., (2015), Motivation and cognitive load in the flipped classroom: definition, rationale and a call for research, High. Educ. Res. Dev., 34(1), 1–14 DOI:10.1080/07294360.2014.934336.
2. Adbo K. and Taber K. S., (2009), Learners’ mental models of the particle nature of matter: A study of 16-year-old Swedish science students, Int. J. Sci. Educ., 31(6), 757–786 DOI:10.1080/09500690701799383.
3. Akaygun S. and Jones L. L., (2014), How does level of guidance affect understanding when students use a dynamic simulation of liquid–vapor equilibrium? in Devetak I. and Glažar S. A. (ed.), Learning with Understanding in the Chemistry Classroom, Dordrecht: Springer Netherlands, pp. 243–263 DOI:10.1007/978-94-007-4366-3_13.
4. Al-Balushi S. et al., (2012), Omani twelfth grade students’ most common misconceptions in chemistry, Sci. Educ. Int., 23(3), 221–240.
5. Bancroft S. F., Jalaeian M. and John S. R., (2021), Systematic review of flipped instruction in undergraduate chemistry lectures (2007–2019): Facilitation, independent practice, accountability, and measure type matter, J. Chem. Educ., 98(7), 2143–2155 DOI:10.1021/acs.jchemed.0c01327.
6. Bergquist W. and Heikkinen H., (1990), Student ideas regarding chemical equilibrium: What written test answers do not reveal, J. Chem. Educ., 67(12), 1000.
7. Bodner G. M., (1986), Constructivism: A theory of knowledge, J. Chem. Educ., 63, 873–878 DOI:10.1021/ed063p873.
8. Burke K. A., Greenbowe T. J. and Windschitl M. A., (1998), Developing and using conceptual computer animations for Cchemistry instruction, J. Chem. Educ., 75(12), 1658–1661.
9. ChemSims, (2020), ChemSims, ChemSims – A Research project made possible with support by the NSF, available at: https://chemsims.com/ (accessed: 6 March 2020).
10. Cheung D., (2009), The adverse effects of Le Châtelier's principle on teacher understanding of chemical equilibrium, J. Chem. Educ., 86(4), 514 DOI:10.1021/ed086p514.
11. Chi M. T. H. and Wylie R., (2014), The ICAP framework: Linking cognitive engagement to active learning outcomes, Educ. Psychol., 49(4), 219–243 DOI:10.1080/00461520.2014.965823.
12. Cooper M. M., Kouyoumdjian H. and Underwood S. M., (2016), Investigating students’ reasoning about acid–base reactions, J. Chem. Educ., 93(10), 1703–1712 DOI:10.1021/acs.jchemed.6b00417.
13. DeKorver B., Chaney A. and Herrington D., (2020), Strategies for teaching chemistry online: A content analysis of a chemistry instruction online learning community during the time of COVID-19, J. Chem. Educ., 97(9), 2825–2833.
14. Demircioğlu G., Demircioğlu H. and Yadigaroglu M., (2013), An investigation of chemistry student teachers’ understanding of chemical equilibrium, Int. J. New Trends Educ. Implicat., 4(2), 192–199.
15. Deslauriers L. et al., (2019), Measuring actual learning versus feeling of learning in response to being actively engaged in the classroom, Proc. Natl. Acad. Sci. U. S. A., 116(39), 19251–19257 DOI:10.1073/pnas.1821936116.
16. Eichler J. F., (2022), Future of the flipped classroom in chemistry education: Recognizing the value of independent preclass learning and promoting deeper understanding of chemical ways of thinking during in-person instruction, J. Chem. Educ., 1c01115 DOI:10.1021/acs.jchemed.1c01115.
17. Eichler J. F. and Peeples J., (2016), Flipped classroom modules for large enrollment general chemistry courses: A low barrier approach to increase active learning and improve student grades, Chem. Educ. Res. Pract., 17(1), 197–208 10.1039/C5RP00159E.
18. Engzell P., Frey A. and Verhagen M. D., (2021), Learning loss due to school closures during the COVID-19 pandemic, Proc. Natl. Acad. Sci. U. S. A., 118(17) DOI:10.1073/pnas.2022376118.
19. Erdemir A.Ö., Geban Ö. and Uzuntiryaki E., (2000), Freshman students misconceptions in chemical equilibrium, Hacettepe Üniversitesi Eğitim Fakültesi Dergisi, 18(18).
20. Ganasen S. and Shamuganathan S., (2017), The Effectiveness of Physics Education Technology (PhET) Interactive Simulations in Enhancing Matriculation Students’ Understanding of Chemical Equilibrium and Remediating Their Misconceptions, in Karpudewan M., Md Zain A. N. and Chandrasegaran A. L. (eds), Overcoming Students’ Misconceptions in Science: Strategies and Perspectives from Malaysia, Singapore: Springer, pp. 157–178 DOI:10.1007/978-981-10-3437-4_9.
21. Gillis A. and Krull L. M., (2020), COVID-19 remote learning transition in spring 2020: Class structures, student perceptions, and inequality in college courses, Teach. Sociol., 48(4), 283–299 DOI:10.1177/0092055X20954263.
22. Google Forms – create and analyze surveys, for free, (2018), available at: https://www.google.com/forms/about/ (accessed: 11 May 2018).
23. Hegarty M., (2004), Dynamic visualizations and learning: Getting to the difficult questions, Learn. Instruct., 14(3), 343–351.
24. Herrington D. G., Sweeder R. D. and VandenPlas J. R., (2017), Students’ independent use of screencasts and simulations to construct understanding of solubility concepts, J. Sci. Educ. Technol., 26(4), 359–371 DOI:10.1007/s10956-017-9684-2.
25. IBM SPSS Statistics 25, (2017), IBM, available at: https://www.ibm.com/products/spss-statistics (accessed: 10 July 2018).
26. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Learn., 7(2), 75–83 DOI:10.1111/j.1365-2729.1991.tb00230.x.
27. Karpudewan M. et al. (2015), Investigating high school students’ understanding of chemical equilibrium concepts, Int. J. Environ. Sci. Educ. [preprint], available at: https://www.ijese.net/makale/23.html (accessed: 28 October 2021).
28. Keehner M. et al., (2008), Spatial reasoning with external visualizations: What matters is what you see, not whether you interact, Cogn. Sci., 32(7), 1099–1132 DOI:10.1080/03640210801898177.
29. Keengwe J. and Kidd T. T., (2010), Towards best practices in online learning and teaching in higher education, 6(2), 9.
30. Kelly R. M. and Jones L. L., (2007), Exploring how different features of animations of sodium chloride dissolution affect students’ explanations, J. Sci. Educ. Technol., 16(5), 413–429 DOI:10.1007/s10956-007-9065-3.
31. Koedinger K. R. et al., (2015), Learning is not a spectator sport: Doing is better than watching for learning from a MOOC, in Proceedings of the Second (2015) ACM Conference on Learning @ Scale, New York, NY: Association for Computing Machinery (L@S ’15), pp. 111–120 DOI:10.1145/2724660.2724681.
32. Lekhavat P. and Jones L. L., (2009), The effect of adjunct questions emphasizing the particulate nature of matter on students’ understanding of chemical concepts in multimedia lessons, Educ. Quím., 20(3), 351–359 DOI:10.1016/S0187-893X(18)30036-3.
33. Liu X. and Lesniak K. M., (2005), Students’ progression of understanding the matter concept from elementary to high school, Sci. Educ., 89(3), 433–450 DOI:10.1002/sce.20056.
34. Martinez B. L. et al., (2021), Improving conceptual understanding of gas behavior through the use of screencasts and simulations, Int. J. STEM Educ., 8(1), 1–13.
35. Mayer R. E., (2011), Applying the science of learning, Upper Saddle River, NJ: Pearson.
36. Mayer R. E. and Anderson R. B., (1991), Animations need narrations: An experimental test of a dual-coding hypothesis, J. Educ. Psychol., 83(4), 484–490 DOI:10.1037/0022-0663.83.4.484.
37. Mayer R. E. and Moreno R., (2003), Nine ways to reduce cognitive load in multimedia learning, Cogn. Psychol., 38(1), 43–52.
38. Nakhleh M. B., (1992), Why some students don’t learn chemistry: Chemical misconceptions, J. Chem. Educ., 69(3), 191–196 DOI:10.1021/ed069p191.
39. Nguyen T. et al., (2021), Insights into students’ experiences and perceptions of remote learning methods: From the COVID-19 pandemic to best practice for the future, Front. Educ., 6, 91 DOI:10.3389/feduc.2021.647986.
40. Potgieter M., Harding A. and Engelbrecht J., (2008), Transfer of algebraic and graphical thinking between mathematics and chemistry, J. Res. Sci. Teach., 45(2), 197–218 DOI:10.1002/tea.20208.
41. Pulukuri S. and Abrams B., (2021), Improving learning outcomes and metacognitive monitoring: Replacing traditional textbook readings with question-embedded videos, J. Chem. Educ., 98(7), 2156–2166 DOI:10.1021/acs.jchemed.1c00237.
42. Quílez-Pardo J. and Solaz-Portolés J. J., (1995), Students’ and teachers’ misapplication of Le Chatelier's principle: Implications for the teaching of chemical equilibrium, J. Res. Sci. Teach., 32(9), 939–957 DOI:10.1002/tea.3660320906.
43. Rau M. A. et al., (2017), Unpacking “active learning”: A Combination of flipped classroom and collaboration support is more effective but collaboration support alone is not, J. Chem. Educ., 94(10), 1406–1414 DOI:10.1021/acs.jchemed.7b00240.
44. Reactions & Rates, (2013), PhET, available at: https://phet.colorado.edu/en/simulation/reactions-and-rates (accessed: 8 June 2018).
45. Sanger M. J., Phelps A. J. and Fienhold J., (2000), Using a computer animation to improve students’ conceptual understanding of a can-crushing demonstration, J. Chem. Educ., 77(11), 1517 DOI:10.1021/ed077p1517.
46. Seery M. K., (2015), Flipped learning in higher education chemistry: emerging trends and potential directions, Chem. Educ. Res. Pract., 16(4), 758–768 10.1039/C5RP00136F.
47. Suits J. P. and Sanger M. J., (2013), Dynamic visualizations in chemistry courses, in Suits J. P. and Sanger M. J. (ed.), Pedagogic Roles of Animations and Simulations in Chemistry Courses, Washington, DC: American Chemical Society, p. 13 DOI:10.1021/bk-2013-1142.ch001.
48. Sweeder R. D. and Herrington D. G., (2020), Formative assessments using text messages to develop students’ ability to provide causal reasoning in general chemistry, Can. J. Chem., 98(1), 15–23.
49. Sweeder R. D., Herrington D. G. and VandenPlas J. R., (2019), Supporting students’ conceptual understanding of kinetics using screencasts and simulations outside of the classroom, Chem. Educ. Res. Pract., 20, 685–698 10.1039/C9RP00008A.
50. Taber K. S., (2013), Revisiting the chemistry triplet: Drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14, 156–168.
51. Talanquer V., (2011), Macro, submicro, and symbolic: The many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33(2), 179–195.
52. Talanquer V., (2014), Chemistry education: Ten heuristics to tame, J. Chem. Educ., 91(8), 1091–1097 DOI:10.1021/ed4008765.
53. Usher E. L. et al., (2021), Psychology students’ motivation and learning in response to the shift to remote instruction during COVID-19, Scholarship Teach. Learn. Psychol. DOI:10.1037/stl0000256.
54. VandenPlas J. R. et al., (2021), Use of simulations and screencasts to increase student understanding of energy concepts in bonding, J. Chem. Educ., 98(3), 730–744 DOI:10.1021/acs.jchemed.0c00470.
55. van Driel J. H., Verloop N. and de Vos W., (1998), Developing science teachers’ pedagogical content knowledge, J. Res. Sci. Teach., 35(6), 673–695 DOI:10.1002/(SICI)1098-2736(199808)35:6<673::AID-TEA5>3.0.CO;2-J.
56. Vygotsky L. S., (1980), Mind in Society: The Development of Higher Psychological Processes, Harvard University Press.
57. Wiggins G. and McTighe J., (2005), Understanding by Design, Alexandria, VA: ASCD.
58. Williamson V. M. and Abraham M. R., (1995), The effects of computer animation on the particulate mental models of college chemistry students, J. Res. Sci. Teach., 32(5), 521–534.

---