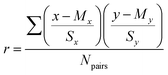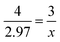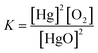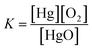Relevance and equity: should stoichiometry be the foundation of introductory chemistry courses?†
Vanessa
Rosa
*a,
Nicole E.
States
b,
Adriana
Corrales
c,
Yvonne
Nguyen
d and
Molly B.
Atkinson
c
aTeaching Engagement Program, Office of the Provost and Department of Chemistry and Biochemistry, University of Oregon, 1585 E 13th Ave, Eugene, Oregon 97403, USA. E-mail: vanessarosa@cuvettecollective.org
bDepartment of Chemistry, University of Iowa, 230 N Madison St, Iowa City, Iowa 52242, USA
cDepartment of Chemistry, University of North Texas, 1508 W Mulberry St, Denton, Texas 76201, USA
dDepartment of Chemistry, University of South Florida, 12111 USF Sweetgum Ln, Tampa, Florida 33620, USA
First published on 15th April 2022
Abstract
Emphasizing stoichiometry appears to be a norm of introductory chemistry courses. In this longitudinal and mixed-methods study, we examined how the emphasis on stoichiometry in assessments of introductory chemistry impacted educational equity and student learning. Using quantitative methods, we identified mole and stoichiometric conversions as two of the most frequently assessed and inequitable competencies, perpetuating systemic inequities in access to pre-college mathematics preparation. Above all other competencies, midterm assessments of stoichiometry were the most impactful as the strongest predictor of students’ scores on both the first and second-semester introductory chemistry final exam. These results informed the development of a think-aloud protocol used to describe how students approached assessments of stoichiometry. Students described stoichiometry as a step-by-step series of calculations, rarely associating this algorithm with the process of a chemical reaction by which reactants break bonds and rearrange to form products. Student responses suggest stoichiometry substitutes learning how to apply chemistry to think about the problems scientists solve for memorizing algorithms to solve math problems in the context of chemistry. Shifting the foundation of introductory chemistry courses from algorithmic to applied competencies reflects scientific practice and maybe one strategy for educators to disrupt systemic barriers to access and retention in STEM Education. Based on these findings and the advancements of other research, we offer implications for supporting educators as they iteratively develop increasingly relevant and equitable assessments of introductory chemistry.
Introduction
The purpose of this research is to support chemistry educators as they evaluate their curricula for which competencies are relevant and equitable to students of science, technology, engineering, and mathematics (STEM).Internationally, there have been calls to reform education from static, industrialized norms to equitably equipping students with competencies relevant to thriving in the rapidly developing disciplines of STEM (OECD, 2018; Freeman et al., 2019; Duschl et al., 2021). Competencies are the skills, abilities, and other qualities practitioners need to participate in a discipline (Albanese et al., 2008; Momsen et al., 2013; OECD, 2018). In the following sections, how we defined relevance and equity for this study is described alongside the prior research to which this work seeks to contribute.
Relevance
The Education Policy Committee of the Organisation for Economic Cooperation and Development (OECD, 2018) developed the Future of Education and Skills 2023 project as an opportunity to reflect on the long-term challenges facing education and to support educators in advancing equitable and evidence-based curriculum reform.The OECD characterized relevance as epistemic knowledge or competencies that allow students to think like a practitioner of a discipline, making a clear distinction between learning to solve problems and learning to think about the problems practitioners solve. Throughout, we will refer to learning to solve problems as algorithmic competencies and learning to think about the problems practitioners solve as applied competencies.
Assessments are a vital component of curricular reform. How students are assessed informs which competencies they perceive as valuable to participating in a discipline (Asikainen et al., 2013; Momsen et al., 2013; Dent and Koenka, 2016; Herrmann et al., 2017; Lynam and Cachia, 2018; Andrade and Brookhart, 2019; Phelps, 2019a, 2019b). Chemistry Education Researchers have developed frameworks to support educators as they differentiate algorithmic and applied competencies and evaluate which competencies should be assessed relative to which are assessed. Some examples include differentiating algorithmic competencies from conceptual understanding (Nakhleh, 1993; Niaz, 1995; Pushkin, 1998), lower- and higher-order cognitive skills (Zoller et al., 1995; Zoller, 2002; Toledo and Dubas, 2016), the thinking processes students are likely to employ when solving different types of assessment tasks (Smith et al., 2010), and the potential of an assessment task to elicit dimensions of scientific knowledge and practice (Laverty et al., 2016).
Despite these advancements, substantial emphases on algorithmic competencies continue to be the norm (Smith et al., 2010; Rosa and Lewis, 2018; Shah et al., 2021; Stowe et al., 2021). For example, Stowe et al. (2021) observed learning environments where more than half of assessment points were awarded to algorithmic competencies with relatively little (less than 5%) emphasis on applied competencies. Algorithmic competencies have also been identified as the most inequitable approach to assessing first (Rosa and Lewis, 2018) and second (Shah et al., 2021) semester introductory chemistry courses.
Equity
In addition to relevance, the OECD expressed aspirations of educational equity, defined as deconstructing barriers preventing students of differing socially constructed identities (e.g., gender, race, ethnicity, socioeconomic status) from attaining favorable academic outcomes; ensuring all students are supported (OECD, 2018; Voogt et al., 2018). Evidence of systemic inequities in STEM education are reported all over the world (Freeman et al., 2019; Duschl et al., 2021), particularly in the United States, where government agencies have identified educational systems as exclusionary to Black, Indigenous, Latinx, and other minoritized identities (National Academies Press, 2011; President's Council of Advisors on Science and Technology, 2012).We argue that the persistent emphasis on algorithmic competencies and inequities in STEM education are related. Evidence of medium to strong correlations between students’ math test scores and achievement in introductory chemistry courses spans decades (Pedersen, 1975; Pickering, 1975; Ozsogomonyan and Loftus, 1979; Craney and Armstrong, 1985; Rixse and Pickering, 1985; Bunce and Hutchinson, 1993; McFate and Olmsted, 1999; Wagner et al., 2002; Nguyen et al., 2017; Berkowitz and Stern, 2018; Thompson et al., 2018; Powell et al., 2020; Williamson et al., 2020).
Often termed “underprepared,” “at risk,” or “low achieving,” students scoring in the bottom quartile of their cohorts are disproportionately at risk of attaining unfavorable academic outcomes in chemistry (Wagner et al., 2002; Gellene and Bentley, 2005; Lewis and Lewis, 2007; Hall et al., 2014; Ye et al., 2016; Rosa and Lewis, 2018; Williamson et al., 2020). Further, students scoring in the bottom quartile are over-represented by those who identify as women, Black, or Latinx (Carmichael et al., 1986; Crisp et al., 2009; Grossman and Porche, 2014; Rosa and Lewis, 2018; Vincent-Ruz et al., 2018; King and Pringle, 2019; Robinson et al., 2019; Witherspoon et al., 2019). Developed as tools for racial prejudice (Selden, 1999; Davis and Martin, 2008; Au, 2010; Knoester and Au, 2017), “standardized” math test scores are still nearly ubiquitously used by educational institutions to prevent the admission and enrollment of students with lower math test scores (Bialek and Botstein, 2004; Nicholas et al., 2015).
As there are no biological differences to explain why students in different socially constructed categories attain different math and chemistry test scores (Selden, 1983; Byrd and Hughey, 2015; Atmaykina and Babayan, 2018), we (1) argue math test scores conflate measures of math aptitude with access to mathematical preparation and (2) posit the emphasis of algorithmic competencies on chemistry assessments is a systemic barrier to education equity in STEM requiring further investigation.
Both studies operationalized inequitable topics within first or second-semester introductory chemistry as those presenting a barrier to students receiving inequitable access to pre-college mathematics preparation. However, coding by topic bounds the evaluation to a single semester of the two-semester course sequence. A longitudinal design allows us to answer whether the competencies assessed across the course sequences were inequitable, highly emphasized (or a substantive portion of the assessments used to define academic success), and impactful (or strongly correlated to students’ future academic outcomes). Neither study incorporated qualitative data analyses describing how students approached inequitable assessment tasks. A mixed-methods design allows us to examine competencies identified as inequitable for their relevance to disciplinary practice.
Purpose
The purpose of this longitudinal and mixed methods research is to provide evidence that can support chemistry educators as they evaluate their curricula for which competencies are relevant and equitable to STEM students. Two research questions guided the work:1. Which competencies assessed across first- and second-semester introductory courses were the most emphasized, impactful, and inequitable to students’ success?
2. How is the knowledge elicited by assessments of highly emphasized, impactful and inequitable competencies relevant to the practice of chemistry?
Methods
This study is of explanatory sequential design, a mixed-methods approach wherein quantitative data inform the collection and analyses of qualitative data (Tashakkori and Teddlie, 2003). Quantitative, longitudinal methods were used to evaluate the emphasis, impact, and equity of competencies assessed across two semesters of introductory chemistry courses (research question 1). Then, qualitative methods were used to characterize the relevance of the competencies identified by the extent to which students experienced them as algorithmic (learning to solve problems) or applied (learning to think about the problems practitioners solve; research question 2). Following a description of the research setting, we outline the quantitative and qualitative methods used to address the research questions.Setting
The following description of the university and classroom structure, along with first-semester chemistry pre-requisites, is provided to support the reader in determining the transferability of these findings to their educational settings (Elo et al., 2014). Data were collected from a large, public, and doctorate-granting research institution in the Southeastern United States, where multiple classes of first- and second-semester introductory chemistry are offered. With 2035 students enrolled in first-semester introductory chemistry courses, class sizes averaged 241 students in the fall. In the spring, second-semester introductory classes were smaller, seating an average of 176 students of the 795 who enrolled.Topics covered in the first semester included properties of substances and reactions, thermochemistry, atomic-molecular structure, bonding, and periodicity. Second-semester topics included solutions, thermodynamics, kinetics, equilibria, electrochemistry, and nuclear chemistry.
Courses were coordinated by a team of instructors who shared a textbook, learning objectives, syllabus, and grading scheme. Instructors chose a peer-reviewed, openly licensed introductory textbook offered through OpenStax (Chemistry: 2e, 2019) for both courses. “Chemistry: 2e” was not atoms-first, introducing the topic of stoichiometry ahead of electronic structure, periodic properties, chemical bonding, and molecular geometry.
Academic success was primarily defined by high-stakes, summative assessment outcomes (70%), online homework completion (10%), and class participation (e.g., clicker responses and quizzes; 20%). Instructors coordinated the implementation of flipped classes and peer-led team learning (Robert et al., 2016) across all sections of first-semester general chemistry and several sections of the second-semester course (Rosa and Lewis, 2020).
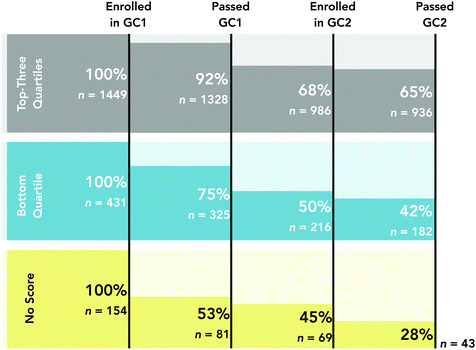
To enroll in first-semester chemistry, the institution required students to attain either a 570 on a pre-college math test known as the SAT or complete a college-level algebra course with a “C” or higher in addition to either one year of high school chemistry or the completion of a chemistry preparation course. The bottom quartile (or 25th percentile) of math test scores for this cohort was 570, suggesting students scoring in the bottom quartile and students without registered math test scores relied on college-level algebra courses to meet the mathematics prerequisites set by the institution. In alignment with prior research (Wagner et al., 2002; Gellene and Bentley, 2005; Lewis and Lewis, 2007; Hall et al., 2014; Ye et al., 2016; Rosa and Lewis, 2018; Williamson et al., 2020), we observed disparate outcomes in longitudinal retention rates for students scoring in the top-three quartiles, bottom quartile or enrolled without pre-college math test scores (see Fig. 1).
 | ||
| Fig. 1 Access or Exclusion? A step-diagram of the longitudinal retention (by frequency, or n, and percentage) observed as students matriculated through first (GC1) and second (GC2) semester introductory chemistry. Student outcomes were grouped by those scoring in the top-three quartiles, bottom quartile, or did not have an incoming math test score (No Score). | ||
Overall, there were 2034 students enrolled in first-semester general chemistry. Of the 1449 students who scored in the top-three quartiles, 936 (or 65%) were retained (i.e., passed GC1, enrolled, and passed GC2). In contrast, the retention rate for students scoring in the bottom quartile was 42%. Students without registered math test scores (“No Score” in Fig. 1) had a retention rate of 28%. Findings suggest that access to pre-college mathematics preparation is critical for success in introductory chemistry courses.
Quantitative methods
| Student Groupc | Sample Size | % T3Qs | % BQ | % No Score |
|---|---|---|---|---|
| a Proportion of students represented in the top-three quartiles (T3Qs), bottom quartile (BQ), or without math test scores (no score). b Pass rates (in parentheses) for chemistry students retained across the course sequence. c Data limited to conflated categorizations of race and ethnicity as collected by the Institution's Registrar. | ||||
| Overall | 2034 | 71a (0.65)b | 21 (0.42) | 8 (0.28) |
| Asian | 288 | 86 (0.77) | 12 (0.48) | 2 (0.00) |
| Black | 192 | 57 (0.68) | 33 (0.39) | 10 (0.21) |
| Foreign national | 94 | 62 (0.64) | 25 (0.38) | 13 (0.17) |
| Indigenous | 20 | 75 (0.73) | 15 (0.33) | 10 (0.50) |
| Latinx | 478 | 64 (0.63) | 28 (0.47) | 8 (0.26) |
| Not reported | 71 | 73 (0.52) | 20 (0.57) | 7 (0.00) |
| White | 891 | 74 (0.61) | 18 (0.38) | 8 (0.36) |
As mentioned previously, there are no biological reasons why students of differing socially constructed identities should perform disparately on presumed measures of “math aptitude” (Selden, 1983; Allen, 1999; Byrd and Hughey, 2015). The exclusion of Black, Foreign National, and Latinx students from (1) having a math test score, (2) scoring in the top-three quartiles, and (3) being retained in introductory chemistry courses suggest these test scores reflect the consequences of systemic racism (Wilson-Kennedy et al., 2020; Madkins and Morton, 2021).
In addition to inequitable representation across subgroups, intersectionality, or observations of the overlapping and interdependent systems of discrimination across other socially constructed categories (Petersen, 2006; López et al., 2018), was observed within subgroups as students scoring in the top-three quartiles were far more likely to be retained in introductory chemistry courses than their peers who scored in the bottom quartile (Petersen, 2006; Bowleg, 2008; López et al., 2018). Thus, pre-college math test scores functioned as a proxy for educational access or exclusion, informing how we operationalized educational equity.
Rodriguez and colleagues (2012) identified the impact of equity operationalization on interpreting a study's results. We operationalized equity as parity (or, more appropriately, equality), defining equitable approaches to assessing chemistry competencies as those resulting in similar outcomes for chemistry students scoring in the top three and bottom quartiles of math test scores (Lynch, 2000; Rodriguez et al., 2012). Having identified our population of interest and a model for operationalizing equity, we then sought a framework to categorize individual chemistry test items by competency.
| Knowledge | Competency |
|---|---|
| Foundational: students are asked to discern definitions or representations to recall or identify pertinent chemical contexts. | Recall: match a term to a definition or vice versa. |
| Identify: apply a definition to categorize chemical species (e.g., acid or base, ionic or covalent). | |
| Translate: interpret qualitative descriptions of observable phenomena (e.g., a change in color), quantitative expressions (e.g., equilibrium expressions, rate laws), or representations (e.g., photographs, particulate diagrams including Lewis structures, chemical equations). | |
| Algorithmic: students are asked to engage in step-by-step solution processes concluding with conversions or multi-step calculations. | Math operations: conduct a single-step calculation (excluding conversions). |
| Macroscopic conversions: convert macroscopic quantities (e.g., volume in mL to L). | |
| Mole conversions: convert between macroscopic and microscopic quantities of the same chemical species (e.g., volume to moles). | |
| Stoichiometric conversions: convert between moles of one chemical to moles of another using the coefficients of a chemical equation (e.g., mol-mol ratios and ICE tables). | |
| Multi-step calculations: substitute the resultant value of one calculation into another (excluding conversions). | |
| Applied: students are asked to use foundational or algorithmic knowledge to predict or explain chemical phenomena, compare chemical species, or evaluate data. | Compare: reason at the interface of measures, structures, and properties to communicate differences between chemical species or phenomena (e.g., use the structures of two chemical species to determine which would have a higher boiling point). |
| Evaluate: interpret quantitative data (e.g., tables, graphs, calculations, expressions) or descriptions to assess the nature of chemical phenomena (e.g., determine the degree to which a solution is saturated using a solubility curve). | |
| Predict or explain: extend relevant models, chemical theories, or laws to predict or explain changes in chemical systems (i.e., apply atomic- and molecular-level models to explain changes in a solution). | |
The first and fourth authors independently coded all midterms and final exams administered across the year-long course sequence. These authors achieved 93.3% agreement with 0.891 for Cohen's Kappa; both measures could be interpreted as strong agreement (Berry and Mielke, 1988).
We explain in Appendix 1 how previously published frameworks and protocols were synthesized and applied according to data collected at the research setting. For exemplar assessment tasks for each competency, see Appendix 2.
Three measures were used to identify the competencies critical to students' success in first- (GC1) and second semester (GC2) introductory chemistry: (1) emphasis was the percent of assessment items represented by a given competency, (2) impact was measured using Pearson correlations (Pearson, 1909) between students’ competency scores on midterm exams and final exams scores in either course and (3) inequity was calculated as the numerator of Cohen*s d (Cohen, 1988) or the mean differential between students scoring in the top three and bottom quartiles (see Table 3).
| Term | Definition | Equation |
|---|---|---|
| Emphasis | The percent of items administered within each course used to assess a given competency |
|
| Impact | The direction (+ or −) and strength (on a scale from 0 to 1) of the linear association between pairs of students' midterm competency scores (x) and final exam scores (y) |
|
| Inequity | A difference in the percentage of chemistry students who selected a correct answer between those scoring in the top-three quartiles (MT3Qs) and bottom quartile (MBQ) of pre-college math composite SAT (and concorded ACT) scores | MD = MT3Qs − MBQ |
Exceedingly challenging or easy competencies could artificially condense student outcomes giving the appearance of equality (Ho and Yu, 2015). However, mean competency scores ranged from 55.1–76.6% suggesting floor/ceiling effects were unlikely to influence measures of inequity.
These quantitative measures were applied to identify particularly frequently assessed, impactful, and inequitable competencies. Then, the quantitative findings informed the design of the qualitative methodology used to answer the second research question.
Qualitative methods
Our colleagues in Physics Education Research developed the modeling framework to characterize different facets in how students apply and integrate knowledge (e.g., principles, concepts, and measurements) to make sense of a phenomenon (Zwickl et al., 2015). The first, second, and fourth authors used the modeling framework to identify the target phenomenon of an assessment task and describe the extent to which students approached the competency as algorithmic (e.g., first, do this, then, do that) or applied (e.g., this principle/concept/measure can be used to make sense of the presented phenomena).
This framework prompted us to use an interview protocol comprised of a variety of prompts capable of eliciting a range of student experiences with a given competency. Developed in education research, phenomenography focuses on producing descriptions of a range of student experiences with a phenomenon (Walsh et al., 2007). Consistent with prior research in physics (Walsh et al., 2007; Ornek, 2008) and chemistry education (Bretz, 2008; Stefani and Tsaparlis, 2009), phenomenography was used in this study to produce descriptions of the range in ways a small group of students perceived and understood a competency as it related to the target phenomenon. A think-aloud protocol, an interview method wherein students are prompted to solve a task or activity aloud to the researchers (Larkin and Rainard, 1984), appeared well suited to the modeling framework and phenomenographic methodology.
Maximum variation sampling (Shaheen et al., 2019) was used to select student participants. We hypothesized that students with high chemistry test scores would approach the competency as more applied than algorithmic. Thus, we alternated between interviewees who scored in the top three and bottom quartiles of the first instructor-authored exam on which the identified competency was assessed.
The number of participants recruited for the study was informed by saturation. Following each interview, meetings were held to discuss prevalent themes and evaluate whether saturation had been achieved (Mack et al., 2005; Curtis and Curtis, 2011; McGrath et al., 2018). Given the specificity of the protocol, emergent themes became repetitive after seven participants. The researchers interviewed eleven students, identifying no new themes in the last four interviews, a sample size appropriate to the phenomenographic methodology implemented (Collins et al., 2006; Bartholomew et al., 2021).
Then, we separated to identify and describe the themes observed, reconvening to condense our collective themes to descriptive patterns, audit for negative cases, and discuss agreements and discrepancies (Ornek, 2008; Wilson, 2015; Ataro, 2020). Once the first and fourth authors reached a consensus, this cycle was repeated with the first and second authors (Miles et al., 2013). Overall, this cycle was consistent with the process of collaborative consensus coding, enabled the analysis to occur through multiple perspectives, and was a more appropriate option than interrater reliability (Sweeney et al., 2013).
Reflexivity and positionality
We seek transparency and accountability in the research we produce and acknowledge the impact of our social identities, professional roles, and prior experiences on our research (Secules et al., 2021). We chose to include these statements in the methods (rather than the Electronic Supplemental Information) to ensure scholarship key to our interpretations of the data is recognized and appropriately cited. Authors are listed alphabetically (by the first initial) and were brought together through Twitter (first, second, third, and fifth authors) and Undergraduate Research (first and fourth authors).Results
An inequitable norm in the assessment of introductory chemistry courses
 | ||
| Fig. 2 Algorithmic competencies were the dominant emphasis in assessments of introductory chemistry. A dot plot (wherein each dot represents an assessment task) grouped by the competency assessed and color-coded by knowledge type with gray representing foundational knowledge, yellow algorithmic knowledge, and teal applied knowledge. | ||
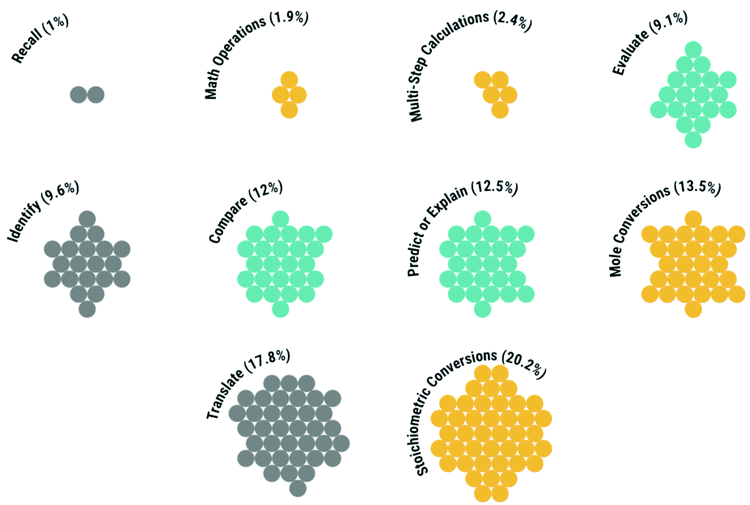
The most frequently assessed competency (nitems = 42) was stoichiometric conversions. Together, mole and stoichiometric conversions (nitems = 70) comprised more than 1/3rd of the assessment tasks administered in the chemistry course sequence.
The types of assessment tasks assigned around these competencies were remarkably diverse, including calculations of molar mass, isotopic abundance, empirical and molecular formulae, percent mass/yield, molarity, molality, mole fraction, serial dilutions, lattice energy, partial/vapor/osmotic pressure, ideal gas laws, Gibbs free energy, the heat of vaporization, molar entropy, equilibrium/rate constants, pH/pOH, titrations, molar solubility, precipitants, common ion effects, electroplating, balancing equations and half-/formation reactions. While mole and stoichiometric conversions originally appeared to be narrowly defined competencies in the deductive coding scheme (see Fig. 1), these tasks were heavily represented, warranting individual categories.
 | ||
| Fig. 3 The most inequitable approach to assessing introductory chemistry was algorithmic competencies. This dot plot is arranged by competency (y-axis) and inequity (x-axis). Inequity is measured by the difference in mean between students scoring in the top-three (T3Qs) and bottom quartile (BQs). The dot plot has been color-coded by knowledge type, with gray representing foundational knowledge, yellow algorithmic knowledge, and teal applied knowledge. | ||
In descending order, the most inequitable competencies were multi-step calculations (where mean differentials were, on average 17.1%), stoichiometric conversions (AVGMD = 17.0%), evaluate (16.4%), and mole conversions (16.4%).
The nuances observed in these data warrant further description. First, the inequity of a competency could differ across the course sequence. The most notable change in inequity observed was in the competency mole conversions, which decreased from 18.9% in GC1 to 14.3% in GC2. This change may relate to attrition as students with inequitable access to pre-college math preparation were much less likely to complete all four exams in each course (31%) than their peers (53%; see Fig. 1). Second, while the assessment of applied knowledge was generally more equitable, evaluate tasks (n = 19), relying on quantitative data (n = 15, AVGMD = 17.2%) to examine the nature of a chemical phenomenon were similar in inequity to solely algorithmic tasks.
However, the range of mean differentials for quantitative, evaluate tasks was 7.8 to 26.9%. The most equitable evaluate tasks relied on math diagrams, requesting (for example) that students use a vapor pressure diagram to identify which substance would have the highest vapor pressure at a given temperature or a solubility curve to identify whether a given quantity of solute is super/un/saturated. The most inequitable evaluate tasks also relied on math diagrams. However, these tasks required some form of conversion. For example, students were given a solubility curve with a y-axis in units of “g of solute per 100 g of solution” with a prompt “how many grams of solute would dissolve in 50 g of water.” In another task, students identified the equivalence point of a weak acid titrated with a strong base or the acidity/basicity of a solution relying on pH calculations (which often accompany mole conversions).
These examples highlight the relative emphasis on assessing the nature of chemical phenomena (applied) versus enacting conversions (algorithmic) as a potential underlying factor in the equity of an evaluate assessment task. These examples also demonstrate the potential for conversions to have the potential for conversions to have an impact on students* trajectory through introductory chemistry courses that may not correspond to the relevance of this competency to the practice of chemistry.
 | ||
| Fig. 4 Stoichiometric conversions were the strongest predictor of students’ success on final exams administered in first (GC1) and second (GC2) semester introductory chemistry courses. This quadrant chart depicts the Pearson correlations of students’ midterm competency scores and final exam scores in GC1 (x-axis) and GC2 (y-axis). We chose to depict only well-represented competencies (those comprised of more than three assessment tasks). | ||
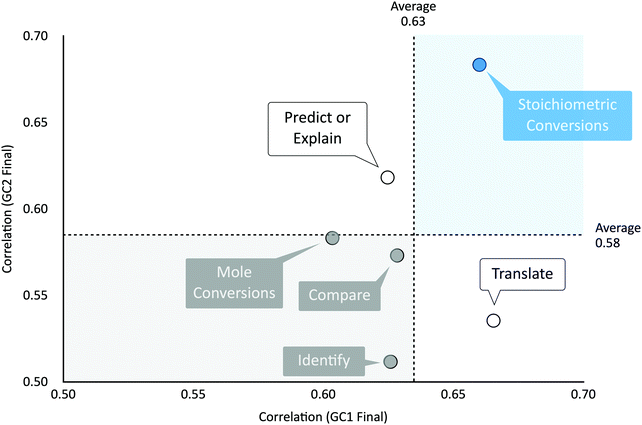
Situated in the top-right quadrant of Fig. 4, midterm assessments of stoichiometric conversions were above average in correlation, accounting for 44–46% of the variance observed on students’ GC1 and GC2 final exam scores.
In summary, stoichiometric conversions were flagged as a highly inequitable and frequently assessed competency strongly correlated to students’ academic success. Should stoichiometry be the foundation of introductory chemistry courses? Is it relevant in supporting students, not just to solve problems, but to think about the problems chemists solve?
Stoichiometric conversions were irrelevant, and may have impeded students’ thinking about the problems chemists solve
Relying on the modeling framework (Zwickl et al., 2015), the target phenomenon of stoichiometric conversions was identified as the process of breaking bonds and rearranging atoms in the reactants to form new bonds and products during a chemical reaction. Thus, if students integrated the target phenomenon in their solutions to the think-aloud prompts, their responses were coded as an applied approach to stoichiometric conversions. In contrast, an algorithmic approach presents itself as a series of quantitative steps disconnected from the target phenomenon (e.g., first, check that the equation is balanced, then, extract the measurements needed for the conversion from the prompt, then convert units of measure into moles, and finally, calculate the desired quantity).As described in the methods, we used maximum variation sampling (Shaheen et al., 2019) to recruit interview participants scoring in the top-three and bottom quartiles of the first midterm exam wherein the competency emerges or Test 1 of first-semester introductory chemistry (see Table 4).
| Pseudonym | Test 1 scores (%) | SAT scores | Stoichiometric competency (GC1, GC2) | Applied |
|---|---|---|---|---|
| Adam | 65.8 | 540 | 0.38, 0.36 | |
| Aimee | 67.1 | No score | 0.28, 0.38 | |
| Eric | 92.4 | 650 | 0.67, 0.40 | |
| Isaac | 64.6 | 430 | 0.48, 0.68 | |
| Jakob | 91.8 | 590 | 0.72, 0.52 | |
| Jean | 43.7 | No score | 0.62, 0.59 | |
| Lily | 100.0 | 750 | 0.67, 0.78 | |
| Maeve | 91.1 | 610 | 0.81, 0.66 | |
| Ola | 64.6 | 550 | 0.90, 0.90 | |
| Rahim | 65.2 | 680 | 0.48, 0.61 | |
| Ruby | 100.0 | No score | 0.86, 0.88 | ✓ |
Despite variations in access to pre-college mathematics preparation and students’ demonstrated proficiency with the competency of stoichiometry, only one student was identified as using an applied approach to stoichiometry. Therefore, neither a students* math test score nor proficiency with the competency of stoichiometry appeared to inform whether or not they adopted an applied approach to thinking about the problems chemists solve.
The prompts used in the think-aloud protocol were related to this chemical equation:
| 2Ni2O3(s) → 4Ni(s) + 3O2(g) |
More moles of nickel will be produced because 2 moles of oxygen atoms will break ionic bonds with nickel and rearrange to form one mole of covalently bound molecular oxygen (O2).
However, students unanimously elicited algorithmic strategies to answer the prompt, often relying on coefficients in the chemical equation. For example, Maeve responded by stating:
I figured because there was there were four moles of nickel, that would mean that the amount of moles of oxygen would be smaller than the amount of moles produced by nickel because there's four moles of nickel as opposed to 3 moles of oxygen.
These justifications lead to an accurate prediction: more moles of nickel are produced than moles of oxygen. However, one reflects an applied approach related to the atomic and molecular behavior of the target phenomenon (i.e., the process of converting reactants to products) and the other an algorithmic approach through a series of quantitative steps disconnected from the target phenomenon.
This disconnection from the target phenomenon appeared to impede some students’ responses, obfuscating the chemical reaction process with algorithmic approaches to understanding coefficients, numbers, or the masses of chemical species. For example, Isaac claimed, “I'm going to say [the moles of O2 produced would be] higher because there's two molecules of O2. And then there's three moles. So, three times two would be six [atoms]. Then there's only four [atoms] of nickel.” Other students emphasized the mass of the atoms, like Lily, who wrote, “higher, the mass is higher,” emphasizing atomic mass as knowledge elicited when considering which product would be produced in a greater quantity of moles. Adam stated, “… nickel would be higher. I just kind of ran through it in my head, and I'm pretty sure that three is a bigger number than what I would get if I were to multiply them by this [underlining the coefficient].”
Some students expressed an aversion to the first prompt, requesting to skip to the next, which involved a (potentially more familiar) unit conversion. For example, Jakob stated: “Do I have to answer this first one?” When prompted as to why they did not want to answer the prompt, Jakob stated, “I just like, I’ve kind of wanted to just jump into it because I don’t really think conceptually like that. I’m just like, oh, let's just do it.” Overall, none of the interviewed students elicited an approach that applied the process of chemical reactions to stoichiometry when responding to the first prompt.
| x = 2.23 mol O2 |
I liked it when it's like this that just makes it looks more like a math equation. So, I think it's easier to understand when it's like that… I like math, so I try to put it in terms of like how you do it in math. But like once you incorporate like the chemicals, I get all confused… It's kind of like, um, like one day you just see the periodic table and they're like, okay, now we're just going to throw all these elements into regular math. And then it's like, what? But yeah.
While the prompt could be solved with a single mole-to-mole conversion, many students elicited a variety of algorithmic approaches, often expressing the need to incorporate grams into the conversion. Jakob started their solution by writing “mass → moles.” Jean had trouble starting the problem, asking, “Well, I know like you have to do the mole equation, but I'm forgetting how you start. Like should I divide this by the whole mass of NiO2 or just?” Even Aimee – who expressed confidence in their solution – stated, “Because I also have the, the grams for nitrogen. And since I also have the moles, I'm trying to figure out how, if I'm trying to see, because I need to cross out for moles and grams for nitrogen.”
Many students drew connections to past problems, like Isaac when they stated, “Um, I feel like a lot of equations use it, so I feel like the molar mass is probably going to be in there somewhere.” Aimee explained how grams are often incorporated, offering this explanation of why they converted to grams:
Well, it just makes it seem like, um, well, when we learned it was like a big thing of it. Like you had the chance to, we usually got the grams. So, you have the change to grams to moles. That's what most of it was like, and then, well, like the mol-to-mol was the hardest one. So, it was like harder to remember how to do that. So, I want to say they tell us an easy way to get from grams from moles to grams and then go back to moles but not moles to moles.
Some students expressed challenges with reconciling algorithmic and applied approaches in chemistry. Jakob explains how the first prompt was hard to grasp:
I was taught how to do like just the math first, not the understanding part. So, I like in the beginning I asked you, do I have to answer with this first? I was thrown off because I was like, oh, I don't really know how to do it. I just know how to do it mathematically. And then, once I do it mathematically, I could explain it to you conceptually. So, I feel like conceptually first threw me off because I just wanted to jump into the math and then explain… I feel like you should know how to do it conceptually first and then do it numerically. But I feel like when people grow up doing math, they jump right into the math. They don't really think about why it's this.
Ola reflects on the lack of engaging with “why” throughout their educational experiences in chemistry:
Yeah. That that's what it is. Is it the fact that um, like every, every time I've been taught at even from high school, it just, it, there is no explanation why. It's just that mole to gram and then that, you know, grams back to moles. It never really clicked, I guess.
Student responses suggest an overemphasis of algorithmic reasoning during the instruction and assessment of chemistry may (1) implicitly communicate to students that chemistry is about word problems using chemical phenomena as the context for calculations, not understanding how and why phenomena occur in terms of atomic and molecular behavior, and (2) impede students’ desire to learn explanations, processes, and applications of the knowledge.
Apart from Ruby, all other students sought to enact an array of calculations. For example, Jakob responded:
… when you take the molar mass of nickel, it is 58.69, but you have two of them. So, you have to multiply that by two. And then same thing for oxygen, it's 16 times the three. And then once you add that up, you have to times it by two because there's like two of each.
Students often elicited knowledge related to the conservation of mass but appeared to be impeded by algorithmic knowledge. For example, Lily invoked the law of mass conservation after multiplying the mass of Ni by the coefficient in the chemical equation when she stated, “the mass of the products a little bit. Um, yeah. So yeah, mass of the products would be like the four times Ni, oh wow. It'd be the same thing, wouldn't it?” Additionally, Isaac expressed, “I don't know how you would see that; I'm not sure.”
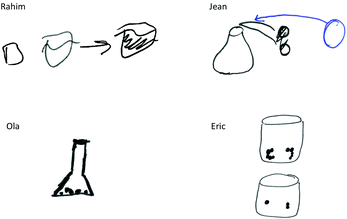
To improve the prompt's accessibility, the interviewers began asking students to draw what would be in a beaker before and after the reaction took place (see Fig. 5).
 | ||
| Fig. 5 The overemphasis of algorithmic competencies may have impeded students’ approaches toward applied competencies. Student participants provided four exemplar illustrations of the mass before and after a chemical reaction. | ||
Using their visual (top-left of Fig. 5), Rahim explains: “Okay. Yes, there are reactants [left two beakers]. So together there are two compounds of Nickel and oxygen…and then after the reaction takes place, there are four moles of the Nickel and then three of the oxygen.” Similarly, Jean enacted a calculation using coefficients and atomic masses and explained their illustration as: “Um, because NiO is just one compound and then Ni, and then O2 [represented with circles later crossed out], it's two different compounds,” later editing their illustration (blue) to emphasize the combination of the reactants to form the products within the beaker. Ola initially answers “491.1786 grams,” describing the use of subscripts and atomic masses in calculating their response, maintaining that the mass of the products remains the same before and after the reaction occurs.
While four students achieved a competency score for stoichiometric conversions exceeding 70% on assessments administered in the first-semester introductory chemistry course (see Table 4), qualitative results suggest that just one student (Ruby) applied the competency of stoichiometry to the process of a chemical reaction. When Ruby was asked by the interviewers how they came to develop this understanding of stoichiometry, Ruby shared that they identify as an international student and describe educational experiences outside of the United States.
Truly, the US education is kind of broad, like the information they brought up. it is not really deep and their solution. …uh, it the same not really complicated, but like in my country, they do some more complicated question…
This response reflects the influence of systemic norms in science education and the potential positive impacts following a shift from emphasizing algorithmic to applied competencies. Subject to this norm of science education, educators may unknowingly perpetuate students’ systemic marginalization by emphasizing algorithmic competencies in introductory STEM courses (Rosa and Lewis, 2018; Shah et al., 2021). In summary, assessment design can convey which competencies are of value to a discipline and whom a discipline selects for participation, informing whether prerequisite STEM courses serve as a point of access or exclusion.
Discussion
Key findings
Situating these findings in the context of prior research suggests these results may reflect a norm in chemistry education. For example, a predominant emphasis on algorithmic competencies on assessments of chemistry has been documented in several studies (Tai et al., 2006; Smith et al., 2010; Momsen et al., 2013; Rosa and Lewis, 2018; Shah et al., 2021; Stowe et al., 2021). For example, chemistry courses offered at three different institutions were observed, assigning (on average) 29.2%, 46.7%, and 59.2% of assessment points to algorithmic competencies (Stowe et al., 2021). Smith and colleagues (2010) report algorithmic emphases on an initiative by the American Chemical Society to emphasize fewer “traditional” (i.e., algorithmic) and more “conceptual” chemistry questions as composed of 23% (first term) and 16% (second), suggesting it is a “tradition” in introductory chemistry to emphasize algorithmic competencies.
When placed alongside efforts to identify inequitable approaches to assessing introductory chemistry, these systemic trends reflect barriers to educational equity. For example, stoichiometry and the mole concept have previously been identified as the most inequitable topics in first-semester chemistry courses (Rosa and Lewis, 2018). In second semester introductory chemistry, researchers identified algorithmic competencies as comprising most assessments, potentially driving the inequity in the topics: chemical equilibria and intermolecular forces and properties (Shah et al., 2021).
The current study contributes a longitudinal analysis of competencies spanning first and second-semester introductory chemistry courses to this literature base. The results reify algorithmic competencies are highly emphasized, impactful, and inequitable to students of introductory chemistry courses. However, math remains a valuable tool supporting chemists as they think about problems as they arise in the modern world. How might educators reconcile the utility of mathematics with the inequity of algorithmic competencies?
This study adopts a mixed-methods approach contributing qualitative descriptions of whether students experience the competency of stoichiometric conversions as solely algorithmic or if this knowledge was a valuable tool in examining chemical phenomena. Relying on the modeling framework advanced by education researchers in the physical sciences (Zwickl et al., 2015), scientists' intellectual work was characterized around (1) a target phenomenon and (2) the knowledge used to model the processes underlying the target phenomena. In the context of stoichiometric conversions, it was theorized that the target phenomenon would be the process of converting reactants into products, with the knowledge used to model this process involving the rearrangements that follow breaking chemical bonds to form new bonds and products. Of the students interviewed, one applied knowledge about the target phenomenon when engaging in stoichiometric conversions. All others relied on an algorithmic approach disjointed from the target phenomenon with varying degrees of success in responding to the prompts correctly.
Competency scores in the assessments of stoichiometric conversions did not reflect a student's integration of mathematics to examine the chemical phenomena and instead more often correlated to students’ math test scores (see Table 4).
Again, when situated in prior research, the observations that students hold stoichiometry as an algorithm and not a tool to understand chemical phenomena appears to be repeatedly reified across several of the works contributed by chemistry education researchers. To provide a few examples, several scholars have reported a students’ reliance on algorithmic approaches to stoichiometry, using the algorithm to solve problems at the expense of applying this knowledge to think about phenomena (Mason et al., 1997; BouJaoude and Barakat, 2003; Arasasingham et al., 2004; Dahsah and Coll, 2007; Cracolice et al., 2008). One prior study could be found connecting the knowledge students elicit to the inequity of the competency of stoichiometric conversions. The evidence presented suggests inequities reflect differences in the rates by which students answer stoichiometric conversions correctly using incoherent chemical reasoning (Rosa and Lewis, 2019), reflecting the inaccurate and algorithmic approaches students expressed in the current study.
We argue this is not a deficit of the student nor the teacher reflecting instead the limitations of an industrialized education system that offers little institutionalized support or incentive to advance curricular and pedagogical reform. Despite this system, these findings reflect the need for a critical conversation about the purpose of chemistry education and how what we choose to perpetuate in our classrooms impacts who gains access to careers in STEM.
Implications for research and practice
 | ||
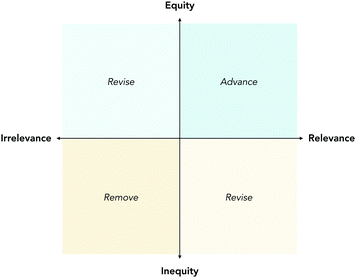| Fig. 6 A visual guide for curriculum evaluation. Envisioning a guiding framework for evaluations along dimensions of relevance (x-axis) and equity (y-axis). | ||
For example, while assessments of applied knowledge (i.e., compare, evaluate, predict, or explain) were generally more equitable than assessments of algorithmic knowledge, the applied tasks administered in this setting were still inequitable, spanning mean differentials between 14 and 16% (see Fig. 4).
Such assessments could be characterized on the plane in Fig. 6 as relevant but inequitable. Thus, the advisable action would be to make evidence-based and data-driven revisions to improve the relevance and equity of our courses.
Some instructors calculate the difficulty of a task using the percentage of students who answered it correctly to evaluate whether a task is too difficult. With support, instructors could calculate inequity using the difference in percentages of students who answered a task correctly between subgroups of interest and evaluate whether a task is inequitable. Iteratively, these adjustments of how we define academic success and who is most impacted by these definitions can potentially impact the relevance and equity of our courses substantially. An example spreadsheet with equations to conduct by-item equity and relevance analyses is available in the ESI.† Specific examples of assessment tasks for each code can be found in Appendix 2.
The Center for Urban Education offers Racial Equity Tools, a suite of resources offering step-by-step guides, measures, and other evaluative tools for advancing racial equity in educational institutions (CUE Racial Equity Tools, 2020). Additionally, institutional efforts to broaden access to student outcomes disaggregated by social constructs (e.g., gender, race, ethnicity) can be used as models for advancement. For example, see the Grades and Equity Gaps Dashboard by Faculty Development at California State University, Chico (Hall, 2022), the Know Your Students web-based application offered by the Center for Educational Effectiveness (Steinwachs, 2021), the Comprehensive Analytics for Student Success project through the Office of the Provost at University of California (Cherland et al., 2019), Irvine, and Equity Data by the Center for Innovations in Teaching and Learning at the University of California, Santa Cruz (Equity Data, 2022).
Other opportunities to advance the current research include examining (1) other competencies (besides stoichiometry) identified as inequitable, and (2) intersections of competencies as each of the codes used in the current student represents a task's primary competency, ignoring when a variety of competencies were assessed within one task. In sum, these research efforts could be used to identify further the hallmarks of equitable approaches to assessing chemistry.
For larger-scale impacts to the equity and value of introductory chemistry courses, we agree with the following quote by Dr. Vincent-Ruz (2020) and encourage instructors to extend the practice of Relevance and Equity beyond practices of assessment design.
“Finally, equity work is not a methodology or the inclusion of diverse groups in a sample. A true commitment to equity research is centering those principles in every decision we make as researchers and practitioners.” (p. 71)
We also agree with our colleagues in education research who call for disaggregating data in evaluative efforts (Mukherji et al., 2017; Bancroft, 2018; Bancroft et al., 2021; Collins and Olesik, 2021).
As researchers engage in this work, we ask that they continue to shift their discourse out of deficit perspectives and into system-level interpretations. For example, prior research has attributed deficits to students with inequitable access to pre-college mathematics, referring to these students as “at-risk” or of “low math aptitude” (Lewis and Lewis, 2007; Shields et al., 2012; Hall et al., 2014; Ye et al., 2016; Rosa and Lewis, 2018, 2019), without acknowledging these measures were historically designed to exclude, and are presently successful in excluding, students by social constructs such as race and ethnicity (Davis and Martin, 2008; Knoester and Au, 2017). To provide a starting point, we encourage our colleagues to seek information about reframing deficit perspectives (Harper, 2010) and engaging in quantitative research critically informed by broader systemic and societal influences (Garcia et al., 2018; Gillborn et al., 2018).
Limitations
A series of limiting methodological decisions made throughout this study should be considered in the interpretation and advancement of the scholarship presented. First, these findings reduce societal, institutional, departmental, and classroom practices, policies, and culture to inequities in student outcomes on assessments highlighting opportunities to examine other systemic practices in the education of chemistry that may be contributing to the exclusion of students marginalized by the broader education system.While relying on data from students scoring within the bottom and top-three quartiles of assessments (e.g., SAT, ACT, or chemistry tests) aptly reflects the quantitative data, a second limitation was purposeful sampling by the maximum variation sampling method. Maximum variation sampling may have introduced bias into the results. As a result, we recognize that the knowledge elicited from the think-aloud interviews may not be generalizable to every institution's population, but given evidence in prior research, it appears pertinent to many. We also acknowledge that the purpose of qualitative methods, particularly from a phenomenological approach, is not meant to be generalizable but to provide a detailed description of individuals’ experiences as they engage with and process specific phenomena.
A third limitation of this work is that only high-stakes, summative assessments were included in the initial analysis. Formative assessments are more likely to reveal students’ progress toward learning goals. Future work could examine the connection between formative and summative assessments and equitable outcomes for chemistry students.
Finally, throughout the quantitative methods, we relied predominantly on descriptive statistics. This choice reflects the purpose of this work, to support educators as they evaluate their curricula. By relying on descriptive statistics (frequencies, percentages, rates) and a relatively familiar parametric statistic (correlation), we prioritized the accessibility of our methods. However, binary measures of the statistical significance between measures (e.g., whether the emphasis of mole conversions in assessment was significantly different from stoichiometry) and other more complex methods could be used to examine networks of associations between students’ competency scores, math test scores, and chemistry assessment outcomes.
Conclusions
In this longitudinal and mixed-methods investigation, quantitative methods were used to identify the most emphasized, impactful, and inequitable competencies assessed across a two-semester course sequence of introductory chemistry. Stoichiometric conversions were represented in over 20% of high-stakes summative assessment tasks, accounting for 44–46% of the variance on students’ final exam scores, and (along with other multi-step calculations) were highly inequitable to students with inequitable access to pre-college mathematics preparation.These quantitative results informed the qualitative methods used to collect students’ response processes and characterize their experiences, engaging in assessments of this competency to evaluate whether the knowledge elicited was relevant to applying chemistry to think about phenomena. Stoichiometric conversions elicited knowledge of step-by-step calculations removed from the chemical contexts they are situated (algorithmic) and were observed to hinder students’ integration of the target phenomena stoichiometry represents: the process of converting reactants to products via the breaking, rearrangement, and forming of new chemical bonds and products. The authors challenge other proprietors of the education system to consider (1) what do our assessments communicate in terms of the intellectual work we value in this discipline, (2) who do our assessments exclude from STEM participation, and (3) how can we improve the relevance of the measures we use to assess academic success equitably and prepare students seeking careers in STEM?
Author contributions
Given the critical lens through which we conducted this work, we sought to normalize the practice of offering author contributions within this chemistry education research to ensure the research team is adequately attributed for the work and to hold ourselves and one another accountable for the work we conducted. We were thrilled to see this practice encouraged by the editors of Chemistry Education Research and Practice and have listed our contributions in Table 5 below as informed by CRediT (2019).| Contribution | Authors’ initials |
|---|---|
| Conceptualization | VRR |
| Methodology | YN & VRR |
| Data curation | YN & VRR |
| Coding | YN, VRR, & NES |
| Formal analysis | VRR & NES |
| Interpretation | MBA, AC, VRR, & NES |
| Literature search | MBA, AC, VRR, & NES |
| Writing – original draft | MBA, AC, VRR, & NES |
| Writing – review and editing | MBA, AC, YN, VRR, & NES |
| Project administration and supervision | MBA & VRR |
Conflicts of interest
There are no conflicts to declare.Appendix 1: synthesizing frameworks to identify competencies in chemistry assessments
Complementary strengths and weaknesses of published frameworks
Smith and colleagues (2010) aimed to characterize knowledge and cognitive process dimensions in an Expanded Framework for Evaluating Chemistry Assessments. This informed many of the code descriptions we used to characterize foundational and algorithmic assessment tasks (see Table 6).| Current | Original (Smith et al., 2010) |
|---|---|
| FOUNDATIONAL | |
| Recall: match a term to a definition or vice versa. | D-R: recognizing a definition in multiple-choice format. |
| Identify: apply a definition to categorize chemical species (e.g., acid or base, ionic or covalent). | D-RUA: recalling, understanding, or applying a definition in an open-ended question. |
| Translate: interpret qualitative descriptions of observable phenomena (e.g., a change in color), quantitative expressions (e.g., equilibrium expressions, rate laws), or representations (e.g., photographs, particulate diagrams including Lewis structures, chemical equations). | C-P: analysis of a pictorial representation (chemical symbols or equations). |
| ALGORITHMIC | |
| Macroscopic conversions: convert macroscopic quantities (e.g., volume in mL to L). | A-MaD: macroscopic-dimensional analysis questions requiring conversions between units of macroscopic quantities. |
| Mole conversions: convert between macroscopic and microscopic quantities of the same chemical species (e.g., volume to moles). | A-MaMi: macroscopic-microscopic conversion questions between moles and volumes or masses. |
| Stoichiometric conversions: convert between moles of one chemical to moles of another using the coefficients of a chemical equation (e.g., mol-mol ratios and ICE tables). | A-Mis: microscopic-symbolic conversion questions requiring stoichiometric conversions of particle or mole quantities of substances usually based on chemical formulas or equations. |
| Multi-step calculations: Substituting the resultant value of one calculation into another (excluding conversions). | A-Mu: multi-step questions involve multiple steps frequently based on the use or algebraic manipulation of mathematical formulas. |
The subsumed competencies of foundational and algorithmic knowledge used in this study are similar to those described by Smith and colleagues, given their applicability and utility in describing assessment items in the research setting. However, changes were made. For example, assessment tasks rarely relied solely on word association (e.g., “definition” codes in the original scheme) and more often required students to apply a definition to categorize symbolically, or otherwise represented, chemical contexts (e.g., acid or base, ionic or covalent, oxidizing or reducing). These competencies were reorganized in the coding scheme used for the current study as “recall” and “identify,” wherein either could be applied to a multiple-choice assessment item. This reflects the difference between students associating a definition with its term and applying this definition toward identifying a relevant chemical context. As this reconceptualization of the “definition” knowledge reflects students' understanding and application of what could be considered introductory course content, the dimension of knowledge was renamed as “foundational” for use in the current study.
Items coded as “conceptual” were the most challenging to nest in the framework, as the competencies described in the original coding scheme did not encompass many of the items observed in the research setting. For example, the code “analysis of pictorial representations” referred to items requiring students to translate pictorial representations into analyzing a chemical phenomenon. At the research setting, several items required translation across scales of representation but did not necessarily rely upon a pictorial representation (i.e., translating qualitative descriptions of a macroscopic phenomenon to symbolic representations that span the molecular, atomic, and subatomic scale). Additionally, there was no code to describe items wherein algorithmic calculations were necessary to evaluate chemical phenomena (e.g., calculate ΔG to evaluate whether the equilibrium of a chemical reaction will favor the reactants or products).
A subset (90 of 298 or 30.2%) of the assessment tasks were coded using each published framework or protocol to evaluate each by its applicability to the data collected. In early examinations of interrater reliability, where percent agreement was measured at 72% (65 of 90 items or Kappa = 0.549, indicating weak agreement), discerning items of the conceptual competencies from foundational and algorithmic contributed many disagreements amongst the researchers (19 of the 25 mismatched items). Then, we discovered complementary strengths and weaknesses between this and other frameworks published in prior research, which informed the decision to combine these frameworks into a single coding scheme.
In Defining Conceptual Understanding by Holme and colleagues (2015), what a “conceptual” assessment task entails was defined by the open-ended responses of 1396 chemistry instructors. The study helped expand descriptions of “conceptual” assessment tasks (see Table 7).
| Current | Original (Smith et al., 2010) | (Holme et al., 2015) | (Laverty et al., 2016) |
|---|---|---|---|
| Applied: students are asked to use foundational or algorithmic knowledge to predict or explain chemical phenomena, compare chemical species, or evaluate data. | Depth: reason about core chemistry ideas using skills that go beyond mere rote memorization or algorithmic problem solving. | ||
| Compare: reason at the interface of measures, structures, and properties to communicate differences between chemical species or phenomena (e.g., use the structures of two chemical species to determine which would have a higher boiling point). | Transfer: apply core chemistry ideas to chemical situations that are novel to the student. | ||
| Evaluate: interpret quantitative data (e.g., tables, graphs, calculations, expressions) or descriptions to assess the nature of chemical phenomena (e.g., determine the degree to which a solution is saturated using a solubility curve). | C-I: questions involving the analysis of interpretation of data. | Problem-solving: demonstrate the critical thinking and reasoning involved in solving problems including laboratory measurement. | Evaluating information: make sense of information presented and demonstrate reasoning to support or deny its validity. |
| Analyzing and interpreting data: given a claim or data, select an interpretation of its meaning. | |||
| Using mathematics and computational thinking: perform a mathematical manipulation and interpret the results in the context of a phenomenon. | |||
| Predict or explain: extend relevant models, chemical theories, or laws to predict or explain changes in chemical systems (i.e., apply atomic- and molecular-level models to explain changes in a solution). | C-E: questions involving the explanation of underlying ideas behind chemical phenomena. | Predict: expand situational knowledge to predict and/or explain behavior of chemical systems. | Developing and using models: given a representation, select an appropriate explanation or prediction about phenomenon. |
| C-O: questions involving the prediction of outcomes. | Constructing explanations and engaging in argument from evidence: Select reasoning and evidence to support a claim. | ||
For example, the code “depth” was instrumental in defining the difference between conceptual and the other two competencies (foundational and algorithmic). Our interpretation of the framework was that it did not minimize the role of memorization or algorithmic computation in learning chemistry but acknowledged the cognitive effort required to commit these competencies to practice via application.
However, two weaknesses were identified in the descriptions provided by Holme and colleagues (Holme et al., 2015). The first was in the code description “transfer – applying core chemistry ideas using scenarios novel to students.” Such a code would require data supporting (or assumptions about) what is and is not novel to individual students. Thus, “transfer” was redefined as “compare” in the synthesized coding scheme. The second issue was tautology. The code “problem solving” was defined as “relating to demonstrations of critical thinking in reasoning.” This use of other vaguely defined terms (“problem-solving,” “reasoning,” and “critical thinking”) to define “conceptual” required an additional perspective to solidify codes relating to “conceptual” knowledge.
Thus, we integrated the Scientific Practices Criteria from the Three-Dimensional Learning Protocol advanced by Laverty and colleagues (2016). The criterion described helped identify “conceptual” competencies. For example, the criterion for “Using Mathematics and Computational Thinking” and “Analyzing and Interpreting Data” helped to differentiate between multi-stepalgorithmic (the performance of the calculation or test) and evaluate (interpreting quantitative data to assess the nature of chemical phenomena) test items. Overall, “conceptual” tasks were often foundational or algorithmic knowledge applications towards a larger goal (e.g., modeling, predicting, explaining). Thus, “conceptual” tasks were relabeled as applied. A limitation of the Three-Dimensional Learning Protocol was in its applicability to the collected dataset. More than half of the assessment tasks collected in the research setting did not meet the criterion established for engaging in Scientific Practices, often because the collected assessment tasks did not require students to justify or explain their answer selections. We were able to clarify characterizations of the assessments collected in the research setting by synthesizing all three frameworks.
Interrater agreement for coding assessment tasks
Once the frameworks were applied, items not yet described or for which agreement was not achieved were taken and reviewed by the researchers who identified relevant features of the items related to what students are asked to accomplish in solving the items. Rounds of open coding and constant comparative analyses wherein the researchers met to discuss emergent codes led to the development of inductive codes used in the culminating framework (Miles et al., 2013; Merriam and Tisdell, 2015). After applying these three frameworks, an emergent code generated by the authors from the assessment items collected was used to describe assessment items that fit none of the previously described categories and required students were to compare two different chemical contexts by structure or property (e.g., given three chemical formulae, discern which are of the highest and lowest boiling point). This emergent code was labeled as “compare.”Appendix 2: examples of assessment tasks in each category of the proposed coding scheme
Each code used in the study is organized by cognitive process (foundational, algorithmic, or applied) below, with exemplar assessment items (answers in bold) collected at the research setting. Contrasting items are used at times to substantiate the differences between codes.Foundational Assessment Items
Defined as items wherein solutions are discerned by applying definitions to either recall or identify relevant chemical contexts.Recall: matching a term to a definition or description and vice versa.
The [A]t expression in an integrated rate law describes which of the following:
(A) The initial rate of the reaction
(B) The rate of the reaction at any point in time
(C) The concentration of a reactant at any point in time
(D) The concentration of a product at any point in time
(E) The initial concentration of a product
Requires students to match the definition for [A]t.
Identify: applying a definition to categorize a relevant chemical context (e.g., acid or base, ionic or covalent, oxidizing or reducing).
Write the equilibrium constant expression for the reaction:
2HgO(s) ⇄ 2Hg(l) + O2(g)
(A) K = [Hg]2[O2]
(B) K = [O2]
(C) 
(D) 
(E) 
Requires students identify this reaction as having heterogeneous equilibrium for which only gaseous and aqueous species would contribute a concentration.
Translate: interpreting (1) qualitative descriptions across scale (e.g., macroscopic observations explained using submicroscopic phenomena), or (2) representations across scale (e.g., photographs or descriptions of chemicals at the macroscopic-level, particulate representations of chemicals at the particulate-level, and symbolic representations of chemicals at the reaction-, molecular-, elemental-, and subatomic-levels).
Consider the following chemical reaction,
HSO4−(aq) + H2O(l) ⇌ SO42−(aq) + H3O+(aq)
Identify all statements that are true regarding the reaction above.
(I) HSO4−(aq) is a base in this reaction.
(II) H3O+(aq) is the conjugate acid of H2O(l).
(III) SO42−(aq) is the conjugate base of HSO4−(aq).
(A) only I (B) only II (C) only III (D) both I and II (E) both II and III
Requires students to translate from the given symbolic representation to consider particulate-level changes to the chemical species.
Algorithmic Assessment Items
Defined as items wherein solutions are derived of procedural cognitive work (i.e., step-by-step solution processes), including algebraic rearrangement, conversions, or multiple steps not used to evaluate or otherwise describe the chemical context.Macroscopic conversions: converting macroscopic quantities (e.g., volume in mL to L).
No items in the research setting were exclusively related to macroscopic conversions. However, many required these conversions as a subsidiary step. For example, the item prior relating to ΔG requires a student to convert ΔH from 65.0 kJ to 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 J to subtract the term TΔS where ΔS is in units of J K−1.
Mole conversions: converting between macroscopic quantities (e.g., volumes, masses) and microscopic quantities (e.g., moles).
Similarly, no items were observed to enact only a mole conversion. For example, in the exemplar for the code “Multi-Step,” students would need to convert from moles of the solvent to the mass of the solvent (in kg) to determine the molality of the solution.
Stoichiometric conversions: converting between chemical contexts (i.e., moles of one chemical to moles of another) via applying a mol–mol ratio or incorporating chemical coefficients in a calculation.
Stoichiometric conversions applied to convert between chemical contexts (e.g., ΔHrxn and Q for 2.05 mole of NH3):
Consider the following balanced chemical equation:
4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(l) ΔHrxn = +1168 kJ
How much heat is absorbed/released when 2.05 mol of NH3(g) reacts with excess O2(g) to produce NO(g) and H2O(l)?
(A) 5.99 × 102 kJ of heat is released.
(B) 5.99 × 10 2 kJ of heat is absorbed.
(C) 2.40 × 103 kJ of heat is released.
(D) 2.40 × 103 kJ of heat is absorbed.
(E) 1.02 × 104 kJ of heat is absorbed.
Stoichiometric conversions are applied in the calculation of a state function (e.g., entropy) as for the item shown below:
Calculate 
for the following reaction. The S° for each species is shown below the reaction.
C2H2(g) + 2H2(g) → C2H6(g)
S° (J (mol K))−1 200.9 130.7 229.2
(A) −102.4 J (mol K)−1
(B) −233.1 J (mol K) −1
(C) 229.2 J (mol K)−1
(D) 303.3 J (mol K)−1
(E) 560.8 J (mol K)−1
Multi-step calculations: substituting the product of one calculation into another to arrive at a solution (excluding unit conversions). Note: not all algorithmic, multi-step items required computation (see the second exemplar).
The mole fraction of KNO3 in an aqueous solution is 0.0194. What is the molality of the solution? (MM of H2O is 18.02 g mol−1)
(A) 0.0194 m
(B) 0.0388 m
(C) 0.194 m
(D) 1.10 m
(E) 2.20 m
This task requires several steps, including:
1. Use the provided mole fraction of KNO3 (0.0194) to determine the moles of solute (the numerator of molality),
2. Subtract these moles of solute from moles of the solution to determine the moles of solvent,
3. Convert moles of solvent to the mass of solvent,
This was in addition to converting mass in g to mass in kg (the denominator of molality) to determine the molality of the solution, which (per the coding scheme) was not included as “steps” in the multi-step calculation.
Which answer best describes how to solve for the pH of a KOH solution when given the concentration of the solution?
(A) Write the base reaction, write an equilibrium table, and solve for [OH−], convert to pOH and then to pH
(B) Write the acid reaction and an equilibrium table, solve for [H3O+] and then pH
(C) Set concentration of KOH equal to [H3O+] and solve for pH
(D) Write the acid reaction, convert Ka to Kb, write an equilibrium table and solve for [OH−], convert to pOH, and then to pH
(E) Set concentration of KOH equal to [OH − ], solve for pOH, and then pH
Requires students to identify the correct sequence of steps in solving the item.
Conceptual Assessment Items
Defined as items wherein solutions extend beyond hallmarks of foundational or algorithmic toward translations across scale or representation, predictions of a chemical phenomenon, analysis of data, or comparisons between chemical context or measures.Compare: reasoning at the interface of measures, structures, and properties to inform differences between chemical species or phenomenon (e.g., relating the structure of a chemical species to compare by differences in boiling point). These two exemplars differ as one requires computation and the other does not.
A voltaic cell is designed with the following cell notation:
Li(s)|Li+(aq)‖Pb2+(aq)|Pb(s)
Which set of concentrations for Li+(aq) and Pb2+(aq) would produce the largest cell potential (Ecell) for this voltaic cell?
| Li+(aq) | Pb2+(aq) | |
|---|---|---|
| (A) | 0.1 M | 1.0 M |
| (B) | 1.0 M | 1.0 M |
| (C) | 1.0 M | 0.1 M |
| (D) | 0.1 M | 0.1 M |
| (E) | Each has the same Ecell | |
Requires students to compare each set of concentrations for which would render the smallest Q ([ion, oxidized]/[ion, reduced]) to produce the largest Ecell.
Which of the following aqueous solutions (solute added to water) would have the lowest freezing point?
(A) 2.0 m KNO3
(B) 2.0 m CaF 2
(C) 2.0 m KF
(D) 2.0 m CH3OH
(E) 2.0 m HClO4
Requires students to compare solutions by the ideal van't Hoff factor produced by each solvent.
Evaluate: interpreting data, quantitative (in the form of a table, graph, or calculations within the context of a mathematical model) or qualitative (descriptions of the context and chemical systems involved), to assess the nature of a chemical context (e.g., determining the degree to which a solution is saturated using a solubility curve).
Determine the rate law for the following reaction using the data provided.
2NO(g) + O2(g) 
2NO2(g)
| Experiment | [NO], M | [O2], M | Reaction rate (mol (L × s)−1) |
|---|---|---|---|
| 1 | 5.5 ×10−3 | 3.0 × 10−2 | 8.55 × 10−3 |
| 2 | 1.1 × 10−2 | 3.0 × 10−2 | 1.71 × 10−2 |
| 3 | 5.5 × 10−3 | 6.0 × 10−2 | 3.42 × 10−2 |
A. Rate = k[NO][O2]
B. Rate = k[NO]2[O2]
C. Rate = k[NO]2[O2]2
D. Rate = k[NO][O2]1/2
E. Rate = k[NO][O 2 ]2
Requires students to use the quantitative data provided to determine the rate law for each reactant.
Predict or explain: extending relevant models, chemical theories, or laws (e.g., the valence bond theory, the law of mass conservation, the laws of definite and multiple properties, the ideal gas laws) beyond algorithmic calculations to predict or select an explanation for changes in chemical systems (e.g., cause-effect relationships, structure-property relationships, and chemical interactions in solution).
Consider the following reaction at equilibrium. What effect will removing NO2 have on the system?
SO2(g) + NO2(g) ⇌ SO3(g) + NO(g)
(A) The reaction will shift in the direction of products.
(B) The reaction will shift in the direction of reactants.
(C) The reaction will shift to decrease the pressure.
(D) The equilibrium constant will decrease.
(E) No change will occur since NO2 is not included in the equilibrium expression.
Requires students to predict the impact removing NO2 will have on the equilibrium of the provided chemical context.
The normal boiling point for hydrazoic acid, HN3, is 37 °C compared to ammonia, NH3, which has a boiling point of −33.34 °C. This is best explained by:
(A) HN3 has a lower pH
(B) HN 3 has larger intermolecular forces
(C) HN3 has a higher vapor pressure
(D) HN3 has a larger van't Hoff factor
(E) HN3 has lower surface tension
Requires students to explain the observed phenomenon (differences in boiling points between two chemical species).
Acknowledgements
This study would not be possible without the cooperation and dedication of instructors and students in the research setting. Partial support for this work was provided by the National Science Foundation's Florida-Georgia Louis Stokes Alliance for Minority Participation Bridge to the Doctorate award HRD-1612347, the University of Iowa Graduate Diversity Fellowship, and early career faculty start-up funding provided by the University of North Texas.Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation or other sources of funding. Finally, the authors wish to acknowledge our mentors, Drs Stacey Lowery Bretz, Renée Cole, Regis Komperda, Scott E. Lewis, Norbert J. Pienta, and Kathy Schuh for their investments in our methodological and philosophical training, the anonymous reviewers whose labor is critical to the advancement of education research, and the community of scholars who readily engaged in critical discussions that informed this research: Leslie Bolda, Megan Y. Deshaye, Kevin Pelaez, Leah J. Scharlott, Nicole Suarez, Andrea Van Wyk, and Drs. Kathryn N. Hosbein, Morgan E. Howe, Nicole M. James, Christiane N. Stachl, and Paulette Vincent-Ruz.
References
- Albanese M. A., Mejicano G., Mullan P., Kokotailo P. and Gruppen L., (2008), Defining characteristics of educational competencies, Med. Educ., 42(3), 248–255.
- Allen G. E., (1999), Modern biological determinism, in The Practices of Human Genetics, Fortun M. and Mendelsohn E. (ed.), Springer Netherlands, pp. 1–23.
- Andrade H. L. and Brookhart S. M., (2019), Classroom assessment as the co-regulation of learning, Assess. Educ.: Princip., Pol. Pract., 1–23.
- Arasasingham R. D., Taagepera M., Potter F. and Lonjers S., (2004), Using knowledge space theory to assess student understanding of stoichiometry, J. Chem. Educ., 81(10), 1517.
- Asikainen H., Parpala A., Virtanen V. and Lindblom-Ylänne S., (2013), The relationship between student learning process, study success and the nature of assessment: A qualitative study, Stud. Educ. Eval., 39(4), 211–217.
- Ataro G., (2020), Methods, methodological challenges and lesson learned from phenomenological study about OSCE experience: Overview of paradigm-driven qualitative approach in medical education, Ann. Med. Surg., 49, 19–23.
- Atmaykina V. and Babayan A. V. B., (2018), Principles of determinism, systemicity and development in the scientific research of social and cultural activities, Sci. Educ. New Time, 198–204.
- Au W., (2010), Unequal by design, Routledge.
- Ausubel D. P., (1968), Educational Psychology: A Cognitive View, Holt, Reinhart and Winston Inc., New York.
- Bancroft S. F., (2018), Toward a critical theory of science, technology, engineering, and mathematics doctoral persistence: Critical capital theory, Sci. Educ., 102(6), 1319–1335.
- Bancroft S. F., Jalaeian M. and John S. R., (2021), Systematic review of flipped instruction in undergraduate chemistry lectures (2007–2019): Facilitation, independent practice, accountability, and measure type matter, J. Chem. Educ., 98(7), 2143–2155.
- Bartholomew T. T., Joy E. E., Kang E. and Brown J., (2021), A choir or cacophony? Sample sizes and quality of conveying participants’ voices in phenomenological research, Methodol. Innov., 14(2), 20597991211040064.
- Becker N. M., Rupp C. A. and Brandriet A., (2017), Engaging students in analyzing and interpreting data to construct mathematical models: An analysis of students’ reasoning in a method of initial rates task, Chem. Educ. Res. Pract., 18(4), 798–810.
- Berkowitz M. and Stern E., (2018), Which cognitive abilities make the difference? Predicting academic achievements in advanced STEM studies, J. Intell., 6(4), 48.
- Berry K. J. and Mielke P. W., (1988), A generalization of cohen's kappa agreement measure to interval measurement and multiple raters, Educ. Psychol. Meas., 48(4), 921–933.
- Bialek W. and Botstein D., (2004), Introductory science and mathematics education for 21st-Century biologists, Science, 303(5659), 788–790.
- Biggs J., (1996), Enhancing teaching through constructive alignment, High. Educ., 32(3), 347–364.
- Biggs J., (2003), Aligning teaching and assessing to course objectives, Teach. Learn. High. Educ.: New Trends Innov., 2(4), 13–17.
- Biggs J., (2014), Constructive alignment in university teaching, HERDSA Rev. High. Educ., 1(1), 5–22.
- Boda P. A., (2019), Culture as inter- and intra-personal mediator: Considering the notion of conceptual porosity and its connection to culture as a concept, Cult. Stud. Sci. Educ., 14(3), 699–722.
- Bodner G. M., (1986), Constructivism: A theory of knowledge, J. Chem. Educ., 63(10), 873.
- BouJaoude S. and Barakat H., (2003), Students’ problem solving strategies in stoichiometry and their relationships to conceptual understanding and learning approaches, Electron. J. Sci. Educ., 7(3), 42.
- Bowleg L., (2008), When Black+ lesbian+ woman$\ne$ Black lesbian woman: The methodological challenges of qualitative and quantitative intersectionality research, Sex Roles, 59(5), 312–325.
- Bretz S. L., (2008), Qualitative research designs in chemistry education research, in Nuts and Bolts of Chemical Education Research, Bunce D. M. and Cole R. S. (ed.), American Chemical Society, pp. 79–99.
- Bunce D. M. and Hutchinson K. D., (1993), The use of the GALT (Group Assessment of Logical Thinking) as a predictor of academic success in college chemistry, J. Chem. Educ., 70(3), 183.
- Byrd W. C. and Hughey M. W., (2015), Biological determinism and racial essentialism: The ideological double helix of racial inequality, Ann. Am. Acad. Pol. Soc. Sci., 661(1), 8–22.
- Campbell S. L., (2020), Ratings in black and white: A quantcrit examination of race and gender in teacher evaluation reform, Race Ethnicity Educ., 1–19.
- Carlone H. B. and Johnson A., (2007), Understanding the science experiences of successful women of color: Science identity as an analytic lens, J. Res. Sci. Teach., 44(8), 1187–1218.
- Carmichael J. W., Bauer S. J., Sevenair J. P., Hunter J. T. and Gambrell R. L., (1986), Predictors of first-year chemistry grades for black Americans, J. Chem. Educ., 63(4), 333.
- Chemistry: 2e, (2019), OpenStax.
- Cherland R., Colestock K. and Dennin M., (2019), The COMPASS Project, University of California, Irvine.
- Chiu M.-H., Guo C.-J. and Treagust D. F., (2007), Assessing students’ conceptual understanding in science: An introduction about a national project in Taiwan, Int. J. Sci. Educ., 29(4), 379–390.
- Clark K. R., (2018), Learning theories: Cognitivism, Radiol. Technol., 90(2), 176–179.
- Cohen J., (1988), Statistical Power 2nd Ed, Lawrence Erlbaum Associates.
- Collins J. S. and Olesik S. V., (2021), The important role of chemistry department chairs and recommendations for actions they can enact to advance black student success, J. Chem. Educ., 98(7), 2209–2220.
- Collins K. M. T., Onwuegbuzie A. J. and Jiao Q. G., (2006), Prevalence of mixed-methods sampling designs in social science research, Educ. Res. Eval., 19(2), 83–101.
- Cooper M. M., (2015), Why ask why? J. Chem. Educ., 92(8), 1273–1279.
- Cooper M. M. and Klymkowsky M., (2013), Chemistry, life, the universe, and everything: A new approach to general chemistry, and a model for curriculum reform, J. Chem. Educ., 90(9), 1116–1122.
- Cooper M. M., Stowe R. L., Crandell O. M. and Klymkowsky M. W., (2019), Organic chemistry, life, the universe and everything (OCLUE): A transformed organic chemistry curriculum, J. Chem. Educ., 96(9), 1858–1872.
- Covarrubias A., Nava P. E., Lara A., Burciaga R., Vélez V. N. and Solorzano D. G., (2018), Critical race quantitative intersections: A testimonio analysis, Race Ethnicity Educ., 21(2), 253–273.
- Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: A cognitive difference, J. Chem. Educ., 85(6), 873.
- Craney C. L. and Armstrong R. W., (1985), Predictors of grades in general chemistry for allied health students. J. Chem. Educ., 62(2), 127.
- CRediT - Contributor Roles Taxonomy, (2019).
- Crenshaw K., (2022), On Intersectionality: Essential Writings, New Press.
- Crisp G., Nora A. and Taggart A., (2009), Student characteristics, pre-college, college, and environmental factors as predictors of majoring in and earning a STEM degree: An analysis of students attending a hispanic serving institution, Am. Educ. Res. J., 46(4), 924–942.
- CUE Racial Equity Tools, (2020), Center for Urban Education.
- Curtis B. and Curtis C., (2011), Social Research: A Practical Introduction, SAGE Publications, Inc.
- Dahsah C. and Coll R. K., (2007), Thai Grade 10 and 11 students’ conceptual understanding and ability to solve stoichiometry problems, Res. Sci. Technol. Educ., 25(2), 227–241.
- Davis and Martin, (2008), Racism, assessment, and instructional practices: Implications for mathematics teachers of African American students, J. Urban Math. Educ., 1(1), 10–34.
- Delgado R. and Stefancic J., (2012), Critical Race Theory: An Introduction, 2nd edn, NYU Press.
- De los Ríos C. V., López J. and Morrell E., (2015), Toward a critical pedagogy of race: Ethnic studies and literacies of power in high school classrooms, Race Soc. Probl., 7(1), 84–96.
- De los Ríos C. V., López J. and Morrell E., (2016), Critical ethnic studies in high school classrooms: Academic achievement via social action, in Race, Equity, and Education: Sixty Years from Brown, Noguera P., Pierce J. and Ahram R. (ed.), Springer International Publishing, pp. 177–198.
- Dent A. L. and Koenka A. C., (2016), The relation between self-regulated learning and academic achievement across childhood and adolescence: A meta-analysis, Educ. Psychol. Rev., 28(3), 425–474.
- Duran A., Dahl L. S., Stipeck C. and Mayhew M. J., (2020), A critical quantitative analysis of students’ sense of belonging: Perspectives on race, generation status, and collegiate environments, J. Coll. Stud. Dev., 61(2), 133–153.
- Duschl R. A., Jorde D., McLoughlin E. and Osborne J., (2021), Policy and pedagogy: International reform and design challenges for science and STEM education, in Engaging with Contemporary Challenges through Science Education Research: Selected papers from the ESERA 2019 Conference, Levrini O., Tasquier G., Amin T. G., Branchetti L. and Levin M. (ed.), Springer International Publishing, pp. 59–72.
- Elo S., Kääriäinen M., Kanste O., Pölkki T., Utriainen K. and Kyngäs H., (2014), Qualitative content analysis: A focus on trustworthiness, SAGE Open, 4(1), 2158244014522633.
- Equity Data, (2022).
- Freeman B., Marginson S. and Tytler R., (2019), An international view of STEM education, in STEM Education 2.0, Brill, pp. 350–363.
- Freire P., (1970), Pedagogy of the Oppressed, Seabury Press.
- Garcia N. M. and Mayorga O. J., (2018), The threat of unexamined secondary data: A critical race transformative convergent mixed methods, Race Ethnicity Educ., 21(2), 231–252.
- Garcia N. M., López N. and Vélez V. N., (2018), QuantCrit: Rectifying quantitative methods through critical race theory, Race Ethnicity Educ., 21(2), 149–157.
- Gee J. P., (2000), Identity as an analytic lens for research in education, Rev. Res. Educ., 25, 99–125.
- Gellene G. I. and Bentley A. B., (2005), A six-year study of the effects of a remedial course in the chemistry curriculum, J. Chem. Educ., 82(1), 125.
- Gillborn D., Warmington P. and Demack S., (2018), QuantCrit: Education, policy, ‘Big Data’ and principles for a critical race theory of statistics, Race Ethnicity Educ., 21(2), 158–179.
- Grossman J. M. and Porche M. V., (2014), Perceived gender and racial/ethnic barriers to STEM success, Urban Educ., 49(6), 698–727.
- Hall K., (2022), Grades and Equity Gaps Dashboard, California State University, Chico.
- Hall D. M., Curtin-Soydan A. J. and Canelas D. A., (2014), The science advancement through group engagement program: Leveling the playing field and increasing retention in science, J. Chem. Educ., 91(1), 37–47.
- Harper S. R., (2010), An anti-deficit achievement framework for research on students of color in STEM, New Dir. Inst. Res., 148, 63–74.
- Hazari Z., Sadler P. M. and Sonnert G., (2013), The science identity of college students: Exploring the intersection of gender, Race Ethnicity, 11.
- Herrmann K. J., McCune V. and Bager-Elsborg A., (2017), Approaches to learning as predictors of academic achievement: Results from a large scale, multi-level analysis, Högre Utbildning, 7(1).
- Ho A. D. and Yu C. C., (2015), Descriptive statistics for modern test score distributions: Skewness, kurtosis, discreteness, and ceiling effects, Educ. Psychol. Meas., 75(3), 365–388.
- Holme T. A., Luxford C. J. and Brandriet A., (2015), Defining conceptual understanding in general chemistry, J. Chem. Educ., 92(9), 1477–1483.
- Irby S. M., Phu A. L., Borda E. J., Haskell T. R., Steed N. and Meyer Z., (2016), Use of a card sort task to assess students’ ability to coordinate three levels of representation in chemistry, Chem. Educ. Res. Pract., 17(2), 337–352.
- Kezar A., Gehrke S. and Bernstein-Sierra S., (2018), Communities of transformation: Creating changes to deeply entrenched issues, J. Higher Educ., 89(6), 832–864.
- King N. S. and Pringle R. M., (2019), Black girls speak STEM: Counterstories of informal and formal learning experiences, J. Res. Sci. Teach., 56(5), 539–569.
- Knoester M. and Au W., (2017), Standardized testing and school segregation: Like tinder for fire? Race Ethnicity Educ., 20(1), 1–14.
- Kozma R. and Russell J., (2005), Students becoming chemists: Developing representational competence, in Visualization in Science Education, Gilbert J. K. (ed.), Models and Modeling in Science Education, Springer Netherlands, pp. 121–145.
- Larkin J. H. and Rainard B., (1984), A research methodology for studying how people think, J. Res. Sci. Teach., 21(3), 235–254.
- Laverty J. T., Underwood S. M., Matz R. L., Posey L. A., Carmel J. H., Caballero M. D., et al., (2016), Characterizing college science assessments: The three-dimensional learning assessment protocol. PLoS One, 11(9), e0162333.
- Lawrenz F. and Huffman D., (2006), Methodological pluralism: The gold standard of STEM evaluation, New Dir. Eval., 109, 19–34.
- Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: Comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
- Libarkin J. C. and Kurdziel J. P., (2002), Research methodologies in science education: Qualitative data, J. Geosci. Educ., 50(2), 195–200.
- López N., Erwin C., Binder M. and Chavez M. J., (2018), Making the invisible visible: Advancing quantitative methods in higher education using critical race theory and intersectionality, Race Ethnicity Educ., 21(2), 180–207.
- Lynam S. and Cachia M., (2018), Students’ perceptions of the role of assessments at higher education, Assess. Eval. High. Educ., 43(2), 223–234.
- Lynch S. J., (2000), Equity and Science Education Reform, Taylor & Francis.
- Mack N., Woodsong C., Macqueen K. M., Guest G. and Namey E., (2005), Qualitative Research Methods, p. 137.
- Madkins T. C. and Morton K., (2021), Disrupting anti-blackness with young learners in STEM: Strategies for elementary science and mathematics teacher education, Canadian J. Sci., Math. Technol. Educ., 21(2), 239–256.
- Malina E. G. and Nakhleh M. B., (2003), How students use scientific instruments to create understanding: CCD spectrophotometers, J. Chem. Educ., 80(6), 691.
- Mason D. S., Shell D. F. and Crawley F. E., (1997), Differences in problem solving by nonscience majors in introductory chemistry on paired algorithmic-conceptual problems, J. Res. Sci. Teach., 34(9), 905–923.
- McFate C. and Olmsted J., (1999), Assessing student preparation through placement tests, J. Chem. Educ., 76(4), 562.
- McGrath C., Palmgren P. J. and Liljedahl M., (2018), Twelve tips for conducting qualitative research interviews, Med. Teach., 1–5.
- Merriam S. B. and Tisdell E. J., (2015), Qualitative research: A guide to design and implementation.
- Miles M., Huberman M. and Saldaña J., (2013), Qualitative Data Analysis: A Methods Sourcebook and The Coding Manual for Qualitative Researchers, SAGE Publications, Inc.
- Mogashoa T., (2014), Applicability of Constructivist Theory in Qualitative Educational Research.
- Momsen J., Offerdahl E., Kryjevskaia M., Montplaisir L., Anderson E. and Grosz N., (2013), Using assessments to investigate and compare the nature of learning in undergraduate science courses, LSE, 12(2), 239–249.
- Mukherji B. R., Neuwirth L. S. and Limonic L., (2017), Making the case for real diversity: Redefining underrepresented minority students in public universities, SAGE Open, 7(2), 2158244017707796.
- Nakhleh M. B., (1993), Are our students conceptual thinkers or algorithmic problem solvers? Identifying conceptual students in general chemistry, J. Chem. Educ., 70(1), 52.
- National Academies Press, (2011), Expanding Underrepresented Minority Participation: America's Science and Technology Talent at the Crossroads, National Academies Press.
- National Research Council, Division of Behavioral and Social Sciences and Education, Board on Behavioral, Cognitive, and Sensory Sciences and Committee on Developments in the Science of Learning with additional material from the Committee on Learning Research and Educational Practice, (2000), How People Learn: Brain, Mind, Experience, and School: Expanded Edition, National Academies Press.
- Nguyen T.-L. K., Williams A. and Ludwikowski W. M. A., (2017), Predicting student success and retention at an HBCU via interest-major congruence and academic achievement, J. Career Assess., 25(3), 552–566.
- Niaz M., (1995), Progressive transitions from algorithmic to conceptual understanding in student ability to solve chemistry problems: A lakatosian interpretation. Sci. Educ., 79(1), 19–36.
- Nicholas J., Poladian L., Mack J. and Wilson R., (2015), Mathematics preparation for university: Entry, pathways and impact on performance in first year science and mathematics subjects, Int. J. Innov. Sci. Math. Educ., 23(1), 37–51.
- Novak J. D., (1977), A Theory of Education, Cornell University Press.
- Nyachwaya J. M., Mohamed A.-R., Roehrig G. H., Wood N. B., Kern A. L. and Schneider J. L., (2011), The development of an open-ended drawing tool: An alternative diagnostic tool for assessing students’ understanding of the particulate nature of matter, Chem. Educ. Res. Pract., 12(2), 121–132.
- OECD, (2018), OECD Future of Education and Skills 2030 – OECD Future of Education and Skills 2030.
- Ornek F., (2008), An Overview of a Theoretical Framework of Phenomenography in Qualitative Education Research: An Example from Physics Education Research.
- Ozsogomonyan A. and Loftus D., (1979), Predictors of general chemistry grades, J. Chem. Educ., 56(3), 173.
- Pashler H., Bain P. M., Bottge B. A., Graesser A., Koedinger K., McDaniel M. and Metcalfe J., (2007), Organizing Instruction and Study To Improve Student Learning, Department of Education.
- Pearson K., (1909), Determination of the coefficient of correlation, Science, 30(757), 23–25.
- Pedersen L. G., (1975), The correlation of partial and total scores of the scholastic aptitude test of the college entrance examination board with grades in freshman chemistry, Educ. Psychol. Meas., 35(1), 509–511.
- Pérez Huber L., Vélez V. N. and Solórzano D., (2018), More than ‘papelitos:’ A QuantCrit counterstory to critique Latina/o degree value and occupational prestige, Race Ethnicity Educ., 21(2), 208–230.
- Petersen A. J., (2006), Exploring intersectionality in education: The intersection of gender, race, disability, and class.
- Phelps A. J., (2019a), “But You Didn’t Give Me the Formula!” and Other Math Challenges in the Context of a Chemistry Course, in It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, ACS Symposium Series, American Chemical Society, pp. 105–118.
- Phelps R. P., (2019b), Test frequency, stakes, and feedback in student achievement: A meta-analysis, Eval. Rev., 43(3–4), 111–151.
- Pickering M., (1975), Helping the high-risk freshman chemist, J. Chem. Educ., 52(8), 512.
- Powell C. B., Simpson J., Williamson V. M., Dubrovskiy A., Walker D. R., Jang B., et al., (2020), Impact of arithmetic automaticity on students’ success in second-semester general chemistry, Chem. Educ. Res. Pract., 21(4), 1028–1041.
- President's Council of Advisors on Science and Technology, (2012), Engage to excel: Producing one million additional college graduates with degrees in science, technology, engineering, and mathematics.
- Pushkin D. B., (1998), Introductory students, conceptual understanding, and algorithmic success, J. Chem. Educ., 75(7), 809.
- Rosa V. and Lewis S. E., (2018), Chemistry topics posing incommensurate difficulty to students with low math aptitude scores, Chem. Educ. Res. Pract., 19(3), 867–884.
- Rosa V. and Lewis S. E., (2019), An explanative basis for the differential performance of students with low math aptitude in general chemistry, Chem. Educ. Res. Pract., 20(3), 570–593.
- Rosa V. and Lewis S. E., (2020), Introducing randomization tests via an evaluation of peer-led team learning in undergraduate chemistry courses, Chem. Educ. Res. Pract., 21(1), 287–306.
- Ramsden P. and Others, (1997), The context of learning in academic departments, Exp. Learn., 2, 198–216.
- Rixse J. S. and Pickering M., (1985), Freshman chemistry as a predictor of future academic success, J. Chem. Educ., 62(4), 313.
- Robert J., Lewis S. E., Oueini R. and Mapugay A., (2016), Coordinated implementation and evaluation of flipped classes and peer-led team learning in general chemistry, J. Chem. Educ., 93(12), 1993–1998.
- Robinson K. A., Perez T., Carmel J. H. and Linnenbrink-Garcia L., (2019), Science identity development trajectories in a gateway college chemistry course: Predictors and relations to achievement and STEM pursuit, Contemp. Educ. Psychol., 56, 180–192.
- Rodriguez I., Brewe E., Sawtelle V. and Kramer L. H., (2012), Impact of equity models and statistical measures on interpretations of educational reform, Phys. Rev. ST Phys. Educ. Res., 8(2), 020103.
- Rodriguez J.-M. G., Stricker A. R. and Becker N. M., (2020a), Exploring the productive use of metonymy: Applying coordination class theory to investigate student conceptions of rate in relation to reaction coordinate diagrams, J. Chem. Educ., 97(8), 2065–2077.
- Rodriguez J.-M. G., Stricker A. R. and Becker N. M., (2020b), Students’ interpretation and use of graphical representations: Insights afforded by modeling the varied population schema as a coordination class, Chem. Educ. Res. Pract., 21(2), 536–560.
- Secules S., McCall C., Mejia J. A., Beebe C., Masters A. S., Sánchez-Peña L. M. and Svyantek M., (2021), Positionality practices and dimensions of impact on equity research: A collaborative inquiry and call to the community, J. Eng. Educ., 110(1), 19–43.
- Seelman K. L., Woodford M. R. and Nicolazzo Z., (2017), Victimization and microaggressions targeting LGBTQ college students: Gender identity as a moderator of psychological distress, J. Ethn. Cult. Divers. Soc. Work, 26(1–2), 112–125.
- Selden S., (1983), Biological determinism and the ideological roots of student classification, J. Educ., 165(2), 175–191.
- Selden S., (1999), Inheriting Shame: The Story of Eugenics and Racism in America, Teachers College Press.
- Sevian H. and Talanquer V., (2014), Rethinking chemistry: A learning progression on chemical thinking, Chem. Educ. Res. Pract., 15(1), 10–23.
- Shah L., Fatima A., Syed A. and Glasser E., (2021), Investigating the impact of assessment practices on the performance of students perceived to be at risk of failure in second-semester general chemistry, J. Chem. Educ. DOI:10.1021/acs.jchemed.0c01463.
- Shaheen M., Pradhan S. and Ranajee, (2019), Sampling in qualitative research, in Qualitative Techniques for Workplace Data Analysis, IGI Global, pp. 25–51.
- Shields S. P., Hogrebe M. C., Spees W. M., Handlin L. B., Noelken G. P., Riley J. M. and Frey R. F., (2012), A transition program for underprepared students in general chemistry: Diagnosis, implementation, and evaluation, J. Chem. Educ., 89(8), 995–1000.
- Siswanto J., Susantini E. and Jatmiko B., (2018), Multi-representation based on scientific investigation for enhancing students’ representation skills, J. Phys. Conf. Ser., 983, 012034.
- Smith K. C., Nakhleh M. B. and Bretz S. L., (2010), An expanded framework for analyzing general chemistry exams, Chem. Educ. Res. Pract., 11(3), 147–153.
- Stefani C. and Tsaparlis G., (2009), Students’ levels of explanations, models, and misconceptions in basic quantum chemistry: A phenomenographic study, J. Res. Sci. Teach., 46(5), 520–536.
- Steinwachs M., (2021), KnowYourStudents, Center for Educational Effectiveness.
- Stowe R. L. and Cooper M. M., (2017), Practicing what we preach: Assessing “critical thinking” in organic chemistry, J. Chem. Educ., 94(12), 1852–1859.
- Stowe R. L. and Cooper M. M., (2019), Assessment in chemistry education, Isr. J. Chem., 201900024.
- Stowe R. L., Herrington D. G., McKay R. L. and Cooper M. M., (2019), The impact of core-idea centered instruction on high school students’ understanding of structure–property relationships, J. Chem. Educ., 96(7), 1327–1340.
- Stowe R. L., Scharlott L. J., Ralph V. R., Becker N. M. and Cooper M. M., (2021), You are what you assess: The case for emphasizing chemistry on chemistry assessments, J. Chem. Educ., 98(8), 2490–2495.
- Sweeney A., Greenwood K. E., Williams S., Wykes T. and Rose D. S., (2013), Hearing the voices of service user researchers in collaborative qualitative data analysis: the case for multiple coding, Health Expect., 16(4), e89–99.
- Syed M., (2010), Disciplinarity and methodology in intersectionality theory and research, Am. Psychol., 65(1), 61–62.
- Tai R. H., Ward R. B. and Sadler P. M., (2006), High school chemistry content background of introductory college chemistry students and its association with college chemistry grades, J. Chem. Educ., 83(11), 1703.
- Talanquer V. and Pollard J., (2010), Let's teach how we think instead of what we know, Chem. Educ. Res. Pract., 11(2), 74–83.
- Talanquer V. and Pollard J., (2017), Reforming a large foundational course: Successes and challenges, J. Chem. Educ., 94(12), 1844–1851.
- Tashakkori A. and Teddlie C., (2003), An expanded typology for classifying mixed methods research into designs, in Advanced mixed methods research designs., Creswell J. W., Plano Clark V. L., Gutmann M. L. and Hanson W. E. (ed.)., SAGE Publications, pp. 159–196.
- Thompson E. D., Bowling B. V. and Markle R. E., (2018), Predicting student success in a major's introductory biology course via logistic regression analysis of scientific reasoning ability and mathematics scores, Res. Sci. Educ., 48(1), 151–163.
- Toledo S. and Dubas J. M., (2016), Encouraging higher-order thinking in general chemistry by scaffolding student learning using Marzano's taxonomy, J. Chem. Educ., 93(1), 64–69.
- Van Dusen B. and Nissen J., (2020), Associations between learning assistants, passing introductory physics, and equity: A quantitative critical race theory investigation, Phys. Rev. Phys. Educ. Res., 16(1), 010117.
- Vincent-Ruz P., (2020), What does it mean to think like a chemist? in Integrating Professional Skills into Undergraduate Chemistry Curricula, ACS Symposium Series, American Chemical Society, pp. 57–79.
- Vincent-Ruz P., Binning K., Schunn C. D. and Grabowski J., (2018), The effect of math SAT on women's chemistry competency beliefs, Chem. Educ. Res. Pract., 19(1), 342–351.
- Voogt J., Nieveen N. and Thijs A., (2018), Preliminary findings from an international literature review on “ensuring equity and innovations”, OECD.
- Wagner E. P., Sasser H. and DiBiase W. J., (2002), Predicting students at risk in general chemistry using pre-semester assessments and demographic information, J. Chem. Educ., 79(6), 749.
- Walsh L. N., Howard R. G. and Bowe B., (2007), Phenomenographic study of students’ problem solving approaches in physics, Phys. Rev. ST Phys. Educ. Res., 3(2), 020108.
- Wenger E., (1999), Communities of Practice: Learning, Meaning, and Identity, Cambridge University Press.
- Williamson V. M., Walker D. R., Chuu E., Broadway S., Mamiya B., Powell C. B., et al., (2020), Impact of basic arithmetic skills on success in first-semester general chemistry, Chem. Educ. Res. Pract., 21(1), 51–61.
- Wilson A. N. S., (2015), A guide to phenomenological research, London Volume, 29(34), 2014.
- Wilson-Kennedy Z. S., Payton-Stewart F. and Winfield L. L., (2020), Toward intentional diversity, equity, and respect in chemistry research and practice, J. Chem. Educ., 97(8), 2041–2044.
- Witherspoon E. B., Vincent-Ruz P. and Schunn C. D., (2019), When making the grade isn’t enough: The gendered nature of premed science course attrition, Educ. Res., 48(4), 193–204.
- Ye L., Shuniak C., Oueini R., Robert J. and Lewis S., (2016), Can they succeed? Exploring at-risk students’ study habits in college general chemistry, Chem. Educ. Res. Pract., 17(4), 878–892.
- Young K. K. and Talanquer V., (2013), Effect of different types of small-group activities on students’ conversations, J. Chem. Educ., 90(9), 1123–1129.
- Zoller U., (2002), Algorithmic, LOCS and HOCS (chemistry) exam questions: Performance and attitudes of college students, Int. J. Sci. Educ., 24(2), 185–203.
- Zoller U., Lubezky A., Nakhleh M. B., Tessier B. and Dori Y. J., (1995), Success on algorithmic and LOCS vs. conceptual chemistry exam questions, J. Chem. Educ., 72(11), 987.
- Zwickl B. M., Hu D., Finkelstein N. and Lewandowski H. J., (2015), Model-based reasoning in the physics laboratory: Framework and initial results, Phys. Rev. ST Phys. Educ. Res., 11(2), 020113.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1rp00333j |
| This journal is © The Royal Society of Chemistry 2022 |