Student thinking profiles within a small group addressing problems in thermodynamics as part of a physical chemistry unit: reflections for students and instructors
Kevin
Charles de Berg

Avondale University, Cooranbong, NSW 2265, Australia. E-mail: kevin.deberg@avondale.edu.au
First published on 11th April 2022
Abstract
This paper reports on how a group of students think when trying to solve a set of thermodynamic revision exercises in the context of collaborative small group conversation at the undergraduate level. The revision exercises involved exploring the relationship between enthalpy and temperature, entropy and temperature, and entropy of a gas under compression. Four students enrolled in a science or science teaching degree comprised the group. Two workshops, conducted about one month apart, were convened and student and instructor diaries were used to explore the thinking profiles illuminated in the diaries. The thinking profiles fitted into the categories: routine-level, object-level, process-level and meta-level. A surprisingly large amount of meta-level thinking was exhibited by the students. It was found advantageous to add adjectival qualifiers to object-level and process-level profiles to more fully interpret what the students had to say. The qualifiers were: incoherent, intuitive, algorithmic, and integrative. The workshops proved beneficial not only to the students but also to the instructor. The use of equations like 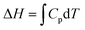 mixes the result of a definite integral symbolic format (left-hand side) with the indefinite integral symbolic format (right-hand side), and leads to students finding it difficult to distinguish between H, dH, and ΔH for enthalpy and S, dS, and ΔS for entropy. Students communicated their feelings freely and there was a general consensus within the group that the workshops were really beneficial.
mixes the result of a definite integral symbolic format (left-hand side) with the indefinite integral symbolic format (right-hand side), and leads to students finding it difficult to distinguish between H, dH, and ΔH for enthalpy and S, dS, and ΔS for entropy. Students communicated their feelings freely and there was a general consensus within the group that the workshops were really beneficial.
Introduction
Thermodynamics is a field in chemistry which demands fluency in basic arithmetic and algebra as well as skill and conceptual understanding in calculus. We know that success in freshman chemistry is correlated with the level of mathematical skill students possess on entry to university or college (Perkins, 1979; Leopold and Edgar, 2008) and success in undergraduate physical chemistry is correlated with students’ undergraduate mathematics grade (Derrick and Derrick, 2002; Hahn and Polik, 2004). However, even when students enter chemistry with a strong mathematics background chemistry staff report that, while such students are able to correctly manipulate a mathematical equation to get a correct answer, they have difficulty identifying the necessary mathematical knowledge and techniques required to solve a chemistry problem (Groves, 2015). Nelson (2018, p. 1440) attributes part of the problem to “decreased attention to math in memory” due to an increasing emphasis on calculators. He uses cognitive science to explain the situation as follows (Nelson, 2018, p. 1441): “If an answer must be looked up or calculated, it occupies space in working memory that is limited. In contrast, for information quickly recallable from long-term memory, space in working memory is essentially unlimited. During the steps of problem solving, if more than a few elements of information are needed that cannot be recalled from long-term memory, some non-memorised information drops out of working memory, and confusion tends to result.” There would appear to be a three-fold issue here: one suggesting that students don’t have regular enough opportunities to apply their mathematical skills; another suggesting that there is an emphasis on getting the chemistry answer at the expense of understanding the mathematical concepts required to get the answer; and finally students report that they are not exposed to the importance of mathematics in chemistry in their undergraduate education (Groves, 2015). Thus the so-called ‘mathematics problem’ in chemistry does not only refer to pre-requisite mathematics for chemistry study but what one might call ‘mathematics inside chemistry’.There is a considerable literature detailing the difficulties students have with the basic concepts of thermodynamics such as: using the concepts of work, heat, and internal energy interchangeably because all these concepts have the same unit being the unit of energy (Loverude et al., 2002); using the concepts of heat and temperature interchangeably due largely to a failure to distinguish between heat as a process and temperature as a state function (de Berg, 2008a); a failure to recognize that q and w are independent means of energy transfer (Meltzer, 2004); a prevalent idea that only thermal energy exchanges can bring about a temperature change in a system (Besson, 2014) and; while students find it relatively easy to substitute values in a mathematical formula and solve for the unknown, they have considerable difficulty in interpreting thermodynamic changes qualitatively (Reif, 1983; Stenhouse, 1985; de Berg, 2008b). This is most likely related to the situation Hadfield and Wieman (2010) observed in their study of the responses of fifty-five physical chemistry students to two surveys related to the first law of thermodynamics: students had difficulty explaining a mathematical equation like, 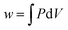 , in words. Becker and Towns (2012) found that the ten undergraduate physical chemistry students they interviewed had significant difficulty in describing mathematically a physical situation like a gas in a cylinder under certain thermodynamic conditions. Difficulty was also experienced in the reverse process: giving a physical description from a thermodynamic mathematical equation.
, in words. Becker and Towns (2012) found that the ten undergraduate physical chemistry students they interviewed had significant difficulty in describing mathematically a physical situation like a gas in a cylinder under certain thermodynamic conditions. Difficulty was also experienced in the reverse process: giving a physical description from a thermodynamic mathematical equation.
The research study discussed in this paper relies on a knowledge of calculus so it is important to briefly glean the mathematics education literature for some insight in this regard. Aspinwell and Miller (1997) observed that students regard calculus primarily as a computational tool. Eichler and Erens (2014, p. 25) claim that, “almost all calculus teachers have the same peripheral goals related to a schema view: calculus is a set of rules and procedures to be memorized and applied in routine tasks.” This was also observed by Mahir (2009) on examining the responses of sixty-two students to a questionnaire containing five questions administered on completion of first year calculus. The students preferred routine calculations over those demanding a more conceptual approach. Grundmeier et al. (2006) asked fifty-two calculus students to complete a survey containing nine questions on integration. It was found that students could calculate an integral but not define it verbally and only one of the fifty-two students could define a definite integral as the limit of a sum. This idea becomes important, for example, when explaining what 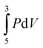 means when determining the work done in compressing a gas from 5 L to 3 L in a cylinder at constant temperature. In a study of one hundred and fifty-seven students from two large colleges in the USA, there was a high prevalence of the anti-derivative conception of the definite integral over the Riemann sum definition and seventy-six percent of the students did not relate ‘dx’ to ‘Δx’ (Jones, 2015). As far as differentiation is concerned, Bingolbali et al. (2007) found that mechanical engineering students tend to focus on ‘rate of change’ while mathematics students were inclined to focus on ‘tangent-oriented’ aspects. Such interdisciplinary observations have been a recent focus of Bain et al. (2019, p. 2086) who consider ways of understanding the relationship between chemistry and mathematics: “…the interface between chemistry and mathematics being a rich area for inquiry, particularly in upper-level chemistry courses that tend to be math-heavy and less represented in the education literature.”
means when determining the work done in compressing a gas from 5 L to 3 L in a cylinder at constant temperature. In a study of one hundred and fifty-seven students from two large colleges in the USA, there was a high prevalence of the anti-derivative conception of the definite integral over the Riemann sum definition and seventy-six percent of the students did not relate ‘dx’ to ‘Δx’ (Jones, 2015). As far as differentiation is concerned, Bingolbali et al. (2007) found that mechanical engineering students tend to focus on ‘rate of change’ while mathematics students were inclined to focus on ‘tangent-oriented’ aspects. Such interdisciplinary observations have been a recent focus of Bain et al. (2019, p. 2086) who consider ways of understanding the relationship between chemistry and mathematics: “…the interface between chemistry and mathematics being a rich area for inquiry, particularly in upper-level chemistry courses that tend to be math-heavy and less represented in the education literature.”
Besson (2014, p. 278) argues that university science courses are “too focused on technical and algorithmic knowledge and skills (with a) disregard (for) conceptual, problematic and cultural aspects.” While this point is well argued particularly from the point of view of a need to incorporate more historical and philosophical aspects of thermodynamics into university courses, there are cases where it is difficult to separate a technical and mathematical skill from a conceptual understanding in thermodynamics and this paper will highlight examples of this taken from students’ responses to questions assigned by an instructor during a semester's work in thermodynamics. The research reported in this paper explores how a small group of students negotiate how to solve problems in an area of thermodynamics dependent on a reasonably sound knowledge of calculus. This research methodology is consistent with an observation made by Becker and Towns (2012, p. 219): “One way to help instructors to better scaffold students’ use of mathematics in chemistry contexts may be to engage students in collaborative problem solving. For instructors of chemistry, observing students working together may offer instructors an opportunity to observe facets of students’ reasoning that may not be made explicit from an examination of student homework and exams.” The research question thus addressed in this study is as follows:
Research Question: What kinds of thinking profiles do university students use in a small group setting when solving problems in thermodynamics that require a knowledge of calculus?
Theoretical foundations
This study draws upon the ideas expressed in the Resources and Conceptual Integration Framework Model of Bain et al. (2019) with some changes incorporated for this study as shown in Fig. 1. The model is instructive for two contexts. Firstly, it reminds us that the concepts in thermodynamics, a key component of physical chemistry, as developed historically in the 19th and early 20th centuries, were expressed using the symbolic and graphical forms of mathematics. That is, thermodynamics is embedded in the language of mathematics. Secondly, the model challenges us not to think of chemistry and mathematics as separate entities in the teaching and learning context as so often happens. In the case of thermodynamics being taught in a physics context, Pollock et al. (2007) interpreted their findings in a way specifying that students hold an isolated understanding of the two subjects (physics and mathematics) rather than an integrated framework. Sometimes mathematics is considered a necessary evil when it comes to solving problems in chemistry. This is reflected in part in the title of the ACS symposium series, It's just Math (Towns et al., 2019).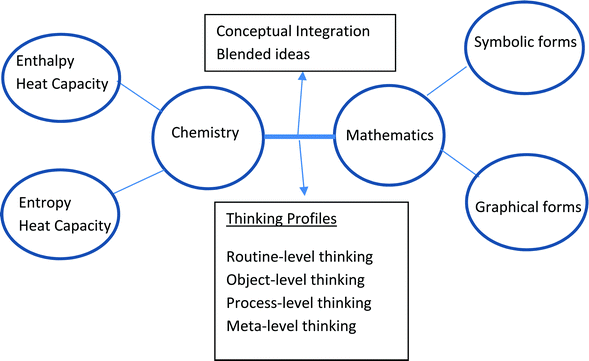 | ||
| Fig. 1 Resource Framework Model of Bain et al. (2019) adapted to this study. | ||
The framework model in Fig. 1 has its origins in cognitive science where symbolic forms and graphical forms in the mathematics space and enthalpy, entropy, and heat capacity in the chemistry space are referred to as occupying mental spaces (Hu and Rebello, 2013). These mental spaces are small conceptual packets of knowledge elements sometimes referred to as fine-grained cognitive units or resources (Bain et al., 2019). Learning is conceived through the human activity of thinking, the individualization of interpersonal communication (Sfard, 2007), activated to engage with mathematics and chemistry resources to construct new information in the blended or integration space. The content of the blended space is by no means fixed. In the process of learning students might decide to combine the knowledge elements in the mathematics and chemistry spaces in a different way to produce a different structure for the blended space. Such an activity is known as ‘running the blend’, a dynamic process from which a new meaning emerges (Hu and Rebello, 2013). So it is more useful to conceive of the blended space as containing emergent information rather than static information.
After analyzing different mathematical definitions and representations Sfard (1991) came to the conclusion that abstract notions, such as number or function, can be conceived in two fundamentally different but complementary ways: structurally as objects, and operationally as process. Sfard (1991) viewed the learning and problem solving process as involving an intricate interplay between the operational (process-level) and structural (object-level) conceptions of the same notion or idea. It is from this study that the ideas of object-level and process-level thinking emerge as thinking profiles in Fig. 1 and Table 2.
The idea of symbolic forms in mathematics originated with the work of Sherin (2001) in the context of simple physics equations. According to Sherin (2001), a symbolic form consists of a template and a conceptual schema. For example, the template, □ = □ + □, shows that some value is obtained by the addition of two other values. A conceptual schema for this template in mechanics is, v = v0+ at, where the boxes are populated with velocity terms. This means that, at, should have the same units as v0. Another possible template which makes this point about units clear is, □ = □ + Δ, where Δ represents a positive change in the value to which it is being added. Sherin (2001) lists twenty-one templates for simple physics equations which do not involve derivatives or integrals. Jones (2013) has listed a variety of integral templates in the context of mathematics education. The template, 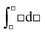 , called function matching, describes the following general conceptual schema (Jones, 2013, p. 135), “The integrand comes from some original function. The differential indicates the relationship between them. The integral seeks to find this original function. The limits represent a measurement between values.” A specific conceptual schema applicable to this study is,
, called function matching, describes the following general conceptual schema (Jones, 2013, p. 135), “The integrand comes from some original function. The differential indicates the relationship between them. The integral seeks to find this original function. The limits represent a measurement between values.” A specific conceptual schema applicable to this study is, 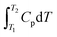 . Populating the boxes of the template with temperature (T) and heat capacity at constant pressure (Cp) will deliver for us a change of enthalpy.
. Populating the boxes of the template with temperature (T) and heat capacity at constant pressure (Cp) will deliver for us a change of enthalpy.
Thinking of differentiation as the reverse of integration leads to the template, d□ = □d□, which on adding the concepts of temperature, heat capacity at constant pressure, and enthalpy leads to, dH = CpdT. Thinking of differentiation as a rate of change leads to the template,  , which on populating with thermodynamic concepts introduced previously leads to,
, which on populating with thermodynamic concepts introduced previously leads to, 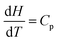 . Thinking of the differential as a rate of change of H as T changes leads to the idea of
. Thinking of the differential as a rate of change of H as T changes leads to the idea of 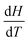 as measuring the slope of a graph of H against T. This leads into a discussion of graphical forms in mathematics.
as measuring the slope of a graph of H against T. This leads into a discussion of graphical forms in mathematics.
The graphical forms relevant to this study are effectively the same as reported by Bain et al. (2019). These are represented in Table 1. In this study students are requested to sketch graphically the relationships indicated in a mathematical equation.
| Graphical form | Conceptual schema |
|---|---|
| Steepness as rate | Varying levels of steepness in a graph correspond to different rates |
| Straight means constant | Straight line indicates a lack of change or a constant rate |
| Curve means change | Curve indicates continuous change or changing rate |
| Trend from shape directionality | General shape of the graph suggests information regarding the graph's tendency to increase or decrease |
To understand and classify student discourse during problem-solving exercises in physical chemistry, one will notice that the model in Fig. 1 draws upon thinking profiles that have received some attention in the chemistry education and mathematics education literature (Sfard, 1991, 2007; Bain et al., 2019). Moon et al. (2016) classify student reasoning in physical chemistry using four modes of thinking or reasoning pertinent to what they call a Chemical Thinking Learning Progression (CTLP). The four modes are descriptive, relational, linear, and multi-component which were found helpful in classifying arguments which did not involve serious mathematics. Since the present study involves mathematical formulae and graphs drawn largely from calculus, the thinking profiles shown in Fig. 1 have been chosen for this study. They are drawn largely from Bain et al. (2019) and Sfard (1991, 2007). The thinking profiles are elaborated upon in Table 2.
| Thinking profile | Definition of thinking profile |
|---|---|
| Routine-level thinking | This can be a practiced procedure almost algorithmically applied in problem solving contexts. The procedure could be endemic to chemistry practice or mathematics practice and in this sense is sometimes referred to as normative or canonical thinking (Becker et al. 2013). Sfard (2007) defines routines as well-defined repetitive patterns of a given discourse which for our present study will reflect chemistry and mathematics. |
| Object-level thinking | This kind of thinking focuses on a mathematical equation or graph as an object. The symbols in the equation and the shape of the graph are the focus. Bain et al. (2019, p. 2092) consider “the object view frames the function as a fixed entity or concept with associated descriptors.” Moore and Thompson (2015) use the term ‘static’ for object-level thinking to distinguish it from process-level thinking described as ‘emergent’ thinking. |
| Process-level thinking | Bain et al. (2019, p. 2092) draw on the work of Sfard (1991) to consider that “the process view of a function emphasizes the relationship between the dependent and independent variables.” This level of thinking is concerned with how changes in one variable impact the other variable. Another term that has been used is ‘covariational’ thinking. David et al. (2019) use the synonym ‘value-thinking’ to describe process-level thinking as distinct from ‘location-thinking’ used for object-level thinking. |
| Meta-level thinking | Typically defined as ‘thinking about thinking’, meta-level thinking is considered a higher order skill. Tanner (2012) provides some examples such as: What do I already know about this topic which could assist me in this activity and in the learning process in general? What was most confusing to me in thinking about the concepts presented on this topic? How has my thinking on this topic changed over time? |
Method
Participants, context, and structure of the study
Four students, one male (with pseudonym Evan) and three females (with pseudonyms Mary, Pamela, and Jessica), were enrolled in a chemistry unit, Environmental Chemistry and Thermodynamics, at a small University and two 2-hour workshop sessions were set aside forthe students to work collaboratively as a group on some project questions related to their work in the thermodynamic section of the unit. No other students were enrolled in this unit. The two workshops were scheduled about one month apart and acted as a contribution to a revision schedule for the semester. A copy of the instructions given to the students prior to the first workshop is given in Fig. 2. The two workshop questions are shown in Fig. 3 and 4. For each workshop one student was assigned to lead the discussion, another was assigned to write a diary outlining the major features of their conversation, another was assigned to write a consensus solution to the questions, and the fourth student was to assist in whatever capacity was needed. The instructor was present during the workshops and kept a diary of the discussions but did not participate in the conversation. The author of this paper was the instructor. It was decided not to use a recorder or video to encourage the students to work as naturally as possible. This led to some limitations for the study detailed later in the paper. The students’ diaries and the instructor's diary along with the group's written consensus solution to the problem provide the data for analysis.
The use of diaries as a data source for the analysis of the teaching and learning context has been an important tool where student and instructor reflections are deemed important, particularly where such reflections become an important catalyst for change (Engin, 2011). It was planned that both students and instructor could potentially benefit from such reflections.
Students were allowed access to their lecture notes, textbook, and the SI Chemical Data Book. In fact, no restrictions were placed on the group as to what resources they chose to use. Of particular relevance is a formula sheet in the students’ lecture notes which could guide the students in the direction of a solution. However, the students needed to be familiar enough with the mathematics and chemistry of the problem at hand to be able to choose the relevant formula and then to be able to manipulate it correctly. The workshop questions were designed to move the students beyond algorithmic substitution to a deeper analysis. The formula sheet the students had at their disposal is shown in Fig. 5. The research project was approved by the institution's research ethics committee.
Data analysis
The diaries were analysed using the Thinking Profiles in Table 2. As an example, evidence for these profiles in Workshop 1 part (a) is provided by excerpts taken from the instructor's written diary shown in Table 3. A similar procedure was used for the student diaries. The task in Workshop 1 part (a) in Fig. 3 is repeated here for convenience.| Task part (a): The constant-pressure heat capacity of a sample of a perfect gas was found to vary with temperature according to the expression: Cp/(J K−1) = 20.17 + 0.3665 × T/K. Calculate ΔH when the temperature is raised from 25 °C to 100 °C at constant pressure |
The data in Table 3 was checked against the definitions in Table 2 by a colleague trained in physical chemistry and in education. The colleague agreed with the classification of the evidence in Table 3 and her comments on meta-level thinking resulted in a tightening of the definition of meta-level thinking in Table 2. The instructor's diary and the students’ diaries were compared by one of the student group members who had not written a diary. While there was, understandably, a difference in content there were no inconsistencies. The student agreed that the instructor and students were reporting on the same event even though there was a variation in the focus of the diaries. This is discussed later in the paper.
Results and discussion
Workshop 1 part (a)
Following on from the instructor's diary account summarized according to thinking profiles in Table 3, the consensus solution to the problem provided by the students is shown alongside the instructor's solution in Fig. 6. It was Mary who had completed the student diary and her reflections on the group consensus solution as written in her diary were as follows. | ||
| Fig. 6 Comparison between the students’ consensus solution and the instructor's solution to part (a) of Workshop 1. | ||
Mary: We decided to commit to our ΔT substitution since there was no strong reason to commit to our T1 or T2 substitution. We are however still confused since the actual equation (for Cp) given in the question does not denote ΔT. We have come to a consensus but are not necessarily convinced that we are correct. We merely want to move on to the next question.
There is a combination of object-level and meta-level thinking in Mary's statement, both making important observations despite the group not being able to solve the problem. The fact that the equation for Cp contains T not ΔT (object-level) was a critical one and led the group to doubt their proposed solution (meta-level). In fact the extent of meta-level thinking shown in Table 3 is quite remarkable given that students don’t always have time to reflect on their thinking in a typical classroom situation where the focus is often on learning procedures to solve problems. The requirement to contribute to making diary entries of collaborative learning in a small group seemed to encourage more reflection by the students. One can make the mistake of dismissing object-level thinking in comparison to process-level thinking but Mary's observation of the equation for Cp as a fixed entity which did not contain ΔT was so important in challenging the group's level of confidence in their thinking strategies.
The kind of process-level thinking shown in the students’ consensus solution in Fig. 6 mirrors that discussed by Cole and Shepherd (2019, pp. 179–180): “But when given Cp = a + bT, many students will evaluate Cp at one (or both) values of temperature defined by the integration range, and then treat Cp as constant when evaluating the integral.” While a similar approach received consensus approval by the students in the current study, they were not convinced of the correctness of their procedure as revealed in Mary's previous statement.
Nowhere in her diary does Mary record Jessica's suggestion that integration might be a strong possibility for a solution (see Table 3). This is unusual given that Mary had studied two years of advanced university calculus at the time the workshop was held. In fact, this difficulty with recognizing when integration is necessary in problem solving and an inability to recognize the conditions under which integration is possible was observed nearly seventy years ago (Williams, 1952). Perhaps one should not be so surprised given the research that shows that a study of mathematics in a physical chemistry context presents different challenges to the study of mathematics in a mathematics classroom (Bain et al., 2014).
Since Jessica suggested integration because the question involved two temperatures (see Table 3), she may have been thinking of the definite integral symbolic template, 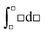 , or more likely,
, or more likely, 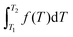 , given her mathematics background. This raises the question of the helpfulness of Sherin's (2001) symbolic forms when student's are presented with a formula sheet containing standard mathematical formulae for the topic in question. The templates Sherin (2001) describes seem very helpful in cases where a student has to develop a mathematical relationship from first principles given certain relationships between the variables. In cases where the formulae are given, it is suggested that the templates may not be so useful. Pamela's suggestion that, “Cp = 20.17 + 0.3665T is in the form of a linear equation” (see Table 3) reflects one's understanding of polynomial functions and their standard expressions. A linear template is not listed as a Sherin (2001) template. In mathematics, y = mx + b, is a linear equation and straight line form when y is plotted against x. General polynomial functions have the form, a0 + a1x + a2x2 + a3x3+…, so, a0 + a1x, is a linear function where ‘x’ is raised to the power 1, a0 + a1x + a2x2, is a quadratic function where ‘x’ is raised to the power 2, and a0 + a1x + a2x2 + a3x3, is a cubic function where ‘x’ is raised to the power 3, and so on. It is to these standard mathematical ideas that Pamela was most likely referring.
, given her mathematics background. This raises the question of the helpfulness of Sherin's (2001) symbolic forms when student's are presented with a formula sheet containing standard mathematical formulae for the topic in question. The templates Sherin (2001) describes seem very helpful in cases where a student has to develop a mathematical relationship from first principles given certain relationships between the variables. In cases where the formulae are given, it is suggested that the templates may not be so useful. Pamela's suggestion that, “Cp = 20.17 + 0.3665T is in the form of a linear equation” (see Table 3) reflects one's understanding of polynomial functions and their standard expressions. A linear template is not listed as a Sherin (2001) template. In mathematics, y = mx + b, is a linear equation and straight line form when y is plotted against x. General polynomial functions have the form, a0 + a1x + a2x2 + a3x3+…, so, a0 + a1x, is a linear function where ‘x’ is raised to the power 1, a0 + a1x + a2x2, is a quadratic function where ‘x’ is raised to the power 2, and a0 + a1x + a2x2 + a3x3, is a cubic function where ‘x’ is raised to the power 3, and so on. It is to these standard mathematical ideas that Pamela was most likely referring.
While the students had access to a formula sheet to assist in problem solving, they had to understand the context in which the formula applied. The formula, 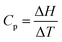 , or, ΔH = Cp. ΔT, only applies when Cp is a constant, that is, does not depend on temperature. When Cp is a function of temperature which it is in part (a), one has to think of the relationship as, dH = CpdT, and recognize that this is a form in which integration can be applied to find ΔH as shown in Fig. 6. But what kind of thinking is behind the solutions shown in Fig. 6? As far as the students’ consensus solution is concerned, it is clear that the choice of the formula, ΔH = Cp. ΔT, represents object-level thinking, and the substitution of values represents process-level thinking if one equates this with value-thinking as defined in Table 2. But there is some incoherency with the confusion between T and ΔT. It seems that the term, process-level thinking, may need to be qualified as, incoherent process-level thinking. Another example of incoherent process-level thinking occurs with Pamela's identification of the process in part (a) as an adiabatic process because of temperature variation but then thought the process was irreversible because the temperature was constant (Pamela according to the instructor's diary: “Since T is varying I think this is an adiabatic process but is it reversible or irreversible? I think it is irreversible since the temperature is constant”.).
, or, ΔH = Cp. ΔT, only applies when Cp is a constant, that is, does not depend on temperature. When Cp is a function of temperature which it is in part (a), one has to think of the relationship as, dH = CpdT, and recognize that this is a form in which integration can be applied to find ΔH as shown in Fig. 6. But what kind of thinking is behind the solutions shown in Fig. 6? As far as the students’ consensus solution is concerned, it is clear that the choice of the formula, ΔH = Cp. ΔT, represents object-level thinking, and the substitution of values represents process-level thinking if one equates this with value-thinking as defined in Table 2. But there is some incoherency with the confusion between T and ΔT. It seems that the term, process-level thinking, may need to be qualified as, incoherent process-level thinking. Another example of incoherent process-level thinking occurs with Pamela's identification of the process in part (a) as an adiabatic process because of temperature variation but then thought the process was irreversible because the temperature was constant (Pamela according to the instructor's diary: “Since T is varying I think this is an adiabatic process but is it reversible or irreversible? I think it is irreversible since the temperature is constant”.).
As far as the instructor's solution is concerned, the choice of, dH = CpdT, and, 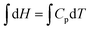 , represents object-level thinking. The evaluation of the integral, requiring reasonable skill, is process-level thinking but it represents a standard procedure in mathematics. To distinguish it from other process-level thinking profiles, the qualifier, algorithmic process-level thinking, may prove helpful. While locating the formula, dH = CpdT, required object-level thinking, recognizing that both sides of the equation were integrable was also an important component of object-level thinking. While some process-level thinking be regarded as algorithmic, this doesn’t mean that significant mathematical skill was not required.
, represents object-level thinking. The evaluation of the integral, requiring reasonable skill, is process-level thinking but it represents a standard procedure in mathematics. To distinguish it from other process-level thinking profiles, the qualifier, algorithmic process-level thinking, may prove helpful. While locating the formula, dH = CpdT, required object-level thinking, recognizing that both sides of the equation were integrable was also an important component of object-level thinking. While some process-level thinking be regarded as algorithmic, this doesn’t mean that significant mathematical skill was not required.
The group did not want to allocate any more time to the problem in part (a) of Workshop 1 for two reasons as recorded by Mary in her diary.
Mary: We merely want to move on to the next question. After discovering that a similar question in the assignment is only worth 6 marks we feel as though we are over-thinking it (Reason 1). We thought that we would learn more effectively if we submitted it (our consensus solution) and let the instructor tell us the actual answer (Reason 2).
The fact that the students located a similar question in their assignments taken from their textbook suggested their thinking had gone astray somewhere and they were ‘overthinking it’ (meta-level thinking). What is evident here in the second reason is the universal tendency of students to pass the responsibility for finding a solution to a problem from themselves to the instructor, although the students were initially happy to engage with the problem and seek a solution without the instructor's assistance. This assessment may be a little harsh on the group given they demonstrated a commitment to each other and spent at least 40 minutes on part (a). The relationship between enthalpy, heat capacity, and temperature is further explored in parts (b), (c), and (d).
Workshop 1 part (b)
The task in part (b) in Fig. 3 is repeated here for convenience.| Task part (b): Which of the following do you think correctly describes the enthalpy, H, of a gas at constant pressure and provide an explanation for your choice? |
| (i) The enthalpy should increase with temperature |
| (ii) The enthalpy should decrease with temperature |
| (iii) The enthalpy should not change with temperature |
According to the instructor's diary and Mary's diary, Pamela suggested that there is a relationship between part (a) and part (b) and in view of the answer to part (a) in Fig. 6 it is obvious that option (i) in part (b) is correct, that is, enthalpy should increase with temperature. Pamela then proceeded to ask the following question listed in the instructor's diary.
Pamela: What is enthalpy? Can we describe it in words? Can formulae give us any guidance?
These are important questions and demonstrate again how the students were not afraid to engage in meta-level thinking. The students were not able to define enthalpy or describe it in words or provide a chemistry context for the concept. They did provide a list of formulae however that contained the symbol for enthalpy. Object-level thinking prompted Mary to list, H = U + PV, ΔH = ΔU + Δ(PV), and Jessica added ΔH = qp. These formulae did not provide any clarity for the students and Mary commented on this in her diary.
Mary: We got a little bit muddled with the plethora of definitions and formulas to take our reasoning from. We feel as though we are over-thinking the question.
This meta-level thinking demonstrated just how confused the students had become. The students were not able to provide a mathematics or chemistry explanation for why enthalpy increases with temperature other than that the answer in Fig. 6 seems to indicate this. There was no attempt to use the particle model of a gas as a resource for an explanation. On the other hand, the supplementary questions were designed to help the students decide on an explanation as to why enthalpy should increase with temperature.
The supplementary questions are repeated here for convenience.
| Supplementary questions: |
| (ia) If enthalpy increases with temperature, what would this tell you about Cp? |
| (iia) If enthalpy decreases with temperature, what would this tell you about Cp? |
| (iiia) If enthalpy did not change with temperature, what would this tell you about Cp? |
Jessica then encouraged the group to consider the supplementary questions (ia), (iia), and (iiia) using ΔH = Cp. ΔT as a guide. This is a good object-level choice since the equation contains the three important ideas in the questions; enthalpy, heat capacity, and temperature. Pamela repeats question (ia) to which Evan replies that, “Cp cannot be negative”, while Jessica replies that, “Cp > 1”, which receives Evan's endorsement even though it would have been more accurate for Jessica to conclude that, Cp > 0. For question (iia) and from the instructor's diary, Mary claims Cp would have to be negative which Jessica endorses but interprets this as equivalent to saying that Cp < 1 rather than Cp < 0. For question (iiia) Evan and Jessica said Cp would have to be zero. Pamela eventually agreed with this conclusion after having stated that Cp is the same as enthalpy.
While the students’ process-level thinking led to the correct conclusion as to whether the heat capacity was positive, negative, or zero, no detailed reasoning was provided. For example, given that, 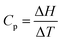 , nobody suggested that “enthalpy increases with temperature” was equivalent to ΔH and ΔT both being positive leading to Cp being positive since the quotient of two positive numbers is always positive. Nobody suggested that “enthalpy decreases with temperature” was equivalent to ΔH being negative and ΔT being positive leading to Cp being negative as the quotient of a negative and a positive number is always negative. Nobody suggested that “enthalpy does not change with temperature” was equivalent to ΔH being zero and ΔT being positive leading to Cp being zero as the quotient of zero and a positive number is always zero. It would seem that the students were thinking intuitively rather than algorithmically or mathematically. Intuitive thinking has been important for some scientific discoveries and some educational settings but has often proved disadvantageous in the teaching–learning space (McCloskey, 1983; Maeyer and Talanquer, 2010). Intuitive thinking connects the word ‘increase’ with the word ‘positive’; connects the word ‘decrease’ with the word ‘negative’; and connects the term ‘no change’ with the word ‘zero’; without any mathematical justification.
, nobody suggested that “enthalpy increases with temperature” was equivalent to ΔH and ΔT both being positive leading to Cp being positive since the quotient of two positive numbers is always positive. Nobody suggested that “enthalpy decreases with temperature” was equivalent to ΔH being negative and ΔT being positive leading to Cp being negative as the quotient of a negative and a positive number is always negative. Nobody suggested that “enthalpy does not change with temperature” was equivalent to ΔH being zero and ΔT being positive leading to Cp being zero as the quotient of zero and a positive number is always zero. It would seem that the students were thinking intuitively rather than algorithmically or mathematically. Intuitive thinking has been important for some scientific discoveries and some educational settings but has often proved disadvantageous in the teaching–learning space (McCloskey, 1983; Maeyer and Talanquer, 2010). Intuitive thinking connects the word ‘increase’ with the word ‘positive’; connects the word ‘decrease’ with the word ‘negative’; and connects the term ‘no change’ with the word ‘zero’; without any mathematical justification.
To confirm that enthalpy increases with temperature as a result of considering the impact on Cp, the students failed to consider the expression for Cp, Cp = 20.17 + 0.3665 × T, and note that Cp can never be negative or zero regardless of temperature. The students simply relied on the results of their calculation in part (a) even though they expressed some doubts about the accuracy of their calculation.
Algorithmic process-level thinking has often been contrasted with what has become known as conceptual thinking since the 1980's (Nurrenbern and Pickering, 1987; Pickering, 1990; Nakhleh, 1993; Cracolice et al., 2008). The thinking above has been entirely mathematical. No chemical concepts have been presented whatsoever. If as instructors we have to strive to integrate chemistry with mathematics more intentionally (Bain et al., 2019), then one must ask the question at this point, “How could one better integrate the concept of heat capacity as a chemistry concept with its mathematical representations?” Let us consider the following questions which attempt to provide examples of integrative process-level thinking.
Question 1. Equal masses of two substances, A and B, at the same temperature are heated by the same amount of thermal energy. A has a larger temperature increase than does B. Which of the two substances has the larger heat capacity? Explain how you arrive at your answer using chemical and mathematical ideas.
Question 2. Ten grams of Neon has a heat capacity of 10.3 J K−1 while ten grams of Argon only has a heat capacity of 5.2 J K−1. Provide a chemical and mathematical explanation for this difference.
Question 3. A certain liquid has a heat capacity given by the formula, Cp = a + bT, where ‘a’ and ‘b’ are constants greater than zero. One kilojoule of thermal energy is added to two 1 L samples (A and B) of the liquid. A is at 25 °C and B is at 50 °C. Which of the two solutions, A or B, will undergo the greatest temperature increase?
All three questions demand an understanding of heat capacity as a measure of a substance's capacity to resist a temperature increase on the addition of thermal energy. The mathematical definition of heat capacity, 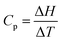 , helps in Question 1 to deduce that the substance with the smaller temperature increase will have the higher heat capacity for the same addition of thermal energy. It also helps in Question 3 to deduce that the liquid with higher heat capacity will have the smaller temperature increase for the same addition of thermal energy. Question 2 requires the student to realize that 10 g of Ne will have twice as many particles as 10 g of Ar given that the molar mass of Ne is half that of Argon. This means that Ne will have twice the capacity to resist a temperature increase compared to Ar because it can distribute the added energy over more particles.
, helps in Question 1 to deduce that the substance with the smaller temperature increase will have the higher heat capacity for the same addition of thermal energy. It also helps in Question 3 to deduce that the liquid with higher heat capacity will have the smaller temperature increase for the same addition of thermal energy. Question 2 requires the student to realize that 10 g of Ne will have twice as many particles as 10 g of Ar given that the molar mass of Ne is half that of Argon. This means that Ne will have twice the capacity to resist a temperature increase compared to Ar because it can distribute the added energy over more particles.
On reflection, according to the instructor's diary, adding questions of this nature would have increased the value of the workshops.
Workshop 1 part (c)
Task (c) from Fig. 3 is repeated here for convenience.| Task (c): Sketch a graph of H against T if Cp is constant. Describe in words how H is varying with T. |
The group agreed that there was a linear relationship between H and T when Cp is constant but there was no substantiation provided by the group apart from the fact that as T increases H increases implicated from part (b). This again appears to be a case of intuitive process-level thinking; process-level because of the emphasis on value thinking for H and T, that is, H values increase as T values increase; intuitive because the students do not provide any mathematical justification for thinking that the graph will be linear. When it comes to graphing, intuitive thinking connects the word ‘constant’ with the word ‘linear’ or the term ‘straight line’; and connects the word ‘variable’ with the word ‘curve’. While Pamela initially suggested the possibility of exponential increase, she finally favored a linear increase but gave no reason for her preference. The group agreed that the line should pass through the origin but again no substantiation was provided.
All four students had studied calculus but failed to consider the relationship between Cp, H, and T in differential form; 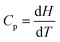 . If Cp is constant, this means that the slope of the graph of H against T is constant which means the relationship must be linear. The group didn’t think to reason this way. If one considers the relationship between Cp, H, and T in indefinite integral form;
. If Cp is constant, this means that the slope of the graph of H against T is constant which means the relationship must be linear. The group didn’t think to reason this way. If one considers the relationship between Cp, H, and T in indefinite integral form; 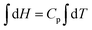 and H = CpT + constant; one can see that the line would pass through the origin only if the constant was zero. It would appear that such object-level thinking should have been a prerequisite to process-level thinking when consideration would have been given to how a graph could be drawn showing how H values would vary with T values. The student consensus solution was a straight line through the origin for a plot of H against T without any object-level descriptions as a backing.
and H = CpT + constant; one can see that the line would pass through the origin only if the constant was zero. It would appear that such object-level thinking should have been a prerequisite to process-level thinking when consideration would have been given to how a graph could be drawn showing how H values would vary with T values. The student consensus solution was a straight line through the origin for a plot of H against T without any object-level descriptions as a backing.
Workshop 1 part (d)
Task (d) from Fig. 3 is repeated here for convenience.| Task (d): Sketch a graph of H against T if Cp/(J K−1) = 20.17 + 0.3665 × T/K. Describe in words how H is varying with T. |
The group atmosphere is captured by quoting directly from Mary's diary.
Mary: We struggled with identifying what type of function this will be. Mary and Jessica thought it was quadratic while Pamela thought it was linear. Pamela then changed her mind to think it was not linear but increased non-linearly perhaps like an exponential but not necessarily an exponential function. Mary and Jessica, though recognizing mathematically that it seemed to be a quadratic, thought it odd that it would be, considering that we have not had to plot any quadratics in class. There was a real issue with using the word ‘exponential’ if the function was not actually an exponential function.
There was some productive meta-level thinking going on here as the students struggled with whether their use of the word, exponential, was appropriate. Mary insisted that the word ‘exponential’ should not be used for a quadratic function but one should use phrases like ‘slope increases with temperature’, or, ‘the graph gets steeper and steeper’, or similar phrases. Mary and Jessica think that the mathematics suggests a quadratic function but think it strange because they have not, to this point, had to plot quadratic functions in the unit. They did not detail why the mathematics suggested a quadratic and one is led to think this might be a case of intuitive object-level thinking; object-level since the emphasis seems to be on the shape of the function; and intuitive since ‘variation’ suggests ‘curve’ of which quadratic is an example. Mary and Jessica also have an expectation that they will be examined on tasks already completed previously in class where the possibility that the only thinking skills required would revolve around routine-level thinking. This turned out not to be the case. The struggle the group had with this task is borne out even more dramatically in the instructor's diary.
Instructor: Pamela is taking the lead in the discussion and says that the required graph will be linear and positive. She still seems to think that heat capacity and enthalpy are equivalent terms and so deduces that enthalpy and heat capacity are linearly related to temperature as shown in the equation, Cp = 20.17 + 0.3665T. Jessica questions this deduction and tells Pamela that we are not plotting Cp against T but H against T and Mary emphasises that we are plotting H not ΔH. Pamela then asks, “Is there another way to relate H and T?” and answers her own question by suggesting, 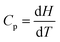 , and interprets the required graph as “increasingly linear”, to which Mary and Jessica say, “It can’t be.” Pamela then suggests there might be an exponential increase of H with T. Jessica suggests T2 would have to be involved if there was an exponential increase. Mary then argues that ‘exponential’ should not be used for a quadratic function; ‘getting steeper and steeper’ or ‘increasing at a faster rate’ might be better. Pamela suggests “increasing by increasingly larger increments”, to which Jessica says, “Is this really important? I think we have missed something.” While they agree to sketch H against T as a quadratic function with increasing slope as T increases, they have a weird feeling that something is not right. Comments were made across the group reflecting the idea that these examples were different to what they had in their notes. The group agreed that these examples were “new territory”.
, and interprets the required graph as “increasingly linear”, to which Mary and Jessica say, “It can’t be.” Pamela then suggests there might be an exponential increase of H with T. Jessica suggests T2 would have to be involved if there was an exponential increase. Mary then argues that ‘exponential’ should not be used for a quadratic function; ‘getting steeper and steeper’ or ‘increasing at a faster rate’ might be better. Pamela suggests “increasing by increasingly larger increments”, to which Jessica says, “Is this really important? I think we have missed something.” While they agree to sketch H against T as a quadratic function with increasing slope as T increases, they have a weird feeling that something is not right. Comments were made across the group reflecting the idea that these examples were different to what they had in their notes. The group agreed that these examples were “new territory”.
There are two ideas that stand out in the instructor's diary. Firstly, the students observed that most of their normal assignment questions reflect routine tasks outlined in their notes or textbook. While this may have explained the difficulty they were experiencing, there was a group consensus view recorded by Mary that doing this workshop, “was a very beneficial experience to do during class time.” Secondly, while the group's consensus quadratic plot of H against T is essentially correct, the reasoning pathway seemed to involve some intuitive guesswork and this explains why the students “had a weird feeling that something is not right.” While the group agreed that the slope of the graph of H against T was increasing with temperature by substituting T values into the Cp equation, the choice of a quadratic function appeared to be a guess. There was no suggestion of rewriting the Cp equation in indefinite integral form, 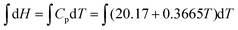 , thus leading to,
, thus leading to, 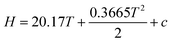 , which clearly shows a quadratic relationship unambiguously.
, which clearly shows a quadratic relationship unambiguously.
It is sometimes difficult to separate out object-level and process-level thinking from a collaborative conversation as witnessed above. The focus on the shape of the graph suggests object-level thinking but a focus on the impact of changing values of T on the slope of the graph would indicate process-level thinking and these can be merged in the one sentence.
Workshop 2 problem
The problem from Workshop 2 in Fig. 4 is repeated here for convenience.| Problem: Calculate the molar entropy of a constant-volume sample of argon gas at 250 K given that it is 154.84 J K−1 mol−1 at 298 K. Use the SI Chemical Data Book if you need relevant information. |
Workshop 2 was held about one month after Workshop 1 so there was an expectation that the students would approach the workshop with more highly developed skills in problem solving than was the case for Workshop 1. The students were able to solve the problem without any real difficulty because Pamela discovered a similar example in the lecture notes and in an assignment about half-way through the problem solving process. The dialogue that led to the solution did however reveal some struggles again. Mary commenced the conversation by suggesting the use of, 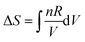 , but then recognized immediately that this wouldn’t work given the sample was at constant volume. Jessica then suggested,
, but then recognized immediately that this wouldn’t work given the sample was at constant volume. Jessica then suggested, 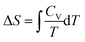 , but Pamela reminded the group that S was needed not ΔS. Jessica replied, “If we can find ΔS, then we can find the unknown S, so we will need to find Cv.” Insight into a solution pathway using process-level thinking was demonstrated by Jessica here.
, but Pamela reminded the group that S was needed not ΔS. Jessica replied, “If we can find ΔS, then we can find the unknown S, so we will need to find Cv.” Insight into a solution pathway using process-level thinking was demonstrated by Jessica here.
Looking up the SI Chemical Data Book she noticed that Cp was given in J K−1 g−1 and recognized that Cv could be obtained through the relationship, Cp − Cv= nR. At this point Jessica had great difficulty knowing how to convert J K−1 g−1 to J K−1 mol−1 until Evan told her to multiply by the molar mass. Jessica then calculated Cvm to be 12.46 J K−1 suggesting mol−1 didn’t need to be part of the unit since the value for Cvm was understood to be for one mol. Evan reminded her that mol−1 still needed to be shown in the unit. At this point Pamela discussed the example from the lecture notes at which point the group was fairly confident that their solution was correct. Mary, in summary, said, “All feel ok actually (about this solution)” (Instructor's and Mary's diary). Evan's consensus solution is shown in Fig. 7.
The mixing of object-level thinking and process-level thinking is again evident here. The way Evan was able to assist Jessica with the question of units demonstrated the value of collaborative learning. Since there was a similar example in their lecture notes, one could argue that the kind of thinking involved was simply routine-level thinking. But the very fact that the lecture notes had to be consulted indicated that the thinking required was beyond routine thinking.
Workshop 2 question 1
Question 1 from Fig. 4 is repeated here for convenience.| Question 1: When heating a constant-volume sample of a gas, which of the following applies? |
| (i) The entropy of the gas should not change with temperature |
| (ii) The entropy of the gas should decrease with temperature |
| (iii) The entropy of the gas should increase with temperature |
All group members agreed that alternative (iii) was the correct choice although Evan initially voted for alternative (ii) having just calculated a decrease in entropy in the problem but then recognized this answer was for a lower temperature. All agreed that their response was consistent with the answer obtained in the problem. Pamela noted that heating a sample of argon at constant volume would lead to an increase in pressure and one would not expect a chemical reaction given argon is a noble gas. She noted in her diary that, “the group felt confident in their answer.” On reflection, I should have asked the students to explain why they chose “entropy increases with temperature” but I just have to consider this a missed opportunity. The opportunity to ask for a mathematical explanation and a chemistry explanation was again lost. So the workshop was beneficial for the instructor as well as the students.
Workshop 2 Question 2
Question 2 from Fig. 4 is repeated here for convenience.| Question 2: Use relevant formulae to sketch a graph of the entropy of a gas against temperature |
Plotting a graph of S against T proved a difficult exercise for the group. A similar difficulty was experienced in Workshop 1 when asked to plot H against T. On this occasion the instructor's diary was more informative than Pamela's diary. Mary recognized that a formula would be helpful even though she recognized that S would increase as T increased from Question 1. Having nominated, 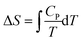 or
or 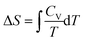 , and suggesting one needed to perform an indefinite integral, Mary was perplexed because the indefinite integral suggested, ΔS = CV
, and suggesting one needed to perform an indefinite integral, Mary was perplexed because the indefinite integral suggested, ΔS = CV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T + c, but the question asked for S not ΔS. What was somewhat disconcerting was that Mary had two years of advanced calculus under her belt and didn’t recognize that the derivative form of the relationship between S and T, from which the integral form was derived, was,
T + c, but the question asked for S not ΔS. What was somewhat disconcerting was that Mary had two years of advanced calculus under her belt and didn’t recognize that the derivative form of the relationship between S and T, from which the integral form was derived, was, 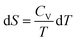 , from which an indefinite integration would give, S = CV
, from which an indefinite integration would give, S = CV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T + c, provided Cv was independent of temperature.
T + c, provided Cv was independent of temperature.
On reflection, the fault didn’t lie entirely with Mary. There was a lesson again for the instructor in drawing up the formula sheet. The left-hand side of the formula, 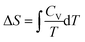 , arises from a definite integral,
, arises from a definite integral, 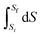 , whereas the right-hand side is in the form of an indefinite integral. The formula should not have mixed the integral types. This is a case where the symbolic templates for integration introduced by Jones (2013) could prove useful:
, whereas the right-hand side is in the form of an indefinite integral. The formula should not have mixed the integral types. This is a case where the symbolic templates for integration introduced by Jones (2013) could prove useful: 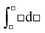 (function matching with limits) and
(function matching with limits) and 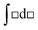 (function matching without limits). Evan's plot on the consensus answer sheet was a plot of ΔS against ln T showing a straight line of positive slope passing through the point where the two axes meet. Pamela noted in her diary that there, “was some uncertainty with this response.” An equation showing S as a function of T could not be derived.
(function matching without limits). Evan's plot on the consensus answer sheet was a plot of ΔS against ln T showing a straight line of positive slope passing through the point where the two axes meet. Pamela noted in her diary that there, “was some uncertainty with this response.” An equation showing S as a function of T could not be derived.
At least Mary recognized the importance of integration on this occasion but was not able to clarify in her mind the difference between S, dS, and ΔS. Recognizing that ΔS arises from, 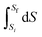 , and S (plus a constant) arises from,
, and S (plus a constant) arises from, 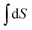 , examples of object-level thinking, would be helpful. Jones (2015) found a similar difficulty between ‘dx’ and ‘Δx’. Cole and Shepherd (2019) noted that it was common for students to have difficulty distinguishing between ‘x’ and ‘dx’ in that when ‘x’ was constant they chose to put ‘x’ equal to zero rather than put ‘dx’ equal to zero. If the group had identified that the slope of S against T was decreasing as T increased, an example of process-level thinking, they would have made some progress in sketching S against T.
, examples of object-level thinking, would be helpful. Jones (2015) found a similar difficulty between ‘dx’ and ‘Δx’. Cole and Shepherd (2019) noted that it was common for students to have difficulty distinguishing between ‘x’ and ‘dx’ in that when ‘x’ was constant they chose to put ‘x’ equal to zero rather than put ‘dx’ equal to zero. If the group had identified that the slope of S against T was decreasing as T increased, an example of process-level thinking, they would have made some progress in sketching S against T.
Workshop 2 question 3
Question 3 from Fig. 4 is repeated here for convenience.| Question 3: What happens to the entropy of a gas when it is compressed at constant temperature? Use an appropriate formula to illustrate your answer |
The group eventually agreed with the idea that the entropy of the gas would decrease when compressed at constant temperature, but the dialogue (particularly that shown in the instructor's diary) that preceded the solution revealed some interesting trends. Jessica commenced the discussion by noting that the pressure should increase when the gas is compressed, a suggestion that can be agreed upon given Boyle's law learnt from high school days. Given the length of time of exposure to this law, one could claim that Jessica was engaged in routine-level thinking here. On the other hand, one could argue for intuitive process-level thinking given the fact that Jessica did not mention Boyle's Law. It is the length of time of exposure that favours a designation of routine-level thinking here.
Mary then suggested, using what we might again claim as intuitive process-level thinking, that the molecules would move faster at the higher pressure, a suggestion that is not consistent with the formula showing that molecular speed only depends on temperature 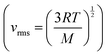 and since the temperature remains constant the root mean square velocity should remain constant. Intuition could have been productive for Mary if she had combined her chemistry thinking with mathematical thinking, that is, integrated her chemistry with mathematics. Compressing the gas is equivalent to doing work on the gas which increases its internal energy (ΔU = w since no thermal energy (q) is initially added to the gas). At the point when the gas is no longer compressed, the temperature must rise (Cv = ΔU/ΔT), which would lead to a rise in the root mean square velocity of the particles. This would have justified Mary's intuition at this point and led to integrative process-level thinking. The fact that the gas was in thermal equilibrium with its surroundings, however, meant that the excess thermal energy was lost to the surroundings and the temperature returned to its initial value.
and since the temperature remains constant the root mean square velocity should remain constant. Intuition could have been productive for Mary if she had combined her chemistry thinking with mathematical thinking, that is, integrated her chemistry with mathematics. Compressing the gas is equivalent to doing work on the gas which increases its internal energy (ΔU = w since no thermal energy (q) is initially added to the gas). At the point when the gas is no longer compressed, the temperature must rise (Cv = ΔU/ΔT), which would lead to a rise in the root mean square velocity of the particles. This would have justified Mary's intuition at this point and led to integrative process-level thinking. The fact that the gas was in thermal equilibrium with its surroundings, however, meant that the excess thermal energy was lost to the surroundings and the temperature returned to its initial value.
At the suggestion that pressure increases, Pamela remembered that increasing the pressure on the NO2/NO equilibrium favoured the side where there was a fewer number of molecules. She queried how this could apply to the case of argon where there was no chemical reaction. Mary remembered applying the concept of entropy to chemical reactions, entropy decreasing if the number of molecules was decreasing, but she wondered how to understand entropy when there is no chemical reaction (meta-level thinking). Since there was no chemical reaction, Mary suggested that the entropy might stay the same on compression at constant temperature. Someone else in the group suggested that the entropy should increase if the pressure was increasing (intuitive process-level thinking). Again, if the chemistry could have been combined with the mathematics using integrative process-level thinking, a resolution could have been reached. Mary made a helpful attempt as shown below.
Mary noted that the equation, 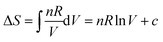 , might help, and noted that ΔS increases as V increases, and “thought that this doesn’t quite line up” with what she previously thought (that S would not change). Pamela reminded everyone that this speaks for ΔS not S. Pamela concludes that, “Either S increases or decreases as V decreases. I am more inclined to think S decreases.” Jessica suggests that one of these alternatives needs to be substantiated by substituting two different values of V in the equation. Pamela then suggests trying a volume decrease from 2 L to 1 L. Evan then calculates ΔS to be −5.76 (doesn’t include the units), using ΔS = 8.314 × ln(1/2) for one mole, and suggests the entropy is decreasing. All agree with this conclusion. The group found it difficult to reason without substituting values. The same trend of preferring value substitution over symbolic reasoning has been noted by Cole and Shepherd (2019).
, might help, and noted that ΔS increases as V increases, and “thought that this doesn’t quite line up” with what she previously thought (that S would not change). Pamela reminded everyone that this speaks for ΔS not S. Pamela concludes that, “Either S increases or decreases as V decreases. I am more inclined to think S decreases.” Jessica suggests that one of these alternatives needs to be substantiated by substituting two different values of V in the equation. Pamela then suggests trying a volume decrease from 2 L to 1 L. Evan then calculates ΔS to be −5.76 (doesn’t include the units), using ΔS = 8.314 × ln(1/2) for one mole, and suggests the entropy is decreasing. All agree with this conclusion. The group found it difficult to reason without substituting values. The same trend of preferring value substitution over symbolic reasoning has been noted by Cole and Shepherd (2019).
The algorithmic process-level and object-level thinking here is hampered again by a formula that mixes indefinite integration with definite integration. It would have been better for the formula to have been written as, 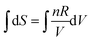 , or,
, or, 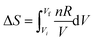 , even though Evan used the definite integral form for both sides of the equation in his calculation. At least the confusion between S and ΔS as noted by Pamela could have been avoided.
, even though Evan used the definite integral form for both sides of the equation in his calculation. At least the confusion between S and ΔS as noted by Pamela could have been avoided.
A summary of adjectival qualifiers for thinking profiles observed across the workshops
Listed in Table 4 is a summary of the adjectival qualifiers attached to thinking profiles observed across the workshops as an aid to the reader.Mary: The class was a little bit frustrated with Mary for not letting them use the word ‘exponential’. We then ensued into a waffle of increasingly using the word ‘increase’.
At the beginning of Workshop 2 Pamela gave us a window into the mood of the group as follows.
Pamela: Pamela was feeling tired; Mary was feeling ok initially; Jessica felt pretty trash in general and Evan tried to lighten the mood with a chemistry joke, to which he received varying responses from the group. Mary was honest enough to admit that she didn’t feel very confident in her knowledge of entropy.
As an instructor I gained a better appreciation of the insecurities students experience in their learning and how they play a part in impacting confidence in activities like problem solving and giving qualitative descriptions of the concepts being learned. The opportunity for students to express themselves led to a higher than expected use of meta-level thinking.
Limitations
The fact that diaries were written during the workshop and the dialogue not digitally recorded meant that some nuances in speech may not have been noticed although every effort was made to record these. This also meant it was not possible to replay the discourse to check details. While every attempt was made to be as objective as possible in recording factual information, the diaries also included reflections and interpretations which may have coloured the information noted. However, it should be noted that reflections were also important pieces of data. When Evan checked what was written in the instructor's diary and compared it to the student diaries, no significant discrepancies were detected.Conclusion
Some of the findings described in this paper have also been found in other studies (Cole and Shepherd, 2019) looking at the relationship between mathematics and physical chemistry and these have been identified earlier in the paper. Findings of importance in the current study emphasize the significance of adjectival qualifiers for describing thinking profiles, and the importance of not mixing integral types when presenting formulas. Some further detail follows.It was confirmed, in the light of the research question, that student thinking around chemistry concepts which are mathematically expressed can be classified under the profiles; routine-level, object-level, process-level, and meta-level. Routine-level was confined to standard procedures that might be expected of a second-year chemistry undergraduate. Standard procedures and thus routine-level thinking for an expert would be much broader of course. Object-level applied to both mathematical formulae and their derivatives as fixed entities and the shape of graphs as fixed entities. When values or changes in values were being considered, process-level was used as the thinking profile. Meta-level applied when students were examining their thinking processes and assessing where they thought they were at in finding a solution to the problem. This was commonly used by the students which suggested they were happy to remain on a learning pathway even though there were some incorrect answers in the workshop. When looking at the written diaries and consensus solutions, it was found necessary to add adjectival qualifiers for object-level and process-level thinking to enhance the value of the classifications.
The qualifiers that proved helpful when studying the diaries in detail were: incoherent, intuitive, algorithmic, and integrative. Incoherent was used when a student said one thing and then implied the opposite. Thankfully there were not too many incidences of this in the diaries. Intuitive was used when a student gave no detailed reasoning for a conclusion but the context suggested there might be a logical reason for the conclusion. For example, an increase in a property leads to a positive answer, a decrease in a property leads to a negative answer, and no change in a property leads to a zero answer. When graphing, constancy implies a straight line, variability implies a curve. Algorithmic applied when a standard procedure was used to calculate an answer as in determining the value of a definite integral. Integrative was used when chemistry concepts and their associated mathematical concepts were used in the thinking profile to generate blended or integrated knowledge. While this thinking profile is highly desirable (Bain et al., 2019), the students found this difficult to achieve.
While the workshops proved beneficial to the students according to their own comments, they also proved of value to the instructor, particularly in the area of the construction of formula sheets. Mixing symbolic formats in the one equation proved disastrous for students, particularly when asked to sketch a graph of H against T and S against T. Using a definite integral format and an indefinite integral format in the one equation made it difficult for students to distinguish between H, dH, and ΔH; and between S, dS, and ΔS. The other lesson for the instructor was to include exercises requiring more integrative thinking in workshops, assignments, and examinations, and to do more modelling of integrating chemistry concepts with mathematical concepts including explicit prompts for students to do so in the exercises.
Conflicts of interest
There are no conflicts of interest to declare.References
- Aspinwell L. and Miller D., (1997), Students’ positive reliance on writing as a process to learn first semester calculus, J. Inst. Psychol., 24, 253–261.
- Bain K., Moon A., Mack M. R. and Towns M.H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15, 320–335.
- Bain K., Rodriguez J. G. and Towns M. H., (2019), Chemistry and mathematics: Research and frameworks to explore student reasoning, J. Chem. Educ., 96, 2086–2096.
- Becker N. and Towns M., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13, 209–220.
- Becker N., Rasmussen C., Sweeney G., Wawro M., Towns M. and Cole R., (2013), Reasoning using particulate nature of matter: An example of a sociochemical norm in a university-level physical chemistry class, Chem. Educ. Res. Pract., 14, 81–94.
- Besson U., (2014), Teaching about Thermal Phenomena and Thermodynamics: The Contribution of the History and Philosophy of Science, in Matthews M., (ed.), International Handbook of Research in History, Philosophy and Science Teaching, Dordrecht: Springer, pp. 245–283.
- Bingolbali E., Monaghan J. and Roper T., (2007), Engineering students’ conceptions of the derivative and some implications for their mathematical education, Int. J. Math. Educ. Sci. Technol., 38(6), 763–777.
- Cole R. and Shepherd T., (2019), Making sense of mathematical relationships in Physical Chemistry, in Towns M. H., Bain K. and Rodriguez J. G., (ed.), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, ACS Symposium Series 136, Washington, DC: American Chemical Society, pp. 173–186.
- Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: A cognitive difference, J. Chem. Educ., 85 (6), 873.
- David E. J., Roh K. H. and Sellers M. E., (2019), Value-thinking and location-thinking: Two ways students visualise points and think about graphs, J. Math. Behav., 54, 100675.
- de Berg K. C., (2008a), The concepts of heat and temperature: The problem of determining the content for the construction of a historical case study which is sensitive to nature of science issues and teaching-learning issues, Sci. & Educ., 17(1), 75–114.
- de Berg K. C., (2008b), Conceptual depth and conceptual usefulness in chemistry: Issues and challenges for chemistry educators, in Eriksson I. V., (ed.), Science Education in the 21st Century, New York: NovaScience Publishers, pp. 165–182.
- Derrick M. E. and Derrick F. W., (2002), Predictors of success in physical chemistry, J. Chem. Educ., 79(8), 1013–1016.
- Eichler A. and Erens R., (2014), Teachers’ beliefs towards teaching calculus, ZDM Math. Educ., 46, 647–659.
- Engin M., (2011), Research diary: A tool for scaffolding, Int. J. Qual. Meth., 10(3), 296–306.
- Groves M., (2015), Is a conceptual understanding of maths vital for chemistry? Educ. Chem., Jan, 11.
- Grundmeier T. A., Hansen J. and Sousa E., (2006), An exploration of definition and procedural fluency in integral calculus, Primus, XVI(2), 178–191.
- Hadfield L. C. and Wieman C. E., (2010), Student interpretations of equations related to the first law of thermodynamics, J. Chem. Educ., 87, 750–755.
- Hahn K. E. and Polik W. F., (2004), Factors influencing success in physical chemistry, J. Chem. Educ., 81(4), 567–572.
- Hu D. and Rebello N. S., (2013), Using conceptual blending to describe how students use mathematical integrals in physics, Phys. Rev. Spec. Top-Phys. Educ. Res., 9(020118), 1–15.
- Jones S. R., (2013), Understanding the integral: Students’ symbolic forms, J. Math. Behav., 32, 122–141.
- Jones S. R., (2015), The prevalence of area-under-a-curve and anti-derivative conceptions over Riemann sum-based conceptions in students’ explanations of definite integrals, Int. J. Math. Educ. Sci. Technol., 46(5), 721–736.
- Leopold D. G. and Edgar B., (2008), Degree of mathematics fluency and success in second semester introductory chemistry, J. Chem. Educ., 85(5), 724–731.
- Loverude M. E., Kautz C. H. and Heron P. R., (2002), Student understanding of the first law of thermodynamics: Relating work to the adiabatic compression of an ideal gas, Am. J. Phys., 70(2), 137– 148.
- Maeyer J. and Talanquer V., (2010), The Role of Intuitive Heuristics in Students’ Thinking: Ranking Chemical Substances, wileyonlinelibrary.com.
- Mahir N., (2009), Conceptual and procedural performance of undergraduate students in integration, Int. J. Math. Educ. Sci. Tech., 40(2), 201–211.
- McCloskey M., (1983), Intuitive physics, Sci. Am., 248(4), 122–130.
- Meltzer D. E., (2004), Investigation of students’ reasoning regarding heat, work, and the first law of thermodynamics in an introductory calculus-based general physics course, Am. J. Phys., 72(11), 1432–1446.
- Moon A., Stanford C., Cole R. and Towns M., (2016), The nature of students’ chemical reasoning employed in scientific argumentation in physical chemistry, Chem. Educ. Res. Pract., 17, 353–364.
- Moore K. C. and Thompson P. W., (2015), Shape thinking and students’ graphing activity, in Fukawa-Connelly T., Infante N., Keene K. and Zandieh M., (ed.), Special Interest Group of the Mathematics Association of America for Research in Undergraduate Mathematics Education, pp. 782–789.
- Nakhleh M. B., (1993), Are our students conceptual thinkers or algorithmic problem solvers? Identifying conceptual students in general chemistry, J. Chem. Educ., 70(1), 52–55.
- Nelson E. A., (2018), ConfChem conference on mathematics in undergraduate chemistry instruction: Addressing math deficits with cognitive science, J. Chem. Educ., 95, 1440–1442.
- Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem soling: Is there a difference? J. Chem. Educ., 64(6), 508–509.
- Perkins R. D., (1979), Do community college introductory chemistry students have adequate mathematics skills? J. Chem. Educ., 56(5), 329.
- Pickering M., (1990), Further studies on concept learning versus problem solving, J. Chem. Educ., 67(3), 254–255.
- Pollock E. B., Thompson J. R. and Mountcastle D. B., (2007), Student understanding of the physics and mathematics of process variables in P-V diagrams, in Proceedings of the 2007 physics education research conference of American Institute of Physics.
- Reif F., (1983), How can chemists teach problem-solving? J. Chem. Educ., 60, 948–953.
- Sfard A., (1991), On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin, Educ. Stud. Math., 22, 1–36.
- Sfard A., (2007), When the rules of discourse change, but nobody tells you: Making sense of mathematics learning from a commognitive perspective, J. Learn. Sci., 16 (4), 565–613.
- Sherin B. L., (2001), How students understand physics equations, Cognit. Instruct., 19 (4), 479–541.
- Stenhouse D., (1985), Active Philosophy in Education and Science, London: Allen & Unwin.
- Tanner K. D., (2012), Promoting student metacognition, CBE Life Sci. Educ., 11(2), 113–120.
- Towns M. H., Bain K. and Rodriguez J. G., (ed.), (2019), It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, ACS Symposium Series 1316, Washington DC: American Chemical Society.
- Williams H. B., (1952), Elementary physical chemistry and mathematics, J. Chem. Educ., 29(2), 77.
| This journal is © The Royal Society of Chemistry 2022 |





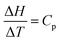

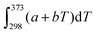
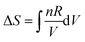
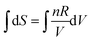
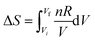
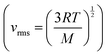
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)