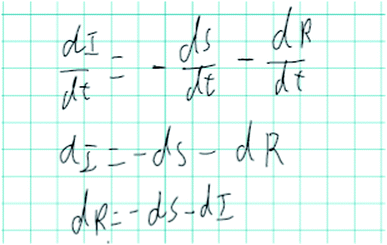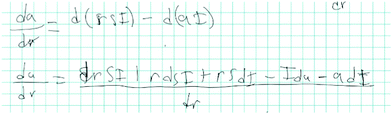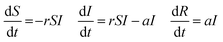Development of a framework to capture abstraction in physical chemistry problem solving
Jessica M.
Karch
* and
Hannah
Sevian
Department of Chemistry, University of Massachusetts Boston, Boston, Massachusetts, USA. E-mail: Jessica.Karch@gmail.com
First published on 1st September 2021
Abstract
Productive problem solving, concept construction, and sense making occur through the core process of abstraction. Although the capacity for domain-general abstraction is developed at a young age, the role of abstraction in increasingly complex and disciplinary environments, such as those encountered in undergraduate STEM education, is not well understood. Undergraduate physical chemistry relies particularly heavily on abstraction because it uses many overlapping and imperfect mathematical models to represent and interpret phenomena occurring on multiple scales; however, studying and identifying abstraction in-the-moment in physical chemistry is challenging, because current conceptions of abstraction neglect the domain-specific features. This work uses an approach guided by informed grounded theory to develop a conceptual framework that makes abstraction in physical chemistry problem solving visible. Problem solving teaching interviews with individuals and pairs (n = 18) on thermodynamics and kinetics topics are analyzed using an abductive approach. The resulting Epistemic Actions of Abstraction framework characterizes eight epistemic actions along two dimensions: increasing abstractness relative to the context (concretizing, manipulating, restructuring, and generalizing) and nature of the object the action operates on (conceptual or symbolic). These actions are used to identify two types of abstraction: horizontal and vertical abstraction. We discuss how abstraction in problem solving is contextually dependent and implications this work has for problem solving in physical chemistry, as well as implications for physical chemistry instruction.
Introduction
Developing deep disciplinary understanding of physical chemistry concepts is challenging. Both students and instructors have called for pedagogical approaches that foster deeper conceptual understanding in physical chemistry (Sözbilir, 2004; Bain et al., 2014); however, the majority of physical chemistry assessments remain mathematical in nature (Fox and Roehrig, 2015). A common instructional approach in physical chemistry to foster and assess student conceptual understanding is through problem solving (Mack and Towns, 2016). When students solve problems in physical chemistry, they may be tasked with applying their knowledge to novel situations and making connections between the different concepts encountered in the problem task. Through this connection making, students may further develop and refine their conceptual understanding of the topic at hand.One approach researchers have taken to investigate how students develop disciplinary conceptual understanding from problem solving is by studying how they abstract—that is, how students extract salient details, make connections, and match to exemplar cases (Sevian et al., 2015). Studies in developmental psychology (Inhelder and Piaget, 1958) suggest that abstraction underlies the development of concepts and generalizations, particularly when learners are still developing their cognitive capacity for abstract thinking at young ages. However, even once learners have developed a capacity for domain-general abstract thinking, they still may not necessarily apply this capacity to increasingly complex and abstract concepts (Davydov, 1972), such as those encountered in learning complex disciplinary material in undergraduate chemistry. Furthermore, studies conducted in different science courses have found that not only is abstraction an important process for learners, but abstraction itself has to be studied in domain-specific ways (Jiménez et al., 2016; Weinrich and Sevian, 2017; Santos and Mortimer, 2019). Thus, to understand how abstraction may support the development of physical chemistry conceptual knowledge, it is important first to be able to recognize abstraction in action.
To this end, we report the development of a domain-specific framework to operationalize abstraction in problem solving. This framework identifies two dimensions to abstracting actions taken in physical chemistry problem solving: the nature of the knowledge the problem solver draws upon (mathematical or conceptual) and how far removed (how abstract) the knowledge constructed in-the-moment is from the established problem space. These two dimensions are used to define two types of abstraction in physical chemistry: horizontal and vertical abstraction.
Research question
This study grew out of an earlier project in our research group examining how abstraction manifests differently in undergraduate engineering and chemistry (Sevian et al., 2015; Weinrich and Sevian, 2017). The analytic framework for that study (representation mapping) focused on how abstractly students represented the problem space and their prior knowledge, as well as how they matched the problem space and their relevant prior knowledge. In preliminary work applying this framework to physical chemistry, we found that although this approach was fruitful, it did not fully capture either the difference in abstractness that emerged from the use of mathematical and conceptual chemistry resources or how abstractness could change over the course of a single problem-solving episode. In mathematics education, some studies have operationalized abstraction as the epistemic actions students make while problem solving (e.g., Williams, 2007; Halverscheid, 2008; Tabach et al., 2017). Combining this approach with theoretical aspects from representation mapping, we designed a study to develop a domain-specific understanding of abstraction in physical chemistry.The overarching research question that guided this study was: How does abstraction occur in students’ reasoning while they are solving complex physical chemistry problems?.
This paper is laid out into four sections: first, we review the state of relevant literature that motivated the development of a domain-specific framework, as well as the literature in which our framework is grounded. Second, we report the process by which the framework was developed. Third, we report the major features of the framework and illustrate them with examples. Finally, we discuss the implications for both research and practice.
Literature review
To motivate the need for a domain-specific framework to study abstraction in physical chemistry problem solving, we will briefly review current literature on physical chemistry problem solving, as well as how abstraction has been previously conceptualized in chemistry and mathematics education research.Problem solving in physical chemistry
In undergraduate physical chemistry, problem solving is an important opportunity for students to develop and apply conceptual understanding. In particular, physical chemistry instructors see problem solving as an opportunity to make new connections and deepen their understanding of new content material (Fox and Roehrig, 2015; Mack and Towns, 2016). Thus, it is important to have a grounded understanding of the approaches students take while solving common types of problems, such as those involving chemical kinetics (Rodriguez et al., 2018) and free energy (Tsaparlis, 2005). Problem solving in undergraduate physical chemistry involves a mix of high level conceptual and mathematical reasoning (Rodriguez et al., 2018), which can be challenging for students in part because the content covered in physical chemistry tends to be removed from concrete references to real systems (Sözbilir, 2004).Bridging conceptual and mathematical reasoning has also been identified as a specific challenge for students, particularly during problem solving. For example, Becker and Towns (2012) showed that students working on Maxwell relation problems were successful in interpreting the physical and mathematical meaning of a partial differential (e.g., (∂V/dT)P) separately; however, they struggled to apply this understanding when solving a problem. Similarly, Rodriguez and collaborators studied the epistemic games students use when solving kinetics problems. They found that students tended to compartmentalize their mathematics and chemistry knowledge, and often had trouble simultaneously navigating these two different sets of conceptual resources, even when they had otherwise productive problem solving approaches. (Rodriguez et al., 2020). The disconnect between conceptual and mathematical reasoning has also been extensively documented in physics problem solving, where expert-like problem solving requires coherence between conceptual and mathematical reasoning (e.g., Kuo et al., 2013, 2020; Niss, 2017).
There are two takeaways from this brief review: (1) problem solving is used as a tool to support students’ conceptual knowledge development, and (2) a salient challenge in physical chemistry involves how students use mathematical and chemistry ideas together. To begin to develop a definition of abstraction specific to physical chemistry, we thus turn to how abstraction has been conceptualized in both mathematics and chemistry education research.
Abstraction in chemistry and mathematics problem solving
A capacity for abstraction is an important skill for chemistry learning. As a process, abstraction involves extracting salient details, recognizing and developing generalities, and recognizing and applying conceptual meaning to symbols (e.g., abstractions). In general chemistry, Frey, Cahill and McDaniel (2017) found that students who learned concepts through abstraction, e.g., through the extraction of salient points, outperformed students who learned through rote memorization of examples. In organic chemistry, Weinrich and Sevian (2017) and Domin and Bodner (2012) found that students who were more flexible in their use of abstraction while solving organic chemistry problems tended to present more plausible solutions. In their study of organic mechanism problem solving, Weinrich and Sevian (2017) identified 4 domain-specific indicators of abstractness: (1) the extent to which students drew on information explicit (low) or implicit (high) in the problem, (2) whether students focused on the sequential order of mechanistic steps (low) or the explanation behind the steps (high), (3) whether students focused on structure (low) or function (high), and (4) the extent to which their representations were specific (low) or general (high). This work operationalized the act of abstracting as a function of how students constructed mental representations of the problem space and relevant prior knowledge, and the relative abstractness of these representations (Hahn and Chater, 1998; Sevian et al., 2015).Santos and Mortimer (2019) built on previous work in middle school science (Jiménez et al., 2016) to propose 4 possible levels of “abstractness” that can be used to characterize chemistry knowledge and representations. Using Legitimation Code Theory (Maton, 2013), they proposed that chemistry knowledge can be categorized in two dimensions. First, chemistry knowledge can be characterized by semantic gravity, or how removed from physical reality a piece of knowledge is, into four levels: description, explanation, generalization, and abstraction. Second, building on Johnstone's triangle (Johnstone, 1991), chemistry knowledge can be characterized into four levels of semantic density, or how much information is encoded into a given representation: macroscopic or phenomenological (the least amount of information encoded), conceptual macroscopic, conceptual submicroscopic, and symbolic (the most amount of information encoded).
These works have largely focused on the conceptual aspects of abstraction or worked to identify domain-specific attributes in other sub disciplines, e.g., in organic chemistry. However, physical chemistry as a sub discipline is unique because it draws not only on highly abstract physical concepts, such as entropy (Sözbilir, 2004), it also utilizes highly abstract mathematics, such as partial differentials. Mathematics and physics education literature have been found to be very fruitful in interpreting student reasoning in physical chemistry (e.g., Bain et al., 2019). Thus, due to the mathematical nature of physical chemistry problem solving, we also draw heavily on literature published in mathematics education. In mathematics education, studies have focused on abstraction as the construction of mathematical knowledge. There are several traditions in mathematics education for investigating abstraction, which can largely be differentiated into two categories: abstraction-from-actions and abstraction-from-objects (Scheiner, 2016).
In abstraction-from-action approaches, abstraction is conceptualized as how learners learn procedures and extract mathematical meaning through reflecting on how these procedures are applied to an object. An object is defined as a mathematical concept that a learner can perform transformations on, such as an equation (Dubinsky and McDonald, 2001). An example of this would be a student who learns a procedure to solve a certain type of problem, and then after solving many of these types of problem, reflects on the similarities between them and recognizes a mathematical concept that underpins the similarities (e.g., Sfard, 1991; White and Mitchelmore, 2010). The concept of reflective abstraction stems primarily from Piaget's theories on empirical abstraction, in which an individual extracts meaning from their encounters with the world (Piaget, 1964).
Abstraction-from-object approaches (structural abstraction) takes an opposite stance. If abstraction-from-action occurs when a learner reflects on the similarities between many different types of similar procedures, abstraction-from-object occurs when a learner takes a single object and places it in different contexts to extract the essence of that object, which gives it meaning (Davydov, 1972). For example, a learner might be trying to develop the concept of “atom.” By considering what an atom is in different contexts, such as the Bohr's model of an atom or an atom as a part of a molecule, they may come to better understand its nature. In mathematics education, this type of abstraction involves trying to deeply understand the mathematical structure of an object. One mathematical tradition that utilizes abstraction-from-objects is the Dutch tradition of Realistic Mathematics Education (RME). In RME, the construction of mathematical knowledge is viewed as how learners bridge the concrete (experiential knowledge) and the abstract (mathematical knowledge) (van den Heuvel-Panhuizen, 2003). RME identifies two ways in which learners may develop mathematical knowledge: horizontal mathematization, or translating between experiential and physical reality and a mathematical object; and vertical mathematization, or the reorganization and consolidation of previous mathematical concepts into a single mathematical construct. Some researchers define abstraction as the process of vertical mathematization (e.g., Hershkowitz et al., 2001).
Instead of trying to reconcile these two approaches into a single definition of abstraction, Scheiner (2016) suggests that both are valid and reflect two different kinds of learners in mathematics. Reflective learners extract meaning from a mathematical object by working with it in order to formalize their understanding of it; that is, they “abstract from actions.” Structural learners primarily learn mathematics by considering it in light of their previous experiences and giving meaning to an object; that is, they “abstract from objects.” Scheiner also proposes a third type of learner, who uses a hybrid of reflective and structural abstraction. These “reflectural” (reflective + structural) learners both extract meaning from and give meaning to objects through abstraction.
Although much of the work done on abstraction in mathematics uses a constructivist theoretical lens, some studies have also conceptualized abstraction using sociocultural theory. Abstraction in Context (Hershkowitz et al., 2001, 2007; Tabach et al., 2017) is a framework that conceptualizes abstraction as “a process that takes place in a complex context that incorporates tasks, tools, and other artifacts; the personal histories of participants; and the social and physical settings” (Hershkowitz et al., 2001, p. 204). That is, how a student abstracts and what tools they use to do so depend on the context in which the abstraction is taking place as well as the historical context of the students.
This review shows that there are many approaches to characterizing abstraction in the literature, and that chemistry and mathematics education research have focused on different aspects of abstraction. In chemistry, researchers have focused largely on the abstractness of the concepts themselves, whereas in math, researchers have largely focused on the construction of mathematical structures and knowledge. However, in physical chemistry, students must grapple with both abstract concepts and dense mathematical equations. This suggests that to understand how students abstract in physical chemistry, it is necessary to bridge chemistry and mathematics education research and develop a conceptual framework that draws on both. In the following section, we describe the details of the conceptual framework that emerged from our iterative development process.
Theoretical and conceptual framework
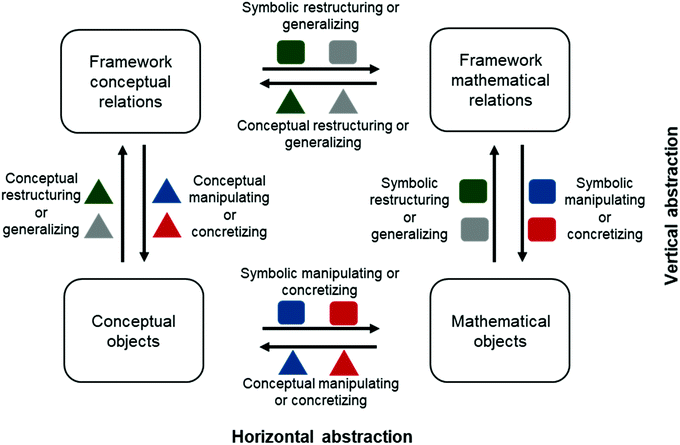
Our orientation to abstraction draws primarily on the work from Scheiner (2016) and the Abstraction in Context framework (Hershkowitz et al., 2001). From Scheiner, we take the stance that abstraction may involve both extracting meaning from and giving meaning to an object. “Object” is defined as a concept that a learner can perform transformations on, such as an equation (Dubinsky and McDonald, 2001). Therefore, abstraction is how a learner makes sense of something like an equation or a conceptual idea, either extracting meaning from it to develop a generalized concept, or giving meaning to it to recognize generalizable features.Although Scheiner's theory categorizes learners by what kind of abstraction they primarily use, we acknowledge that learners may use different types of abstraction processes depending on the context in which they are being asked to abstract, and depending on their personal histories. There are thus two important parts of our framework: what learners do (which we will characterize as epistemic actions), and the context in which they are working (which we will characterize as the problem space).
Abstraction as epistemic actions (what learners do)
To capture abstraction as something that is sociohistorically situated, a sociocultural theoretical framework was used as the overarching framework for the study: first-generation activity theory (Davydov, 1972; Leont’ev, 1978; Hershkowitz et al., 2001). Through activity theory, abstraction is characterized as an activity: practical human work that uses tools and occurs within a particular context in response to a need. Activity is constituted by a series of actions mediated by sociocultural tools that an actor does to resolve a need. For example, an activity in a chemistry lab may be synthesizing a product. A chemist synthesizes a product toward a goal, for example developing a new pharmaceutical to treat cancer (the need). She may use procedures (tools) to design the synthesis, which she carries out in discrete steps (actions): mix the reactants, run the synthesis, separate and purify the product, characterize the results. This all occurs in a context: the methods she uses depend on what is available to her in the lab, such as tools and the physical space (her current sociocultural context), and what has been previously published and is considered to be the standard in drug discovery (sociohistorical context). The individual actions the chemist takes (mixing the reactant, etc.) all work toward resolving the need for a new product, and thus constitute one activity: drug synthesis.Similarly, we view abstraction as a mental activity—an activity that is carried out using mental tools and actions. For example, while solving a problem in chemistry, a student may be faced with an equation they do not understand (the need). To understand it, they may need to give meaning to the equation by abstracting (the activity). They may use concepts (mental tools) they already know to define the different variables in the equation, and figure out the meaning by reasoning about how the variables relate. How they do this depends on things like what concepts and problem solving approaches they learn in their chemistry class and in previous classes (sociohistorical context), and how they view and personally relate to the problem at hand (current sociocultural context).
The individual actions the learner takes while abstracting are epistemic actions: goal-mediated mental actions learners take when they are constructing knowledge (Pontecorvo and Girardet, 1993). Previous work in mathematics education has identified the four epistemic actions that constitute abstraction as recognizing, building-with, constructing, consolidating. That is, when a learner abstracts in math, they may (1) recognize a previously learned schema, (2) use that schema to make sense of what has been given in the problem (building-with), (3) construct a piece of knowledge, e.g., by recognizing a deep structure, and (4) consolidate it to make it more readily available for future use (Hershkowitz et al., 2001; Tabach et al., 2017). However, these actions rely on a definition of abstraction as “vertical mathematization,” which may not be true in a different domain, such as physical chemistry.
In order to characterize abstraction in physical chemistry, the goal of this study is to identify the types of epistemic actions students take that give meaning to or extract meaning from objects in the problem space—that is, the epistemic actions that constitute abstraction in physical chemistry problem solving.
Abstractness as a function of the problem space (the context)
The conditions under which an activity occurs guide the specifics of the activity. For this study, the condition is problem solving during teaching interviews. In problem solving, part of what determines the knowledge that is relevant to use in a given situation and what path the problem solver may take is the problem space. The problem space is defined by how the problem solver interprets the task that is being given to them (Bodner and McMillen, 1986; Reimann and Chi, 1989; Jonassen, 2010).For example, a student in physical chemistry may be tasked with solving a problem that requires calculating the entropy of a system based on the possible orientations of the molecule (e.g., that relies on a statistical mechanical view of entropy). This student may cue on the notion of “entropy” and try to apply the Second Law to calculate an entropy change (e.g., an approach that utilizes a thermodynamic view of entropy), because that is the type of entropy problem they are most familiar with. If the student cues on the idea of possible orientations and probability, they may use the Boltzmann equation. This initial view of the problem and the prior knowledge cued change the pieces of information that the student cues on (Chi et al., 1981), as well as the subsequent actions the student takes toward solving the problem.
Abstractness (a quality that describes how removed something is from the context at hand) has been previously related to the idea of problem space. In this view, something in problem solving is more or less abstract relative to the knowledge cued as relevant to the problem solver. The further removed from the initial problem space, the more abstract it is. For example, Domin and Bodner (2012) used this definition to investigate the abstractness of mental representations in graduate organic problem solving. They considered a mental representation to be more abstract when it was more strongly associated with the prior knowledge the learner had that was not directly relevant to the problem context. This suggests that what is abstract during problem solving depends on how the problem solver interprets the problem. Going back to the physical chemistry example, this means that for the thermodynamics student, it would be abstract to think about entropy as being related to microstates, because that is not how they interpret the problem. For the statistical mechanics student, it would be abstract to think about entropy as being related to the heat transfer of a system.
Epistemic actions and abstractness
To bridge activity theory and the idea of problem space, we consider that the problem task is part of what defines the current sociocultural context. The problem task, which is the problem as it is written, will be interpreted by students according to their mental tools, what they have previously learned in their courses, and their personal histories. This interpretation of the problem as written is what we call the problem space. We assume that the problem space prescribes the actions a student takes during problem solving, and not just the knowledge that is relevant to solving the problem. That is, some actions may be cued by the problem space (less abstract), whereas others may be drawn from previous experiences initially considered irrelevant to the task at hand (more abstract). That is, we assume that epistemic actions have the characteristic of abstractness. We thus looked for actions using the follow definition, revised from Domin and Bodner (2012): “Abstractness reflects the degree to which students’ actions rely primarily on the representations and paths explicitly cued by the problem space.” That is, actions are more abstract if the student does something that is not explicitly cued by the problem space, and less abstract if the student seems to be following a prescribed path. This definition guided our development of the conceptual framework. Table 1 provides an overview of the key terms in the framework.| Important theoretical terms | Definition used in this study |
|---|---|
| Object | Something a learner can perform transformations on (e.g., an equation) |
| Problem space | How a problem solver understands what a problem is about (their mental representation of the problem and the allowable problem solving paths) |
| Abstractness | The degree to which students’ actions rely primarily on the representations and paths explicitly cued by the problem space |
| Abstraction | The process of extracting meaning from and giving meaning to an object |
| Epistemic action | Goal-mediated mental action |
Methods
This study aimed to develop a conceptual framework to operationalize abstraction in physical chemistry problem solving. We began with the initial definition that abstraction is the construction of knowledge through the connection of ideas from different sources (Scheiner, 2016), and designed data collection procedures that may emerge abstraction. Through iterative data analysis procedures, we tested and refined this preliminary definition, until we arrived at a domain-specific definition of abstraction and an operationalization that could be used to make abstraction in physical chemistry visible. In this section, we describe data collection and data analysis procedures that were used to develop the conceptual framework.Design of interviews
Examples of abstraction in action are necessary to characterize abstraction as an activity. Consequently, we designed the interview situation to facilitate the emergence of abstraction and to promote the student framing the interview as a sense-making interaction (Russ et al., 2012), and drew on literature that studied abstraction in other fields to identify three design features.First, participants were invited to participate in teaching interviews (Kapon and diSessa, 2012). Teaching interviews have been used in studies of abstraction (Hershkowitz et al., 2001), because they allow the interviewer to probe deeply what a participant is thinking, and to scaffold connections participants are capable of making but may not immediately notice (Broman et al., 2018; Caspari and Graulich, 2019). This facilitated observation of the co-construction of knowledge during problem solving and the emergence of abstraction through this process.
Second, the problems participants solved consisted of seemingly disparate parts that had to be pieced together conceptually for participants to succeed in solving the problems. Although several expert solutions to the problem exist, participants generally did not have the prior knowledge to be able to access these solutions (e.g., the experience with ordinary differential equations to recognize the inflection point or the experience with autocatalysis to quickly map the problem to a two-step reaction). That is, there is a gap between the solution state, and the students’ most likely problem space. To bridge these two, the student would be expected to abstract. The problems used related to the course content the participants were learning at the time, but were multi-disciplinary and covered content beyond the scope of what students had covered in the course so far, so participants could not rely on memorized procedures to solve the problem.
Finally, we conducted both pair and individual interviews, because literature suggests that students working in pairs may solve problems at a higher level of abstractness than they do working alone (Schwartz, 1995; Dreyfus et al., 2001). However, we also wanted to collect data about how students solve problems alone, as this better resembles how students solve problems in physical chemistry classrooms. To ensure that all participants were interviewed both individually and in a pair, two rounds of data were collected at different points in the semester.
The first round of interviews served as a pilot for the teaching interview approach, in order to better understand how to facilitate the emergence of abstraction during an interview context. During the interviews, the first author noticed that certain aspects of the design constrained abstraction: for example, providing the participants an equation sheet, the phrasing of certain probing questions, and the nature of the problem. These insights guided the second round of interviewing, resulting in data that were richer and thus more fruitful for theory building. These data (from the kinetics interview) were the primary source of data for developing the epistemic actions framework, and data collected during the first round were used to validate the applicability of the framework to data beyond those from which the theory was developed.
Interview task
The interview instruments were taken from the course textbook (Atkins and de Paula, 2014). In the entropy problem, participants were asked to solve for the residual entropy of a DNA molecule, in which the order of the binucleotides was random and they were given the length of the DNA ladder. In the kinetics problem, participants were given the rates of change of 3 populations (susceptibles, infectives, and removed class) and tasked with finding the ratio a/r that controlled the disease spread. The problem was based on the epidemiological SIR model, which models disease spread in a constant population as a set of 3 coupled differential equations that depend on the effective transmission rate (r) and the removal rate (a) (Kermack et al., 1927).Although the problems were close-ended (there is one correct answer), there were multiple possible ways to solve the problem (see Appendix 1 for full problem texts and discussions of possible solutions). At the time the interviews were conducted, participants had just begun learning about entropy (round 1) and about chemical kinetics (round 2) in their physical chemistry course. They were expected to be able to recognize that dx/dt represented the change in x over time (e.g., a rate) and to have used this formalism in the context of chemical kinetics. Participants were not necessarily familiar with the SIR model beforehand, and were not expected to have taken an ordinary differential equations course.
Data collection
Upper-level undergraduates were recruited with IRB approval from a physical chemistry (thermodynamics and kinetics) course in Spring 2018 at a highly diverse public institution in the Northeastern United States (IRB # 2013-010). With the professor's permission, participants were offered 10 extra credit points as a token of appreciation for participation (equivalent to one homework assignment). To assign pairs, the 18 study participants were asked to identify classmates with whom they would feel comfortable working (n pairs = 9). Participants were interviewed twice, once during the unit on entropy (in early part of semester) and once during the unit on chemical kinetics (near the end of the semester). They were randomly assigned to participate in one interview individually and in one as a pair, such that there were an equal number of participants interviewing as pairs and individuals each round (26 total interviews). Participants used a LiveScribe pen; in pair interviews, participants were asked to share a pen and pad of paper as they solve the problem. They were audio-recorded as they solved the problems, and encouraged to talk through their solution aloud. The first author conducted the interviews, and took informal field notes on salient gestures or interpersonal dynamics that emerged during the problem solving that would not be captured by the audio recordings.Informed grounded theory approach
To develop our conceptual framework, the theoretical foundations of which are described above and the specific operationalization of which is described below in the results, principles of informed grounded theory guided our approach (Thornberg, 2012). Classic grounded theory is a purely inductive endeavor, drawing conclusions and developing theory from data, and using strategies like theoretical sampling to collect more data to explore emergent phenomenon (Glaser and Strauss, 1967). Recent ground theory scholars have pointed out the limitations of this method, such as the fact that it is impossible, and perhaps even undesirable, for researchers to be theoretical blank slates (e.g., Charmaz, 2006). Informed grounded theory, developed from this new constructivist grounded theory tradition, instead draws on an abductive methodological approach. In abduction, hypotheses are adopted as the best understanding of a phenomenon at the time, and are then tested, and refined or transformed through an ideological interrogation (Schurz, 2008; Douven, 2011). Similar to the classic grounded theory approach, informed grounded theory seeks to generate theory from data. However, informed grounded theory includes a dialogue with the literature as a part of this methodology.To remain grounded in data and not fall into the trap of deductive research and prejudiced interpretations, Thornberg (2012) suggests three data sensitizing principles that have been used by other ground theorists: theoretical agnosticism, which involves the researcher taking a critical stance toward theoretical positions and gaps found in the literature, and treating all extant theories as modifiable; theoretical pluralism, which involves the research being flexible in which extant theories may be applicable to their data; and theoretical sampling of the literature, which involves the researcher deliberately seeking out new literature based on their emergent theories. In this study, we adopted the theoretical agnostic and theoretical sampling approaches. We remained open to the notion that any prior work on abstraction could be relevant to our emergent theory (theoretical agnosticism), and as the conceptual structure of our theory on abstraction developed, we deliberately sought out literature that could deepen our emergent understandings (theoretical sampling).
Two other activities of informed grounded theory were particularly relevant to the study at hand: memoing extant knowledge associations and constant reflexivity (Thornberg, 2012). Theoretical and analytical memos were used extensively throughout our project. Memos are “theoretical notes about the data and the conceptual connections between categories” (Glaser and Holton, 2004, para. 61), and they both help the researcher capture and track how the theory is emerging, as well as act as analytical tools to make sense of those conceptual connections. Constant reflexivity involves the researcher confronting their own biases, assumptions, and theoretical lenses throughout the project. In this study, constant reflexivity was vital to interrogate and challenge how prior beliefs about abstraction biased our interpretation of the data.
Although we largely took an informed grounded theory approach, this work builds upon a deductive study (Sevian et al., 2015). True to the abductive process, we began with a “best hypothesis” that abstraction is a process of representation mapping (Hahn and Chater, 1998; Weinrich and Sevian, 2017), and applied this approach to an already collected set of physical chemistry problem solving data (Sevian et al., 2015). When the representation mapping approach did not account for or capture emergent characteristics of abstraction that seemed specific to physical chemistry, we collected the data reported in the study at hand using a method designed to emerge abstraction. The process we describe in the next section is the abductive analysis approach we took through theoretical sampling of literature to generate and refine our construct of abstraction in physical chemistry.
Development of the conceptual framework
Data analysis was carried out in multiple stages (see Fig. 1). First, each transcript was read through in its entirety while listening to the audio and looking at the written student work, to capture intonation and written referents. Our first idea about abstraction was that it involved how students made sense of a task at hand. To capture this idea, a representation mapping framework was applied (Hahn and Chater, 1998; Sevian et al., 2015) to identify participants’ new instance representations (how they interpret the problem task and combine their stored knowledge with the problem text) and use of stored knowledge. However, it became clear that these chunked pieces of knowledge did not capture how ideas built on each other, connected, and changed over time, which seemed to be important aspects of our emergent ideas around abstraction. To capture this dynamic piece, a narrative summary was written of participants’ problem solving, and then insights from this narrative summary were used to segment each transcript into 5–10 turn long chunks, in which a coherent idea was being developed or a particular strategy was used. These early chunks provided the basis of the grain size for what was ultimately operationalized as an epistemic action. | ||
| Fig. 1 Overview of the constant comparative analytic process used to develop the epistemic actions framework. | ||
These smaller coherent chunks were used to develop modified concept maps, which allowed us to visualize the connections participants made to advance their ideas forward (see Appendix 2). These concept maps were constructed using CmapTools (Cañas et al., 2004) and explored the idea that abstraction was about the connection of ideas. Each node in the concept map consists of a coherent idea identified by the representation mapping (Hahn and Chater, 1998), and how the participant seemed to be connecting them in their problem solving (Novak and Cañas, 2006). This way of organizing the data led to two important and data-driven insights: first, abstraction seemed to be related to how a learner used transformed ideas over the course of problem solving. Second, abstraction seemed to be related to how students drew on and coordinated knowledge from different knowledge sources, e.g., mathematical or chemical knowledge. These insights led to sampling from literature that theorizes abstraction as connection (e.g., Scheiner, 2016).
Triangulating the narrative analysis with the concept map analysis led to an initial set of codes for the actions. From the concept maps, we saw that there were typical ways students combined ideas to move forward in problem solving, and that these related to the “coherent strategy” chunks identified in the narrative analysis. Operationalizing this unit of analysis as “action,” we turned to the literature again to make sense of what these actions could be. Specifically, we drew on two previously developed frameworks that capture the epistemic actions of abstraction (Hershkowitz et al., 2001) and levels of abstraction for chemistry knowledge (Santos and Mortimer, 2019) to try to differentiate the action types. When developing these initial codes, we centered what was happening in the data, and used the literature constructs as a lens to interpret the data-driven phenomenon, rather than trying to strictly map concepts. The preliminary codes for the actions were concretization (reframing the problem to make it more concrete), manipulation (manipulating variables without moving beyond bounds of the problem), interpretation (interpreting information given in problem with information outside of problem space), mapping (restructuring information in a novel way that moves beyond specific problem space), and construction (constructing generalized principle or knowledge).
Combining these two approaches helped to flesh out the definition of action, because the concept map made it clear how the students connected and developed ideas over multiple steps. Common patterns were identified in how connections were being made, which became the basis of the 4 types of actions: concretizing, manipulating, restructuring, and generalizing (see Fig. 2).
 | ||
| Fig. 2 Schema of the four actions, (a) concretizing, (b) manipulating, (c) restructuring, and (d) generalizing. | ||
Drawing on the concept of theoretical sampling, four transcripts in the kinetics dataset were identified that were the strongest examples of these initial definitions of the actions. Each of these transcripts were used to develop an exemplar of each of these actions with initial definitions. Then, these actions were used to code the rest of the kinetics data, which served to refine the definitions of the actions. One major outcome of this refinement process was the characterization of two types of actions based on the type of knowledge source: conceptual (in which the action was operating on meanings and conceptual ideas) and symbolic (in which the action was operating on symbols or mathematics). The refined actions framework was then used to analyze all of the entropy data. Analyzing the entropy data served to validate that the framework could be used to analyze problem solving that involved a different content area (thermodynamics rather than kinetics).
The analysis and development process was iterative; through each stage of analysis, theoretical notions of abstraction were refined and tested. At each stage, we also theoretically sampled the literature to check how our developing understanding aligned with previously published works, and to see how those works further refined our emerging definitions and codebook (Thornberg, 2012). This process ended once we had developed a codebook (the actions) that could be reliably applied to the data, and developed a working definition of abstraction that captured both these data-driven insights and insights from literature (see Fig. 1 for an overview of this process), and that generated a theory that explained the structure of abstraction as a concept.
Reliability
Each iteration of data analysis was staged by inter-rater reliability processes with researchers outside of the authors. At each stage of developing an operational definition of abstraction and integrating a new stage of analysis, the first author met with a group of 8–10 researchers and discussed the interpretation of the data and the alignment of the analysis to theory. These discussions and feedback were incorporated into the evolving framework. These reliability measures enabled us to develop construct validity via consistent operationalization of the analysis (Dalgety et al., 2003).After developing a finalized version of the framework, inter-rater reliability was conducted. An external researcher coded 20% of the data (both kinetics and thermodynamics data) using the finalized codebook, and she and the first author discussed their coding until they reached 100% agreement.
Results
Through this constant comparison approach and codebook refinement, we identified 8 epistemic actions that students took while solving a problem related to kinetics and to entropy (see Table 2 for an overview). These actions could be distinguished by common patterns in how representations in problem solving were connected in the concept maps (see Fig. 2). Because the kinetics interviews were used to develop the actions, exemplars are primarily shown from that subset of the data.| Symbol | Action | Description |
|---|---|---|
|
Symbolic concretizing | Putting a mathematical constraint on the problem space |
|
Conceptual concretizing | Putting a conceptual constraint on the problem space |
|
Symbolic manipulation | Advancing toward a solution/understanding by working with math or variables in a procedural way |
|
Conceptual manipulation | Advancing toward a solution/understanding by thinking through meanings and connections between conceptual aspects in a procedural way |
|
Symbolic restructuring | Transforming mathematical relationships to represent something that they were familiar with from another context, applying those constraints and meanings (focuses on changing the representation and mathematical relationships) |
|
Conceptual restructuring | Reimagining the meaning of the mathematics or the concepts, which transforms the relationship between math and the variables (focuses on changing the meaning and conceptual underpinnings) |
|
Symbolic generalization | Connecting ideas and meanings to produce new mathematical relationships within the problem space |
|
Conceptual generalization | Connecting ideas and meanings to develop a new concept/idea within the problem space |
The results section is organized into two parts. First, we will describe the 8 actions in detail and illustrate each one with an example from student data. Then, we will describe how the actions were used to operationalize two forms of abstraction: vertical and horizontal abstraction. Using a student vignette, we will illustrate the power of the epistemic actions framework to analyze student problem solving.
Actions
8 actions were identified based on two dimensions: the abstractness of the action (vertical dimension) and the type of resources the actions related to (horizontal dimension). Abstractness was operationalized as the extent to which the action transformed the problem space by utilizing resources that were not within the students’ initial representation of the problem.In the vertical dimension (abstractness of the action), we identified 4 types of action: concretizing (making the problem space more concrete by constraining it), manipulating (performing procedural changes within the problem space), restructuring (transforming the problem space by integrating other forms of knowledge), and generalizing (generating a new representation or relationship in the problem space) (Karch and Sevian, 2020). Compared to the initial abstractness of the problem space, restructuring and generalizing were considered to be actions that made the problem space more abstract. In a restructuring move, a student uses prior knowledge to redefine the constraints of the problem space—that is, they abstract away from the problem space to generate a transformed problem space. In generalizing, the student draws on sense making done during the problem solving as well as prior knowledge to generate a new understanding—that is, they abstract a new relationship. Manipulating is at the same level of abstractness, because the student follows the procedures and problem solving paths dictated by the problem space at hand, and concretizing was a lower level of abstractness, because the student makes the problem space more concrete.
In the horizontal dimension (type of resource), we identified two types of resources: conceptual and symbolic. We characterized an action as conceptual or symbolic based on the object that the action was performed on; that is, if the action (e.g., a manipulating action) was being performed on a concept or meaning, such as a description of the infectives, it was characterized as a conceptual action. If it was performed on a symbolic or mathematical representation, such as an equation or a graph it was characterized as symbolic.
The n value listed with each action lists the number of participants who performed this epistemic action (see Table 3). These values are included to provide additional context about how often they occurred in the data; however, because actions are contextually dependent, we do not make generalized claims about the relationship between the frequency of actions and the nature of the actions in physical chemistry problem solving.
| Conceptual actions | Symbolic actions | |||||||
|---|---|---|---|---|---|---|---|---|
| # Occurrences | # Participants | # Occurrences | # Participants | |||||
| Kinetics | Entropy | Kinetics | Entropy | Kinetics | Entropy | Kinetics | Entropy | |
| Concretizing | 58 | 30 | 16 | 13 | 18 | 5 | 7 | 4 |
| Manipulating | 73 | 79 | 16 | 16 | 62 | 53 | 17 | 14 |
| Restructuring | 24 | 29 | 14 | 16 | 13 | 3 | 9 | 3 |
| Generalizing | 10 | 2 | 6 | 3 | 1 | 0 | 1 | 0 |
Symbolic concretizing: in symbolic concretizing, a constraint was put on the problem by assigning a mathematical value to the variables, which allowed the participants to work with numbers rather than the variables in the abstract. In the kinetics problem, no values were provided in the problem. Students who symbolically concretized had to invent a situation that would allow them to assign numerical meanings to the values. A pair of participants, Akeyo and Jamila, invented a hypothetical population in which the disease spread was occurring:
Interviewer: And so how does what you just came up with relate to whether the disease will spread or die out?.
Jamila: That's a good question.
Akeyo: So since we just said that r, the constant, is depending on the number of people were infective. So [[10s]] if you plug in like random numbers. So if you said that S is 5 and I is 10, that's 50, negative 2. Negative 100. It can’t be negative 100 people. [[7s]] So let's say in a population we have 300 people.
Jamila: How will you know if a disease will die out?.
Akeyo: No, but see, if you think about it—Let's say if the city has like 300 people, right?.
Jamila: Hmm hmm.
Akeyo: You say 25 are—
Jamila: Susceptible.
Akeyo: I can’t say that word. And then—
Jamila: Ten are infected or something.
Akeyo: Okay, 10, 11, 25. And then 250. That's the only way I can do that math. 250 are, yeah, removed, isolated, and whatever. Right?.
In this excerpt, Akeyo and Jamila had been struggling to make sense of the problem after an extended period of unproductive mathematical manipulation they called “magic math,” in which they had set up differential expressions for the two parameters, a and r. The interviewer asked them to elaborate on how their mathematical solution related to the original problem task of determining the spread and decline of the disease, which they struggled to answer. Connecting their work back to the idea of disease spread cued them to reframe the variables more specifically as representing populations. They concretized the problem by inventing a real-world situation with numbers they could work with, rather than trying to make sense of the variables in the abstract. Akeyo suggested a hypothetical situation where the populations belonged to a city with a specific number of people, and assigned numbers to each of the three populations. Using these numbers, they could modulate how the populations were changing according to the rate equations given in the problem. By symbolically concretizing, they put constraints on the problem space that allowed them to think productively about what the equations represented (e.g., the change in numbers of people in a disease event).
Conceptually concretizing: conceptual concretizing, similar to symbolic concretizing, resulted in the students putting more constraints around the problem space. A common example of conceptual concretizing was when participants defined or assigned a meaning to a particular variable, and then using that definition or meaning to make sense of the problem. For example, when Philip tried to make sense of the problem task, he first tried to define the parameters a and r:
Philip: So I’m not exactly sure. The whole thing is a. The a is what's getting me stuck. Cause I would say it's the amount of people, but that wouldn’t make sense because then there wouldn’t be any susceptibles.
Interviewer: Where do you notice a on these equations?.
Philip: So it's only for the infective and the removed class. So it's people that can actually be infected. Oh, wait, susceptible, sorry, they catch the disease. So it's people who have the disease and/or have recovered, died, immune, or isolated. So a equals have disease. Okay.
One aspect of the problem prompt was to figure out a potential meaning for a and r. Philip had previously defined t as time and r as rate, and was trying to make sense of what a could mean in the context of the problem. This action is a concretizing move, because he used those definitions as constraints to facilitate further sense making and had not arrived to them through any incorporation of outside knowledge.
Symbolic manipulation: symbolic manipulation, or mathematical manipulation, occurred when students moved and worked with variables in procedural ways. Students used a range of manipulation strategies: rearranging the equations to solve for a and r separately then dividing to return the ratio, integrating the differential equations, taking the derivative of the equations, and a substitution strategy. A key aspect of manipulation was that it involved the resources and symbols that were explicit in the problem space—both what was explicit in the text (e.g., the equations) and what was cued by the participant's framing of the problem space.
Chao: I thought about first that, if we want to calculate a divided by r, it should be something related with a and r, right? So here has an r, here has an a. I tried to just substitute to this equation, because this, you can, is an r and a. But what I substituted is only can [?] an issue with R and an I, like here, I, it's only R, S, and I. It's not a and r. So, but if I try to substitute again, it will be back. It will be back to here, and not meaning anything. Meaningless. So maybe some some some things I didn’t find out from these questions. But.
In this example, Chao had noticed that dS/dt and dR/dt could be substituted into the dI/dt equation. His goal had been to manipulate the equations to try to algebraically solve for the ratio a/r, but his substitution strategy meant that the resultant equation did not include a or r, which were required by the problem as written (see Fig. 3 for student work). Here, he applied several algebraic strategies (substitution, division) to transform the equations in a procedural way.
 | ||
| Fig. 3 Chao's (partial) written work during the kinetics problem. | ||
Because the problem space is a result of how the student interprets the problem, manipulating actions may vary in how mathematically complex they are. For example, some students cued on the partial derivatives and tried to apply calculus techniques (integration or derivation), whereas others noticed that the equations could be substituted for each other (e.g., Chao), whereas still others tried to algebraically isolate a and r.
Conceptual manipulation: conceptual manipulation involved participants focusing on the concepts or meanings of representations explicit in the problem space; for example, the definitions of S, I, and R as susceptibles, infectives or removed class. When a participant conceptually manipulated, they advanced toward a solution state by reasoning through the meanings of conceptual aspects of the problem in a procedural way. One common way this manifested was by participants substituting the meanings of variables in for the symbol, and talking through the mathematical transformation aloud. Another way this emerged is illustrated by this example from the entropy interview. Alex is trying to figure out how the different parts of the problem text (the length of the DNA, the idea of entropy, and the idea of DNA) connect:
Alex: Yeah. but I know that, I know that, I don't know if this is the rungs or whatever, so I know that A binds with T but the T binds with A, but the order, I'm not sure if it has to do with stability.
Interviewer: Mmm
Alex: So let's say we have AT next to a GC, it might not have to do with stability, but if you're saying randomizing and it still has its double helix shape and stuff like that and it still has its double helix structure, this might not apply. But if it's randomized and it has something to do with stability and it has an effect on the stability of the DNA structure, it might have associated with the residual entropy.
Here Alex is trying to reason through how all of these aspects are connected. Each of the ideas he brings up (e.g., “AT”, “CG”, “stability”, “order”) are ideas he had already introduced to the problem space. He is trying to figure out how they connect to each other, but is not doing so through the framework of some prior piece of knowledge. Instead, it seems to be a sort of one-to-one mapping: reasoning through how random connects to stability and to helix. This kind of reasoning was considered to be conceptual manipulation, because the participant is taking the concepts in the problem space and trying to manipulate them to figure out what they mean in terms of each other. However, it is “procedural” because it is not introducing new meaning or constraints.
Symbolic restructuring: when a participant symbolically restructured, they transformed the equations to represent something that they were familiar with from another context, usually changing it mathematically. For example, when Philip tried to find the ratio a/r, he developed a strategy to solve for da/dr:
Philip: So I think would be da over dr.
Interviewer: Okay. Why do you think that? What made you think of that?.
Philip: Um, because the um, you’d have to take the derivative of it, I think. I’m not sure. It's just kind of a little guess to try to get me thinking as to how I can figure that out. But that means—But they’re all for dt. So you’d have to have this equal to something. You’d have to, so you’d have to take the derivative of like say that, but you want it in terms of r, little r. So let me see. So this is off of a wing.
[…]
Philip: So I decided to differentiate it because it made me think of like the Maxwell equations for p-chem. It made me think of how you have formulas that you can, you can make them, you can change them after you differentiate them, because then you can pretty much combine like terms that aren’t pretty much defined as like correlating. You can kind of like, like with Maxwell equations, it's like, I can’t think of one off the top of my head,
but it's one that equals another, and then if you’re, if you find one of them inside an equation, you then know if you have to get it in specific terms of say N or G or pressure or temperature, you then know you can plug that in to be able to figure it out to find out the answer, like the, yeah, the fundamental equations.
In this example, Philip cued on two aspects of the problem that invoked a similarity to Maxwell relations: the need to “combine terms that aren’t pretty much defined as like correlating,” and the presence of differential expressions. Maxwell relations are the set of derived partial differential expressions that relate the 4 thermodynamic potentials (internal energy, Helmholtz energy, enthalpy, and Gibbs’ free energy) with mechanical and thermal variables like pressure and entropy. Earlier in the semester, the course instructor had introduced Maxwell's relations as the “fundamental equations,” which could allow the students to make relationships between different thermodynamic variables. Here, Philip restructured the equations symbolically by using the chain rule to differentiate the expression by d/dr.
By cueing on the familiar feature of derivatives, Philip moved away from the problem space to reason about Maxwell's relations, and then restructured the problem space to be one that could be solved using the “Maxwell relations” approach (see Fig. 4 for student work). This changed the possible actions Philip could take to include taking the derivative of a and r. It also transformed the relationship the variables had with each other to be “uncorrelated things that could be correlated.”
 | ||
| Fig. 4 Philip's (partial) written work during the kinetics problem. | ||
Conceptual restructuring: in contrast to symbolic restructuring, which involved changing the mathematical relationships the variables had to each other, conceptual restructuring integrated prior knowledge to transform the meanings of the variables in the problem. Unlike conceptual concretizing, in which a meaning was assigned to a variable as a way to concretize the problem space, conceptually restructuring resulted in reimagining the meaning of the mathematics, which transformed the relationship between the math and the variables it stood for.
The interview task had a biological context (disease spread) and many of the participants were biology or biochemistry majors, which may explain why conceptual restructuring in this dataset tended to occur when participants integrated formal biological and biochemical knowledge to make sense of the relationships between an epidemic and the equations. For example, one participant struggled to understand what the equations meant, and conceptualized the meaning of the equations to be that they each represented the number of the populations (that dS/dt, dI/dt, and dR/dt were conceptually equivalent to S, I, and R). However, he soon expressed that he was stuck and did not know how to move forward with the problem. The interviewer and participant spent several minutes discussing what the participant, a biochemistry major, knew about disease spread, before the interviewer asked him to bridge these two aspects (their biological knowledge and the model in the problem), to try to elicit abstraction:
Interviewer: Okay. So if we think about that in terms of these three classes of people, how do those two models work together? So not necessarily thinking about the math, but just thinking about infected people, people who can catch it and people who can’t catch it. How does that work with this model of disease spread that you were just telling me about?.
Joshua: Well susceptible people have a higher chance of getting the disease, so it would require like less transmission to get to them, I guess, than an average person, it would require more interactions with people who are infected, so I guess that's why it's infected people times the—Well I guess, you know what? The derivative doesn’t necessarily mean like that, like S doesn’t have to equal—dS over dt doesn’t have to equal like S. So it's like the number of susceptible people times the number of infected people. So this ratio actually could be the number of people, number, the increasing number of people becoming, or reducing the number of people becoming less susceptible, because, like what am I saying? So susceptible people times infected people times a variable that's negative. So it's reducing the susceptibili-, the number of people being susceptible over time is decreasing, because of the negative number, I think, just because they’re becoming infected as the number of people that are infected increase. There are like the higher chance that they can be—I guess, the transmission can happen. I don’t know.
Prompted by the question from the interviewer, Joshua moved away from the problem space to think about how disease spread occurs in general in terms of transmission and contact. He then applied this understanding back to the problem space to restructure and reinterpret the conceptual meanings of the derivatives as representing this new idea of transmission over time. Although this understanding is closer to the canonical interpretation of the equations, this was a restructuring move for Joshua, because he had previously defined the rate equations as equivalent to the population variables.
Symbolic generalization: symbolic generalizing actions result in the generation of a mathematical or representational relationship that was more abstract than the problem space and that could not be accessed through manipulating without integrating prior knowledge beyond what was cued in the problem space. Symbolic generalization occurred infrequently in our dataset. During a pair interview, one participant (Hoa) engaged in symbolic generalization when she proposed an inequality to model the relationship between a and r. Prior to this point in the problem solving, the pair had gone through two concretizing cycles, in which they plugged in different numbers for the three rates, and looked at how these changed the relationships between the three rate equations. They found that the sign of dI/dt depended on whether dR/dt or dS/dt was larger, and were trying to make sense of this finding:
Avni: I think that makes more sense, because the disease will spread less, and more people, I mean less people will be affected by it, and maybe like people over here, they already had the immunity when the disease is like spreading. They are making their immunity in their body.
Interviewer: Okay. That could definitely be what's happening.
Hoa: So like it's telling us what condition. So I think it really depends on rSI, I guess, because if you look at this—[[10]] Because if rSI is greater than aI, which is right here, that means that the rate is larger. What does it mean when the rate is larger?.
Avni: That it will spread more.
Hoa: Spread more? Do you think that's right? Do you think that's a good statement? ((directed toward her partner)) And then rSI is less. This is 2, and 1. This is 1 right here. Do you get what I’m saying or no? So this will die out. What do you think? I guess this is the condition. What do you think?.
Avni: So in order to be, in order to increase this one—
Hoa: Yeah, so this one would be like 3, and then this would like 1, so rSI is greater.
In this example, Hoa and Avni connected their conceptual reasoning to the mathematical formalism of a negative or positive rate. They figured out that the rate of change of the infectives determined whether the disease spread. They then realized that the sign of the rate of change of the infectives was influenced by whether the rate of change of the susceptibles or of the infectives was higher. This allowed them to perform a symbolic generalization move and abstracted away from their concrete examples to set up two inequalities: that rSI > aI when the disease is spreading, and rSI < aI when the disease is dying out.
It is important to note that the interviewer utterance (“That could definitely be what's happening”) was a deliberate move as part of the teaching interview design, as the goal of the interviewer was to support the emergence of abstraction, not to probe how participants solve problems without interference. The influence of interviewer interventions will be investigated more deeply in future works.
Conceptual generalization: conceptual generalization moves resulted in defining an idea that emerged from the problem space but can be viewed as separate from (more general than) the problem space. For example, a conceptual generalization move may result in extracting the idea of independent parameters from the data, or making a generalization about disease spread that emerged from examining the rate laws. Conceptual generalization had a fairly low frequency in our findings. One participant who engaged in conceptual generalization tried to make sense of the meanings of the parameters a and r. This moment occurred at the end of the interview, after he had spent a considerable amount of time conceptually and symbolically manipulating the equations:
Chao: a and r, mmm, by the time [you released]. It maybe means—Ah, and also. Hey maybe it's only the constant, how the, how new things can, how stable for these things catch disease, because it's relatable if it's remove and catch, right? And the R should be the [?] of disease, and this one also how catch it, and, I don’t know. R is too complex.
Interviewer: I actually don’t know what a and r are, so that's—
Chao: Okay, so I thought—
Interviewer: It's definitely what your thoughts are.
Chao: I don’t know.
Interviewer: But you think that r has something to do with how people catch the disease?.
Chao: No no, I said a. a is how stable, how stable the things catch disease, catch some things, because if it's relatable, it's catch, and is remove, right? This means, where maybe a is less, it's easy to remove. When a is high, it's hard to remove.
Here, Chao is trying to figure out the meanings of a and r. Unlike the participants who assigned meanings to a and r in order to reduce the concreteness of the problem space, Chao is trying to coordinate different lines of reasoning about the mathematical nature of the parameters (“constant”) and prior reasoning about how the disease progresses to figure out what the variables may stand for. That is, Chao was trying to pull meaning out of the problem, rather than imposing meaning on it (a conceptual concretizing move).
Vertical and horizontal abstraction
Coding for actions based on the relationship of the objects to the problem space and the types of knowledge being leveraged allowed us to see how the problem solving was progressing from moment to moment. However, according to Activity Theory, an activity is a sequence of several actions; thus, to define abstraction, we needed to look at how actions worked together during problem solving. As shown in Fig. 5, we characterized two types of abstraction activities based on the two dimensions of the epistemic actions (abstractness and conceptual-symbolic). | ||
| Fig. 5 Depiction of vertical and horizontal abstraction. Figure shows how actions move between objects and frameworks, and how actions are related to the two forms of abstraction (vertical and horizontal). | ||
The first type is horizontal abstraction, in which participants move between symbolic and conceptual forms of an action at the same level of abstractness (e.g., symbolically and then conceptually manipulating). When horizontal abstracting, a learner gives meaning to or extracts meaning from an object by navigating between a conceptual and symbolic understanding of the same object (e.g., a particular equation). This is horizontal because the learner stays at the same level of abstractness with reference to the problem space (e.g., conceptual followed by symbolic concretizing). It is abstraction because the learner moves between sources of knowledge to make sense of and give meaning to an object—e.g., the learner is abstracting away from one context (the mathematics) to give meaning to the object in another context (the conceptual meaning).
The second type of abstraction activity is vertical abstraction, in which participants move between actions at different levels of abstractness. Vertical abstraction involves participants taking actions in problem solving that moved them between different levels of abstractness (e.g., manipulating to restructuring). Similar to vertical mathematization (van den Heuvel-Panhuizen, 2003), vertical abstraction is the process of reorganizing conceptual or mathematical knowledge within the problem space to create new relationships. Following our definition of abstraction, vertical abstraction can be a process of giving meaning to or extracting meaning from an object in the problem space. For example, when a problem solver restructures the problem space, they change the relationships between the objects in the problem space by recontextualizing the problem within the meaning space of another piece of knowledge. This may give new meaning to one of the objects, such as an equation. When a problem solver generalizes, they extract meaning by identifying and generating new relationships and objects. These processes are vertical, because the problem solver shifts the level of abstractness with reference to the problem space. They are abstraction because the learner moves away from the original problem space to make sense of the problem—e.g., the problem solver abstracts away from the context of disease spread (the initial problem space) to the context of chemical reactions (a restructuring move), which changes the problem space and the relationships between the variables.
To illustrate how the actions can be used to make abstraction in student problem solving visible, below we present an example in which both horizontal and vertical abstraction occur.
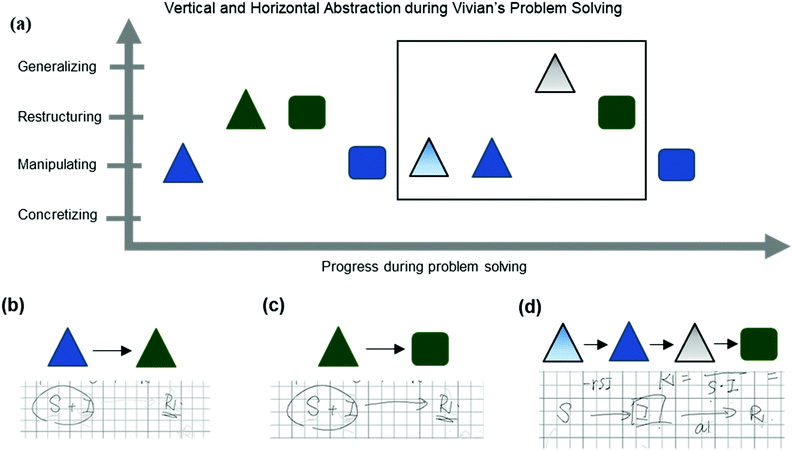
Illustrating how the actions can provide insight into problem solving
Coding for abstraction using the actions across a problem-solving episode can give insight into how a student navigates the use of resources drawn from different contexts as they make sense of the problem space. To illustrate this, a vignette of Vivian's problem solving is presented as an exemplar of how the actions can reveal both horizontal and vertical abstraction, and how horizontal and vertical abstraction can work in tandem as a participant refines their understanding of a problem over time (see Fig. 6). | ||
| Fig. 6 Epistemic actions and work during Vivian's kinetics problem solving. (a) Diagram shows how Vivian progressed in problem solving over several minutes. The section in the box represents the interviewer-scaffolded discussion, and icons with gradient fills are interviewer interventions. Triangles represent conceptual actions and squares represent symbolic actions. (b) Diagram shows how Vivian's representation of the relationship between the variables progressed through (b) vertical, (c) horizontal, and (d) diagonal abstraction. | ||
When Vivian tried to solve the kinetics problem, she initially took an arithmetic approach to solve for the ratio a/r. After a back and forth with the interviewer, she reasoned that the three populations are ratios themselves, and that S, I, and R are subsets of a constant population (an assumption that is embedded in the problem). She decided that to figure out S, I, and R, she needed to understand what the total population is, and performed several manipulating actions. However, these led her to a surprising result—when she added the three rate equations together to find the total population, she instead found that they sum to zero. This forced her to rethink her assumptions about what the equations represent, which led to a conceptual manipulation action in which she considered how the disease spread:
Vivian: 
So I think when the times goes by, they probably have least people they can catch of the disease, because they will be either already catch the disease, or they won’t do anything. So when we have more people catch the disease, the S should be decrease. I mean, for me it's r and a, one would be negative and one would be—no, wait.
This conceptual manipulation move solidified her understanding that the three variables (S, I, and R) represented different populations, and set her up for a conceptual restructuring move. She then vertically abstracted by changing the problem space to represent the population as having two groups (S + I and R). She used the different elements she brought into the problem space through her previous actions (a conceptual understanding of the problem and the idea of change over time) to reorganize the relationships to recognize that there was one total, unchanging population:
Vivian: 
Okay, probably what I’d do is plus I, and compare with R, because R is either people die or recover, and here is the people going to catch the disease. Or they can increase the number, and here would be decrease the number. So if I can compare the relationship between them, so I guess I can know what's happening there. [[long pause]] Yeah. I don’t really have any idea how to solve that.
Conceptually restructuring the three populations as two groups of people that change over time was followed by a symbolic restructuring move (horizontal abstraction), in which she represented the change over time as if it were a chemical reaction (see Fig. 6c):
Interviewer: Okay. So what were you just thinking about?.
Vivian: 
[[long pause, ∼30 s before adding arrow to relation written before]] [[long pause, ∼15 s]] I’m thinking these people, they can catch the disease, and these people, they have disease or they can transmit that. At the end, they will all end up with the R. So.
Interviewer: The disease totally spreads to the entire population, right?.
Vivian: 
Hmm hmm, so they will be all to the R or recover. They’ll also go to R. Then the rate law would be [long pause, ∼20 s], if we’re using the rate in chemistry. [[silence while writing]]
She then used her restructured problem space (S + I → R) and immediately tested it with a manipulating move, in which she tried to apply the equation for finding the rate constant of a chemical equation. Through a scaffolded discussion with the interviewer in which they conceptually manipulated to understand how the disease spread occurred, she revises her restructured problem space to be a two-step chemical equation through a symbolic restructuring move (see Fig. 6d):
Interviewer: Okay. So if the number of I is increasing, then the disease will spread.
Vivian: Yeah.
Interviewer: And what about if the number of I is decreasing?.
Vivian: 
I mean, they still have changed the spread out, but compared with I's larger [the] possible, it's less.
Interviewer: 
Okay. So then does the spread of the disease—In the spread of the disease, which of these three populations does it depend most on? Does it depend most on I, or does it also depend on the other two? In your opinion, from what you’ve been, how you think about the problem.
Vivian: 
Okay, right now I’m thinking, just as we say S, they can become an I, and I can become R. So I would be the intermediate.
Later in her problem solving, Vivian uses this two-step chemical reaction model to solve for a/r, by recognizing that a is a parameter that's related to the rate of change from I → R (step 2), and r is a parameter related to the rate of change from S → I (step 1). When she does this, it was coded as “manipulating.” Restructuring the relationships between the three populations shifted the scope of the problem space to be about a familiar problem type, the kinetics of two-step reactions, which she could solve using known procedures.
This example demonstrates three important features of abstraction. First, previous actions set the stage for abstracting moves e.g., the work she did to develop the initial relationship S + I → R was crucial for setting up the problem space to make S → I → R possible. Second, horizontal and vertical abstraction worked in tandem to shift and deepen her understanding of the problem space as she made sense of the problem. Third, she engaged in “diagonal” abstraction during the discussion with the interviewer. After she conceptually manipulates, the interviewer scaffolds through a conceptual generalizing action when she asks which population group the spread depends on the most. Vivian then directly shifts to a new symbolic restructuring move, shifting across different levels of vertical abstractness as well as shifting from conceptual to symbolic directly.
Discussion
Developing a disciplinary approach to operationalizing abstraction is key to understanding how students apply and appropriate knowledge during problem solving. In this study, we used an approach inspired by informed grounded theory to build from literature that studied abstraction in other domains (e.g., mathematics) to propose a set of epistemic actions in kinetics and thermodynamics problem solving. These actions led to two major outcomes. First, they provide a way to operationalize and identify abstraction processes during problem solving, adding a theoretical contribution to the literature that investigates abstraction, especially abstraction in context (e.g., Hershkowitz et al., 2001). Second, they led to the development of a framework that captures abstraction processes in physical chemistry specifically on two dimensions: horizontal abstraction and vertical abstraction (see Fig. 5).Abstraction in problem solving is contextual and dynamic
In developing this framework, we refined the definitions of abstractness and abstracting presented in previous work by this group (Sevian et al., 2015; Weinrich and Sevian, 2017). Weinrich and Sevian (2017) used representation mapping to operationalize abstractness (noun) as “the degree of abstraction (non-concrete references, additional symbol systems, or underlying relations) present in a way a person imagines a problem” (p. 171). In the study at hand, we refined this definition to specify that what is considered “non-concrete” depends on how the person imagines the problem. That is, abstract is considered relative to the problem space, rather than something that can be defined absolutely, i.e., we do not consider a piece of knowledge to be inherently abstract or inherently concrete. Shifting this definition of abstractness to be contextual and relative also required a shift in what it means to abstract (verb). Weinrich and Sevian (2017) defined abstracting on two dimensions: how strictly a problem solver matches their new instance and prior knowledge representations, and how abstract those representations are. This work builds on this definition to relate abstracting to (1) how a problem solver uses their prior knowledge to make sense of the problem at hand and (2) how their approaches relate to how they initially view the problem. This also represents a shift from abstraction as a static capacity dependent on internal representations, to abstraction as something contextually dependent and constituting dynamic actions. In other words, by relating abstraction to the problem space, we suggest that abstractness is both contextual to the problem space and dynamic as the problem space shifts.These two features (contextual and dynamic) have important implications for how we can study abstraction. First, if abstractness is contextual, what is abstract is determined by the context. Although our study primarily focused on how students leveraged prior knowledge, this definition opens up several possibilities to study the contextualized nature of abstraction from an explicitly sociocultural perspective (Hershkowitz et al., 2001). For example, later generations of activity theory describe activities as mediated by sociocultural elements of the activity system such as rules, division of labor, and community (Engeström, 1999). If we think of abstraction as contextually dependent, and can study the situated nature of it, this allows us to ask questions such as, “How do the rules of the classroom influence how, whether, and when students abstract in problem solving? How does the community change the actions students take toward abstraction?” In particular, previous studies have shown that group dynamics influence the nature of abstraction during problem solving (Schwartz, 1995; Dreyfus et al., 2001; Tabach et al., 2017). The epistemic actions framework provides a lens to understand how these dynamics are enacted and how they influence how abstraction is carried out in the moment.
Second, because abstractness is dynamic, the problem space can shift and be transformed throughout the course of problem solving. That is, what may be considered abstract at the beginning of problem solving may become concrete through the process of solving the problem, as the problem solver grapples with identifying relevant pieces of knowledge and resources and testing hypotheses. As these ideas become more concrete, they can be manipulated by the problem solver and leveraged for further meaning making. This is similar to the concept of consolidation proposed by Hershkowitz and colleagues (2007). In their model of Abstraction in Context, consolidation occurs after abstracting mathematical structures and is the process of a piece of knowledge becoming “progressively more readily available to the learner” (p. 45). In the epistemic actions framework, this consolidation process is enabled through the transformation of the problem solving space through moves like restructuring. Thus, the dynamic nature of abstraction as observed through the use of epistemic actions may give insight into how students consolidate and begin to construct knowledge during problem solving.
Abstraction in physical chemistry problem solving is domain-specific
The second major contribution of our work is a physical chemistry-specific conceptualization of abstraction, extending previous research that has examined the disciplinarily situated nature of abstractness in other domains, such as organic chemistry (Weinrich and Sevian, 2017). In particular, we observed that in our data, the ways in which students worked with and transformed conceptual pieces seemed distinct from how they worked with mathematical pieces, even when they used the same epistemic action, e.g., concretizing. Following our informed grounded theory approach, we made sense of this phenomenon through the lens of physical chemistry and mathematics education literature. Our observation was congruent with previous work suggesting that students often work with mathematical and conceptual objects in physical chemistry problem solving separately (Becker and Towns, 2012; Rodriguez et al., 2020). Drawing on realistic mathematics education, or RME, (van den Heuvel-Panhuizen, 2003), we generated the concepts of horizontal and vertical abstraction to capture movement among conceptual and symbolic objects.In mathematics education, vertical mathematization, i.e., the reorganization of mathematical structures, has often been equated to abstraction, as it captures how students recognize and generate mathematical structures (e.g., Hershkowitz et al., 2001). In our data, we found that concept salient to capture how students reorganized, appropriated, and constructed mathematical and conceptual knowledge structures through actions such as restructuring and generalizing. To conceptualize horizontal abstraction, this framework appropriates the RME concept of “horizontal mathematization” as how a learner navigates between symbolic and conceptual forms of knowledge. In mathematics education, horizontal mathematization generally refers to how a learner grounds a mathematical concept in real world phenomena. In other words, horizontal mathematization is a concretizing action. In physical chemistry, however, horizontal abstraction provides an additional mechanism to understand how the physical and mathematical interpretations of a concept can be navigated, which has been noted as a particular problem of practice in physical chemistry teaching and learning. (Becker and Towns, 2012, Bain et al., 2018; Rodriguez et al., 2020). In addition, horizontal abstraction can occur at multiple levels of abstractness, not just at the level of the concrete. Horizontal abstraction provides a framework to understand how students connect mathematical structures to their conceptual underpinnings. Thus, there is opportunity to understand at what level of abstractness these challenges to horizontal abstraction are particularly pressing and consequently how they can be overcome.
Ultimately, the power of the epistemic actions framework lies at the intersection of its conceptualization of abstraction as domain-specific, contextual, and dynamic. Studying patterns of epistemic actions and of abstraction during problem solving may give insight into how concept formation is enacted (Inhelder and Piaget, 1958) and into how students make sense of and use physical chemistry concepts. Defining abstract relative to the problem space emphasizes the situated nature of these processes and of the abstraction activity (Leont’ev, 1978). This is particularly important for physical chemistry, as we noted in the introduction that problems are often intended to foster concept development (Fox and Roehrig, 2015). However, while previous studies of abstraction have focused on the acquisition of stable concepts (Sfard, 1991; White and Mitchelmore, 2010), and on the use of abstracting to solve problems (Weinrich and Sevian, 2017), our epistemic actions framework highlights the transformative potential of abstraction in problem solving to practice, develop, and consolidate situated knowledge that instructors can leverage to support students’ mastery of physical chemistry concepts. The epistemic actions framework provides a lens to make these processes visible, and further research is needed to understand the patterns of abstraction in problem solving and instruction in order to develop opportunities to support student learning in physical chemistry.
Conclusions and implications
In this article, we present a framework to study and operationalize abstraction in physical chemistry through the epistemic actions students take during problem solving. We characterized actions along two dimensions: conceptual vs symbolic and degree of abstractness, which allowed us to identify two types of abstraction in physical chemistry: horizontal abstraction and vertical abstraction.The framework expands the existing and limited literature on problem solving in physical chemistry. It provides a lens through which student actions during problem solving can be viewed, and which can co-exist with existing problem solving frameworks that examine problem solving at a larger grain size, such as epistemic games (Tuminaro and Redish, 2007; Sevian and Couture, 2018; Rodriguez et al., 2020). It also presents a novel way of understanding abstraction and abstractness as contextual. Here, abstraction is defined in relation to a problem space; that is, the context in which abstraction occurs determines which resources are considered abstract (implicit) and which are considered concrete (explicit). This definition can be applied beyond physical chemistry, to understand and investigate how student problem solving is cued by the type of problem at hand.
Implications for research
The Epistemic Actions framework was developed by interpreting data in kinetics and thermodynamics problem solving. This work provides a novel tool researchers can use in tandem with other frameworks to investigate student problem solving in physical chemistry, in particular to investigate how students leverage prior knowledge and make sense of problem tasks. It also provides an operational tool to identify and characterize abstraction in problem solving, which we previously mentioned is critical in learning physical chemistry, but is as of yet understudied.This framework was also developed from a wide range of literature and tested in two contexts. Because it draws on such a wide base of knowledge, and because it was fruitful in analyzing data from fairly different types of problems, we speculate that this framework can be applied beyond physical chemistry. There are two dimensions to the framework: a domain-general dimension, which is represented by the types of actions and their levels of relative abstractness (the vertical abstraction dimension); and a domain-specific dimension, which is represented by the integration of conceptual and symbolic forms of each action (the horizontal abstraction dimension). The 4 domain-general actions (concretizing, manipulating, restructuring, and generalizing) could be adapted to other disciplines to investigate abstraction in other areas of chemistry, science, and beyond.
Finally, the Epistemic Actions framework may also have utility for investigating a broad range of meaning making in physical chemistry, not just in problem solving. The RBC-C, a similar framework in mathematics education and an inspiration for this work, has been used in a range of contexts, including individual and group problem solving and documenting collective meaning making in math classes, and has been fruitfully combined with other theoretical frameworks (Dreyfus et al., 2001; Hershkowitz et al., 2007; Özçakir Sümen, 2019; Tabach et al., 2020).
Implications for practice
There is intriguing theoretical work that suggests that deliberately modelling abstraction practices can support students’ fluency in making sense of and navigating abstract representations (Maton, 2013; Blackie, 2014). Often, chemistry instructors model how to problem solve, and implicitly assume that students share their mental representation of the problem and prior knowledge; however, there is evidence from organic chemistry that this is not necessarily true (Caspari et al., 2018). This study provides a set of actions that students may engage in while problem solving, and thus provides a framework for instructors in physical chemistry to (1) be more intentional in how they model abstraction and (2) more carefully attend to how students make sense of complex mathematical and conceptual objects.To illustrate this, imagine a physical chemistry professor who wants to emphasize that calculating an entropy change from the Second Law depends on the nature of the system at hand. The professor may start from an expression of the Second Law and define the system they are working in (concretizing)—for example, the isothermal expansion of a gas. They may then vertically abstract to talk through what kind of boundaries this system has (conceptual restructuring), and how those can be represented mathematically (symbolic restructuring). While solving the equation for entropy change of an isothermal expansion, the professor may engage in horizontal abstraction to reinforce how each calculation step corresponds to something meaningful about the system. By being deliberate in showing how the physical system and mathematical representations relate (horizontal abstraction), and how these relationships change the expression of the second law (vertical abstraction), the professor can model the reasoning they expect from their students during this type of problem solving.
Furthermore, there exists a discrepancy between instructional goals and assessment practices in physical chemistry in the United States—the majority of instructors report that their assessment goals for students are conceptual understanding, yet their assessments primarily consist of mathematical problem solving (Fox and Roehrig, 2015). This gap may be bridged by either intentionally modelling horizontal or vertical abstraction. The professor may intentionally design opportunities for horizontal and vertical abstraction into problems. For horizontal abstraction, the professor may ask students to think about the connections between concept and mathematics and deepen their understanding of an object. For vertical abstraction, they can design problems that require students to integrate and test different lines of reasoning and build toward concept construction.
Limitations
As a study that sought to build theory grounded in data, the analyses were based on an interview task that specifically sought to elicit abstraction. In more conventional physical chemistry tasks, abstraction may serve different purposes. For example, the task students were provided in the interviews required them to think about an unfamiliar context (disease spread), so abstraction activities often served the purpose of trying to understand what the problem was tasking them to do. In more familiar problem contexts, abstraction may serve a different role—for example, restructuring to try to figure out what equation may be the most appropriate for the problem at hand.Furthermore, although we report the frequencies of each action to contextualize the data, these frequencies are deeply situated in the study context and do not necessarily suggest generalizable findings. For example, we observed that conceptual actions were much more frequent than symbolic tasks; however, the task had a biological context and several variables participants found to be ambiguous, which resulted in a higher frequency of conceptual than of symbolic actions as participants attempted to make sense of the variables’ meanings. As we note above, abstraction is contextual, so frequencies of actions are likely to be related to the nature of the problem task. The frequency of the epistemic actions was also based on what participants vocalize. It is possible that participants made connections that they did not vocalize, and thus that we could not code for, or that were implicit. This may explain diagonal abstraction, when participants moved directly between a conceptual and symbolic move at two different levels of abstractness. It is possible that these participants had a “blended” understanding; that is, that their conceptual understanding of an object was tied to its mathematical representation, and so they moved through a blended framework of relations (Bain et al., 2018). It is also possible that they did the intermediate step (e.g., translating between conceptual and symbolic) in their heads, or that it was the interaction with the interviewer that induced this leap. To better understand this phenomenon, further research is needed. In particular, further research is needed about the role of interaction, e.g., with a perceived authority, on abstraction.
Future work
The study at hand investigated one part of an activity (the actions), in order to identify when the activity occurs. Ongoing work pursues a deeper understanding of the other two aspects of the activity system: motives and conditions. This work investigates what interactions motivate changes in abstraction to occur in context (motive), as well as how these changes in abstraction play out in a classroom setting (condition).There are also opportunities for other researchers to build off this work in both physical chemistry education and beyond. This study developed and facilitated an interview situation that sought to specifically elicit abstraction processes. However, by studying how students abstract while solving more conventional or traditional physical chemistry problems, there is an opportunity to better understand how students interact with different tasks. This may be a way to start to bridge the gap between instructor motivation and problem design for facilitating student learning we noted in the introduction.
Conflicts of interest
There are no conflicts to declare.Appendix
Appendix 1: interview tasks
The tasks for the two rounds of interviews are shown in Box 1. For both rounds of interviews, the “Warm Up Question” was treated as open-ended and the interviewer primarily sought to elicit participants’ thinking around the topic without guiding them toward any particular end. Both of the “novel problems,” upon which the data analysis is based, were closed-ended (had one correct solution); however, there were several different approaches students could take to solve the problem.Box 1. Text for the interview tasks. Novel questions for both tasks are adapted from Atkins P. and de Paula J. (2014). Atkins’ Physical Chemistry (10th ed). Oxford University Press, with permission from Oxford University Press.Interview 1: EntropyWarm-up question: What happens when a hot stone is dropped into cold water? Novel question: An average human DNA molecule has 5 × 108 binucleotides (rungs on the DNA ladder) of four different kinds. If each rung were a random choice of one of these four possibilities, what would be the residual entropy associated with this typical DNA molecule? Interview 2: Kinetics Warm-up question: You’ve been asked to improve the rate of a chemical reaction. How will you do this? What might you need to know about the system? Novel question: Many biological and biochemical processes are catalyzed by the presence of the product (this process is called autocatalysis). In the SIR model of the spread and decline of infectious diseases the population is divided into three classes: the ‘susceptibles,’ S, who can catch the disease; the ‘infectives,’ I, who have the disease and can transmit it; and the ‘removed class,’ R, who have either had the disease and recovered, are dead, are immune, or are isolated. The model mechanism for this process implies the following rate laws: |
For the kinetics problem, one possible solution relied on recognizing that when the disease is epidemic, the number of infectives is growing (dI/dt is positive). When the disease is dying out, the number of infectives is shrinking (dI/dt is negative). Then, students could solve for a/r for each of these conditions: that the epidemic condition is a/r < S, whereas the dying out condition is a/r > S.
For the entropy task, one possible solution involved recognizing that the question was asking about a statistical view of entropy; thus, students had to use the Boltzmann formula. They then had to figure out the number of possible combinations of how DNA could be organized and relate that to the idea of microstates.
Appendix 2: development of the actions from the concept maps
As part of the third iteration of data analysis (Fig. 1), we developed concept maps to visualize how participants brought objects into the problem space and connected them over the course of solving the problem. Over the course of developing the concept maps, we found patterns in how objects were connected and transformed over the course of solving the problem that were related to abstraction. These patterns are depicted in Fig. 2.Below we show a piece of Philip's concept map that corresponds to restructuring (Fig. 7). This example was discussed in detail in the Symbolic restructuring section above. In the concept map (Fig. 7a), objects were included as nodes. The piece that corresponds to the restructuring move is outlined in purple in Fig. 7a. First, Philip used a substitution strategy to combine the three rate equations together, which yielded dI/dt = −dS/dt − dR/dt. This is depicted in the box on the bottom left of Fig. 7a, which depicts the connections between three nodes to show the substitution strategy that yielded the combined equation. He then introduces the idea that “uncorrelated things can be uncorrelated,” which came from his familiarity with Maxwell relations (middle top of 7a). This new piece of information led to Philip shifting the goal state from solving for a/r to solving for da/dr.
 | ||
| Fig. 7 Relationship between concept map and actions coding. (a) An example of a part of a concept map from Philip's problem solving that led to the restructuring action. Here, Philip realized that the three equations could be put together into one equation (bottom left). This triggered him to remember Maxwell relations and the idea that uncorrelated things can be correlated through differentiating them (top center). Drawing on this piece of knowledge, he changed the structure of the ratio he was being asked to solve (a/r) by differentiating it, resulting in da/dr (bottom right). (b) The abstracted form of the restructuring action, which is the mediated transformation of an object (e.g., the ratio a/r) through a piece of prior knowledge (e.g., Maxwells relation) to a new form of the object (e.g., da/dr). | ||
Fig. 7b shows the abstracted form of this pattern. In Fig. 7b, the transformation of an object (bottom left) into a new object (bottom right) is mediated through another piece of knowledge that is brought it from outside of the original problem space (top middle). Similar to the concept map, the transformation of the equations, which Philip manipulated as part of his strategy to solve for a/r, into a “differentiated” form, represented here as da/dr, was mediated through his familiarity with the “Maxwell relations” strategy, which allowed him to correlate things that were otherwise uncorrelated.
The three other patterns depicted in Fig. 2 similarly arose from concept maps. Concretizing depicts the transformation of an object (bottom left) to another object (bottom right) through the application of a constraint (top middle). Manipulating depicts the transformation of an object (left) to another object (right) through a procedural transformation (middle). This manipulating pattern can also be seen in the bottom left part of Philip's concept map in Fig. 7a, where the procedural transformation is substitution. Generalizing depicts the generation of a new object (left) through the coming together of e.g., two other objects (right top and bottom). In the next iteration of data analysis, these actions were qualified as conceptual or symbolic. This theory development was supported in part by the concept maps as well, as the nodes were coded for the knowledge source of the object.
Acknowledgements
This paper is based, in part, on the doctoral dissertation of the first author (J. M. K.). The authors are grateful to the students who participated in the study, as well as the professor who allowed access to the course. We also thank the Sevian Group research team members who helped to strengthen construct validity in the analysis: Raúl Orduña Picón, Klaudja Caushi, Stephanie Murray, as well as visiting professor Edenia Amaral. In particular, we would like to thank Clarissa Keen for fruitful discussions and inter-rater reliability, and Ira Caspari for feedback on this manuscript. The authors acknowledge the funding sources that supported our work, National Science Foundation Graduate Research Fellowship award 1842403, NSF DRL-1621228, NSF DUE-1348722.References
- Atkins P. and de Paula J., (2014), Atkins’ Physical Chemistry, 10th edn, Oxford University Press.
- Bain K., Moon A., Mack M. and Towns M., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15(3), 320–335 10.1039/C4RP00011K.
- Bain K., Rodriguez J.-M. G., Moon A. and Towns M. H., (2018), The characterization of cognitive processes involved in chemical kinetics using a blended processing framework, Chem. Educ. Res. Pract., 19(2), 617–628 10.1039/C7RP00230K.
- Bain K., Rodriguez J.-M. G. and Towns M. H., (2019), Chemistry and Mathematics: Research and Frameworks To Explore Student Reasoning, J. Chem. Educ., 96(10), 2086–2096 DOI:10.1021/acs.jchemed.9b00523.
- Becker N. and Towns M., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220 10.1039/C2RP00003B.
- Blackie M. A. L., (2014), Creating semantic waves: Using Legitimation Code Theory as a tool to aid the teaching of chemistry, Chem. Educ. Res. Pract., 15(4), 462–469 10.1039/C4RP00147H.
- Bodner G. M. and McMillen T., (1986), Cognitive Restructuring as an Early Stage in Problem Solving, J. Res. Sci. Teach., 23(8), 727–737.
- Broman K., Bernholt S. and Parchmann I., (2018), Using model-based scaffolds to support students solving context-based chemistry problems, Int. J. Sci. Educ., 40(10), 1176–1197 DOI:10.1080/09500693.2018.1470350.
- Cañas A. J., Hill G., Carff R., Suri N., Lott J., Gómez G., Eskridge T. C., Arroyo M. and Carvajal R., (2004), CmapTools: A Knowledge Modeling and Sharing Environment, Proceedings of the First International Conference on Concept Mapping, Pamplona, Spain: Concept Maps: Theory, Methodology, Technology.
- Caspari I. and Graulich N., (2019), Scaffolding the structure of organic chemistry students’ multivariate comparative mechanistic reasoning, Int. J. Phys. Chem. Educ., 11(2), 31–43.
- Caspari I., Weinrich M. L., Sevian H. and Graulich N., (2018), This mechanistic step is “productive”: Organic chemistry students’ backward-oriented reasoning, Chem. Educ. Res. Pract., 19(1), 42–59 10.1039/C7RP00124J.
- Charmaz K., (2006), Constructing grounded theory: A practical guide through qualitative analysis, Sage.
- Chi M. T. H., Feltovich P. J. and Glaser R., (1981), Categorization and Representation of Physics Problems by Experts and Novices*, Cognit. Sci., 5(2), 121–152 DOI:10.1207/s15516709cog0502_2.
- Dalgety J., Coll R. K. and Jones A., (2003), Development of chemistry attitudes and experiences questionnaire (CAEQ), J. Res. Sci. Teach., 40(7), 649–668 DOI:10.1002/tea.10103.
- Davydov V. V., (1972), Types of Generalization in Instruction: Logical and Psychological Problems in the Structuring of School Curricula. Soviet Studies in Mathematics Education. Volume 2, National Council of Teachers of Mathematics.
- Domin D. and Bodner G., (2012), Using Students’ Representations Constructed during Problem Solving To Infer Conceptual Understanding, J. Chem. Educ., 89(7), 837–843 DOI:10.1021/ed1006037.
- Douven I., (2011, March 9), Abduction, Stanford Encyclopedia of Philosophy, https://plato.stanford.edu/entries/abduction/?utm_campaign=%F0%9F%A6%89%2010x%20curiosity&utm_medium=email&utm_source=Revue%20newsletter.
- Dreyfus T., Hershkowitz R. and Schwarz B. B., (2001), Abstraction in context II: The case of peer interaction, Cognit. Sci. Q., 1(3/4), 307–368.
- Dubinsky E. and McDonald M. A., (2001), APOS: A Constructivist Theory of Learning in Undergraduate Mathematics Education Research, in D. Holton, M. Artigue, U. Kirchgräber, J. Hillel, M. Niss and A. Schoenfeld (ed.), The Teaching and Learning of Mathematics at University Level: An ICMI Study, Netherlands: Springer, pp. 275–282 DOI:10.1007/0-306-47231-7_25.
- Engeström Y., (1999), Activity theory and individual and social transformation, in Y. Engeström, R. Miettinen and R.-L. Punamäki-Gitai (ed.), Perspectives on Activity Theory, Cambridge University Press, pp. 19–38.
- Fox L. J. and Roehrig G. H., (2015), Nationwide Survey of the Undergraduate Physical Chemistry Course, J. Chem. Educ., 92(9), 1456–1465 DOI:10.1021/acs.jchemed.5b00070.
- Frey R. F., Cahill M. J. and McDaniel M. A., (2017), Students’ Concept-Building Approaches: A Novel Predictor of Success in Chemistry Courses, J. Chem. Educ., 94(9), 1185–1194 DOI:10.1021/acs.jchemed.7b00059.
- Glaser B. G. and Holton J., (2004), Remodeling Grounded Theory, Forum Qualitative Sozialforschung/Forum: Qualitative Social Research, 5(2), 2 DOI:10.17169/fqs-5.2.607.
- Glaser B. and Strauss A., (1967), The Discovery of Grounded Theory: Strategies for Qualitative Research, Aldine Transaction.
- Hahn U. and Chater N., (1998), Similarity and rules: Distinct? Exhaustive? Empirically distinguishable? Cognition, 65(2–3), 197–230.
- Halverscheid S., (2008), Building a local conceptual framework for epistemic actions in a modelling environment with experiments, ZDM, 40(2), 225–234.
- Hershkowitz R., Schwarz B. B. and Dreyfus T., (2001), Abstraction in context: Epistemic actions, J. Res. Math. Educ., 32(2), 195–222.
- Hershkowitz R., Hadas N., Dreyfus T. and Schwarz B., (2007), Abstracting processes, from individuals’ constructing of knowledge to a group's “shared knowledge,” Math. Educ. Res. J., 19(2), 41–68 DOI:10.1007/BF03217455.
- Inhelder B. and Piaget J., (1958), The growth of logical thinking: From childhood to adolescence, (A. Parsons and S. Milgram, Trans.), Basic Books.
- Jiménez J. P. C., Melo G., Bacigalupo F. and Manghi D., (2016), Semantic waves in teacher-student interaction: Analysis of two Natural Science lessons in 6th grade, Ciência Educação, 22(2), 335–350 DOI:10.1590/1516-731320160020005.
- Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem. J. Comput. Assisted Learn., 7(2), 75–83 DOI:10.1111/j.1365-2729.1991.tb00230.x.
- Jonassen D. H., (2010), Learning to Solve Problems: A Handbook for Designing Problem-Solving Learning Environments, Routledge DOI:10.4324/9780203847527.
- Kapon S. and diSessa A. A., (2012), Reasoning Through Instructional Analogies, Cognit. Instr., 30(3), 261–310 DOI:10.1080/07370008.2012.689385.
- Karch J. M. and Sevian H., (2020), ‘Abstraction in Disciplinary Problem Solving,’ in M. Gresalfi and I. S. Horn (ed.), The Interdisciplinarity of the Learning Sciences: Proceedings of 14th International Conference of the Learning Sciences (ICLS) 2020, Nashville, TN, 19–23 June, 2020, pp. 831–832.
- Kermack W. O., McKendrick A. G. and Walker G. T., (1927), A contribution to the mathematical theory of epidemics, Proc. R. Soc. London, Ser. A, 115(772), 700–721 DOI:10.1098/rspa.1927.0118.
- Kuo E., Hull M. M., Gupta A. and Elby A., (2013), How students blend conceptual and formal mathematical reasoning in solving physics problems, Sci. Educ., 97(1), 32–57 DOI:10.1002/sce.21043.
- Kuo E., Hull M., Elby A. and Gupta A., (2020), Assessing mathematical sensemaking in physics through calculation-concept crossover, Phys. Rev. Phys. Educ. Res., 16, 1–24.
- Leont’ev A. N., (1978), Activity, Consciousness, and Personality, Englewood Cliffs, Nj: Prentice-Hall.
- Mack M. R. and Towns M. H., (2016), Faculty beliefs about the purposes for teaching undergraduate physical chemistry courses, Chem. Educ. Res. Pract., 17(1), 80–99 10.1039/C5RP00148J.
- Maton K., (2013), Making semantic waves: A key to cumulative knowledge-building, Linguist. Educ., 24(1), 8–22 DOI:10.1016/j.linged.2012.11.005.
- Niss M., (2017), Obstacles Related to Structuring for Mathematization Encountered by Students when Solving Physics Problems, Int. J. Sci. Math. Educ., 15(8), 1441–1462 DOI:10.1007/s10763-016-9754-6.
- Novak J. D. and Cañas A. J., (2006), The Theory Underlying Concept Maps and How to Construct Them, Technical Report IHMC CmapTools 2006–01, Florida Institute for Human and Machine Cognition.
- Özçakir Sümen Ö., (2019), Primary School Students’ Abstraction Levels of Whole-Half-Quarter Concepts According to RBC Theory, J. Math. Educ., 10(2), 251–264.
- Piaget J., (1964), Part I: Cognitive development in children: Piaget development and learning, J. Res. Sci. Teach., 2(3), 176–186.
- Pontecorvo C. and Girardet H., (1993), Arguing and Reasoning in Understanding Historical Topics, Cognit. Instr., 11(3 & 4), 365–395.
- Reimann P. and Chi M. T. H., (1989), Human Expertise, in K. J. Gilhooly (ed.), Human and Machine Problem Solving, US: Springer, pp. 161–191 DOI:10.1007/978-1-4684-8015-3_7.
- Rodriguez J.-M. G., Bain K., Hux N. P. and Towns M. H., (2018), Productive features of problem solving in chemical kinetics: More than just algorithmic manipulation of variables, Chem. Educ. Res. Pract., 20, 175–186 10.1039/C8RP00202A.
- Rodriguez J.-M. G., Bain K. and Towns M. H., (2020), The Role of Epistemology and Epistemic Games in Mediating the Use of Mathematics in Chemistry: Implications for Mathematics Instruction and Research on Undergraduate Mathematics Education, Int. J. Res. Undergrad. Math. Educ., 6, 279–301.
- Russ R. S., Lee V. R. and Sherin B. L., (2012), Framing in cognitive clinical interviews about intuitive science knowledge: Dynamic student understandings of the discourse interaction, Sci. Educ., 96(4), 573–599.
- Santos B. F. dos and Mortimer E. F., (2019), Ondas semânticas e a dimensão epistêmica do discurso na sala de aula de química, Investigações em Ensino de Ciências, 24(1), 62–80 DOI:10.22600/1518-8795.ienci2019v24n1p62.
- Scheiner T., (2016), New light on old horizon: Constructing mathematical concepts, underlying abstraction processes, and sense making strategies, Educ. Stud. Math., 91(2), 165–183 DOI:10.1007/s10649-015-9665-4.
- Schurz G., (2008), Patterns of abduction, Synthese, 201–234 DOI:10.1007/s11229-007-9223-4.
- Schwartz D. L., (1995), The Emergence of Abstract Representations in Dyad Problem Solving, J. Learn. Sci., 4(3), 321–354 DOI:10.1207/s15327809jls0403_3.
- Sevian H. and Couture S., (2018), Epistemic games in substance characterization, Chem. Educ. Res. Pract., 19(4), 1029–1054 10.1039/C8RP00047F.
- Sevian H., Bernholt S., Szteinberg G. A., Auguste S. and Pérez L. C., (2015), Use of representation mapping to capture abstraction in problem solving in different courses in chemistry, Chem. Educ. Res. Pract., 16(3), 429–446 10.1039/C5RP00030K.
- Sfard A., (1991), On the Dual Nature of Mathematical Conceptions: Reflections on Processes and Objects as Different Sides of the Same Coin, Educ. Stud. Math., 22(1), 1–36.
- Sözbilir M., (2004), What Makes Physical Chemistry Difficult? Perceptions of Turkish Chemistry Undergraduates and Lecturers, J. Chem. Educ., 81(4), 573–578 DOI:10.1021/ed081p573.
- Tabach M., Rasmussen C., Dreyfus T. and Hershkowitz R., (2017), Abstraction in Context and Documenting Collective Activity, Dublin, Ireland: CERME 10https://hal.archives-ouvertes.fr/hal-01948869.
- Tabach M., Rasmussen C., Dreyfus T. and Apkarian N., (2020), Towards an argumentative grammar for networking: A case of coordinating two approaches, Educ. Stud. Math., 103(2), 139–155 DOI:10.1007/s10649-020-09934-7.
- Thornberg R., (2012), Informed Grounded Theory, Scand. J. Educ. Res., 56(3), 243–259 DOI:10.1080/00313831.2011.581686.
- Tsaparlis G., (2005), Non-algorithmic quantitative problem solving in university physical chemistry: A correlation study of the role of selective cognitive factors, Res. Sci. Technol. Educ., 23(2), 125–148 DOI:10.1080/02635140500266369.
- Tuminaro J. and Redish E. F., (2007), Elements of a cognitive model of physics problem solving: Epistemic games, Phys. Rev. Spec. Top. – Phys. Educ. Res., 3(2), 1–22 DOI:10.1103/PhysRevSTPER.3.020101.
- van den Heuvel-Panhuizen M., (2003), The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage, Educ. Stud. Math., 54(1), 9–35 DOI:10.1023/B:EDUC.0000005212.03219.dc.
- Weinrich M. L. and Sevian H., (2017), Capturing students’ abstraction while solving organic reaction mechanism problems across a semester, Chem. Educ. Res. Pract., 18(1), 169–190 10.1039/C6RP00120C.
- White P. and Mitchelmore M. C., (2010), Teaching for Abstraction: A Model, Math. Thinking Learn., 12(3), 205–226 DOI:10.1080/10986061003717476.
- Williams G., (2007), Abstracting in the context of Spontaneous Learning, Math. Educ. Res. J., 19(2), 69–88 DOI:10.1007/BF03217456.
| This journal is © The Royal Society of Chemistry 2022 |