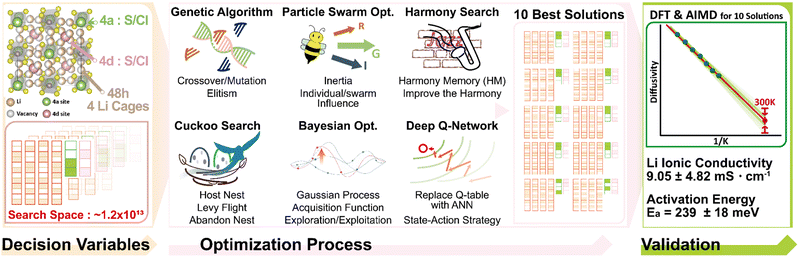
Open Access Article
Open Access ArticleArgyrodite configuration determination for DFT and AIMD calculations using an integrated optimization strategy†
Byung Do Lee‡
a,
Jin-Woong Lee‡a,
Joonseo Parka,
Min Young Choa,
Woon Bae Park*b and
Kee-Sun Sohn *a
*a
aFaculty of Nanotechnology and Advanced Materials Engineering, Sejong University, Seoul 05006, Republic of Korea. E-mail: kssohn@sejong.ac.kr
bDepartment of Advanced Components and Materials Engineering, Sunchon National University, Chonnam 57922, Republic of Korea. E-mail: wbpark@scnu.ac.kr
First published on 31st October 2022
Abstract
When constructing a partially occupied model structure for use in density functional theory (DFT) and ab initio molecular dynamics (AIMD) calculations, the selection of appropriate configurations has been a vexing issue. Random sampling and the ensuing low-Coulomb-energy entry selection have been routine. Here, we report a more efficient way of selecting low-Coulomb-energy configurations for a representative solid electrolyte, Li6PS5Cl. Metaheuristics (genetic algorithm, particle swarm optimization, cuckoo search, and harmony search), Bayesian optimization, and modified deep Q-learning are utilized to search the large configurational space. Ten configuration candidates that exhibit relatively low Coulomb energy values and thereby lead to more convincing DFT and AIMD calculation results are pinpointed along with computational cost savings by the assistance of the above-described optimization algorithms, which constitute an integrated optimization strategy. Consequently, the integrated optimization strategy outperforms the conventional random sampling-based selection strategy.
Introduction
Alkali superionic conductors (solid electrolytes for use in all-solid-state rechargeable alkali-ion batteries) have recently attracted a great deal of attention for their improved safety and potentially higher energy density in comparison to traditional organic liquid electrolytes.1–3 In parallel with the experimental development of solid electrolytes, theoretical approaches also deserve to be highlighted to facilitate the development of more promising solid electrolytes. In this context, density functional theory (DFT) and ab initio molecular dynamics (AIMD) calculations have been actively pursued for solid electrolyte materials.4–6 A well-known solid electrolyte material, Li6PS5Cl (argyrodite),7–15 has a partially occupied structure that gives rise to configuration issues when constructing the input model structure for use in DFT and AIMD calculations. The configuration issue is one of the most exasperating problems in the theoretical approach to partially occupied inorganic compounds.When the configuration issue is to be considered, virtual crystal approximation (VCA)16–20 and coherent pseudopotential approximation (CPA)21 are viable solutions. The VCA (i.e., an effective pseudopotential represented as a weighted sum of different pseudopotentials) has been suggested for solid solutions, but the VCA is available only for limited compounds that are composed of metallic elements with similar electronic configurations. The CPA approximates a random configuration with an effective medium that is determined self-consistently from the condition of stationary scattering.21 Although the CPA has actually outperformed the VCA,21 it is not well suited to total energy calculations and geometry optimization.22 Likewise, the configurational average approximation also seems unrealistic for relatively large supercells because the enhanced configurational diversity in a large supercell would lead to more scattered ab initio calculation results.23,24 In addition, the configurational average strategy could increase both cost and time.25–28 The cluster expansion method (CEM)29–33 could be an alternative approach to address the configuration issue in a solid electrolyte material. Since the cluster expansion is fitted using a DFT-calculated property for a set of representative configurations, the CEM still requires extra and expensive DFT-calculated data in the regression fitting procedures. Therefore, none of the strategies described above seems ideally suited to address the configurational issue in solid electrolyte materials.
A general and simple solution to address the configuration issue, which has been widely accepted in the field,34–39 is random sampling from the large number of viable configurations (for instance, the total number of viable configurations for Li6PS5Cl amounts to ∼1013 even for a single unit cell model) and the ensuing choice of some configurations based on a certain selection criterion. The criterion utilized for the configuration selection following the random sampling is the electrostatic energy (Coulomb potential or energy),34–39 which can be evaluated by a very fast, low-cost computation and is reliable enough to roughly approximate the DFT-calculated total energy, although the structure that minimizes the electrostatic energy is not always the lowest energy structure based on DFT calculations. Despite the swift evaluation of the Coulomb energy that is much faster than the DFT calculations, the complete enumeration for the huge number of configurations is practically impossible. The selection of a few low-Coulomb-energy entries from the nominal number (∼1000) of random configurations, which is a current method in the field, would be inefficient to find the lowest-Coulomb-energy configurations that might be better matched with real-world ground state structures.
While the computationally inexpensive Coulomb energy is still being utilized as a selection criterion, we propose a more systematic methodology to nominate plausible configurations for use in the ensuing DFT and MD calculations—an optimization algorithm that enables us to nominate a greater number of low-Coulomb-energy configurations with incredible cost savings. This optimization algorithm makes it possible to search the enormous configuration search space and nominate a number of configurations that could represent real-world ground state structures for argyrodite. A series of optimization algorithms are applied in parallel to select argyrodite configurations that have minimum Coulomb energy values and thus could be used as input model structures for the subsequent DFT and MD calculations.
The adopted optimization algorithm includes four well-known metaheuristics: the genetic algorithm (GA),40–42 particle swarm optimization (PSO),43,44 harmony search (HS),45 and cuckoo search (CS).46 In addition to metaheuristic algorithms, we introduce Bayesian optimization (BO).47,48 Although the deep Q-network (DQN)49 is not dogmatically designed for optimization tasks, we modify it for use in a simple optimization task such as the argyrodite configuration search. The metaheuristic, which is inspired by generally acknowledged disciplines such as biology, ethology, and music, is known to outperform the traditional Jacobian/Hessian-based optimization.50 The metaheuristic has the merit of offering a higher possibility of escaping from local optima. We take on the four most frequently utilized metaheuristics: GA, PSO, HS, and CS. Along with the metaheuristic, we also employ Bayesian optimization, which has been known to be more efficient for optimization tasks that require the extremely expensive evaluation of an objective function. DQN, a recently devised reinforcement learning algorithm, represents a merger between traditional Q-learning and a more recent deep neural network.51 In principle, the DQN is not designed for use in such a simple optimization but for more complicated dynamic problems such as games. The DQN capability is far beyond a simple optimization. A truncated (or modified) DQN algorithm, called a single-episode DQN, is fully adapted to the optimization task.
We systematically compare all the above-described optimization algorithms for the argyrodite configuration search. In addition, the validity of each optimization algorithm is preconfirmed using well-known benchmark test functions. Although some previous reports have dealt with a single optimization algorithm, such as a genetic algorithm or particle swarm optimization, for a similar configuration selection task,52–55 we introduce six optimization algorithms, involving four metaheuristics, a Bayesian optimization, and a reinforcement learning algorithm (=DQN), which constitute an integrated optimization strategy.
Computational methods
Metaheuristics
The GA, PSO, HS, and CS algorithms are coded by referring to the general fundamentals.56–58 We heavily borrowed GA and PSO codes from others57,58 but the HS and CS codes originated from this work. Hyperparameters are also inherited from the original algorithms.56 We also tested other sets of hyperparameters using benchmark functions, but they never outperformed the original set of hyperparameters. The final adopted hyperparameters are given in Tables 1 and S2.† The codes for all the metaheuristics, such as the GA, PSO, HS, and CS algorithms, are available at https://github.com/socoolblue/optimization.| Method | Hyperparameter | Coulomb energy (eV f.u.−1) |
|---|---|---|
| Random | — | −247.20 |
| GA | Mutation probability: 0.1, elite size: 0.01, crossover probability: 0.5 | −249.27 |
| PSO | C1: 2, C2: 2, w: 0.85 | −248.10 |
| HS | HMCR: 0.7, PAR: 0.3, bw: 0.01 | −248.72 |
| CS | Pa: 0.25, β: 1.5 | −248.80 |
| BO | α: 10−5, β: 10−7 | −247.54 |
| DQN | Episode length: 2500, learning rate: 0.001 | −248.01 |
BO
BO works best for many expensive optimization tasks, the objective function evaluation for which is time-consuming. Two optimization steps are required for BO: one for maximum likelihood estimation (MLE) for the hyperparameter determination process during Gaussian process regression (GPR) and the other for acquisition function optimization for the determination of the next position to be evaluated. Well-known gradient- and Hessian-based optimization algorithms were used for both optimization processes in BO execution. Both optimization processes do not guarantee global optimization, and the choice of acquisition functions is also heuristic. Even a single-objective BO execution does not always yield an acceptable result when the objective function terrain is not continuous and smooth. Even worse performance would be expected in the case of multiobjective optimization problems.48The BO performance depends significantly on the objective function terrain; if a continuous and smooth benchmark function is of concern, the GPR works better; on the other hand, if a benchmark function has a nonsmooth terrain with abrupt transitions, then the GRP would not be appropriate as a surrogate function. Very recently, Lei et al.59 reported a much more improved BO performance using different surrogate functions rather than GPR, so-called Bayesian multivariate adaptive regression splines (BMARS)60,61 and Bayesian additive regression trees (BART).62 However, Lei et al.59 adopted a truncated search space in the decision variable range [−2, 2] with 4D (for Rosenbrock) and 10D (for Rastrigin) search spaces. The decision variable ranges that Lei et al.59 adopted are far narrower than those generally recommended. We adopted the decision variable range [−5, 5] with a 6D search space for six benchmark functions: the Ackley, Egg Crate, Griewank, Rastrigin, Rosenbrock, and Sphere functions. More importantly, since the metaheuristics, such as GA, PSO, HA, and CS, greatly outperformed BO, the improved BO algorithms would make no sense in the present investigation. However, we also adopted alternative surrogate functions, which are four ensemble-learning algorithms such as random forest, AdaBoost, gradient Boost, and extreme gradient (XG) Boost.
DQN
It is obvious that the DQN is a sort of early-stage reinforcement learning algorithm that is generally used for dynamic problems. Its use in such a simple optimization that we are dealing with in the present investigation seems to be a waste of computational resources. The conventional DQN capability is far beyond such a simple optimization task. If a standard DQN model was fully trained and thereafter the ensuing test was executed, a start at any point in the decision variable space would definitely end up with the convergence to the global optimum. However, such a standard training process must require a large number of episodes, which means that a huge number of object function evaluations are needed.We altered the operation method to make it possible to use the DQN algorithm for a simple optimization task. A so-called one-episode training scheme was developed to save computational cost. It is unnecessary to fully train the DQN, but instead it would be satisfactory as far as we can manage to reach (or pass through) the global optimum (or one of promising local optima) in the course of the one-episode training. Since it is highly likely to find the global optimum (or one of promising local optima) during an episode at the expense of minimum computational costs, we do not need to learn the complete terrain of the objective function.
The state was defined as decision variable vectors in a six-dimensional decision variable space. The action was defined as small-step movement from the current state. A remarkable measure that we newly took for our modified DQN approach is the inclusion of the step length in the output layer of the deep neural network, such that it can be adjustable during the training, and depending on the state of concern (i.e., the step length differed for every position in the decision variable space, presumably, the step length would be shorter if we get closer to the optimum, otherwise longer). The reward was defined as two fixed numbers; if the action from the current state to the next state gives rise to an improvement in the objective function, then the reward is +0.1; otherwise, it is −100. More details for the one-episode DQN can be recognized from the code available at https://github.com/socoolblue/optimization.
DFT & AIMD calculations
First-principles calculations were performed using conventional lab-scale computational inventories based on the Vienna Ab initio Simulation Package (VASP5.4).63–67 The generalized gradient approximation (GGA) parameterized by Perdew, Burke, and Ernzerhof (PBE)63 was employed for the entire computational process. Projector-augmented wave potentials,68,69 a cutoff energy of 520 eV and a k-mesh interval maintained below 0.2 Å−1 were adopted using the Monkhorst–Pack scheme for all input model structures, which ensured that the total energy converged at less than 10−6 eV. All structural aspects (atomic position, lattice size, and shape) were allowed to relax until the final force on all relaxed atoms was less than 0.01 eV Å−1 for structure relaxation. To evaluate the room-temperature ionic conductivity of the selected candidates, AIMD70,71 calculations were implemented at 600, 700, 800, 900, 1,000, 1,100, and 1200 K. Each candidate was heated to the desired temperature for 2 ps in the microcanonical (NVE) simulations. The AIMD simulation for 150 ps, with a time step of 2 fs, and was based on the canonical ensemble (NVT) and Nosé–Hoover thermostat algorithm.Results and discussion
Problem setting
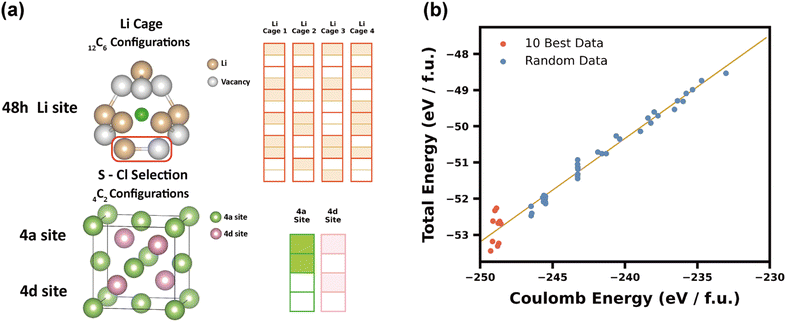
Fig. 1 schematically shows the entire concept for the integrated optimization strategy, i.e., the integrated optimization platform consisting of the GA, PSO, HS, CS, BO, and DQN algorithms. The decision variable and objective function setting is the first prerequisite for the optimization task. The decision variable setting and its simplified graphical representation, which can be utilized instead of actual unit cell structures for brevity, is well described in Fig. 2a. Six decision variables designating the configuration were extracted from the argyrodite structure. There are four Li cages with the same shape in the argyrodite unit cell. Fig. 2a shows a cage partially filled with Li ions, representing an arbitrary configuration. The partially occupied Li distribution in a cage was assigned to a decision variable, which means that four decision variables were assigned to the Li distribution in the four cages in a unit cell. For both practicality and brevity, an equal number of Li ions was assigned to every cage, such that a total of 7 × 1011 Li configurations were viable in the unit-cell-based model structure for argyrodite. If this restriction (i.e., the equal number of Li ions for each cage) was removed, the total number of available configurations would skyrocket to nearly infinity, and the decision variable extraction would be unviable. It is fortunate, however, that an uneven starting Li distribution in the four cages would mostly result in an even distribution in the four cages when Coulomb energy minimization was completed by the optimization algorithms.40–51 The other two decision variables are extracted from the Cl/S distribution. There are four S sites assigned to each of the 4a and 4d sites, and two for each can be occupied by Cl. In this regard, the fifth and sixth decision variables represent the Cl/S distribution at sites 4a and 4d, respectively. The total number of viable configurations that these six decision variables constitute amounts to 1013.Coulomb energy is assigned to the objective function to be minimized. The Coulomb energy could be a rough measure of the total internal energy, although a complete coincidence would not be viable. A plot of Coulomb energy vs. DFT-calculated total internal energy is shown in Fig. 2b, wherein some randomly chosen configuration data were presented along with the ideal linear fit. It is reasonable to recommend Coulomb energy as a rough measure of total energy and thereby to use it as an objective function for the optimization process, wherein the appropriate ground state configuration can be found. The use of Coulomb energy has an economical merit in comparison to the use of DFT-calculated total energy, since it takes less than a second to complete the Coulomb energy calculation for a single configuration. We adopted Okhotnikov et al.'s Coulomb energy calculation code.72
There have been well-established codes for crystal structure prediction such as USPEX73,74 and CALYPSO.75,76 These codes exhibit either the similarity or the dissimilarity in comparison to our approach. In view of the optimization algorithm, an evolutional algorithm is adopted for USPEX73,74 and a PSO algorithm for CALYPSO.75,76 Presumably, both the well-established codes would give a similar result to what we produced. It should be noted, however, that we employed six optimization algorithms even including both the PSO and evolutionary algorithm that the USPEX and CALYPSO adopted.
Brief discussion of optimization algorithms and benchmark function test results
The metaheuristics are a series of optimization algorithms inspired by well-known disciplines such as biology, ethology, psychology, and music. There are a number of metaheuristics, among which we adopted four relatively popular algorithms for the argyrodite configuration optimization task. The GA has been known as the most renowned metaheuristic,40–42 and its applicability has recently spanned to multiobjective optimization tasks.77 Natural selection in the evolution process for organisms is a backbone principle for the GA, which makes the system of concern artificially evolve in a desirable (predetermined) direction. The decision variable is treated as a chromosome in organisms. The social behavior of a swarm is a backbone principle for PSO. PSO is as popular as the GA, although its establishment lagged behind the GA.43,44 Although all kinds of decision variables, such as real numbers, integers, booleans, etc., are available for PSO as well as in the GA, PSO works best in the continuous real number decision variable space. The HS algorithm is inspired by jazz musician improvisations, wherein the decision variable is treated as a note in music.45 The CS algorithm is the most recently developed among those used here and inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of host birds of other species, wherein a nest can be treated as a decision variable.46 In addition to metaheuristic algorithms, the BO algorithm has recently attracted a great deal of attention due to its outstanding merit, i.e., low-cost optimization with a relatively small number of samples to be evaluated.47,48 DQN is also introduced for use in the optimization, although DQN, a sort of early-stage reinforcement learning algorithm, is not a typical optimization algorithm but instead a sort of dynamic programing that was devised to sort out more complicated problems such as computer games.49 More details on each of the algorithms introduced above will be described in the Computational methods section.In advance of their use in the argyrodite configuration optimization task, we tested all the optimization algorithms using several well-known benchmark test functions, such as the Ackley,78 Egg Crate,79 Griewank,80 Rastrigin,81 Rosenbrock,82 and Sphere83 functions, each of which is schematically described in Fig. S1, ESI.† The search space constituted by the 6-dimensional decision variable vector span with each vector component was restricted in the range [−5, 5]. This preliminary benchmark function test was executed in hopes that the same codes could work for the argyrodite configuration optimization as well. Table S1, ESI,† shows the final optimized objective function (benchmark function) values that were reached by each of the metaheuristic (GA, PSO, HS, and CS), BO, and DQN algorithms. All the algorithms worked out, although it is not clear whether the minimum objective function value at the last generation was close to the global optimum. Although the PSO algorithm is conspicuously superior to others in terms of the final optimized objective function value in the last generation for most benchmark functions, it is not possible to find a definite relative dominance among those optimization algorithms by considering all the benchmark function test results on average, as evidenced in Table S1.† In principle, the performance of optimization algorithms strongly depends on the benchmark test function. Although we can roughly predict the terrain of all the benchmark functions, no one knows what the Coulomb energy terrain in the argyrodite configuration space looks like. That is why we have to pretest more than several benchmark functions that dramatically differ from one another. Moreover, we have to employ as many optimization algorithms as possible because it would be thoroughly impossible to know which algorithm works for which benchmark function. In this context, we employed the six optimization algorithms for Coulomb energy minimization over the large argyrodite configuration space, and these six optimization algorithms were pretested using six benchmark functions. Thus, the integrated optimization strategy we propose here would be more promising than a typical single-algorithm strategy.
For a systematic comparison among those optimization algorithms, the same number of objective function evaluations was applied for every algorithm, that is, the population size was 25 and the generation number was 100, leading to the total number of evaluations fixed at 2500. In the exceptional case of the DQN algorithm, however, a higher number of objective function evaluations was required to obtain a similar level of optimization in comparison to the other optimization algorithms. Although it appears that a much higher number of evaluations is required for the DQN algorithm, the required number of evaluations varies on a case-by-case basis. The initial decision variable vector (the starting point) that is to be determined randomly had a great influence on the performance of the DQN-based optimization, since we adopted a single episode training, as discussed in the Computational methods section. Fig. S1, ESI,† shows the instantaneous objective function (benchmark function) value versus the generation number (which equals the number of objective function evaluations multiplied by the population size of 25) for every optimization algorithm. Fig. S1† also shows that there is no obvious superiority or inferiority among the optimization algorithms for all the benchmark functions, and every algorithm ultimately leads to an acceptable convergence close to the global optimum. For some optimization algorithms (in particular, for BO and DQN), neither the global optimum nor one of promising local optima was reached, but this sort of incomplete optimization is customary for the heuristic nature of the algorithm. The benchmark function test results shown in Table S1 and Fig. S1† imply that some of the aforementioned algorithms with the same hyperparameters refined from these benchmark function tests should definitely work out for the argyrodite configuration optimization problem as well. The hyperparameter screening results are also given in Table S2.†
Argyrodite configuration optimization
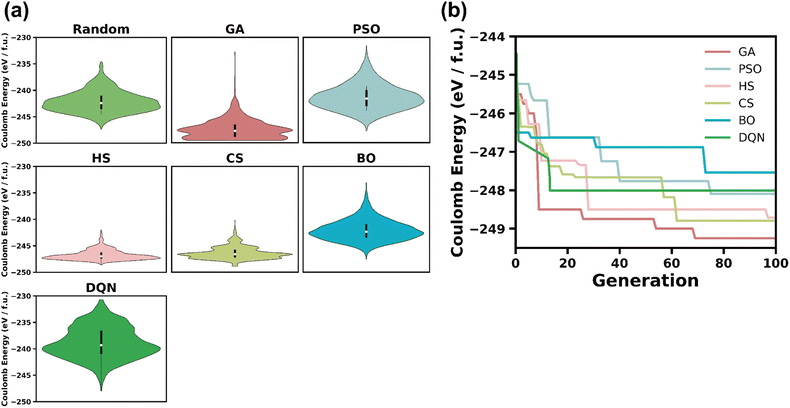
There might be a common misunderstanding that random sampling is appropriate for the selection of argyrodite configurations for use in the ensuing DFT and AIMD calculations. According to the fundamental statistics, even sampling approximately 2500 configurations would be sufficient to represent the total configurations, the number of which amounts to 1013, since the sample mean and variance would not deviate considerably from the ground truth for all configurations. It should be noted, however, that we are not concerned with the mean and variance prediction but instead with the search for an extreme value from the sample, namely, in pursuit of the lowest Coulomb energy. Accordingly, random sampling cannot catch up with this sort of extreme (minimum) search. We have to focus on only an extreme entry out of a sample batch that is randomly selected, and thereafter, we have to repeat this kind of extreme-targeted sampling procedure countless times. For instance, we have to reiterate the random sampling of 2500 configurations 100 times and the nomination of an extreme entry from every sample, which will finally secure 100 configurations with relatively low Coulomb energy values. The resultant average of these extremes was −247.20 eV f.u.−1 with a standard deviation of 0.35 eV f.u.−1. Fig. 3a shows violin plots for the distribution for an extreme sample nominated out of the 100 random samples (the size of each sample is 2500). This random-based extreme sampling process is hereinafter referred to simply as random sampling. Fig. 3a also shows the other data distributions produced by all the optimization algorithms. The configuration selection from the random sample distribution would be time-consuming, and the selected entries would not represent the ground state configuration. Violin plots for the data produced by the GA, HS, and CS algorithms are located toward the lower Coulomb energy side, while the others, including the random sample, distribute upward. It appears that the PSO, BO, and DQN algorithms did not work out by considering the fact that the data distributions produced by these three optimization algorithms do not seem to be improved from the random sample distribution. However, the extreme value (the minimum) obtained by these three algorithms is slightly lower than that for the random sampling, as shown in Table 1. This finding is extraordinarily differs from the benchmark function test result. The violin plot for the benchmark function data distribution exhibits the ordinary propensity, namely, where all the distributions produced by the optimization algorithms are located toward the far lower Coulomb energy side than that for the random sampling, as evidenced in Fig. S3.†Rather than the nomination of minimum Coulomb energy from a single random sampling, the 100 extreme (minimum) values were extracted from the 100 random samples, each of which consists of 2500 configurations. This means that we reached the averaged minimum of −247.20 eV f.u.−1 from the 100 samples (250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations in total), but a conventional single random sampling (even if we enhanced the number of configurations in the sample) would never make it possible to reach this level. The optimization algorithm should be employed to reach as close to the global minimum as possible. The use of the optimization algorithm would be more appropriate in finding energetically stable configurations than the present random sampling that is even more reasonable than the conventional single random sampling. On this ground, Table 1 shows the Coulomb energy values that were minimized by every optimization algorithm and includes a random sampling result at the same expense of computational costs (that is, the same number of objective function evaluations). All the optimization algorithms gave rise to lower Coulomb energy than random sampling. In particular, GA exhibits an outstanding record (−249.27 eV f.u.−1), which might be presumed to be close to a global optimum. Despite the 100 times greater number of evaluations, random sampling could never reach this level.
000 configurations in total), but a conventional single random sampling (even if we enhanced the number of configurations in the sample) would never make it possible to reach this level. The optimization algorithm should be employed to reach as close to the global minimum as possible. The use of the optimization algorithm would be more appropriate in finding energetically stable configurations than the present random sampling that is even more reasonable than the conventional single random sampling. On this ground, Table 1 shows the Coulomb energy values that were minimized by every optimization algorithm and includes a random sampling result at the same expense of computational costs (that is, the same number of objective function evaluations). All the optimization algorithms gave rise to lower Coulomb energy than random sampling. In particular, GA exhibits an outstanding record (−249.27 eV f.u.−1), which might be presumed to be close to a global optimum. Despite the 100 times greater number of evaluations, random sampling could never reach this level.
Fig. 3b shows the argyrodite configuration optimization execution results for all the algorithms, namely, the plot of Coulomb energy (objective function) as a function of the generation number. The Coulomb energy gradually decreases as the algorithm proceeds toward later generations. The term ‘generation’ originated from the GA, but we used it in common for every algorithm for convenience since all the algorithms are population-based. Of course, both the BO and DQN algorithms are not population-based. The generation can be, however, regarded simply as the 25 evaluations of the objective function in these cases. The plot of Coulomb energy versus the generation number is in a typically decreasing form, similar to those for the benchmark function-based optimization shown in Fig. S1, ESI.† The initial drastic drop was followed by a retarded decrease for all the metaheuristics, as shown in Fig. 3b. In particular, the GA appears to outperform the other metaheuristics, but it was proven that every metaheuristic worked out to a certain extent and thereby gave acceptable Coulomb energy values that are lower than those from random sampling. While PSO outperforms the other metaheuristics for most benchmark function tests, as shown in Fig. S1, ESI,† the GA is the best for the argyrodite configuration optimization, as evidenced in Fig. 3a and b, wherein the objective function value converged earlier for the GA and the converged value is lower than any other algorithms. In contrast to the benchmark function test, PSO gave a disappointing result, namely, the PSO-nominated minimum Coulomb energy is relatively high in comparison to the GA-nominated, and the PSO data distribution, shown in Fig. 3a, also looks to be the worst, which is almost identical to the random data distribution. Although the minimum objective function values obtained from the PSO, BO, and DQN algorithms are still lower than the minimum from random sampling, the overall data distribution for the PSO, BO, and DQN data never appears to be improved from the random data distribution, as shown in Fig. 3a. This sort of disappointing performance for the PSO algorithm seems unusual when referring to the benchmark function-based optimization shown in Fig. S1, ESI.† By invoking the fact that the optimization performance is strongly dependent on the shape of the objective function, the successful benchmark function test never guarantees success for a real-world optimization task since the objective function terrain for the real-world optimization task always remains unknown. That is why we had a discrepancy between the benchmark function test result and the real-world argyrodite configuration optimization result.
Rather than using the comparison between the optimization algorithms adopted in the present investigation, it is more important to refer to the result from the conventional random sampling and to mention the superiority of the optimization algorithm to the random sampling. We eventually sampled 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations (2500 configurations/sample × 100 samples) in total through the random process, and the minimum Coulomb energy among all those samples was −248.18 eV f.u.−1. As described above, the average of minimum values that were extracted from 100 random samples, each of which includes 2500 configurations, was −247.20 eV f.u.−1. A comparison should be made between the optimization algorithm result and the averaged minimum from the 100 random samples, including 250
000 configurations (2500 configurations/sample × 100 samples) in total through the random process, and the minimum Coulomb energy among all those samples was −248.18 eV f.u.−1. As described above, the average of minimum values that were extracted from 100 random samples, each of which includes 2500 configurations, was −247.20 eV f.u.−1. A comparison should be made between the optimization algorithm result and the averaged minimum from the 100 random samples, including 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations, to secure a more consistent rationale for using the optimization algorithms. Note that all the optimization algorithms were equally executed based on 2500 evaluations. The random sampling results, at −247.20 eV f.u.−1 (the average of the minimums from 100 samples), are higher than those recommended by any of the optimization algorithms, although the PSO and DQN algorithms yielded a minimized Coulomb energy that is only slightly improved from the random sampling result.
000 configurations, to secure a more consistent rationale for using the optimization algorithms. Note that all the optimization algorithms were equally executed based on 2500 evaluations. The random sampling results, at −247.20 eV f.u.−1 (the average of the minimums from 100 samples), are higher than those recommended by any of the optimization algorithms, although the PSO and DQN algorithms yielded a minimized Coulomb energy that is only slightly improved from the random sampling result.
It should be noted that the total number of objective function evaluations for all the adopted optimization algorithms was equally 2500 (population sizes of 25 and 100 generations). Even DQN reached −248.1 eV f.u.−1 with less than 500 evaluations (Fig. 3b). The BO algorithm yielded a slightly worse performance in comparison to the other optimization algorithms. As shown in Fig. 3b, the minimum Coulomb energy obtained from the BO execution was slightly higher than those obtained from the other optimization algorithms, as shown in Table 1 and Fig. 3b, although it is still better than the random sampling result. There is no doubt that all the optimization algorithms used in the present investigation led to argyrodite configurations that exhibit lower Coulomb energy than the minimum obtained from the random sampling at the expense of the same computational cost, which implies that an equal number of evaluations on average led to a better outcome when adopting the integrated optimization strategy rather than the conventional random sampling.
We do not blindly trust the capabilities of BO, since it is our opinion that BO capability has been slightly exaggerated due to its outstanding merit that BO significantly reduces the computational cost for some expensive optimization problems. The expensive optimization problem represents a time- and cost-consuming objective function evaluation. Although the BO execution yielded an acceptable result and remarkably outperformed the random sampling when using the simple benchmark functions (Table S1†), it showed no such conspicuous improvement in comparison to the random sampling for the real-world argyrodite configuration optimization. The use of GPR seems inappropriate to simulate the Coulomb energy terrain over the configurational space. GPR is only suitable in smooth, continuous objective function terrain. However, the Coulomb energy terrain over the argyrodite configuration is supposed to be neither smooth nor continuous. The introduction of other surrogate functions would improve the BO performance for real-world argyrodite configuration optimization, as suggested by Lei et al.59 However, the alternative surrogate functions that we adopted did not outperform the existing GPR-based BO for the Coulomb energy optimization for the argyrodite configuration determination, as shown in Fig. S4.† More importantly, since the metaheuristics, such as GA, PSO, HA, and CS, greatly outperformed BO, the improved BO algorithms would make no sense in the present investigation.
DFT and MD calculations for selected argyrodite configurations
In advance of the DFT and AIMD calculations, it is a prerequisite to confirm a strong correlation between the Coulomb energy and the DFT-calculated total energy since we employed the easy-to-evaluate Coulomb energy instead of the expensive DFT-calculated total energy as an objective function for the configuration optimization process. Fig. 2b shows a clear linear relationship between the Coulomb energy and the DFT-calculated total energy for some randomly chosen argyrodite configurations. The DFT-calculated total energy for the ten nominated configurations are also included in Fig. 2b and marked with red dots. Based on this finding, it was proven that the Coulomb energy is acceptable as a surrogate criterion for use in configuration selection, and thereby, we secured the ten argyrodite configurations with the lowest Coulomb energies, regardless of which optimization algorithm recommended them. Eight of them came from the GA algorithm, and the other two came from HS and CS. Fig. 4 shows the ten nominated configurations in the simplified schematic manner. These low-Coulomb-energy entries were further DFT-relaxed and finally used for the ensuing AIMD calculations.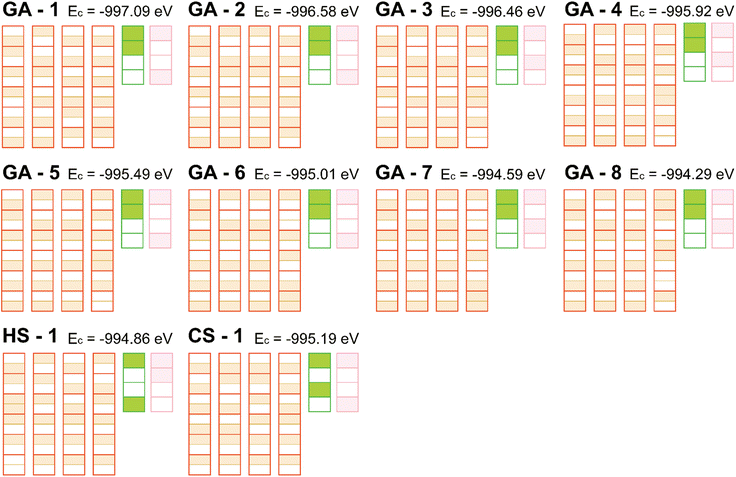 | ||
| Fig. 4 Ten configurations in the simplified schematic manner, nominated by the integrated optimization strategy. | ||
The ten finally nominated argyrodite configurations are utilized for the ensuing DFT and AIMD calculations, and thereby, we validated that the calculated result is more convincing in comparison with those from the random sampling. The AIMD calculations for the ten selected argyrodite configurations enabled us to estimate the Li+ ionic conductivity. Seven temperatures were selected for the calculation of mean-squared displacement (MSD) as a function of time interval (Δt). The diffusivity was obtained from the slope of the MSD over Δt by referring to the Einstein relation. The Li+ ionic conductivity was also obtained from the diffusivity calculated according to the Nernst–Einstein relation. The activation energy was obtained from the Arrhenius plot of diffusivity vs. temperature, and thereby, the Li+ ionic conductivity at room temperature was finally evaluated through the extrapolation process. Fig. 5 shows the Arrhenius plot of diffusivity vs. temperature for the ten nominated configurations. We used pymatgen34,84 and mostly followed the protocol for the AIMD-based diffusivity calculation suggested by Ong et al.34 and He et al.84 The extrapolated room temperature diffusivity is marked in red, and the blue pentacle with an error bar stands for the average room temperature diffusivity obtained from the ten extrapolated data points (the mean and standard deviation for all ten red dots in Fig. 5). Table 2 shows the calculated room-temperature Li+ ionic conductivity values for the ten low-Coulomb-energy configurations along with some other calculated and experimental results reported in the literature. We suggest that the average conductivity value from the ten Li+ ionic conductivity values should be a more representative value for argyrodite. Since the previously reported values from the literature are lacking and even the calculated and experimental values are scattered, a legitimate Li+ ionic conductivity value for argyrodite is not clearly defined. However, the Li+ ionic conductivity values for some of the suggested configurations (4.67 and 4.28 mS cm−1) were similar to the experimental values (2.7 ± 1.26 mS cm−1), despite the overall overestimation of the calculated conductivity, which is a general trend. The proposed strategy would be a starting guideline for future computational Li+ ionic conductivity.
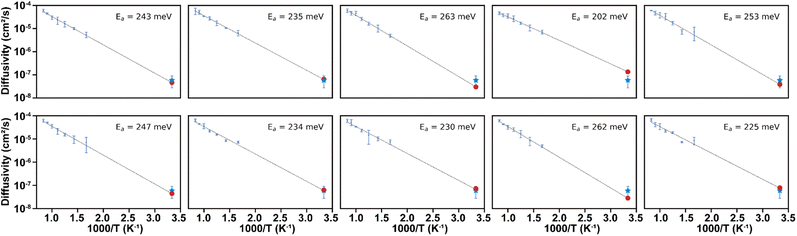 | ||
| Fig. 5 Arrhenius plot for ten selected low-Coulomb-energy configurations. The error bar stands for the uncertainty for the diffusivity at each temperature. | ||
| Material | Ea (meV) | Diffusivity (cm2 s−1) | Conductivity (mS cm−1) | Source |
|---|---|---|---|---|
| a a: ref. 4, b: ref. 5, c: ref. 6, d–i: ref. 10–15. | ||||
| Li6PS5Cl (GA-1) | 243 | 4.63 × 10−8 | 7.08 | Ab initio (MSD) |
| Li6PS5Cl (GA-2) | 235 | 6.33 × 10−8 | 9.68 | Ab initio (MSD) |
| Li6PS5Cl (GA-3) | 263 | 3.06 × 10−8 | 4.67 | Ab initio (MSD) |
| Li6PS5Cl (GA-4) | 202 | 1.36 × 10−7 | 20.87 | Ab initio (MSD) |
| Li6PS5Cl (GA-5) | 253 | 3.93 × 10−8 | 6.01 | Ab initio (MSD) |
| Li6PS5Cl (GA-6) | 247 | 4.41 × 10−8 | 6.75 | Ab initio (MSD) |
| Li6PS5Cl (GA-7) | 234 | 6.00 × 10−8 | 9.19 | Ab initio (MSD) |
| Li6PS5Cl (GA-8) | 230 | 6.71 × 10−8 | 10.27 | Ab initio (MSD) |
| Li6PS5Cl (HS-1) | 262 | 2.80 × 10−8 | 4.28 | Ab initio (MSD) |
| Li6PS5Cl (CS-1) | 225 | 7.64 × 10−8 | 11.69 | Ab initio (MSD) |
| Li6PS5Cla | 524 | — | 2 × 10−3 | Ab initio (MSD) |
| Li6PS5Clb | 130–270 | — | 40 | Ab initio (MSD) |
| Li6PS5Clc | 190 | — | — | Ab initio (MSD) |
| Li6PS5Cld | 350 | — | 3.1 | Experimental |
| Li6PS5Cle | 340 | — | 2.5 | Experimental |
| Li6PS5Clf | 330 | — | 1.33 | Experimental |
| Li6PS5Clg | 160 | — | 4.96 | Experimental |
| Li6PS5Clh | — | — | 2.4 | Experimental |
| Li6PS5Cli | 380 | — | 1.9 | Experimental |
Conclusions
Based on the correlation between the Coulomb energy and DFT-calculated total internal energy, we pursued the ground-state energy of argyrodite by screening the large configurational space in terms of the easy-to-evaluate Coulomb energy. The screening process was greatly facilitated by adopting several optimization algorithms, such as the GA, PSO, HS, CS, BO and DQN. The usability and validity of these algorithms was confirmed by employing six well-known benchmark test functions: the Ackley, Egg Crate, Griewank, Rastrigin, Rosenbrock, and Sphere functions.Although the benchmark function test resulted in an acceptable result for all the optimization algorithms, the real-world argyrodite configuration optimization resulted in a disappointing result for some optimization algorithms. The GA, HS, and CS exhibited promising optimization performances both for the benchmark function test and the real-world argyrodite configuration optimization. However, PSO gave a disappointing performance for the real-world argyrodite configuration optimization, while an excellent performance was observed for the benchmark function test. In particular, the BO algorithm was worst among all the optimization algorithms for real-world argyrodite configuration optimization. It was found that the optimization performance is extremely dependent upon the objective function terrain, but no one method can surmise the objective function terrain in advance of the adoption of optimization algorithms. In this regard, the integrated optimization strategy that we suggested in the present investigation would work out rather than the use of a single specific optimization algorithm only.
Ten final argyrodite configuration candidates exhibiting the lowest Coulomb energies were identified by the GA, CS, and HS (eight from the GA and two from CS and HS). Although the lowest-Coulomb-energy entry could not directly lead to a ground state configuration corresponding to the lowest DFT-calculated total internal energy, several lowest-Coulomb-energy entries were recommended, and their averaged DFT-calculated total internal energy could represent a real-world ground state.
The diffusivity at several temperatures was calculated via AIMD calculations to constitute the Arrhenius plot, from which the activation energy and eventually the room temperature Li+ ionic conductivity were evaluated. A representative room temperature Li+ ionic conductivity value was ultimately estimated to be 9.05 ± 4.82 mS cm−1 by averaging the ten final argyrodite configurations. Although it is not possible to pinpoint a definite true conductivity value since all the reported values are diverse irrespective of whether they are experimental or computational, it is worth appreciating our averaged conductivity value thanks to the concrete rationale behind the evaluation procedures.
Code availability
The code used for this study is available at https://github.com/socoolblue.Data availability
The data used for this study are available in the ESI.†Author contributions
K.-S. S. and W. B. P. conceived the concept for the entire process and directed the computational process. W. B. P. and B. D. L. performed DFT and AIMD calculations. B. D. L., J. P., and J. W. L. participated in coding optimization algorithms. W. B. P., M.-Y. C., and B. D. L. prepared the figures and tables. K.-S. S. wrote the paper. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT, and Future Planning (2021R1A2C1009144), (2021R1A2C1011642) and (2021M3A7C2089778) and partly by the Alchemist project (20012196) funded by MOTIE, Korea. Byung Do Lee and Jin-Woong Lee contributed equally to this work.References
- J. O. Besenhard, Handbook of Battery Materials, Wiley-VCH, New York, 1999 Search PubMed.
- D. Linden and T. B. Reddy, Handbook of Batteries, McGraw-Hill, New York, 3rd edn, 2002 Search PubMed.
- G. Pistoia, Lithium Batteries: New Material, Developments and Perspectives, Elsevier, New York, 1994 Search PubMed.
- Z. Deng, Z. Y. Zhu, I. H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288 CrossRef CAS.
- N. J. J. de Klerk, I. Rosłoń and M. Wagemaker, Chem. Mater., 2016, 28, 7955–7963 CrossRef CAS.
- A. R. Stamminger, B. Ziebarth, M. Mrovec, T. Hammerschmidt and R. Drautz, Chem. Mater., 2019, 31, 8673–8678 CrossRef CAS.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758 CrossRef CAS.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858 CrossRef CAS.
- P. Adeli, J. D. Bazak, A. Huq, G. R. Goward and L. F. Nazar, Chem. Mater., 2021, 33, 146–157 CrossRef CAS.
- P. Adeli, J. D. Bazak, K. H. Park, I. Kochetkov, A. Huq, G. R. Goward and L. F. Nazar, Angew. Chem., Int. Ed., 2019, 58, 8681–8686 CrossRef CAS PubMed.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1–5 CrossRef CAS.
- C. Yu, S. Ganapathy, J. Hageman, L. van Eijck, E. R. H. van Eck, L. Zhang, T. Schwietert, S. Basak, E. M. Kelder and M. Wagemaker, ACS Appl. Mater. Interfaces, 2018, 10, 33296–33306 CrossRef CAS.
- L. Zhou, K.-H. Park, X. Sun, F. Lalère, T. Adermann, P. Hartmann and L. F. Nazar, ACS Energy Lett., 2019, 4, 265–270 CrossRef CAS.
- R. P. Rao and S. Adams, Phys. Status Solidi A, 2011, 208, 1804–1807 CrossRef CAS.
- A. N. Andriotis, R. M. Sheetz, E. Richter and M. Menon, J. Phys.: Condens. Matter, 2014, 26, 055013 CrossRef CAS.
- L. Bellaiche and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7877–7882 CrossRef CAS.
- S.-H. Jhi, J. Ihm, S. G. Louie and M. L. Cohen, Nature, 1999, 399, 132–134 CrossRef CAS.
- N. J. Ramer and A. M. Rappe, J. Phys. Chem. Solids, 2000, 61, 315–320 CrossRef CAS.
- N. J. Ramer and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R743–R746 CrossRef CAS.
- R. Niklaus, J. Minár, J. Hausler and W. Schnick, Phys. Chem. Chem. Phys., 2017, 19, 9292–9299 RSC.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- Y. S. Meng and M. E. Arroyo-de Dompablo, Energy Environ. Sci., 2009, 2, 589–609 RSC.
- A. Van der Ven, M. K. Aydinol, G. Ceder, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2975–2987 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- P. Rivero, I. D. P. R. Moreira, R. Grau-Crespo, S. N. Datta and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085108 CrossRef.
- T. Shibuya, Y. Goto, Y. Kamihara, M. Matoba, K. Yasuoka, L. A. Burton and A. Walsh, Appl. Phys. Lett., 2014, 104, 021912 CrossRef.
- B. Winkler, C. Pickard and V. Milman, Chem. Phys. Lett., 2002, 362, 266–270 CrossRef CAS.
- L. Barroso-Luque, J. H. Yang and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 104, 224203 CrossRef CAS.
- D. de Fontaine, Solid State Phys., 1994, 47, 33–176 Search PubMed.
- F. Ducastelle, Order and Phase Stability in Equilibrated, Elsevier Science, New York, 1994 Search PubMed.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Phys. A, 1984, 128, 334–350 CrossRef.
- A. Seko, Y. Koyama and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165122 CrossRef.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6, 148–156 RSC.
- L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, Y. Park, J.-M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048–3055 CrossRef CAS.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef CAS.
- Q. Bai, X. He, Y. Zhu and Y. Mo, ACS Appl. Energy Mater., 2018, 1, 1626–1634 CrossRef CAS.
- Q. Bai, L. Yang, H. Chen and Y. Mo, Adv. Energy Mater., 2018, 8, 1702998 CrossRef.
- R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10, 1903719 CrossRef CAS.
- H. J. Bremermann, The Evolution of Intelligence: The Nervous System as a Model of Its Environment, University of Washington, Department of Mathematics, Washington, 1958 Search PubMed.
- J. H. Holland, Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence, MIT Press, Cambridge, 1992 Search PubMed.
- J.-W. Lee, S. P. Singh, M. Kim, S. U. Hong, W. B. Park and K.-S. Sohn, Inorg. Chem., 2017, 56, 9814–9824 CrossRef CAS.
- J. Kennedy and R. C. Eberhart, Particle swarm optimization, in Proceedings of the IEEE International Conference on Neural Networks, Piscataway, 1995 Search PubMed.
- M. Kim, S. P. Singh, S. Shim, W. B. Park and K.-S. Sohn, Chem. Mater., 2020, 32, 6697–6705 CrossRef CAS.
- Z. W. Geem, J. H. Kim and G. V. Loganathan, Simulation, 2001, 76, 60–68 CrossRef.
- X. S. Yang and S. Deb, Cuckoo Search via Levy Flights, in Proc. World Congress on Nature and Biologically Inspired Computing, Coimbatore, 2009 Search PubMed.
- J. Mockus, Bayesian Approach to Global Optimization: Theory and Applications, Springer, Dordrecht, 1989 Search PubMed.
- B. D. Lee, J.-W. Lee, M. Kim, W. B. Park and K.-S. Sohn, npj Comput. Mater., 2022, 8, 83 CrossRef CAS.
- V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra and M. Riedmiller, 2013, preprint, arXiv:1312.5602.
- H. B. Curry, Q. Appl. Math., 1944, 2, 258–261 CrossRef.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS.
- H. Fang and P. Jena, Nat. Commun., 2022, 13, 2078 CrossRef CAS PubMed.
- P. B. Jensen, S. Lysgaard, U. J. Quaade and T. Vegge, Phys. Chem. Chem. Phys., 2014, 16, 19732–19740 RSC.
- S. Lysgaard, D. D. Landis, T. Bligaard and T. Vegge, Top. Catal., 2014, 57, 33–39 CrossRef CAS.
- L. B. Vilhelmsen and B. A. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef.
- K.-S. Sohn, Optimization, 2022, https://github.com/socoolblue/optimization Search PubMed.
- R. M. Solgi, Geneticalgorithm, 2020, https://github.com/rmsolgi/geneticalgorithm Search PubMed.
- N. Rooy, Particle-Swarm-Optimization, 2016, https://github.com/nathanrooy/particle-swarm-optimization Search PubMed.
- B. Lei, T. Q. Kirk, A. Bhattacharya, D. Pati, X. Qian, R. Arroyave and B. K. Mallick, npj Comput. Mater., 2021, 7, 194 CrossRef.
- D. G. T. Denison, B. K. Mallick and A. F. M. Smith, Stat. Comput., 1998, 8, 337–346 CrossRef.
- J. H. Friedman, Multivariate adaptive regression splines, Ann. Stat., 1991, 19, 1–67 Search PubMed.
- H. A. Chipman, E. I. George and R. E. McCulloch, Ann. Appl. Stat., 2010, 4, 266–298 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- Z. Li, J. R. Kermode and A. D. Vita, Phys. Rev. Lett., 2015, 114, 096405 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminf., 2016, 8, 17 Search PubMed.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- W. G. Han, W. B. Park, S. P. Singh, M. Pyo and K.-S. Sohn, Phys. Chem. Chem. Phys., 2018, 20, 26405–26413 RSC.
- D. H. Ackley, A connectionist machine for genetic hillclimbing, Springer New York, NY, 1987 Search PubMed.
- M. Jamil and X.-S. Yang, Int. J. Math. Model. Numer. Optim., 2013, 4, 150–194 Search PubMed.
- A. O. Griewank, J. Optim. Theory Appl., 1981, 34, 11–39 CrossRef.
- L. A. Rastrigin, Systems of External Control Systems, Nauka, Moscow, 1974 Search PubMed.
- H. H. Rosenbrock, Comput. J., 1960, 3, 175–184 CrossRef.
- M. Schumer and K. Steiglitz, IEEE Trans. Autom. Control, 1968, 13, 270–276 CrossRef.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05889h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |