Synthesis of Ca(OH)₂ and Na₂CO₃ through anion exchange between CaCO₃ and NaOH: effect of reaction temperature

Abstract

The CO₂ released upon calcination of limestone accounts for the largest portion of the emissions from the cement, lime, and slaked lime manufacturing industries. Our previous works highlighted the possibility for a no-combustion decarbonisation of CaCO₃ through reaction with NaOH solutions to produce Ca(OH)₂ at ambient conditions, while sequestrating the process CO₂ in a stable mineral Na₂CO₃·H₂O/Na₂CO₃. In this study, the effect of temperature was assessed within the range of 45–80 °C, suggesting that the process is robust and only slightly sensitive to temperature fluctuations. The proportioning of the precipitated phases Na₂CO₃·H₂O/Na₂CO₃ was also assessed at increasing NaOH molalities and temperatures, with the activity of water playing a crucial role in phase equilibrium. The activation energy (E_a) of different CaCO₃ : NaOH : H₂O systems was assessed between 7.8 kJ·mol⁻¹ and 32.1 kJ·mol⁻¹, which is much lower than the conventional calcination route. A preliminary energy balance revealed that the chemical decarbonisation route might be ∼4 times less intensive with respect to the thermal one. The present work offers a further understanding of the effect of temperature on the process with the potential to minimise the emissions from several energy-intensive manufacturing processes, and correctly assess eventual industrial applicability.

---

1 Introduction

The calcination of limestone to give lime (CaCO₃ → CaO + CO₂) is a crucial step for the production of Portland cement (PC), lime (CaO), slaked lime (Ca(OH)₂), and soda ash (Na₂CO₃), whose worldwide markets exceed 4 Gt,¹ ∼55 Mt, ∼15 Mt,² and 50 Mt ³ per year, respectively. Given the heavy carbon footprint of such calcination step,⁴ these industrial realities are responsible for a significant portion of the total CO₂ emissions worldwide.^1,5,6 Depending on the targeted product, the very energy-intensive⁷ calcination of limestone might occur in different calcination designs, with varying efficiencies and carbon emissions;⁸ specifically, 0.8, 1.0–1.8, and 0.4 t CO₂ are emitted to produce 1 t of cement, lime/slaked lime, and soda ash, respectively. However, independently from the calcination unit considered, the emissions arising from this step arise from both the fuel-derived and process CO₂. While the process CO₂ results from the stoichiometry of CaCO₃ decomposition, the fuel-derived emissions arise from combustion of fuels (primarily fossil fuels) necessary to achieve the calcination temperature (above 900 °C).⁹ The achievement of those environmental goals set by the UN in 2015 (at least 80% of CO₂ emission cut from the industry sector by 2050¹⁰) requires a significant contribution from the cement, lime, and soda ash industries. To achieve this, the application of carbon capture and storage (CCS) technologies¹¹ and the use of alternative fuels¹² are expected to be the best candidates; however, both these solutions assume that the thermal calcination of limestone (and the process CO₂) is unavoidable. In contrast to this, recent investigations^13–16 highlighted the possibility for alternative decarbonisation routes which apply no-combustion approaches for the synthesis of the essential chemical CaO¹⁷ from CaCO₃. As far as we are aware, the chemical decarbonisation route here characterised represents the only alternative for the sustainable co-synthesis of Ca(OH)₂ and Na₂CO₃. The stoichiometry of the key-reaction is reported in eqn (1); it occurs at ambient conditions and implies the reaction between CaCO₃ and aqueous NaOH solutions.

CaCO₃ + 2NaOH + xH₂O → Ca(OH)₂ + Na₂CO₃·xH₂O (1)

The process is relatively simple; however, the full fundamental understanding of the system is necessary to determine the feasibility of any scaled-up industrial process, and the reaction rate is assessed in this work. The reaction rate may be defined through eqn (2),¹⁸ where the variables t, T, and α (with 0 < α < 1) represent the reaction time, temperature, and extent of reaction, respectively.¹⁸ The function f(α) represents the kinetic reaction model depending on the mechanism assessed,¹⁹ while f(T) reflects the Arrhenius equation (eqn (3)), depending on the temperature (T), the activation energy (E_a), and the pre-exponential factor (A).

∂α/∂t = f(T) × f(α) (2)

Despite the mild temperature range here considered (45–80 °C), it is crucial to assess the response of a given process to eventual fluctuations; ideally, a robust route would not be significantly affected by these variations in the processing parameters. The title study aims to gain a deeper insight into the behaviour of the system considered at increasing temperatures, therefore providing essential information for any eventual scale-up.

2 Materials and methods

2.1 Experimental procedure

The materials used in this work are reagent grade chemicals: Sigma-Aldrich CaCO₃ (≥99%), Honeywell Fluka NaOH (≥97%), and distilled water. The ternary composition (wt%) 26.9 (CaCO₃) : 32.7 (NaOH) : 40.4 (H₂O) was first investigated, allowing for a 0.86 conversion efficiency (α) in a previous study;¹⁶ therefore, a 20 M NaOH (mol kg_H2O⁻¹) was first considered. The relatively high water to solids ratio (1.5 g g⁻¹) ensured homogeneous mixing of the solid powders even at milder stirring conditions, as described below, with respect to a previous characterisation.¹⁴

The experimental set up is illustrated in Fig. 1. The 20 m NaOH solutions were prepared in a polypropylene plastic vessel, and placed in the pre-heated water bath for 30 min at the target temperatures T_k of 45 °C, 60 °C, or 80 °C.

Fig. 1 Illustration of the experimental set up discussed above, highlighting the indirect temperature control on the reaction system by setting the surrounding water environment at a T_k temperature through external thermocouple.

Direct contact between the hot plate and the bottom of the reaction vessel was avoided through the placement of an insulating glass disk. The CaCO₃ powders were also pre-heated at 80 °C for 2 hours to remove excess water. The CaCO₃ was then quickly added to the NaOH solutions and manually mixed, at first, to prevent the agglomeration of the solids. Subsequently, the vessel was covered with a lid to minimise the loss of water and heat throughout the reaction; a magnetic stirring of 300 rpm was set up at increasing residence times of 1, 2, 3, 4 and 5 min. Longer residence times were not considered, since our previous study¹⁴ highlighted that negligible reaction progression would occur beyond 5 min. The reaction was also performed in non-isothermal conditions, upon initial heating of the NaOH solutions at the targeted temperatures T_i of 45 °C, 60 °C, and 80 °C (to be referred as 45 °C_5 min_RT, 60 °C_5 min_RT, and 80 °C_5 min_RT, respectively). A residence time of 5 min was solely considered to produce these samples.

Upon reaction, all the pastes were mixed with methanol (30 mL) for further 5 min, ensuring the removal of the unreacted NaOH, whose solubility in methanol is 238 g L⁻¹;²⁰ whereas, the negligible solubility of CaCO₃,²¹ Ca(OH)₂,²² Na₂CO₃ (ref. 23) and Na₂CO₃·H₂O²³ in methanol would ensure an unmodified solid phase assemblage upon washing. The solid products and the liquid streams could then be collected separately using Buchner filtration. The solids were dried at 80 °C for 2 h, before being manually ground and sieved below 63 μm for subsequent characterisation though thermogravimetry and X-ray diffraction.

An additional set of experiments was conducted to estimate the E_a of the decarbonisation reaction at different ternary compositions (Table 1), selected from our previous study.¹⁶ The same procedure described above was applied here, with the solids being reacted for 1 min at constant temperatures T_k of 30 °C, 45 °C, 60 °C and 70 °C. The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.

Table 1 Starting compositions (wt%) and the molar ratio NaOH/CaCO₃ of the samples. The parameter labelled as α reflects the conversion extent values (0 < α < 1) of CaCO₃ into Ca(OH)₂ reported in our previous study

ID	NaOH (wt%)	CaCO3 (wt%)	H2O (wt%)	NaOH/CaCO3 (mol mol^−1)	H2O/CaCO3 (g g^−1)	H2O/NaOH (mol mol^−1)	α^16
NaOH_10m	14.3	14.3	71.4	2.5	3.0	5.5	0.07
NaOH_12m	24.5	24.5	51.0	2.5	2.1	4.6	0.46
NaOH_15m	30.1	20.0	49.9	3.8	2.5	3.7	0.69
NaOH_17m	37.2	8.1	54.7	11.5	6.7	3.3	0.96

---

2.2 Characterisation techniques

2.2.1 X-ray diffraction (XRD). The reaction products were qualitatively identified by X-ray diffraction (XRD) and following analysis on the Highscore-Plus software with the PDF⁻⁴ 2019 database. The measurements were performed using a Bruker D2 PHASER desktop X-ray diffractometer in the Bragg–Brentano geometry equipped with a CuKα radiation source running at 30 kV and 10 mA. The instrument is equipped with a one-dimensional LYNXEYE detector and a 1 mm divergence slit. All samples were in a powder form, and they were loaded onto the sample holder with 2.5 cm diameter and 1 mm deep. All the analyses were conducted between 5° and 80° (2θ) with a step size of 0.02° at 0.5 s per step, with the stage rotating at 15 rpm to improve counting statistics.

2.2.2 Thermogravimetry (TG/DTG). A PerkinElmer TGA 4000 was used to provide thermogravimetric analysis (TGA) for the reaction products; approximately 40 mg of sample were subjected to a temperature ramp from 30 °C to 800 °C at the heating rate of 10 °C min⁻¹, with a 40 mL min⁻¹ of N₂ flow. The heating program was set up to held the sample at 800 °C for 1 hour to ensure complete loss of CO₂ from CaCO₃; the analysis temperature was not exceeding 800 °C to avoid the melting or weight loss from Na₂CO₃. To identify evolving gases, a Hiden mass spectrometer (HPR-20 GIC EGA) was used to record the signals for CO₂ and H₂O. An example of TG analysis is presented in Fig. 2, where the mass loss events are linked to Ca(OH)₂, Na₂CO₃·H₂O and CaCO₃. Together with the weight loss, the DTG trend is also reported to ensure the distinction of eventual overlapping signals. The extent of reaction was calculated based on the amount of Ca(OH)₂ (ref ²⁴) and unreacted CaCO₃,²⁵ based on the respective thermal decompositions. The content of Na₂CO₃·H₂O could similarly be estimated in the temperature range 50–130 °C.²⁶

Fig. 2 Generic temperature-trend of the TG data (wt%) and DTG data (wt%/⁰C), red and black lines, respectively, showing the weight loss events of the sample associated with: Na₂CO₃·H₂O, Ca(OH)₂, and CaCO₃.

The measurement was repeated 6 times for each sample to estimate the measurement error (±0.16 wt%, ± 0.10 wt% and ± 0.16 wt% for Na₂CO₃·H₂O, Ca(OH)₂ and CaCO₃, respectively).

3 Theory

This investigation aims to provide the scientific community with a deeper insight into the chemistry and energetic demand of a novel CaCO₃ decarbonisation route,¹⁶ with the potential to lead the transition towards sustainable cement, lime, and soda ash industries. To highlight this, an energetic comparison with the state-of-the-art processes is presented in Section 5, highlighting the potential advantages of the alternative one. To do that, the concomitant by-production of soda ash Na₂CO₃ was also considered, whose conventional manufacturing route through Solvay process requires a high energy supply. This early-stage investigation, together with other ones focusing on the processing conditions¹⁴ and the nature of the raw materials used,¹⁵ will provide a strong base to the potential scale-up of the process. In these terms, future work will aim to design a laboratory-scale process simulating the ideal industrial one, providing a stronger dataset to assess the effective energy requirements of the route, and therefore allowing for a proper techno-economic analysis.

4 Results and discussion

4.1 Effect of temperature and CO₂ capture

The XRD analysis of the 45 °C_n, 60 °C_n, and 80 °C_n samples are shown in Fig. 3A–C, respectively.

Fig. 3 XRD patterns for the samples produced at a constant temperature of 45 °C (A), 60 °C (B), and 80 °C (C), and increasing residence times; the patterns also include those samples produced at ambient conditions and with an initial temperature of 45 °C, 60 °C, and 80 °C.

Upon reaction, only Ca(OH)₂ (ICSD collection code: #191851), Na₂CO₃ (ICSD collection code: #5009), Na₂CO₃·H₂O (ICSD collection code: #1852), and unreacted CaCO₃ (ICSD collection code: #80869) could be detected, with respective main reflection angles at 2θ of 29.5°,²⁷ 34.1°,²⁸ 16.9° (ref. 29) and 30.1°.³⁰ No additional phases were detected, suggesting the absence of secondary and competing reactions. The TG data for the 45 °C_n, 60 °C_n and 80 °C_n series is shown in Fig. 4A–C, respectively.

Fig. 4 TG/dTG analysis for the samples series 45 °C_n (A), 60 °C_n (B), and 80 °C_n (C) showing the weight losses in the temperature ranges of 50–130 °C, 310–470 °C and 560–800 °C corresponding to the presence of Na₂CO₃·H₂O, Ca(OH)₂ and CaCO₃, respectively.

The phase quantification was performed through the weight losses observed in the TG data for CaCO₃ (at 560–800 °C), Ca(OH)₂ (at 310–470 °C) and Na₂CO₃·H₂O (at 50–130 °C). The estimated quantities for all the samples discussed are summarised in Table 2, where the processing conditions used are also reported.

Table 2 Processing conditions and phases composition (wt%) gained from thermogravimetric analysis, together with the Loss On Ignition (LOI) expressed in % and the Na₂CO₃·H₂O/Ca(OH)₂ molar ratio registered for all the samples discussed

Sample ID	CaCO3 (wt%)	Ca(OH)2 (wt%)	Na2CO3·H2O (wt%)	Na2CO3 (wt%)	LOI (%)	Na2CO3·xH2O/Ca(OH)2 (mol%/mol%)
45 °C_1 min	13.7	34.5	6.6	45.2	15.4	1.1
45 °C_2 min	6.4	35.6	23.6	34.4	14.9	1.1
45 °C_3 min	4.2	34.3	55.9	5.6	18.3	1.1
45 °C_4 min	4.8	32.9	59.6	2.7	18.8	1.1
45 °C_5 min	3.2	33.5	61.6	1.7	18.5	1.1
45 °C_RT_5 min	4.6	34.7	57.0	3.7	18.7	1.1
60 °C_1 min	8.9	34.8	15.1	41.2	14.6	1.1
60 °C_2 min	4.5	36.8	18.0	40.7	13.5	1.1
60 °C_3 min	4.2	37.7	8.6	49.5	12.2	1.1
60 °C_4 min	4.3	36.7	8.9	50.1	15.0	1.1
60 °C_5 min	3.1	37.8	11.1	48.0	12.2	1.1
60 °C_RT_5 min	3.2	33.5	61.6	1.7	18.5	1.1
80 °C_1 min	8.5	34.7	11.1	45.7	13.8	1.2
80 °C_2 min	6.1	35.9	11.0	47.0	13.0	1.2
80 °C_3 min	5.2	36.1	6.6	52.1	12.0	1.2
80 °C_4 min	5.5	36.1	7.9	50.5	12.3	1.2
80 °C_5 min	5.2	35.8	11.2	47.8	12.6	1.2
80 °C_RT_5 min	6.0	35.2	15.0	43.8	13.4	1.2

---

It must be mentioned that the content of Na₂CO₃ was calculated by subtracting the sum of the other quantified phases Ca(OH)₂, CaCO₃ and Na₂CO₃·H₂O from the total mass (100%). In fact, since Na₂CO₃ would start decomposing above 851 °C,³¹ it could not be directly quantified by TG analysis (up to 800 °C) through the detection of the relevant peak. A higher content of Na₂CO₃ could also be suggested by the lower LOI registered for samples with similar reaction efficiencies (Table 2). This aspect will be extensively discussed in Section 3.2. However, the quantification was considered reliable since the XRD analysis confirmed the absence of any additional phases in the solid products. Moreover, the ratio between the precipitated Na₂CO₃·H₂O/Na₂CO₃ and Ca(OH)₂ (mol%/mol%) revealed a good accordance to the stoichiometry expressed in eqn (1) (Table 2). In fact, 1 mol of both Ca(OH)₂ and Na₂CO₃·H₂O/Na₂CO₃ should precipitate for each mol of CaCO₃ reacted, and the resulting molar ratio between Na₂CO₃·H₂O/Na₂CO₃ and Ca(OH)₂ was expected to be close to unity. Specifically, the ratios were suggesting a slight over-precipitation of Na₂CO₃·H₂O and Na₂CO₃ with respect to Ca(OH)₂ for all the systems studied and that could possibly be reflecting the distribution of the positive (Ca²⁺) and negative (CO₃²⁻) charged sites on the surface of the CaCO₃. Statistically, a 27% excess of negatively charged sites may be found on the CaCO₃ surface,³² justifying the greater affinity of the CaCO₃ to interact with the cationic species Na⁺ in the liquid bulk to form Na₂CO₃·H₂O/Na₂CO₃.

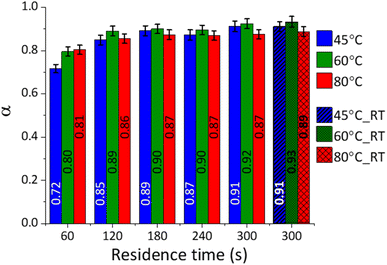
Based on the TG data, the extent of reaction (α) was calculated for each system, and the outcomes are reported in Fig. 5.

Fig. 5 Extent of reaction (α) for the samples at different temperatures (45, 60 and 80 °C)and increasing residence times, based on TG analysis; the outcomes are also reported for those samples produced without actively maintaining the temperature throughout the reaction.

The conversion of CaCO₃ was high (0.7 < α < 0.8) in the tested reaction conditions, in line with the qualitative XRD data (Fig. 3A–C), showing progressive decrease in the intensity of the CaCO₃ main peak at 29.5° 2θ. During the first minute, the system temperature had a significant impact on the extent of the reaction; enhanced conversion efficiencies were gained at higher temperatures, while limited effects were observed at longer residence times. It seems likely that the higher conversion registered at short residence times and higher temperatures could be linked to the lower viscosity of the NaOH solutions, favouring the ionic mobility and the enhanced interaction between the dissolved species and the solid surface and bulk.

The efficiency of the system may also be expressed in terms of CO₂ capture, expressed as moles of CO₂ precipitated as Na₂CO₃·xH₂O per second of reaction progression. As reported in Fig. 6, the CO₂ capture rate was decreasing from ∼4.5 × 10⁻⁴ mol sec⁻¹ of CO₂ in the first minute of reaction down to two orders of magnitude below (∼10⁻⁶ mol sec⁻¹ of CO₂) after 5 min of contact time. In other terms, around the 80% of the total process CO₂ initially introduced was effectively captured after 1 min of reaction.

Fig. 6 CO₂ capture rate, expressed in moles of CO₂ precipitated as Na₂CO₃·xH₂O per second of reaction progression, for all the residence times considered at constant temperature; the samples reacted at ambient conditions were not considered for this graph. The lines only work as a guide for the eye.

The samples reacted at ambient conditions (45 °C_5 min_RT, 60 °C_5 min_RT, and 80 °C_5 min_RT) indicated extent of reactions like those reacted at a constant temperature after 5 min (Fig. 5). Decreasing temperature trends could be detected for 45 °C_5 min_RT, 60 °C_5 min_RT, and 80 °C_5 min_RT, with final temperatures of 21.5, 42.1, and 53.6 °C, respectively, after 5 min of residence time. Evidently, the temperature of the system was not significantly influencing the progression of the reaction for a residence time of 5 min.

4.2 Partitioning of Na₂CO₃·H₂O and Na₂CO₃

The reaction at different conditions resulted in the sequestration of the process CO₂ through precipitation of Na₂CO₃·H₂O and Na₂CO₃ in different proportion, with the x value (eqn (1)) equal to 1 and 0, respectively. Based on the data obtained from TGA (Fig. 4A–C), the molar fraction ν of precipitated Na₂CO₃, with 0 < ν < 1, was calculated by dividing the moles of Na₂CO₃ in the samples by the total moles of Na₂CO₃·H₂O and Na₂CO₃. As introduced in Section 2.1, most samples were produced at a constant temperature (T_k = 45 °C, 60 °C, and 80 °C) whereas others were only initially set up at targeted temperature values (T_i = 45 °C, 60 °C, and 80 °C), following which the system was left at ambient conditions and was allowed to achieve Tf (with T_f < T_i). As reported in Fig. 7, the precipitation of Na₂CO₃ was dominant at T_k = 45 °C up to 2 min of reaction; beyond that, the precipitation of Na₂CO₃·H₂O was larger despite the constant temperature. Whereas, when considering the systems at T_k = 60 °C and T_k = 80 °C, the precipitation of Na₂CO₃ was dominant for all the residence times investigated.

Fig. 7 Molar fraction ν of Na₂CO₃, expressed as molar ratio between Na₂CO₃ and Na₂CO₃·H₂O, for the samples produced at 45, 60 and 80 °C at increasing residence times.

Different outcomes were observed when considering the samples reacted at ambient conditions, suggesting a key-role of the temperature on the equilibrium between Na₂CO₃·H₂O and Na₂CO₃. In fact, while Na₂CO₃·H₂O was dominant at T_i = 45 °C and T_i = 60 °C, with respective T_f values of 21.5 °C and 42.1 °C, Na₂CO₃ was the main species precipitating at T_i = 80° (T_f = 53.5 °C). Likely, such a different proportion gained at different values of T_i and T_f might be explained by considering the standard enthalpy of reaction ΔH_R for x = 0, 1 in eqn (1). The calculation was performed by application of the Hess law and considering standard enthalpies of formation of −1207.4, −426.7, −285.8, −986.1, −1429.7, and −1129.2 kJ mol⁻¹ for CaCO₃,³³ NaOH,³⁴ H₂O,³⁴ Ca(OH)₂,³⁴ Na₂CO₃·H₂O,³³ and Na₂CO₃,³³ respectively. It appears that the precipitation of Na₂CO₃·H₂O is enhanced at lower temperatures (ΔH_R = −69.2 kJ mol⁻¹) than that of Na₂CO₃ (ΔH_R = −54.5 kJ mol⁻¹), justifying the results just discussed. The XRD analysis (Fig. 3A–C) was qualitatively in accordance with the quantification of Na₂CO₃·H₂O and Na₂CO₃ gained from TGA for both the samples reacted at constant and varying temperatures. In fact, low contents of Na₂CO₃·H₂O (main peak at 16.9° 2θ) were suggested for all the samples reacted at T_k = 80 °C, whereas increased intensities were observed for the T_k = 45 °C series above 2 min of residence time and the sample reacted at ambient conditions with T_i = 60 °C.

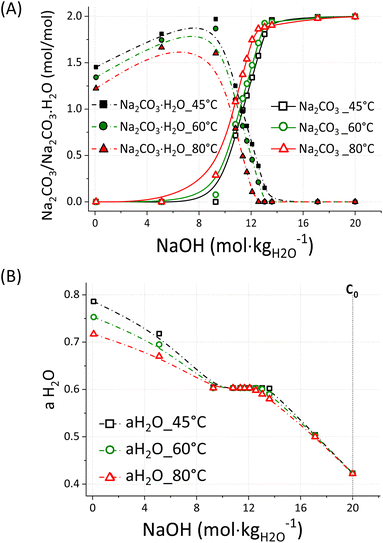
The equilibrium between Na₂CO₃·H₂O and Na₂CO₃ was studied by performing targeted simulations of a simplified system using the PHREEQC software³⁵ with the PITZER₍₂₀₁₈₎ database; an overview of the outcomes is reported in Fig. 8A and B.

Fig. 8 PHREEQC simulation showing the molar ratio between the precipitated Na₂CO₃ and Na₂CaO₃·H₂O (A) and the activity of water aH₂O (B) at 45, 60 and 80 °C and increasing NaOH molalities, up to 20 m; the concentration C₀ (B) indicates the initial NaOH concentration considered for the samples here discussed.

The simulations were conducted for a system composed of 1 mole of Na₂CO₃·H₂O and 1 mole of Na₂CO₃, both dissolved in 0.1 kg of water at T_k = 45 °C, T_k = 60 °C, and T_k = 80 °C, with increasing concentrations of NaOH up to 20 m. The simulated system does not contain Ca²⁺ ions as in the experimentally tested systems but it is useful to understand the general behaviour of Na₂CO₃·H₂O and Na₂CO₃ in highly concentrated NaOH solutions. As reported in Fig. 8A, Na₂CO₃·H₂O and Na₂CO₃ are the dominant species at [NaOH] < 10 m and [NaOH] > 12.5 m, respectively, while the co-precipitation of both species occurs at 10 m < [NaOH] < 12.5 m. Such behaviour might likely depend on the activity of water, which lowers at increasing solute concentrations and system temperature.³⁶ Given the higher proportion of Na₂CO₃ at T_k = 60 °C and T_k = 80 °C with respect to T_k = 45 °C, it is likely that such phase is favoured at a lower activity of water, i.e. higher temperature. However, an unexpected trend is shown in Fig. 7 for the samples reacted at T_k = 45 °C; in fact, Na₂CO₃ was the main phase up to 2 min of reaction, whereas the content of Na₂CO₃·H₂O sharply increased beyond that. Likely, the consumption of alkalinity related to the progression of eqn (1) resulted in a lower activity of water, allowing for the precipitation of Na₂CO₃·H₂O rather than Na₂CO₃. In fact, a higher conversion extent (α = 0.89) was registered after 3 min of reaction, if compared with the outcome after 1 min (α = 0.72) and 2 min (α = 0.85). Most likely, a low activity of water could be maintained at T_k = 60 °C and T_k = 80 °C, even upon enhanced reaction progression, i.e. alkalinity consumption. Whereas the alkalinity drop occurring at an enhanced conversion extent was enough to increase the activity of water in those systems reacted at T_k = 45 °C. This is also confirmed by the experiments conducted at ambient conditions, since the system at T_i = 60 °C mostly formed Na₂CO₃·H₂O at the end of the reaction, when T_f = 42.1 °C was registered.

A deeper insight allows for the explanation of the dynamic situation occurring at 10 m < [NaOH] < 12.5 m; in such interval, the system achieves a transitionary aH₂O value of 0.603. That corresponds to a chemical potential u of −241.3 kJ mol⁻¹ (eqn (6)), where u₀ is the standard chemical potential of formation of pure water,³⁷ R the gas constant, and T the temperature in K.

u = u₀ + RT ln a_w (6)

At this point, the transition Na₂CO₃·H₂O/Na₂CO₃ is swapped (Fig. 8A), promoting the precipitation of Na₂CO₃·H₂O and Na₂CO₃ above and below an activity of water of 0.603, respectively. To explain the constant water activity value of 0.603, the gradual formation of Na₂CO₃ to the detriment of Na₂CO₃·H₂O must be considered; as a result, water is released into the liquid bulk and it counterbalances the further addition of NaOH. In fact, when all the sodium into the system is converted to Na₂CO₃ and no more H₂O is released by the dissolution of Na₂CO₃·H₂O, the activity of water rapidly drops down to just above 0.400 at NaOH 20 m. That corresponds to a higher water activity aH₂O within the liquid phase of the system (Fig. 8B), and therefore resulting in a higher proportioning of Na₂CO₃·H₂O with respect to Na₂CO₃ (Fig. 8A).

4.3 Calculation of E_a

An additional set of experiments was conducted to estimate the activation energy E_a of the decarbonisation reaction at the different starting compositions reported in Table 1, selected from our previous study.¹⁶ Based on the amount of CaCO₃ and Ca(OH)₂ in the reaction products estimated from their TGA data (ESI I–IV†), the extent of reaction (α) was calculated for each reaction. As reported in Fig. 9, beneficial effects of raising temperatures were observed at different levels depending on the starting composition.

Fig. 9 Conversion extent values (α) of the samples NaOH_10m_n, NaOH_12m_n, NaOH_15m_n and NaOH_17m_n plotted against the temperature initially set up and kept constant throughout the reaction.

In these terms, the effects of temperature (T) is commonly expressed in the reaction rate constant (k) using Arrhenius equation (eqn (7)),³⁸ depending on the pre-exponential factor (A), activation energy (E_a) and gas constant (R).

k = A e^(−E_a/RT) (7)

The rate constant k is a change in the extent of reaction (α) per unit time (t). Since the reactions in this sub-set of experiments were all conducted for 1 min, the extent of reaction obtained (Fig. 9) was directly used in eqn (7) as representative of the reaction rate, and thus:

α = A e^(−E_a/RT) (8)

Taking the natural logarithm, eqn (8) can also be expressed as:

By plotting ln α against T⁻¹ (Fig. 10), the activation energy E_a can be calculated from the slope (−E_a/RT); the experimental data for NaOH_10m, NaOH_12m, NaOH_15m, and NaOH_17m led to the fitting eqn (10)–(13), respectively.

y = 3865.1x + 10.254 R² = 1.00 (10)

y = 2054.3x + 5.638 R² = 0.91 (11)

y = 1242.1x + 3.507 R² = 0.94 (12)

y = 933.3x + 2.591 R² = 0.93 (13)

Fig. 10 Linearized Arrhenius plot showing the correlation between ln k and −1/T (K⁻¹) for the samples series NaOH_10m_n, NaOH_12m_n, NaOH_15m_n and NaOH_17m_n, reflected by the equations, 9, 10, 11, and 12, respectively.

Based on these, the apparent activation energies for NaOH_10m, NaOH_12m, NaOH_15m and NaOH_17m are estimated as 32.1, 17.1, 10.3 and 7.8 kJ mol⁻¹, respectively, and therefore reflecting the limited kinetics at lower NaOH molality. Despite that, lower activation energies were highlighted here, with respect to the conventional calcination route of CaCO₃ under inert atmospheres (164–225 kJ mol^{−1 39}) and with varying CO₂ partial pressures (213.3–2142.2 kJ mol^{−1 40}). Naturally, this first comparison does not consider the embodied energy required to produce the required NaOH to carry out the chemical calcination of CaCO₃. For this reason, the next section will introduce crucial aspects to fully consider when assessing its real feasibility from an industrial point of view.

5 Industry-oriented considerations

The authors understand that a proper life-cycle assessment needs to be done to understand the industrial feasibility of this novel chemical decarbonisation process, but this is not the aim of the present investigation. Nevertheless, some crucial considerations are reported below to better highlight the potential of the decarbonisation route presented here.

It is highlighted that eventual fluctuations of temperature would not negatively affect the reaction yield; moreover, the mild processing conditions required suggest convenient operating costs. However, the energy input required for the synthesis of the stoichiometric NaOH would represent the major obstacle in sight of an industrial application. In fact, 7.7 GJ is required to produce 1 t of NaOH, which occurs alongside the synthesis of 0.03 t of hydrogen gas and 1.1 t of chlorine gas, through the chlor-alkali process.⁴¹ Such hydrogen is typically wasted and vented to the atmosphere, whereas the in situ recirculation for power production would lower the energy demand by approximately 34%.⁴² In these conditions, considering that 0.8 t of stoichiometric NaOH are required for each tonne of CaCO₃ reacted, about 3.9 GJ_Equivalent of electricity should be supplied through usage of fresh fuel. Whereas, the conventional cement production route requires an energy input of 2.5–2.9 GJ per tonne of CaCO₃ to decarbonise, considering the theoretical heat of dissociation of CaCO₃ (1819.4 kJ⁴³) and efficiencies between 41 and 62%.⁴⁴ At first glance, our route does not appear economically desirable, since it requires 1.4–1.6 times the energy involved in the conventional route. However, it must be considered that the co-production of Na₂CO₃ occurs whilst synthetising Ca(OH)₂, and important energetic considerations would arise from that. In fact, the production of 1 tonne of Na₂CO₃ requires 13.6 GJ through the conventional Solvay process,⁴⁵ which would be completely avoided by supplying the product via the chemical route proposed. According to the stoichiometry depicted in eqn (1), a Na₂CO₃/Ca(OH)₂ weight ratio of 1.43 occurs at the end of the reaction, assuming total conversion of CaCO₃. The following considerations are done by normalising all the calculations with respect to cement, lime, and slaked lime, treating Na₂CO₃ as an added-value by-product. For the calculations, a 1 : 1 weight ratio between the decarbonised CaCO₃ and the resulting cement was considered; in fact, the CaO proportion in PC is around 60–70%,⁴⁶ and a 0.56 weight ratio occurs between the produced CaO (upon dehydration of Ca(OH)₂) and the reacted CaCO₃. For clarity, these numbers are reported in Table 3, alongside the cases for lime and slaked lime productions.

Table 3 Amounts of NaOH reacted and Na₂CO₃ produced through the chemical route by considering the stoichiometry depicted in eqn (1), together with the amount of CaCO₃ required for both the thermal and chemical approach. The values reported refer to the normalisation of the products, case by case, PC, Lime and Slaked lime

Production type	PC	Lime	Slaked lime	CaCO3 reacted	NaOH reacted	Na2CO3 produced
PC	1	—	—	1	0.8	1.0
Lime	—	1	—	1.6	1.3	1.8
Slaked lime	—	—	1	1.2	1.0	1.4

---

All these considerations were used to produce the energetic comparisons displayed in Fig. 11, where the electrical energy input required to produce the stoichiometric NaOH is reported alongside the thermal energy to be supplied to decarbonise CaCO₃ plus the one to produce soda ash. The extremes of the energy efficiencies reported for the PRK design are labelled as “Thermal_1” (η = 41%) and “Thermal_2” (η = 62%) for the PC case, whereas the novel decarbonisation route is displayed as “Chemical” both for PC, lime, and slaked lime. It must be mentioned that the energies outlined were normalised with respect to 1 tonne of PC, according to the stoichiometry just discussed, and therefore expressed in GJ_Equivalent, i.e., the energy required to produce 1 tonne of PC and the stoichiometric amount of Na₂CO₃ (1.0 t). It must be mentioned that these values solely refer to the decarbonisation step, without considering additional consumptions associated with the further processing of both reactants and products. It is revealed that chemical decarbonisation allows for ∼4 times lower energy consumption with respect to the thermal route, considering the synthesis of 1.0 tonne of PC and 1.0 tonnes of Na₂CO₃ (Table 3). For the calculation of the energy requirement from the chemical route, a 10% surplus was considered to include the handling and separation of the materials.

Fig. 11 Comparison of the energy consumption between the thermal and chemical approaches to the decarbonisation of CaCO₃, referred to the cement, lime and slaked lime industries; the values only depend on the decarbonisation step, considering a PRK design for the thermal calcination in PC production, and PFRK one for lime and slaked lime.

Regarding the production of lime, 1.6 tonnes of initial CaCO₃ are required to ensure 1 tonne of product, corresponding to a higher consumption of NaOH with respect to PC. For this reason, the normalisation with respect to lime shows that a higher amount of soda ash is produced, and that is considered for the calculation of the thermal power required from the conventional route. In these terms, the calcination design adopted in the lime/slaked lime industry allows for higher efficiencies (75% < η < 99%⁴⁴); in Fig. 11, the labels “Thermal_1” and “Thermal_2” refer to the efficiency extremes of 75 and 99%, respectively. The larger consumption of NaOH reflects a higher energy input for the chemical route with respect to PC; despite that, even in this case the thermal route would require ∼4 times the energy employed in the chemical decarbonisation, when 1 and 1.8 tonnes of CaO and Na₂CO₃ are produced, respectively (Table 3). Finally, the case study for slaked lime Ca(OH)₂ highlighted a 3.7–3.8 times lower energy input for the chemical route with respect to the conventional one for the synthesis of 1 and 1.4 tonnes of slaked lime and soda ash, respectively.

The preliminary energetic balance appears promising when sodium carbonate is considered as a co-product (i.e., replacing market soda ash); however, the global market demand of the chemicals involved must be considered. In fact, the current global demand for PC and soda ash is 4 Gt¹ and 50 Mt,⁴⁷ respectively; if the whole global production of PC is performed chemically, an excess production of soda ash would occur. However, the demand for soda ash might significantly grow given the increasing importance of geopolymers in the global perspective, with Na₂CO₃ used as activator to produce these low-carbon binders.⁴⁸ Furthermore, in case the excess of soda ash could not be reused, Na₂CO₃ would represent a safer option for permanent CO₂ storage with respect to the current geological disposal of liquid and compressed CO₂, whose long-term effects have not been fully understood yet.⁴⁹

Another drawback of the chemical route is represented by the production of chlorine gas arising from the chlor-alkali process to produce NaOH;⁴¹ if the size of the market increases to fulfil the demand for cement production, such emissions might have a heavy impact on the environment. The development of chlorine-based binders, such as alinite,⁵⁰ could help to mitigate the issue. In fact, despite that the presence of Cl leads to the failure of reinforced concrete through corrosion of the mild steel,⁵¹ ∼75% of the worldwide cement is used for unreinforced purposes.⁵² In addition, an enhancement of the chlor-alkali process with the in situ hydrogen processing and re-use would contribute to the mitigation of the drinkable water crisis expected in the next decades.⁵³ In fact, Na⁺ and Cl⁻ are removed from the brine (concentrated seawater) fed into the chlor-alkali process, and pure water is a by-product from the reprocessing of hydrogen.⁵⁴

Alternatively, both the excess production of soda ash and the increasing emissions of chlorine gas might be limited by solely applying the novel route to produce lime and slaked lime, whose markets (50 Mt and 20 Mt, respectively²) are currently closer to that of soda ash (50 Mt⁴⁷).

6 Conclusions

The effects of temperature on the efficiency of a chemical decarbonisation process for CaCO₃ was assessed. The reaction appeared effective for the sequestration of the process CO₂ partitioned into CaCO₃, with over the 80% of it captured within the first minute of reaction. The short residence times and mild heating conditions required look promising in sight of an eventual scale-up. It is supposed that the process might be thermally self-sustained, given (1) the exothermic dissolution of NaOH into water, and (2) the high conversion degrees observed even at ambient conditions. That would reflect a significant advantage from an industrial point of view, suggesting that the process is robust and that no additional costs would be associated with the control of the reaction temperature.

The capture of the process CO₂ occurs through precipitation of Na₂CO₃·H₂O at milder temperature and pH, whereas Na₂CO₃ is the dominant Na-based species at higher temperature and alkalinity. Given the need for a final separation of Ca(OH)₂ from Na₂CO₃. xH₂O, not discussed here, Na₂CO₃·H₂O might be favourable given the higher solubility with respect to Na₂CO₃ (330 and 307 g L⁻¹ at 25 °C and 1 atm, respectively). In fact, given the much lower solubility of Ca(OH)₂ (1.5 g L⁻¹ at 25 °C and 1 atm), the separation can be carried out in excess of water, and the yield would be maximised when the solubility gap between the phases of interest is large.

The activation energy E_a was determined for different ternary compositions previously tested. Generally, the activation energy barrier was smaller for the system with the higher initial NaOH concentration; moreover, the rate of the chemical decarbonisation appeared much higher with respect to the conventional CaCO₃ calcination for all the conditions tested.

Preliminary energetic considerations were also reported, and the comparison between the thermal and chemical route to produce PC, lime, slaked lime, and soda ash was shown. As outlined, the chemical route was ∼4 times more convenient in terms of energy input, if only the decarbonisation step of CaCO₃ is considered and when soda ash is considered as a co-product.

Overall, the chemical decarbonisation of CaCO₃ may have the potential to drastically reduce the carbon footprint of the related industries, potentially removing the need for high temperature calcination. The main obstacle to overcome is still represented by the general concept that the thermal decarbonisation of CaCO₃ is unavoidable, and that a transition would be technically too difficult to operate. However, the current environmental crisis demands for brave and optimistic approaches/decisions backed by the desire for real change towards a sustainable future.

Author contributions

Theodore Hanein and Hajime Kinoshita discovered and conceptualized the technology. Marco Simoni developed the technology and designed the methodology and experiments. Marco Simoni and Chun Long Woo carried out experiments. Marco Simoni drafted the original manuscript. Theodore Hanein, Hajime Kinoshita, and John L. Provis acquired funding, and supervised Marco Simoni and Chun Long Woo. Theodore Hanein, Hajime Kinoshita, John Provis, Mark Tyrer, and Magnus Nyberg reviewed and edited the manuscript.

Conflicts of interest

The authors declare that they have no competing interests as defined by RSC Advances, or other interests that might be perceived to influence the interpretation of the article.

Acknowledgements

This work was funded by the Engineering and Physical Science Research Council (EPSRC) and CEMEX under grant ID EP/R025959/1. This research utilised the HADES/MIDAS facility at the University of Sheffield established with financial support from EPSRC and BEIS, under grant EP/T011424/1. The group would also express gratitude to Alan Maries, Juan-Carlos Martinez, John Stennet, and Nestor I. Quintero-Mora for the support and knowledge received.

References

1. R. M. Andrew, Global CO₂ emissions from cement production, Earth Syst. Sci. Data, 2018, 10(1), 195–217.
2. J.-M. de Vet, et al., Competitiveness of the European Cement and Lime Sectors, WIFO Studies, 2018.
3. W. P. Bolen, Mineral Commodity Summaries–Soda Ash, United States Geological Survey, Reston, VA, 2015.
4. P. D. Warwick, et al., US Geological Survey Carbon Sequestration–Geologic Research and Assessments, Energy Procedia, 2014, 63, 5305–5309.
5. E. Gartner and H. Hirao, A review of alternative approaches to the reduction of CO₂ emissions associated with the manufacture of the binder phase in concrete, Cem. Concr. Res., 2015, 78, 126–142.
6. G. Steinhauser, Cleaner production in the Solvay Process: general strategies and recent developments, J. Cleaner Prod., 2008, 16(7), 833–841.
7. E. Worrell, et al., Carbon dioxide emissions from the global cement industry, Annu. Rev. Environ. Resour., 2001, 26(1), 303–329.
8. F. Schorcht, et al., Best available techniques (BAT) reference document for the production of cement, lime and magnesium oxide, European Commission Joint Research Centre Institute for Prospective Technological Studies (Report EUR 26129 EN), Publications Office of the European Union, Luxembourg, 2013.
9. L. Barcelo, et al., Cement and carbon emissions, Mater. Struct., 2014, 47(6), 1055–1065.
10. J. Rogelj, et al., Paris Agreement climate proposals need a boost to keep warming well below 2 C, Nature, 2016, 534(7609), 631.
11. D. Leeson, et al., A Techno-economic analysis and systematic review of carbon capture and storage (CCS) applied to the iron and steel, cement, oil refining and pulp and paper industries, as well as other high purity sources, Int. J. Greenhouse Gas Control, 2017, 61, 71–84.
12. M. Schneider, et al., Sustainable cement production—present and future, Cem. Concr. Res., 2011, 41(7), 642–650.
13. L. D. Ellis, et al., Toward electrochemical synthesis of cement—An electrolyzer-based process for decarbonating CaCO₃ while producing useful gas streams, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(23), 12584–12591.
14. M. Simoni, et al., Decarbonisation of calcium carbonate in sodium hydroxide solutions under ambient conditions: effect of residence time and mixing rates, Phys. Chem. Chem. Phys., 2022, 16125–16138.
15. M. Simoni, et al., Effect of Impurities on the Decarbonization of Calcium Carbonate Using Aqueous Sodium Hydroxide, ACS Sustainable Chem. Eng., 2022, 11913–11925.
16. T. Hanein, et al., Decarbonisation of calcium carbonate at atmospheric temperatures and pressures, with simultaneous CO ₂ capture, through production of sodium carbonate, Energy Environ. Sci., 2021, 14(12), 6595–6604.
17. A. Dowling, J. O'Dwyer and C. C. Adley, Lime in the limelight, J. Cleaner Prod., 2015, 92, 13–22.
18. O. T. Sørensen and J. Rouquerol, Sample controlled thermal analysis: origin, goals, multiple forms, applications and future, Springer Science & Business Media, 2013, vol. 3.
19. O. Levenspiel, Chemical reaction engineering, John Wiley & Sons, 1998.
20. A. Seidell, Solubilities of inorganic and metal organic compounds, 1940.
21. G. W. Morey, The action of water on calcite, magnesite and dolomite, Am. Mineral., 1962, 47(11–12), 1456–1460.
22. A. Farhad and Z. Mohammadi, Calcium hydroxide: a review, Int. Dent. J., 2005, 55(5), 293–301.
23. J. L. Ellingboe and J. H. Runnels, Solubilities of Sodium Carbonate and Sodium Bicarbonate in Acetone-Water and Methanol-Water Mixtures, J. Chem. Eng. Data, 1966, 11(3), 323–324.
24. J. Zelić, D. Rušić and R. Krstulović, Kinetic analysis of thermal decomposition of Ca (OH)₂ formed during hydration of commercial Portland cement by DSC, J. Therm. Anal. Calorim., 2002, 67(3), 613–622.
25. P. K. Gallagher and D. W. Johnson Jr, The effects of sample size and heating rate on the kinetics of the thermal decomposition of CaCO₃, Thermochim. Acta, 1973, 6(1), 67–83.
26. M. Hartman, et al., Thermal dehydration of the sodium carbonate hydrates, Chem. Eng. Commun., 2001, 185(1), 1–16.
27. S. M. Antao and I. Hassan, Temperature dependence of the structural parameters in the transformation of aragonite to calcite, as determined from in situ synchrotron powder X-ray-diffraction data, Can. Mineral., 2010, 48(5), 1225–1236.
28. T. Nagai, et al., Compression mechanism and amorphization of portlandite, Ca (OH)₂: structural refinement under pressure, Phys. Chem. Miner., 2000, 27(7), 462–466.
29. K. K. Wu and I. D. Brown, A neutron diffraction study of Na₂CO₃. H₂O, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31(3), 890–892.
30. A. Arakcheeva, et al., The incommensurately modulated structures of natural natrite at 120 and 293 K from synchrotron X-ray data, Am. Mineral., 2010, 95(4), 574–581.
31. K. Motzfeldt, The thermal decomposition. of sodium carbonate by the effusion method, J. Phys. Chem., 1955, 59(2), 139–147.
32. S. L. Stipp and M. F. Hochella Jr, Structure and bonding environments at the calcite surface as observed with X-ray photoelectron spectroscopy (XPS) and low energy electron diffraction (LEED), Geochim. Cosmochim. Acta, 1991, 55(6), 1723–1736.
33. R. A. Robie and B. S. Hemingway, Thermodynamic properties of minerals and related substances at 298.15 K and 1 bar (105 Pascals) pressure and at higher temperatures, US Government Printing Office, 1995, vol. 2131.
34. M. W. Chase Jr, NIST-JANAF thermochemical tables, J. Phys. Chem., Ref. Data, Monograph, 4th edn, 1998, vol. 9, pp. 1–1951.
35. D. L. Parkhurst and C. A. J. Appelo, Description of input and examples for PHREEQC version 3: a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations, US Geological Survey. 2013.
36. J. Balej, Water vapour partial pressures and water activities in potassium and sodium hydroxide solutions over wide concentration and temperature ranges, Int. J. Hydrogen Energy, 1985, 10(4), 233–243.
37. J. G. Speight, Lange's handbook of chemistry, McGraw-Hill, New York, 2005, vol. 1.
38. K. J. Laidler, The development of the Arrhenius equation, J. Chem. Educ., 1984, 61(6), 494.
39. L. Fedunik-Hofman, A. Bayon and S. W. Donne, Kinetics of solid-gas reactions and their application to carbonate looping systems, Energies, 2019, 12(15), 2981.
40. K. M. Caldwell, P. K. Gallagher and D. W. Johnson Jr, Effect of thermal transport mechanisms on the thermal decomposition of CaCO₃, Thermochim. Acta, 1977, 18(1), 15–19.
41. S. Lakshmanan and T. Murugesan, The chlor-alkali process: work in progress, Clean Technol. Environ. Policy, 2014, 16(2), 225–234.
42. A. Kumar, F. Du and J. H. Lienhard, Caustic Soda Production, Energy Efficiency, and Electrolyzers, ACS Energy Lett., 2021, 6(10), 3563–3566.
43. B. R. Stanmore and P. Gilot, Calcination and carbonation of limestone during thermal cycling for CO₂ sequestration, Fuel Process. Technol., 2005, 86(16), 1707–1743.
44. M. Simoni, et al., Decarbonising the lime industry: State-of-the-art, Renewable Sustainable Energy Rev., 2022, 168, 112765.
45. J. T. Houghton, Intergovernmental Panel on Climate Change, Revised 1996 IPCC Guidelines for National Greenhouse Gas Inventories: Greenhouse Gas Inventory Workbook, OECD. 1996.
46. H. F. W. Taylor, Cement Chemistry, 2nd edn, 1997, 0727725920, 9780727725929.
47. S. Jewell and S. Kimball, USGS mineral commodities summaries: 2014, US Geological Survey, p. 2014, http://minerals.usgs.gov/minerals/pubs/mcs/2014/mcs2014.pdf, accessed, 2014 12(12).
48. J. L. Provis and S. A. Bernal, Geopolymers and related alkali-activated materials, Annu. Rev. Mater. Res., 2014, 44, 299–327.
49. C.-F. Tsang, J. Birkholzer and J. Rutqvist, A comparative review of hydrologic issues involved in geologic storage of CO₂ and injection disposal of liquid waste, Environ. Geol., 2008, 54(8), 1723–1737.
50. M. Simoni, et al., Producing cement clinker assemblages in the system: CaO-SiO₂-Al₂O₃-SO₃-CaCl₂-MgO, Cem. Concr. Res., 2021, 144, 106418.
51. G. K. Glass and N. R. Buenfeld, The presentation of the chloride threshold level for corrosion of steel in concrete, Corros. Sci., 1997, 39(5), 1001–1013.
52. U. N. Environment and K. L. Scrivener, et al., Eco-efficient cements: Potential economically viable solutions for a low-CO₂ cement-based materials industry, Cem. Concr. Res., 2018, 114, 2–26.
53. W. A. Jury and H. J. Vaux Jr, The emerging global water crisis: managing scarcity and conflict between water users, Adv. Agron., 2007, 95, 1–76.
54. H. Khasawneh, et al., Utilization of hydrogen as clean energy resource in chlor-alkali process, Energy Explor. Exploit., 2019, 37(3), 1053–1072.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05827h

---