Reactivity of anatase (001) surface from first-principles many-body Green's function theory

Abstract

The anatase (001) surface has attracted a lot of interest in surface science due to its excellent performance. However, its reactivity is under debate since it can undergo a (1 × 4) reconstruction. Herein, we applied the many-body Green's function theory to investigate the electronic properties and excitons as well as the water adsorption behavior of the (1 × 4) unreconstructed anatase (001) surface and two reconstructed patterns, namely ADM and AOM. Our results revealed that the high reactivity of the (001) surface is probably not relevant to the reconstructed shape. The unreconstructed (001) surface and reconstructed ADM surface were very reactive for dissociating H₂O molecules among three surfaces, but the lower-energy singlet exciton for ADM was completely confined within the inner atomic layers in TiO₂, which is unfavorable for hole transfer to the reactant on the surface. Also, the required photon energy for initiating photochemical reactions on the reconstructed ADM surface should be higher than for the unreconstructed (001) surface, implying it is more difficult for the reaction to happen on the former surface. The unreconstructed (001) surface exhibited the highest reactivity due to the smaller optical absorption edge and the photoholes distributed on surface sites.

---

1 Introduction

Titanium dioxide (TiO₂) has been intensively studied and widely applied in photocatalysis,^1,2 photoelectrocatalysis,³ solar cells,^4–6 and in the remediation of pollutants⁷ due to its excellent performances. TiO₂ exists in three typical crystal phase structures: anatase, rutile, and brookite, among which the anatase polymorph exhibits the highest photocatalytic activity.⁸ The anatase crystals expose majority (101) facets and minority (001) facets. Early experimental⁹ and theoretical investigations¹⁰ on anatase concluded that the minority (001) surface is more reactive. In contrast, a recent experimental study¹¹ reported distinctly different insights into the (001) surface regarding its lower activity in photocatalytic reactions. The reactivity of (001) facets is thus still under debate. It is known that the catalytic performance is strongly dependent on the surface state and atomic structure of a catalyst. The anatase (001) surface usually favors a (1 × 4) reconstruction due to its high surface energy,^8,12,13 which may result in remarkably different properties. For this reason, it is necessary to study the atomic structure and properties of reconstructed anatase (001) surfaces, which would enable us to gain a better understanding of the intrinsic reactivity of the (001) surface.

The (1 × 4) reconstruction of the (001) surface has been detected by various experimental techniques to date,^12,14–18 including scanning tunneling microscopy (STM), (scanning) transmission electron microscopy (STEM), and low-energy electron diffraction. In combination with theoretical calculations, several surface models have been proposed for this reconstruction. The add-molecule model (ADM),¹³ in which rows of bridging oxygen atoms on the surface are replaced with rows of TiO₃ groups in a (1 × 4) periodicity, is the most widely accepted and studied. A simulated STM image based on it agreed with the experimental results. Moreover, an in situ spherical aberration corrected STEM study on the anatase reconstructed surface performed by Yuan et al.,¹⁶ also provided direct evidence to verify the ADM model. Both experimental and theoretical studies^19,20 on ADM reconstructed surfaces have found that several small molecules are dissociatively adsorbed on the ADM surface in the same way as in the adsorption behavior on the pristine (001) surface,^10,21,22 indicating the anatase (001) surface possesses higher reactivity among TiO₂ surfaces. However, another STM experiment showed that there were no fourfold-coordinated Ti atoms on the surface and proposed a surface reconstruction added-oxygen model (AOM) that was constructed by adding one oxygen atom to the TiO₃ ridges of ADM.¹⁵ That study also found that²³ the anatase (001)–(1 × 4) surface was inert for molecular adsorption except at the intrinsic defects sites, which could explain the experimental results for the lower activity of the (001) surface. Nevertheless, this is not enough to judge the reactivity according to the absorbed state on the surface, and a proper assessment of the photoreactivity of the surface also requires an accurate description of its energy-level alignment and excitonic behavior. To date, a few theoretical works have investigated the electronic properties of the (001) surface,^24–26 but the calculations utilized in these studies were based on density functional theory (DFT). Also, the excitonic properties of the reconstructed (001) surface have rarely been covered. Current achievements and advances to date are far from meeting the final goal. In this work, we applied the more advanced first-principles many-body Green's function theory (MBGFT) including the GW method and Bethe–Salpeter equation (BSE), to systematically study the quasiparticle band structures and excitonic properties of the reconstructed anatase (001) surface, including ADM and AOM, and the interfacial properties of a single water molecule adsorbed on the surfaces, with an overall aim to explore the photoreactivity of the surface. The GW method has been demonstrated to compute the electronic levels of semiconductor and insulators with higher accuracy than DFT,^27,28 while the BSE is a state-of-the-art approach to describe the behavior of electron–hole pairs.^27,29

2 Computational detail

2.1 Ground-state geometries

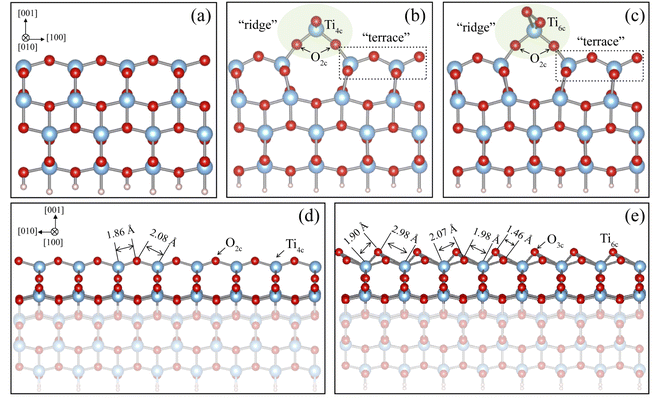
In our calculations, the structures of ADM and AOM were constructed according to ref. 13 and 15. The experimental lattice parameters^23,30 of anatase TiO₂ were adopted. As shown in Fig. 1, all the (001) surfaces were constructed by a periodically repeated (1 × 4) orthorhombic slab containing four O–Ti–O trilayers, corresponding to a 3.776 × 15.104 Ų area. Just as in our previous work on the rutile TiO₂(110) surface,^31,32 all the fivefold-coordinated Ti and twofold-coordinated O atoms on the bottom layer were saturated by pseudohydrogen atoms with nuclear charges of +4/3 and +2/3, respectively. This protocol aims to maintain the TiO₂ bulk-like coordination environment. A 30 Å vacuum layer above the surface was included in this model, whose convergence was tested in our previous work on other TiO₂ surfaces.^31,32 Geometry optimization was performed within the plane-wave pseudopotential scheme employing the Vienna ab initio simulation package (VASP).^33,34 The Perdew–Burke–Ernzehof (PBE) generalized gradient approximation³⁵ was chosen for describing the exchange–correlation interaction. The projector-augment-wave pseudopotentials of Ti (3s²3p⁶3d²4s²) and O (2s²2p⁴) were adopted in this calculation. An energy cutoff of 450 eV was set for the wave functions. The bottom trilayers were fixed at their bulk positions, while the other three trilayers were relaxed until the residual force acting on each ion was less than 0.02 eV Å⁻¹. For the calculations of the (001)/water interface, a (3 × 4) surface supercell was used in this work (see Fig. S1†). The PBE-D3 dispersion interaction correction was used to describe the van der Waals interaction between the surface and the water molecule.

Fig. 1 Relaxed structures of the unreconstructed anatase (001) surface (a) and the reconstructed ADM model (b) and the AOM model (c). The “ridge” and “terrace” parts of the reconstructed surface are highlighted by light green ellipses and black dotted lines in (b) and (c), respectively. The ADM and AOM structural parameters along the [010] directions are marked in (d) and (e). Light blue, red, and gray balls represent Ti, O, and H atoms, respectively.

2.2 GW method and the Bethe–Salpeter equation

In the GW method, electronic structures are calculated via the quasiparticle (QP) equation:^27,28where ∑(r,r′,E) is the electron self-energy operator, which describes the exchange and correlation interactions among electrons. It is a non-local, energy-dependent operator, which can be evaluated within GW approximation by the convolution of one-particle Green's function (G) and the screened Coulomb potential (W). W is linked to the bare Coulomb potential υ through , where ε is the dielectric function. Moreover, solutions of the QP equation are QP energies and QP wave functions. The QP energy E^QP_nk corresponds to the energy differences E(N) − E(N − 1) and E(N + 1) − E(N), where N is the total number of electrons in the system, as measured by direct and inverse photoelectron spectra. This is another advantage of the quasiparticle equation. In DFT, the empirical exchange and correlation functional are applied to describe the interactions among electrons. The calculated results for the electronic band structure of a semiconductor system are heavily affected by the exchange–correlation functionals. The energy gaps obtained are generally small. Although some hybrid exchange–correlation functionals have been developed in order to improve the accuracy of DFT calculations for band gap prediction, empirical parameters still imbedded in these functionals may limit their transferability.

In BSE, the exciton wave functions χ_S(r,r′) is described as follows:³⁶

where c(v) is the conduction (valence) band, and r(r′) is the coordinates of the excited electron (hole). With eqn (2), the Bethe–Salpeter equation could be reformulated into the eigenvalue form:^27,37where Ω_S is the excitation energy. In eqn (3), the first term describes the independent-particle transition, whereby the energies of the valence and conduction bands were calculated by the GW method in this work. The second term accounts for the interaction between the bound electron–hole pair. K_{vc,v^′c^′}(Ω_S) is the electron–hole interaction kernel, consisting of the exchange term caused by the bare Coulomb potential υ and the direct term caused by the screened Coulomb potential W.

Our GW and BSE calculations were performed using a Gaussian-orbital-based code.^37–39 The local density approximation (LDA) was used as the starting point to construct the physical quantities needed in GW. Atom-centered Gaussian orbitals with the decay constants (in atomic unit) for Ti atoms, O atoms, and pseudohydrogen atoms were the same as those in our recent studies on TiO₂.^31,32,40 In the calculation of the (1 × 4) supercell, we went one further step beyond the G₀W₀ level to evaluate more accurate quasiparticle energies and wave functions by diagonalizing the full G₀W₀ Hamiltonian, including both the diagonal and off-diagonal elements. Electronic screening was calculated by employing the random-phase approximation and the plasmon-pole model proposed by von der Linden and Horsch.^38,41 To reduce the huge computational cost of the GW method, unoccupied states whose energies were 91 eV and 158 eV above the conduction band minimum were not considered in the band summation for constructing the electronic screening and self-energy in GW, respectively. From the convergence test on the band summation, as shown in Fig. S2,† the total effect of the two cutoffs on the orbital energy and band gap was within 0.1 eV. Also, k-point meshes of 6 × 2 × 1 and 8 × 2 × 1 in the first Brillouin zone were respectively employed for the evaluation of the dielectric matrix and self-energy. In the BSE, excitonic wave functions were represented by a converged 12 × 3 × 1 k-point mesh, which could converge the optical absorption onset well.

3 Results and discussion

3.1 Structural parameters and stability

The optimized structures of the clean (1 × 4) anatase (001) surface, ADM, and AOM are shown in Fig. 1. There is a ridge along the [100] direction on both the ADM and AOM (1 × 4) surfaces, respectively. The Ti–O bond length along this direction on the ADM and AOM is about 1.80 Å, which is shorter than that on the unreconstructed (001) surface. The Ti and O atoms on the ridge of ADM is four-coordinated (Ti_4c) and two-coordinated (O_2c), but the added O atom on the ridge of AOM can form two Ti–O bonds with adjacent Ti atoms, changing Ti_4c to six-coordinated Ti. The bond lengths of Ti_4c–O_2c bonds and Ti_6c–O_3c bonds along the [010] direction on the ridge for the ADM and AOM surfaces are also marked in this figure. The bonds lengths are strongly inequivalent and asymmetric, indicating the possible high activity of the reconstructed surface.

The relative stabilities of different reconstructed surface structures can be evaluated by the formation energies, which can be calculated by where E_tot and E_ref represent the total energies of the reconstructed surface and the unreconstructed (001) surface, respectively; n_Ti and n_O are the number of excess Ti and O atoms of the reconstructed surface, respectively; μ_Ti and μ_O are the chemical potentials for Ti and O, respectively; and N is the number of surface unit cells in the supercell. There exist the constraints: and μ_Ti + 2μ_O = E_TiO2, where E_O2 and E_TiO2 are the total energies of an isolated O₂ molecule and the bulk anatase TiO₂. The permitted range of μ_O is The computed formation energies of the ADM and AOM surface structures with respect to the potential of O are shown in Fig. 2. Clearly, ADM possessed the lowest formation energy, suggesting that it has the highest stability and tends to be formed. The unreconstructed (001) surface was less stable and 0.42 eV higher in formation energy than ADM, but it was energetically more favorable than AOM within the μ_O range −9.54 eV to −6.27 eV. For μ_O > −6.27 eV, the reconstructed AOM was more stable than the unreconstructed surface, and its formation energy was close to that of ADM, indicating that AOM probably exists under high O-rich conditions. These results are in line with the results obtained by Sun et al.²³ and Xu et al.²⁵ Moreover, the results are the same as the results from the perspective of the binding energy (Table S1†). Therefore, both the reconstructed ADM and AOM surface structures will likely be formed.

Fig. 2 Computed formation energies of the reconstructed surface as a function of chemical potentials of O.

3.2 Electronic structures and excitons

Fig. S3† and 3 show the DFT–LDA and GW band structures for three surfaces. All the surfaces were indirect-gap materials. The LDA bandgaps for the unreconstructed surface, ADM, and AOM were 1.26, 1.73, and 1.18 eV, respectively. The band dispersions of the conduction band are similar in these three surfaces. The conduction band minimum (CBM) of all the surfaces originated from the d orbitals of the Ti bulk atoms (Fig. S3†). The electrons at the valence band maxima (VBM) for the unreconstructed surface are delocalized on the surface O atoms. However, the ridges of ADM and AOM generate new levels above the valence bands of the unreconstructed surface as illustrated in Fig. S3.† These states are localized on the O atoms at the ridge. From DFT to GW, the band dispersion and band sequence dispersion are changed little (see Fig. S3† and 3). Also, the electron distributions are also unchanged. The higher-energy states originate from the surface ridge O atoms (Fig. 4), but the spacing between the new bands originating from the ridge and other valence bands was reduced in the GW calculations. The band gaps were enlarged by 2.1, 2.4, and 2.7 eV, respectively. The GW gaps for ADM and AOM were larger than that of the unreconstructed surface, which were unfavorable for the absorption of lower-energy light. The VBM/CBM positions relative to the vacuum and NHE scales calculated by the GW method for the unreconstructed surface, ADM, and AOM are shown in Fig. S4.† Their respective CBM positions were found to be above the H⁺/H₂ level and the VBM was below the O₂/H₂O potential. Because of the suitable VBM and CBM energy levels for both the oxygen evolution reaction and hydrogen evolution reaction, the photogenerated holes and electrons created on these surfaces have strong reduction and oxidation capabilities. However, it was hard to assess which one possesses higher photoactivity from these electronic properties.

Fig. 3 GW band structures of the unreconstructed anatase (001) (a), ADM (b) and AOM (c). VBM and CBM of the band structures in each panel are marked by red circle and green circle, respectively. The VBM is set to zero.

Fig. 4 Charge distributions of the VBM and CBM calculated by GW for the unreconstructed anatase (001) (a), ADM (b), and AOM (c).

The optical properties are also the key factors to determine the photochemical reactivity. It was thus necessary to investigate the characteristic of the electron–hole pairs for the three structures. In this section, we discuss the excitonic properties that were calculated by BSE. Fig. 5 shows the optical absorption spectra of the three surfaces. The lowest excited state (S₁) was located at 3.10 eV for the unreconstructed (001) surface, which agreed with the experimental absorption edge of anatase TiO₂. The lowest electronic excitation (S₁) for ADM emerged at 3.70 eV, which was higher than the optical absorption edge of the unreconstructed (001) surface. Thus, the photochemical process on the reconstructed ADM surfaces could be initiated only when the excitation energy is higher than 3.70 eV. In addition, the exciton was almost confined within the inner atomic layers in TiO₂ (Fig. 5(e)), which acts against the hole transfer to the reactant on the surface. In general, the surface hole could readily transfer to the reactant. Although the hole could be localized on the surface O atom for higher excitation (see Fig. S5† for the exciton at 3.8 eV or 4.0 eV), the system would decay quickly to the lower excited states. Also, the holes for the excited states below 4.0 eV are mostly confined within bulk atoms. Fig. 5(d) and S5† display the exciton distribution at S₁ and 3.45 eV for the unreconstructed surface, in which it can be seen that the holes at a relatively lower excitation are delocalized widely on the surface O atoms, which is in favor of hole transfer to the reactant. Likewise, the optical absorption edges (S₁) for AOM arose from the ridge O atoms on the surface (see Fig. 5(f)). Nevertheless, the energy of S₁ (3.38 eV) for AOM was higher than that of the unreconstructed surface, which means the required photon energy for initiating the photochemical reaction on the reconstructed AOM surface could be higher. The reaction on the surface for excitations below 3.38 eV fails to be initiated. To sum up, the required excitation energy to activate the reaction on the reconstructed surface should be higher, making it harder for the process to happen. It seems that the unreconstructed surface possesses superior photocatalytic activity relative to the reconstructed surface, both in terms of excitation energy or excitonic behavior.

Fig. 5 Optical absorption spectra for the unreconstructed anatase (001) (a), ADM (b) and AOM (c) calculated by BSE. S₁ is the lowest excited states. (d–f) Illustrate the exciton distributions for S₁ in (a)–(c), respectively, where electron and hole are represented in blue and green isosurfaces, respectively.

3.3 Water adsorption

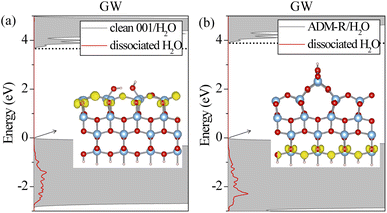
To examine in depth the photoactivity of the (001) surface, we analyzed the interfacial properties of a single water molecule adsorbed on unreconstructed and reconstructed (001) surfaces. It is challenging to calculate the excitonic properties for the anatase (001)/H₂O interfaces in which the total number of atoms is about 180 by BSE owing to the huge computational cost. Thus, we only discuss the ground-state geometries and electronic levels. As shown in Fig. S1,† the five anatase (001)/H₂O interfaces were investigated. A water molecule could be adsorbed at the ridge (ADM-R or AOM-R) or terrace (ADM-T or AOM-T) sites of the reconstructed surfaces. We found that a water molecule is adsorbed on the AOM surface in a molecular form. For the ADM surface, the water molecule was adsorbed in a molecular state at the terrace and in a dissociative state at the ridge. The dissociation of the water molecule at the ridge leads to the formation of two neighboring OH groups, which is in agreement with previous studies.¹⁹ Experiments also have shown the dissociative H₂O structure on the ADM surface.^19,20 The water molecule also spontaneously dissociates into the bridge O_2cH and terminal OH for the clean (001) surface, which results in unsymmetrical Ti–O bond lengths with the same Ti atom on the surface. This structure provides more active sites for water dissociation. In terms of the atomic surface structures, the unreconstructed (001) surface and ADM surface exhibited superior reactivity due to the fact that the water molecule adsorbed on these surfaces exhibited the dissociative state. However, a proper assessment of an interface's photoactivity requires an accurate description of its frontier levels' alignment. In our previous work,³¹ it was found that the dissociated H₂O possessed a higher capability to capture holes than the molecular H₂O, which also supports the higher activity of the unreconstructed (001) surface and ADM. We thus calculated the G₀W₀ DOS of these two interfaces with the dissociative state (see Fig. 6). The GW gap of the ADM surface remained unchanged upon water adsorption; whereas the gap of the unreconstructed (001) surface was enlarged by 0.5 eV upon water adsorption, which was still smaller than that of ADM surface. We speculated that the S₁ was also probably lower according to the BSE results on the three surface structures above. The electrons at the VBM for these two surfaces were also still delocalized on TiO₂ (Fig. 6). Also, the highest energy edge of PDOS on the dissociated H₂O lay below the VBM, which was in line with our previous GW results for the TiO₂(110)/water interface.³¹ The holes may be trapped by the dissociated H₂O under the irradiation by higher-energy UV light. In comparison with the ADM-R/H₂O interface, the gap between the highest energy edge on the dissociated H₂O and the CBM at the unreconstructed (001)/H₂O interface was smaller (see Fig. 6). Therefore, the hole can be captured by the dissociated H₂O on the latter surface at a relatively lower excitation energy, suggesting the reaction prefers to happen. The unreconstructed (001) surface seemed to have higher photoactivity than ADM in the photooxidation reaction. In other words, the unreconstructed (001) surface exhibited the highest reactivity of them. The experimental results for the lower activity of the (001) surface could be explained by the reconstruction.

Fig. 6 Total (gray) and projected DOS (PDOS) on dissociated H₂O calculated by G₀W₀ for the unreconstructed anatase (001)/H₂O interface (a) and the ADM-R/H₂O interface (b). VBM is set to zero in each panel. CBM is marked by the dotted lines. The inset displays the charge distribution of the VBM.

4 Conclusions

In summary, we investigated the electronic and excitonic properties of the unreconstructed anatase (001) surface and two reconstructed patterns that were experimentally observed, namely the ADM and AOM models. Our results show that the band gap and optical absorption edge for the reconstructed surface were higher than that of the unreconstructed, implying that the required photon energy for initiating the photochemical reaction on the unreconstructed (001) surface could be the lower than that for the reconstructed ADM and AOM surfaces. The reaction on the clean (001) surface could thus more easily happen. The photogenerated holes after photon excitation were spread over the surface O atoms, which was in favor of hole transfer to the reactant. By contrast, the excitons for ADM were completely confined within the bulk atoms. Our calculations also showed that the gap for the reconstructed ADM was still larger than that for the clean (001) surface upon water adsorption. Although the clean (001) surface and the ridge of ADM surface were intrinsically reactive toward water, the unreconstructed (001) surface seemed to have superior reactivity due to the smaller optical gap. Given the relative stability of the reconstructed surfaces, the reactivity of the (001) surface likely played a negligible or reduced role in the material's overall reactivity. The two reconstructed shapes could explain the experimental results for the lower activity of the (001) surface. The results provide a new explanation of the reactivity of the (001) surface. As for the reactivity of other surfaces of anatase, further systematic studies on the issue may be required.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Basic Research Program in Shanxi Province under the Grant No. 20210302124345, the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (Grant No. 2020L0556), the Doctoral research funds of Yuncheng University (YQ-2019023), the Doctoral research funds in Shanxi (QZX-2020004) and Applied Research Project of Yuncheng University (CY-2021016).

References

1. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
2. Q. Guo, Z. Ma, C. Zhou, Z. Ren and X. Yang, Chem. Rev., 2019, 119, 11020–11041.
3. Y. Wang, M. Zu, X. Zhou, H. Lin, F. Peng and S. Zhang, Chem. Eng. J., 2020, 381, 122605.
4. Y. Bai, I. Mora-Sero, F. De Angelis, J. Bisquert and P. Wang, Chem. Rev., 2014, 114, 10095–10130.
5. L. Hao, F.-Q. Bai, C.-P. Kong, S. Bibi and H.-X. Zhang, RSC Adv., 2015, 5, 79868–79873.
6. L. Hao, J. Wang, F. Q. Bai, M. Xie and H. X. Zhang, Eur. J. Inorg. Chem., 2015, 2015, 5563–5570.
7. R. Li, T. Li and Q. Zhou, Catalysts, 2020, 10, 804.
8. G. Li, K. Fang, Y. Ou, W. Yuan, H. Yang, Z. Zhang and Y. Wang, Prog. Nat. Sci.: Mater. Int., 2021, 31(1), 1–13.
9. X. Han, Q. Kuang, M. Jin, Z. Xie and L. Zheng, J. Am. Chem. Soc., 2009, 131, 3152–3153.
10. X.-Q. Gong and A. Selloni, J. Phys. Chem. B, 2005, 109, 19560–19562.
11. J. Pan, G. Liu, G. Q. Lu and H.-M. Cheng, Angew. Chem., Int. Ed., 2011, 50, 2133–2137.
12. Y. Xia, K. Zhu, T. C. Kaspar, Y. Du, B. Birmingham, K. T. Park and Z. Zhang, J. Phys. Chem. Lett., 2013, 4, 2958–2963.
13. M. Lazzeri and A. Selloni, Phys. Rev. Lett., 2001, 87, 266105.
14. Y. Liang, S. Gan, S. A. Chambers and E. I. Altman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 235402.
15. Y. Wang, H. Sun, S. Tan, H. Feng, Z. Cheng, J. Zhao, A. Zhao, B. Wang, Y. Luo, J. Yang and J. G. Hou, Nat. Commun., 2013, 4, 2214.
16. W. Yuan, H. Wu, H. Li, Z. Dai, Z. Zhang, C. Sun and Y. Wang, Chem. Mater., 2017, 29, 3189–3194.
17. K. Fang, G. Li, Y. Ou, W. Yuan, H. Yang, Z. Zhang and Y. Wang, J. Phys. Chem. C, 2019, 123, 21522–21527.
18. G. S. Herman, M. R. Sievers and Y. Gao, Phys. Rev. Lett., 2000, 84, 3354–3357.
19. I. Beinik, A. Bruix, Z. Li, K. Adamsen, S. Koust, B. Hammer, S. Wendt and J. Lauritsen, Phys. Rev. Lett., 2018, 121, 206003.
20. W. Yuan, B. Zhu, X.-Y. Li, T. W. Hansen, Y. Ou, K. Fang, H. Yang, Z. Zhang, J. B. Wagner, Y. Gao and Y. Wang, Science, 2020, 367, 428–430.
21. X. Lang, Y. Liang, J. Zhang, L. Li, L. Cao and H. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 1371–1380.
22. J. Geiger, M. Sprik and M. M. May, J. Chem. Phys., 2020, 152, 194706.
23. H. Sun, W.-C. Lu and J. Zhao, J. Phys. Chem. C, 2018, 122, 14528–14536.
24. X. Ma, X. Wu, X. Zhao and H. Sun, Phys. Chem. Chem. Phys., 2017, 19, 25456–25462.
25. M. Xu, S. Wang and H. Wang, Phys. Chem. Chem. Phys., 2017, 19, 16615–16620.
26. M. Harb, G. Jeantelot and J.-M. Basset, J. Phys. Chem. C, 2019, 123, 28210–28218.
27. X. Leng, F. Jin, M. Wei and Y. Ma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 532–550.
28. G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659.
29. D. J. Mowbray and A. Migani, J. Chem. Theory Comput., 2016, 12, 2843–2852.
30. X. Ma, Y. Dai, W. Wei, B. Huang and M.-H. Whangbo, J. Phys. Chem. Lett., 2015, 6, 1876–1882.
31. F. Jin, M. Wei, T. Chen, H. Ma, G. Liu and Y. Ma, J. Phys. Chem. C, 2018, 122, 22930–22938.
32. F. Jin, X. Zhang, M. Wei, T. Chen, H. Ma and Y. Ma, J. Mater. Chem. A, 2020, 8, 20082–20090.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. A. L. Fetter and J. D. Walecka, Quantum theory of many-particle systems, Courier Corporation, 2012.
37. M. Rohlfing and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944.
38. M. Rohlfing, P. Krüger and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17791–17805.
39. M. Rohlfing, P. Krüger and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1905–1917.
40. F. Jin, X. Zhang, M. Wei and Y. Ma, Electron. Struct., 2019, 1, 044002.
41. W. von der Linden and P. Horsch, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8351–8362.

---

Footnote

† Electronic supplementary information (ESI) available: The convergence tests of the thickness of the surface slab and GW calculations; the DFT–LDA results, some electronic and excitonic properties for the unreconstructed anatase (001) surface, ADM and AOM; and the ground-state geometries of the anatase (001)/H₂O interfaces. See https://doi.org/10.1039/d2ra05058g

---