Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A first-principles investigation of the linear thermal expansion coefficients of BeF2: giant thermal expansion
Chee Kwan Gan *a,
Abdullah I. Al-Sharifb,
Ammar Al-Shormanb and
Abdallah Qteish*b
*a,
Abdullah I. Al-Sharifb,
Ammar Al-Shormanb and
Abdallah Qteish*b
aInstitute of High Performance Computing, 1 Fusionopolis Way, #16-16 Connexis, 138632, Singapore. E-mail: ganck@ihpc.a-star.edu.sg
bDepartment of Physics, Yarmouk University, Irbid-21163, Jordan. E-mail: aqteish@yu.edu.jo
First published on 20th September 2022
Abstract
We present the results of a theoretical investigation of the linear thermal expansion coefficients (TECs) of BeF2, within a direct Grüneisen formalism where symmetry-preserving deformations are employed. The required physical quantities such as the optimized crystal structures, elastic constants, mode Grüneisen parameters, and phonon density of states are calculated from first-principles. BeF2 shows an extensive polymorphism at low pressures, and the lowest energy phases [α-cristobalite with space group (SG) P41212 and its similar phase with SG P43212] are considered in addition to the experimentally observed α-quartz phase. For benchmarking purposes, similar calculations are performed for the rutile phase of ZnF2, where the volumetric TEC (αv), derived from the calculated linear TECs along the a (αa) and c (αc) directions, is in very good agreement with experimental data and previous theoretical results. For the considered phases of BeF2, we do not find any negative thermal expansion (NTE). However we observe diverse thermal properties for the distinct phases. The linear TECs are very large, especially αc of the α-cristobalite phase and its similar phase, leading to giant αv (∼175 × 10−6 K−1 at 300 K). The giant αv arises from large Grüneisen parameters of low-frequency phonon modes, and the C13 elastic constant that is negatively signed and large in magnitude for the α-cristobalite phase. The elastic constants, high-frequency dielectric constants, Born effective charge tensors, and thermal properties of the above phases of BeF2 are reported for the first time and hence serve as predictions.
1. Introduction
Beryllium fluoride (BeF2) is known to exist in glass and crystalline phases and has a variety of technological applications. BeF2 glass has a large bandgap of about 13.8 eV, the lowest refractive index and highest Abbe number of any inorganic material, and exceptional resistance to damage. These properties have enabled the manufacturing of special glasses (from BeF2 and its mixtures with fluorides and other difluorides) that have excellent transmittance in the UV region1,2 and for use in high-power laser systems.3 The LiF–BeF2 mixture is a primary coolant and fuel solvent in molten salt nuclear reactors.4 In protein crystallography, BeF2 is used to restrict protein motion to facilitate the crystallography process.5 Very recently, crystalline BeF2 is predicted to be a better neutron filter than MgF2, which has been considered an effective neutron filter candidate.6 The main aim of this work is to investigate, for the first time, the linear thermal expansion coefficients (TECs) of a few low-energy crystalline phases of BeF2. We also consider a benchmark system ZnF2 that has exceptional electric and optical properties, and interesting technological applications ranging from catalysis to spectroscopy and laser applications.7Single crystal BeF2 has been grown and found to have a crystal structure remarkably similar to that of the α-quartz (SiO2) structure,8 which has a trigonal symmetry with space group (SG) P3121 (#152). A recent first-principles study has revealed that BeF2 shows extensive polymorphism at low pressures.9 Interestingly, three crystal phases [namely, (i) the α-cristobalite phase that has a tetragonal symmetry with SG P41212 (#92), (ii) a similar phase to the α-cristobalite phase (hereafter referred to as the α′-cristobalite phase) with SG P43212 (#96), and (iii) the C2/c-2 × 4 phase with SG C12/c1 (#15)] are predicted to be energetically more stable than α-quartz. However, these phases have a very small stability pressure range (less than 0.4 GPa), and the α-quartz phase transforms to the coesite-I phase SG C2/c at 3.1 GPa. The high-pressure phases of BeF2 have been the subject of other first-principles calculations.10 Very recently, first-principles calculations have also been employed to construct the P–T phase diagram of BeF2.11 The HSE06 optical bandgap of the α-quartz structure is found to be about 10.6 eV, and increases by increasing the applied pressure.9 The lattice vibrations, inelastic scattering cross-sections, and neutron transmission of BeF2 have been thoroughly investigated6 using first-principles calculations and compared to those of MgF2.
The benchmark system ZnF2 crystallizes in the tetragonal rutile structure with SG P42/mnm (#136). Very recently, Raman scattering measurements with the use of the diamond anvil cell have been employed to investigate the structural phase transformations of ZnF2 under high pressures.12 This experimental work is supplemented by first-principles calculations. In addition to the structural stability and pressure variation of the Raman active phonon modes, the electronic bandgap of the considered phases as a function of pressure has been investigated at the HSE06 level. Neutron diffraction has been employed to study the temperature dependence of the lattice parameters and unit cell volume of ZnF2,13 and NTE has been observed in a small temperature range (below 75 K). This NTE behavior has been supported by first-principles calculations.13,14 However, only the volumetric TEC has been theoretically investigated.
In the present work, the linear TECs of BeF2 and ZnF2 are investigated by employing the recently introduced direct approach15 in which the symmetry of the deformed structures could be preserved. Since this approach has not been applied to systems with tetragonal symmetry, ZnF2 is thus chosen as a suitable benchmark system because of its tetragonal crystal structure, in addition to the existence of experimental and previous theoretical results of its volumetric thermal expansion. The elastic constants and phonon frequencies required to compute linear TECs are calculated from first-principles. For BeF2, the α-quartz, α-cristobalite and α′-cristobalite phases will be considered. Moreover, the relative stability of the above three phases of BeF2 are also investigated using different levels of approximation of the exchange-correlation potential.
2. Methodology
The linear TECs of the considered phases of ZnF2 and BeF2 are calculated within the Grüneisen formalism following the procedure described in ref. 16–22. To compute the mode Grüneisen parameters we considered two types of symmetry-preserving deformations obtained by changing the in-plane (a) or out-of-plane (c) lattice parameters by ±0.5%. These deformations allow for the full utilization of the tetragonal or trigonal point-group symmetry23 of the considered systems, which minimizes the required number of independent atomic displacements (i.e., number of supercells) to calculate the phonon frequencies within the direct method.24–28 The amplitude of atomic displacements, from the corresponding equilibrium positions, is 0.015 Å. The supercell sizes are of 2 × 2 × 3 for ZnF2, and 2 × 2 × 2 for the α-quartz, α-cristobalite, and α′-cristobalite phases of BeF2. The adequacy of these supercells have been checked by considering larger ones for each of these systems, and we found that such actions do not alter appreciably our main results and conclusions. The determination of the linear TECs also requires the elastic constants that may be obtained through fittings of energy versus strain curves.29,30 Specifically, these TECs at temperature T in the a (αa) and c (αc) directions of the above systems are given by
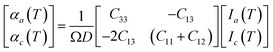 | (1) |
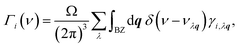 | (2) |
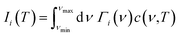 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r)2 is the contribution of the phonon modes with frequency ν to the specific heat. Here, r = hν/2kBT, and h and kB are the Planck and Boltzmann constants, respectively. The maximum (minimum) frequency is denoted by νmax (νmin).
r)2 is the contribution of the phonon modes with frequency ν to the specific heat. Here, r = hν/2kBT, and h and kB are the Planck and Boltzmann constants, respectively. The maximum (minimum) frequency is denoted by νmax (νmin).
The DFT calculations of the optimized structural parameters, phonon frequencies, and elastic constants are performed by employing the projector augmented wave (PAW) method, as implemented in the Vienna Ab Initio Simulation Package (VASP). A relatively high cutoff energy of 600 eV is used for the plane-wave basis. Geometry optimization is stopped when the maximum force on each atom is less than 10−3 eV Å−1. We find that phonon frequency shifts are more consistent when we use the local density approximation (LDA) for BeF2, and the PBE_sol functional of the generalized gradient approximation (GGA) for ZnF2. Therefore, for the linear TECs only the results of these calculations are reported.
3. Results and discussion
3.1. Structural properties
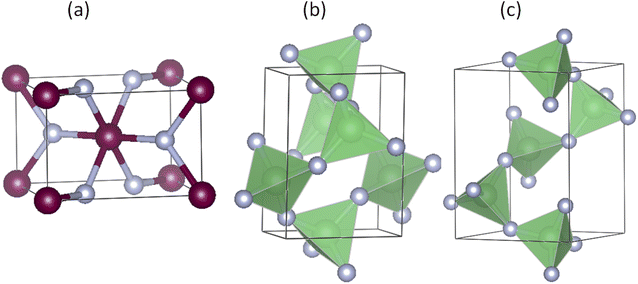
We start with the benchmark system, ZnF2, which at ambient conditions crystallizes in the rutile structure, shown in Fig. 1(a). This crystal structure has a tetragonal symmetry and six atoms per primitive unit cell. The two Zn atoms occupy the Wyckoff 2a(0, 0, 0) sites and the four F atoms are located at the 4f(x, x, 0) sites. Therefore, this structure is characterized by three crystallographic parameters: two lattice parameters (a and c) and an internal parameter for the coordinates of the four F atoms (x). The structural parameters obtained using the PBE_sol functional are (a, c, x) = (4.7194 Å, 3.1376 Å, 0.3037), while the corresponding LDA results are (4.6373 Å, 3.0990 Å, 0.3033). These calculated values are in very good agreement with the experimental data (4.7038 Å, 3.1336 Å, 0.3035)32 and (4.7034 Å, 3.1335 Å, 0.303).13 As expected, the LDA lattice parameters are underestimated while those of the PBE_sol are slightly overestimated.For BeF2, the three considered crystal structures are α-quartz [Fig. 1(b)], α-cristobalite [Fig. 1(c)] and α′-cristobalite. The α-quartz phase has trigonal symmetry and nine atoms in the conventional hexagonal unit cell. The three Be atoms occupy the Wyckoff 3a(x1, x1, 0) sites and the six F atoms occupy the 6c(x2, y2, z2) sites. On the other hand, the α-cristobalite phase has a tetragonal symmetry and twelve atoms per primitive unit cell. The four Be atoms occupy the Wyckoff 4a(x1, x1, 0) sites and the eight F atoms occupy the 8c(x2, y2, z2) sites. Therefore, each of these two structures has six crystallographic parameters: two lattice parameters (a and c), and four internal parameters (denoted as x1, x2, y2 and z2). The atomic coordinates of the α′-cristobalite phase can be obtained from those of the α-cristobalite by mirror-image transformation (x, y, z) → (−y, −x, z), and the lattice parameters of the two structures are identical. Therefore, only the structure parameters of the first two crystal structures are reported. Our LDA, PBE_sol, and PBE results, shown in Table 1, are in good agreement with available experimental data and other theoretical calculations. The PBE_sol results lie between the corresponding LDA and PBE results and show the best agreement with the experimental data for the α-quartz.
| Phase | Approach | Lattice constants | Internal parameters | ΔE (meV) | ||||
|---|---|---|---|---|---|---|---|---|
| a (Å) | c (Å) | x1 | x2 | y2 | z2 | |||
| α-Quartz | LDA | 4.5958 | 5.0529 | 0.4579 | 0.4098 | 0.2867 | 0.2290 | |
| PBE_sol | 4.7301 | 5.1814 | 0.4662 | 0.4138 | 0.2737 | 0.2188 | ||
| PBE | 4.8497 | 5.3070 | 0.4756 | 0.4176 | 0.2575 | 0.2053 | ||
| PBE6 | 4.8282 | 5.2837 | 0.4740 | 0.4171 | 0.2601 | 0.2075 | ||
| LDA31 | 4.6663 | 5.1608 | ||||||
| Expt.8 | 4.7390 | 5.1875 | 0.4700 | 0.4164 | 0.2671 | 0.2131 | ||
| α-Cristobalite | LDA | 4.5967 | 6.1773 | 0.3226 | 0.2230 | 0.1454 | 0.2000 | 25 |
| PBE_sol | 4.8087 | 6.5984 | 0.3044 | 0.2378 | 0.1112 | 0.1825 | −2 | |
| PBE | 4.8934 | 6.7428 | 0.2988 | 0.2400 | 0.1001 | 0.1769 | −9 | |
| LDA31 | 4.695 | 6.318 | ||||||
| LDA11 | 4.684 | 6.373 | ||||||
| PBE11 | 4.960 | 6.910 | ||||||
3.2. Elastic properties and stability
We show in Table 1 the LDA, PBE_sol and PBE relative energies (ΔE) of the α-cristobalite phase with respect to those of α-quartz. According to the PBE and PBE_sol calculations the latter phase is slightly more stable, in accordance with the Nelson et al.9 GGA calculations. However, the LDA calculations lead to an opposite conclusion. Similar conclusions have recently been reached by Masoumi,11 using both LDA and GGA calculations. These results show that these two phases have extremely close cohesive energies.The α-quartz phase of BeF2 with a trigonal crystal symmetry has six independent elastic constants.34 On the other hand, the rutile phase of ZnF2 and α-cristobalite phase of BeF2 (both have a tetragonal crystal symmetry) also have six independent elastic constants.34 The elastic constants of these phases, obtained by using the LDA and PBE_sol functionals are shown in Table 2. There are two features to note from this table. First, our results for the rutile ZnF2 are in very good agreement with the available experimental values.33 Secondly, the PBE_sol values are systematically smaller than the corresponding LDA values, which is expected since the PBE_sol GGA functional leads to softer materials than LDA (see above). The calculated elastic constants are used in the calculations of the linear TECs (see Sec. 2).
| System | Phase | Approach | Elastic constants (GPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C14 | C33 | C44 | C66 | |||
| BeF2 | α-Quartz | LDA | 46.975 | 14.223 | 12.067 | −6.401 | 75.287 | 31.745 | |
| PBE_sol | 42.278 | 4.991 | 3.760 | −9.077 | 53.009 | 30.548 | |||
| α-Cristobalite | LDA | 33.309 | 7.300 | −5.087 | 22.487 | 35.810 | 13.731 | ||
| PBE_sol | 32.589 | 4.839 | −5.336 | 24.412 | 37.813 | 16.078 | |||
| ZnF2 | Rutile | LDA | 139.442 | 121.550 | 109.127 | 220.673 | 36.583 | 91.826 | |
| PBE_sol | 128.470 | 98.717 | 94.547 | 200.902 | 35.523 | 83.001 | |||
| Expt.33 | 125.5 | 91.8 | 83.0 | 192.2 | 39.5 | 80.7 | |||
The elastic constants could be used to investigate the mechanical stability of the crystal structure. For α-quartz structure, the Born stability criteria34 are
| D = (C11 + C12)C33 − 2C132 > 0, | (4) |
| (C11 − C12)C44 − 2C142 > 0. | (5) |
3.3. Phonon dispersion relations
Since the considered crystals are polar in character we perform non-analytical correction (NAC) to their dynamical matrices. To do that, we have calculated the high-frequency dielectric constant and Born effective charge tensors, and the results are listed in Table 3. The features to note from this table are the following. (i) The calculated results have a very weak dependence on the used exchange-correlation functional. (ii) The effective charges in the ZnF2 are larger than in BeF2, which shows that the ionicity of Zn–F bond is larger than that in Be–F. This is consistent with the corrected Allred–Rochow electronegativity values39 (larger for Be). (iii) Our calculated xx and yy components of the dielectric constant are in very good agreement with available experimental data,36 while that of zz is larger than the measured one. However, the comparable values of diagonal components of the dielectric constant in our calculations are consistent with the experimental and calculated values for other metal fluorides crystallizing in the rutile structure (such as MgF2 and FeF2).40| System | Phase | Approach | DC | Atom | Born effective charge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xx = yy | zz | xx | xy | xz | yx | yy | yz | zx | zy | zz | ||||
| BeF2 | AQ | PBE_sol | 1.902 | 1.912 | Be | 1.728 | 0.000 | 0.000 | 0.000 | 1.914 | 0.081 | 0.000 | −0.079 | 1.866 |
| F | −0.747 | 0.221 | −0.115 | 0.213 | −1.074 | 0.337 | −0.095 | 0.345 | −0.933 | |||||
| LDA | 1.887 | 1.896 | Be | 1.727 | 0.000 | 0.000 | 0.000 | 1.918 | 0.080 | 0.000 | −0.0758 | 1.864 | ||
| F | −0.746 | 0.226 | −0.124 | 0.218 | −1.076 | 0.343 | −0.104 | 0.356 | −0.932 | |||||
| BeF2 | AC | PBE_sol | 1.723 | 1.718 | Be | 1.832 | 0.005 | −0.045 | 0.005 | 1.832 | 0.049 | 0.100 | −0.101 | 1.810 |
| F | −1.221 | −0.117 | 0.377 | −0.101 | −0.611 | 0.061 | 0.380 | 0.100 | −0.905 | |||||
| LDA | 1.827 | 1.818 | Be | 1.823 | 0.005 | − 0.036 | 0.005 | 1.823 | 0.036 | 0.110 | −0.110 | 1.790 | ||
| F | −1.199 | −0.135 | 0.329 | −0.120 | −0.624 | 0.076 | 0.333 | 0.115 | −0.896 | |||||
| ZnF2 | Rutile | PBE_sol | 2.549 | 2.664 | Zn | 2.222 | −0.162 | 0.000 | −0.162 | 2.222 | 0.00 | 0.000 | 0.000 | 2.424 |
| F | −1.111 | −0.409 | 0.000 | −0.409 | −1.111 | 0.000 | 0.000 | 0.000 | −1.200 | |||||
| LDA | 2.547 | 2.653 | Zn | 2.206 | −0.1493 | 0.000 | −0.1493 | 2.206 | 0.000 | 0.000 | 0.000 | 2.392 | ||
| F | −1.103 | −0.395 | 0.000 | −0.395 | −1.103 | 0.000 | 0.000 | 0.000 | −1.196 | |||||
| Expt.36 | 2.6 | 2.1 | ||||||||||||
Fig. 2 shows the calculated phonon dispersion relations and PDOS of the rutile ZnF2, with and without NAC. Also shown are the calculated Zn and F projected PDOS, with NAC, and the available experimental data.37,38 The frequency spans across an interval of about 500 cm−1. The features to note from this figure are the following. (i) As expected, the NAC leads to longitudinal optical-traverse optical (LO-TO) splitting, near the Γ point. The strongest effects are felt by high-frequency optical modes. However, the effects of the NAC on the calculated PDOS are quite small. (ii) Experimental data are available only for infrared37 and Raman12,38 active modes at the Γ-points. The reported frequencies of the latter modes are in very good agreement with each other, and hence only those of ref. 38 are shown in Fig. 2. For the designation of these phonon modes see ref. 40. Fig. 2 shows that these experimental data agree reasonably well with our first-principles results.
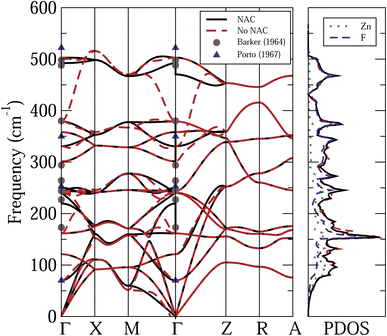 | ||
| Fig. 2 Calculated phonon dispersion relations and PDOS of ZnF2, with (black solid curves) and without (red dashed curves) non-analytic correction (NAC). The Zn and F projected PDOS, with NAC, and also shown. Symbols: available experimental data.37,38 | ||
Fig. 3 shows the phonon dispersion relations of the α-quartz and α-cristobalite phases of BeF2, taking into account the NAC. Also shown are the PDOS, and Be and F projected PDOS of the α-cristobalite phase. The results of the α′-cristobalite phase are very similar to those of α-cristobalite and hence are not shown. The features to note from this figure are the following. (i) The very wide frequency range of the phonon modes in these systems, compared to that of ZnF2. This can be understood as a consequence of the rather large mass difference between Be and Zn atoms. (ii) The frequency range of both phases of BeF2 can be separated, according to the character of the phonon modes, into three sub-regions. (a) The lower frequency region between 0 and about 700 cm−1, where the phonon modes are mainly due to the vibrations of F atoms. The contribution of the Be atoms becomes appreciable above 300 cm−1. It is worth noting that in the case of ZnF2 the dominance of the vibrations of the F atoms occurs in the upper part of the frequency range because the Zn atom is heavier than the F atom. (b) A narrow intermediate region at about 770 cm−1, where the rather localized phonon modes originate from vibrations involving both Be and F atoms. (c) The upper-frequency region, where the phonon modes originate mainly from vibrations of Be atoms. (iii) The opening of two frequency gaps, between (a) and (b), and between (b) and (c) sub-regions. These frequency gaps can be understood as a consequence of the localization of phonon modes in the (b) sub-region.
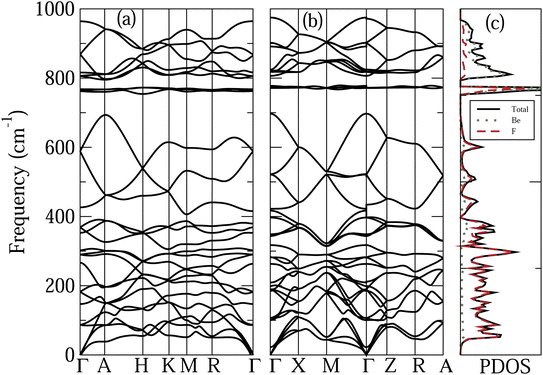 | ||
| Fig. 3 Calculated phonon dispersion relations of the (a) α-quartz and (b) α-cristobalite phases of BeF2. (c) PDOS, and the Be and F projected PDOS of the α-cristobalite phase. | ||
3.4. Thermal expansion
The calculated linear and volumetric TECs of the considered phases of ZnF2 and BeF2, according to the procedure described in Sec. 2, are depicted in Fig. 4 and 5, respectively. It is worth mentioning that, as expected, the NACs to the dynamical matrices have negligible effects on the calculated linear TECs.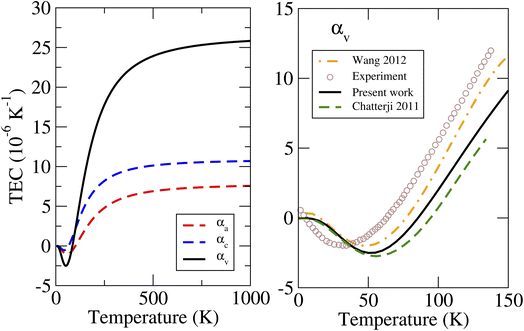 | ||
| Fig. 4 Calculated linear and volumetric TECs of ZnF2 using the LDA, compared to the available experimental data13 and previous theoretical results.13,14 | ||
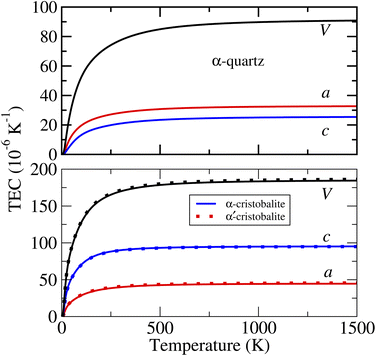 | ||
| Fig. 5 Calculated linear and volumetric TECs with PBE_sol of the three considered phases of BeF2. Note the difference in the scales of the two panels. | ||
We will first look at the TECs of ZnF2. The important features to note from Fig. 4 are the following. (i) The NTE at low temperatures is mostly due to αa. The negative values of αc are smaller (in magnitude) than those of αa and lie in a considerably shorter T-range. This is clear from the magnitude and the location of the minimum values: αa ∼ −1.05 × 10−6 K−1 at 55 K, and αc ∼ −0.5 × 10−6 K−1 at 40 K. These results are consistent with observed T-variations of the a and c lattice parameters at low temperatures (see Fig. 3 of ref. 13). (ii) The calculated αv from the linear TECs (i.e., αv = 2αa + αc) are in good agreement with the previous direct theoretical calculations,13,14 and the results of all these theoretical calculations are in a qualitative agreement with experimental data.13 This finding reflects the accuracy and reliability of our calculated linear TECs. (iii) αc is systematically and appreciably larger than αa. For example, at 300 K the calculated value of αc (of 8.9 × 10−6 K−1) is about 60% larger than that of αa (of 5.6 × 10−6 K−1).
As for the thermal expansion of the considered phases of BeF2, the features to note from Fig. 5 are the following. (i) Unlike ZnF2, the calculated values of both αa and αc are always positive for all of the considered phases of BeF2. (ii) Both αc and αa of the α-cristobalite structure are very close to those of α′-cristobalite, and hence only those of the former phase will be discussed below. (iii) In the considered T-range, αa(T) of the α-quartz structure is slightly larger than αc(T), whereas αa(T) of the α-cristobalite phase is much smaller than αc(T). (iv) The large αc and αa lead to very large αv for both phases of BeF2. For example, at 300 K, the values of αv are of 77.6 and 169.9 × 10−6 K−1 respectively for the above two phases of BeF2, compared to that of 20.0 × 10−6 K−1 for ZnF2. Our largest calculated linear TEC is of ∼95 × 10−6 K−1 at 300 K for αc of the α-cristobalite phase. This is indeed large compared to the experimental linear TECs at 300 K of four fluorites, i.e., CaF2, SrF2, BaF2, and PbF2 (ref. 41) that range between 18.1 and 29 × 10−6 K−1, but still is somewhat smaller than the measured linear TEC value of 163.9 × 10−6 K−1 of an Ti–Nb alloy.42
The key physically insightful quantity for the interpretation of the above results is the PDOS weighted by the Grüneisen parameters, Γi(ν), defined in eqn (2). Fig. 6 shows Γi(ν) of ZnF2, and the α-quartz and α-cristobalite phases of BeF2. The important features to note from this figure are the following. (i) For ZnF2, the low-frequency modes (ν < 150 cm−1) have negative Grüneisen parameters, which lead to negative Γi(ν) in this ν range. Since low-frequency modes are easily thermally excited, this finding explains the observed NTE in ZnF2. Moreover, by inspecting the differences between Γa(ν) and Γc(ν) one can easily understand why αa is always lower than αc. (ii) The Γi(ν) of the considered phases of BeF2 are always positive, which reflects the dominance of positive mode Grüneisen parameters in these phases. This explains the lack of NTE in the considered phases of BeF2. (iii) The Γa(ν) and Γc(ν) of α-quartz BeF2 have comparable magnitudes, with Γc(ν) being smaller than Γa(ν) for ν < 100 cm−1, which explain the comparable magnitudes and ordering of its αc and αa. (iv) The peak in Γc(ν) of the α-cristobalite phase around ν ∼ 34 cm−1 is much higher than that of the Γa(ν), which results in a large αc compared to αa. This finding means that, in this ν-range, the positive mode Grüneisen parameters associated with the out-of-plane deformation are significantly larger than those associated with the in-plane deformation. The large Grüneisen parameters can be viewed as a manifestation of strong anharmonic effects in the α-cristobalite and α′-cristobalite structures of BeF2. However, it should be noted that large Grüneisen parameters are not the only factor that is responsible for the giant αv of the α-cristobalite: the elastic property via the negative (and with a large magnitude) C13 elastic constant (see Table 2 and eqn (1)) plays also a major role. The above findings explain the much larger volumetric TEC of the α-cristobalite phase of BeF2, compared to that of the α-quartz phase, which, in turn, is larger than that of ZnF2.
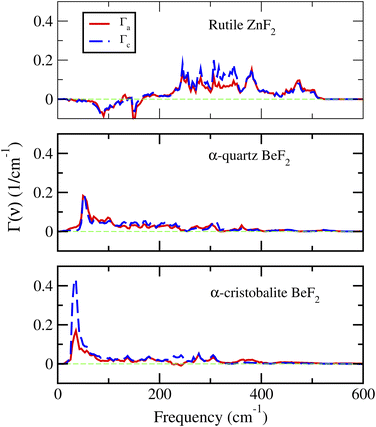 | ||
| Fig. 6 The PDOS weighted by the Grüneisen parameters of the rutile ZnF2, and the α-quartz and α-cristobalite phases of BeF2. | ||
4. Summary
First-principles calculations are performed to investigate the structural, elastic, and vibrational properties of the rutile structure of ZnF2 and three crystal structures of BeF2 (α-quartz, α-cristobalite and its similar phase with space group P43212). The so-obtained phonon density of states, mode Grüneisen parameters, and elastic constants are used to study the linear thermal expansion coefficients (TECs) of the compounds mentioned above, within a Grüneisen formalism. We have used deformations that preserve the symmetry of the crystal to obtain the Grüneisen parameters. The considered crystal structures of both systems are found to be mechanically stable. The calculated physical quantities for both systems are in very good agreement with the available experimental data and previous theoretical results. For ZnF2, the calculated linear TECs, αa and αc, along the a and c directions are consistent with the experimental T-variations of the corresponding lattice parameters, respectively. The volumetric TEC αv computed from these linear TECs is in qualitative agreement with experiment at low temperatures, including negative thermal expansion (NTE) behavior. The considered phases of BeF2 are not NTE materials, and their linear TECs are much higher than those of ZnF2, especially for the α-cristobalite phase. The elastic constants, high-frequency dielectric constants, Born effective charge tensors, and TECs of the considered phases of BeF2 are reported in this work for the first time and could serve as predictions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Supercomputing Center, Singapore (NSCC) and A*STAR Computational Resource Center, Singapore (ACRC) for computing resources. We also thank Iyad Al-Qasir for fruitful discussions. This work is supported by RIE2020 Advanced Manufacturing and Engineering (AME) Programmatic grant no. A1898b0043.References
- J. Parker and P. France, in Glasses and glass-ceramics, ed. M. H. Lewis, Chapman and Hall, 2011, p. 156 Search PubMed.
- F. Gan, Optical properties of fluoride glasses: a review, J. Non-Cryst. Solids, 1995, 184, 9 CrossRef CAS.
- M. J. Weber, C. F. Cline, W. L. Smith, D. Milam, D. Heiman and R. Hellwarth, Measurements of the electronic and nuclear contributions to the nonlinear refractive index of beryllium fluoride glasses, Appl. Phys. Lett., 1978, 32, 403 CrossRef CAS.
- L. Mei, X. Cai, D. Jiang, J. Chen, W. Guo and W. Xiong, Investigation of thermal neutron scattering data for BeF2 and LiF crystals, J. Nucl. Sci. Tech., 2013, 50, 419 CrossRef CAS.
- R. Kagawa, M. Montgomery, K. Braig, A. Leslie and J. Walker, The structure of bovine F1-ATPase inhibited by ADP and beryllium fluoride, EMBO J., 2004, 23, 2734 CrossRef CAS PubMed.
- I. Al-Qasir and A. Qteish, Neutron filter efficiency of beryllium and magnesium fluorides, J. Appl. Crystallogr., 2017, 50, 441 CrossRef CAS.
- Z. Kaawar and B. Paulus, A computational study of the structure of zinc fluoride surfaces, AIP Conf. Proc., 2015, 1653, 020051 CrossRef.
- P. Ghalsasi and P. S. Ghalsasi, Single crystal X-ray structure of BeF2: α-quartz, Inorg. Chem., 2011, 50, 86 CrossRef CAS.
- J. R. Nelson, R. J. Needs and C. J. Pickard, High-pressure phases of group II difluorides: polymorphism and superionicity, Phys. Rev. B, 2017, 95, 054118 CrossRef.
- M. S. Rakitin, A. R. Oganov, H. Niu, M. M. D. Esfahani, X.-F. Zhou, G.-R. Qian and V. L. Solozhenko, Novel phase of beryllium fluoride at high pressure, Phys. Chem. Chem. Phys., 2015, 17, 26283 RSC.
- N. Masoumi, First-principles DFT study of imide and fluoride analogs of silicon oxide, silicon oxynitride, and their alloys, PhD thesis, Arizona State University, Cambridge, MA, 2021 Search PubMed.
- D. Kurzydlowski, A. Oleksiak, S. B. Pillai and P. K. Jha, High-pressure phase transitions of zinc difluoride up to 55 GPa, Inorg. Chem., 2020, 59, 2584 CrossRef CAS PubMed.
- T. Chatterji, M. Zbiri and T. C. Hansen, Negative thermal expansion in znf2, Appl. Phys. Lett., 2011, 98, 181911 CrossRef.
- L. Wang, P. -F. Yuan, F. Wang, Q. Sun, E. -J. Liang and Y. Jia, Theoretical study of negative thermal expansion mechanism of ZnF2, Mater. Res. Bull., 2012, 47, 1113 CrossRef CAS.
- C. K. Gan and K. T. E. Chua, Large thermal anisotropy in monoclinic niobium trisulfide: a thermal expansion tensor study, J. Phys.: Condens. Matter, 2019, 31, 265401 CrossRef CAS PubMed.
- E. Grüneisen, Handb. Phys., 1926, 10, 1 Search PubMed.
- T. H. K. Barron, J. G. Collins and G. K. White, Thermal expansion of solids at low temperatures, Adv. Phys., 1980, 29, 609 CrossRef CAS.
- P. K. Schelling and P. Keblinski, Thermal expansion of carbon structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035425 CrossRef.
- Y. Ding and B. Xiao, Thermal expansion tensors, Grüneisen parameters and phonon velocities of bulk MT2 (M = W and Mo; T = S and Se) from first principles calculations, RSC Adv., 2015, 5, 18391 RSC.
- C. K. Gan, J. R. Soh and Y. Liu, Large anharmonic effect and thermal expansion anisotropy of metal chalcogenides: the case of antimony sulfide, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235202 CrossRef.
- G. Liu, H. M. Liu, J. Zhou and X. G. Wan, Temperature effect on lattice and electronic structures of WTe2 from first-principles study, J. Appl. Phys., 2017, 121, 045104 CrossRef.
- J. Liu and P. B. Allen, Internal and external expansions of wurtzite ZnO from first principles, Comput. Mater. Sci., 2018, 154, 251 CrossRef CAS.
- C. K. Gan, Y. Liu, T. C. Sum and K. Hippalgaonkar, Efficacious symmetry-adapted atomic displacement method for lattice dynamical studies, Comput. Phys. Commun., 2021, 259, 107635 CrossRef CAS.
- W. Frank, C. Elsässer and M. Fähnle, Ab initio force-constant method for phonon dispersions in alkali metals, Phys. Rev. Lett., 1995, 74, 1791 CrossRef CAS PubMed.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, First-principles determination of the soft mode in cubic ZrO2, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- G. Kresse, J. Furthmüller and J. Hafner, Ab initio force constant approach to phonon dispersion relations of diamond and graphite, Europhys. Lett., 1995, 32, 729 CrossRef CAS.
- C. K. Gan, X. F. Fan and J. -L. Kuo, Composition-temperature phase diagram of BexZn1−xO from first principles, Comput. Mater. Sci., 2010, 49, S29 CrossRef CAS.
- Y. Liu, K. T. E. Chua, T. C. Sum and C. K. Gan, First-principles study of the lattice dynamics of Sb2S3, Phys. Chem. Chem. Phys., 2014, 16, 345 RSC.
- A. Dal Corso, Elastic constants of beryllium: a first-principles investigation, J. Phys.: Condens. Matter, 2016, 28, 075401 CrossRef PubMed.
- C. K. Gan and C. H. Lee, Anharmonic phonon effects on linear thermal expansion of trigonal bismuth selenide and antimony telluride crystals, Comput. Mater. Sci., 2018, 151, 49 CrossRef CAS.
- F. Yu, M. Xu, M. Jiang and J. -X. Sun, The phase transitions and electronic structures of crystalline BeF2 under high-pressure: First-principle calculations, Solid State Commun., 2013, 169, 14 CrossRef CAS.
- N. O'Toole and V. Streltsov, Synchrotron X-ray analysis of the electron density in CoF2 and ZnF2, Acta Cryst. B, 2001, 57, 128 CrossRef PubMed.
- D. S. Rimai, Elastic properties of ZnF2 between 4.2 and 300 K, Phys. Rev. B: Solid State, 1977, 16, 4069 CrossRef CAS.
- W. Pabst and E. C. Gregorová, Elastic properties of silica polymorphs – a review, Ceram.-Silik., 2013, 57, 167 CAS.
- F. Mouhat and F. -X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- R. E. Alaoui-Bichri, J. Giordano, R. Almairac, C. Benoit and P. Nassiri, Properties, J. Phys., 1980, 41, 543 CrossRef.
- J. A. S. Barker, Transverse and longitudinal optic mode study in MgF2 and ZnF2, Phys. Rev., 1964, 136, A1290 CrossRef.
- S. P. S. Porto, P. A. Fleury and T. C. Damen, Raman spectra of TiO2, MgF2, ZnF2, FeF2, and MnF2, Phys. Rev., 1967, 154, 522 CrossRef CAS.
- A. Qteish, Electronegativity scales and electronegativity-bond ionicity relations: a comparative study, J. Phys. Chem. Solids, 2019, 124, 186 CrossRef CAS.
- C. Benoit and J. Giordano, Dynamical properties of crystals of MgF2, ZnF2 and FeF2. II. Lattice dynamics and infrared spectra, J. Phys. C: Solid State Phys., 1988, 21, 5209 CrossRef CAS.
- R. B. Roberts and G. K. White, Thermal expansion of fluorites at high temperatures, J. Phys. C: Solid State Phys., 1986, 19, 7167 CrossRef CAS.
- M. Bönisch, A. Panigrahi, M. Stoica, M. Calin, E. Ahrens, M. Zehetbauer, W. Skrotzki and J. Eckert, Giant thermal expansion and α-precipitation pathways in Ti-alloys, Nat. Commun., 2017, 8, 1429 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |