Open Access Article
Open Access ArticleEffects of flow history on extensional rheological properties of wormlike micelle solution
In-Hyuk Janga,
Won Jun Leea,
Daekwon Jina and
Ju Min Kim *ab
*ab
aDepartment of Energy Systems Research, Ajou University, South Korea. E-mail: jumin@ajou.ac.kr; Fax: +82-31-219-1612; Tel: +82-31-219-2475
bDepartment of Chemical Engineering, Ajou University, South Korea
First published on 16th November 2022
Abstract
A wormlike micelle (WLM) solution is a complex fluid that forms when the surfactant concentration is high. It has rheological properties similar to those of polymer solutions. However, unlike polymer molecules, WLM chains possess the dynamic microstructure that can be reversibly broken and reassembled in flows. Therefore, the rheological properties and flow behavior of WLM solutions have attracted much attention owing to their unique dynamic microstructures. However, the effects of the flow history on the extensional rheological properties of WLM solutions remain unclear. In this study, the change in the extensional rheological properties of WLM solutions depending upon on their shear flow histories was investigated by combining the dripping-onto-substrate/capillary break-up extensional rheometry technique with a compressed gas flow (stop-flow) control method. This approach precisely controls the shear flow histories of the WLM solutions. The results revealed that the shear flow history has a substantial impact on elongational rheological properties such as relaxation time. They also showed that the effects of the characteristic shear rate are highly dependent on the surfactant concentration. We expect that the current findings can be applied to understand the extensional rheological properties of complex fluids in industrially relevant processes such as coating and printing.
Introduction
A wormlike micelle (WLM) solution forms entanglements at low surfactant concentrations, has rheological properties comparable to those of polymer solutions, and possesses a microstructure that can be dynamically broken and reassembled in flows, making it a very interesting fluid.1 Therefore, a WLM solution has attracted significant interest, and it has been extensively studied, including those on shear-induced phase transitions and flow instability,2 shear banding and its corresponding structural change in shear flows,3 elongational flow-induced structures,4,5 pre-shear effects on elongational properties,6 and effects of the initial step strain on elongational rheological properties.7 However, complex fluids frequently experience shear flows before entering the elongational flow region in many practical applications, such as contraction flows. In the previous study, pre-shear was imposed on a WLM solution between two disks by rotating the upper disk (flow, flow gradient, and vorticity directions are θ, z and r in cylindrical coordinates in this case, respectively).8 Subsequently the filament was stretched to measure its elongational rheological properties.6 However, the principal stretching axis in the pre-shearing stage of the previous study6 differs from that in the typical Poiseuille flow scenario (flow direction: z; flow gradient direction: r; vorticity direction: θ), which is frequently experienced immediately before the contraction flow.Capillary-thinning of a fluid filament, which is induced by surface tension, occurs in various flow situations, such as saliva stretching between two fingers.9 Quantitative analysis of capillary-thinning and break-up dynamics yields the extensional viscosities and characteristic time scales related to complex fluids.9,10 For example, the capillary-thinning phenomenon between droplets formed during a jetting process from a nozzle has been used to determine the short relaxation times of weakly elastic solutions.11 Capillary break-up extensional rheometry (CaBER), which is commercially available, imposes a step strain on a complex fluid placed between two plates, causing capillary-thinning of the formed liquid bridge. Subsequently, the neck-thinning dynamics are captured with a laser-based micrometer or a high-speed camera.12 The benefit of the CaBER setup is that the capillary-thinning dynamics can be observed in the Eulerian framework without requiring fluid element tracking during its flow.12 However, for weakly elastic fluids with low viscosity [η (shear viscosity) < 20 mPa s; λ (relaxation time of a viscoelastic fluid) < 1 ms], measuring the extensional rheological properties is difficult because the capillary break-up occurs before the CaBER measurement.9,13 In addition, the initial step strain necessary for the formation of a liquid bridge in a CaBER experiment can significantly alter the equilibrium microstructure of the complex fluid, thereby influencing its elongational rheological properties.7,13
Dripping-onto-substrate (DoS)/CaBER was developed to overcome the limitations of conventional CaBER by bridging the liquid from the nozzle by dripping it onto the substrate.13,14 By lowering the dispensing speed of the liquid released from the nozzle, microstructure disruption can be minimized.13,14 The capillary-thinning and break-up processes are captured with a normal- or high-speed camera after the liquid bridge formation, and the thickness evolution of the fluid filament is obtained using an imaging processing technique.13,14 It has been demonstrated that the elongational properties of weakly elastic fluids with low viscosities (η < 20 mPa s; λ < 1 ms) can be measured using DoS/CaBER.13,15
In this study, we investigated the effects of the shear flow histories of WLM solutions on their elongational rheological properties by combining DoS/CaBER13 with a compressed gas-based flow (stop-flow) control technique.16 In the original DoS/CaBER method, a syringe pump is used to control the liquid flow rate from the nozzle; however, a long transient time is required to reach the steady state.16 In this study, we improved the original DoS/CaBER method by adopting the stop-flow technique,16 which controls the flow rate more accurately using a compressed gas than a syringe pump. In our experimental setup, the liquid first experiences the Poiseuille flow, and subsequently the elongational rheological properties are measured, mimicking practical flow conditions such as contraction flows. We showed that our novel experimental setup can be applied to demonstrate the significant impact of the shear (Poiseuille) flow history of a WLM solution on its elongational rheological properties.
Experimental
Materials and test fluid preparation
The monohydrate product of cetylpyridinium chloride (CPyCl, Sigma-Aldrich) (Molecular Weight (M.W.): 358.00 g mol−1) was used as the surfactant, and sodium salicylate (NaSal, Sigma-Aldrich) (M.W.: 160.10 g mol−1) and sodium chloride (NaCl, Sigma-Aldrich) were used as the salts. Following the previous study,17 WLM solutions were prepared by first dissolving the surfactant in deionized water in target concentrations with a magnetic stirrer at 120 rpm and 40–50 °C. Following this, NaSal and NaCl were added, and the solution was mixed for 2 h. In this study, three different WLM solutions were prepared: 50/25/100, 60/30/100, and 100/50/100 mM (CPyCl/NaSal/NaCl). The prepared solutions were stored at room temperature for 24 h to stabilize and remove air bubbles generated during sample preparation. A 95 wt% glycerin (Sigma-Aldrich) aqueous solution was also prepared to investigate the characteristics of the stop-flow system.Measurement of shear rheological properties of WLM solution
The shear rheological properties of each WLM solution were measured using a rotational rheometer (DHR-3, TA Instruments). Steady- and small-amplitude oscillatory shear (SAOS) tests were conducted with a cone-and-plate geometry (1°, 40 mm diameter) at 23 °C. Since the rheological properties of a WLM solution can be affected by pre-shear,6 the measurements were conducted after a 1 min waiting time following sample loading.DoS/CaBER with stop-flow system
A schematic of the DoS/CaBER setup13 used in this study is presented in Fig. 1. In the original DoS/CaBER setup,13 the liquid flow rate is controlled with a syringe pump, and the pump switch is deactivated when the droplet from the nozzle reaches the underlying substrate. Since the flow does not completely stop even after the syringe pump is turned off as demonstrated later in this work, a compressed gas-based flow control (stop-flow) method was adopted in this study.16 Fig. 1 shows that the solution flows from a solution reservoir (15 mL conical tube, Falcon) to a nozzle [inner diameter (ID): 0.833 mm; outer diameter (OD): 1.27 mm (D0)] along a Tygon tube (ID = 1.016 mm; length: 30 cm). This occurs under the imposed pressure (nitrogen) in the reservoir, forming a droplet at the nozzle tip. Subsequently, the fluid flow is stopped by decreasing the reservoir pressure to ambient pressure with a solenoid valve16 immediately as the formed droplet at the nozzle reaches the substrate (diameter: 3.00 mm, length: 6.00 mm) located at a fixed distance from the nozzle (H = 3D0). The stop-flow system consists of a pneumatic regulator (Type 120-BA, ControlAir) and a solenoid valve (Type 0330, Bürkert) connected to a single-module USB carrier (NI USB-9162, National Instruments) and a digital module (NI-9472, National Instruments). The solenoid valve is controlled using LabVIEW software (National Instruments). When a liquid bridge is formed between the nozzle tip and the substrate, the filament gradually thins under the capillary force and is finally pinched off. These procedure images are captured at 1000–5000 fps using a high-speed camera (VEO-E 310L, Phantom). In this study, the sessile drop contact line was pinned to the edge of a 3 mm-diameter circular glass substrate, isolating the capillary-thinning dynamics from the droplet spreading effects.18,19 As also shown in Fig. 1, the optical components consist of a light source, a light diffuser, and an infinity-corrected objective (5×, Edmund Optics). The captured images were processed and analyzed using Image J (NIH) software and a homemade MATLAB code based on the Canny edge detection algorithm.20 The capillary-thinning profiles were obtained through three independent experiments. The surface tension, σ, was also measured using the current DoS/CaBER setup at 23 °C. Still images were captured after the pendent drop hanging from the nozzle reached a steady state. The surface tension was subsequently obtained by analyzing the acquired images using Opendrop software.21 The surface tension of all WLM samples considered in this study was 0.032 N m−1, which is consistent with the literature value.22 | ||
| Fig. 1 Schematic of improved DoS/ CaBER experimental setup: flow rate from fluid reservoir to substrate is controlled by stop-flow method. | ||
Results and discussion
First, we investigated the characteristics of the stop-flow system that was newly implemented in the DoS/CaBER system. For comparison, a 95 wt% glycerin aqueous solution (shear viscosity = 480 cP) was first forced out of the nozzle with a syringe pump and the stop-flow system separately to form droplets on the nozzle tip. The flow was stopped by switching off the syringe pump and changing the reservoir pressure to the ambient pressure, respectively, when the droplets touched the substrate. The capillary-thinning and pinch-off dynamics of the liquid bridge formed between the nozzle tip and the substrate were recorded with a high-speed camera [refer to the inset snapshots in Fig. 2(a)]. When the flow rate from the nozzle was controlled by the syringe pump, the pinch-off time was ∼7 ms longer than when the stop-flow system was used [Fig. 2(a)]. In the case of the syringe pump, the prolonged pinch-off time can be attributed to the fact that the fluid continued to flow from the top after the pump had been shut off. We investigated the size changes of the droplets remaining on the nozzle tip after the pinch-off, to understand the difference in the pinch-off times observed in Fig. 2(a). The size of the droplet hanging on the nozzle tip after the pinch-off slightly changes when the stop-flow system is employed. However, the droplet size continuously increases when the syringe pump is used for the flow rate control, as shown in Fig. 2(b). The above results confirm that when the syringe pump is employed, the fluid continues to flow out from the nozzle even after the pump is turned off, which can delay the capillary-thinning and pinch-off dynamics. In addition, these findings are consistent with those of the previous study on flow control in microfluidic channels.16 The previous study demonstrated that when a syringe pump is used to change the flow rate, a non-negligible transitory period is caused by the compressibility of the liquid in the tubes, which is significantly reduced when it is replaced by the stop-flow system.16 Therefore, we conclude that the stop-flow system is suitable for precisely controlling the flow rate in DoS/CaBER measurements.Next, we characterized the shear rheological properties of the three different WLM solutions [50/25/100, 60/30/100, and 100/50/100 mM (CPyCl/NaSal/NaCl)] with the rotational rheometry at 23 °C. The shear viscosity [η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )] of each WLM solution measured as a function of the shear rate (
)] of each WLM solution measured as a function of the shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is shown in Fig. 3. The WLM solutions show a clear zero-shear viscosity (η0) region at low shear rates (
) is shown in Fig. 3. The WLM solutions show a clear zero-shear viscosity (η0) region at low shear rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) < 1), whereas they present a strong shear thinning behavior at high shear rates. The zero-shear viscosities of the WLM solutions are obtained using the Carreau model as follows:
< 1), whereas they present a strong shear thinning behavior at high shear rates. The zero-shear viscosities of the WLM solutions are obtained using the Carreau model as follows:
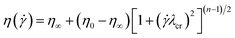 | (1) |
 | (2) |
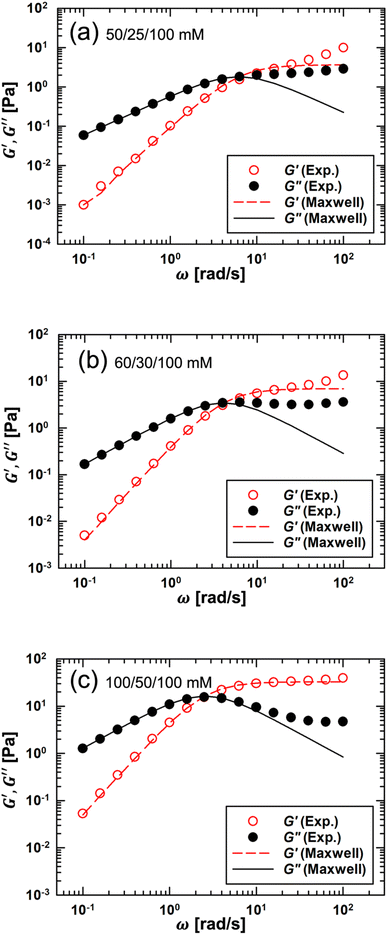 | ||
| Fig. 4 Shear storage (G′) and loss (G′′) moduli as functions of angular frequency (rad s−1) for three different WLM solutions: (a) 50/25/100, (b) 60/30/100, (c) 100/50/100 mM (CPyCl/NaSal/NaCl). | ||
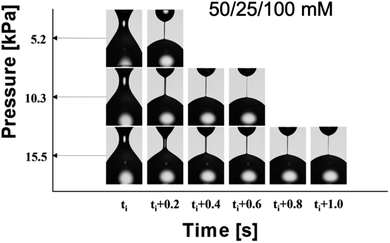
As shown in Fig. 5, we presented the representative images of the temporal evolutions of the filament necks observed for the three different solutions at the fixed imposed pressure (4.1 kPa) in the reservoir, when our current DoS/CaBER combined with stop-flow control system (SF-DoS/CaBER) was employed. Each neck shape generated between the nozzle and the substrate is a cylindrical, slender filament typical of a highly viscous or elastic fluid.9,14 This cylindrical neck shape differs from the conical neck shapes observed in inviscid and power-law fluids.9,14 In addition, the images show that the thinning rate decreases, and the pinch-off time increases with increasing concentration. The time evolutions of the neck shapes presented in Fig. 6 quantitatively show that the pinch-off dynamics decelerates as the surfactant concentration increases. The plots comprise at least two separate regions, which will ultimately form straight lines (elasto-capillary regions) in semi-log plots.
 | ||
| Fig. 6 Time evolutions of normalized neck radii [R(t)/R0] for three different WLM solutions: 50/25/100, 60/30/100, and 100/50/100 mM (CPyCl/NaSal/NaCl). Every 50 data points, the average values with error bars obtained from three measurements are presented. Extensional relaxation times (λE) are determined by fitting the average values in elasto-capillary region using eqn (3) (refer to straight lines). Reservoir is subjected to constant imposed pressure of 4.1 kPa during all experiments, and R0 denotes outer radius of nozzle. | ||
For viscous fluids, in the initial neck-thinning stage, the evolution dynamics are determined by the competition between the capillary, gravity, inertial and viscous forces.9,23 As the diameter becomes thinner, the gravitational effects are irrelevant,23 and the thinning dynamics are determined by the competition between the inertial and viscous forces.9 The Ohnesorge number, Oh  , is dimensionless number and denotes the relative ratio of the viscous-capillary
, is dimensionless number and denotes the relative ratio of the viscous-capillary  to Rayleigh (or inertio-capillary;
to Rayleigh (or inertio-capillary; 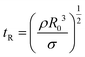 ) time scales, where R0 denotes the outer nozzle radius (=D0/2).9,13 Clasen et al.24 demonstrated that the viscous force dominates the inertial force, and the dynamics of fluid filament thinning are determined by the balance of the viscous and capillary forces when Oh > 0.2.24 The current study corresponds to a viscous-dominant case because Oh > 4.0 for all the experimental conditions of the WLM solutions. The capillary-thinning dynamics of a Newtonian fluid follow the relationship of
) time scales, where R0 denotes the outer nozzle radius (=D0/2).9,13 Clasen et al.24 demonstrated that the viscous force dominates the inertial force, and the dynamics of fluid filament thinning are determined by the balance of the viscous and capillary forces when Oh > 0.2.24 The current study corresponds to a viscous-dominant case because Oh > 4.0 for all the experimental conditions of the WLM solutions. The capillary-thinning dynamics of a Newtonian fluid follow the relationship of  under high-Oh number conditions, where tc is the pinch-off time, and R(t) is the neck radius of the fluid filament at time t.25 For power-law fluids with constitutive relationship η(
under high-Oh number conditions, where tc is the pinch-off time, and R(t) is the neck radius of the fluid filament at time t.25 For power-law fluids with constitutive relationship η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = Kc
) = Kc![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1 (n: power-law index, Kc: consistency index), R(t)/R0 is proportional to (tc − t)n when n > 2/3. However, there is no simple theoretical model to predict capillary-thinning occurrence for n < 2/3 because the filament shape violates the slenderness assumption.9,26,27 When elasticity dominates both inertial and viscous forces in a viscoelastic fluid, the elasto-capillary region appears as a straight line in a semi-log plot (see Fig. 6), as predicted by Entov and Hinch:10
n−1 (n: power-law index, Kc: consistency index), R(t)/R0 is proportional to (tc − t)n when n > 2/3. However, there is no simple theoretical model to predict capillary-thinning occurrence for n < 2/3 because the filament shape violates the slenderness assumption.9,26,27 When elasticity dominates both inertial and viscous forces in a viscoelastic fluid, the elasto-capillary region appears as a straight line in a semi-log plot (see Fig. 6), as predicted by Entov and Hinch:10
 | (3) |
Subsequently, the changes in the extensional rheological properties were investigated based on the flow histories of the WLM solutions, as they flow from the reservoir to the nozzle through the tube. The representative images in Fig. 7 show that the imposed pressure in the reservoir for the 50/25/100 mM WLM solution alters the dynamics of capillary-thinning and pinch-off. The images correspond to the same diameter and the time interval between the selected images is Δt = 0.2 s. Moreover, the filament lifetime and the pinch-off time increase with increasing imposed pressure in the reservoir. The flow history in the tube as a function of the applied pressure is represented as a characteristic shear rate, and the results are summarized in Table 1 for the three different WLM solutions. The characteristic shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c) is defined as
c) is defined as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ≡ Q/πRi3, where Q is the mean volumetric flow rate from the reservoir to the nozzle tip, and Ri is the inner radius of the nozzle. The Weissenberg number (Wi) is the relative ratio of the elastic to viscous forces defined as Wi = λM
c ≡ Q/πRi3, where Q is the mean volumetric flow rate from the reservoir to the nozzle tip, and Ri is the inner radius of the nozzle. The Weissenberg number (Wi) is the relative ratio of the elastic to viscous forces defined as Wi = λM![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c. The pressures applied to the WLM solutions with three different concentrations were intended to have similar levels of characteristic shear rates, i.e., (1)
c. The pressures applied to the WLM solutions with three different concentrations were intended to have similar levels of characteristic shear rates, i.e., (1) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ≈ 20, (2)
c ≈ 20, (2) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ≈ 300, and (3)
c ≈ 300, and (3) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c ≈ 1000. The effects of the flow history on the dynamics of capillary-thinning and pinch-off are notably dependent on the WLM concentration, as shown in Fig. 8 [the labeled numbers denote the relaxation times (unit: s) of the corresponding curves]. At the lowest concentration (50/25/100 mM), the relaxation time significantly increased as the imposed pressure (or
c ≈ 1000. The effects of the flow history on the dynamics of capillary-thinning and pinch-off are notably dependent on the WLM concentration, as shown in Fig. 8 [the labeled numbers denote the relaxation times (unit: s) of the corresponding curves]. At the lowest concentration (50/25/100 mM), the relaxation time significantly increased as the imposed pressure (or ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c) in the reservoir increased. The extensional relaxation time also increased when Couette flow was imposed on WLM solutions prior to CaBER measurements.7 However, the relaxation time increased by no more than 20%, in contrast to the multifold increase observed in this study (50/25/100 mM WLM solution). The matching orientations of alignment of wormlike micelles by the Poiseuille flow and the elongational flow, whereas they are normal for the Couette flow case,7 can account for the discrepancy in the relaxation time increase. At the surfactant concentration of 60/30/100 mM, the capillary-thinning dynamics did not significantly change until the pressure reached 13.4 kPa. However, the dynamics of capillary-thinning notably decelerated when the pressure was further increased to 17.9 kPa. At the highest concentration of 100/50/100 mM, the pinch-off time decreased as the imposed pressure increased, whereas the relaxation times obtained in the elasto-capillary region were similar regardless of the imposed pressure. We also computed the transient extensional viscosities [ηE(ε)] as a function of the Hencky strain (ε) from the capillary-thinning dynamics data, where ηE(ε) and ε are defined as
c) in the reservoir increased. The extensional relaxation time also increased when Couette flow was imposed on WLM solutions prior to CaBER measurements.7 However, the relaxation time increased by no more than 20%, in contrast to the multifold increase observed in this study (50/25/100 mM WLM solution). The matching orientations of alignment of wormlike micelles by the Poiseuille flow and the elongational flow, whereas they are normal for the Couette flow case,7 can account for the discrepancy in the relaxation time increase. At the surfactant concentration of 60/30/100 mM, the capillary-thinning dynamics did not significantly change until the pressure reached 13.4 kPa. However, the dynamics of capillary-thinning notably decelerated when the pressure was further increased to 17.9 kPa. At the highest concentration of 100/50/100 mM, the pinch-off time decreased as the imposed pressure increased, whereas the relaxation times obtained in the elasto-capillary region were similar regardless of the imposed pressure. We also computed the transient extensional viscosities [ηE(ε)] as a function of the Hencky strain (ε) from the capillary-thinning dynamics data, where ηE(ε) and ε are defined as 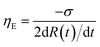 and ε = −2
and ε = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(R(t)/R0), respectively. The differential value for R(t) was obtained after its B-spline regression.29 The effect of the flow history on the extensional viscosity can be also seen in Fig. 9. All the transient extensional viscosities slightly changed until ε = 3, and subsequently increased considerably when ε was further increased. In addition, the effect of
ln(R(t)/R0), respectively. The differential value for R(t) was obtained after its B-spline regression.29 The effect of the flow history on the extensional viscosity can be also seen in Fig. 9. All the transient extensional viscosities slightly changed until ε = 3, and subsequently increased considerably when ε was further increased. In addition, the effect of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c (or imposed pressure in the reservoir) on the extensional viscosity is similar to that on the capillary-thinning dynamics described before. At the lowest surfactant concentration (50/25/100), the elongational viscosity increased as the characteristic shear rate increased. For the 50/25/100 mM solution, it maintained a similar level until the imposed pressure = 13.4 kPa. However, when the pressure was further increased to 17.9 kPa, it abruptly increased. In contrast, the extensional viscosity slightly changed with increasing imposed pressure at the highest concentration (100/50/100 mM).
c (or imposed pressure in the reservoir) on the extensional viscosity is similar to that on the capillary-thinning dynamics described before. At the lowest surfactant concentration (50/25/100), the elongational viscosity increased as the characteristic shear rate increased. For the 50/25/100 mM solution, it maintained a similar level until the imposed pressure = 13.4 kPa. However, when the pressure was further increased to 17.9 kPa, it abruptly increased. In contrast, the extensional viscosity slightly changed with increasing imposed pressure at the highest concentration (100/50/100 mM).
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c
c
| Solution (CPyCl/NaSal/NaCl) | 50/25/100 mM | 60/30/100 mM | 100/50/100 mM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Pressure [kPa] | 5.2 | 10.3 | 15.5 | 8.6 | 13.4 | 17.9 | 27.2 | 40.3 | 62.1 |
| Mean volumetric flow rate [mL h−1] | 18.3 | 253.1 | 755.1 | 18.1 | 269.3 | 651.2 | 19.9 | 265.1 | 999.7 |
| Characteristic shear rate [s−1] | 22.4 | 309.7 | 924 | 22.2 | 329.6 | 796.9 | 24.4 | 324.4 | 1223.4 |
| Wi [—] | 3.6 | 49.6 | 147.9 | 5.3 | 79.1 | 191.3 | 9.7 | 129.8 | 489.4 |
 | ||
| Fig. 8 Changes in normalized radius [R(t)/R0] of filament neck under various imposed pressure conditions in reservoir: (a) 50/25/100 mM, (b) 60/30/100 mM, (c) 100/50/100 mM. Every 50 data points, the average values with error bars obtained from three measurements are presented, and the relaxation times were determined by fitting the average values in the elasto-capillary region with eqn (3). Straight lines denote example regression lines in the elasto-capillary region, and number attached to each curve is extensional relaxation time (λE; unit: s). | ||
 | ||
| Fig. 9 Transient elongational viscosities of WLM solutions having three different concentrations as functions of Hencky strain: (a) 50/25/100 mM, (b) 60/30/100 mM, (c) 100/50 /100 mM. | ||
At low surfactant solutions (50/25/100 and 60/30/100 mM), it is inferred from the current experimental results that the microstructure of the WLMs is aligned in the flow direction under the flow history in the tube, as predicted and observed in previous studies.30,31 This consequently increases the extensional relaxation time. In contrast, the capillary-thinning dynamics and their corresponding extensional viscosities are interesting at the highest concentration (100/50/100 mM) because capillary-thinning accelerates in the initial stage (short time interval from the start of capillary-thinning) with increasing imposed pressure. However, the relaxation time determined in the elasto-capillary region (final stage) does not change significantly even if ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c (or imposed pressure) is increased. One hypothesis that can account for these interesting behaviors at the highest WLM concentration is the shear banding formation,32 which might occur as the WLM solution flows through the tube. In this scenario, short WLMs form near the wall (high shear rate region),6,32 the draining progresses at the initial stage in the extensional flow, and the WLMs inside dominate the late-stage dynamics of elasto-capillary-thinning.
c (or imposed pressure) is increased. One hypothesis that can account for these interesting behaviors at the highest WLM concentration is the shear banding formation,32 which might occur as the WLM solution flows through the tube. In this scenario, short WLMs form near the wall (high shear rate region),6,32 the draining progresses at the initial stage in the extensional flow, and the WLMs inside dominate the late-stage dynamics of elasto-capillary-thinning.
Finally, to compare the results of this study with those obtained using the conventional syringe pump,13–15 we conducted DoS/CaBER tests for the three different WLM solutions using a syringe pump (PHD ULTRA, Harvard). In the syringe pump experiments, after the WLM solutions were filled in the tube between the syringe and the nozzle tip, the liquids were dripped onto the substrate at the lowest possible flow rate. The pinch-off times were longer when the syringe pump, which has been typically utilized for DoS/CaBER experiments,13–15 was employed, compared to the experimental results at the lowest pressure at each surfactant concentration (Fig. 8). As observed in the glycerin–water mixture experiments, the prolonged pinch-off time in the syringe pump case can be attributed to the flow persisting from the nozzle even after the syringe pump is stopped.
In this study, we investigated changes in the extensional rheological properties of the WLM solution according to the surfactant concentration and the flow history, which showed that the extensional relaxation time and viscosity were significantly affected by them. These two properties increase monotonically with increasing surfactant concentration. However, the increase in the characteristic shear rate in the tube flow experienced prior to the onset of capillary-thinning at each concentration did not coincide with the increase in the relaxation time and elongational viscosity. This can be attributed to the formation of different microstructures owing to the tube flow, such as WLM alignment along the flow and shear banding, depending on the surfactant concentration.
Conclusions
In this study, the conventional syringe pump used in DoS/CaBER was replaced with a stop-flow system to minimize the response time when the flow from the nozzle was halted. We demonstrated that the modified DoS/CaBER setup can dramatically reduce the response time after flow cessation. We investigated the changes in the extensional rheological properties of WLM solutions as a function of the surfactant concentrations, as well as the characteristic shear rate in tube flow experienced by the WLM solutions prior to the onset of capillary-thinning. Our results showed that the extensional relaxation time and viscosity monotonically increased with increasing surfactant concentration. However, the effects of increasing the characteristic shear rate of the tube flow on the rheological properties were highly dependent on the surfactant concentration. At low surfactant concentrations, both the relaxation time and elongational viscosity increased with increasing characteristic shear rate. In contrast, the relaxation time insignificantly changed when the characteristic shear rate increased at high surfactant concentrations. We proposed that the difference in the effects of the characteristic shear rate on the rheological properties originates from the difference in the flow-induced microstructure. We expect that our results can be used to understand the relationship between the flow-induced microstructure of a WLM solution and its elongational rheological properties.Conflicts of interest
A Korean patent application (10-2021-0140908) is filed for the DoS/CaBER system combined with the stop-flow system.Acknowledgements
This study was supported by National Research Foundation of Korea (NRF) grants funded by the Korean government (NRF-2022R1F1A1074036 and NRF-2018R1A5A1024127). The authors are thankful to Dr S. O. Hong at currently Lotte Chemical for helping us with setting up the DoS/CaBER system. The authors are also thankful to Prof. K. S. Cho at Kyungpook National University for providing us with the B-spline regression software.References
- J. P. Rothstein and H. Mohammadigoushki, J. Non-Newtonian Fluid Mech., 2020, 285, 104382 CrossRef CAS.
- S. Lerouge and J.-F. Berret, in Polymer Characterization: Rheology, Laser Interferometry, Electrooptics, ed. K. Dusek and J.-F. Joanny, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, 1–71 Search PubMed.
- M. M. Britton and P. T. Callaghan, Phys. Rev. Lett., 1997, 78, 4930–4933 CrossRef CAS.
- D. Sachsenheimer, C. Oelschlaeger, S. Müller, J. Küstner, S. Bindgen and N. Willenbacher, J. Rheol., 2014, 58, 2017–2042 CrossRef CAS.
- M. Vasudevan, E. Buse, D. Lu, H. Krishna, R. Kalyanaraman, A. Q. Shen, B. Khomami and R. Sureshkumar, Nat. Mater., 2010, 9, 436–441 CrossRef CAS PubMed.
- A. Bhardwaj, D. Richter, M. Chellamuthu and J. P. Rothstein, Rheol. Acta, 2007, 46, 861–875 CrossRef CAS.
- E. Miller, C. Clasen and J. P. Rothstein, Rheol. Acta, 2009, 48, 625–639 CrossRef CAS.
- A. U. Oza and D. C. Venerus, Phys. Fluids, 2021, 33, 023102 CrossRef CAS.
- G. H. McKinley, Rheol. Rev., 2005, 1–48 CAS.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–53 CrossRef CAS.
- B. Keshavarz, V. Sharma, E. C. Houze, M. R. Koerner, J. R. Moore, P. M. Cotts, P. Threlfall-Holmes and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 222, 171–189 CrossRef CAS.
- L. E. Rodd, T. P. Scott, J. J. Cooper-White and G. H. McKinley, Appl. Rheol., 2004, 15, 12–27 Search PubMed.
- J. Dinic, Y. Zhang, L. N. Jimenez and V. Sharma, ACS Macro Lett., 2015, 4, 804–808 CrossRef CAS PubMed.
- J. Dinic, L. N. Jimenez and V. Sharma, Lab Chip, 2017, 17, 460–473 RSC.
- S. Sur and J. Rothstein, J. Rheol., 2018, 62, 1245–1259 CrossRef CAS.
- K. W. Bong, S. C. Chapin, D. C. Pregibon, D. Baah, T. M. Floyd-Smith and P. S. Doyle, Lab Chip, 2011, 11, 743–747 RSC.
- N. J. Kim, C. J. Pipe, K. H. Ahn, S. J. Lee and G. H. McKinley, Korea-, Korea Aust. Rheol. J., 2010, 22, 31–41 Search PubMed.
- Y. Zhang and S. J. Muller, Phys. Rev. Fluids, 2018, 3, 043301 CrossRef.
- S. Wu and H. Mohammadigoushki, Phys. Rev. Fluids, 2020, 5, 053303 CrossRef.
- J. Canny, IEEE Trans. Pattern Anal. Mach. Intell., 1986, PAMI-8, 679–698 Search PubMed.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- B. Akers and A. Belmonte, J. Non-Newtonian Fluid Mech., 2006, 135, 97–108 CrossRef CAS.
- C. Clasen, Korea Aust. Rheol. J., 2010, 22, 331–338 Search PubMed.
- C. Clasen, P. M. Phillips, L. Palangetic and J. Vermant, AIChE J., 2012, 58, 3242–3255 CrossRef CAS.
- D. T. Papageorgiou, Phys. Fluids, 1995, 7, 1529–1544 CrossRef CAS.
- P. Doshi, R. Suryo, O. E. Yildirim, G. H. McKinley and O. A. Basaran, J. Non-Newtonian Fluid Mech., 2003, 113, 1–27 CrossRef CAS.
- P. Doshi and O. A. Basaran, Phys. Fluids, 2004, 16, 585–593 CrossRef CAS.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids, Wiley Interscience, New York, 1987 Search PubMed.
- K. S. Cho, Viscoelasticity of polymers, Springer, 2016 Search PubMed.
- A. Sambasivam, A. V. Sangwai and R. Sureshkumar, Phys. Rev. Lett., 2015, 114, 158302 CrossRef PubMed.
- B. Arenas-Gómez, C. Garza, Y. Liu and R. Castillo, J. Colloid Interface Sci., 2020, 560, 618–625 CrossRef PubMed.
- E. Miller and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2007, 143, 22–37 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |