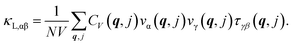Structural diversity of CuZn₂InSe₄ quaternary chalcogenides: electronic and phonon properties from first principles

Abstract

First principles simulations are utilized to calculate the electronic and vibrational properties of several metastable structural phases of the CuZn₂InSe₄ quaternary chalcogenide, including stanite, kesterite, primitive mixed CuAu, wurtzite-stanite, and wurtzite-kesterite lattices. We find that although each phase is formed by nearest cation-chalcogen bonds, the structural diversity due to cation and polyhedral arrangements has direct consequences in the electronic structure. The simulations further indicate that hybrid functionals are needed to account for the s–p and p–d orbital hybridization that is found around the Fermi level, which leads to much enhanced energy band gaps when compared with standard exchange-correlation approaches. We also find that the thermal conductivities for all phases are relatively low, and the main scattering channel comes from a low frequency optical band hybridized with acoustic phonons. Given that CuZn₂InSe₄ is a material from a larger class of quaternary chalcogenides, other materials may exhibit similar electronic and vibrational properties, which may be useful for electronic and thermal management applications.

---

Introduction

Multinary chalcogenides are diverse materials that can accommodate different types of metallic atoms in their structures. Quaternary chalcogenides can exist in a variety of structural phases with tunable properties, which makes them of great interest in many applications, including thermoelectricity,¹ superconductivity,² and nonlinear optics³ among others. Recently, chalcogenide systems containing multiple atoms in their structures have also been suggested as high-entropy compounds for possible thermoelectric applications^4,5 Many such materials have a common origin associated with II–VI binary zinc blende structures, and recently a new array of compositions with the chemical formula I–II₂–III–VI₄ (I = Cu, Ag; II = Cd, Zn, Ca, Co, Fe, V; III = In, Ga, Al, Tl; VI = S, Se, Te) have been synthesized. These new systems have been realized in the laboratory showing that the electric properties can be tuned by stoichiometry variations or doping.^6–11

Recent experiments have shown that CuZn₂InSe₄, CuZn₂InTe₄, CuCd₂InTe₄, CuMn₂InTe₄, and AgZn₂InTe₄ have low thermal conductivity.^11–21 These results are consistent with the low measured thermal conductivity for related systems such as Cu₂ZnSnS₄ and Cu₂CdSnSe₄, which belong to the widely studied class I₂–II–IV–VI₄ (I = Cu, Ag; II = Cd, Zn, Ca, Co, Fe, V; IV = Si, Sn, Ge; VI = S, Se, Te).^22,23 The close connection between I–II₂–III–VI₄ and I₂–II–IV–VI₄ is also evident in the similar structural phases these materials can have. Kesterite, stannite, modified cubic, wurtzite-kesterite, and wurtzite-stannite lattices are possible for both types of materials classes, as shown by experimental and computational studies.^{11,14–16,24,25}

While most computational studies focus on I₂–II–IV–VI₄, recent investigations of I–II₂–III–VI₄ representatives report on high through-put calculations for one hundred and fifty structures and their basic electronic properties.¹⁴ Simulations for the vibrational and phonon characteristics of selected representatives are also available.²⁶ Given the limited number of such studies, our basic understanding of this emerging class of systems needs further advancement, especially in the context of deeper knowledge of the structure–property relations and transport characteristics.

In this study, using first principles simulations we investigate CuZn₂InSe₄ and its structural and dynamical stability by simulating five atomic phases previously found for I–II₂–III–VI₄ materials.^14,27 This is a recently synthesized material,²⁸ which has not been investigated in detail from first principles. In-depth calculations for the electronic and vibrational properties together with the lattice thermal conductivity are also performed and analyzed. This investigation helps us develop a better picture for the effects of the phase diversity in a given composition from I–II₂–III–VI₄ systems, which can be used to translate to other similar materials. The comparison with prior results for Te-based I–II₂–III–VI₄ systems and other Se-based II₂–I–IV–VI₄ materials^20,29 is especially useful to find commonalities and differences between these related classes.

Methodology

The structural and electronic calculations are based on Density Functional Theory (DFT)³⁰ and are carried out with the Vienna Ab initio Simulations Package (VASP),³¹ a state-of-the-art code relying on periodic boundary conditions. The exchange-correlation energy is taken into account using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.²⁷ The convergence criteria for the atomic relaxation process are 10⁻⁸ eV (total energy criteria) and 10⁻⁷ eV Å⁻¹ (force criteria), and the energy cut-off is taken at 295.45 eV for all cases. To address the partial occupancies for each orbital, we employed Gaussian smearing method with smearing width of 0.05 eV. We also choose the tetrahedron integration method and Blöchl corrections for the relaxation of the structures with a 12 × 12 × 12 k-mesh.³² The energy band structure and DOS are calculated within the Heyd–Scuseria–Ernzerhof (HSE06) screened Coulomb hybrid density functional.³³ This hybrid functional is regarded as a superior method especially for obtaining more accurate energy gaps in semiconductors, in which prominent s–p and p–d hybridization exists. The HSE06 calculations were facilitated by the VASPkit software³⁴ with an optimized 5 × 5 × 2 k and q grids for the KS, PMCA, and ST phases, while 4 × 4 × 4 was used for the WST and WKS k and q grids.

The unit cell for each phase is shown in Fig. 1 and it is constructed by following the initial symmetry as described in what follows. After relaxation, the resultant structures are further used to calculate the phonon band structures, phonon density of states (PDOS), and Grüneisen parameters for each CuZn₂InSe₄ phase by using the PHONOPY code.^35,36 The computations were performed based on supercell displacements with central differences within GGA-PBE, by setting energy cutoff values to be 1.3 times the largest default cutoff energy of the atomic pseudopotentials of the CuZn₂InSe₄ phase (384.08 eV), as recommended by the VASP developer. The atomic displacements are also taken at their default value of 0.03 Å. The phonon properties rely on calculations of the interatomic force constants (IFCs), whose harmonic and anharmonic contributions are obtained by second and third order derivatives of the total energies obtained from VASP in terms of the atomic displacements defined over finite translation groups.³⁷ For the harmonic IFCs, we construct 3 × 3 × 3 supercells with 432 atoms for KS and ST, while the 4 × 4 × 2 supercell are used for the PMCA containing 512 atoms. For the WKS and WST, supercells of 2 × 2 × 4 with 256 atoms and a 3 × 3 × 4 with 576 atoms are constructed, respectively. The third-order anharmonic IFCs are further calculated using the PHONO3PY to find three-phonon interaction matrix elements.^35,36

Fig. 1 Crystal structures for CuZn₂InSe₄ with (a) kesterite (KS), (b) primitive mixed CuAu (PMCA), (c) stannite (ST), (d) wurtzite-kesterite (WKS), (e) wurtzite-stannite (WST) phases.

The PHONO3PY code is also used to calculate the lattice thermal conductivity, whose tensor components in α, β directions are

In the above expression, the summation is in the first Brillouin zone over phonon modes labeled by their wave vector q and polarization j. Also, N is the number of sampled points and V is the unit cell volume. The lattice thermal conductivity is determined by the heat capacity C_V(q, j), group velocity components v_α(q, j), and the transport lifetime tensor τ(q, j) of each vibration mode. Among those, the heat capacity is calculated as C_V(q, j) = k_Bn(q, j)(n(q, j) + 1)(ℏω(q, j)/k_BT)² with ω(q, j) being the frequency and n(q, j) – the Bose–Einstein occupation number at equilibrium of the phonon mode (q, j). The group velocity components are defined as v_α(q, j) ≡ ∂ω(q, j)/∂q_α. Also, the repeating index α, β, γ in the above expression implies coordinates.

The PHONO3PY code obtains a full solution of the Peierls–Boltzmann transport equation, beyond the relaxation time approximation.^38,39 The transport lifetime components follow from the Peierls–Boltzmann equation as they are obtained from the nonequilibrium distribution functions. These depend on transition scattering probabilities, which are found based on perturbation theory by including both normal and Umklapp processes.⁴⁰ The phonon self-energies needed for the thermal conductivity calculations involve harmonic and anharmonic IFCs that can be obtained via the PHONOPY and PHONO3PY packages. We also consider the phonon-isotope scattering for isotopic mass variations in the atoms. The lattice thermal conductivity is then solved based on the phonon Boltzmann equation with the previously obtained IFCs on a 6 × 6 × 6 q-grid. The anharmonic cutoff-pair distances are taken as 6 Å since larger values do not affect the κ_L convergency significantly. Convergence tests for the lattice thermal conductivity are given in the ESI† (Fig. S3 and S4†) showing that the chosen size of the q-grid and the magnitude of the cutoff-pair distance result in a good numerical accuracy for the results to follow.

The mode Grüneisen parameter describes the anharmonicity in the lattice. Here it is calculated based on the anharmonic IFCs using the expression γ(q, j) = −(V/ω(q, j))(∂ω(q, j)/∂V), which involves numerical derivatives of the frequency for each phonon mode and can be obtained using central finite difference method that requires the value of ω(q, j) at the equilibrium volume and at slightly larger and smaller than the equilibrium volumes.⁴¹ Electron and phonon band structures and densities of states are obtained by using the VASPKIT package.^34,35 The crystal structures are visualized with the VESTA software.⁴²

Results and discussions

The quaternary I–II₂–III–VI₄ group of materials are derivatives of simpler, binary II–VI systems. They are obtained by cation substitution following the chain through binary and ternary compounds II–VI →–I–III–VI₂ → I–II₂–III–VI₄. During the substitution process, charge neutrality and the octet rule are maintained for energetic stability of each new material.^43,44 The I–II₂–III–VI₄ quaternary chalcogenides can be found in five metastable phases Kesterite, KS; primitive mixed CuAu, PMCA; Stannite, ST; wurtzite-kesterite, WKS and wurtzite-stannite, WST.⁴⁵ To initiate the calculations, the unit cells of these phases are constructed following their associated symmetries as follows: I4̄ (KS), I4̄2m (ST), P4̄2m (PMCA), Pmn2₁ (WKS), and Pc (WST).^45,46 The lattice parameters of each structural phase after relaxation are summarized in Table 1, showing a marginal difference from the originally prescribed symmetries (a common situation for many complex systems).

Table 1 Calculated lattice constants (a, b, c) and angles (α, β, γ) for all considered phases are given. The energy difference ΔE = E_phase − E_KS formation energy per atom where E_phase is the total energy of the compound in a given structural phase, μ_i is the chemical potential of each constituent atom, and N is the number of atoms in the unit cells. The energy gaps E_G, obtained via PBE and HSE06 approximations, are also given

Phases	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	ΔE (eV)	Ef (eV)	E^PBEG (eV)	E^HSEG (eV)
KS	5.517	5.517	10.998	90.000	90.000	90.000	0.000	−0.523	0.756	1.887
PMCA	5.508	5.508	11.044	90.000	90.000	90.000	0.022	−0.521	0.691	1.800
ST	5.506	5.506	11.052	90.000	90.000	90.000	0.001	−0.523	0.816	1.932
WKS	7.785	7.789	6.402	90.079	89.961	120.020	0.206	−0.510	0.449	1.538
WST	7.783	7.778	6.398	90.000	90.000	119.980	0.103	−0.516	0.757	1.862

---

The atomic structures for the CuZn₂InSe₄ quaternary chalcogenide phases are displayed in Fig. 1, where explicit polyhedral arrangements are also given. It shows that the KS and ST lattices have tetragonal symmetry, while the PMCA is very close to an orthorhombic space group, and the wurtzites are hexagonal structures. The lattice parameters for the KS, PMCA, and ST phases share the relation a = b ≈ c/2, while for the WKS and WST, we find that a ≈ b > c. Experimentally, CuZn₂InSe₄ was recently reported²⁸ in a PMCA-like lattice structure with a = 5.7316 Å, which is about 4% greater than the computational values. Having the lattice parameters, the cell volume for the wurtzites is found as V_wurtzite = a × b × c ≈ 389 ų, while V_tetra = a × b × c ≈ 333 ų for the tetragonal-like symmetries. Given that the atomic volumes in the unit cells are the same for all the phases (V_atoms = 2V_Cu + 4V_Zn + 2V_In + 8V_Se ≈ 143.9 ų), the packing density of the KS, PMCA, and the ST phases is ρ_packing = V_atoms/V_tetra = 0.43, which is greater than that of the WKS and WST phases ρ_packing′ = V_atoms/V_Wurtzite = 0.37.

For all lattices, the atomic bonds always involve a cation and a Se atom. We further find that within each frame, each cation X (X = Cu, Zn, and In) is bonded with the four adjacent Se atoms to form tetrahedron structures [XSe₄]. The distinct features between the different phases describe how the cations are distributed around the chalcogen atoms, which gives some diversity in the relative position of the faces and vertices of the tetrahedra. For instance, Fig. 1a–c, and e illustrate that KS, PMCA, ST, and WST have staggered patterns of [CuSe₄] tetrahedra. Specifically, along the [201] direction which covers the adjacent tetrahedra of [CuSe₄] in (001) planes, the KS and ST phases line up tetrahedra centralized by different types of cations, such that KS obtains the sequence of [ZnSe₄] − [InSe₄] − [CuSe₄] while ST holds the [InSe₄] − [ZnSe₄] − [CuSe₄] pattern. Similarly, the arrangement in PMCA transforms to [CuSe₄] − [ZnSe₄] − [CuSe₄] with no [CuSe₄] tetrahedra touching each other. In contrast, the [CuSe₄] tetrahedra in WKS phase share one vertex Se atom along [001] direction with other [CuSe₄] tetrahedra, showing a different alternation of the stacking pattern.

The different phases are also studied by examining the total energy difference ΔE and the formation energy per atom E_f. Taking the KS as a reference, we find that the ST phase has practically the same energetic stability. On the other hand, ΔE = 206 meV indicates that the WKS has the least energetic stability. The formation energies of the phases render additional information of how difficult it is to synthesize single crystal CuZn₂InSe₄ in its different structural phases. We find that E_f for the KS, PMCA, and ST phases is practically the same indicating that these three structures are metastable. The fact that their formation energy values are more negative than the WKS and WST structures shows that the KS, PMCA, and ST lattices are easier to synthesize.

The electronic structure is considered next by analyzing the calculated electronic band structure and density of states (DOS) for each phase, shown in Fig. 2. Standard DFT approximations (GGA and Local-density approximations (LDA) and their variations) are inadequate in finding the energy band gap in many semiconductors that have strong s–p or p–d orbital hybridization around the Fermi level.^47–49 Zinc blende derived quaternary chalcogenides fall in that category, thus we perform calculations with the HSE06 hybrid functional (also discussed in Methodology). The band gaps obtained by the standard PBE-GGA approximation are typically 2.5 to 3 times smaller than those found via HSE06 as reported in Table 1. We find that all phases are large gap semiconductors with E^HSE_G being the largest for the ST phase and smallest for the WKS phase. This is commensurate with the band gap ranges (1.2–1.8 eV) of quaternary compounds from the related I₂–II–IV–VI₄ family of compounds.^50,51

Fig. 2 Orbitally projected band structure and atom projected density of states of the CuZn₂InSe₄ phases: (a) and (b) KS; (c) and (d) PMCA; (e) and (f) ST; (g) and (h) WKS, and (i) and (j) WST. All results are obtained using the HSE06 hybrid functional.

The energy bands, shown in Fig. 2, indicate that all the CuZn₂InSe₄ phases possess a direct energy gap at the Γ-point. Since the Fermi level is almost at the top of the highest valence band, each phase is a p-type semiconductor. Besides, all phases exhibit one CBM at the Γ point in the Brillouin zone, however, secondary conduction minima are found: for the PMCA at the M-point (higher by 0.39 eV than its peak at Γ), for the WKS at the Y-point (higher by 0.59 eV than its Γ peak), and for the WST at the B-point (higher by 0.61 eV than its Γ peak). These are commensurate with DOS peaks in the conduction band region and are the result of strong s–p orbital hybridization. The conduction regions in the orbitally projected bands and the DOS given in Fig. 2 indicate that the CBM edges mainly contain In-5s and Se-4p orbitals, and that the DOS above the gap is essentially contributed by the Indium and Selenium atoms. The valence bands of all phases mainly contain Se-4p and Cu-3d orbitals in the (−2, 0) eV region as illustrated in Fig. 2. This p–d orbital hybridization not only accounts for the dispersion behaviors at the top of the valence band, but it also shapes the band curves around valence band maximum (VBM) edges. Another perspective of the s–p–d hybridization can be found in Fig. S1 in the ESI,† where the atomic orbitally projected DOS for the Cu, In, and Se atoms is given. The semiconducting behavior of CuZn₂InSe₄ phases can also be seen in the calculated conductivity at T = 300 K as a function of the chemical potential shown in Fig. S2† (details in the ESI†).

The calculated band structure can also be used to obtain the band effective masses m* for the different phases by using 1/m* = (1/ℏ²)(∂²E/∂k_i∂k_j) where E is the band energy around the CBM and VBM edges and k_i,j are the components of the wave vector k. In Table 2, we show characteristic m* for the different phases (in terms of the electron mass m₀) along some directions in the Brillouin zone. Our results show that the effective masses of the holes are larger than the ones of the electrons in magnitude along the same direction indicating greater mobilities for the electrons. For each phase, the effective band masses have similar values in different directions around CBM, while larger variations are found around the VBM, especially for PMCA and WKS. Comparing with the values m_h* = 0.6–0.8 m₀ of the explored quaternary chalcogenide compounds reported by others,²⁸ the effective masses of the KS and ST phases fall in that range while the PMCA and the wurtzite phases are greater than that benchmark.

Table 2 The effective mass of the electron m_e* and hole m_h* carriers around CBM and VBM, respectively, are given. The group velocities of two transverse acoustic branches (v_TA1 and v_TA2) as well as the longitudinal acoustic branch (v_LA) around Γ in the directions from one high symmetry point to another for all phases, are also summarized. The effective mass is given in terms of electron mass m₀ and the unit of the group velocity is m s⁻¹

Phase	Direction	me* (m0)	mh* (m0)	vTA1 (m s^−1)	vTA2 (m s^−1)	vLA (m s^−1)
KS	Γ → N	0.121	0.607	2284	2287	3785
KS	Γ → M	0.130	0.910	2092	2132	3998
PMCA	Γ → M	0.131	3.064	2279	2510	4157
PMCA	Γ → Z	0.125	0.560	2519	2519	4022
ST	Γ → N	0.117	0.605	2287	2254	3754
ST	Γ → M	0.123	0.630	1952	2240	4059
WKS	Γ → X	0.137	1.111	2135	1859	4030
WKS	Γ → Z	0.139	0.195	1841	1850	4029
WST	Γ → B	0.127	1.457	1809	1826	4427
WST	Γ → A	0.127	1.391	1941	2452	4046

---

According to Pauling's theory, not only the sharing of the polyhedron elements but also the coordinate number of the polyhedrons influence the lattice stabilities and the electronic properties.⁴³ Therefore, some of the band structure features can be linked with the atomic polyhedral arrangements (Fig. 1), which are typically associated with band edge shifting. Especially, in quaternary chalcogenide compounds such as the CuZn₂InSe₄, the valence band shifting is mainly attributed to the arrangement of [CuSe₄] tetrahedra, while the conduction band shifting comes from the [InSe₄] tetrahedra.^26,51 For example, given that two nearest [InSe₄] tetrahedra in all phases are separated by the similar distance (d ≈ 5.5 Å), the sharing corners of [CuSe₄] tetrahedra in WKS result in closer distance between the Cu atoms. This leads to enhanced Coulomb interaction and reduced lattice stability, as also indicated by the WKS smallest total energy, as discussed earlier. As a result, the VBM of WKS phase is pushed up giving a reduced band gap. For the other phases, the separation distance of the nearest [CuSe₄] tetrahedra are almost the same (d ≈ 5.5 Å). The staggered patterns of [CuSe₄] tetrahedra along [201] shows no touching between adjacent [CuSe₄] tetrahedra. However, since the coordination number of [CuSe₄] tetrahedra is 6 for the PMCA and WST phases, which is larger than that of the remaining phases (coordination number is 4), the band gaps of PMCA and WST are relatively smaller than KS and ST phases.

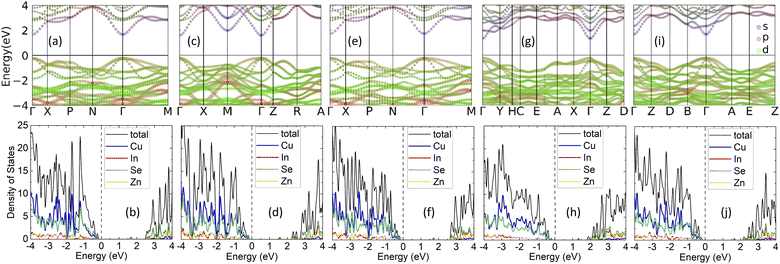
Further insight into the type of bonding in each phase can be gained by the calculated Electron Localization Function (ELF), with ELF ∼ 1 representing strong localization and ELF ∼ 0.5 corresponding to an electron gas.⁵² Fig. 3 shows calculations for ELF with explicitly given projection planes in each case. For all structural phases, the cations are surrounded by the chalcogens within the [XSe₄] tetrahedra. The alignment patterns of [XSe₄] are also presented by showing the (102) plane in KS, PMCA, and ST phases and (001) plane in WKS and WST phases. Fig. 3 shows that the Cu–Se, Zn–Se bonds exhibit localized electrons around the Se atom, which is indicative of ionic-like type of bonding. For the In–Se bond, on the other hand, the rather large degree of localization in the region between the In and Se atoms shows a covalent-like bonding. The four adjacent ELF basins of Se surrounding the In atom constitute the sp³ hybridization in [InSe₄] tetrahedra. This is also consistent with features of the orbitally projected band structure which indicates the conduction band minimum (CBM) edge is mainly composed of In-5s and Se-4p orbitals.

Fig. 3 Electron localization function for (a) KS, (b) PMCA, (c) ST, (d) WKS, and (e) WST phases of CuZn₂InSe₄ compounds. The different projections are shown at the right top corner next to each panel. The atomic composition and the ELF color scale are also displayed.

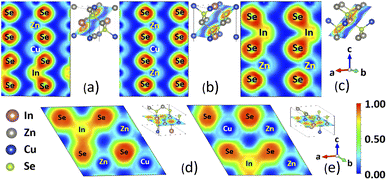
In addition to the electronic band structure, the vibrational properties are also calculated from first principles, as discussed in Methodology. The results for the phonon band structure and PDOS for the considered CuZn₂InSe₄ structures are given in Fig. 4. The absence of negative branches in the phonon frequency dispersions indicates that all phases are dynamically stable. In all cases, a dense band of low optical phonons is found in the (1, 2.5) THz region. These types of relatively flat low frequency optical phonons have been obtained for other quaternary chalcogenides in their ST and KS phases, such as the case for Se-based I₂–II–IV–VI₄ representatives^17,18 and Te-based materials from I₂–II–IV–VI₄ and I–II₂–III–VI₄ classes.²⁰ The atomically resolved PDOS further show how specific atoms contribute to the phonon dynamics.

Fig. 4 Phonon dispersions and atomically resolved phonon density of states for the considered CuZn₂InSe₄ phases for CuZn₂InSe₄: (a) and (b) KS; (c) (d) PMCA; (e) and (f) ST; (g) and (h) WKS, and (i) and (j) WST.

The peak in the centered around ∼1.8 THz comes from vibrations of the Se and all cations, re-enforcing the direct cation-chalcogen bonding in all phases. This feature is associated with the relatively flat dense low-frequency optical phonon bands from the band structure. In the range (2.5, 5) THz, a relatively dispersed phonon band structures stands out.

The PDOS atomic decomposition shows that this frequency range is predominately determined by vibrations involving the Cu, Zn and chalcogen atoms, while the In contributions are rather less important. All phases exhibit a gap at ∼4.8 THz, followed by a frequency range (5, 7) THz primarily again composed of contributions from all atoms. Distinct peaks from Cu–Se at ∼5.3 THz and from In–Se at ∼6.2 THz in that region are found for KS, PMCA, ST, and WST phases. It appears that all structural phases have similar phonon properties with an especially low frequency optical phonon bands but with varying spreads. Among all the phases, the largest spread of this band is WST (1.30–2.35 THz) while the narrowest spread of the band goes to PMCA (1.52–2.32 THz).

From the phonon band structure, we can also find the sound velocities for the transverse acoustic (TA) and longitudinal acoustic (LA) branches around Γ point. Calculated group velocities for the TA and LA branches along certain directions in the Brillouin zone are summarized in Table 2. From these data, v_TA = 2519 m s⁻¹ (PMCA phase) is the largest, while v_TA = 1809 m s⁻¹ (WST phase) is the smallest. Similarly, the range of the LA group velocities are set by the lower limit of 3754 m s⁻¹ for ST and the upper limit of 4427 m s⁻¹ for WST. We note that the phonon velocities for all CuZn₂InSe₄ phases compare well with the ones of typical thermoelectric materials, including Bi₂Te₃ with v_TA = 1870 m s⁻¹, v_LA = 3390 m s⁻¹ and PbTe with v_TA = 1210 m s⁻¹, v_LA = 3570 m s⁻¹.^21,53

Another important property for the phonon transport is the degree of anharmonicity of the atomic bonds in each lattice. For this purpose, we calculate the Grüneisen parameter γ(q, j) for each mode transition via PHONOPY and the results are shown in Fig. 5. For each CuZn₂InSe₄ structural phases most of the negative values in the low frequency regime are attributed to transverse acoustic mode scattering, while the higher frequency range with predominantly positive γ(q, j) come from optical phonon mode scattering. One finds a rather constant average γ(q, j) for the ω >3THz region with the KS phase (Fig. 5a) showing largest dispersion. In all cases, the average Grüneisen parameter is found to be 1.8 ± 0.2 for ω >3THz. For comparison, we note that for covalently bonded materials γ ≈ 1.0, while for ionic alkali halides (γ ≈ 2.2).⁵⁴ The average Grüneisen parameters found here are consistent with mixed ionic-covalent hybridization, as discussed earlier (also, see Fig. 3). Additionally, the magnitude of the average γ in each phase is comparable with the values of other quaternary chalcogenides further re-enforcing the structural connection of these materials.²⁰ The phonon scattering rates are also a measurement of the anharmonicity of the systems. Here these are calculated from three-phonon scattering processes within the relaxation time approximation Γ = 1/τ_RTA(q, j). The given scattering rate in Fig. 5 display significant similarities for all studied phases. There is a local minimum in the 1−2 THz range, which corresponds to the flat band of low frequency optical phonons (Fig. 4). The maximum ∼4 THz reflects transitioning to higher lying optical phonons followed by Γ around 5 THz, which reflects the corresponding gaps observed in the PDOS for the CuZn₂InSe₄ phases.

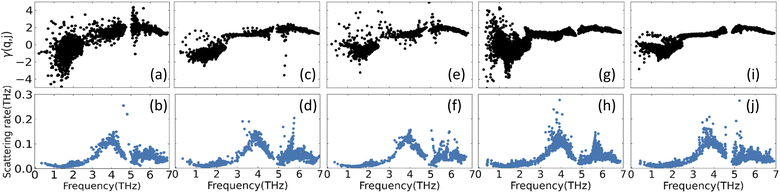Fig. 5 Mode Grüneisen parameters γ(q, j) and room-temperature phonon scattering rates of (a) and (b) KS; (c) and (d) PMCA; (e) and (f) ST; (g) and (h) WKS and (i) and (j) WST of CuZn₂InSe₄.

The results for the calculated temperature dependent thermal conductivities are presented in Fig. 6. The thermal conduction is anisotropic for the studied latices. Examining the ratio |κ_xx − κ_zz|/κ_xx shows the largest anisotropic degree of 28% for the WST and smallest one of 6% for the ST phases at T = 300 K. It is further interesting to note that from the tetragonal structures, the smallest thermal conductivity overall is obtained for the PMCA lattice (κ_xx = 1.35, κ_zz = 1.20 W m⁻¹ K⁻¹ at T = 300 K). From the hexagonal lattices, this distinction belongs to the WKS phase (κ_xx = 1.24, κ_zz = 1.36 W m⁻¹ K⁻¹ at T = 300 K). On the other hand, κ_xx = 1.74, κ_zz = 1.63 W m⁻¹ K⁻¹ reflect the overall largest thermal conductivity found for the ST phase.

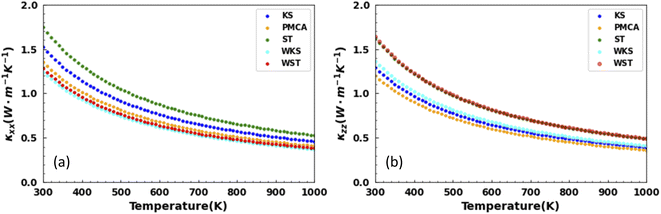Fig. 6 Lattice thermal conductivity components as a function of temperature along the (a) x-axis and (b) z-axis for the lattice phases of CuZn₂InSe₄.

It is further instructive to compare our results to the thermal conductivity for other related quaternary chalcogenides. Although extensive transport measurements are scarce, existing data for AgZn₂InTe₄ (κ ∼1.5 W m⁻¹ K⁻¹) and Cu₂ZnSnS₄ (κ ∼1.69 W m⁻¹ K⁻¹) bulk compounds compare well with the values found for the CuZn₂InSe₄ phases. Notably, the thermal conductivity for CuZn₂InTe₄ (κ ∼3.3 W m⁻¹ K⁻¹), Cu₂CdSnTe₄ (κ ∼2.8 W m⁻¹ K⁻¹), and the Cu₂ZnSnSe₄ (κ ∼4.44 W m⁻¹ K⁻¹) exhibits higher values than the ones found here.^11,17,55,56 It appears that the studied CuZn₂InSe₄ is characterized by rather low κ, even in the context of other chalcogenides.

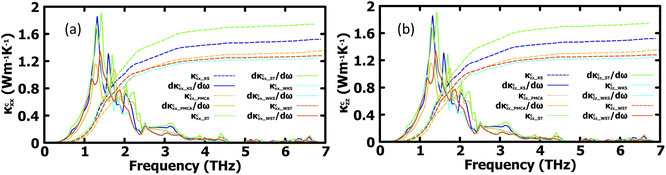
More insight into the vibrational properties can be gained by examining the cumulative lattice thermal conductivity calculated as a function of frequency in the high temperature regime using 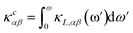(κ_L,αβ – defined in Methodology). Fig. 7 shows κ^c_xx and κ^c_zz and their derivatives with respect to frequency for all studied phases. The derivatives of κ^c_xx and κ^c_zz indicate the density of the phonons that carry heat with respect to ω whose maxima is in the (1, 2) THz range for the different phases. This is also the range with very small scattering rates (Fig. 5) primarily attributed to acoustic phonons. The (2, 4) THz region corresponds to the low frequency optical phonons hybridized to the acoustic modes, whose heat carrying capacity decreases as seen is in the decreasing dκ^c_xx,zz/dω as a function of ω. As the phonon DOS goes to zero (Fig. 4) at ω ∼4 THz the cumulative κ^c_xx,zz reaches a plateau indicating the onset of higher optical phonons with much reduced heat capacity. This also corresponds to the behavior of scattering rates experiencing a maximum at that frequency followed by a gap, as seen in Fig. 5. While these are common features for all structural phases, the various peaks of the derivatives of κ^c_xx and κ^c_zz show how different heat carrying phonons contribute to the lattice thermal conductivity for the considered CuZn₂InSe₄ phases. The cumulative thermal conductivity also gives another qualitative perspective of the anisotropy of the different CuZn₂InSe₄ structural phases.

Fig. 7 Cumulative lattice thermal conductivity components and the first derivatives as a function of phonon frequency at 300 K along the (a) x-axis and (b) z-axis for the lattice phases of CuZn₂InSe₄.

Conclusions

The compound CuZn₂InSe₄ belongs to the I–II₂–III–VI₄ class of materials, which is similar to I₂–II–IV–VI₄ quaternary chalcogenides as both types of system are derivatives of the simpler binary II–VI zincblendes. The five structural phases for CuZn₂InSe₄ can also be found for other representatives of both I–II₂–III–VI₄ and I₂–II–IV–VI₄,^13,45 although the dynamical stability, electronic and vibrational properties, and associated transport behaviors depend on the particular chemical composition. Here applying first-principles simulations we study in depth the ST, KS, PMCA, WKS, and WST CuZn₂InSe₄ for their structure–property relations. Drawing similarities with prior studies, the results reported here can serve as a representative example for other quaternary chalcogenides.

The hybrid functional calculations yield 2–3 times larger energy gaps as compared with the standard DFT simulations. Experimental measurements report energy gap values consistent with the ones found via the HSE06 hybrid functional.³³ This is not surprising since all chalcogenides from both I–II₂–III–VI₄ and I₂–II–IV–VI₄ experience strong s–p or p–d orbital hybridization around the Fermi level, which cannot be captured adequately via standard DFT approximations. Thus, in order to obtain electronic transport properties that are in potentially good agreement with experiments, DFT simulations beyond the GGA and LDA methods are needed. Nevertheless, the energy gaps found for CuZn₂InSe₄ are in the 1.5–1.9 eV range, which is comparable with the band gap ranges (1.2–1.8 eV) of the I₂–II–IV–VI₄ counterpart family from reports.^50,51

Regardless of the chemical composition, for all structures each chalcogen is surrounded by metallic atoms, such that there are only direct metal-chalcogen bonds. At the same time, the specific arrangement of cations gives the specificity for each lattice, which can be seen in terms of polyhedral [XSe₄] building block patterns. The shared corners and edges sequence can be related to stability of each lattice as well as conduction and valence band shifts and orbital hybridization which may be unique for each phase of the same material.

Other important results to be noted are the low thermal conductivity values for all CuZn₂InSe₄ phases, which are similar to several other I–II₂–III–VI₄ and I₂–II–IV–VI₄ representatives, as found experimentally and computationally.^11,17,55,56 Usually, materials with complex lattices and atom constituents with highly dissimilar masses are characterized with low κ. However, the lattice structure of quaternary chalcogenides is relatively simple given its resemblance to the parent zinc blende, and the constituent atoms come from light mass elements. It appears that the cation-chalcogen direct bonds making up all structural phases may be key to the origin of their low κ. The PDOS and scattering rates show that in the low frequency regime all atoms contribute to the scattering. As a result, the hybridized optical-acoustic phonon band is an effective phonon scattering channel resulting in much reduced κ. We expect that due to the omnipresence of the direct cation-chalcogen bonds such a source of anharmonicity is present regardless of the chemical composition of the I–II₂–III–VI₄ and I₂–II–IV–VI₄ materials or their structural phases. Consequently, all such materials are expected to have low thermal conductivity properties.

Author contributions

L. M. and W. S. performed the simulations for all considered phases and their properties. L. M. W. conceived the idea, performed the analysis, and wrote the paper.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We acknowledge financial support from the U.S. National Science Foundation under Grant No. DMR-1748188. Computational resources were provided by USF Research Computing.

References

1. C. Han, Q. Sun, Z. Li and S. X. Dou, Adv. Energy Mater., 2016, 6, 1600498.
2. J. Ranninger, Z. Phys. B Condens. Matter, 1991, 84(2), 167–178.
3. I. Chung and M. G. Kanatzidis, Chem. Mater., 2014, 26, 849–869.
4. R.-Z. Zhang, F. Gucci, H. Zhu, K. Chen and M. J. Reece, Inorg. Chem., 2018, 57, 13027–13033.
5. R. Liu, H. Chen, K. Zhao, Y. Qin, B. Jiang, T. Zhang, G. Sha, X. Shi, C. Uher, W. Zhang and L. Chen, Adv. Mater., 2017, 29, 1702712.
6. Y. Dong, H. Wang and G. S. Nolas, Phys. Status Solidi RRL, 2014, 8, 61–64.
7. W. G. Zeier, Y. Pei, G. Pomrehn, T. Day, N. Heinz, C. P. Heinrich, G. J. Snyder and W. Tremel, J. Am. Chem. Soc., 2013, 135, 726–732.
8. G. S. Nolas, H. Poddig, W. Shi, L. M. Woods, J. Martin and H. Wang, J. Solid State Chem., 2021, 297, 122058.
9. G. E. Delgado, J. L. Villegas, P. Silva and V. Sagredo, Chalcogenide Lett., 2009, 6, 293–298.
10. D. Hobbis, W. Shi, A. Popescu, K. Wei, R. E. Baumbach, H. Wang, L. M. Woods and G. S. Nolas, Dalton Trans., 2020, 49, 2273–2279.
11. D. Hobbis, K. Wei, H. Wang and G. S. Nolas, J. Alloys Compd., 2018, 743, 543–546.
12. D. Hobbis, W. Shi, A. Popescu, K. Wei, R. E. Baumbach, H. Wang, L. M. Woods and G. S. Nolas, Dalton Trans., 2020, 49, 2273.
13. W. Shi, A. R. Khabibullin, D. Hobbis, G. S. Nolas and L. M. Woods, J. Appl. Phys., 2019, 125, 155101.
14. W. Shi, A. R. Khabibullin and L. M. Woods, Adv. Theory and Simul., 2020, 3, 2000041.
15. V. L. Bekenev, V. v. Bozhko, O. v. Parasyuk, G. E. Davydyuk, L. v. Bulatetska, A. O. Fedorchuk, I. v. Kityk and O. Y. Khyzhun, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 559–566.
16. M. v. Jyothirmai, J. Electron. Mater., 2020, 50(4), 1707–1712.
17. J. M. Skelton, A. J. Jackson, M. Dimitrievska, S. K. Wallace and A. Walsh, APL Mater., 2015, 3, 041102.
18. T. Gürel, C. Sevik and T. ÇaǧIn, Phys. Rev. B, 2011, 84, 205201.
19. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
20. W. Shi, T. Pandey, L. Lindsay and L. M. Woods, Phys. Rev. Mater., 2021, 5, 045401.
21. X. Gao, M. Zhou, Y. Cheng and G. Ji, Philos. Mag., 2016, 96, 208–222.
22. F. J. Fan, L. Wu and S. H. Yu, Energy Environ. Sci., 2013, 7, 190–208.
23. F. S. Liu, J. X. Zheng, M. J. Huang, L. P. He, W. Q. Ao, F. Pan and J. Q. Li, Sci. Rep., 2014, 4, 1–7.
24. Y. Xu, Q. Fu, S. Lei, J. Xiong, S. Sun, Q. Bian, Y. Xiao and B. Cheng, Inorg Chem., 2019, 58, 15283–15290.
25. A. Shavel, J. Arbiol and A. Cabot, J. Am. Chem. Soc., 2010, 132, 4514–4515.
26. K. Pal, Y. Xia, J. Shen, J. He, Y. Luo, M. G. Kanatzidis and C. Wolverton, npj Comput. Mater., 2021, 7, 1–13.
27. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
28. G. S. Nolas, M. S. Hassan, Y. Dong and J. Martin, J. Solid State Chem., 2016, 242, 50–54.
29. C. Wang, S. Chen, J. H. Yang, L. Lang, H. J. Xiang, X. G. Gong, A. Walsh and S. H. Wei, Chem. Mater., 2014, 26, 3411–3417.
30. R. O. Jones, Rev. Mod. Phys., 2015, 87, 897.
31. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558.
32. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B, 1994, 49, 16223.
33. B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454.
34. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
35. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B, 2015, 91, 094306.
36. L. Chaput, Phys. Rev. Lett., 2013, 110, 265506.
37. G. Deinzer, G. Birner and D. Strauch, Phys. Rev. B, 2003, 67, 144304.
38. L. Lindsay, Nanoscale Microscale Thermophys. Eng., 2016, 20, 67–84.
39. OXFORD CLASSIC TEXTS IN THE PHYSICAL SCIENCES.
40. Y. Wang, Z. Lu and X. Ruan, J. Appl. Phys., 2016, 119, 225109.
41. D. Cuffari and A. Bongiorno, Phys. Rev. Lett., 2020, 124, 215501.
42. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
43. L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026.
44. R. J. Gillespie and E. A. Robinson, J. Comput. Chem., 2007, 28, 87–97.
45. S. Chen, A. Walsh, Y. Luo, J. H. Yang, X. G. Gong and S. H. Wei, Phys. Rev. B, 2010, 82, 195203.
46. N. Kattan, B. Hou, D. J. Fermín and D. Cherns, Appl. Mater. Today, 2015, 1, 52–59.
47. S. Chen, X. G. Gong, A. Walsh and S. H. Wei, Phys. Rev. B, 2009, 79, 165211.
48. R. B. Wexler, G. S. Gautam and E. A. Carter, Phys. Rev. B, 2020, 102, 054101.
49. S. Botti, D. Kammerlander and M. A. L. Marques, Appl. Phys. Lett., 2011, 98, 241915.
50. L. Weston and C. Stampfl, Phys. Rev. Mater., 2018, 2, 085407.
51. A. Hong, Y. Tang and J. Liu, J. Phys. Chem. C, 2021, 125, 24796–24804.
52. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew Chem. Int. Ed. Engl., 1997, 36, 1808–1832.
53. Y. Amouyal, Materials, 2017, 10, 386.
54. W. F. Sherman, J. Phys. C: Solid State Phys., 1980, 13, 4601.
55. G. S. Nolas, M. S. Hassan, Y. Dong and J. Martin, J. Solid State Chem., 2016, 242, 50–54.
56. Y. Dong, A. R. Khabibullin, K. Wei, Z.-H. Ge, J. Martin, J. R. Salvador, L. M. Woods and G. S. Nolas, Appl. Phys. Lett., 2014, 104, 252107.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04261d

---