Open Access Article
Open Access ArticleExploring the adsorption ability with sensitivity and reactivity of C12–B6N6, C12–Al6N6, and B6N6–Al6N6 heteronanocages towards the cisplatin drug: a DFT, AIM, and COSMO analysis†
Md. Golam Muktadir,
Ariful Alam,
Afiya Akter Piya and
Siraj Ud Daula Shamim
and
Siraj Ud Daula Shamim *
*
Department of Physics, Mawlana Bhashani Science and Technology University, Tangail, Bangladesh. E-mail: sdshamim@mbstu.ac.bd
First published on 18th October 2022
Abstract
The DFT study on the adsorption behaviour of the C24, B12N12, and Al12N12 nanocages and their heteronanocages towards the anticancer drug cisplatin (CP) was performed in gas and water media. Among the three pristine nanocages, Al12N12 exhibited high adsorption energy ranging from −1.98 to −1.63 eV in the gas phase and −1.47 to −1.39 eV in water media. However, their heterostructures C12–Al6N6 and B6N6–Al6N6 showed higher interaction energies (−2.22 eV and −2.14 eV for C12–Al6N6 and B6N6–Al6N6) with a significant amount of charge transfer. Noteworthy variations in electronic properties were confirmed by FMO analysis and DOS spectra analysis after the adsorption of the cisplatin drug on B12N12 and B6N6–Al6N6 nanocages. Furthermore, an analysis of quantum molecular descriptors unveiled salient decrement in global hardness and increments in electrophilicity index and global softness occurred after the adsorption of CP on B12N12 and B6N6–Al6N6. On the other hand, the above-mentioned fluctuations are not so noteworthy in the case of the adsorption of CP on Al12N12, C12–B6N6, and C12–Al6N6. Concededly, energy calculation, FMO analysis, ESP map, DOS spectra, quantum molecular descriptors, dipole moment, COSMO surface analysis, QTAIM analysis, and work function analysis predict that B12N12 and B6N6–Al6N6 nanocages exhibit high sensitivity towards CP drug molecules.
1. Introduction
Cancer is the leading contributor to the ailment burden across the globe, and studies predict that the global cancer burden will continue to grow for the forthcoming 20 years. Chemotherapy is a sheet anchor for cancer treatment along with surgical intervention and radiotherapy. However, it is a matter of fact that chemotherapeutic drugs inevitably attack normal cells along with proliferating cancerous cells, causing adverse effects. The adverse side effects include loss of immunity to other diseases, fall in appetite, nausea, loss of hair, etc. For this reason, advanced chemotherapeutics, which are capable of targeting cancerous cells (either actively or passively) and thereby omitting the adverse side effects, is a crying need. To guide and unload a drug at a specific predestined biological site in an efficient and controlled targeted drug delivery system may provide the best solution.In 1844 M. Peyrone first synthesized cisplatin1 and in 1965 Rosenberg elucidated the anticancer activity of cisplatin following the growth of bacteria under the influence of electrolysis products from platinum-based electrodes.2,3 Clinically proven reports undoubtedly support cisplatin to combat different types of cancers, including lung cancer, sarcomas, ovarian cancer, carcinoma, breast cancer, and brain cancer.1,4,5 However the therapeutic application of cisplatin is hindered by numerous (approximately 40 types) toxicities associated with it, including gastrointestinal toxicity, nephrotoxicity, cardiotoxicity followed by low specificity and poor solubility.6–8 A high-resolution crystallographic study conducted by Nicolla Pontillo et al. concluded that ferritin nanocages can be prominent cisplatin delivery platforms to minimize the off-target toxicity.9 In addition to this, numerous DFT approaches have been performed to reduce the side effects of cisplatin and enhance the therapeutic outcomes.5,10–12 For this reason, we are enthusiastic to explore the adsorption ability of cisplatin drug on C24 and its derivative nanocages for the first time.
Nanomaterial-based delivery systems are making a noteworthy difference in cancer immunotherapy because of their unique biological characteristics. Owing to their large surface area to volume ratio, tiny size, binding or adsorption, and carrying anticancer agents with them is really feasible. Among different nanostructures, including nanodots, nanosheets, nanocage, nanowires, nanocones, and nanotubes, nanocages owing to their unique spherical shape, lesser adverse side effects, and enhanced sensitivity to drug molecules, have extensively drawn the attention of researchers.13–15 Due to the good thermodynamic stability of C24 fullerene, numerous investigations have been conducted by considering C24 as an adsorbent.16–18 Bodgan et al. have studied the adsorption behaviour of the ephedrine drug on C24 using DFT and TD-DFT theory and they have proposed C24 to be a potential carrier.16 According to the investigation of Hosseinian et al., the interaction between 5-fluorouracil and C24 fullerene was found to be a weak interaction, which was later enhanced by substituting one carbon atom with a boron atom.17 To improve the interaction behaviour of C24, its derivatives such as B12N12 and Al12N12 were widely studied by Javan et al. who theoretically proposed that B12N12 could be a favourable drug carrier for 5-fluorouracil drug by DFT.19 Soltani et al. investigated the interaction of 5-AVA drug molecules on B12N12 and B16N16 nano-cages and concluded that B12N12 is more preferable for the drug than B16N16.20 Using DFT computations, Fatemeh Azarakhshi et al. investigated the adsorption behaviour of sulfanilamide drugs on B12N12 and Al12N12. Afterward, they concluded that B12N12 fullerene can be suitable for the delivery of SLF drug.21 Padash et al. studied the adsorption of sulfamide drugs employing DFT onto the exterior surface of Al12N12, Al12P12, B12N12, and B12P12 and concluded that Al12N12 showed the best adsorbent property.22 Recently, different heteronanocages have been studied and proposed as drug delivery systems due to their unique properties, such as high interaction behaviour with drug molecules.23–25 Muz et al. studied C30B15N15 heteronanocages as a drug carrier for flavipiravir and Hazrati et al. investigated the same heteronanocages as isoniazid drug vehicles by DFT.24,26 C12–B6N6 and C12–Al6N6 heteronanocages have been studied by X. F. Fan et al. and Paul et al. by theoretical studies and confirmed to be energetically stable.25,27
This study is aimed to set forth the adsorption ability of the C24 fullerene and its derivatives (substituting the C atoms with B, Al, and N atoms in equal proportions) for the controlled delivery of Cisplatin. Firstly, we investigated the sensitivity of C24 towards CP and found a weak interaction. Secondly, C24 nanocages were modified by substituting 12 C atoms with equal proportions of B, N, and Al atoms to enhance the adsorption characteristics. In order to further explore the bio-sensing of CP, we further modified the C24 nanocage and modelled fullerene-like heteronanocages, i.e. C12–B6N6, C12–Al6N6, and B6N6–Al6N6, and performed adsorption computations under DFT framework. To investigate the reactivity of our proposed nanocages towards CP, quantum molecular descriptors and work function analysis along with the quantum theory of atoms in molecules (QTAIM) and COSMO surface analysis were performed.
2. Computational details
This presented investigation under spin unrestricted DFT framework conditions illustrates the adsorption calculations of cisplatin over Al12N12, B12N12, C24, C12–B6N6, C12–Al6N6, and B6N6–Al6N6 nanocages in gas and water phases implemented in Dmol3 module.28,29 In order to optimize the structures of the nanocages along with the complexes of cisplatin, generalized gradient approximation (GGA) (instead of LDA) was used, since local density approximation (LDA) estimates inflated results as observed in numerous previous studies for results of equilibrium distance and bond energy. To describe the exchange–correlation interaction, the Perdew–Burke–Ernzerhof (PBE) functional within GGA was used.30,31 For the core treatment, DFT semi-core pseudopotentials along with double numerical basis set plus polarization (DNP) was applied in the absence of any symmetry restriction. The geometries have been optimized under spin unrestricted condition.32 In order to account for the van der Waals interaction, all the investigations were carried out by implementing Tkatchenko–Scheffler (TS) dispersion corrected PBE, which also accounts for the long-range electron effect.33 To account for the dispersion forces in the interactions precisely, the dispersion corrected DFT (DFT-D) scheme was adopted.34 It is irrefutable that computations are prone to be affected by BSSE (basis set superposition error) if interacting molecules are present. Therefore, BSSE (basis set superposition error) correction is one of the important factors for obtaining precise energy of the complexes, and in this case, the DNP basis set has better accuracy since it can offset the effects of BSSE errors. In this study, the maximum displacement, maximum force, and convergence tolerance of energy were 0.005 Å, 0.004 Ha Å−1, and 2 × 10−5 Ha, respectively.35 The convergence of the electronic SCF was set to 1 × 10−5 eV. A 0.005 Ha smearing point and a 5 Å real space global cut-off radius for better computational accuracy and speedy geometry optimization were set.36 Adsorption is defined as a surface phenomenon in which the adsorbate species from the solution accumulate on the solid adsorbent surface by van der Waals interaction, and it is mainly a consequence of the surface energy. The energy (Ead) of cisplatin to get adsorbed on the surface of Al12N12, B12N12, and C24 nanocages is defined as follows:37| Ead = Ecom − Edrug − Ecage | (1) |
In the above equation Ecom, Edrug, Ecage denote the total energies of complexes, cisplatin drug, and nanocages, respectively. The electronic properties are well described by EL (energy of the lowest unoccupied molecular orbital (LUMO)) and EH (energy of the highest occupied molecular orbital (HOMO)) and the energy gap Eg fluctuations and relation among these mentioned parameters are as follows:
| Eg = EL − EH | (2) |
The change in the energy gap (% ΔEg) of Eg is obtained as follows:
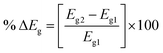 | (3) |
| Electrophilicity, ω = μ2/2η | (4) |
| Softness, S = 1/2η | (5) |
| Hardness, η = (ELUMO − EHOMO)/2 | (6) |
| Chemical potential, μ = −(EHOMO + ELUMO)/2 | (7) |
The analysis of the normal mode of vibrations was performed in order to ascertain that the structures after adsorption belongs to real local minima. The charge transfer among drug and nanocages were studied based on the Hirshfeld charge analysis. It analyses the electron density as a function of space, to know whether cisplatin acts as a donor or acceptor.42 In a water solvent, the interaction of cisplatin drug with the nanocages was investigated by applying a dielectric constant of 78.54 by introducing the conductor-like screening model (COSMO).43 To gain a further better revelation about the characteristics of the interactions, QTAIM analysis was performed on the considered complexes.44,45 In this investigation, all parameters mentioned earlier were computed and all states were optimized once again in water media using the same theories.
3. Results and discussion
3.1. Geometry optimization
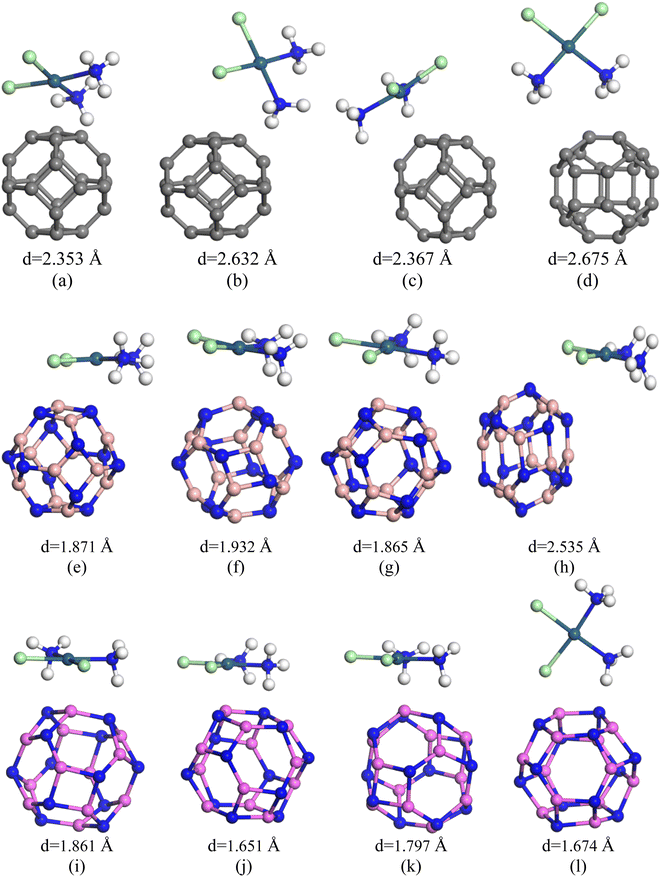
The nanocages we were interested (C24, Al12N12, B12N12, C12–B6N6, C12–Al6N6, and B6N6–Al6N6 for drug delivery) were relaxed both in gas and water media. The optimized illustrations of the adsorbent nanocages are depicted in Fig. 1. The C24 nanocage consists of six 4-component rings (4-CR) attached to eight 6-component rings (6-CR) with m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Oh) symmetry and contains no 5-component ring (5-CR). In 4-CR, C–C bond lengths are equal and have been computed at about 1.490 Å, and in 6-CR, C–C bond lengths are also equal and have been computed at about 1.38 Å. Hence, the average C–C length in C24 nanocage is 1.435 Å, which is consistent with the previous studies by Chang et al. and Soliman et al.46,47 In order to study the electron-rich and deficient regions, the HOMO and LUMO maps of the nanocages were analysed. For C24, except for some of the C–C bonds in 4-CR and 6-CR, 6-CR, and 6-CR junctions, the HOMO and LUMO levels were located throughout the entire cage. In the case of B12N12 and Al12N12, the HOMO levels were above the N atoms and LUMO levels were situated over the B and Al atoms of the nanocages. Based on the results of the simulation, the energy gaps (Eg) were computed at about 1.577 eV, 4.972 eV, and 2.644 eV for C24, B12N12, and Al12N12, respectively. The calculated Eg of C24 (1.577 eV) is consistent with the result obtained by Kosar et al. employing the B3LYP hybrid functional (1.81 eV).48 The Eg of B12N12 was in good agreement with the result (4.43 eV) obtained employing B3LYP/6-31G(d,p) by Rakib Hossain et al. and mass spectrometric analysis by Oku et al.49,50
m (Oh) symmetry and contains no 5-component ring (5-CR). In 4-CR, C–C bond lengths are equal and have been computed at about 1.490 Å, and in 6-CR, C–C bond lengths are also equal and have been computed at about 1.38 Å. Hence, the average C–C length in C24 nanocage is 1.435 Å, which is consistent with the previous studies by Chang et al. and Soliman et al.46,47 In order to study the electron-rich and deficient regions, the HOMO and LUMO maps of the nanocages were analysed. For C24, except for some of the C–C bonds in 4-CR and 6-CR, 6-CR, and 6-CR junctions, the HOMO and LUMO levels were located throughout the entire cage. In the case of B12N12 and Al12N12, the HOMO levels were above the N atoms and LUMO levels were situated over the B and Al atoms of the nanocages. Based on the results of the simulation, the energy gaps (Eg) were computed at about 1.577 eV, 4.972 eV, and 2.644 eV for C24, B12N12, and Al12N12, respectively. The calculated Eg of C24 (1.577 eV) is consistent with the result obtained by Kosar et al. employing the B3LYP hybrid functional (1.81 eV).48 The Eg of B12N12 was in good agreement with the result (4.43 eV) obtained employing B3LYP/6-31G(d,p) by Rakib Hossain et al. and mass spectrometric analysis by Oku et al.49,50
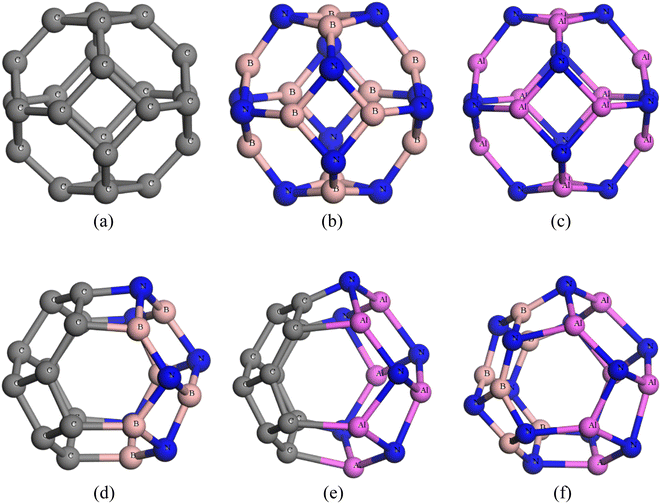 | ||
| Fig. 1 Optimized structures of (a) C24, (b) B12N12, (c) Al12N12, (d) C12–B6N6, (e) C12–Al6N6 and (f) B6N6–Al6N6. | ||
Increased electronegativity difference leads to an increased ionic character as well as increased bond polarity. The electronegativity values of boron (B), nitrogen (N), and aluminium (Al) were 2.051, 3.066, and 1.613, respectively. According to this, the difference in the electronegativity of N and B in B12N12 is 1. For Al12N12, the difference in electronegativity of the constituent molecules was 1.43, which is greater than the electronegativity difference of B12N12. Therefore, Al12N12 shows enhanced ionic character than B12N12. As B12N12 exhibits covalent character, its HOMO–LUMO gap (Eg) is greater than Al12N12.51 The CP drug molecule was optimized and the relaxed structure along with its respective HOMO–LUMO profile and ESP map are depicted in Fig. SI1.† Previous experimental results agree with our observation on the bond lengths of the optimized CP drug.52 Two kinds of N–H bonds have been perceived in CP having lengths of 1.035 Å and 1.023 Å. The Pt–N and Pt–Cl bond lengths were found to be 2.110 Å and 2.315 Å, respectively. While experimental values of these bonds were 2.06 Å and 2.347 Å; in fact, previous studies suggested the theoretically observed values of these bonds as 2.09 Å and 2.307 Å, respectively. The HOMO profile of the CP drug suggests that the HOMO levels are located on the Pt and Cl atoms at −5.029 eV. The LUMO profile shows that the LUMO level is located on the Pt–Cl and Pt–N bonds and H atoms at 2.36 eV. The accumulation of negative and positive charges around Cl atoms and the NH3 molecules, respectively, was confirmed from the ESP map of CP.
3.2. Adsorption of CP on C24 nanocage
In search for suitable adsorbents for the CP drug, ample adsorption parameters of CP/C24, CP/B12N12, and CP/Al12N12 complexes were investigated. Initially, on different adsorption domains of C24 nanocage, CP was adsorbed (both in gas and water media) and among them, four different orientations of the CP drug over C24 were chosen. The description of the states are as follows: (i) the S1 state where CP was placed parallel to the C24 nanocage, (ii) the S2 state where CP was placed perpendicular to the C24 nanocage and one Cl atom of the CP drug was close to the nanocage, (iii) the S3 state where central Pt atom of the drug molecule was slightly far for the central top C atom of C24 than the S1 and the drug was parallel to the nanocage, (iv) the S4 state where two NH3 of the CP were close to the central top C atom and the drug molecule was slightly inclined outwards from the nanocage perpendicularly. In the case of the complex molecules, the geometry of C24 was found unchanged and the bond lengths around the 4-CR and 6-CR junctions and 6-CR–6CR junctions were observed to vary about 0.044 Å and 0.046 Å, respectively. The optimized geometries, as well as the adsorption distances of all states (in the gas phase), were demonstrated in Fig. 2. Negative adsorption energies were observed for all the states, which indicates attractive interactions between the drug and the nanocages. Based on the results of the simulation, the S1, S2, S3, and S4 states of CP/C24 complexes were adsorbed with −0.74 eV, −0.26 eV, −0.77 eV, and −0.41 eV adsorption energies at 2.353 Å, 2.632 Å, 2.367 Å, and 2.675 Å distances, respectively. Thus, S3 is the most favourable state, i.e., when the drug molecule is juxtaposed to the nanocage. The adsorption energy maintains an inversely proportional relationship with the interaction distance. After the adsorption of the CP drugs on the C24 nanocages, the nanocages remain almost symmetric (geometrically) as they were before adsorption, while the bond lengths varied slightly. If the value of the adsorption energy is greater than −0.8 eV then it is called chemisorption, while less than −0.6 eV is referred to as physisorption.53 According to this definition, no chemisorption was observed for CP/C24 complexes, all the adsorption energies of the four states exhibit physisorption. When cisplatin is inserted into the body environment, the main challenge, which the therapeutic of cisplatin meets is that the drug has to cross multiple biological barriers namely mouth mucosa, blood–brain barrier (BB), and gastrointestinal tract with the least generic accumulation. The efficacy of cisplatin therapeutics can be limited by premature release of the drug on undesired biological sites if there is weak binding between cisplatin and the studied nanocages. Therefore, strong binding between the drug and the nanocages is indispensable.To verify the structural stability of the S3 state of CP/C24, vibrational frequency analysis was performed. The vibrational frequency analysis ensured that there was no existence of imaginary frequency for the S3 state and the vibrational frequencies varied within the limit of 24.9 cm−1 to 3522 cm−1. The energy gap (Eg), Frontier molecular orbital (FMO) analysis, and charge transfer (Q) (tabulated in Table 2) were studied to investigate the degree of sensitivity of C24 nanocages toward the CP drug. The FMO of the most favourable state of the CP/C24 complex (both top and side views) is depicted in Fig. SI2.† The HOMO and LUMO levels were randomly localized throughout the drug and the nanocage. For S1, S2, S3, S4 states of C24, the LUMO energy (EL) increases from −4.593 eV to −4.105 eV, −4.395 eV, −4.119 eV and −4.853 eV and HOMO energy (EH) increased from −6.17 eV to −5.012 eV, −5.384 eV, −5.096 eV, −5.607 eV, respectively. Thus, energy gap of C24 decreases from 1.577 eV to 0.907 eV, 0.989 eV, 0.979 eV and 0.754 eV for S1, S2, S3 and S4 states, respectively. The calculated percentage reductions in the energy gap (% Eg) for S1, S2, S3, and S4 states were 42.5%, 37.286%, 37.9201%, and 52.1877%, respectively. A reduction in energy gap (Eg) leads to an exponential increment of conduction electron density, which is desired for targeted drug delivery. It should be taken into consideration that the conduction electron density (Nc) and energy gap (Eg) are related by the following relation:54
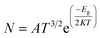 | (8) |
Hirshfeld charge analysis to get an insight into the net charge transfer from the CP drug to the nanocages was performed. For S1, S2, S3, and S4 states, 0.260e, 0.097e, 0.266e, and 0.095e of charges, respectively, were transferred to the nanocages from the drug molecule. Hence, C24 nanocages acted as electron acceptors, whereas CP acted as the electron donor.
In the water medium, similar to the gas phase, attractive exothermic reactions between CP and C24 nanocage were observed. The maximum adsorption energy was found at about −0.769 eV when the drug molecule was placed parallel to the C24 nanocage at a distance of 2.287 Å from the nanocage. The electrical properties (e.g., Eg, HOMO, LUMO energies) change after having been CP adsorbed on C24 nanocage surfaces. The Eg of C24 was reduced by about 27.6% for the S1 and 23.7% for the S3 state after adsorption, while the energy gap reduction for the S3 state was tremendous (∼38%) in the gas phase as mentioned earlier. What is more, in the water phase, the drug is adsorbed on the nanocage at a closer distance than it was thought to be adsorbed previously in the gas phase. Therefore, in comparison with the gas phase, a slightly enhanced interaction between CP and C24 in the water phase was observed.
3.3. Adsorption of CP on B12N12 nanocage
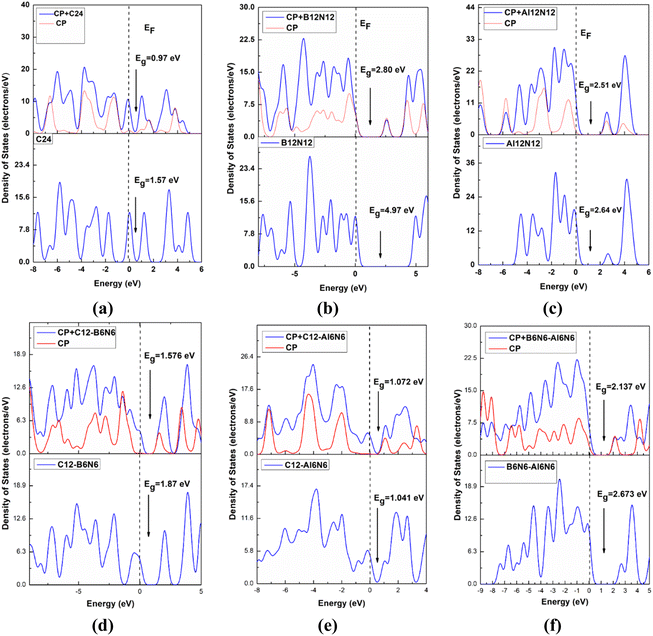
From the above discussion, it is obvious that the degree of sensitivity exhibited by C24 towards the CP drug molecule is not intense enough. For this reason, we altered the C24 nanocage so that we can obtain the B12N12 nanocage. After having the B12N12 nanocage optimized, CP drug molecules were adsorbed on it at different adsorption sites. Among the different orientations, four different states were considered, such as the ones we considered for the CP/C24 complex earlier. Adsorption energy and electronic properties were studied for the four states (Fig. 2). The CP drug was observed to be adsorbed on B12N12, 1.871 Å apart, and with an adsorption energy of −0.93 eV for the S1 state.The observed adsorption energies were −1.195 eV, −0.956 eV, and −0.485 eV for S2, S3 and S4 states, respectively (tabulated in Table 2). Therefore, the S2 state can be considered a more favourable state for the adsorption of CP on B12N12. According to the definition of adsorption energy, chemisorption occurs in the case of S1, S2, and S3 states, while physisorption occurs in the case of the S4 state. According to a previous theoretical investigation, it is a matter of fact that chemisorption is more favourable for the purpose of drug delivery.55,56 B12N12 nanocages have been observed to deform near the adsorption site after the adsorption. A trend of increasing the 4CR–6CR junction bond lengths and of decreasing the 6CR–6CR junction bond lengths has been observed for all four states. According to the predictions of the Hirshfeld charge analysis, CP and B12N12 molecules act as electron donors and electron acceptors, respectively, by receiving an amount of charge (0.254e–0.364e) from CP. The ESP maps play a pivotal role as it gives a crystal clear insight into the visualization of the reactive sites depending on the distribution of charge density. In the ESP maps, the blue (positive domains) and the yellow (negative domains) colours signify relative inanition and accumulation of electronic charges, respectively. Fig. SI3(b)† depicts the ESP and EDM maps of the S2 state of the CP/B12N12 complex. Between CP and B12N12, overlapping electron densities were observed which was confirmed by the electron density map (EDM). Additionally, the ESP map ensured that charge transfer occurred from CP to the B12N12 nanocage. EH, EL, Eg, and % ΔEg are tabulated in Table 2. Significant changes in HOMO, LUMO energies and Eg of CP/B12N12 which are greater than CP/C24 complexes were observed. The HOMO and LUMO levels are localized on the CP drug molecule. After having CP adsorbed on the B12N12 surface, downward and upward shifts of EH and EL values for all states were observed. Increment in LUMO energy and a decrement in HOMO energy leads to the reduction of the energy gap. From 4.972 eV of the energy gap, drastic decrements to 2.564 eV, 2.806 eV, 2.582 eV, and 2.627 eV for S1, S2, S3, and S4 states, respectively, were observed. This trend of reduction in the band gap is supported by another finding by Saeid Onsori et al., who investigated the adsorption of CP on B12N12 by employing B3LYP as a hybrid functional.57 The changes in the energy gap (% ΔEg) after adsorption of CP on B12N12 were 48.43% (S1), 43.56% (S2), 48.06% (S3), and 47.16% (S4), respectively. Reduced Eg increases the reactivity and sensitivity of B12N12 nanocages toward the CP drug. For CP/C24, S3 (which is the preferable state according to adsorption energy) the energy gap reduces to about 37.92% and in the CP/B12N12 complex, decrement in Eg occurs around 43.56%.
The adsorption energy for the S2 state of CP/B12N12 in a water medium was observed at around −0.84 eV, which is coherent with the results of the gas medium. The CP molecule was observed to be adsorbed almost perpendicularly with B12N12 at a distance of 2.087 Å from the central top B atom. The CP drug molecule loses an amount of 0.175e. Analogous to the gas phase, the HOMO, LUMO, and Eg are not stagnated after adsorption. EH is shifted from −7.144 eV to −6.283 eV, while the EL is shifted from −2.077 eV to −3.13 eV for the S2 state. The reduction of the energy gap observed was about 37.77% (S2 state) after having the CP adsorbed. The above-mentioned fluctuations are indicative of a strong interaction between CP and B12N12 both in the gas and water phase.
3.4. Adsorption of CP on A12N12 nanocage
In view of enhancing the adsorption behaviour, C24 nanocages were further modified by substituting C atoms with equal proportions of Al and N atoms to form Al12N12 nanocage. After the optimization of Al12N12, CP drug was adsorbed on the surface of Al12N12 nanocages on different reactive sites and among them, 4 states were selected (Fig. 2) as we did before in the case of the previous two nanocages. For S1, S2, S3 and S4 states the obtained adsorption energies were −1.974 eV, −1.744 eV, 1.98 eV and −1.628 eV, respectively (Table 1). All four structures demonstrate chemisorption according to the definition of adsorption energy. The adsorption distances were observed at 1.861 Å (S1), 1.651 Å (S2), 1.797 Å (S3), and 1.674 Å (S4), respectively. The shortest adsorption distance corresponds to the S2 state. The shortest adsorption distance between CP and Al12N12 nanocage of the most favourable state (S3) depending upon the adsorption energy is about 1.797 Å, which is shorter than the interaction distances of the most favourable states of C24 (2.367 Å) and B12N12 (1.932 Å). The vibrational frequency analysis, which ensures structural stability unveils that there is no existence of any imaginary frequency for the S3 state of CP/Al12N12 and the vibrational modes were found within the range of 35.5 cm−1 to 3513.4 cm1. The Hirshfeld charge analysis indicates that, during the interaction, the CP drug molecule donates 0.122e charge to the Al12N12 nanocage.| Structure | State | Gas phase | Water phase | ||||
|---|---|---|---|---|---|---|---|
| d | Ead | Q | d | Ead | Q | ||
| CP/C24 | S1 | 2.353 | −0.744 | 0.260 | 2.306 | −0.744 | 0.386 |
| CP/C24 | S2 | 2.632 | −0.256 | 0.097 | 2.709 | −0.256 | 0.058 |
| CP/C24 | S3 | 2.367 | −0.769 | 0.266 | 2.287 | −0.769 | 0.394 |
| CP/C24 | S4 | 2.675 | −0.412 | 0.095 | 2.781 | −0.412 | 0.052 |
| CP/B12N12 | S1 | 1.871 | −0.933 | 0.364 | 2.010 | −0.712 | 0.463 |
| CP/B12N12 | S2 | 1.932 | −1.195 | 0.254 | 2.070 | −0.838 | 0.355 |
| CP/B12N12 | S3 | 1.865 | −0.956 | 0.355 | 2.003 | −0.738 | 0.445 |
| CP/B12N12 | S4 | 2.535 | −0.485 | 0.338 | 2.048 | −0.522 | 0.636 |
| CP/Al12N12 | S1 | 1.861 | −1.974 | 0.130 | 1.938 | −1.450 | 0.233 |
| CP/Al12N12 | S2 | 1.651 | −1.744 | 0.219 | 1.804 | −1.447 | 0.305 |
| CP/Al12N12 | S3 | 1.797 | −1.98 | 0.122 | 1.932 | −1.468 | 0.239 |
| CP/Al12N12 | S4 | 1.674 | −1.628 | 0.202 | 1.827 | −1.394 | 0.321 |
| CP/C12–B6N6 | S1 | 2.077 | −0.776 | 0.254 | 2.248 | −0.446 | 0.378 |
| CP/C12–B6N6 | S2 | 2.426 | −0.627 | 0.312 | 2.359 | −0.395 | 0.298 |
| CP/C12–B6N6 | S3 | 1.910 | −0.930 | 0.220 | 2.00 | −0.688 | 0.575 |
| CP/C12–Al6N6 | S1 | 1.919 | −1.933 | 0.149 | 2.478 | −1.541 | 0.352 |
| CP/C12–Al6N6 | S2 | 1.797 | −2.204 | 0.193 | 1.697 | −1.655 | 0.372 |
| CP/C12–Al6N6 | S3 | 1.798 | −2.215 | 0.192 | 1.897 | −0.373 | 0.152 |
| CP/B6N6–Al6N6 | S1 | 1.852 | −1.993 | 0.221 | 2.067 | −1.568 | 0.363 |
| CP/B6N6–Al6N6 | S2 | 1.740 | −2.136 | 0.312 | 2.336 | −1.861 | 0.839 |
| CP/B6N6–Al6N6 | S3 | 1.871 | −2.115 | 0.173 | 2.147 | −1.666 | 0.400 |
The FMO maps of the S3 state of the CP/Al12N12 complex are depicted in Fig. SI2(c) and (f).† Unlike CP/B12N12, the HOMO levels are localized on the Al12N12 nanocage and LUMO levels are located on the CP drug molecule. A trend of increasing HOMO and LUMO energies was observed for all the selected four states of CP/Al12N12 after adsorption. For S1, S2, S3 and S4 states, Eg decreases from 2.644 eV to 2.484 eV, 2.197 eV, 2.517 eV and 2.125 eV, respectively. The DOS spectra of Al12N12 are illustrated in Fig. 3(c), which depicts that no additional major peaks are generated after adsorption in the near vicinity of the Fermi level. EDM and ESP maps guarantee the event of electron density overlapping and hybridization between the CP and Al12N12 nanocage. Analogous to the gas media, for the S3 state of Al12N12 the adsorption energy was found at about −1.468 eV. The charge transfer for this state is about 0.239e from CP to Al12N12. Significant variations in the electronic properties were also observed after the adsorption of CP on the Al12N12 nanocage. Thus, the adsorption behaviours of Al12N12 are preferable in both gas and water medium.
3.5. Adsorption of CP on C12–B6N6 heteronanocage
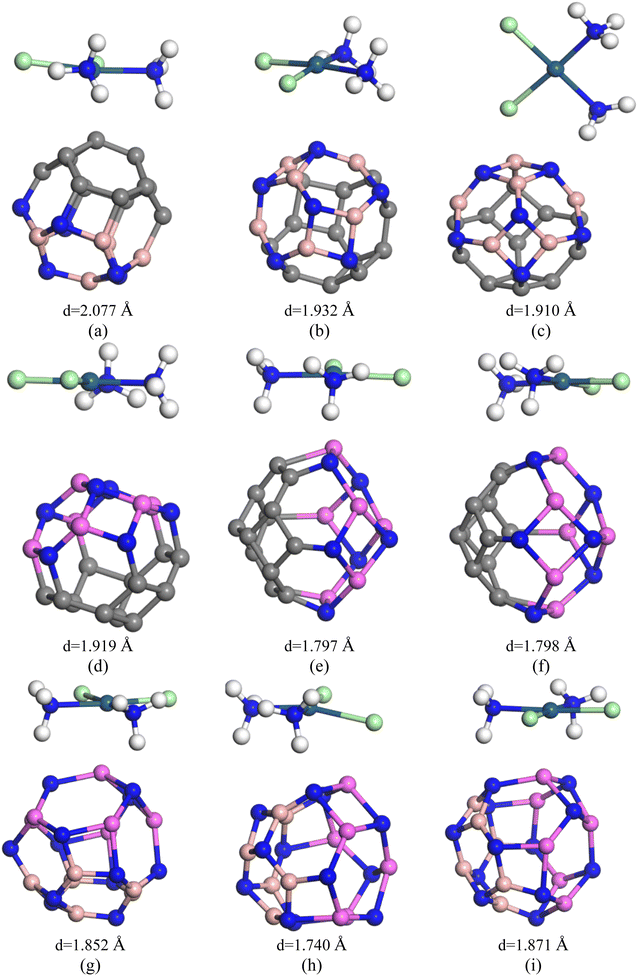
Our inquiry still continues as we have customized the C24 nanocage by introducing 6 B and 6 N atoms at the cost of eliminating 12 C atoms to form the heteronanocage: C12–B6N6 (Fig. 1(d)). It contains 5 types of bonds, which are C–C, B–B, B–C, C–N (at the junction of 4 and 6 component rings), and C–C (at the junction of 6 and 6 component rings) and, the magnitudes happen to be 1.502 Å, 1.383 Å, 1.553 Å, 1.497 Å, and 1.370 Å respectively. X. F. Fan et al. in 2008 investigated the structural stability of C12–B6N6 fullerene by employing bond counting (BCR) rules coupled with a B3LYP-based DFT approach and confirmed the structural stability of the nanocage. This result further motivates our investigation of C12–B6N6 and supports our vibrational mode analysis. In our vibrational frequency analysis, we have not found any imaginary frequencies. The range of the vibrational modes is 313.9–1577.6 cm−1. Surprisingly, our calculated Eg of C12–B6N6 agrees well with them.58In the case of our hetero-nano-cage, we have considered three different states of the complexes, which are (i) adsorption on the C12 site, (ii) adsorption of the B6N6 site, and (iii) adsorption on their interface of the C12–B6N6 hetero-nano-cage. Fig. 4 depicts the selected 3 states of the CP/C12–B6N6 complex. The negative sign of the adsorption energies infers attractive interactions but the adsorption energies of both 2 states correspond to the physisorption range (except the S3 in the gas phase) in both the gas and water phases, as tabulated in Table 1. In the gas phase, the adsorption energies are −0.776 eV, −0.627 eV, and −0.930 eV, and the interaction distances are 2.077 Å, 2.426 Å, and 1.910 Å, for the water phase, the Ead are −0.446 eV, −0.395 eV, and −0.688 eV and the interaction distances are 2.248 Å, 2.359 Å and 2.00 Å for S1, S2, S3 states, respectively. The Hirshfeld charge analysis predicts that 0.254e, 0.312e, and 0.220e charges are transported from the CP drug molecule to C12–B6N6 nanocage for S1, S2, and S3 states, respectively.
Upon FMO analysis, the data we have obtained are illustrated in Fig. SI4(a) and (d),† which indicate that the LUMO levels are located on the CP drug molecule and the HOMO levels are located on the C12–B6N6 nanocage. The FMO analysis also suggests that the reduction in the energy gap is quite trivial, as tabulated in Table 2. The reductions in energy gaps are about 11.39% and 13.36% in the gas phase for S1 and S2 states, respectively. It is to be noted that the most stable complex (which is in terms of adsorption energy) S3 has a reduction in the energy gap of about only 15.72% in the gas phase. The full and partial DOS spectra for the most stable complex are displayed in Fig. 3(d) and it implies that no dominant peaks are introduced in the near vicinity of the Fermi level. Therefore it is obvious for us to infer that, based on the electrical properties, the C12–B6N6 nanocage shows the least preferable sensitivity towards the CP drug molecule.
| Structure | State | Gas phase | Water phase | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Eg | % Eg | D.M | EHOMO | ELUMO | Eg | % Eg | D.M | ||
| C24 | −6.17 | −4.593 | 1.577 | 0 | −5.714 | −4.492 | 1.22 | 0 | |||
| CP/C24 | S1 | −5.012 | −4.105 | 0.907 | −42.4 | 9.33 | −5.038 | −4.153 | 0.885 | −27.5 | 17.39 |
| CP/C24 | S2 | −5.384 | −4.395 | 0.989 | −37.2 | 9.22 | −5.557 | −4.457 | 1.1 | −9.9 | 15.19 |
| CP/C24 | S3 | −5.098 | −4.119 | 0.979 | −37.9 | 9.07 | −5.073 | −4.141 | 0.932 | −23.7 | 17.12 |
| CP/C24 | S4 | −5.607 | −4.853 | 0.754 | −52.1 | 6.89 | −5.683 | −4.59 | 1.093 | −10.5 | 17.12 |
| B12N12 | −7.132 | −2.16 | 4.972 | 0 | −5.506 | −2.461 | 3.05 | 0 | |||
| CP/B12N12 | S1 | −5.791 | −3.227 | 2.564 | −48.4 | 11.52 | −5.763 | −2.88 | 2.883 | −43.4 | 18.45 |
| CP/B12N12 | S2 | −6.11 | −3.304 | 2.806 | −43.5 | 8.99 | −6.283 | −3.13 | 3.153 | −37.7 | 16.23 |
| CP/B12N12 | S3 | −5.789 | −3.207 | 2.582 | −48.0 | 11.64 | −5.784 | −2.876 | 2.908 | −42.6 | 18.25 |
| CP/B12N12 | S4 | −5.746 | −3.119 | 2.627 | −47.1 | 14.19 | −5.74 | −2.993 | 2.747 | −45.7 | 24.29 |
| Al12N12 | −5.696 | −3.052 | 2.644 | 0 | −5.506 | −2.461 | 3.045 | 0 | |||
| CP/Al12N12 | S1 | −5.482 | −2.998 | 2.484 | −6.0 | 7.41 | −5.69 | −3.019 | 2.671 | −1.5 | 14.05 |
| CP/Al12N12 | S2 | −5.176 | −2.979 | 2.197 | −16.9 | 9.75 | −5.55 | −2.954 | 2.596 | −4.2 | 16.63 |
| CP/Al12N12 | S3 | −5.502 | −2.985 | 2.517 | −4.8 | 7.36 | −5.701 | −3.026 | 2.675 | −1.3 | 14.14 |
| CP/Al12N12 | S4 | −5.155 | −3.03 | 2.125 | −19.6 | 10.17 | −5.494 | −2.942 | 2.552 | −5.8 | 16.54 |
| C12–B6N6 | −5.735 | −3.856 | 1.87 | 1.95 | −5.732 | −3.809 | 3.00 | 3.44 | |||
| CP/C12–B6N6 | S1 | −5.184 | −3.527 | 1.65 | −11.3 | 7.3 | −6.052 | −3.228 | 2.82 | −6.1 | 21.9 |
| CP/C12–B6N6 | S2 | −5.275 | −3.655 | 1.62 | −13.3 | 10.1 | −5.036 | −3.402 | 1.63 | −45.6 | 26.6 |
| CP/C12–B6N6 | S3 | −4.983 | −3.407 | 1.57 | −15.7 | 11.9 | −6.045 | −3.288 | 2.75 | −8.3 | 17.4 |
| C12–Al6N6 | −4.525 | −3.484 | 1.041 | 8.5 | −4.893 | −3.496 | 1.39 | 13.3 | |||
| CP/C12–Al6N6 | S1 | −4.39 | −3.49 | 0.9 | −13.5 | 12.2 | −4.729 | −3.28 | 1.44 | 3.7 | 24.2 |
| CP/C12–Al6N6 | S2 | −4.365 | −3.293 | 1.07 | 2.9 | 6.0 | −4.686 | −3.267 | 1.41 | −2.0 | 13.9 |
| CP/C12–Al6N6 | S3 | −4.369 | −3.303 | 1.06 | 2.4 | 5.4 | −4.892 | −3.544 | 1.34 | −3.5 | 23.4 |
| B6N6–Al6N6 | −5.912 | −3.239 | 2.67 | 7.3 | −6.306 | −3.298 | 3.0 | 11.1 | |||
| CP/B6N6–Al6N6 | S1 | −5.757 | −3.484 | 2.27 | −14.9 | 11.3 | −6.052 | −3.228 | 2.82 | −6.1 | 21.9 |
| CP/B6N6–Al6N6 | S2 | −5.337 | −3.2 | 2.13 | −20.0 | 4.9 | −5.036 | −3.402 | 1.63 | −45.6 | 26.6 |
| CP/B6N6–Al6N6 | S3 | −5.737 | −3.463 | 2.27 | −14.9 | 8.98 | −6.045 | −3.288 | 2.75 | −8.3 | 17.4 |
3.6. Adsorption of CP on C12–Al6N6 heteronanocage
To trace a better adsorbent for the targeted delivery of the CP drug molecule, we further adsorbed it on the surface of C12–Al6N6 (Fig. 4). The optimized structure of C12–Al6N6 contains 7 types of bonds and they are C–Al (1.966 Å), N–Al (1.867 Å), C–C shared between 4 and 6-CR (1.446 Å), C–C shared between 6 and 6-CR (1.81 Å), C–N shared between hetero-rings (1.361 Å), C–N shared between 4 and 6-CR (1.849 Å) and C–N shared between 6 and 6-CR (1.81 Å). The structural stability was confirmed by vibrational frequency analysis in which no imaginary frequency was found and the range of vibrational modes was 167.1–1571.8 cm−1 (Table 3). The calculated adsorption energies along with interaction distances and charge transfer for the 3 chosen states of CP/C12–Al6N6 are tabulated in Table 1. Observations suggest that the CP drug molecule gets adsorbed on the surface of C12–Al6N6 with adsorption energies of −1.933 eV, −2.204 eV, and −2.215 eV for S1, S2, and S3 states in the gas phase with the interaction distances of 2.492 Å, 1.79 Å, and 1.798 Å, respectively. Our calculated Eg of C12–Al6N6 agrees well with the findings of Paul et al.59 It may apparently seem that the S3 state is the most stable complex, but in the water phase, this state has an adsorption energy of −0.373 eV with an interaction distance of 1.897 Å. While in the water phase, the S2 state shows adsorption energy (−1.655 eV), which is way too consistent compared with the S3 state. The interaction distance of the S2 state is the shortest in both water and gas media, as we can see from Table 1. The Hirshfeld charge analysis predicts that an appreciable amount of charge is transferred from the CP drug molecule to the nanocage, which is 0.372e (in water medium) and 0.193e (in gas medium) for the S2 state. The other two states have lower charge transfers, as suggested by the Hirshfeld charge analysis. The HOMO levels are situated at the nanocage and the LUMO levels are situated at the drug molecule, as can be seen from the FMO analysis in Fig. SI4(b) and (e).† Table 2 shows the variation of the electronic parameters of the nanocages after adsorption. In the gas phase, only the S1 state exhibits a reduction in the energy gap of 13.5%, while the S2 and S3 states exhibit an increment of the energy gap of 2.9% and 2.4%, respectively. However, this scenario is exactly the opposite in the water phase, where the S1 state undergoes an increment in the energy gap of 3.7%, while the S2 and S3 states exhibit a decrement in the energy gap of 2% and 3.5%, respectively. Full and partial DOS spectra analysis as depicted in Fig. 3(e) shows that no extra dominant peaks are generated near the Fermi level. It can be concluded that C12–Al6N6 nanocages show less sensitivity toward the CP drug molecule.| Structure | Vibrational mode ranges (cm−1) |
|---|---|
| CP/C24/S3 | 24.9–3522.1 |
| CP/B12N12/S2 | 64.4–3400.7 |
| CP/Al12N12/S3 | 35.5–3513.4 |
| CP/C12–B6N6/S3 | 14.7–3526 |
| CP/C12–Al6N6/S2 | 23.6–3523.4 |
| CP/B6N6–Al6N6/S2 | 40.6–3525.7 |
3.7. Adsorption of CP on B6N6–Al6N6 heteronanocage
Ultimately, in search of a potent adsorbent for the CP drug to be adsorbed, we further modified the previous nanocage by removing all the carbon atoms and introducing 6 N and 6 B atoms in the place of the C atoms of the nanocage to form B6N6–Al6N6. We studied the bond types of the nanocage and found 6 types of bonds, which are B–N (1.427 Å) shared between 6 and 6-CR, B–N (1.506 Å) shared between 4-CR and 6-CR (hetero ring), B–N (1.481 Å) shared between 4 and 6-CR, Al–N (1.863 Å) shared between 4 and 6-CR, Al–N (1.841 Å) shared between 4 and 6-CR (hetero), Al–N (1.8 Å) shared between 6 and 6-CR. The positive vibrational modes were found in the range of 179.1–1385.6 cm−1 which verified the structural stability of the heteronanocage. Exceptionally high negative adsorption energies were observed, which are listed in Table 1 along with interaction distances. The main contrast between the previously studied nanocages and B6N6–Al6N6 nanocage is that B6N6–Al6N6 exhibits preferable high negative Ead in both gas and water media for all the states as well as the interaction distance is optimum. In the gas phase, S1 and S3 states both exhibit Ead of −1.852 eV and 1.871 eV, respectively, which is slightly higher than the Ead of the S2 state (−1.740 eV). On the other hand, the S2 state exhibit an adsorption energy of −1.861 eV, which is far better than the adsorption energies of both the S1 and S3 states (−1.568 eV and −1.666 eV, respectively). The Hirshfeld charge analysis unveils that a large proportion of charge transfer occurs for the most stable state (i.e., S2), especially in the water phase, the amount of charge transferred from CP to the nanocage is about 0.839e, which is the largest amount of charge transfer we have observed so far in this investigation. Results obtained from the FMO analysis are listed in Table 2. For the S1 and S3 states, the reduction in the energy gap is about 14.9%, while the S2 state shows a reduction of about 20%. In the water phase, we can see the S2 state undergoes an outstanding reduction of 45.6% in Eg. The LUMO and HOMO profiles of the S2 state show that the HOMO levels are located in both the drug and nanocage while the LUMO levels are located on the drug molecule only. The ESP and EDM maps of the most stable complex of CP/B6N6–Al6N6 are illustrated in Fig. SI5(c) and (f).† The full and partial DOS spectra are illustrated in Fig. 3(f) which, ensures the energy gap reduction phenomenon of the S2 state.3.8. Quantum molecular descriptors and dipole moment
In Table 4, global descriptors of the complexes are tabulated to gain a better insight into the stability as well as the reactivity of our complexes under study. The resistance to the deformation of alignment of the electron cloud of atoms, ions, or molecules is defined as global hardness (η). The stability of the structure increases with increasing global hardness thereby leading to a substantial decrement in reactivity.53 Another vital parameter is the electrophilicity index (ω) which defines the electrophilic behaviour of a compound. The electrophilicity index (ω) maintains an inversely proportional relationship with global hardness (η). The higher the electrophilicity index and softness, the higher the reactivity of the complexes. In our investigation, a decreasing trend of hardness and increasing trend of electrophilicity index (ω) and global softness (S) are observed.| Structure | State | μ (eV) | η (eV) | ω (eV) | S (eV−1) |
|---|---|---|---|---|---|
| CP | −3.694 | 1.334 | 5.114 | 0.374 | |
| C24 | −5.381 | 0.788 | 18.364 | 0.634 | |
| CP/C24 | S1 | −4.558 | 0.453 | 22.910 | 1.102 |
| CP/C24 | S2 | −4.889 | 0.494 | 24.173 | 1.011 |
| CP/C24 | S3 | −4.608 | 0.486 | 21.693 | 1.021 |
| CP/C24 | S4 | −5.23 | 0.377 | 36.277 | 1.326 |
| B12N12 | −4.646 | 2.486 | 4.341 | 0.201 | |
| CP/B12N12 | S1 | −4.509 | 1.282 | 7.929 | 0.390 |
| CP/B12N12 | S2 | −4.707 | 1.403 | 7.895 | 0.390 |
| CP/B12N12 | S3 | −4.498 | 1.291 | 7.835 | 0.387 |
| CP/B12N12 | S4 | −4.432 | 1.313 | 7.478 | 0.380 |
| Al12N12 | −4.374 | 1.322 | 7.235 | 0.378 | |
| CP/Al12N12 | S1 | −4.24 | 1.242 | 7.237 | 0.402 |
| CP/Al12N12 | S2 | −4.077 | 1.098 | 7.567 | 0.455 |
| CP/Al12N12 | S3 | −4.243 | 1.258 | 7.154 | 0.397 |
| CP/Al12N12 | S4 | −4.092 | 1.062 | 7.881 | 0.470 |
| C12–B6N6 | −4.8 | 0.935 | 12.320 | 0.534 | |
| CP/C12–B6N6 | S1 | −4.355 | 0.828 | 11.448 | 0.603 |
| CP/C12–B6N6 | S2 | −4.465 | 0.81 | 12.306 | 0.617 |
| CP/C12–B6N6 | S3 | −4.195 | 0.788 | 11.166 | 0.634 |
| C12–Al6N6 | −4.004 | 0.520 | 15.404 | 0.960 | |
| CP/C12–Al6N6 | S1 | −3.94 | 0.45 | 17.248 | 1.111 |
| CP/C12–Al6N6 | S2 | −3.829 | 0.536 | 13.676 | 0.932 |
| CP/C12–Al6N6 | S3 | −3.836 | 0.533 | 13.803 | 0.938 |
| B6N6–Al6N6 | −4.575 | 1.336 | 7.832 | 0.374 | |
| CP/B6N6–Al6N6 | S1 | −4.620 | 1.136 | 9.392 | 0.439 |
| CP/B6N6–Al6N6 | S2 | −4.268 | 1.068 | 8.526 | 0.467 |
| CP/B6N6–Al6N6 | S3 | −4.6 | 1.137 | 9.305 | 0.439 |
The calculated hardnesses for C24, B12N12, and Al12N12 are 0.755 eV, 2.486 eV, and 1.322 eV, respectively. However, the hardness decreases from 0.755 eV to 0.377–0.494 eV for C24, from 2.486 eV to 1.282–1.403 eV for B12N12, from 1.322 eV to 1.062–1.258 eV after adsorption. To sum up, the chemical stability of the complexes of CP/C24, CP/B12N12, and CP/Al12N12 decreases but reactivity increases. Furthermore, the computed values of softness and electrophilicity index of the three nanocages were observed to shift to higher values, which is an indication of the increased reactivity. The global softness is incremented from 0.634 eV−1 to 1.021 eV−1, from 0.201 eV−1 to 0.356 eV−1, from 0.378 to 0.397 eV−1 for the S3, S2, and S3 states of CP/C24, CP/B12N12 and CP/Al12N12, respectively. The computed hardness of C12–B6N6, C12–Al6N6, and B6N6–Al6N6 nanocages are 0.935 eV, 0.520 eV, and 1.336 eV, respectively. C12–B6N6 and B6N6–Al6N6 nanocages were observed to have a reduced global hardness (0.788 eV and 1.068 eV, respectively), while the hardness of the C12–Al6N6 nanocage increases to 0.536 eV after adsorption. With an initial value of global softness of 0.534 eV−1 and 0.374 eV−1, C12–B6N6 and B6N6–Al6N6 nanocages exhibited an increment of 0.634 eV−1 and 0.467 eV−1, respectively, while C12–Al6N6 showed a decrement in its softness (from 0.960 eV−1 to 0.932 eV−1). A trend of the decreasing electrophilicity index was observed in the case of C12–B6N6 and C12–Al6N6 (except for the S1 state) nanocages, while an increasing trend of electrophilicity index was observed in the case of B6N6–Al6N6 (except for the S2 state) nanocage.
The measurement of symmetricity of the complex dipole moment (D.M) is a significant study. The dipole moment study in the water phase provides a deeper insight into the solubility of a complex. The higher value of dipole moment indicates higher solubility, reactivity, and higher transit of charge between the drug and nanocage.60–62 Through the dipole moment study, we investigated the asymmetry of the charge distribution of our complexes. The calculated D.M for C24, B12N12, and Al12N12 were all 0 D. On the other hand, D.M increases outstandingly for all the preferable states after adsorption (Table 2). After adsorption, the solubility of the complexes in the human body is thus ensured by a noticeable rise in the dipole moment values. In the water medium, the computed dipole moments of the nanocages were also 0 D. After adsorption in the water medium, the dipole moments were highly increased by about 17.13 D, 16.23 D and 14.14 D for S3, S2, and S3 states of CP/C24, CP/B12N12 and CP/Al12N12 complexes, respectively. Unlike C24, B12N12, or Al12N12 nanocages, the dipole moments of C12–B6N6, C12–Al6N6, and B6N6–Al6N6 nanocages are non-zero before adsorption and the values happen to be 1.95 D, 8.54 D, and 7.39 D, respectively. The dipole moment of C12–B6N6 increases to 11.992 D, while the dipole moments of C12–Al6N6 and B6N6–Al6N6 tend to decrease to 6.036 D and 4.943 D after adsorption from their initial values before adsorption. However, this scenario in the water phase is obviously different since all three stable complexes of C12–B6N6, C12–Al6N6, and B6N6–Al6N6 show dipole moment values of 23.39 D, 13.96 D, and 26.66 D (after adsorption) incremented from their initial dipole moment values of 3.44 D, 13.39 D, and 11.14 D (before adsorption).
3.9. Work function analysis
To justify the sensitivity of the CP drug molecule toward the nanocages, the work function (φ) study is a pivotal investigation. Whether the CP drug is affecting or not the work function of the nanocages was studied in this analysis. The work function is referred to be the minimum thermodynamic work (energy) required to remove an electron from a solid surface to vacuum instantaneously and is defined by the following relation,63| φ = Ve(+∞) − EF | (9) |
The field emission characteristics of the nanocages are altered by varying the work function, which may consequently end up changing the gate voltage.64,65 This is well explained by Richardson Dushman equation66
| j = AT2e(−φ/KT) | (10) |
The change in the work function after adsorption can be calculated using the following formula:
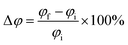 | (11) |
Tables SI1 and SI2† illustrate the computed work function values. In our study, the work function of C24 was found about 5.12 eV. Observations indicate that during the adsorption of the drug on our nanocages under study, work functions are outstandingly fluctuating. Negative and positive signs of the variation of work function (φ) indicate increment and decrement of φ of adsorbents after adsorbing CP, respectively. In the gas phase, C24 and Al12N12 φ were observed to increase about 9.824% and 1.365% and decrease about 0.71% for B12N12 after the adsorption of CP. φ is increased by about 8.672% and 2.673% for C24 and Al12N12 and decreased by about 0.967% for B12N12 after the adsorption of CP drug in the water medium. Therefore, according to work-function analysis, C24 and Al12N12 nanocages show higher sensitivity than B12N12 towards the CP drug. For all three stable complexes, the nanocages tend to exhibit a decrement in their work function after adsorption. In the gas phase, the decrements was observed to be about 5.97%, 2.63%, and 7.04% for the S3, S2, and S3 states of CP/C12–B6N6, CP/C12–Al6N6 and CP/B6N6–Al6N6 complexes, respectively. Similarly, in the water phase, we observed analogous decrement of about 5.19%, 0.86%, and 8.27% for S3, S2, and S3 states of CP/C12–B6N6, CP/C12–Al6N6 and CP/B6N6–Al6N6 complexes, respectively. Upon the work function analysis, it was quite obvious to infer that C12–B6N6 and B6N6–Al6N6 showed less sensitivity toward the CP drug molecule. To draw a conclusion, in view of the work function analysis among the studied nanocages, C24 shows better sensitivity toward CP.
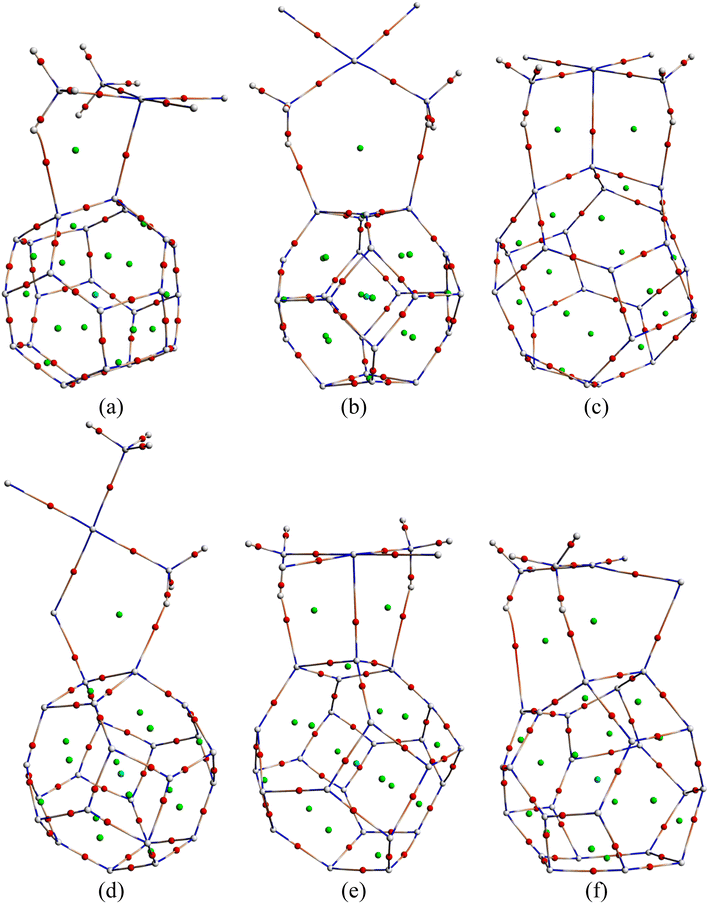
3.10. COSMO surface analysis
Previously, we have discussed how the presence of solvent dominates the adsorption process of CP on nanocages under study through energy calculations, the variation of electronic properties, dipole moment analysis, etc. in the water medium to mimic the body's biochemical environment and to reach experimental conditions. To obtain a more detailed insight into the polarity of the drug and nanocage complexes, a COSMO surface analysis was performed. Fig. 5 shows the COSMO surfaces of C24, B12N12, Al12N12, C12–B6N6, C12–Al6N6, and B6N6–Al6N6. Whereas, Fig. 6 depicts the illustrations of COSMO surface analysis of drug–nanocage complexes under study. The green segments correspond to non-polar neutral parts of the molecules. The blue areas denote the highly positive region. Therefore, they form the hydrogen bond donor (HBD) region to the solvent media. Conversely, the red regions report the highly negative region, which is the hydrogen bond acceptor (HBA) region to the solvent. As we can see from Fig. 5, the COSMO surface of C24 is almost green everywhere, which indicates that the polarity of C24 is neutral before adsorption. The HBD regions are situated over the nitrogen atoms in the case of both B12N12 and Al12N12 nanocages. While the HBA regions are located on the B and Al atoms. In the case of the C12–B6N6 and C12–Al6N6 heteronanocages, the HBD regions are located on the C12 portion of the nanocages, while HBA regions are located on the B6N6 and Al6N6 portions of the nanocages, respectively. Similarly, we can observe the locations of the HBA and HBD regions in the case of the B6N6–Al6N6 nanocage. After adsorption, it is clear from Fig. 6 that NH3 portions of the CP drug molecule denote the negative polarity region in the case of all the complexes, while the majority portion of the nanocages denotes the positive polarity region. Finally, it can be inferred that CP adsorption on the nanocages drastically enhanced the polarity of the nanocages, which is coherent with our dipole moment analysis.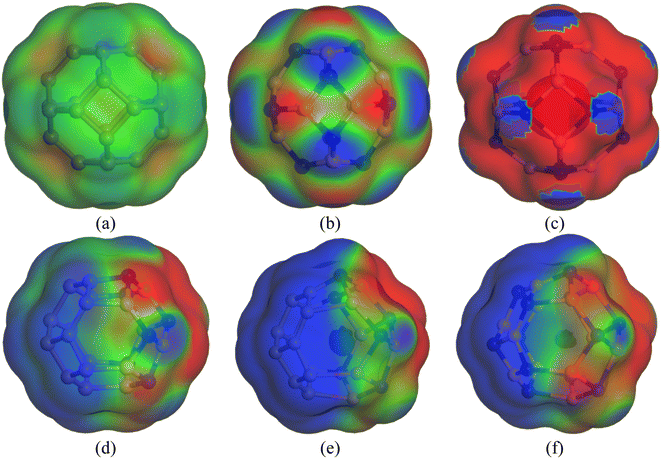 | ||
| Fig. 5 COSMO surfaces for (a) C24, (b) B12N12, (c) Al12N12, (d) C12–B6N6, (e) C12–Al6N6 and (f) B6N6–Al6N6, respectively. | ||
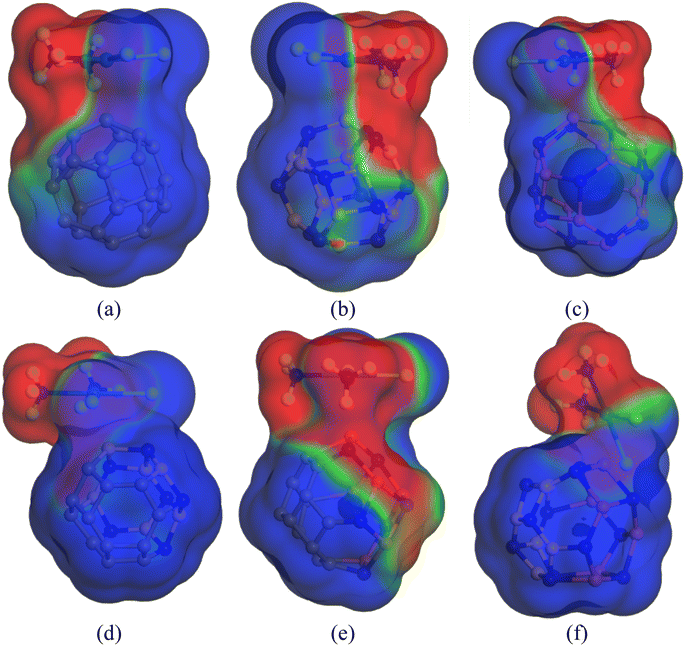 | ||
| Fig. 6 COSMO surfaces of our most stable states (a) CP/C24 (S3), (b) CP/B12N12 (S2), (c) CP/Al12N12 (S3), (d) CP/C12–B6N6 (S3), (e) CP/C12–Al6N6 (S2) and (f) CP/B6N6–Al6N6 (S2), respectively. | ||
3.11. QTAIM analysis
QTAIM analysis was performed since we were interested in explaining the intermolecular interactions and the bonding types. The quantum theory of atoms is an indispensable tool as it helps to visualize the non-covalent, hydrogen, or halogen-type chemical interactions.67 The molecular graphs for the most stable complexes in the water phase are depicted in Fig. 7. The figure demonstrates all the critical points and bond paths between the drug and the nanocages. As can be seen from Table 5, the charge density (ρb) values range from 0.0212–0.0818 a.u. and the Laplacian of charge density (∇2ρb) values lie within −1.3588 and 0.1301 a.u. A positive value of ∇2ρb is indicative of non-covalent interaction, i.e., a closed shell interaction (including van der Waals and ionic interaction), whereas a negative value of ∇2ρb implies a shared interaction in the same way as in covalent interaction. It is obvious from Table 5 that all Laplacian of charge density values are positive except for BCP 50 of CP/C12–B6N6 and BCP 82 of CP/B6N6–Al6N6. The ratio of −Gb/Vb also plays an unquestionable role in determining the bonding nature. For −Gb/Vb positive and greater than 1, the interaction is assumed to be purely non-covalent, while the bond is considered covalent if the ratio is smaller than 0.5. The total electron energy density Hb at a BCP can play a decisive role in getting a better insight into the bond type and interaction. A positive value of total electron energy density (Hb) indicates a closed-shell interaction, whereas, a negative Hb indicates a covalent bond.68 For BCP-46 CP/C24 and BCP-68 CP/B12N12, Hb > 0, ∇2ρb > 0, and −Gb/Vb > 1 indicating these interactions to be non-covalent in nature. For BCP-42 CP/C24, BCP-44 CP/B12N12, BCP-59, 75, 85 CP/Al12N12, BCP-46 CP/C12–B6N6, BCP-54, 72 CP/C12–Al6N6, BCP-65, 77, 82 CP/B6N6–Al6N6, Hb<0, −Gb/Vb < 1 and ∇2ρb > 0, which is an indicator of stronger interaction with partially covalent character. It is worth pointing out that the obtained QTAIM results for the CP/B12N12 and CP/B6N6–Al6N6 complexes are in good agreement with the interactions predicted by the adsorption energy calculation, FMO analysis, DOS spectra analysis.| Complex | BCP | ρb | ρb × 103 | ∇2ρb | Gb | Vb | Hb | −Gb/Vb |
|---|---|---|---|---|---|---|---|---|
| CP/C24 (S3) | 42 | 0.0653 | 65.337 | 0.1054 | 0.0480 | −0.0696 | −0.0216 | 0.68917 |
| 46 | 0.0212 | 21.248 | 0.0572 | 0.0142 | −0.0141 | 0.0009 | 1.0064 | |
| CP/B12N12 (S2) | 44 | 0.0372 | 37.279 | 0.1144 | 0.0310 | −0.0334 | −0.0024 | 0.9280 |
| 68 | 0.0222 | 22.268 | 0.0855 | 0.0193 | −0.0172 | 0.0020 | 1.1199 | |
| CP/Al12N12 (S3) | 59 | 0.0410 | 41.051 | 0.0695 | 0.0256 | −0.0338 | −0.0082 | 0.7568 |
| 75 | 0.0429 | 42.989 | 0.0977 | 0.0314 | −0.0384 | −0.0069 | 0.8179 | |
| 85 | 0.0428 | 42.859 | 0.0973 | 0.0312 | −0.0382 | −0.0069 | 0.8179 | |
| CP/C12–B6N6 (S3) | 46 | 0.0321 | 32.164 | 0.0886 | 0.0241 | −0.0260 | −0.0019 | 0.9249 |
| 50 | 0.0818 | 81.844 | −0.0600 | 0.0342 | −0.0835 | −0.0492 | 0.4102 | |
| CP/C12–Al6N6 (S2) | 54 | 0.0433 | 43.361 | 0.0702 | 0.0270 | −0.0365 | −0.0095 | 0.7401 |
| 72 | 0.0244 | 24.467 | 0.0555 | 0.0151 | −0.0164 | −0.0012 | 0.9213 | |
| 88 | 0.0441 | 44.173 | 0.0989 | 0.0323 | −0.0399 | −0.0075 | 0.8097 | |
| CP/B6N6–Al6N6 (S2) | 65 | 0.0453 | 45.305 | 0.1301 | 0.0382 | −0.0439 | −0.0056 | 0.8704 |
| 77 | 0.0487 | 48.729 | 0.1054 | 0.0362 | −0.0461 | −0.0098 | 0.7858 | |
| 82 | 0.3229 | 322.97 | −1.3588 | 0.2100 | −0.7598 | −0.5497 | 0.2764 |
4. Conclusions
To predict a suitable CP drug nanocarrier, we first studied the adsorption behaviour of the CP drug towards C24, B12N12, Al12N12, C12–B6N6, C12–Al6N6, B6N6–Al6N6 nanocages and adsorption calculations of CP over B12N12, Al12N12 and B6N6–Al6N6 revealed preferable adsorption energies for drug delivery purposes both in gas and water phases. To gain a better insight into the sensitivity and reactivity of the nanocages, FMO analysis was performed, which revealed that EL was shifted to downward values while the EH was shifted to upward values after the adsorption of CP on the B12N12, Al12N12, and B6N6–Al6N6 nanocages. In gas and water phases, the energy gap tremendously decreased by about 43.56% and 37.77% for B12N12 and 20% and 45.67% for the B6N6–Al6N6 nanocage, respectively, which is not so appreciable (4.80% and 1.36% respectively) in case of Al12N12 after the adsorption of CP. The Hirshfeld charge analysis revealed that the charge transfer between CP and Al12N12 is not quite good enough (0.122e and 0.239e in the gas and water phases, respectively) whereas a significant amount of charge transfer was observed in the case of B12N12 (0.254e and 0.355e in gas and water phases, correspondingly) and B6N6–Al6N6 (0.312e in the gas phase and 0.839e in the water phase). The global descriptors also project that B12N12 nanocages exhibit high sensitivity and reactivity since the decrement of the global hardness and increment of global softness and the electrophilicity index of B12N12 is more preferable than that of Al12N12 after adsorption. We investigated the variations of quantum molecular descriptors of the heteronanocages as well as observed the propensity of the downfall of global hardness and rise of global softness and electrophilicity index in the case of B6N6–Al6N6. Dipole moment, work function, and COSMO surface analysis are also in favour of B6N6–Al6N6 being a potent candidate in CP drug delivery. Therefore, adsorption energy, electronic properties, Hirshfeld analysis, and quantum molecular descriptors indicate that B12N12 and B6N6–Al6N6 are promising candidates for targeted delivery of CP.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.References
- R. a Alderden, M. D. Hall and T. W. Hambley, J. Chem. Educ., 2006, 83, 728–734 CrossRef CAS.
- J. Topps and R. C. Elliott, Nature, 1965, 205, 498–499 CrossRef.
- B. Rosenberg, E. Renshaw, L. Vancamp, J. Hartwick and J. Drobnik, J. Bacteriol., 1967, 93, 716–721 CrossRef CAS PubMed.
- R. S. Go and A. A. Adjei, J. Clin. Oncol., 1999, 17, 409–422 CrossRef CAS PubMed.
- M. Perveen, S. Nazir, A. W. Arshad, M. I. Khan, M. Shamim, K. Ayub, M. A. Khan and J. Iqbal, Biophys. Chem., 2020, 267, 106461 CrossRef CAS PubMed.
- F. ud Din, W. A. Aman, I. Ullah, O. S. Qureshi, O. Mustapha, S. Shafique and A. Zeb, Int. J. Nanomed., 2017, 12, 7291–7309 CrossRef CAS PubMed.
- J. H. Moon, J. W. Moxley, P. Zhang and H. Cui, Future Med. Chem., 2015, 7, 1503–1510 CrossRef CAS PubMed.
- L. Qi, Q. Luo, Y. Zhang, F. Jia, Y. Zhao and F. Wang, Chem. Res. Toxicol., 2019, 32, 1469–1486 Search PubMed.
- N. Pontillo, F. Pane, L. Messori, A. Amoresano and A. Merlino, Chem. Commun., 2016, 52, 4136–4139 RSC.
- A. A. Piya, S. U. D. Shamim, M. N. Uddin, K. N. Munny, A. Alam, M. K. Hossain and F. Ahmed, Comput. Theor. Chem., 2021, 1200, 113241 CrossRef CAS.
- N. Wazzan, K. A. Soliman and W. S. A. Halim, J. Mol. Model., 2019, 25, 1–19 CrossRef CAS PubMed.
- Q. Luo and W. Gu, Mol. Phys., 2020, 118, 1–7 CrossRef.
- T. C. Johnstone, K. Suntharalingam and S. J. Lippard, Chem. Rev., 2016, 116, 3436–3486 CrossRef CAS PubMed.
- R. Singh and J. W. Lillard, Exp. Mol. Pathol., 2009, 86, 215–223 CrossRef CAS PubMed.
- A. N. Al-Kenani, Open J. Discrete Math., 2012, 02, 1–4 CrossRef.
- B. T. Tomić, C. S. Abraham, S. Pelemiš, S. J. Armaković and S. Armaković, Phys. Chem. Chem. Phys., 2019, 21, 23329–23337 RSC.
- A. Hosseinian, E. Vessally, S. Yahyaei, L. Edjlali and A. Bekhradnia, J. Cluster Sci., 2017, 28, 2681–2692 CrossRef CAS.
- P. R. C. Kent, M. D. Towler, R. J. Needs and G. Rajagopal, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15394–15397 CrossRef CAS.
- M. B. Javan, A. Soltani, Z. Azmoodeh, N. Abdolahi and N. Gholami, RSC Adv., 2016, 6, 104513–104521 RSC.
- A. Soltani, A. Sousaraei, M. Bezi Javan, M. Eskandari and H. Balakheyli, New J. Chem., 2016, 40, 7018–7026 RSC.
- F. Azarakhshi, S. Shahab, S. Kaviani and M. Sheikhi, Lett. Org. Chem., 2020, 18, 640–655 CrossRef.
- R. Padash, M. R. Esfahani and A. S. Rad, J. Biomol. Struct. Dyn., 2020, 1–11 Search PubMed.
- A. Hosseinian, A. Bekhradnia, E. Vessally, L. Edjlali and M. D. Esrafili, Comput. Theor. Chem., 2017, 1115, 114–118 CrossRef CAS.
- M. K. Hazrati, Z. Bagheri and A. Bodaghi, Phys. E, 2017, 89, 72–76 CrossRef CAS.
- X. F. Fan, Z. Zhu, Z. X. Shen and J. L. Kuo, J. Phys. Chem. C, 2008, 112, 15691–15696 CrossRef CAS.
- İ. Muz, F. Göktaş and M. Kurban, Phys. E, 2022, 135, 114950 CrossRef.
- D. Paul, J. Deb, B. Bhattacharya and U. Sarkar, J. Mol. Model., 2018, 24, 1–13 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B, 1993, 48, 4978 CrossRef CAS PubMed.
- N. A. Benedek, I. K. Snook, K. Latham and I. Yarovsky, J. Chem. Phys., 2005, 122, 144102 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef.
- Y. Inada and H. Orita, J. Comput. Chem., 2007, 29, 225–232 CrossRef PubMed.
- X. Chen, J. Jiang, Q. Liang, R. Meng, C. Tan, Q. Yang and X. Sun, J. Mater. Chem. C, 2016, 4, 7004–7012 RSC.
- S. U. Daula Shamim, M. K. Hossain, S. M. Hasan, A. Hossain and F. Ahmed, Mol. Simul., 2020, 46, 1135–1145 CrossRef CAS.
- A. S. Rad, S. S. Shabestari, S. A. Jafari, M. R. Zardoost and A. Mirabi, Mol. Phys., 2016, 114, 1756–1762 CrossRef CAS.
- P. K. Chattaraj and R. G. Parr, in Chemical Hardness, 2006, pp. 11–25 Search PubMed.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- S. N. Ema, M. A. Khaleque, A. Ghosh, A. A. Piya, U. Habiba and S. U. D. Shamim, RSC Adv., 2021, 11, 36866–36883 RSC.
- T. Ahmed, M. Aminur Rahman, R. Islam, A. Akter Piya and S. Ud Daula Shamim, Comput. Theor. Chem., 2022, 1214, 113797 CrossRef CAS.
- S. U. D. Shamim, M. H. Miah, M. R. Hossain, M. M. Hasan, M. K. Hossain, M. A. Hossain and F. Ahmed, Phys. E, 2022, 136, 115027 CrossRef CAS.
- Y. F. Chang, J. P. Zhang, H. Sun, B. Hong, Z. An and R. S. Wang, Int. J. Quantum Chem., 2005, 105, 142–147 CrossRef CAS.
- K. A. Soliman and S. A. Aal, Diamond Relat. Mater., 2021, 117, 108458 CrossRef CAS PubMed.
- N. Kosar, H. Tahir, K. Ayub and T. Mahmood, J. Mol. Graphics Modell., 2021, 105, 107867 CrossRef CAS PubMed.
- T. Oku, A. Nishiwaki and I. Narita, in Science and Technology of Advanced Materials, 2004, vol. 5, pp. 635–638 Search PubMed.
- M. Rakib Hossain, M. Mehade Hasan, S. Ud Daula Shamim, T. Ferdous, M. Abul Hossain and F. Ahmed, Comput. Theor. Chem., 2021, 1197, 113156 CrossRef CAS.
- G. Xiuying, G. Fengsheng, T. Yamaguchi, H. Kan and M. Kumagawa, Cryst. Res. Technol., 1992, 27, 1087–1096 CrossRef.
- I. Georgieva, N. Trendafilova, N. Dodoff and D. Kovacheva, Spectrochim. Acta, Part A, 2017, 176, 58–66 CrossRef CAS PubMed.
- A. Shokuhi Rad, S. Alijantabar Aghouzi, N. Motaghedi, S. Maleki and M. Peyravi, Mol. Simul., 2016, 42, 1519–1527 CrossRef CAS.
- J. Mawwa, S. U. D. Shamim, S. Khanom, M. K. Hossain and F. Ahmed, RSC Adv., 2021, 11, 32810–32823 RSC.
- A. Soltani, E. Tazikeh-Lemeski and M. B. Javan, J. Mol. Liq., 2020, 297, 111894 CrossRef CAS.
- H. Zhu, C. Zhao, Q. Cai, X. Fu and F. R. Sheykhahmad, Inorg. Chem. Commun., 2020, 114, 107808 CrossRef CAS.
- S. Onsori and E. Alipour, J. Mol. Graphics Modell., 2018, 79, 223–229 CrossRef CAS PubMed.
- X. F. Fan, Z. Zhu, Z. X. Shen and J. L. Kuo, J. Phys. Chem. C, 2008, 112, 15691–15696 CrossRef CAS.
- D. Paul, J. Deb, B. Bhattacharya and U. Sarkar, J. Mol. Model., 2018, 24, 1–13 CrossRef CAS PubMed.
- M. R. Hossain, M. M. Hasan, N. E. Ashrafi, H. Rahman, M. S. Rahman, F. Ahmed, T. Ferdous and M. A. Hossain, Phys. E, 2021, 126, 114483 CrossRef CAS.
- S. U. D. Shamim, T. Hussain, M. R. Hossian, M. K. Hossain, F. Ahmed, T. Ferdous and M. A. Hossain, J. Mol. Model., 2020, 26, 1–17 CrossRef PubMed.
- M. Shahabi and H. Raissi, J. Biomol. Struct. Dyn., 2018, 36, 2517–2529 CrossRef CAS PubMed.
- S. U. D. Shamim, D. Roy, S. Alam, A. A. Piya, M. S. Rahman, M. K. Hossain and F. Ahmed, Appl. Surf. Sci., 2022, 596, 153603 CrossRef CAS.
- M. G. Campbell and M. Dincă, Sensors, 2017, 17, 1–11 CrossRef PubMed.
- F. Li, X. Gao, R. Wang, T. Zhang and G. Lu, Sens. Actuators, B, 2017, 248, 812–819 CrossRef CAS.
- S. D. O. Richardson, Phys. Rev., 1924, 23, 153 CrossRef.
- R. F. Matta and C. F. Bader, Proteins: Struct., Funct., Bioinf., 2002, 48, 519–538 CrossRef PubMed.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04011e |
| This journal is © The Royal Society of Chemistry 2022 |