Molecular dynamics simulation insights into the cellular uptake of elastic nanoparticles through human pulmonary surfactant

Abstract

The interaction between inhaled nanoparticles (NPs) and the pulmonary surfactant (PS) monolayer has drawn significant attention due to its potential in drug delivery design and application for respiratory therapeutics in active and passive cellular uptake pathways. Even though much attention has been given to explore the interaction between NPs and the PS monolayer, the effects of the NP elasticity on the translocation across the PS monolayer have not been thoroughly studied. Here, we performed a series of coarse-grained (CG) molecular dynamics simulations to study active or passive cellular uptake pathways of three NPs with different elasticities through a PS monolayer. The differences between active and passive pathways underly the enhanced targeting ability by ligand–receptor interaction (L–R interaction). In the active or passive cellular uptake pathways, it is found that the increase in stiffness level leads to a higher penetrability of NPs at the same time range. The soft NP has always been withheld inside the PS monolayer due to the lowest level of elasticity, while the other two types of NPs penetrate through the PS monolayer as the simulation progresses toward the end. The NPs in the active cellular uptake pathways take a longer time to penetrate the PS monolayer, resulting in a longer average penetration distance of approximately 40.55% and a higher average number of contacts, approximately 36.11%, than passive cellular uptake pathways, due to the L–R interaction. Moreover, it demonstrates that NPs in active cellular uptake pathways have a significantly higher targeting ability with the PS monolayer. We conclude that the level of NP elasticities has a substantial link to the penetrability in active or passive cellular uptake pathways. These results provide valuable insights into drug delivery and nanoprobe design for inhaled NPs within the lungs.

---

Introduction

Lung diseases such as lungs cancer, asthma, tuberculosis, chronic obstructive pulmonary disease (COPD), and acute lower respiratory tract infections are the five well-known diseases that cause extreme illness and death worldwide.¹ Conventional treatment of these diseases relies on antibiotics, and anti-oxidant and anti-inflammatory drugs via oral and intravenous routes.^2,3 The oral route could be inefficient due to the unpredictable absorption in the gastrointestinal tract, and it is unsuitable for an emergency as rapid and precise administration of the drug is required. Moreover, disadvantages of the intravenous route include the possibility of infection and pain to patients from the injection and other side effects such as blood vessel inflammation, blood clots, and air embolism.^4,5 In order to overcome these disadvantages, inhalation therapy with higher treatment efficiency has been developed.⁶ It provides favourable properties such as precise localization of a drug to the lung, and a lower dose of drugs required than systemic drug delivery (oral and intravenous). So far, inhalation therapy devices including nebulizer, pressurized metered-dose inhaler, and dry powder inhaler have been developed and administered in an inhalation route of treatment at present.^7,8 However, these devices have not been designed with the consideration of biological barriers of lungs diseases such as specific-site, airway mucus, and interaction with the targeted cells.^9,10

Nanomedicine has been employed since nanoparticles (NPs) can provide new diagnosis and treatment tools in biomedical applications such as bioimaging, drug delivery, biosensors, theranostic medicine, etc.^11–21 For instance, there have been a large number of NP-based respiratory therapeutic studies.^22–27 Furthermore, NPs as drug nanocarriers with fascinating features such as improved biodistribution, controlled release, and site-specific targeting have shown a capability to overcome lung's biological barriers.^28,29 Hence, using NPs for inhalation therapy sheds light on improving the treatment capabilities and efficiencies for respiratory system diseases. Therefore, a number of types of NPs have been used for inhalation therapy of lungs diseases, such as liposome NPs,³⁰ polymer NPs,³¹ solid-lipid nanoparticles (SLNs),³² dendrimer NPs³³ and inorganic NPs.³⁴ Still, after inhalation, the NPs may interact with a group of cellular and biological barriers at all levels of lung structures, resulting in elongated lung retention, which is purposed to achieve specific-site localization, reduce the dosage frequency, and avoid undesired side effects. On the other hand, the longer lung retention might cause a potential pulmonary nanotoxicity.³⁵ Thus, in order to enhance the applications of NPs in NP-based therapy for respiratory diseases, NP's penetrability and the potential side effects need to be balanced and further studied. For the efficient design of NPs, their characteristics such as size, shape, charge, elasticity and wettability have been extensively investigated for optimizing treatment efficiencies.³⁶ Among these characteristics, elasticity has drawn great attention for its role in NP drug delivery,^37,38 cell translocation,^39,40 and membrane wrapping efficiency.⁴¹ While the benefits of elasticity adjustment are widely investigated in NP–cell interaction, similar studies on the role of elastic NPs penetration on the pulmonary surfactant (PS) monolayer systems are severely lacking and long-overlooked as only a few studies focus on NP permeation processes within PS system without a consideration on the effects of the elasticity variation.^42–46 Therefore, it is of great importance to unveil the underlying mechanisms of the effects of inhaled NPs elasticity on the interaction between NPs and PS monolayer.

As the NPs elasticity variation could significantly affect the therapeutic efficiency of NPs-based drug delivery treatment,⁴⁷ it is important to investigate how NPs elasticity affects the cellular uptake process within the PS monolayer in both NP-based active and passive pathways of drug delivery.⁴⁸ Typically, the active cellular uptake is prone to increase the number of designated nanocarriers to the location of the targeted cell and therapeutic sites to avoid unrelated normal tissues by using genes delivery, drugs, ligands–receptor binding, and theranostic technique,⁴⁹ while the passive cellular uptake is based on nanocarriers characteristics (total circulation runtime, size, shapes) and the tissue biology (the enhanced permeability and retention effects).^50,51 Many previous attempts have been introduced to mimic soft NPs in different formats such as polymeric NPs,⁵² lipid-coated NPs,⁵³ core–shell NPs with lipid shell compose of adjustable volume of water,⁵⁴ or varying NPs rigidity with different constraints,⁵⁵ size, and shapes.^41,56–59 Despite these studies, it can be seen that most of the studies were focused on creating soft NPs by scoping on a lipid-like strategy since softer NPs show a great potential in drug delivery due to higher solubility, higher drug release, and lower toxicity.^60,61 The method of modulating the elasticity by varying the whole NPs spring constant has not yet been thoroughly studied. For example, Zhang et al. conducted a soft NP using a double layer lipid coating method compared to a rigid NP. They found that rigid NPs can achieve a complete internalization, while soft NPs only reach 40% surface coverage by membrane lipids.⁵³ Shen et al. created soft NPs under the rigidity bending scheme inspired by modelling red blood cells as a single NP matrix and defining a number of ligand beads throughout the whole NP matrix. They showed that soft NPs have a lower efficiency than stiff NPs during the membrane wrapping process.⁵⁸ Sun et al. have synthesized soft NP by varying the water content and rigidity of the core–shell poly(lactic-co-glycolic acid) (PLGA)–lipid NP. The particle rigidity can be adjusted by changing the volume of the interfacial water between the PLGA core and the lipid shell. Their simulations revealed that the soft NP is deformed and inappropriate for cellular uptake.⁵⁴ Wang et al. modelled soft NP based on a hydrophobic and hydrophilic core–shell structure by varying their bending constant and shear stress, which leads to the deformation of the NP at the penetration process. They found that stiffness increment of hydrophilic NPs increases the permeation capabilities, while the effects of the translocation of hydrophobic NPs decreased by the stiffness increment effects.⁵⁵ These findings imply that the elasticity of the NPs highly affects the penetration process of NPs.

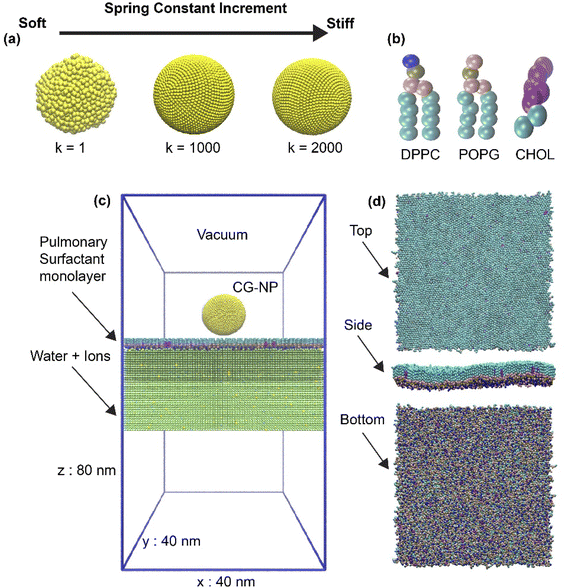
In this work, we used coarse-grained (CG) molecular dynamics simulations to investigate the effects of the elasticity of NPs on the translocation across the PS monolayer at the air–water interface in active or passive cellular uptake pathways. The NP elasticity is tuned by using different spring constant (k) values among NP's building block beads. The three different elasticities are achieved by tuning value from 1 to 1000 and 2000 kJ mol⁻¹ nm⁻², corresponding to the soft, intermediate and stiff NP (Fig. 1a). Active cellular uptake was simulated by introducing a ligand–receptor interaction (L–R interaction).⁶² In contrast, the default parameters provided passive cellular uptake settings (non-L–R interaction). We compared the three different elastic NPs permeability across the PS monolayer at the air–water interface. Further simulations discovered that a higher level of stiffness leads to a better penetrability of NPs in both active and passive cellular uptake processes. Our computational results provide useful insights into the design of respiratory drug nanocarrier.

Fig. 1 The initial configuration the of simulation system. (a) Illustration of CG-NP elasticity adjustment by the variation of spring constant (k) has been shown. The increment trend of spring constant (k) in kJ mol⁻¹ nm⁻² leads to higher stiffness of CG-NP. The diameter of all three CG-NPs is 11.8 nm. (b) Coarse-grained surfactant lipids (DPPC, POPG, and CHOL) with the framework of MARTINI forcefield. (c) Detailed of the simulation box with information provided. The water molecules are shown in light green, sodium cations in yellow, while chloride anions in light cyan. (d) Top, side and bottom views of pulmonary surfactant monolayer.

Modelling and methods

Molecular dynamic simulations

In this study, we used the MARTINI CG model (version 2.2)⁶³ and the GROMACS simulation package (version 5.1)⁶⁴ for all CG simulations. In the MARTINI model, a group of atoms are converted to one CG bead based on a general four-to-one mapping rule. These beads are categorized into four classes, namely, polar (P), apolar (C), nonpolar (N), and charged (Q), each type of beads can be further divided into 4 or 5 different levels based on the hydrogen-bonding capabilities (0: none, a: acceptor, d: donor, da: both) or the degree of polarity number (from 1 to 5, low to high polarity) are used to categorized subtypes of each particle types, which result in a total of 20 subtypes. All CG simulation system in this work were run with a constant pressure and temperature, and periodic boundary conditions were used in all three dimensions. NPs, lipids, and water plus ions were coupled separately by V-rescale heat baths⁶⁵ at T = 310 K with τ = 1 ps. The systems were simulated at 1 bar pressure using a semi-isotropic Berendsen pressure coupling scheme⁶⁶ with a coupling constant of τ = 5 ps and compressibility of 3 × 10⁻⁴ bar⁻¹. The coulombic potential with a cutoff of 1.2 nm was used for the calculation of electrostatic interactions, which was smoothly shifted to zero within the range of 0 to 1.2 nm. The relative dielectric constant of the force field was 15 for explicit screening, which was the default value of the forcefield.⁶³ The Lennard-Jones potential was smoothly shifted between 0.9 and 1.2 nm for van der Waals interactions, which a cutoff of 1.2 nm to reduce the cutoff noise. Each simulation was run for 0.15 μs with a step of 10 fs.

Modelling of nanoparticles

In this work, spherical NPs have been constructed using in-house code based on MARTINI CG beads with a packing constant of 0.5 nm. The core diameter is about 11.8 nm and consists of 7890 CG beads. NP forcefield parameters followed the work of Lin et al.,^67,68 where Nda type CG beads were used for hydrophilic NPs as it has shown the capabilities of translocating and overcoming the energy barrier of a PS monolayer⁶⁹ (Nda is a bead type in the MARTINI forcefield). To investigate the level of NP's elasticity affecting cellular uptake process, a spring constant (k) of NP has been adjusted to achieve the elasticity modification throughout the whole NP (Fig. 1a). The level of modification of k is set as 1, 1000 and 2000 kJ mol⁻¹ nm⁻², corresponding to the soft, intermediate and stiff NP.

Simplified pulmonary surfactant monolayer model

A pulmonary surfactant monolayer system, which has been validated in many types of researches,^42,46,70,71 was used to investigate the interactions with the inhaled NPs. The air space was represented by vacuum. In our simplified pulmonary surfactant monolayer system, we chose a well-known three components consisting of saturated dipalmitoyl phosphatidyl-choline (DPPC), unsaturated palmitoyl oleoyl phosphatidyl-glycerol (POPG), and cholesterol (CHOL) molecules (Fig. 1b) in a molar ratio of 62 : 32 : 6 (ref.72 and 73) and they were built using the INSANE script.⁷⁴ Thus, the whole simulation system consists of 1 NP, 1550 DPPC, 800 POPG, 150 CHOL, 226 400 water molecules represented with P4 MARTINI bead, and 0.15 M NaCl (Qd and Qa MARTINI beads for sodium cations and chloride anions, respectively). The initial box size is 40 nm × 40 nm × 80 nm, as shown in Fig. 1c and d. NP was placed in a vacuum 10 nm above the center of the simulation system and the simulation was kept for 150 ns at body temperature (310 K). In addition, the variation of the lipid or pulmonary surfactant monolayer composition may affect the simulation results in terms of translocation time (see the ESI†), and such effects will be further examined in the future since we concentrate on the NP's elasticity changes in this work.

Ligand–receptor interactions

For the investigation of the binding potential between the NPs and the pulmonary surfactant monolayer, the L–R interactions have been utilized, and the default CG MARTINI forcefield (version 2.2) has been adjusted by initiating two new CG beads, namely, L: ligand and R: receptor. The Lennard-Jones interaction parameter (ε = 8 kJ mol⁻¹, σ = 0.47 nm) between L and R CG beads can mimic the stronger attractive L–R interaction.⁶² Meanwhile, the interactions of L/R beads with other beads are the same as the lipid head-group (Nda). When the L–R interactions are introduced, the simulation systems are used for studying the active uptake pathway. Otherwise, the system without L–R interactions means the passive cellular uptake.

Analysis of trajectories

Number of contacts. For our pulmonary surfactant monolayer, to compare the effects of elasticity modification throughout the whole NP in active/passive cellular uptake, the number of contacts between NP and pulmonary surfactant monolayer was calculated by using the GROMACS tool (gmx mindist) with a cutoff value of 0.6 nm.

Area per lipid. Visualization and analysis of elasticity modification effects in active/passive cellular uptake of NP across pulmonary surfactant monolayer were done by APL@Voro software.⁷⁵ APL@Voro is capable of creating a two-dimensional geometric representation of the lipid membrane by using a Voronoi tessellation analysis. The lipid inside the pulmonary surfactant monolayer is divided into polygon parts, which each polygonal part indicating the area of a single lipid type. Area per lipid is calculated based on the uses of polygon individual layers combination, in which every single layer stored information of every atom.

Results and discussion

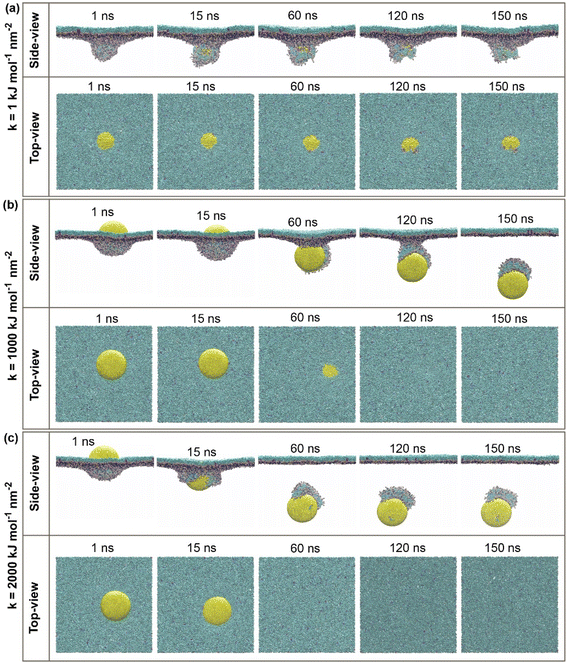
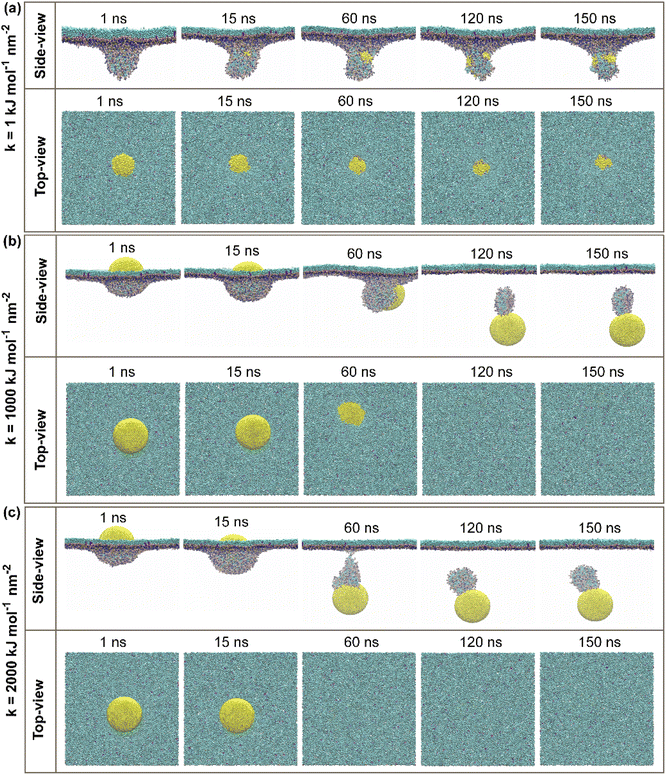
CG molecular dynamic simulations were conducted to investigate the underlying mechanisms of hydrophilic NPs with a different range of elasticities through the PS monolayer. Simulations were performed in both active and passive cellular uptake settings. Due to our simulation settings, the hydrophilic NPs have been steered downwards across the PS monolayer on the minus Z-axis. As a result, it is found that there is a crucial relationship between the variation of elasticities and the penetrability of NPs across the PS monolayer. In addition, the additional independent simulation repeats were performed for each of the simulation systems to ensure the penetrability of the elastic NPs and the correctness of the permeations, and it is shown in Fig. S3 and S4.†

In our work, hydrophilic NP's elasticity has been adjusted by tuning the NPs spring constant (k) in a unit of kJ mol⁻¹ nm⁻², and three spherical NPs with spring constant (k) values of 1, 1000 and 2000 kJ mol⁻¹ nm⁻² were studied. We name these three NPs as the “soft, intermediate and stiff” NP (see Fig. 1a). Simulation snapshots of three NPs during the active or passive cellular uptake process were shown in Fig. 2 and 3. In addition, we have extended the simulation runtime to 1 μs. As a result, we did not see much difference in the NP's penetrability, which supports that 150 ns is a suitable and reliable parameter for studying the effects of NP's elasticity adjustment in this research. The previous studies have shown that the elasticity of NPs can cause a substantial effect on the translocation ability of cellular uptake.^53,54,58 It is noteworthy to focus on both active and passive cellular uptake as these two processes are linked to therapeutic efficiency.⁷⁶

Fig. 2 Side and top views of simulation systems for active cellular uptake of a 11.8 nm-in-diameter CG-NP (yellow). (a) The soft CG-NP with spring constant (k) equal 1 kJ mol⁻¹ nm⁻², (b) intermediate CG-NP with spring constant (k) equal 1000 kJ mol⁻¹ nm⁻², and (c) stiff CG-NP with spring constant (k) equal 2000 kJ mol⁻¹ nm⁻². Water and ions have been removed for greater visualization.

Fig. 3 Side and top views of simulation systems for passive cellular uptake of a 11.8 nm-in-diameter CG-NP (yellow). (a) The soft CG-NP with spring constant (k) equal 1 kJ mol⁻¹ nm⁻², (b) intermediate CG-NP with spring constant (k) equal 1000 kJ mol⁻¹ nm⁻², and (c) stiff CG-NP with spring constant (k) equal 2000 kJ mol⁻¹ nm⁻². Water and ions have been removed for greater visualization.

For the active cellular uptake, a soft NP has penetrated the PS monolayer at the initial 1–15 ns of the simulation, as shown in the side-view snapshots (Fig. 2a); on the other hand, the top-view snapshots confirm the incomplete wrapping of the soft NP by the PS monolayer, as the top part of the soft NP is still visualizable. The simulations also show that the soft NP has been withheld inside the PS monolayer during the full period of simulations from 1 to 150 ns. In contrast, the intermediate NP has started to penetrate through the PS monolayer at the runtime of 60 ns (Fig. 2b). At the runtime of 120 ns, the whole intermediate NP is almost translocating through the PS monolayer as being supported by the side-view snapshots and only a small quantity of the top part is visualized in the top view. Then, the side-view and top-view snapshots with the runtime of 150 ns confirm that the intermediate NP has entirely permeated through the PS monolayer. Next, the stiff NP has partially translocated through the PS monolayer at the runtime of 15 ns, as indicated in the side-view snapshots (Fig. 2c). Later on, as the simulation has progressed to 60 ns, the stiff NP has achieved a complete translocation together with an attachment of a small part of the PS monolayer as being supported by the side-view and top-view snapshots of the simulation runtime at 60, 120 and 150 ns, respectively.

For the passive cellular uptake (Fig. 3), the series of interactions between NP and PS monolayer simulation results are considerably similar in terms of penetration speed. The only significant difference from the active cellular uptake pathway is at 120 ns of the simulation runtime of the intermediate NP (Fig. 3b). The side-view snapshots pinpoints that the intermediate NP has successfully penetrated across the PS monolayer with a large distance away from the PS monolayer. Overall, the simulation results of active/passive cellular uptake signify three preeminent findings. Firstly, the soft NP has penetrated and been withheld inside the PS monolayer. Secondly, the stiff NP shows the fastest penetrability for both active and passive cellular uptakes, followed by the intermediate NP. Finally, the significant difference between active and passive uptakes is that the former shows a better wrapping by the PS monolayer than the latter. At the end of the simulations, it can be clearly seen that the level of elasticity adjustment has resulted in differences in penetration capabilities and speed within the same time range. The larger spring constant (k) corresponds to stronger stiffness of NP. The spring constant (k) and the penetration speed have been shown to have a directly proportional relationship, as the stiff NPs has the fastest penetration rate.

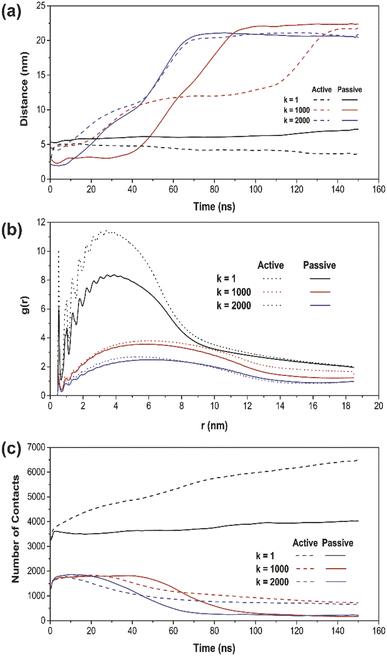
To further verify the penetration ranges of NPs with different elasticities by tuning the k values, the distance plot analysis was performed. The distance plots refer to the measurement of the center-of-mass (COM) distances between the NP and the PS monolayer, as shown in Fig. 4a. The penetration ranges measurement boundary is within the PS monolayer with a size of 40 nm × 40 nm × 20 nm, fixed at the center of the simulation system box. The distance plot has proved the penetrated location with respect to the simulation runtime. The increasing interval of the graph, specifically for k = 1000 and 2000 kJ mol⁻¹ nm⁻² (red and blue line) confirms the translocated location according to the simulation results. On the other hand, for k = 1 kJ mol⁻¹ nm⁻² (black line), there is no increasing interval due to the fact that the soft NP has been withheld and does not pass through the PS monolayer.

Fig. 4 (a) The time evolution of distance between COM of CG-NPs and COM of pulmonary surfactant monolayer with active/passive cellular uptake. (b) The radial distribution function (RDF) of active cellular uptake (dot) and passive cellular uptake (solid line) between COM of CG-NP beads and COM of pulmonary surfactant monolayer for 150 ns. (c) Number of contacts of all three types of CG-NP in all simulations between CG-NP and pulmonary surfactant monolayer.

Moreover, the radial distribution function (RDF) analysis was conducted in order to take the attractive interaction of the three elastic NPs further examined. The RDF of the PS monolayer and three types of NPs are illustrated in Fig. 4b. The RDF plot describes how density varies as a function of a distance from a reference particle; that is, in essence, alternative ways of determining the level of adsorbed interaction between NP and the PS monolayer. For all simulations with a runtime of 150 ns, the higher amplitude of plots indicates a more vital adsorbed interaction. The spring constant (k) and the amplitude of g(r) have been shown to establish an inversely proportional relationship. The soft NP has the highest adsorbed interaction, followed by the intermediate and stiff NP. For every NPs of the same type, all the RDF in active cellular uptake is higher than that in passive cellular uptake.

Also, we have investigated the number of contacts between the whole NP and the PS monolayer to support the targeting ability of NPs quantitatively. The number of contacts plot of all three types of NPs and the PS monolayer is shown in Fig. 4c as a function of time. The most apparent differences occur in a simulation system with k = 1 kJ mol⁻¹ nm⁻² (black line). Active cellular uptake has a considerably higher number of contacts compared to passive cellular uptake. In the other two cases, with k = 1000 and 2000 kJ mol⁻¹ nm⁻² (red and blue line), the number of contacts is within the same range at the starting point of the simulations. However, as the simulation has progressed close to the end, the active cellular uptake showed a slightly higher number of contacts for both cases. This shows the consistency with the system snapshots (Fig. 2 and 3), where NP crossed the PS lipid monolayer and a few lipids were dragged out.

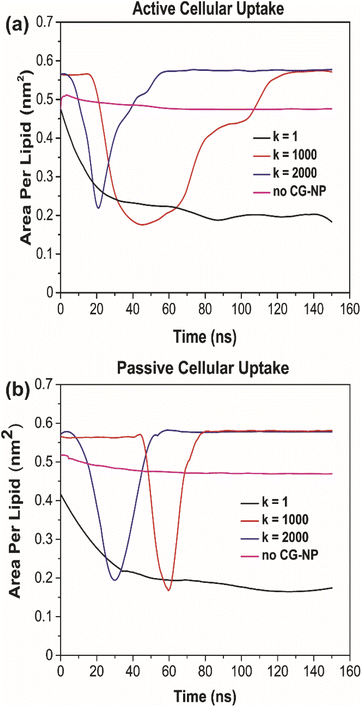
To further probe into the influence of different NPs elasticities on the structure of the PS monolayer, the area per lipid (APL in nm²) have been studied. APL is one of the most important analysis parameters needed to ensure the accurate structure of a lipid membrane and the validity of molecular dynamic simulations.⁷⁷ For the APL plot (Fig. 5a and b), non-NPs pink line represents the control system with an average APL, approximately 0.48 nm², whereas the other three plots k = 1, 1000 and 2000 kJ mol⁻¹ nm⁻² represents each individual type of NPs. All plots have a major difference to the non-NPs plot, due to the penetration of NPs. For k = 1 kJ mol⁻¹ nm⁻² (black line) in active/passive cellular uptake, the average APL decreases substantially, as shown in Fig. 6, and the value does not rise to the starting point level due to the fact that the NPs have been kept within the PS monolayer for the whole simulation runtime. In contrast to k = 1 kJ mol⁻¹ nm⁻², for k = 1000 and 2000 kJ mol⁻¹ nm⁻², it is evident that there is an inflection point that pinpoints the time that NPs present inside the PS monolayer. As NPs pass through the PS monolayer, the APL value increase to the starting point level. The APL Voronoi diagram of NPs permeating through the PS monolayer for all systems are shown in Fig. S5 and S6.†

Fig. 5 Area per lipid of (a) active and (b) passive cellular uptake simulation systems.

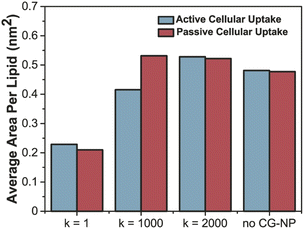Fig. 6 Average area per lipid (nm²) of active (sapphire)–passive (red) cellular uptake of all variation of CG-NP in all simulation systems.

The increment trend of spring constant (k) value has caused a significant difference in all four analysis parameters, for active/passive cellular uptake, as shown in Table 1. The spring constant (k) have a directly proportional relationship with average distance and average APL. On the other hand, the average number of contacts and radial distribution plots are inversely proportional to the spring constant (k) value. Our data analysis indicated that in both active and passive cellular uptake cases, the permeation abilities of the NPs had a substantial link to the spring constant (k) value. The penetrability of NPs deteriorated with decreasing spring constant (k) value. The soft NPs were observed to be withheld within the PS monolayer throughout the whole simulation runtime, while the intermediate and the stiff NPs translocated through the PS monolayer at a respectable time. All NPs translocation with reduction trend of k values has significantly decreased the average distance and average APL. The RDF plots demonstrated that the NPs with lower spring constant (k) values have a more vital adsorbed interaction. The average number of contacts confirmed that active cellular uptake settings intensify the cellular wrapping process with a higher number of contacts than passive cellular uptake settings. Therefore, we concluded that tuning the NPs elasticity impacts their permeability through the PS monolayer.

Table 1 Comparison of spring constant increment effects in active/passive cellular uptake

Analysis parameters	Active cellular uptake			Passive cellular uptake
	k = 1	k = 1000	k = 2000	k = 1	k = 1000	k = 2000
Avg. distance (nm)	4.353	12.421	16.216	6.206	8.284	18.239
Avg. number of contacts	5460.453	1190.453	962.560	3762.600	938.103	706.180
Avg. area per lipid (nm^2)	0.228	0.415	0.528	0.210	0.522	0.531
Adsorbed interaction (RDF)	Strongest	Intermediate	Weakest	Strongest	Intermediate	Weakest

---

Conclusion

In summary, we explored the active and passive cellular uptakes of the soft, intermediate, and stiff NPs in the PS monolayer using coarse-grained molecular dynamic simulations. Active cellular uptake simulations were conducted by introducing the ligand–receptor interaction, while passive cellular uptakes were done by using provided default coarse-grained molecular dynamic simulation parameters. Three NPs with different spring constant (k) equal 1, 1000 and 2000 kJ mol⁻¹ nm⁻² were considered in our simulations. As a result of spring constant adjustment, representing three hydrophilic NP types with different elasticities, the simulations showed that the soft NP was the only type that could not pass through the PS monolayer, while the other two types could pass through as the simulation had advanced to the end. In addition, increasing the spring constant (k) value in active/passive cellular uptake settings had a directly proportional relationship, with the average distance and average APL, which leads these two analysis parameters achieved an average higher value of approximately 233.20% and 142.22%, respectively. In contrast, increasing the spring constant (k) from 1 kJ mol⁻¹ nm⁻² to 2000 kJ mol⁻¹ nm⁻² not only lowered the average number of contacts by 81.80% but also decreased the radial distribution plot's most vital adsorbed interaction to the weakest interaction. Importantly, the active cellular uptake enhanced the cellular wrapping process, resulting in a prominent higher number of contacts and slower translocation time than passive cellular uptake. Overall, our coarse-grained computational results could help to understand the effects of NPs elasticity on active/passive cellular uptake pathways within PS monolayer from a molecular perspective and provide valuable insights information for designing drug delivery systems and nanocarriers for inhaled NPs within the lungs.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge the financial support from the National Natural Science Foundation of China (No. 81871401), the Science and Technology Commission of Shanghai Municipality (No. 19441905300, 21511102100), Shanghai Jiao Tong University (No. YG2019QNA28), and the Shanghai Key Laboratory of Gynecologic Oncology.

References

1. M. T. Barbosa, M. Morais-Almeida, C. S. Sousa and J. Bousquet, Pulmonology, 2021, 27, 71.
2. M. Passi, S. Shahid, S. Chockalingam, I. K. Sundar and G. Packirisamy, Int. J. Nanomed., 2020, 15, 3803.
3. C. Velino, F. Carella, A. Adamiano, M. Sanguinetti, A. Vitali, D. Catalucci, F. Bugli and M. Iafisco, Front. Bioeng. Biotechnol., 2019, 406.
4. J.-f. Jin, L.-l. Zhu, M. Chen, H.-m. Xu, H.-f. Wang, X.-q. Feng, X.-p. Zhu and Q. Zhou, Patient Prefer. Adherence, 2015, 9, 923.
5. B. Homayun, X. Lin and H.-J. Choi, Pharmaceutics, 2019, 11, 129.
6. J. M. Borghardt, C. Kloft and A. Sharma, Can. Respir. J., 2018, 2018, 2732017.
7. S. P. Newman, Ther. Delivery, 2017, 8, 647–661.
8. S. Pramanik, S. Mohanto, R. Manne, R. R. Rajendran, A. Deepak, S. J. Edapully, T. Patil and O. Katari, Mol. Pharm., 2021, 18, 3671–3718.
9. C. A. Ruge, J. Kirch and C.-M. Lehr, Lancet Respir. Med., 2013, 1, 402–413.
10. T. Sécher, A. Mayor and N. Heuzé-Vourc'h, Front. Immunol., 2019, 10, 2760.
11. J. Liu, Z. Xiong, J. Zhang, C. Peng, B. Klajnert-Maculewicz, M. Shen and X. Shi, ACS Appl. Mater. Interfaces, 2019, 11, 15212–15221.
12. S. Suárez-García, T. V. Esposito, J. Neufeld-Peters, M. Bergamo, H. Yang, K. Saatchi, P. Schaffer, U. O. Hafeli, D. Ruiz-Molina and C. Rodríguez-Rodríguez, ACS Appl. Mater. Interfaces, 2021, 13, 10705–10718.
13. A. M. Ferretti, S. Usseglio, S. Mondini, C. Drago, R. La Mattina, B. Chini, C. Verderio, M. Leonzino, C. Cagnoli and P. Joshi, J. Colloid Interface Sci., 2021, 582, 678–700.
14. D. Chen, H. Jiang, D. Guo, W. Yasen, J. Ao, Y. Su, D. Pan, X. Jin and X. Zhu, Biomater. Sci., 2019, 7, 336–346.
15. L. Wang, C. Shi, X. Wang, D. Guo, T. M. Duncan and J. Luo, Biomaterials, 2019, 215, 119233.
16. F. Ding, S. Yang, Z. Gao, J. Guo, P. Zhang, X. Qiu, Q. Li, M. Dong, J. Hao and Q. Yu, Front. Chem., 2019, 7, 770.
17. J. Li, L. Chen, X. Xu, Y. Fan, X. Xue, M. Shen and X. Shi, Small, 2020, 16, 2005661.
18. A. Alba-Patiño, S. M. Russell, M. Borges, N. Pazos-Pérez, R. A. Álvarez-Puebla and R. de la Rica, Nanoscale Adv., 2020, 2, 1253–1260.
19. E. Karakuş, E. Erdemir, N. Demirbilek and L. Liv, Anal. Chim. Acta, 2021, 1182, 338939.
20. C. Verry, S. Dufort, B. Lemasson, S. Grand, J. Pietras, I. Troprès, Y. Crémillieux, F. Lux, S. Mériaux and B. Larrat, Sci. Adv., 2020, 6, eaay5279.
21. Q. Wei, J. He, S. Wang, S. Hua, Y. Qi, F. Li, D. Ling and M. Zhou, J. Nanobiotechnol., 2021, 19, 1–17.
22. S. K. Debnath, S. Saisivam and A. Omri, J. Pharmaceut. Biomed. Anal., 2017, 145, 854–859.
23. S. Castellani, A. Trapani, A. Spagnoletta, L. Di Toma, T. Magrone, S. Di Gioia, D. Mandracchia, G. Trapani, E. Jirillo and M. Conese, J. Transl. Med., 2018, 16, 1–15.
24. S. K. Debnath, S. Saisivam, M. Debanth and A. Omri, PLoS One, 2018, 13, e0190976.
25. S. Nozohouri, R. Salehi, S. Ghanbarzadeh, K. Adibkia and H. Hamishehkar, Mater. Sci. Eng., C, 2019, 99, 752–761.
26. M. D. Buhecha, A. B. Lansley, S. Somavarapu and A. S. Pannala, J. Drug Delivery Sci. Technol., 2019, 53, 101128.
27. V. Codullo, E. Cova, L. Pandolfi, S. Breda, M. Morosini, V. Frangipane, M. Malatesta, L. Calderan, M. Cagnone and C. Pacini, J. Controlled Release, 2019, 310, 198–208.
28. R. T. Sadikot, Arch. Med. Res., 2018, 6, 5.
29. F. U. Din, W. Aman, I. Ullah, O. S. Qureshi, O. Mustapha, S. Shafique and A. Zeb, Int. J. Nanomed., 2017, 12, 7291–7309.
30. T.-T. Tran, H. Yu, C. Vidaillac, A. Y. Lim, J. A. Abisheganaden, S. H. Chotirmall and K. Hadinoto, Int. J. Pharm., 2019, 559, 382–392.
31. S. A. Cohen, P. S. Kingma, J. Whitsett, R. Goldbart, T. Traitel and J. Kost, Int. J. Pharm., 2020, 585, 119387.
32. E. Maretti, L. Costantino, F. Buttini, C. Rustichelli, E. Leo, E. Truzzi and V. Iannuccelli, Drug Delivery Transl. Res., 2019, 9, 298–310.
33. R. S. Heyder, Q. Zhong, R. C. Bazito and S. R. da Rocha, Int. J. Pharm., 2017, 520, 181–194.
34. Y. Ding, Z. Jiang, K. Saha, C. S. Kim, S. T. Kim, R. F. Landis and V. M. Rotello, Mol. Ther., 2014, 22, 1075–1083.
35. J. Bourquin, A. Milosevic, D. Hauser, R. Lehner, F. Blank, A. Petri-Fink and B. Rothen-Rutishauser, Adv. Mater., 2018, 30, 1704307.
36. C. Auría-Soro, T. Nesma, P. Juanes-Velasco, A. Landeira-Viñuela, H. Fidalgo-Gomez, V. Acebes-Fernandez, R. Gongora, M. J. Almendral Parra, R. Manzano-Roman and M. Fuentes, Nanomaterials, 2019, 9, 1365.
37. X. Yi and H. Gao, Nanoscale, 2017, 9, 454–463.
38. A. C. Anselmo, M. Zhang, S. Kumar, D. R. Vogus, S. Menegatti, M. E. Helgeson and S. Mitragotri, ACS Nano, 2015, 9, 3169–3177.
39. T. Chen, Y. Zhang, X. Li, C. Li, T. Lu, S. Xiao and H. Liang, J. Chem. Theory Comput., 2021, 17, 7850–7861.
40. L. Chen, X. Li, Y. Zhang, T. Chen, S. Xiao and H. Liang, Nanoscale, 2018, 10, 11969–11979.
41. Z. Shen, H. Ye, X. Yi and Y. Li, ACS Nano, 2018, 13, 215–228.
42. S. I. Hossain, N. S. Gandhi, Z. E. Hughes, Y. Gu and S. C. Saha, Biochim. Biophys. Acta, Biomembr., 2019, 1861, 1458–1467.
43. F. Jiao, J. Sang, Z. Liu, W. Liu and W. Liang, Biophys. Chem., 2020, 266, 106457.
44. X. Bai, M. Li and G. Hu, Nanoscale, 2020, 12, 3931–3940.
45. S. I. Hossain, Z. Luo, E. Deplazes and S. C. Saha, J. R. Soc., Interface, 2021, 18, 20210402.
46. S. I. Hossain, N. S. Gandhi, Z. E. Hughes and S. C. Saha, J. Phys. Chem. B, 2021, 125, 1392–1401.
47. Z. Xu, H. M. Mansour and A. J. Hickey, J. Adhes. Sci. Technol., 2012, 25, 451–482.
48. A. J. Omlor, J. Nguyen, R. Bals and Q. T. Dinh, Respir. Res., 2015, 16, 1–9.
49. D. Peer, J. M. Karp, S. Hong, O. C. Farokhzad, R. Margalit and R. Langer, Nano-Enabled Med. Appl., 2020, 61–91.
50. J. Fang, H. Nakamura and H. Maeda, Adv. Drug Delivery Rev., 2011, 63, 136–151.
51. H. Maeda, J. Wu, T. Sawa, Y. Matsumura and K. Hori, J. Controlled Release, 2000, 65, 271–284.
52. Y. Li, X. Zhang and D. Cao, Nanoscale, 2015, 7, 2758–2769.
53. L. Zhang, H. Chen, J. Xie, M. Becton and X. Wang, J. Phys. Chem. B, 2019, 123, 8923–8930.
54. J. Sun, L. Zhang, J. Wang, Q. Feng, D. Liu, Q. Yin, D. Xu, Y. Wei, B. Ding, X. Shi and X. Jiang, Adv. Mater., 2015, 27, 1402–1407.
55. S. Wang, H. Guo, Y. Li and X. Li, Nanoscale, 2019, 11, 4025–4034.
56. Z. Luo, S. Li, Y. Xu, Z. Yan, F. Huang and T. Yue, Environ. Sci.: Nano, 2018, 5, 1921–1932.
57. X. Lin, Y. Y. Zuo and N. Gu, Sci. China Mater., 2015, 58, 28–37.
58. Z. Shen, H. Ye and Y. Li, Phys. Chem. Chem. Phys., 2018, 20, 16372–16385.
59. T. Lunnoo, J. Assawakhajornsak and T. Puangmali, J. Phys. Chem. C, 2019, 123, 3801–3810.
60. T. Yue and X. Zhang, Soft Matter, 2013, 9, 559–569.
61. S. Li, Z. Luo, Y. Xu, H. Ren, L. Deng, X. Zhang, F. Huang and T. Yue, Biochim. Biophys. Acta, Biomembr., 2017, 1859, 2096–2105.
62. K. Yang and Y.-Q. Ma, Nat. Nanotechnol., 2010, 5, 579–583.
63. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
64. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. Van Der Spoel, Bioinformatics, 2013, 29, 845–854.
65. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
66. H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
67. X. Lin, T. Bai, Y. Y. Zuo and N. Gu, Nanoscale, 2014, 6, 2759–2767.
68. X. Lin and N. Gu, Nano Res., 2014, 7, 1195–1204.
69. K. Yue, X. Sun, J. Tang, Y. Wei and X. Zhang, Int. J. Mol. Sci., 2019, 20, 3281.
70. S. I. Hossain, N. S. Gandhi, Z. E. Hughes and S. C. Saha, MRS Adv., 2019, 4, 1177–1185.
71. S. I. Hossain, N. S. Gandhi, Z. E. Hughes and S. C. Saha, Phys. Chem. Chem. Phys., 2020, 22, 15231–15241.
72. E. Parra and J. Pérez-Gil, Chem. Phys. Lipids, 2015, 185, 153–175.
73. S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822.
74. T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155.
75. G. Lukat, J. Kruger and B. Sommer, J. Chem. Inf. Model., 2013, 53, 2908–2925.
76. T. D. Clemons, R. Singh, A. Sorolla, N. Chaudhari, A. Hubbard and K. S. Iyer, Langmuir, 2018, 34, 15343–15349.
77. N. Kučerka, F. A. Heberle, J. Pan and J. Katsaras, Membranes, 2015, 5, 454–472.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03670c

---