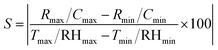Open Access Article
Open Access ArticleFabrication of a graphene-based sensor to detect the humidity and the temperature of a metal body with imprecise data analysis
Usama Afzal *ad,
Muhammad Aslam
*ad,
Muhammad Aslam b,
Fatima Afzalc,
Kanza Maryamc,
Naveed Ahmadd,
Qayyum Zafar
b,
Fatima Afzalc,
Kanza Maryamc,
Naveed Ahmadd,
Qayyum Zafar e and
Zahid Farooqf
e and
Zahid Farooqf
aVisiting Lecturer, Faculty of Science, Gift College, Hafizabad 52110, Pakistan. E-mail: mohammadusamafzal7@gmail.com
bDepartment of Statistics, Faculty of Science, King Abdulaziz University, Jeddah 21551, Saudi Arabia. E-mail: aslam_ravian@hotmail.com
cBachelor Student, School of Chemistry, University of the Punjab, Lahore 54000, Pakistan. E-mail: f.afzal.edu@gmail.com; k.maryam.edu@gmail.com
dDepartment of Physics, University of Education, Township Campus, Lahore 54000, Pakistan. E-mail: dr.naveedahmadsammar@ue.edu.pk
eDepartment of Physics, University of Management and Technology, Lahore 54000, Pakistan. E-mail: qayyumzafar@gmail.com
fDepartment of Physics, University of Education, Faisalabad Campus, Pakistan. E-mail: Zahid.farooq@ue.edu.pk
First published on 2nd August 2022
Abstract
Graphene is a 2D material with remarkable properties. The present study demonstrates the fabrication of a graphene-based sensor for measuring the temperature and humidity of a metal body. The graphene sensor was fabricated by depositing a thin film of graphene nanoparticles between silver electrodes (separated by ∼50 μm) on a glass substrate. The graphene thin film was characterized by XRD, Raman spectroscopy and UV-vis techniques. The capacitance and resistance for both the relative humidity (in the range of 0–100% RH) and temperature (in the range of 230–310 K) were measured using an LCR meter at 1 kHz in a controlled chamber. The graphene-based sensor expressed high sensitivity with fast response and recovery times for both humidity and temperature with long stability and low hysteresis curves. The sensor was also tested on a metal body, which expressed a good response time. Moreover, the measured data of capacitance and resistance was analyzed with classical and neutrosophic analysis as an application of modern material statistics. It was observed that neutrosophic analysis is more flexible for analyzing the capacitance and resistance of the fabricated sensor.
1. Introduction
Studies on microelectronics and nanotechnology are on the rise and researchers have been working on flexible circuits as well as devices. Many nanomaterials have been used for this purpose, such as carbon-containing materials, i.e., carbon nanofibers (CNFs)1 and carbon nanotubes (CNTs).2,3 Graphene is one of the well-known carbon-containing materials. It is a zero-bandgap4 allotropic form of carbon having a two-dimensional hexagonal lattice structure. Graphene is more advantageous than other materials such as graphite due to its mechanical properties (since it may be single-layered or multilayered5), thermal conductivity (graphene has very high thermal properties) of about 5000 W m−1 K (ref. 6), electric conductivity (about 104 to 105 S m−1 for pure graphene7) and large surface area.8 Researchers have also used the oxide form of graphene which is produced through different methods. The Hummers' method is one of the commonly known methods, which is used by different researchers in their work as explained in the following ref. 9–12. Due to the remarkable properties of graphene, it has been used in the fabrication of different devices such as sensors,13 solar cells14 and others. For example, a humidity sensor based on the thin films of graphene oxide with thermal annealing at the temperature of 1200 °C was proposed.15 A highly sensitive humidity graphene oxide was also fabricated with evenly dispersed multi-walled carbon nanotubes.16 Similarly, a wearable temperature sensor based on graphene nano-walls was proposed.17 For further examples, the reader may be interested in the following ref. 16, 18–26. From the abovementioned references, it was observed that the data measured (whether resistance or capacitance) were analyzed through classical graphs and tables, which are based on the fixed-point values, i.e., fixed values of capacitance and resistance at a specific point of humidity and temperature. However, if someone measures data in the interval, classical methods do not analyze the data well. This is why we should move on to some novel statistics approaches, such as the neutrosophic approach, etc.A neutrosophic approach is used for the analysis of the data variance, as proposed by Smarandache.27 It is a flexible and reliable technique of statistics, which has numerous advantages over the classical approach. The neutrosophic approach uses interval data for the analysis,28 which is its biggest advantage because classical analysis is only specified around the fixed-point or determined data. This is why the use of this approach has gained importance for the variance analysis of different problems in several fields, e.g. medicine,29 applied sciences,30 astrophysics31 and material statistics like resistance and capacitance analysis,32–34 etc. Moreover, the neutrosophic technique is more helpful than classical techniques; see the following references for examples.35–37 Different statistical techniques have been developed under neutrosophic statistics by Muhammad Aslam.38,39
Herein, we report the fabrication of a graphene-based sensor for measuring the humidity and temperature effects of the metal body. A thin film of graphene nanoparticles was deposited on a glass substrate between two silver electrodes whose capacitance and resistance with respect to temperature and relative humidity were measured at 1 kHz with an LCR meter. The data were analyzed through classical and neutrosophic approaches (a similar analysis was performed for the interval data of the humidity sensor based on methyl green40). Through this work, we have tried to develop an application of material statistics (a study in which data regarding material properties are analyzed through different methods of statistics) for the said graphene sensor's imprecise data based on modern statistics methods.
2. Experimental
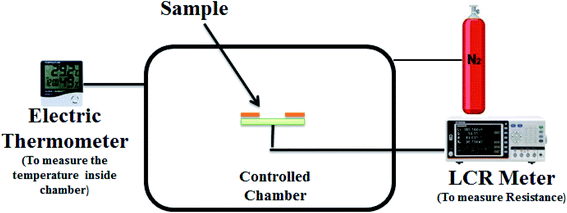
Graphene with 99.9% purity has been used in this experiment. For the fabrication of the sensor, the glass substrate (25 × 25 mm) was cleaned with ethanol (for 15 minutes) and then dried with the help of a nitrogen gun. Silver electrodes (separated about 50 μm) were deposited on the substrate by thermal evaporation with a shadow mask at 10−5 mbar pressure. After this, a solution of graphene nanoparticles was prepared by taking about 40 mg graphene and 1.6 ml naphtha. The solution was stirred for five hours and then filtered. About 50 μl of the solution was deposited between the electrodes through a micropipette. In the end, our fabricated sensor (of dimension 25 × 25 mm) was ready for characterization having a 2 μm thickness of the thin film of graphene nanoparticles with an 8 mm × 25 mm surface area as shown in Fig. 1. The whole process was performed at room temperature, i.e. 20 °C.The structure of the graphene nanoparticle thin film was characterized by X-ray diffraction (XRD), the optical properties of the sample were studied by the UV-vis technique and the quality of the thin film was investigated by Raman spectroscopy. The electrical study was performed in the laboratory using an AT2816B LCR meter at 10 kHz, which was associated with a controlled chamber. This controlled chamber contained a heater to increase the temperature of the chamber and a humidifier to produce humidity inside the chamber. The characterization setup is shown in Fig. 2. First, we measured the variances in capacitance and resistance with respect to changes in temperature (from 230 to 310 K). After this, we measured the capacitance and resistance variance with respect to changes in the relative humidity inside the chamber (from 0 to 90% RH). All the data were collected at intervals, with both maximum and minimum value changes in capacitance and resistance at a specific point of relative humidity, as well as temperature. Also, the sample has shown high sensitivity with high response and recovery times for both relative humidity (% RH) and temperature (K). We repeated the whole experiment several times but found very minor variations (about 1 to 1.5%, which can be neglected).
3. Results and discussion
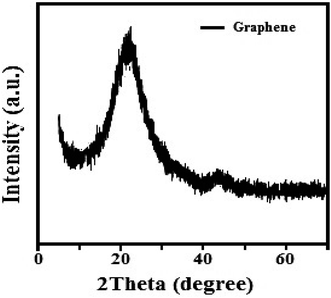
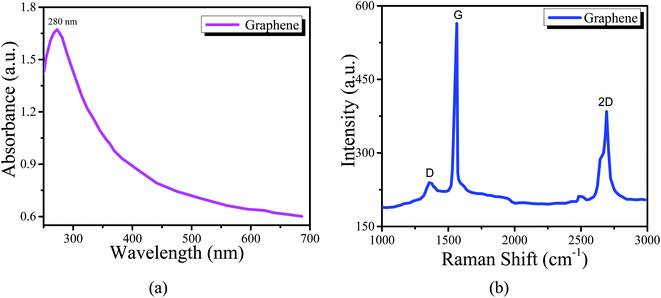
The structure of the graphene thin film has been studied by the XRD technique, as shown in Fig. 3. The following pattern was ben observed in the range 5° < 2° theta < 70°. The pattern satisfies the standard value. There is a sharp peak, i.e. (002), at about 25°, which expresses the (002) plane with a d-spacing of 3.562 Å based on Bragg's law and also provides information about the size of the lattice constant, i.e., 2.46 Å.41Fig. 4(a) shows the UV-vis spectrum of the graphene thin film. The peak of the spectrum is found at 280 nm, which indicates that the thin film is a good absorber of UV-C light. The absorption efficiency indicates that it can be used in light sensing, photodiodes, or solar cell applications. Also, Fig. 4(b) shows the Raman spectrum. We observed three peaks as D, G and 2D at about 1376, 1649 and 2725 cm−1, respectively. ‘D’ is a defect peak, which highlights the defects as well as disorders between layers of graphene. ‘G’ is the characteristic peak of the carbon structure sp2, which highlights the symmetry as well as the crystallization of the graphene structure. ‘2D’ is a double-phonon-resonance peak, which expresses the graphene stacking degree, i.e., indicating the presence of graphene.42,43
 | ||
| Fig. 4 (a) UV-vis spectrum of the graphene nanoclusters thin film. (b) Raman spectrum of the graphene nanoclusters thin film. | ||
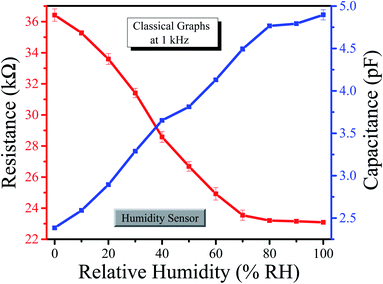
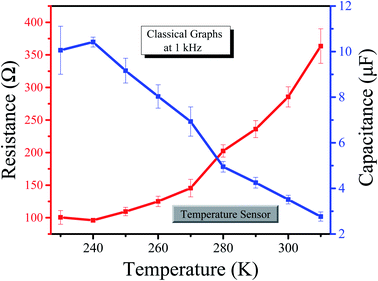
We investigated the electric properties of the sample for humidity and temperature sensing, which were measured in the lab as shown in Tables 1 and 2 for humidity and temperature sensors, respectively. We measured the interval values of capacitance and resistance because we wanted to observe the whole variance of the sensor's capacitance and resistance (i.e., the minimum change value and maximum change value as in our previous work3) at a specific value of temperature and relative humidity.
| Relative humidity (% RH) | Capacitance (pF) | Resistance (kΩ) |
|---|---|---|
| 0 | [2.345, 2.923] | [36.024, 36.820] |
| 10 | [2.421, 3.213] | [35.122, 35.422] |
| 20 | [2.710, 3.312] | [33.245, 33.945] |
| 30 | [3.001, 3.299] | [31.108, 31.708] |
| 40 | [3.398, 3.663] | [28.378, 28.930] |
| 50 | [3.419, 3.824] | [26.378, 26.991] |
| 60 | [3.721, 4.143] | [24.524, 25.321] |
| 70 | [3.921, 4.521] | [23.216, 23.879] |
| 80 | [4.007, 4.791] | [23.116, 23.290] |
| 90 | [4.172, 4.810] | [23.102, 23.208] |
| 100 | [4.671, 4.957] | [23.079, 23.102] |
| Temperature (K) | Capacitance (μF) | Resistance (Ω) |
|---|---|---|
| 230 | [10.01, 11.12] | [90, 111] |
| 240 | [10.21, 10.63] | [94, 98] |
| 250 | [8.62, 9.71] | [103, 116] |
| 260 | [7.52, 8.55] | [117, 133] |
| 270 | [6.29, 7.58] | [132, 159] |
| 280 | [4.72, 5.18] | [193, 212] |
| 290 | [4.02, 4.49] | [223, 249] |
| 300 | [3.32, 3.70] | [270, 301] |
| 310 | [2.56, 2.97] | [337, 390] |
3.1. The effect of humidity on the capacitance and resistance of the sample
It can be seen from Table 1 that the capacitance of the humidity sensors increased. Initially, the sensors showed a small variation in capacitance; however, the capacitance increased sharply as the humidity in the air in the chamber increased. This is because initially, there were several immobile layers of sensing thin films but as the humidity of the air in the chamber increased and was absorbed by the films, the immobile layers were converted into mobile layers.44 This means that the capacitance of the humidity sensors is directly proportional to the absorption of humidity. If ‘εd’ is the dielectrics permittivity of the sensing thin films with ‘ε0’ as the vacuum permittivity and ‘d’ is the distance between the electrodes and ‘A’ is the area of electrodes, the capacitance for the humidity sensors is written as follows:
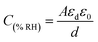 | (1) |
Since the capacitance changes with the changes in the humidity of the air, it can be defined by some factors like the surface morphology of the sensing film, the polarizability of the material, the dielectric constant of the water and material and electrode distance. Dielectric permittivity is an important factor that can cause capacitance to increase. The relative permittivity of water is very high (i.e., 80), which is significantly higher than the relative permittivity of organic semiconductors.45 This high relative permittivity of water increases the dielectric permittivity of the sensing film; therefore, the relationship between the capacitance and the dielectric constant under dry and humid conditions can be written as follows:46
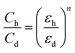 | (2) |
In eqn (2), ‘εh’ is the humid dielectric constant, ‘εd’ is the dry dielectric constant, ‘Ch’ is the humid capacitance and ‘Cd’ is the dry capacitance with ‘n’ being the morphology element of the dielectric. The absorption of humidity on films can also be observed with weak hydrogen bonding and van der Waals interactions of humidity with sensing films.47 If an external electric field acts on the water molecules and the molecules become polarized, it can be written as follows:
| P = αE | (3) |
In eqn (3) above, ‘P’ is the polarity, ‘α’ is the polarizability and ‘E’ is the external field. Moreover, it was observed that the polarizability of the thin films is directly proportional to the dielectric constant.48 This polarization may have an electronic nature, dipolar nature or ionic nature.49 If ‘ε0’ represents the free space permittivity and ‘εd’ represents the relative permittivity, the relation between polarization and dielectric constant by using the Clausius Mossotti equation50 is as follows:
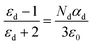 | (4) |
From eqn (4), we can write a simulation equation for the capacitance of sensors51 as follows:
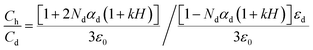 | (5) |
Table 1 shows the resistance variance of the humidity sensors. The resistance decreased as the humid air level increased in the chamber. Initially, the sensors showed high variation but as the humidity increased, the variation became small. The change in the resistance of the sensors is related to the absorption of humidity on the sensing films. As the sensing films absorb humidity, this humidity becomes a reason for an increase in charge carriers, i.e., water molecules also work as dopants (because the molecules of water interact with the atoms/molecules of graphene and provide a path to pass the electric charge from the graphene). Also, it is seen that the absorption of humidity may lead to the dissociation of ions. These ions increase the conductivity of the sensing film and the resistance starts to decrease because both are inversely proportional to each other.52 If ‘A’ is the area of sensing films, ‘l’ is the length and ‘α’ is the conductivity of sensing films, then resistance for sensors can be written as
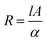 | (6) |
From eqn (6), it is clear that the resistance depends on the absorption rate of the films, length of films, conductivity, and the area of films.
3.2. The effects of temperature on the capacitance and resistance of the sample
Table 2 shows the effects of temperature on the capacitance and resistance of the sample. It is seen that first resistance starts to decrease till 245 K because graphene also has conductive properties53,54 but then it gradually starts to increase. This shows that the thin film of graphene nanoparticles is a good conductor at room temperature. However, as the temperature starts to rise, then the air (present in the chamber) starts to expand in the nanoparticle layers, which becomes a reason for thermal distribution.55 Due to the thermal distribution, the thermal expansion between the layers of nanoparticles increases and contact between layers decreases. This phenomenon leads to a decrease in the tunnel area. As the tunneling effects become weaker, then resistance starts to increase. From eqn (6), the temperature increased and the conductivity decreased due to the change in atomic motion of the sensing layer and electrodes, hence the resistance of the sample increased but the capacitance decreased. There is an inverse relationship between resistance and capacitance (for LCR40) as follows:
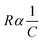 | (7) |
3.3. Sensitivity with response and recovery time
Sensitivity can be defined as “a tiny variation in measuring, sensor signal to premier sensor signal”.56 The formula for finding sensitivity is written as follows:• ‘Cmax’ and ‘Rmax’ are the maximum measured values of capacitance and resistance, respectively.
• ‘Cmin’ and ‘Rmin’ are the minimum measured values of capacitance and resistance, respectively.
• ‘Tmax’ and ‘RHmax’ are the maximum measured values of temperature and relative humidity, respectively.
• ‘Tmin’ and ‘RHmin’ are the minimum measured values of temperature and relative humidity, respectively.
The sensitivities of the samples for both humidity and temperature sensors are shown in Table 3. Comparisons of the present work with previous work can be seen in Tables 4 and 5 for humidity and temperature, respectively.
| Sensors | Frequency | Band gap | Sensitivity (%) | Response time | Recovery time | |
|---|---|---|---|---|---|---|
| Capacitance | Resistance | |||||
| Humidity | 1 kHz | 0–100% RH | 2.612 (pF/% RH) | 12.927 (kΩ/% RH) | 1.60 s | 2.15 s |
| Temperature | 1 kHz | 230–310 K | 8.8 (μF/K) | 375 (Ω/K) | 3 s | 8.1 s |
| Nano-materials | Band gap | Sensitivity | Response time | Recovery time |
|---|---|---|---|---|
| SnO2 (ref. 57) | 30–85% RH | 2–33 pF/RH% | 120–170 s | 20–60 s |
| Multi-wall carbon nanotubes58 | 11–97% RH | 0.026 pF/% RH | 45 s | 15 s |
| Methyl green40 | 40–80% RH | (122.37 pF/% RH) & (31 KΩ/% RH) | 200 s | 60 s |
| Methyl red59 | 30–95% RH | (16.92 pF/% RH) & (0.307 MΩ/% RH) | 10 s | 10 s |
| Graphene nanoparticles (present study) | 0–100% RH | (2.612 pF/% RH) & (12.927 kΩ/% RH) | 1.60 s | 2.15 s |
| Nano-materials | Band gap | Sensitivity | Response time | Recovery time |
|---|---|---|---|---|
| CNTs on PET60 | 40–100 °C | 0.4% °C | 300 ms | 4 s |
| Graphene on PDMS61 | 30–100 °C | 2.11% K | 3 s | 20 s |
| rGO on PET62 | 30–100 °C | 0.6345% °C | 1.2 s | — |
| rGO on PI63 | 25–45 °C | 1.30% °C | 0.443 s | 0.330 s |
| Graphene nanoparticles (present study) | 230–310 K | (8.8 μF/K) & 375 (Ω/K) | 3 s | 8.1 s |
3.4. Hysteresis curves and long stability for humidity and temperature
Hysteresis curves of the graphene sensor for the humidity and temperature have been studied by calculating the calibration curves during humidity absorption and desorption as well as heat-absorbing and releasing processes as shown in Fig. 5 (here, we have only measured the capacitance, instead of both capacitance and resistance, because the sample is same; however, one can also measure the resistance). The hysteresis curve for the humidity sensor is the average value for the total span of humidity.64 We used the same process for temperature. The average hysteresis for humidity was estimated at 2% with the relative humidity in the range of 0 to 100% RH. For temperature, about 1.5% average hysteresis was estimated in the temperature range of 230 to 310 K. The obtained hysteresis value suggests competency for this sensing device since it is below the threshold of 3%, a maximum value set for a practically competent sensor.65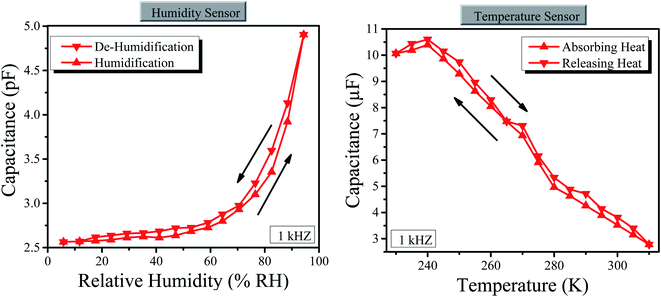 | ||
| Fig. 5 (Left) Hysteresis curves of the humidity sensor. (Right) Hysteresis curves of the temperature sensor. | ||
Similarly, the long stability of the graphene-based sensor was checked for humidity and temperature. We checked the stability for one week at room temperature, i.e. 295 K and room level relative humidity i.e. 36% RH as shown in Fig. 6, where the graphene sensor has shown high stability of both temperature and humidity. However, the stability of the temperature sensor is greater than the stability of the humidity sensor depending on graphene nanoparticles.
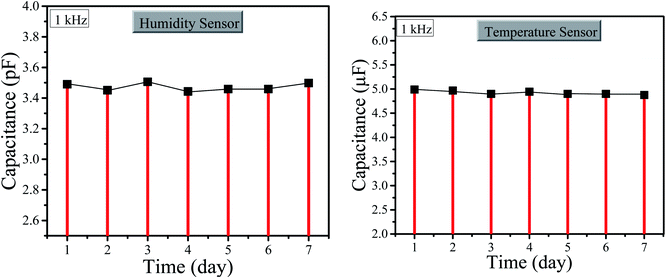 | ||
| Fig. 6 (Left) Stability graph of the humidity sensor. (Right) Stability graph of the temperature sensor. | ||
3.5. Use of sensors for a steel body
We have used the above sensor on the surface of steel glass to observe the humidity and temperature effect (here, we have only measured the resistance, instead of both capacitance and resistance, because the sample is the same; however, one can also measure the capacitance). This experiment was performed at room temperature of about 22 °C with a relative humidity of about 30% RH. For temperature observation, initially, the glass was empty and the sensor was showing the minimum resistance but as the hot water was poured into the glass, the resistance of the sensor started to increase as shown in Fig. 7.Similarly, for humidity, the sensor was expressing high resistance. However, as we put the glass in a chamber having about 60% RH, the resistance started to decrease as shown in Fig. 8.
3.6. Analysis of capacitance and resistance
It was already mentioned that two types of approaches have been used for the analysis of data, i.e., classical and neutrosophic analysis. For classical analysis, a classical average formula [(maximum value + minimum value)/2] for each interval has been used. Through this, we want to convert interval values into fixed-point values (as classical analysis deals with fixed-point values). However, for neutrosophic analysis, the same interval values (without any modification) have been used by developing a neutrosophic formula for resistance. The measured data of capacitance and resistance are shown in Tables 1 and 2.| ZiN = ZiL + ZiUIN (i = 1, 2, 3,… nN) | (8) |
The size of the neutrosophic variable is nN ∈ [nL, nU]. The variable AiN ∈ [ZiL, ZiU] has two parts: the lower value ZiL is a classical part and the upper value AiUIN is an indeterminate part having an indeterminacy interval IN ∈ [IL, IU].
Similarly, the neutrosophic mean ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) N = [
N = [![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) L, ZU] is defined as follows:
L, ZU] is defined as follows:
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) N = N = ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) L + L + ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) UIN; IN ∈ [IL, IU] UIN; IN ∈ [IL, IU]
| (9) |
We can use these preliminaries for developing the neutrosophic formula for the present condition. Since the resistance of the graphene nanoparticles depends on the variation of temperature (T) and relative humidity (RH), we can write it as a function of them, i.e. r(T) and r(I). The neutrosophic formula for resistance depending on the variance of temperature can be written as follows:
| r(T)N = r(T)L + r(T)UIN; IN ∈ [IL, IU] | (10) |
From the above resistance formula r(T)N ∈ [r(T)L, r(T)U] is an extension under the classical analysis. The equation contains two parts, i.e. r(T)L determined and r(T)UIN indetermined. Moreover, IN ∈ [IL, IU] is known as an indeterminacy interval. Also, the measured resistance interval r(T)N ∈ [r(T)L, r(T)U] can be reduced to the classical or determined part if we choose IL = 0 and IU can be calculated by (r(T)U − r(T)L)/r(T)U. Similarly, the neutrosophic formula for capacitance and resistance depending on the variance of relative humidity and temperature can be written as follows:
| r(% RH)N = r(% RH)L + r(% RH)UIN; IN ∈ [IL, IU] | (11) |
| C(% RH)N = C(% RH)L + C(% RH)UIN; IN ∈ [IL, IU] | (12) |
| C(T)N = C(T)L + C(T)UIN; IN ∈ [IL, IU] | (13) |
The classical analysis of the capacitance and the resistance variance with respect to changes in temperature and relative humidity are shown in Table 6. The neutrosophic analysis is shown in Tables 7 and 8 for humidity and temperature, respectively.
| Humidity sensor | Temperature sensor | ||||
|---|---|---|---|---|---|
| Relative humidity (% RH) | Capacitance (pF) | Resistance (kΩ) | Temperature (K) | Resistance (Ω) | Capacitance (μF) |
| 0 | 2.384 | 36.422 | 230 | 100.5 | 10.061 |
| 10 | 2.597 | 35.272 | 240 | 96 | 10.421 |
| 20 | 2.894 | 33.595 | 250 | 109.5 | 9.165 |
| 30 | 3.289 | 31.408 | 260 | 125 | 8.033 |
| 40 | 3.652 | 28.582 | 270 | 145.5 | 6.933 |
| 50 | 3.813 | 26.6845 | 280 | 202.5 | 4.949 |
| 60 | 4.131 | 24.9225 | 290 | 236 | 4.250 |
| 70 | 4.494 | 23.5475 | 300 | 285.5 | 3.513 |
| 80 | 4.767 | 23.203 | 310 | 363.5 | 2.766 |
| 90 | 4.793 | 23.155 | |||
| 100 | 4.897 | 23.0905 | |||
| Relative humidity (% RH) | Capacitance (pF) | Resistance (kΩ) |
|---|---|---|
| 0 | 2.345 + 2.923IN; INε[0, 0.022] | 36.024 + 36.820IN; INε[0, 0.012] |
| 10 | 2.421 + 3.213IN; INε[0, 0.008] | 35.122 + 35.422IN; INε[0, 0.012] |
| 20 | 2.710 + 3.312IN; INε[0, 0.021] | 33.245 + 33.945IN; INε[0, 0.012] |
| 30 | 3.001 + 3.299IN; INε[0, 0.019] | 31.108 + 31.708IN; INε[0, 0.006] |
| 40 | 3.398 + 3.663IN; INε[0, 0.024] | 28.378 + 28.930IN; INε[0, 0.006] |
| 50 | 3.419 + 3.824IN; INε[0, 0.023] | 26.378 + 26.991IN; INε[0, 0.006] |
| 60 | 3.721 + 4.143IN; INε[0, 0.031] | 24.524 + 25.321IN; INε[0, 0.006] |
| 70 | 3.921 + 4.521IN; INε[0, 0.028] | 23.216 + 23.879IN; INε[0, 0.012] |
| 80 | 4.007 + 4.791 IN; INε[0, 0.007] | 23.116 + 23.290IN; INε[0, 0.010] |
| 90 | 4.172 + 4.810IN; INε[0, 0.006] | 23.102 + 23.208IN; INε[0, 0.007] |
| 100 | 4.671 + 4.957IN; INε[0, 0.001] | 23.079 + 23.102IN; INε[0, 0.024] |
| Temperature (K) | Capacitance (μF) | Resistance (Ω) |
|---|---|---|
| 230 | 10.01 + 11.12IN; INε[0, 0.189] | 90 + 111IN; INε[0, 0.189] |
| 240 | 10.21 + 10.63IN; INε[0, 0.041] | 94 + 98IN; INε[0, 0.041] |
| 250 | 8.62 + 9.71IN; INε[0, 0.112] | 103 + 116IN; INε[0, 0.112] |
| 260 | 7.52 + 8.55IN; INε[0, 0.120] | 117 + 133IN; INε[0, 0.120] |
| 270 | 6.29 + 7.58IN; INε[0, 0.170] | 132 + 159IN; INε[0, 0.170] |
| 280 | 4.72 + 5.18IN; INε[0, 0.090] | 193 + 212IN; INε[0, 0.090] |
| 290 | 4.02 + 4.49IN; INε[0, 0.104] | 223 + 249IN; INε[0, 0.104] |
| 300 | 3.32 + 3.70IN; INε[0, 0.103] | 270 + 301IN; INε[0, 0.103] |
| 310 | 2.56 + 2.97IN; INε[0, 0.136] | 337 + 390IN; INε[0, 0.136] |
The above tables show the classical and neutrosophic analysis of the resistance variance with respect to changes in temperature as well as relative humidity. Classical analysis belongs to or deals with only classical assumptions; this means that the classical approach relates to the classical average value, generally used by researchers in their studies (to avoid complication, we have used this classical average formula as the classical analysis). On the other hand, neutrosophic analysis deals with a novel neutrosophic formula that contains indeterminacy for each measured interval of resistance. We have compared the classical analysis and neutrosophic analysis through graphs for both humidity and temperature sensors. The classical graphs for humidity and temperature are shown in Fig. 9 and 10, respectively.
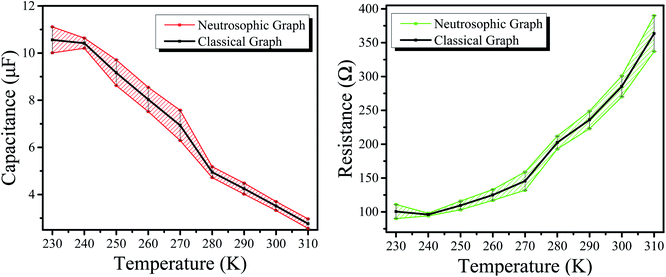
The neutrosophic graphs for the humidity and temperature sensors are shown in Fig. 11 and 12, respectively.
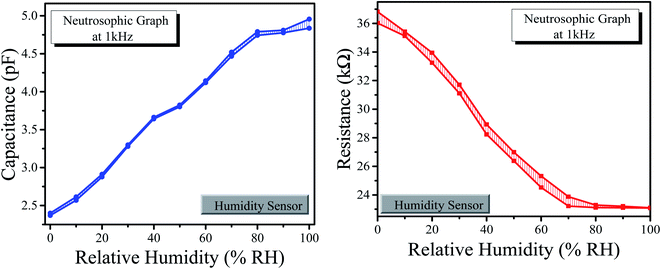 | ||
| Fig. 11 (Left) Neutrosophic graphs of capacitance for the humidity sensor. (Right) Neutrosophic graphs of resistance for humidity sensor. | ||
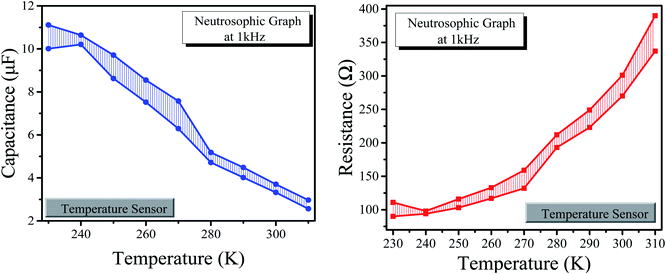 | ||
| Fig. 12 (Left) Neutrosophic graphs of capacitance for the temperature sensor. (Right) Neutrosophic graphs of resistance for the temperature sensor. | ||
The graphs above express the comparison between classical analysis and neutrosophic analysis. It can be seen that the graphs of classical analysis are not very flexible because they are drawn at fixed-point values; however, the graphs of the neutrosophic analysis show more flexibility. Also, one can observe the classical graphs through neutrosophic graphs as these are at the center of neutrosophic graphs (which shows that the neutrosophic analysis is a generalization of classical graphs) as shown in the combined graphs of Fig. 13 and 14. This means that neutrosophic statistics are more effective for analyzing the resistance of the sample.66 As a result, the neutrosophic analysis is more informative, flexible and adequate than the classical analysis.
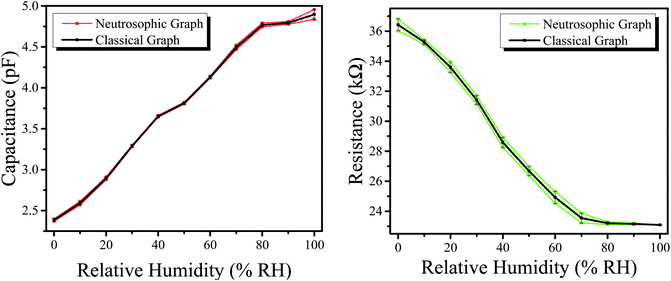 | ||
| Fig. 13 (Left) Combined graphs of capacitance for the humidity sensor. (Right) Combined graphs of resistance for the humidity sensor. | ||
4. Conclusion
This work is based on the fabrication of a graphene nanoparticle thin-film-based sensor for the detection of humidity and temperature on a metal body. A thin film of graphene nanoparticles was deposited between two silver electrodes on a clean glass substrate. The structural properties of the thin film were studied via XRD, the quality was investigated via Raman spectroscopy and optical properties by UV-vis. The electric properties (capacitance and resistance) of the sample with respect to relative humidity (% RH) and temperature (K) were determined separately using an LCR meter in a controlled chamber. The graphene sensor expressed good sensitivity with fast response and recovery times, i.e. 1.6 s and 2.15 s for the humidity and 3 s and 8.1 s for the temperature, respectively. It also expressed long stability for both humidity and temperature and low average hysteresis, i.e. 2% for humidity and 1.5% for temperature. The classical and neutrosophic analyses of the capacitance and resistance were performed via the application of material statistics, and it was found that neutrosophic analysis is more informative and flexible for explaining the capacitance and resistance of the sensors.Conflicts of interest
There are no conflicts to declare.References
- M. Dimchev, R. Caeti and N. Gupta, Effect of carbon nanofibers on tensile and compressive characteristics of hollow particle filled composites, Mater. Des., 2010, 31(3), 1332–1337 CrossRef CAS.
- Z. Zhang, et al., Fabrication and characterization of closed-cell aluminum foams with different contents of multi-walled carbon nanotubes, Mater. Des., 2015, 88, 359–365 CrossRef CAS.
- U. Afzal, et al., Fabrication of flexible temperature sensors to explore indeterministic data analysis for robots as an application of Internet of Things, RSC Adv., 2022, 12, 17138–17145 RSC.
- A. K. Geim and K. S. Novoselov, The rise of graphene, in Nanoscience and technology: a collection of reviews from nature journals, World Scientific, 2010, pp. 11–19 Search PubMed.
- C. Lee, et al., Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321(5887), 385–388 CrossRef CAS PubMed.
- J.-W. Jiang, J.-S. Wang and B. Li, Thermal conductance of graphene and dimerite, PPhys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(20), 205418 CrossRef.
- J.-H. Chen, et al., Intrinsic and extrinsic performance limits of graphene devices on SiO2, Nat. Nanotechnol., 2008, 3(4), 206–209 CrossRef CAS PubMed.
- A. K. Geim, Graphene: status and prospects, Science, 2009, 324(5934), 1530–1534 CrossRef CAS PubMed.
- N. Zaaba, et al., Synthesis of graphene oxide using modified hummers method: solvent influence, Procedia Eng., 2017, 184, 469–477 CrossRef CAS.
- N. Cao and Y. Zhang, Study of reduced graphene oxide preparation by Hummers’ method and related characterization, J. Nanomater., 2015, 2015, 168125 Search PubMed.
- Y. Hou, et al., High-quality preparation of graphene oxide via the Hummers' method: understanding the roles of the intercalator, oxidant, and graphite particle size, Ceram. Int., 2020, 46(2), 2392–2402 CrossRef CAS.
- S. N. Alam, N. Sharma and L. Kumar, Synthesis of graphene oxide (GO) by modified hummers method and its thermal reduction to obtain reduced graphene oxide (rGO), Graphene, 2017, 6(1), 1–18 CrossRef CAS.
- E. W. Hill, A. Vijayaragahvan and K. Novoselov, Graphene sensors, IEEE Sens. J., 2011, 11(12), 3161–3170 CAS.
- D. H. Shin and S.-H. Choi, Use of graphene for solar cells, J. Korean Phys. Soc., 2018, 72(12), 1442–1453 CrossRef CAS.
- D.-T. Phan and G.-S. Chung, Effects of rapid thermal annealing on humidity sensor based on graphene oxide thin films, Sens. Actuators, B, 2015, 220, 1050–1055 CrossRef CAS.
- X. Li, et al., High-sensitive humidity sensor based on graphene oxide with evenly dispersed multiwalled carbon nanotubes, Mater. Chem. Phys., 2018, 207, 135–140 CrossRef CAS.
- J. Yang, et al., Wearable temperature sensor based on graphene nanowalls, RSC Adv., 2015, 5(32), 25609–25615 RSC.
- N. Dong, et al., Pressure and temperature sensor based on graphene diaphragm and fiber Bragg gratings, IEEE Photonics Technol. Lett., 2017, 30(5), 431–434 Search PubMed.
- Y. Wang, et al., High-sensitivity wearable and flexible humidity sensor based on graphene oxide/non-woven fabric for respiration monitoring, Langmuir, 2020, 36(32), 9443–9448 CrossRef CAS PubMed.
- M. Hilal and J. I. Han, Development of a highly flexible and durable fiber-shaped temperature sensor based on graphene/Ni double-decked layer for wearable devices, IEEE Sens. J., 2020, 20(10), 5146–5154 CAS.
- M. Soni, et al., Printed temperature sensor based on PEDOT:PSS-graphene oxide composite, IEEE Sens. J., 2020, 20(14), 7525–7531 CAS.
- Z. Chen, et al., Flexible temperature sensors based on carbon nanomaterials, J. Mater. Chem. B, 2021, 9(8), 1941–1964 RSC.
- D. Wang, et al., Electrospinning of flexible poly(vinyl alcohol)/MXene nanofiber-based humidity sensor self-powered by monolayer molybdenum diselenide piezoelectric nanogenerator, Nano-Micro Lett., 2021, 13(1), 1–13 CrossRef CAS PubMed.
- L. Zhang, et al., Triboelectric nanogenerator based on Teflon/vitamin B1 powder for self-powered humidity sensing, Beilstein J. Nanotechnol., 2020, 11(1), 1394–1401 CrossRef CAS PubMed.
- X. Liu, et al., A humidity sensing and respiratory monitoring system constructed from quartz crystal microbalance sensors based on a chitosan/polypyrrole composite film, J. Mater. Chem. A, 2021, 9(25), 14524–14533 RSC.
- D. Wang, et al., Multifunctional latex/polytetrafluoroethylene-based triboelectric nanogenerator for self-powered organ-like MXene/metal–organic framework-derived CuO nanohybrid ammonia sensor, ACS Nano, 2021, 15(2), 2911–2919 CrossRef CAS PubMed.
- F. Smarandache, Introduction to neutrosophic measure, neutrosophic integral, and neutrosophic probability, Infinite Study, 2013 Search PubMed.
- M. Aslam, A study on skewness and kurtosis estimators of wind speed distribution under indeterminacy, Theor. Appl. Climatol., 2021, 143(3), 1227–1234 CrossRef.
- J. Ye, Improved cosine similarity measures of simplified neutrosophic sets for medical diagnoses, Artif. Intell. Med., 2015, 63(3), 171–179 CrossRef PubMed.
- V. Christianto, R. N. Boyd and F. Smarandache, Three possible applications of neutrosophic logic in fundamental and applied sciences, Infinite Study, 2020 Search PubMed.
- M. Aslam, Enhanced statistical tests under indeterminacy with application to earth speed data, Earth Sci. Inform., 2021, 1–7 Search PubMed.
- U. Afzal, et al., Neutrosophic statistical analysis of resistance depending on the temperature variance of conducting material, Sci. Rep., 2021, 11(1), 1–6 CrossRef PubMed.
- U. Afzal, M. Aslam and A. H. Al-Marshadi, Analyzing imprecise graphene foam resistance data, Mater. Res. Express, 2022, 9, 045007 CrossRef.
- F. Smarandache, The Neutrosophic Research Method in Scientific and Humanistic Fields, 2010 Search PubMed.
- F. Smarandache, Introduction to neutrosophic statistics: Infinite Study, Romania-Educational Publisher, Columbus, OH, USA, 2014 Search PubMed.
- J. Chen, J. Ye and S. Du, Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics, Symmetry, 2017, 9(10), 208 CrossRef.
- J. Chen, et al., Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers, Symmetry, 2017, 9(7), 123 CrossRef.
- M. Aslam, Design of the Bartlett and Hartley tests for homogeneity of variances under indeterminacy environment, J. Taibah Univ. Sci., 2020, 14(1), 6–10 CrossRef.
- M. Aslam, On detecting outliers in complex data using Dixon's test under neutrosophic statistics, J. King Saud Univ., Sci., 2020, 32(3), 2005–2008 CrossRef.
- U. Afzal, et al., Fabrication of a surface type humidity sensor based on methyl green thin film, with the analysis of capacitance and resistance through neutrosophic statistics, RSC Adv., 2021, 11(61), 38674–38682 RSC.
- G. Yang, et al., Structure of graphene and its disorders: a review, Sci. Technol. Adv. Mater., 2018, 19(1), 613–648 CrossRef CAS PubMed.
- A. C. Ferrari, et al., Raman spectrum of graphene and graphene layers, Phys. Rev. Lett., 2006, 97(18), 187401 CrossRef CAS PubMed.
- B. Qin, et al., Crystalline Molybdenum Carbide–Amorphous Molybdenum Oxide Heterostructures: In Situ Surface Reconfiguration and Electronic States Modulation for Li–S Batteries, Energy Storage Materials, 2022, 14752 Search PubMed.
- C.-L. Dai, A capacitive humidity sensor integrated with micro heater and ring oscillator circuit fabricated by CMOS–MEMS technique, Sens. Actuators, B, 2007, 122(2), 375–380 CrossRef CAS.
- R. M. Metzger, Unimolecular and Supramolecular Electronics I: Chemistry and Physics Meet at Metal-Molecule Interfaces, Springer Science & Business Media, vol. 312, 2012 Search PubMed.
- J. Korvink, et al., Accurate 3D capacitance evaluation in integrated capacitive humidity sensors, Sens. Mater., 1993, 4, 323 CAS.
- M. Matsuguchi, et al., Characterization of polymers for a capacitive-type humidity sensor based on water sorption behavior, Sens. Actuators, B, 1998, 49(3), 179–185 CrossRef CAS.
- M. A. Omar, Elementary solid state physics: principles and applications, Pearson Education India, 1975 Search PubMed.
- M. Tahir, et al., Humidity, light and temperature dependent characteristics of Au/N-BuHHPDI/Au surface type multifunctional sensor, Sens. Actuators, B, 2014, 192, 565–571 CrossRef CAS.
- M. Shah, et al., Carbon nanotubes' nanocomposite in humidity sensors, Solid-State Electron., 2012, 69, 18–21 CrossRef CAS.
- P. Li, et al., Humidity sensor based on electrospun (Na0. 5Bi0. 5) 0.94 TiO3–Ba0. 06TiO3 nanofibers, Ceram. Int., 2015, 41(10), 14251–14257 CrossRef CAS.
- N. M. Kiasari, et al., Room temperature ultra-sensitive resistive humidity sensor based on single zinc oxide nanowire, Sens. Actuators, A, 2012, 182, 101–105 CrossRef.
- M. Haditale, R. Dariani and E. Ghasemian Lemraski, Electrical behavior of graphene under temperature effect and survey of I–T curve, J. Theor. Appl. Phys., 2019, 13(4), 351–356 CrossRef.
- E. Gibney, Graphene conducts electricity ten times better than expected, Nature, 2014, 2(6), 2–4 Search PubMed.
- M. Dewapriya, A. S. Phani and R. Rajapakse, Influence of temperature and free edges on the mechanical properties of graphene, Modell. Simul. Mater. Sci. Eng., 2013, 21(6), 065017 CrossRef CAS.
- C. Wang, et al., Metal oxide gas sensors: sensitivity and influencing factors, Sensors, 2010, 10(3), 2088–2106 CrossRef CAS PubMed.
- Q. Kuang, et al., High-sensitivity humidity sensor based on a single SnO2 nanowire, J. Am. Chem. Soc., 2007, 129(19), 6070–6071 CrossRef CAS PubMed.
- W.-P. Chen, et al., A capacitive humidity sensor based on multi-wall carbon nanotubes (MWCNTs), Sensors, 2009, 9(9), 7431–7444 CrossRef CAS PubMed.
- Z. Ahmad, et al., Humidity-dependent characteristics of methyl-red thin film-based Ag/methyl-red/Ag surface-type cell, Phys. E, 2008, 41(1), 18–22 CrossRef CAS.
- V. S. Turkani, et al., A carbon nanotube based NTC thermistor using additive print manufacturing processes, Sens. Actuators, A, 2018, 279, 1–9 CrossRef CAS.
- J.-S. Kim, K.-Y. Chun and C.-S. Han, Ion channel-based flexible temperature sensor with humidity insensitivity, Sens. Actuators, A, 2018, 271, 139–145 CrossRef CAS.
- Q. Liu, et al., A high-performances flexible temperature sensor composed of polyethyleneimine/reduced graphene oxide bilayer for real-time monitoring, Adv. Mater. Technol., 2019, 4(3), 1800594 CrossRef.
- N. Neella, et al., Scalable fabrication of highly sensitive flexible temperature sensors based on silver nanoparticles coated reduced graphene oxide nanocomposite thin films, Sens. Actuators, A, 2017, 268, 173–182 CrossRef CAS.
- M. I. Azmer, et al., Humidity sensor based on electrospun MEH-PPV: PVP microstructured composite, RSC Adv., 2016, 6(42), 35387–35393 RSC.
- M. Ueda, et al., Water-resistant humidity sensors based on sulfonated polyimides, Sens. Actuators, B, 2007, 127(2), 463–470 CrossRef CAS.
- U. Afzal, J. Afzal and M. Aslam, Analyzing the Imprecise Capacitance and Resistance Data of Humidity Sensors, Sens. Actuators, B, 2022, 132092 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |