Open Access Article
Open Access ArticleA study of the mechanical properties of the NEPE binders by molecular dynamic simulations and experiments
La Shi ,
Li Ren,
Yang Li,
Xiaolong Fu*,
Saiqin Meng and
Jiangning Wang
,
Li Ren,
Yang Li,
Xiaolong Fu*,
Saiqin Meng and
Jiangning Wang
Xi'an Modern Chemistry Research Institute, Xi'an 710065, China. E-mail: fuxiaolong204@163.com
First published on 1st June 2022
Abstract
In this study, the crosslinking structures of nitrate ester plasticized polyether (NEPE) binders were constructed by a computational procedure. Based on the final crosslinking models, the glass transition temperatures, mechanical properties, and thermal expansion coefficients of polyethylene glycol400/multi-functional isocyanate (PEG400/N-100), polyethylene glycol400/toluene diisocyanate (PEG400/HDI), polyethylene glycol400/hexamethylene diisocyanate (PEG400/TDI) and polyethylene glycol400/isophorone diisocyanate (PEG400/IPDI) models were simulated by molecular dynamics, and could be confirmed by experiments. Then the bond-length distributions, conformation properties and cohesive energy densities were used to analyze in detail how the different cured structures influenced the mechanical and thermal properties. Furthermore, the radial distribution function, mean square radius of gyration, volume shrinkage and fraction free volume were calculated, which could directly explain the relationships between the intermolecular chains and macroscopical properties of the NEPE binders. Lastly, PEG400/N-100 and PEG400/HDI systems were chosen for the experiments. The dynamic mechanical analysis results explained that PEG400-HDI showed better flexibility and its Tg value was 45 °C lower than that of PEG400-N100. The mechanical properties illustrated that the ultimate tensile strength and Young's modulus of PEG400/N-100 were both to an extent higher than that of PEG400/HDI in the temperature range of −40 °C to 50 °C, according to the results provided by a universal tensile test machine. The experimental results were in good agreement with the simulation analysis. This work can help us to have an efficient comprehension on the crosslinking structures and micro-property relationships of the NEPE binders and act as a guidance for designing applicable polyurethanes in propellant applications.
1 Introduction
There has been a lot of effort put into the research performances of energetic polymer binders for solid rocket propellants.1 Nitrate ester plasticized polyether (NEPE) propellants are new crosslinking solid propellants, which have a polyurethane network with excellent mechanical and thermal properties.2,3 The function of the binder system is to form a three-dimensional (3D) space,4,5 and stabilize plasticizers, oxidizing agents, additives and other propellant grains. The microstructure can affect the mechanical, viscoelastic and thermal properties, and the rocket motor could suffer a failure.6,7 Therefore, it is essential to explore the correction between the microstructures and macro-properties.8–11Molecular dynamics (MD) simulations of NEPE propellants have received increasing attention recently as a result of their capability to gain insightful structure–property information at the microscopic scale instead of experiments.12–16 During the curing stage, the hydroxyl groups of polyethylene glycol (PEG400) react with the isocyanate groups and produce polyurethane, and simulating the crosslinking of polymers is needed to modify the parameters repeatedly to gain useful insights. The crosslinking of polyurethanes can be affected by various factors, including the ratios of raw materials and conversion rates during the processing conditions.17 To overcome these barriers, many scientists have attempted various methods, such as quantum mechanics, coarse grain molecular simulations, kinetic Monte Carlo methods and cutoff distance methods. When analyzing the crosslinked polymers generated by a mapping procedure, Komarov et al.18 found that Tg increased with the increase in the degree of crosslinking. Schichtel et al.19 explored a modified method to model the curing crosslink structure, minimizing high potential energy reaction groups with practical flexibility. Aniruddh et al.10 replicated the polymerization process by a method called accelerated ReaxFF, which embraced the barrier energy, cutoff distance and the effect of molecular chemistry. Sun et al.20 simulated polymers under two typical force fields. Hall et al.21 created a new crosslink model construction technique, which indicated the prediction of the glass transition temperature, which was in good agreement with experimental results. Shen et al.22 discussed the effect of the crosslink density on the network topology by MD methods and experiments. Fankhänel et al.23 used MD simulations with atomic strain to estimate the elastic interphase properties. Radue et al.24 confirmed that MD simulations could be used to study the mechanical behavior of epoxies with the Reax force field. Yan et al.25 controlled the cutoff distances gradually and made the final crosslink density to 90% by MD simulations. Okabe et al.26 reproduced the actual curing reaction by MD methods and simulated the mechanical properties of epoxy resin, whose results confirmed the experimental data. Patil et al.27 used numerical simulated methods to predict the thermomechanical changes of the curing compounds. Zhang et al.28 simulated PEG at different polymerization degrees and found that EPEG became more stable when the polymerization degree was 90%.
In this study, MD simulation techniques and experiments were applied for assessing the mechanical properties of the binder systems in the NEPE propellant. First, by controlling the reaction distance, different crosslinking degree structures were obtained. Then based on the equilibrium crosslink structure, whose crosslinking rate of OH group was 100%, the mechanical and thermodynamic properties were analyzed. Simultaneously, some more simulations, for example, bond-length distribution analysis, conformation properties, cohesive energy density, radial distribution function, mean square radius of gyration, volume shrinkage and fractional free volume were assessed to verify the associations between the crosslinking structure and mechanical and thermal properties in the four NEPE binder systems. Lastly, PEG400/N-100 and PEG400/HDI systems were chosen for the experiments, including the dynamic mechanical and uniaxial tensile analysis.
2 Models and methods
2.1 Molecular model construction details
The models were built by Materials Studio. The chemical structures of polyethylene glycol400 (PEG400), multi-functional isocyanate (N-100), toluene diisocyanate (TDI), hexamethylene diisocyanate (HDI) and isophorone diisocyanate (IPDI) are shown in Fig. 1. The PEG polymer chains were built with repeat units in the Builder Polymers module, and the mean molecular weight was 400 g mol−1. All models were optimized with Compass II force field29 in the Forcite module. The oxygen atoms of PEG400 were named as R2, and the carbon atoms of isocyanate in the curing agents (N-100, IPDI, HDI and TDI) were labeled as R1, which could be recognized by the procedure.2.2 Computational details
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 step energy minimization. Then, the amorphous bends needed annealing from 298 K to 598 K, with 20 K ramps per cycle and 5 annealing cycles. There were 200 ps NPT dynamics in every temperature ramp and 40
000 step energy minimization. Then, the amorphous bends needed annealing from 298 K to 598 K, with 20 K ramps per cycle and 5 annealing cycles. There were 200 ps NPT dynamics in every temperature ramp and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of the total number. Further, these bends were subsequently optimized for 400 ps with a time step of 1 fs, which involved selecting the NVT ensemble and NHL30 thermostat at 298 K in the Forcite module, in which the decay constant was 1 ps. Then, the ensemble was converted into NPT, NHL thermostat and Berendsen31 barostat under 10−4 GPa pressure and 5
000 steps of the total number. Further, these bends were subsequently optimized for 400 ps with a time step of 1 fs, which involved selecting the NVT ensemble and NHL30 thermostat at 298 K in the Forcite module, in which the decay constant was 1 ps. Then, the ensemble was converted into NPT, NHL thermostat and Berendsen31 barostat under 10−4 GPa pressure and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy deviation, with other parameters unchanged. When the temperature and energy were in equilibrium, the amorphous system reached a balance. Next, the cure reactions occurred between the isocyanates and hydroxide radicals of the equilibrium binder systems. The models of the NEPE binder system are shown in Fig. 1.
000 energy deviation, with other parameters unchanged. When the temperature and energy were in equilibrium, the amorphous system reached a balance. Next, the cure reactions occurred between the isocyanates and hydroxide radicals of the equilibrium binder systems. The models of the NEPE binder system are shown in Fig. 1.The steps of the crosslinking mechanism algorithm are shown in Fig. 3, which were accomplished automatically by Perl scripts written according to the mechanism of the double bond addition reaction of alcohols with isocyanates. Some assumptions made are as follows: (i) the PEG400 chains and curing agents were selected equiprobably. Also, all the reactive groups, including the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and O–H, were assumed to be spheres of a certain radius. (ii) The reactive groups were activated when they met within a set distance. (iii) The activated groups shifted into the crosslinking groups. If there were no more reactive groups within the distance, the reaction radius was gradually added by 0.5 Å. The reaction would halt until the OH groups had run out. The conversion, temperature (T), min reaction radius (Rmin), max reaction radius (Rmax) and other parameters were stipulated. For example, the conversion (α) was 100%, T was 600 K and Rmin and Rmax were at 3.5 Å and 14 Å, respectively. When the active groups just met in the distance between Rmin and Rmax, the crosslinking reaction would happen and the atoms would be connected. If they were a cured group, there would be no reaction.
O and O–H, were assumed to be spheres of a certain radius. (ii) The reactive groups were activated when they met within a set distance. (iii) The activated groups shifted into the crosslinking groups. If there were no more reactive groups within the distance, the reaction radius was gradually added by 0.5 Å. The reaction would halt until the OH groups had run out. The conversion, temperature (T), min reaction radius (Rmin), max reaction radius (Rmax) and other parameters were stipulated. For example, the conversion (α) was 100%, T was 600 K and Rmin and Rmax were at 3.5 Å and 14 Å, respectively. When the active groups just met in the distance between Rmin and Rmax, the crosslinking reaction would happen and the atoms would be connected. If they were a cured group, there would be no reaction.
Finally, the crosslinked models were optimized, carried out by the molecular dynamic simulation in NVT and NPT ensembles. Furthermore, the optimized crosslinked models were annealed. All these parameters were identical to those in the section 2.1. The curing degree of binders is defined as the number of reacted hydroxyl sites over the total number hydroxyl sites of PEG400.
2.3 Materials and experiments
The dynamic mechanical properties of the samples were tested by dynamic mechanical analyzers (DMA850, Single Cantilever), fixed with a tensile clamp. The sample size prepared was 35 mm × 13 mm × 3 mm. The test temperature was swept from −120 °C to 100 °C with the liquid nitrogen refrigerant. The heating rate was 3 °C min−1 and the loading frequency was 1 Hz. The mechanical properties were obtained at a crosshead speed of 500 mm min−1 by a universal testing machine (AG-X plus, 5 kN, Shimadzu, Japan) by processing into JANNAF dog bones (length 75 mm × narrow parallel width 4 mm × thickness 2 mm) as shown in Fig. 5.
3 Results and discussion
3.1 Simulation parts
| σij = Cijεij | (1) |
In the molecular simulation, stress could be provided from eqn (2).
 | (2) |
For the isotropic polymers, the stiffness matrix could provide the effective Lame's constants λ and μ according to the equations below.
 | (3) |
 | (4) |
Lastly, the Young's modulus E, shear modulus G, bulk modulus K and Poisson' ratio ν could be calculated from the following equations.
 | (5) |
| G = μ | (6) |
 | (7) |
 | (8) |
The mechanical properties of the NEPE binders at 273.15 K were calculated and are listed in Table 1, obtained through formulations eqn (3)–(9) by MD simulations. As the results show, PEG400/HDI has the highest Young's modulus 8.272 GPa and shear modulus 3.087 GPa but PEG400/IPDI has the highest bulk modulus 7.730 GPa. This indicates that the curing agents have an important impact on the mechanical properties.
| System | Bulk modulus (GPa) | Shear modulus (GPa) | Young's modulus (GPa) | Poisson ratio |
|---|---|---|---|---|
| PEG400/N-100 | 8.644 | 2.298 | 6.332 | 0.378 |
| PEG400/HDI | 8.617 | 3.087 | 8.272 | 0.340 |
| PEG400/TDI | 8.546 | 2.254 | 6.215 | 0.379 |
| PEG400/IPDI | 7.730 | 2.532 | 6.849 | 0.352 |
 | (9) |
CTE would fluctuate dramatically around Tg, thus the volume of the high and low temperature range is chosen to obtain β. The values of CTE were calculated from the volume as a function of temperature, referred to in eqn (9). The results of the volume coefficient of thermal expansion are listed in Table 2. For the four binder systems, CTE below Tg were appreciably smaller than the values above Tg. CTE from the glassy state to rubbery state changed most significantly in the PEG400/TDI system.
| System | Below Tg (K−1) | Above Tg (K−1) |
|---|---|---|
| PEG400/N-100 | 4.32 × 10−4 | 5.50 × 10−4 |
| PEG400/HDI | 1.24 × 10−4 | 2.80 × 10−4 |
| PEG400/TDI | 6.12 × 10−5 | 3.03 × 10−4 |
| PEG400/IPDI | 1.54 × 10−4 | 2.61 × 10−4 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, N
O, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–N bonds of the crosslink structure changed at the left of the original monomers in all the systems. Also, from the molecular model in Fig. 7, the bond details are provided between the no curing monomers and cured structures.
C and C–N bonds of the crosslink structure changed at the left of the original monomers in all the systems. Also, from the molecular model in Fig. 7, the bond details are provided between the no curing monomers and cured structures.
 | ||
| Fig. 8 The torsion rotation of the special bonds φ1 and φ2 in the NEPE binders: (a) PEG400/N-100, (b) PEG400/HDI, (c) PEG400/TDI, (d) PEG400/IPDI. | ||
The cohesive energy (Ecoh) is described as the average energy required per mole of the system if all intermolecular forces were overcome. It can be calculated by the following eqn (10).41
| Ecoh = 〈Einter〉 = 〈Etotal〉 − 〈Eintra〉 | (10) |
CED is the cohesive energy density per unit volume, and is given by the formula (11) below.
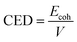 | (11) |
The simulated cohesive energy density results for the NEPE binders in the four systems are presented in Table 3. Here, PEG400-N100 has the highest value 8.590 × 108 J m−3, which shows that the intermolecular forces in PEG400-N100 are the strongest. On the contrary, PEG-IPDI with 2.402 × 108 J m−3 has the weakest intermolecular forces among the different binder systems in this study. Through the CED analysis, the Tg and modulus of PEG400-N100 were found to be the highest, and are highly consistent with the properties determined by molecular dynamic simulations.
| System | PEG400-N100 | PEG400-HDI | PEG400-TDI | PEG400-IPDI |
|---|---|---|---|---|
| CED (J m−3) | 8.590 × 108 | 4.449 × 108 | 4.527 × 108 | 2.402 × 108 |
 | (12) |
 to
to  .
.In brief, the intermolecular interactions usually refer to the hydrogen bonding (2.0 Å ≤ r < 3.1 Å), van der Waals forces 3.1 Å ≤ r < 5 Å and weak van der Waals forces 5 Å < r.42,43 Fig. 10 shows the peak position (r) and g(r) intensities of the four kinds of NEPE binder systems. For the radial distribution functions of the NEPE binders, there are some peaks from the distance 1.1 Å to 2.0 Å, corresponding to the bond-length distribution. Comparing and contrasting intramolecular chemical bonding and intermolecular nonbonding, the hydrogen bonding and van der Waals forces are smaller forces.
 | ||
| Fig. 10 Radial distribution function of the NEPE binders in PEG400/N-100, PEG400/HDI, PEG400/TDI and PEG400/IPDI systems. | ||
Most of the imines of various groups in polyurethane can form hydrogen bonds, with most of them formed with a carbonyl group in the hard segment, and a small part formed between ether the oxygen group or ester carbonyl group in the soft segment.44,45 Fig. 11 shows the radial distribution functions between the donor H atoms and accepter 0 atoms or N atoms. The first peak of the four systems were all around 1.1 Å between H and N atoms, which were the intramolecular N–H bonds of the crosslinking structure. The most obvious peaks were in the distance range from 2 Å to 3.1 Å, which meant that strong hydrogen bonding existed in the crosslinking structure. Also, the hydrogen bonding of PEG400-TDI was partly weaker than in others. These analysis results are consistent with the wonderful mechanical properties of the NEPE binders from the simulations. Further, vdW and hydrogen bonding played important roles in the crosslinking structure of this study.
 | (13) |
If the polymer chain contains many chain units, and the mass of each chain unit is mi, then the distance from the center of mass of the polymer chain to the first chain unit is ri.
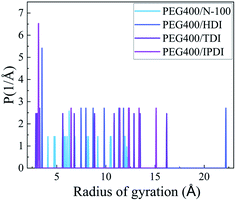
The mean square radius of gyration curves of the NEPE binders about different systems are shown in Fig. 12. The radius of gyration of PEG400-N100, PEG400-HDI, PEG400-TDI and PEG400-IPDI widely ranged from 4.06 Å to 12.27 Å, 3.36 Å to 22.24 Å, 2.83 Å to 16.24 Å and 3.09 Å to 15.15 Å, respectively. The least dispersed radius of gyration distribution and lowest peak were for PEG400-N100, while PEG400-HDI had the most scattered one, which reflected that the latter had a small polymer chain nematic size. This analysis is in accordance with the earlier Tg and conformation properties.
 | ||
| Fig. 13 The free volume distribution of the NEPE binders: (a) PEG400/N-100, (b) PEG400/HDI, (c) PEG400/TDI and (d) PEG400/IPDI. | ||
The mechanical and thermal properties of polyurethane are largely determined by the free volume and movement of molecular chain segments. According to the free volume theory, the volume VT of liquid and solid substances consists of two parts, one is the van der Waals volume occupied by molecules, V0, and the other is the unoccupied volume, Vf, namely the free volume. Due to the different volumes of different polymer systems, it is generally not possible to directly compare the free volume of each system. The distributions of V0 and Vf are shown in Fig. 13, and the calculated results are shown in Table 4. Therefore, the fractional free volume (FFV) was introduced to represent the relative size of the free volume, and is expressed by eqn (14).
 | (14) |
| System | V0 (Å3) | Vf (Å3) | FFV (%) |
|---|---|---|---|
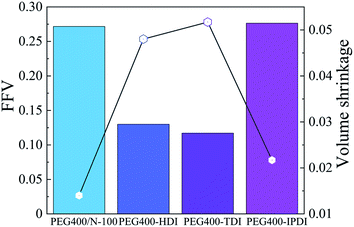
| PEG400/N-100 | 22283.14 | 8312.28 | 27.17 |
| PEG400/HDI | 17135.73 | 2560.54 | 13.0 |
| PEG400/TDI | 16409.96 | 2176.41 | 11.71 |
| PEG400/IPDI | 18516.52 | 7071.24 | 27.64 |
Also, the free volume fraction and volume shrinkage of NEPE binder in the four systems are presented in Fig. 14. The FFV values of PEG400/N-100, PEG400/HDI, PEG400/TDI and PEG400/IPDI were 27.17%, 13.0%, 11.7% and 27.64%, respectively. This indicates that the spatial crosslinking structure of PEG400/N-100 and PEG400/IPDI can supply more interspace. In addition, these also resulted in volume shrinkage during the curing progress.
3.2 Experimental parts
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of two different binder systems as a function of temperature at the frequency 1 Hz. On account of the interactions being weakened among the molecular chains, the E′ of the two systems were in a continuous downward trend with increasing temperature. The storage modulus of PEG-HDI was higher than that of PEG-N100 at the same temperature and was influenced more significantly by the temperature change. The loss modulus is a mechanical loss, which describes the phenomenon of energy transformation into heat when materials are in viscosity deformation. Although the loss modulus of PEG400/N-100 was higher than that of PEG-HDI below −50 °C, PEG400/HDI quickly went beyond the latter. When the temperature increased, the ability of the polymer chains to move and deform viscously would be aggrandized.
δ) of two different binder systems as a function of temperature at the frequency 1 Hz. On account of the interactions being weakened among the molecular chains, the E′ of the two systems were in a continuous downward trend with increasing temperature. The storage modulus of PEG-HDI was higher than that of PEG-N100 at the same temperature and was influenced more significantly by the temperature change. The loss modulus is a mechanical loss, which describes the phenomenon of energy transformation into heat when materials are in viscosity deformation. Although the loss modulus of PEG400/N-100 was higher than that of PEG-HDI below −50 °C, PEG400/HDI quickly went beyond the latter. When the temperature increased, the ability of the polymer chains to move and deform viscously would be aggrandized.
Tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is equal to the ratio of the loss modulus to the storage modulus and its curve peak point corresponding temperature is defined as Tg.46 The loss factor tan
δ is equal to the ratio of the loss modulus to the storage modulus and its curve peak point corresponding temperature is defined as Tg.46 The loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curves of the various samples are shown in Fig. 16. It is obvious that the Tg values of PEG400/N-100 and PEG400/HDI are 15.74 °C and −29.29 °C, respectively. PEG400/HDI showed better flexibility and the value of Tg was 45 °C lower than that of PEG400/N-100. The simulation Tg values were somewhat higher than the DMA experiment results, mainly because the cooling rates of the simulated temperature differed a lot from the real experimental sets.47
δ curves of the various samples are shown in Fig. 16. It is obvious that the Tg values of PEG400/N-100 and PEG400/HDI are 15.74 °C and −29.29 °C, respectively. PEG400/HDI showed better flexibility and the value of Tg was 45 °C lower than that of PEG400/N-100. The simulation Tg values were somewhat higher than the DMA experiment results, mainly because the cooling rates of the simulated temperature differed a lot from the real experimental sets.47
| System | T (°C) | σm (MPa) | εb (%) | Eexp (MPa) |
|---|---|---|---|---|
| PEG400/N-100 | −40 | 55.45 ± 10.45 | 10.18 ± 1.38 | 5752 ± 363.32 |
| 20 | 9.63 ± 0.02 | 81.70 ± 2.45 | 98 ± 35.50 | |
| 50 | 8.98 ± 1.65 | 862.98 ± 40.68 | 63 ± 10.20 | |
| PEG400-HDI | −40 | 13.63 ± 1.65 | 255.62 ± 78.02 | 1558 ± 220.45 |
| 20 | 6.74 ± 1.58 | 1277.26 ± 144.82 | 74 ± 11.00 | |
| 50 | 4.38 ± 0.91 | 61.48 ± 8.85 | 40 ± 6.53 |
In the initial loading stage, the steep rise trends indicated the high elastic modulus of the NEPE binders. The two binder systems showed similar behaviors at different testing temperatures. The stress–strain curves reached a maximum tensile strength and then the curve curl stopped, corresponding to the break strain.
Obviously, the σm and Eexp of both systems decreased gradually with the increase in temperature. These phenomena mainly resulted from the freezing movements of the molecular chains and more external force would be needed at a lower temperature. When the temperature was −40 °C, i.e. under the glass transition temperature, the σm and Eexp of PEG400/N-100 and PEG400/HDI showed ideal values of 55.45 ± 22.45 MPa and 13.63 ± 1.65 MPa, 5752 ± 363.32 MPa and 1558 ± 220.45 MPa, respectively. These results confirmed the DMA analysis that the mechanical properties would change a lot around the glass transition temperature. Furthermore, the σm and Eexp of PEG400/N-100 were consistently higher than the values of PEG400/HDI at the same temperature and the former had a tougher binder system. The reason was that the curing agent N-100 modified by HDI would present a more perfect 3D network in the NEPE binder system. The elongation at break of PEG400/N-100 was reduced when the temperature increased, while the εb values of PEG400/HDI would increase first and decrease later with the rising temperature. Generally speaking, the uniaxial tensile analytical results were in good agreement with the DMA results.
4 Conclusions
In this paper, the molecular dynamics simulation combined with experimental ways were applied to study how the crosslinking molecular structure was connected with the mechanical and thermal properties of the NEPE binders in four different polyurethane systems, namely PEG400/N-100, PEG400/HDI, PEG400/TDI and PEG400/IPDI. Further, the following results are presented.To begin with, we constructed the basic blend model, obtained the high crosslinking (100%) structure by Perl scripts and optimized this until the system reached equilibrium.
Then, the glass transition temperature of PEG400/N-100, PEG400/HDI, PEG400/TDI and PEG400/IPDI were found to be 335 K, 304 K, 283 K and 292 K, respectively. The simulation results for the mechanical properties indicated that PEG400/HDI had the highest bulk modulus, shear modulus and Young's modulus among the four systems at 273.15 K. As expected, the thermal expansion coefficient shifted from below Tg to above Tg. The bond-length distributions of the original prepolymer and curing agents all differed from the final crosslink structure, including the appearance of some new bonds (C–O) and some old bond positions changed. The conformation properties analysis proved that PEG400/HDI had the lowest synergetic rotational energy barrier and PEG400/IPDI had the highest one. The cohesive energy density results verified that PEG400-N100 had the highest value of 8.590 × 108 J m−3 and PEG-IPDI had the least value of 2.402 × 108 J m−3. Strong hydrogen bonding was found in the crosslink structure through the radial distribution function. PEG400-N100 exhibited the most regular radius of gyration distribution, but PEG400-HDI built the most dispersive one. The volume shrinkage and fractional free volume results verified that the mechanical properties were closely connected with the 3D network.
Lastly, the dynamic mechanical analysis results indicated that PEG400-HDI showed better flexibility and the value of Tg was 45 °C lower than that of PEG400-N100. The mechanical property data demonstrated the better flexibility of the PEG400/HDI system connected with the significant broad elongation at break. The maximal tensile stress and Young's modulus corresponded to the crosslink structure analysis by the simulation methods.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This study has been financially supported by National Natural Science Foundation of China (21975150).References
- Y. Wang, H. Rong, X. Zhang, Y. Chen, W. Luo, Y. Liu, W. Yao and Y. Tian, Propellants, Explos., Pyrotech., 2021, 46, 950–961 CrossRef CAS.
- C. M. Roland and B. P. Mason, Rubber Chem. Technol., 2019, 92, 1–24 CrossRef.
- H. Tan, The Chemistry and Technology of Solid Rocket Propellant, Beijing Institute of Technology Press, 2015 Search PubMed.
- R. G. Stacer and D. M. Husband, Propellants Explos. Pyrotech., 1991, 16, 167–176 CrossRef CAS.
- W. Xu, J. Deng and l. Zhang, J. Solid Rocket Technol., 2010, 33, 560–563 CAS.
- Y. Chen, Y. Liu and H. Tan, Chin. J. Explos. Propellants, 2008, 31, 56 Search PubMed.
- W. e. Wu, C. Chen, X. Fu, C. Ding and G. Wang, Propellants, Explos., Pyrotech., 2017, 42, 541–546 CrossRef CAS.
- X. Yang, Y. Wan, X. Wang, Y. Fu, Z. Huang and Q. Xie, Composites, Part B, 2019, 164, 659–666 CrossRef CAS.
- Z. Yu, W. Wang, W. Yao, W. Zhang, W. Xie, Y. Liu, Y. Zhao, H. Tan and Y. Chen, J. Energ. Mater., 2021, 39, 74–84 CrossRef CAS.
- A. Vashisth, C. Ashraf, C. E. Bakis and A. V. Duin, Polymer, 2018, 158, 354–363 CrossRef CAS.
- W. Zhang, Q. Yang, W. Zhong, S. Gang and X. Yang, React. Funct. Polym., 2017, 111, 60–67 CrossRef CAS.
- X. Fernàndez-Francos, À. Serra and X. Ramis, Eur. Polym. J., 2014, 53, 22–36 CrossRef.
- G. Wang, S. Hou, W. Wu and H. Li, J. Solid Rocket Technol., 2015, 38, 684–688 Search PubMed.
- M. An, B. Demir, X. Wan, H. Meng, N. Yang and T. R. Walsh, Adv. Theory Simul., 2019, 2, 1800153 CrossRef.
- P. Zhang, T. Li, S. Liu and J. Deng, Comput. Mater. Sci., 2020, 171, 109135 CrossRef CAS.
- L. A. Richards, A. Nash, M. Phipps and N. Leeuw, New J. Chem., 2018, 42, 17420–17428 RSC.
- K. Chen, S. Yuan, X. Wen, C. Sang and Y. Luo, Propellants, Explos., Pyrotech., 2021, 46, 428–439 CrossRef CAS.
- P. V. Komarov, C. Yu-Tsung, C. Shih-Ming, P. G. Khalatur and P. Reineker, Macromolecules, 2007, 40, 8104–8113 CrossRef CAS.
- J. J. Schichtel and A. Chattopadhyay, Comput. Mater. Sci., 2020, 174, 109469 CrossRef CAS.
- Y. Sun, C. Lin, C. Liu, Y. Zhang and X. Du, Comput. Mater. Sci., 2018, 143, 240–247 CrossRef CAS.
- S. A. Hall, B. J. Howlin, I. Hamerton, A. Baidak, C. Billaud and S. Ward, PLoS One, 2012, 7, e42928 CrossRef CAS PubMed.
- J. Shen, X. Lin, J. Liu and X. Li, Macromolecules, 2019, 52, 121–134 CrossRef CAS.
- J. Fankhänel, B. Arash and R. Rolfes, Composites, Part B, 2019, 176, 107211 CrossRef.
- M. S. Radue, B. D. Jensen, S. Gowtham, D. R. Klimek-Mcdonald, J. A. King and G. M. Odegard, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 255–264 CrossRef CAS PubMed.
- S. Yan, W. Verestek, H. Zeizinger and S. Schmauder, Polymers, 2021, 13, 3085 CrossRef CAS PubMed.
- T. Okabe, Y. Oya, K. Tanabe, G. Kikugawa and K. Yoshioka, Eur. Polym. J., 2016, 78–88 CrossRef CAS.
- A. S. Patil, R. Moheimani and H. Dalir, Therm. Sci. Eng. Prog., 2019, 14, 100419 CrossRef.
- P. Zhang, A. Pang, G. Tang and J. Deng, Appl. Surf. Sci., 2019, 493, 131–138 CrossRef CAS.
- H. Sun, Z. Jin, C. Yang, R. L. C. Akkermans, S. H. Robertson, N. A. Spenley, S. Miller and S. M. Todd, J. Mol. Model., 2016, 22, 47 CrossRef PubMed.
- B. Leimkuhler, E. Noorizadeh and O. Penrose, J. Stat. Phys., 2011, 143, 921–942 CrossRef.
- H. J. Berendsen, J. V. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- P. Zhang, J. Yuan, A. Pang, G. Tang and J. Deng, Composites, Part B, 2020, 195, 108087 CrossRef CAS.
- J. Konrad, R. H. Meißner, E. Bitzek and D. Zahn, ACS Polym. Au, 2021, 1, 165–174 CrossRef CAS.
- J. Pascault and R. Williams, J. Polym. Sci., Part B: Polym. Phys., 1990, 28, 85–95 CrossRef CAS.
- N. R. Jadhav, V. L. Gaikwad, K. J. Nair and H. M. Kadam, Asian J. Pharm., 2009, 3, 82–89 CrossRef.
- G. Roudaut, D. Simatos, D. Champion, E. Contreras-Lopez and M. Le Meste, Innovative Food Sci. Emerging Technol., 2004, 5, 127–134 CrossRef CAS.
- J. Forrest, K. Dalnoki-Veress, J. Stevens and J. Dutcher, Phys. Rev. Lett., 1996, 77, 2002 CrossRef CAS PubMed.
- K. Fu, Q. Xie, L. Fangcheng, Q. Duan and Z. Huang, Polymers, 2019, 11, 975 CrossRef PubMed.
- Y. Qing, X. Li, L. Shi, X. Yang and G. Sui, Polymer, 2013, 54, 6447–6454 CrossRef.
- G. Liang, Q. Zhang, H. Li, S. Yu, W. Zhong, G. Sui and X. Yang, Polym. Chem., 2017, 8, 2016–2027 RSC.
- J. H. Hildebrand, Regular and related solutions: the solubility of gases, liquids, and solids, 1970 Search PubMed.
- H. Li, Y. Zhao and Y. Ning, J. Hazard. Mater., 2019, 362, 303–310 CrossRef PubMed.
- T. Steiner and G. R. Desiraju, Chem. Commun., 1998, 891–892 RSC.
- J. Blackwell and K. H. Gardner, Polymer, 1979, 20, 13–17 CrossRef CAS.
- C. Hepburn, Prog. Polym. Sci., 1991, 16, 695–836 CrossRef.
- Y. Du, J. Zheng and G. Yu, Polymers, 2020, 12, 403 CrossRef CAS PubMed.
- S. Kawana and R. Jones, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 021501 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |