Open Access Article
Open Access ArticlePerformance experiments with a gas wave ejector equipped with curved channels and an analysis of the influence of channel angles
Yiming Zhao ,
Haoran Li and
Dapeng Hu*
,
Haoran Li and
Dapeng Hu*
Department of Chemical Machinery, Dalian University of Technology, Dalian 116012, China. E-mail: hudp@dlut.edu.cn
First published on 16th June 2022
Abstract
Gas wave ejectors (GWEs) utilize pressure waves to efficiently transfer energy between gases, and they have broad applications in the chemical industry. In order to improve the performance of GWEs, the influence of bending angles on GWE performance was studied and experiments involving a GWE equipped with curved channels were carried out for the first time in this study. The research results show that when the exhaust angle difference (φdout) is ≤−3.9° and the incident angle difference (φdin) is >5.0° or ≤−5.0°, the equipment performance decreases with an increase in the absolute values of the angle differences. The maximum efficiency of the backward-curved-channel device is 61.6% within the experimental range. The experimental efficiency of the curved-channel device and the static-pressure proportion of the total pressure of the medium-pressure gas are enhanced in comparison with a traditional straight-channel device, and the operating power consumption is relatively reduced. Due to the difference between the gas incident and exhaust angles, the manner in which the performance of the curved-channel device varies with the rotation speed is different depending on the working conditions.
1. Introduction
Compared with traditional energy sources such as oil and coal, natural gas, as a safer and cheaper clean fuel, is used much more widely in daily life.1 Meanwhile, the plentiful global reserves of natural gas could satisfy long-term requirements based on relevant assessments.2 Therefore, solutions that can promote the extraction and transportation efficiencies of natural gas have drawn much attention. Commonly, tight gas wells or newly opened wells whose pressures are higher than required for gathering and transportation are throttled to meet unified requirements, resulting in the wasting of the pressure energy of high-pressure gas.3 Meanwhile, the pressures of shallow gas wells and medium/late-stage wells are often lower than the unified requirements and, because of this, turbo-charged mining methods are often applied, which can result in large amounts of power consumption.4 To solve the problems mentioned above, static ejectors and gas wave ejectors (GWEs) are often introduced to achieve energy transfer between high- and low-pressure gases. The utilization of excess pressure energy from high-pressure gas to boost low-pressure gas can not only reduce the wasting of gas energy, but this can also increase production from low-pressure wells via conserving energy and reducing emissions. This is an effective way to solve the problem of pressure inconsistency between gas wells.A static ejector is a stationary device that can realize direct-contact energy transfer between gases. It primarily utilizes the turbulent diffusion of the high-speed jet created by a high-pressure fluid to entrain a low-pressure fluid, and energy transfer between fluids is completed via their direct mixing.5,6 A static ejector has the advantages of a simple structure and low manufacturing cost,7 but it mainly achieves energy transfer via intermolecular collisions, resulting in high levels of viscous dissipation during the transfer process. As a result, when the pressure ratio between the high- and low-pressure gases is small, the isentropic efficiency of this device is low and its pressurization capacity is severely limited.8
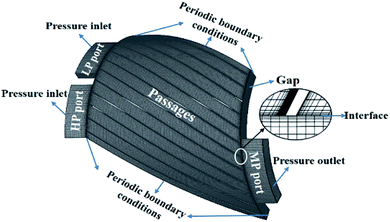
Compared with a static ejector, a GWE primarily employs pressure waves to transfer energy between gases, making its working efficiency significantly higher than that of a traditional static ejector under applicable conditions. The fundamental components of a GWE include a wave rotor composed of homogeneous channels and fixed end-plates with pressure ports (as shown in Fig. 1). A GWE usually has the advantages of a low rotational speed, simple structure, low manufacturing and maintenance costs, and strong liquid carrying capacity, since the rotor channels serving as the container for gas energy exchange have simple geometry and high strength. It has the potential to provide an effective technical method for resolving natural gas transportation issues, improving chemical engineering energy utilization efficiency, and reducing engineering energy consumption.
Currently, wave rotor technology has been successfully applied in the gas turbine top cycle,9–11 gas expansion refrigeration cycle,12–14 and some other fields.15–17 As an important component of wave rotor technology, GWEs have been investigated by several scientific research institutions, as shown in Fig. 2.12,17,23 Power Jets Co., Ltd18 first proposed the concept of a GWE, and then Spalding19 performed preliminary related theoretical research. Kentfield et al.20 of Imperial College London accomplished the first test of this technology in conjunction with a gas-wave divider,21 proving that these two three-port wave rotor devices can achieve equivalent efficiency to turbomachinery when the pressures at each port are close enough. Kharazi et al.22,23 of Michigan State University proposed the application of this technology to the R718 refrigeration cycle, using liquid water to eject and compress water vapor for condensation, instead of using a condenser and first-stage compressor. This can help to reduce the overall structure size and the manufacturing and operating costs of this system by nearly 50%. Hu et al.27–29 of Dalian University of Technology began to conduct in-depth numerical and experimental research on GWEs based on their extensive experience in the area of gas-wave technology.24–26 They obtained the complete performance curves of GWEs equipped with straight rotor channels30 and determined the laws governing the effects of parameters such as rotational speed on equipment performance.31
 | ||
| Fig. 2 Research progress relating to GWE technology. The numbers in square brackets indicate the reference work from which each panel is adapted. | ||
The research related to GWEs mentioned above has defined appropriate functional wave systems and preliminarily verified the application feasibility of this technology in the field of pressure equalization. However, since all existing gas flow and gas wave theories related to GWEs are based on equal-section straight rotor channels, the GWE devices investigated by various institutions are all equipped with straight channels.20,27 According to the relevant studies, there is large flow loss in straight channels during the gas injection process.31,32 Furthermore, the viscous dissipation of gas and other flow losses can be promoted due to the medium-pressure gas being exhausted along the rotor rotational direction. Because the expansion and compression waves are isentropic in theory and the theoretical boosting efficiency of the shock wave can reach more than 75% when the pressure ratio is less than 5.0, the above-mentioned gas flow loss phenomena are proposed to be a major factor affecting the performance of GWEs with straight channels over a certain range of operating conditions.12 This study applied a curved rotor channel in GWE technology in order to resolve this issue. The mechanism of influence of the channel bending angle on equipment performance was obtained via analyzing the impact of angles on the gas wave and gas flow processes. Also, the practical application effects of curved channels in GWEs were verified via comparative experiments. Different from internal combustion wave rotors or gas wave superchargers, which both employ curved channels to provide shaft power output,33–36 this research focuses on using a curved channel to reduce the energy loss inside a GWE and improve its working efficiency. The research results can play a certain role in promoting theoretical improvements and extending the application of this technology.
2. Working principles and performance evaluation parameters of a GWE
The essential operating principle of a GWE can be better explained via expanding the wave rotor and pressure ports into an x–t (axial position-time) planar coordinate system. The pressure distribution (as shown in Fig. 3) demonstrates that the high-pressure gas enters into the channels and forms an incident shock wave S to compress the original gas in channels when the channels rotate to connect with the high-pressure port (translation in the plane development). The opening reflection of S happens as the channels move to connect with the medium-pressure port, forming an expansion wave E1 that accelerates the gas in the channels for discharge via the medium-pressure port. When the channels deviate from the high-pressure port, an expansion wave E2 forms to decelerate and depressurize the gas in the channels, and gas discharge comes to a halt when E2 arrives at the outlet end of the channels. Because of E1 and E2, a deep expansion region with pressure lower than the low-pressure gas is generated in the channels, and the low-pressure gas will be sucked into channels when the channels connect to the low-pressure port. A compression wave C is generated during the closing of the medium-pressure port. The low-pressure gas stops entering the channels when C arrives at the inlet end of the channels. The channels close at both ends when they deviate from the low-pressure port, and the intensity of the oscillating pressure waves existing in the channels gradually weakens after multiple reflections. The gas in the channels eventually enters a stable state with a rather uniform pressure distribution before reconnecting to the high-pressure port.The energy exchange between gases can be divided into two processes based on the above-mentioned working principle of a GWE: the high-pressure gas expands to output work; and the low-pressure gas is compressed via receiving the expansion work. Wep and Weps are used to represent the high-pressure gas actual output work and the isentropic expansion work, respectively, in this study, and they can be expressed as follows:
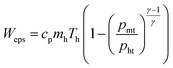 | (1) |
| Wep = Wepsηep | (2) |
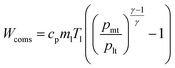 | (3) |
 | (4) |
 | (5) |
In addition to the isentropic efficiency η, as an ejection device, the ejection rate ξ can be given as follows:
 | (6) |
The working conditions of a GWE can be represented using the expansion ratio α and the compression ratio β, and the specific expressions of both are as follows:
 | (7) |
 | (8) |
3. Numerical simulations
3.1 Model for numerical simulations
As shown in Fig. 5a, this paper proposes using the single-directrix scanning method to construct the inner cylinder blades. Via changing the alignment parameters, this method can achieve not only variable channel bending angles but also a smooth transition between angles at both ends. Meanwhile, the thickness of partitions can be ensured to be uniform and the partitions can be radially distributed on the rotor end faces through this construction approach. As demonstrated in Fig. 5b, the single directrix bc used in this paper is a curve segment intercepting the generatrix ao according to the channel length and bending angle requirements, where r represents the radius of the rotor middle surface, and α1 and β1 represent the envelope angle (set to 90° in this paper) and the outlet angle of the generatrix ao, respectively.
 | ||
| Fig. 5 Schematic diagrams of the channel forming method: (a) a schematic diagram of blade forming; (b) an extended diagram of a single directrix. | ||
The equation of the arc-type generatrix is as follows:
 | (9) |
 | (10) |
| l = πrmα1t/180 (0 ≤ t ≤ 1) | (11) |
As shown in Fig. 6, the flow domains of the three-dimensional numerical model established in this research primarily consisted of the fixed pressure ports, rotating rotor channels, and static gaps between the ports and channels. The borders of the high- and low-pressure ports were defined as the pressure inlet boundaries, and the border of the medium-pressure port was set as the pressure outlet boundary. The end faces of channels, end faces of pressure ports close to the channels, and end faces of gaps were all set as sliding mesh interfaces to connect each flow domain. Since the motion process of each rotor channel between the pressure ports is identical, the calculation model only considered some channels to save computing resources, and the cyclic motion of channels between the pressure ports was realized via setting periodic boundaries. Except for the above-mentioned boundary surfaces, the other model surfaces were set as walls. Pressure wave propagation and the pressure exchange processes between gases in the rotor channels are extremely fast, and the temperature differences between gases in the flow channels are small, so there is not enough time for heat exchange between the gas and the walls. Therefore, the wall surfaces were all set to be adiabatic. The boundary settings of the calculation model are shown in Table 1.
| Part of geometry | Boundary condition type |
|---|---|
| High-pressure end face | Pressure inlet |
| Low-pressure end face | Pressure inlet |
| Medium-pressure end face | Pressure outlet |
| Interfaces of fluid domains | Sliding mesh interface |
| Side faces of the passages on both sides of the model | Periodic boundary conditions |
| Walls | Adiabatic/smooth |
The fluid medium used in this study was air (at room temperature with pressure less than 0.3 MPa), which can be assumed to be an ideal gas. The state equation is as follows:
| p = ρRT | (12) |
The calculations satisfy the following basic conservation equations used in fluid mechanics:
the mass conservation equation:
 | (13) |
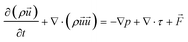 | (14) |
 | (15) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) represent the gas pressure, density, temperature, and velocity vector, respectively;
represent the gas pressure, density, temperature, and velocity vector, respectively; ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) represents the external volume force and τ represents the viscous force tensor; and E represents the gas total energy and k represents the effective thermal conductivity.
represents the external volume force and τ represents the viscous force tensor; and E represents the gas total energy and k represents the effective thermal conductivity.
The turbulent gas flow inside a GWE device always undergoes significant interactions with the walls. The gas incidence and exhaust may generate a strong swirling flow because of channel rotation, and direct contact processes between gases with different pressures in the channels can generate strong interactions. In order to ensure the reliability of calculations, it is critical to select a suitable turbulence model according to the flow characteristics mentioned above. In this research, a new scale adaptive model, the SST-SAS turbulence model,38,39 was chosen for numerical calculations, considering the computing accuracy and economic requirements. In the stable flow domain, the SST-SAS model behaves like the RANS model; however, in the unstable flow domain it can dynamically adjust the solution structure to capture more turbulent pulsation, so as to yield calculation results similar to the LES model. Because of these properties, the SST-SAS model has excellent computing capabilities for powerful swirling and contact flows. It can not only maintain calculation accuracy for near-wall events, but it can also reveal the vortex flow and other phenomena in detail. Kurec et al.40 used PIV technology to prove that the SST-SAS model can accurately calculate the distribution of state parameters in the wave rotor channels, and it can determine gas contact and mixing conditions that cannot be obtained using the classical RANS model. It can save large amounts of computing resources compared with the LES model, and it is perfectly suitable for researching gas wave technology. All the simulations in this study were conducted with double precision to ensure the accuracy of the calculations. Some other related settings used in this study, such as the discrete method, are shown in Table 2.
| Property | Parameter |
|---|---|
| Dimensions of model | 3D |
| Solver type | Density-based |
| Time | Transient |
| Fluid | Air |
| Density | Ideal gas |
| Energy model | Activated |
| Species transport model | Activated |
| Turbulence model | SST-SAS |
| Convective flux type | AUSM |
| Spatial discretization | |
| Flow parameters | Second-order upwind |
| Turbulent kinetic energy | Second-order upwind |
| Specific dissipation rate | Second-order upwind |
| Transient formulation | Second-order implicit |
| Time step | Minimum = 1 × 10−6 s |
| Convergence criteria | 1 × 10−3 for nonaxial velocity components |
| 5 × 10−4 or smaller for the rest |
Because of the regular shape of each flow domain in this model, a hexahedral mesh was used for mesh division. Because the gaps are small and the changing gradients of each physical parameter throughout the channel opening and shutting processes are substantial, mesh refinement was conducted along the interfaces of the pressure ports, rotor channels, and gaps, as shown in Fig. 6. The boundary layer meshes were also set on the channel walls. The optimal number of model cells was determined via grid independence verification. Fig. 7 shows the parameter distribution curves 0.6 ms after the channel started to connect with the high-pressure port. When the number of single-channel cells reaches 4.2 × 104, as shown in Fig. 7a, the calculation model can more accurately capture the low-pressure region (created by the vortex) and the small pressure fluctuations (caused by the multiple compression waves) at the channel entry. At this single-channel mesh scale of 4.2 × 104, the composition distribution curve shown in Fig. 7b is notably different from models using fewer single-channel cells, indicating that this grid size can also capture the contact surface shape more accurately. When the single-channel cell number exceeds 4.2 × 104, the calculation results no longer change, proving that further grid refinement has no effect on the calculation results. Therefore, 4.2 × 104 was chosen as the single-channel mesh division standard in order to economize computing resources and enhance the computing efficiency while ensuring computational correctness. The minimum grid size using this standard was 2.5 × 10−5 m and the total cell number in this model was about 8.8 × 105.
3.2 Analysis of numerical simulation results
The effects of bending angles on device performance are closely related to the gas jet direction. As shown in Fig. 8, this paper defines the gas incident angle φvin and exhaust angle φvout for the convenience of analysis. According to the trigonometric function relationship, these two can be expressed as follows:
 | (16) |
 | (17) |
 | ||
| Fig. 8 Schematic diagrams of the gas incident and exhaust angles: (a) gas incident angle φvin; (b) gas exhaust angle φvout. | ||
The incident angle difference φdin and the exhaust angle difference φdout are defined to represent the difference between the channel bending angle and the gas flow angle. The expressions are as follows:
| φdin = φpin − φvin | (18) |
| φdout = φpout − φvout | (19) |
In order to compare the effects of forward bending (channel bends in the direction of rotor rotation where the angles satisfy the conditions φpin > 90° and φpout > 90°), backward bending (φpin < 90°, φpout < 90°), and reversed bending at both channel ends (φpin > 90°, φpout < 90° or φpin < 90°, φpout > 90°) on equipment performance, different models were established and calculated via choosing two values as the channel inlet and outlet angles from the possible selections of 30°, 45°, 60°, 75°, 90°, and 105°.
 | ||
| Fig. 9 Changing relationships involving φdout and η under the conditions of α = 1.5 and β = 1.25: (a) variation of φdout with φpout; (b) variation of η with φdout. | ||
| φpin | φpout | mmp (kg s−1) | voutv (m s−1) |
|---|---|---|---|
| 30° | 30° | 0.045 | 50.2 |
| 30° | 45° | 0.068 | 63.3 |
| 75° | 30° | 0.078 | 74.8 |
| 75° | 45° | 0.090 | 84.3 |
Fig. 9b shows the variation of the total pressure efficiency η, obtained via numerical calculations, with the exhaust angle difference φdout at different fixed channel inlet angles φpin. η drops dramatically with a decrease in φdout when φdout ≤ −3.9°. When φdout > −3.9°, the η values of the φpin = 30° and φpin = 45° models essentially remain unchanged as φdout increases. When φdout > −10°, the η values of the 60° ≤ φpin ≤ 105° models increase first and then fall as φdout increases. Furthermore, the variation of η is within the range of 9%, and the highest efficiency η value for each model in the 60° ≤ φpin ≤ 105° range is achieved when φdout is in the range of 4.6–6.3°. Within the calculation range, the isentropic efficiency of the model with φpin = 60° and φpout = 75° is the highest.
When the channel inlet angle φpin is fixed, the variation of the outlet angle φpout primarily changes the flow direction of the medium-pressure gas, which impacts the equipment performance. When a traditional straight channel (φpin = φpout = 90°) is connected to the medium-pressure port, the exhaust gas not only has a velocity component along the channel extension direction (perpendicular to the end faces of the pressure ports in straight channels), but it also has a velocity component in the direction of rotor rotation. Therefore, as shown in Fig. 10c, the exhaust gas flows obliquely in the rotation direction, forming a low-speed and low-pressure region near the right-side wall of the medium-pressure port and causing gas backflow. Furthermore, because of the substantial difference in velocity distributions between the exhaust stream and the low-speed region, vortices form easily at their intersection, which impairs the gas flow and causes a certain amount of flow loss. There are always multiple rotor channels connected to the medium-pressure port at the same time. The velocities and energies of the exhaust gas from these channels are different since each channel is at a different stage of the exhaust process. As a result, the exhaust gas from different channels converges and mixes in the medium-pressure port, resulting in a certain loss of gas energy. Since the exhaust gas from each channel contains a rotational velocity component, the mainstream generated upon convergence is inclined to the rotation direction. Before discharging from the pressure port, the flow direction of the mainstream is changed due to obstruction by the wall. Even if the rotational velocity component of the mainstream is not completely consumed during this collision process, it is difficult to effectively recover this in the medium-pressure port or in the equipment cavity. In addition, after the mainstream is obstructed by the wall and changes direction, it will flow perpendicular to the port end-face and adhere to the wall, causing a certain amount of viscous friction loss in the subsequent flow process. As shown in Table 4, under the calculation conditions, the gas total pressure loss in the medium-pressure port ΔTP can reach 1.83 kPa using the straight channel model because of the above-mentioned flow losses.
 | ||
| Fig. 10 A comparison of velocity distributions in the medium-pressure port under the conditions of α = 1.5 and β = 1.25 (the white arrow lines show streamlines). | ||
| φpin | φpout | vmpi | ΔTP | φpin | φpout | vmpi | ΔTP |
|---|---|---|---|---|---|---|---|
| 60° | 30° | 113.9 | 4.63 | 90° | 30° | 107.2 | 3.40 |
| 60° | 75° | 71.6 | 1.08 | 90° | 90° | 103.5 | 1.83 |
| 60° | 105° | 123.0 | 2.51 | 90° | 105° | 122.5 | 2.26 |
Compared with a straight channel, the exhaust angle difference φdout of a curved channel with φpin = 60° and φpout = 105° reaches 33.6°, which is greater than the value of 21.3° for a straight channel. Therefore, the exhaust gas flow inclines more seriously, strengthening the flow losses. The total pressure loss in the medium-pressure port ΔTP rises to 2.26 kPa in this model, as shown in Fig. 10b. The flow loss in the medium-pressure port is also the main reason why the efficiencies of the models with 60° ≤ φpin ≤ 90° decrease as φdout rises when φdout > 5° (as shown in Fig. 9b). The medium-pressure gas exhaust flow rate and velocity of the model with φpin = 30° and φpin = 45° are smaller than the models with 60° ≤ φpin ≤ 90° (as shown in Table 3), and the influence of deflection flow phenomena is also relatively minimal. As a result, within the range of 5° < φdout < 25°, the efficiency values of the models with φpin = 30° and φpin = 45°, as shown in Fig. 9b, are almost identical.
In contrast with the models shown in Fig. 10b and c, since the rotor channels in the φpin = 60° and φpout = 75° model shown in Fig. 10a bend in the opposite direction to rotor rotation and the gas flows along channels before being exhausted, the medium-pressure gas generated in this model discharges vertically to the channel end-face (the exhausting angle difference φdout = 6.3°) with a velocity lower than that of the straight channel. There is no large low-pressure and low-speed region at the right wall of the port, which greatly reduces vortex and backflow phenomena in the exhaust port. Furthermore, in this model, the exhaust velocity of each channel is reasonably average and the directions are nearly identical. During the convergence process of streams from each channel, there are no strong interactions or mixing, and the uniform mainstream does not collide with or adhere to the wall. Instead, the mainstream is directly discharged vertically, reducing the exhaust flow loss in the medium-pressure port. As illustrated in Table 4, compared with the straight model, the total pressure loss in the medium-pressure port of this curved channel can be reduced by nearly 41%, which is one of the main reasons that the model with φpin = 60° and φpout = 75° has optimal performance, as shown in Fig. 9b.
As shown in Fig. 10d, because the outlet end of the channel with φpin = 90° and φpout = 30° bends backwards excessively (the exhaust angle difference φdout reaches 32.8°), a large amount of exhaust gas flows to the lower sidewall of the medium-pressure port, which connects with the channels earlier, and discharges at high speed, adhering to the wall surface. The above-mentioned flow characteristics of the medium-pressure gas cause the violent collision of gas with the lower sidewall of the port, creating a low-velocity region together with flow vortexes on the upper sidewall of the port, resulting in a significant increase in the total pressure loss in the medium-pressure port (as shown in Table 4). In addition to the reasons mentioned above, Fig. 11b shows the uneven pressure distribution in the medium-pressure port, demonstrating a more fundamental reason for the inferior performance of the device using this angle combination. Different from the clear and regular pressure distribution seen in the model with φpin = 60° and φpout = 75° (as shown in Fig. 11a), the pressure on the inlet side of the lower sidewall of the medium-pressure port is higher than at other positions in the φpin = 90° and φpout = 30° model due to the convergence of exhaust gas. The pressure at the port inlet end is also significantly higher than the average pressure of channels in the stable pressure region. As a result, a strong reversed compression wave is created when the channels gradually connect to the medium-pressure port. As shown in Fig. 11b, the pressure at the channel inlet end is significantly enhanced due to the reversed compression wave. There is a backflow phenomenon when the channel connects to the low-pressure port, and this causes energy loss and prevents low-pressure gas inflow. The negative effects of the reversed compression wave are also the primary explanation for the dramatic reduction in the efficiency of the model when φdout <−3.9° at each inlet angle (as shown in Fig. 9b). When φdout in each model reaches about −32.5°, the efficiency reduction ratio relative to the optimal value exceeds 61%.
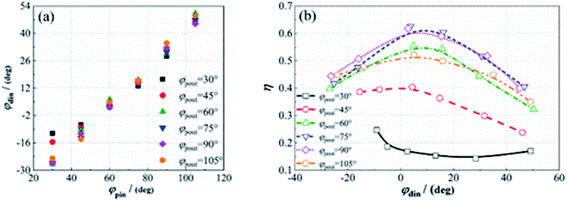 | ||
| Fig. 12 Changing relationships involving φdin and η under the conditions of α = 1.5 and β = 1.25: (a) the variation of φdin with φpin; (b) the variation of η with φdin. | ||
Fig. 12b shows the variation of the efficiency η with the incident angle difference φdin at each fixed channel outlet angle φpout value. When φpout is fixed at 30°, η decreases first and then increases slightly with an increase in φdin. When φdin rises from −15.5° to 4.4° at a fixed φpout of 45°, η increases slightly and reaches to its maximum when φdin = 4.4°; when φdin > 4.4°, η declines rapidly with a rise in φdin. In th range of 60° ≤ φpout ≤ 105°, η also reaches its maximum in the φdin range of 2.5–5.0°, and when φdin is less than the optimal value φdino, the efficiency decline rate is higher than that for φpout = 45°. The optimal performance value for each φpout displays a tendency of first increasing and then decreasing with the growth of φpout under the calculation conditions.
For the convenience of subsequent research, this study defines the entire opening time tpo as follows:
 | (20) |
Fig. 13 shows contour maps of the pressure distributions in channels at an incident pressure ratio αin of 1.5 (the initial pressure in the channels ps = 101 kPa) and with topen/tpo = 0.2. In the channel with the highest efficiency (φpin = 60° and φpout = 75°), the radial compression wave system created in the initial stage of channel opening is slightly inclined relative to the channel walls, and the inclination degree is significantly less than the channel with φpin = 90° and φpout = 75° (the entrance angle is the same as a traditional straight channel). The compression wave system in the channel with φpin = 60° and φpout = 75° is closer to propagating in the direction of channel extension, which can effectively weaken compression wave reflection in the channel with φpin = 90° and φpout = 75°. When φpin = 30°, however, the excessive curvature of the channel entrance causes the left channel sidewall (connecting to the high-pressure port earlier) to impede the propagation of the compression wave system, resulting in multiple reflected waves and local high pressure near the left sidewall.
 | ||
| Fig. 13 A comparison of pressure distributions in channels with topen/tpo = 0.2 (the white arrow lines depict streamlines). | ||
As shown in Fig. 14a, when the channel is fully connected to the high-pressure port (topen/tpo = 1.0), the multiple reflections of the compression waves at the channel entrance weaken the strength of the compression wave system, resulting in the pressure distributions at the entrances of the channels with φpin = 30° and φpin = 90° being much more uneven than that of the φpin = 60° channel. This also makes the velocity field at the channel inlet more turbulent, resulting in larger flow vortexes in the channels with φpin = 30° and φpin = 90°. The vortex in the φpin = 90° channel is generated near the left sidewall, which connects to the high-pressure port earlier, while the vortex in the φpin = 30° channel is formed when the incident gas flow is blocked from rotating around by the channel wall. As shown in Fig. 14b, since the flow vortexes occupy flow space in the channels and obstruct the incident gas flow, the gas interfaces in channels with φpin = 30° and φpin = 90° become more distorted relative to the channel wall; this not only increases the friction and collisions between the gas and the walls, but it also strengthens mixing between the incident high-pressure gas and the original low-pressure gas in the channels (especially in the channel with φpin = 30°). The energy transfer efficiency between gases is significantly impacted due to the flow phenomena described above. As shown in Fig. 15, the average pressures of gas compressed in the φpin = 30° and φpin = 90° channels are lower than that in the φpin = 60° channel. However, the average moving speed of the wave does not differ much between the different models, which indicates that the optimal port geometry size at various φpin values will not be significantly different under the same working conditions and rotational speed.
 | ||
| Fig. 14 A comparison of the parameter distributions in the rotor channels: (a) pressure distributions (the curves show the velocity contours); (b) component distributions. | ||
The gas vorticity magnitude ωt, given as follows:
 | (21) |
 | (22) |
4. Experimental section
4.1 Experimental platform
A gas wave ejection experimental system was established in this study, as shown in Fig. 17, in order to verify the numerical simulation results and to clarify the actual improvement effects from the use of appropriate channel bending angles on the GWE performance. The parameters of the relevant components used in this experimental system are shown in Table 5. The operating process is as follows for experiments: first, the frequency converter was controlled so that the GWE equipment rotation speed could reach the set value before gas flowed in; the high-pressure valve was opened slowly to set the pressure of the high-pressure gas to the experimental requirements while fully opening the medium-pressure valve; the equipment low-pressure valve was opened, and the air in the surrounding environment was directly sucked in as the low-pressure gas during experiments; and the medium-pressure valve was closed gradually to adjust the medium-pressure gas pressure when the pressure of the high-pressure gas met the predetermined value. The adjustment of the medium-pressure valve changes the pressure of the high-pressure gas, and these two valves must be dynamically altered at the same time to attain the experimental working conditions. The medium-pressure gas was eventually exhausted to the outside environment through an eduction pipe connected to the GWE medium-pressure port. In the experiments, the pressure, temperature, and mass flow rate of each gas were measured using a micromanometer and pressure sensor, temperature sensor, and vortex flowmeter, respectively.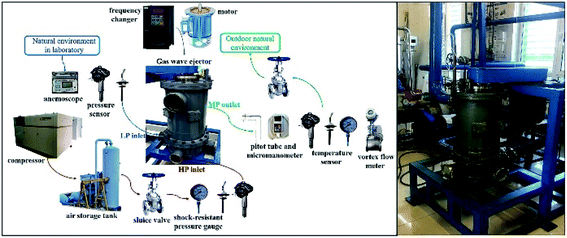 | ||
| Fig. 17 A schematic diagram of the components and procedure used for the GWE experimental system with a photograph of the set up. | ||
| Instrumentation | Brand | Measuring/controlling range | Measurement accuracy |
|---|---|---|---|
| Frequency convertor | KEWO | 7.5 kW/0–50 Hz | 0.01 Hz |
| Driving motor | HUANGHAI | 7.5 kW/0–50 Hz | — |
| Screw compressor | FUSHENG | 1.0/1.05 MPa | — |
| Temperature sensor | SinoMeasure | −50–250 °C | ±0.05% |
| Pressure sensor | Asmik | 0–0.6 MPa | ±0.3% |
| Vortex flowmeter | GALLOP | DN80/DN100 | ±1.5% |
| Anemoscope | KANOMAX | 0.1–50 m s−1 | ±0.1 m s−1 |
| Micromanometer | YIOU | ±100 kPa | 0.01 kPa |
Fig. 18 shows the GWE device that was used in this experiment. The device structure allows for the external adjustment of the gap size and the declination angles between the pressure ports, substantially simplifying equipment installation and debugging. The performances of a traditional ejection rotor (I90O90 rotor) with φpin = φpout = 90° and an arc curved channel rotor with φpin = 60° and φpout = 75° (I60O75 rotor, achieving optimum performance under the calculation conditions in this study) were primarily compared in this experiment. Except for the different channel bending angles, the two rotors had identical specifications, such as axial length and middle diameter, in order to avoid interference from other factors and to facilitate rotor exchange. The exact specifications of the wave rotors are shown in Fig. 19 and Table 6.
| Geometry | Value | Geometry | Value |
|---|---|---|---|
| φpin of the I60O75 rotor | 60° | Passage axial length l | 250 mm |
| φpout of the I60O75 rotor | 75° | Number of passages x | 72 |
| φpin of the I90O90 rotor | 90° | Blade thickness θ | 1.5 mm |
| φpout of the I90O90 rotor | 90° | Middle diameter of rotor d | 256 mm |
| Passage height h | 16 mm | Passage width w | 9.6 mm |
4.2 Analysis of experimental results
Fig. 20 shows the variation of the isentropic efficiency η with the compression ratio β when the expansion ratio α is fixed at 1.5. The differences in η between experiments and simulations are only in the range of 3–8% for both working conditions, and the variation trends of η obtained via experiments are completely consistent with the numerical calculation results, proving the accuracy of the GWE calculation model employed in this study.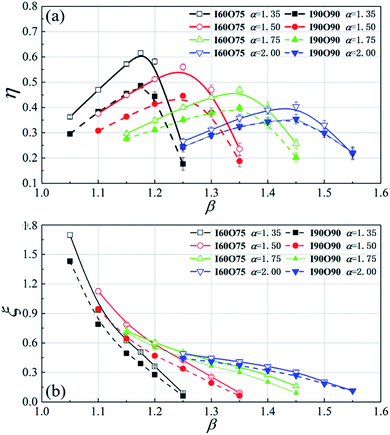 | ||
| Fig. 21 The values of performance parameters obtained via comparison experiments: (a) changes in η with β and (b) changes in ξ with β at different α values. | ||
The gas incident and exhaust velocities will change with the working conditions according to the above research findings. As a result, when the channel bending angles are fixed, the differences between the gas incident and exhaust angles are different based on the working conditions, resulting in different performance improvements in the case of the I60O75 rotor relative to the I90O90 rotor. At a constant α value, the experimental efficiency difference between these two rotors increases first and then decreases with a rise in the compression ratio β, and the β value corresponding to the maximum efficiency difference increases with rising α. The maximum relative improvement ratio in efficiency at each α value exceeds 14.2% over the experimental range. When α = 1.50 (the expansion ratio used in the numerical analysis), the efficiency increase and growth rate for the I60O75 rotor both reach their maximum values under the conditions of β = 1.25, and the values are 11.3% and 25.3%, respectively. Also, this compression ratio is consistent with the numerical simulation results, which illustrates the correctness of the simulations in terms of the impact of angle on device efficiency to a certain extent.
As shown in Fig. 21b, at each fixed expansion ratio α, the ejection rate ξ of the I60O75 rotor decreases monotonically with an increase in the compression ratio β, which is consistent with the I90O90 rotor. The ξ values of the I60O75 rotor are higher than those of the I90O90 rotor under the same working conditions, proving that the use of backward curved channels with an appropriate bending angle can improve the suction capacity of the GWE. When α is fixed, the improvement in ξ for the I60O75 rotor compared to the I90O90 rotor essentially decreases with an increase in β, and the maximum improvement in ξ at each α value exceeds 5% within the experimental range (when α ≤ 1.5, it reaches 26.6%). The relative improvement in ξ obtained from experiments reaches 8.6% under the working conditions employed in the numerical analysis (α = 1.50, β = 1.25). Within the experimental scope of this study, the highest ejection rate of the I60O75 rotor at each α exceeds 49.0% and the highest value is 169.7%; these values are both higher than the values of 44.2% and 143.1% for the I90O90 rotor, respectively.
The curved channels can not only effectively improve the energy exchange efficiency and the boosting capacity of the GWE, but they can also affect the medium-pressure gas velocity, resulting in the ratio of static pressure as a proportion of the total pressure of the gas products to be different from that using traditional straight channels. As an ejector, a larger ratio of static pressure out of the total pressure usually means a higher utility value of the gas products, and it also indicates that the equipment is more effective in pressurizing the low-pressure gas. In order to compare the capability for improving the static pressure of low-pressure gas, the static pressure increment ratio ψmsp can be defined as follows:
 | (23) |
 | (24) |
Fig. 22a shows the variation of ψmsp with the compression ratio β. At each fixed expansion ratio α, the ψmsp values of the two rotors both increase with an increase in β, indicating that the capacity of these two rotors to improve the low-pressure gas static pressure has a positive relationship with β when α is fixed. Meanwhile, the direct utility value of the medium-pressure gas products also rises with an increase in β. Although the ψmsp variation trends of these two rotors are identical, the ψmsp values of the I60O75 rotor are always higher than those of the I90O90 rotor under the same working conditions. In particular, when ψcom ≤ 0.4, the ψmsp increase of the I60O75 rotor compared with the I90O90 rotor is more than 10%. Despite the fact that the difference in ψmsp between the two rotors decreases as β increases, the ψmsp values of the I60O75 rotor are higher than those of the I90O90 rotor by at least 4.2%, even at the maximum relative compression ratio (ψcom = 0.7). The above experimental results show that the backward-bending channels can effectively reduce the medium-pressure gas exhaust velocity compared with traditional straight channels under various working conditions, so the static pressure proportion of the medium-pressure gas can be higher under the premise of meeting compression ratio requirements. At a fixed expansion ratio, the ability of the curved channels to lift the static pressure of low-pressure gas continues to weaken with an increase in the compression ratio β.
 | ||
| Fig. 22 The experimental results regarding (a) the static pressure increase ratio ψmsp and (b) the gas loading power consumption Pcon. | ||
In addition to differences in the composition of the medium-pressure gas pressure, the influence of channel curvature on the flow velocity and direction of the incident and exhaust gas also causes differences in working power consumption between the curved-channel rotor and the traditional straight-channel rotor. The rotor power consumption caused by the gas flow Pcon can be calculated according to eqn (25), where Pw and Ps represent the total power consumption and idling power consumption of the equipment, respectively:
| Pcon = Pw − Ps | (25) |
Fig. 22b shows the variations of Pcon with the compression ratio β. The Pcon values of the I90O90 rotor are always larger than 0, indicating that the flowing gas inevitably generates a certain amount of power consumption during operation. The exhaust gas generated in the I90O90 rotor deflects in the direction of rotor rotation, according to the simulation results, and the Pcon values of the I90O90 rotor are mostly used to provide rotational transport velocity for the axially incident gas. As a result, when the expansion ratio α is fixed, Pcon gradually drops as β increases with a decrease in the gas flow rate. As shown in Fig. 22b, the Pcon value of the I60O75 rotor is close to 0 under the conditions of α = 1.50 and β = 1.25, which is due to the macroscopic flows of the incident and exhaust gas both being in the axial direction, according to the numerical research. When α = 1.50 and β < 1.25, the increase in the flow velocity of the medium-pressure gas generated in the I60O75 rotor channels causes the gas to exhaust in the opposite rotational direction, driving the rotor to rotate. Therefore, Pcon becomes negative, indicating that the gas flow reduces the device operating power consumption. With a decrease in β, increases in the medium-pressure gas flow rate and exhaust velocity lead to a continuous drop in Pcon, indicating that the effects of the flowing gas on rotor rotation are strengthened. Because the medium-pressure gas output is reduced when α = 1.50 and β > 1.25, the flow velocity of the medium-pressure gas is decreased and the exhaust gas deflects in the rotating direction, like the I90O90 rotor, resulting in Pcon > 0. Also, as β increases, Pcon rises as well. Under the conditions of other expansion ratios, the Pcon variation trends for the I60O75 rotor are similar to the condition of α = 1.50, but the β requirement for Pcon = 0 increases as α rises. Under various experimental conditions, the I60O75 rotor can reduce the operating power consumption of the equipment by at least 21.8 W relative to the traditional I90O90 rotor, with a maximum of 473.3 W. The above experimental results show that the curved channels can not only improve the isentropic efficiency of the energy exchange process inside the device, but they can also help minimize the device power consumption, thereby reducing the operating costs and increasing the total application benefits of GWEs.
 | ||
| Fig. 23 The variations in the I60O75 rotor efficiency η with rotor rotation speed: (a) fixed pressure ports; (b) pressure ports satisfying optimal matching. | ||
According to the gas flow characteristics in the rotor channels, both the high-pressure gas incident velocity and the medium-pressure exhaust velocity decrease with a decrease in the compression ratio β; alternatively, they rise as β increases. The calculation results show that when β = 1.15, both φdin and φdout at the design speed nd are no longer the optimal values for achieving the highest equipment performance, and both are lower by roughly 4° relative to at β = 1.25. It can be shown based on Fig. 9b and 12b that the efficiency reduction rate is relatively higher when φdin and φdout are smaller than the optimal values. As a result, when β = 1.15, a slightly lower rotor speed than the design value has no noticeable effect on the opening time of the medium-pressure port, while it can move φdin and φdout closer to the optimal values, resulting in ni < nd under these working conditions. The speed ni that achieves the optimal equipment performance is equal to the design speed nd when β = 1.30, and the efficiency decline rate as the speed rises at nd < n < 2844 rpm is smaller than at β = 1.25. Since the incident velocity of the high-pressure gas rises with an increase in β, a slightly higher rotational speed than the design value makes φdin closer to the optimal value at β = 1.30, reducing the efficiency decline at higher speed.
Relevant research results show that an acceleration of the channel opening process can significantly reduce the flow loss during the incident process and mitigate the damage to the ideal wave system that is generated, since the channels cannot open and close instantaneously when the pressure waves arrive at the channel ends.32 However, according to the numerical analysis results, if the increase in rotational speed amplifies the deviation of the incident and exhaust angle differences from the optimal values, flow losses, such as viscous dissipation, will also be enhanced, which negatively impacts the equipment performance. Therefore, when the pressure ports constantly have the optimal matching relationship with the rotation speed, the influence of changing rotation speed on the rotor performance is governed by a combination of the two influencing factors mentioned above.
Fig. 23b shows the variation of the working efficiency of the I60O75 rotor with the rotation speed n at different compression ratio conditions when α = 1.50. When the compression ratio β is 1.25 (the reference condition for designing the bending angles), φdin and φdout increase from the optimal values of 2.5° and 6.3° to 14.2° and 18.3°, respectively, during the process of increasing the rotation speed from the design value nd = 2676 rpm to 4260 rpm. According to the previous numerical analysis results, this change in φdin has a significant negative impact on the equipment efficiency. As a result, even if the channel opening process is accelerated to some extent, the increase in viscous loss caused by the increase in φdin leads to only a small increase in the equipment efficiency when the rotation speed increases within this range: the maximum increase is less than 6%. The most efficient rotation speed is only 3984 rpm. When n = nd, the medium-pressure gas exhaust velocity at β = 1.20 is higher than that at β = 1.25, causing the exhaust gas to deflect in the opposite direction to rotor rotation. A certain amount of acceleration helps to weaken this deflection, reducing the flow loss in the exhaust port. As a result, when 2676 rpm ≤ n≤ 3702 rpm, the efficiency improvement ratio at β = 1.20 is slightly higher than at β = 1.25. In addition, the efficiency reduction rate at β = 1.20 is slightly lower than at β = 1.25 when n > 3702 rpm. Because the exhaust velocity at β = 1.30 is lower than at β = 1.25, φdout is always greater than 0 over the experimental speed variation range, and the effects of exhaust loss in the medium-pressure port on equipment efficiency only result in a slight change with rotation speed. The incident velocity of high-pressure gas at β = 1.30 is higher than at β = 1.25, and increasing the speed within a certain range is conducive to moving φdin closer to the optimal value. Furthermore, since the incident pressure ratio is larger at β = 1.30, the effects of acceleration on reducing the incident loss are more obvious.31 As a result, the efficiency improvement at β = 1.30 is larger than at β = 1.25 for the same speed increase. When α = 1.50, at each compression ratio within the experimental range, the variations of equipment efficiency with rotation speed exceed 5.4%, while the maximum value reaches about 7.3%.
5. Conclusions
An ejection wave rotor with curved channels was investigated for the first time in this research in order to overcome the defects of gas wave ejectors (GWEs) equipped with traditional straight channels. The mechanism of influence of the channel bending angle on the wave system and gas flow was analyzed, and the first applied experiments involving curved rotor channels in GWE technology were carried out. The following are the main findings of this study.1. A single-directrix scanning method for the construction of curved rotor channels was proposed in this study. This approach can establish curved channels with different line types and angles via adjusting the basic directrix equation and its key parameters, such as the envelope angle and the outlet angle. The angles at both channel ends can allow a smooth transition using this method, and both end-faces of the channels may remain radially distributed.
2. The angle difference between the gas flow and channel bending has a significant impact on device performance. In the scope of this research, when the exhaust angle difference φdout is ≤ -3.9°, the exhaust gas from each channel flows in an opposite direction relative to the rotor rotation in the medium-pressure port; this increases the gas viscosity dissipation and generates reversed compression waves, resulting in the backflow of the incident low-pressure gas. The equipment performance is significantly influenced by the above-mentioned reasons, and the efficiency of the equipment declines with a decrease in φdout. In contrast, when φdout is >−3.9°, the effects of changing φdout on device performance are relatively minimal. When the incident angle difference φdin is >5.0° or ≤−5.0°, the channel walls reflect or obstruct the propagation of compression waves and the incident gas flow, weakening the wave system and causing a great deal of gas energy loss. As a result, device performance basically deteriorates monotonically as |φdin| increases.
3. The experimental results from a curved-channel rotor (the I60O75 rotor, the inlet and outlet angles are φpin = 60° and φpout = 75°), when compared with a traditional straight-channel rotor (the I90O90 rotor), show that backward curved channels can improve the equipment performance under all working conditions within the research range. In comparison with the I90O90 rotor, the equipment efficiency and ejection rate of the I60O75 rotor are improved by 11.3% and 8.6%, respectively, under conditions where the expansion ratio α is 1.50 and the compression ratio β is 1.25. The highest isentropic efficiency of the I60O75 rotor reaches 61.6% within the experimental range.
4. The curved channels can effectively change the velocity and direction of the gas flow, increasing the proportion of static pressure out of the total pressure of the medium-pressure gas and reducing the equipment operating power consumption. Under all experimental working conditions with a relative compression ratio ψcom ≤ 0.4, the static pressure increase ratio ψmsp of the I60O75 rotor can be increased more than 10% compared with the I90O90 rotor. The operating power consumption of the I60O75 rotor can be reduced by 21.8–473.3 W compared with the I90O90 rotor under the experimental conditions used in this study.
5. Because the gas jet velocity varies depending on the working conditions, the incident and exhaust angle differences are different according to the working conditions when the device operates at the designed rotation speed with the bending angles used in the I60O75 rotor. The influence of the variations of angle differences on device performance varies as the rotation speed changes. Because the acceleration of rotor rotation can weaken the energy loss generated during the gradual opening and closing of channels, the working efficiency of the I60O75 rotor can be increased by up to about 7.4% with an increase in rotation speed within the experimental range when the rotational speed is optimally matched with the pressure ports.
This study advances theory related to GWEs and it provides a new method for improving their performance. The relevant research findings are useful for the popularization and application of GWEs, and they have some reference value for the research and development of other wave rotor technologies, such as gas wave refrigeration.
Author contributions
Yiming Zhao: conceptualization, methodology, investigation, writing-original draft. Haoran Li: software, writing-review and editing. Dapeng Hu: conceptualization, resources, project administration.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was funded by the National Key Research and Development Program of China (grant no. 2018YFA0704600).References
- Y. Shen, Carbon dioxide bio-fixation and wastewater treatment via algae photochemical synthesis for biofuels production, RSC Adv., 2014, 4, 49672–49722 RSC.
- X. Wang and Y. Song, Mesoporous carbons: recent advances in synthesis and typical applications, RSC Adv., 2015, 5, 83239–83285 RSC.
- D. Chong, J. Yan, G. Wu and J. Liu, Structural optimization and experimental investigation of supersonic ejectors for boosting low pressure natural gas, Appl. Therm. Eng., 2009, 29, 2799–2807 CrossRef CAS.
- M. G. Drouven and I. E. Grossmann, Mixed-integer programming models for line pressure optimization in shale gas gathering systems, J. Pet. Sci. Eng., 2017, 157, 1021–1032 CrossRef CAS.
- S. Park and H. Yang, Flow and Oxygen-Transfer Characteristics in an Aeration System Using an Annular Nozzle Ejector, Ind. Eng. Chem. Res., 2013, 52, 1756–1763 CrossRef CAS.
- Y. Fang, M. D. Lorenzo, P. Lafon, S. Poncet and Y. Bartosiewicz, An Accurate and Efficient Look-up Table Equation of State for Two-phase Compressible Flow Simulations of Carbon Dioxide, Ind. Eng. Chem. Res., 2018, 57, 7676–7691 CrossRef CAS.
- S. Elbel and N. Lawrence, Review of recent developments in advanced ejector technology, Int. J. Refrig., 2016, 62, 1–18 CrossRef.
- S. Tao, Y. Dai, D. Zhao and J. Zou, Characteristics of static pre-cyclonic steam ejector, Int. J. Therm. Sci., 2017, 120, 244–251 CrossRef.
- F. Iancu, J. Piechna and N. Müller, Basic design scheme for wave rotors, Shock Waves, 2008, 18, 365–378 CrossRef.
- S. Chan, H. Liu and F. Xing, Defining the Thermodynamic Efficiency in a Wave Rotor, J. Eng. Gas Turbines Power, 2016, 138, 112601 CrossRef.
- S. Chan, H. Liu, F. Xing and H. Song, Wave rotor design method with three steps including experimental validation, J. Eng. Gas Turbines Power, 2018, 140, 111201 CrossRef.
- D. P. Hu, Y. Yu and P. Q. Liu, Enhancement of refrigeration performance by energy transfer of shock wave, Appl. Therm. Eng., 2018, 130, 309–318 CrossRef.
- D. P. Hu, R. F. Li, P. Q. Liu and J. Q. Zhao, The design and influence of port arrangement on an improved wave rotor refrigerator performance, Appl. Therm. Eng., 2016, 107, 207–217 CrossRef.
- D. P. Hu, J. X. Wang, M. Wu, T. J. Liu, Y. M. Zhao and Y. Yu, Unsteady heat transfer between gas and tube in a wave rotor refrigerator, J. Therm. Sci. Eng. Appl., 2020, 12, 054502 CrossRef.
- G. Lenoble and S. Ogaji, Performance analysis and optimization of a gas turbine cycle integrated with an internal combustion wave rotor, Proc. Inst. Mech. Eng., 2010, 224, 889–900 CrossRef.
- M. R. Nalim, P. H. Snyder and M. Kowalkowski, Experimental Test, Model Validation, and Viability Assessment of a Wave-Rotor Constant-Volume Combustor, J. Propul. Power, 2016, 33, 1–13 Search PubMed.
- Li. Jianzhong, G. Erlei, Y. Li, Li. Wei and Z. Kaichen, Experimental Investigation on Pressure Rise Characteristics in an Ethylene Fuelled Wave Rotor Combustor. Energy Fuels Am, Chem. Soc. J., 2017, 31, 10165–10177 Search PubMed.
- P. Akbari, R. Nalim and N. Mueller, A review of wave rotor technology and its applications, J. Eng. Gas Turbines Power, 2006, 128, 717–735 CrossRef.
- J. Kentfield, Wave rotors and highlights of their development, 34th AIAA/ASME/SAE/ASEE Jt. Propul. Conf. Exhib, 1998, pp. 1–9 Search PubMed.
- J. Kentfield, The performance of pressure-exchange dividers and equalizers, J. Basic Eng., 1969, 91, 361–370 CrossRef.
- J. Wilson, An experimental determination of losses in a three-port wave rotor, J. Eng. Gas Turbines Power, 1998, 120, 833–842 CrossRef.
- A. A. Kharazi, P. Akbari and P. Mkbari, Preliminary study of a novel R718 compression refrigeration cycle using a three-port condensing wave rotor, J. Eng. Gas Turbines Power, 2005, 127, 539–544 CrossRef CAS.
- A. A. Kharazi, P. Akbari and N. Müller, Implementation of 3-Port condensing wave rotors in R718 cycles, J. Energy Resour. Technol., 2006, 128, 325–334 CrossRef CAS.
- Y. Q. Dai, D. P. Hu, J. P. Zou and J. Q. Zhao, Gas Flow in Unilateral Opening Pulse Tubes Based on Real Gas Equation of State. Chin, J. Chem. Eng., 2009, 17, 914–918 CAS.
- Y. Q. Dai, J. P. Zou, C. Zhu, P. Q. Liu, J. Q. Zhao, L. Zhang and D. P. Hu, Thermodynamic Analysis of Wave Rotor Refrigerators, J. Therm. Sci. Eng. Appl., 2010, 2, 021011 CrossRef.
- D. P. Hu, Y. Yu, P. Q. Liu, X. L. Wu and Y. M. Zhao, Improving Refrigeration Performance by Using Pressure Exchange Characteristic of Wave Rotor, J. Energy Resour. Technol., 2018, 141, 022004 CrossRef.
- W. Zhao, D. Hu, P. Liu, Y. Dai, J. Zou, C. Zhu and J. Zhao, The port width and position determination for gas wave ejector, J. Eng. Gas Turbines Power, 2012, 134, 064502 CrossRef.
- W. Zhao, D. Hu, P. Liu, Y. Dai, C. Rong and J. Zhao, Influence of port angle on performance of gas wave ejector and prediction for optimal angle, CIESC. J., 2012, 63, 6 Search PubMed.
- P. Liu, S. Liu, X. Li and D. Hu, Experimental Research of Ejecting Performance of Pressure Oscillation Tube, J. Eng. Thermophys., 2020, 41, 369–373 Search PubMed.
- D. Hu, Y. Zhao, T. Wu, Z. H. Li, Y. Yu and J. X. Wang, The complete performance map of gas wave ejector and analysis on the variation laws and limitation of performance, J. Eng. Gas Turbines Power, 2019, 142, 021012 CrossRef.
- D. Hu, Y. Zhao, W. Teng, Y. Yu and J. Wang, The experimental research and mechanism analysis on the influence of wave rotor rotational speed on the wave system and flow losses of gas wave ejector, Chem. Eng. Process. Process Intensif., 2019, 144, 107638 CrossRef CAS.
- D. P. Hu, R. F. Li, P. Q. Liu and J. Q. Zhao, The loss in charge process and effects on performance of wave rotor refrigerator, Int. J. Heat Mass Transfer, 2016, 100, 497–507 CrossRef.
- R. Jagannath, S. P. Bane, M. E. Feyz and M. R. Nalim, Assessment of incidence loss and shaft work production for wave rotor combustor with non-axial channels, 55th, Am. Inst. Aeronaut. Astronaut, 2017, pp. 1–16 Search PubMed.
- R. Jagannath, S. P. Bane and N. M. Razi, Numerical modeling of a wave turbine and estimation of shaft work, J. Fluids Eng., 2018, 140, 101106 CrossRef.
- S. Tüchler and C. D. Copeland, Experimental results from the Bath μ-wave rotor turbine performance tests, Energy Convers. Manage., 2019, 189, 33–48 CrossRef.
- S. Tüchler and C. D. Copeland, Experimental and numerical assessment of an optimised, non-axial wave rotor turbine, Appl. Energy, 2020, 268, 115013 CrossRef.
- S. Tüchler and C. D. Copeland, Numerical optimisation of a micro-wave rotor turbine using a quasi-two-dimensional CFD model and a hybrid algorithm, Shock Waves, 2021, 31, 271–300 CrossRef.
- Y. Egorov and F. Menter, Development and application of SST-SAS turbulence model in the DESIDER project, Springer Berlin Heidelberg, 2008, vol. 97, pp. 261–270 Search PubMed.
- A. Mehdizadeh, H. Foroutan, G. Vijayakumar and A. Sadiki, A new formulation of scale-adaptive simulation approach to predict complex wall-bounded shear flows, J. Turbul., 2014, 15, 629–649 CrossRef.
- K. Kurec, J. Piechna and K. Gumowski, Investigations on unsteady flow within a stationary passage of a pressure wave exchanger, by means of PIV measurements and CFD calculations, Appl. Therm. Eng., 2017, 112, 610–620 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |