Linear unit BN₂: a novel birefringence-enhanced fundamental module with sp orbital hybridization

Abstract

Inorganic planar π-conjugated groups are advantageous to generate large birefringence in optical functional materials, and many excellent materials contain CO₃, BO₃ or B₃O₆, such as CaCO₃, α/β-BaB₂O₄ (α/β-BBO), and KBe₂BO₃F₂ (KBBF). In view of their microscopic structures, the common characteristics are the planar structures, which are regarded as birefringence-enhanced fundamental modules (FMs). Nowadays, exploring novel birefringence-enhanced FMs is becoming a burning issue. Herein, we investigated the birefringence-enhanced FMs in B–N systems and found that the BN₂ linear unit could produce great birefringence. Through the investigation based on the Inorganic Crystal Structure Database, some compounds with the BN₂ linear group were screened out with the formulas A₃BN₂ (A = Li, Na), A₃BN₃ (A = Mg, Ca), and Ba₃(BN₂)₂. Particularly, Ca₃(BN₂)N exhibits a great birefringence of about 0.411 at 1064 nm, which is 3.5, 2.5 and 2.0 times those of the most commercially used birefringent crystals α-BaB₂O₄ (Δn = 0.116 at 1064 nm), CaCO₃ (Δn = 0.164 at 1064 nm) and YVO₄ (Δn = 0.208 at 1064 nm), respectively. To find the origins of the optical properties of compounds with the BN₂ linear group, the first-principles, REDA and polarizability anisotropy analysis methods were used. Owing to the structural arrangement and the polarization anisotropy of the BN₂ linear group, it can influence the birefringence significantly. This work will provide a general way for exploring birefringence-enhanced FMs in B–N compounds.

---

1. Introduction

In the field of optical functional crystals, birefringence plays an important role in material processing, laser phase-matching, optical measurements, photolithography, and polarizing microscopic observation.^1–13 Standing out from the discovered birefringent crystal materials, CaCO₃,¹⁴ YVO₄,¹⁵ and α-BaB₂O₄,^16,17 are widely applied in optical devices such as polarizers, optical isolators, and compensators.^18–20

Nowadays, many studies about birefringent crystals with large optical anisotropy have been carried out. For instance, Ca(BO₂)₂ (ref. 21) with the largest reported birefringence (0.247 at 193 nm) in the deep-ultraviolet (DUV) region is regarded as the most promising DUV birefringent material, while (NH₄)₂C₂O₄·H₂O²² has also been identified as a promising UV birefringent material with a large birefringence (0.248 at 546 nm). Meanwhile, introducing F atoms into micro groups (e.g. from PO₄ to PO₃F and from SO₄ to SO₃F) can enhance the polarizability anisotropy significantly, and subsequently increase the birefringence to a certain extent.²³ The original difference in the birefringence of Ba₂BP₃O₁₁ and Ba₂BP₂O₈F (from 0.013 to 0.034) mainly comes from the BO₃F tetrahedra.²⁴ Introducing different numbers of fluorine atoms into B–O groups can modulate the polarizability anisotropy.^25–29 Consequently, the introduction of the F atom has become a feasible strategy to enlarge the polarizability anisotropy and enhance the birefringence.

Generally speaking, crystal structures and the corresponding microscopic groups are inextricably linked with the optical properties of materials, for instance, the arrangement of anionic frameworks or diverse combinations with metal cation polyhedrons will influence the birefringence in significant ways.^30–32 Consequently, a feasible strategy to enhance the birefringence is introducing some functional modules with large optical anisotropy such as coplanar groups with π-conjugation systems (CO₃, BO₃, B₃O₆, C₃N₃O₃, etc.).^22,33–37 At the same time, the isolated parallel distribution, quasi-one dimensional (1D) chain, and quasi-2D plane of anionic groups are proper arrangement modes that contribute to the microscopic effects in FMs. The current research on π-conjugated microscopic groups mainly focuses on the B–O unit (BO₂, BO₃, B₂O₅ and B₃O₆)³⁸ and C–O unit (CO₃, C₂O₄, C₂O₆, C₄O₄, and C₆O₆),²² which make great contributions to the birefringence due to their large anisotropy of polarizabilities. Despite the enormous promise in their chemical and physical functionalities, the sheer amounts of boron nitrides are much smaller than those of the oxides, for reasons well known to chemists,^39,40 and the units containing N have rarely been utilized in the optical functional crystals field. Nevertheless, it does not mean that the units containing N cannot make a contribution to the optical properties.

To the best of our knowledge, there are only a few systematic studies that unveil the contribution of B–N groups towards enhancing birefringence. Based on the analysis of B–O groups, we propose an idea that BN₂ is a linear group containing sp orbital hybridization that contributes greatly to birefringence. Through the investigation of the BN₂ unit based on the Inorganic Crystal Structure Database (Version 4.7.1 build 20211220-1548, ICSD), seven ternary nitride borates with the formulas A₃BN₂ (A = Li, Na), A₃BN₃ (A = Mg, Ca), and Ba₃(BN₂)₂ were screened out.^41–47 In order to explore the origin of the optical properties of the selected compounds, multiple analytical methods have been applied. The birefringence was calculated from the dielectric functions by the first-principles method, along with polarizability anisotropy and REDA analysis to further prove the contribution of the BN₂ unit to birefringence. Essentially, a new birefringent-enhanced FM was screened.

2. Computational details

The electronic structures and optical properties of the target compounds were calculated by first-principles calculations based on the density functional theory (DFT) method⁴⁸ implemented in the CASTEP package.⁴⁹ The exchange-correlation functional⁵⁰ was Perdew–Burke–Ernzerhof (PBE) within the generalized gradient approximation (GGA). The norm-conserving pseudopotentials (NCP)⁵¹ were selected for structural optimization and calculating the electronic and optical properties. The electronic configurations were treated as follows: Li 2s¹, B 2s² 2p¹, N 2s² 2p³, Na 2s² 2p⁶ 3s¹, Mg 2s² 2p⁶ 3s², Ca 3s² 3p⁶ 4s², and Ba 5s² 5p⁶ 6s², the cutoff energy was set at 880 eV for Ca₃(BN₂)N, 990 eV for Mg₃BN₃, and 770 eV for Li₃BN₂ (P2₁/c), Li₃BN₂ (P4₂/mnm), Li₃BN₂ (I4₁/amd), Na₃BN₂, and Ba₃(BN₂)₂. The scissor operators of 1.18 eV for Li₃BN₂ (P2₁/c), 1.21 eV for Li₃BN₂ (P4₂/mnm), 1.22 eV for Li₃BN₂ (I4₁/amd), 1.24 eV for Na₃BN₂, 1.18 eV for Mg₃BN₃, 0.61 eV for Ca₃(BN₂)N and 1.00 eV for Ba₃(BN₂)₂ were applied to move the simulated conduction bands to the right place. Furthermore, to reach the convergence of this calculation, the Brillouin zone comprised 3 × 3 × 3 Monkhorst–Pack k-point sampling with a separation of 0.04 Å⁻¹. The other calculation parameters and convergent criteria were employed as the default values of the CASTEP code.

To explore the optically anisotropic hierarchy and the functionality of the B–N units on birefringence, we investigated their polarizability anisotropy characteristics using the DFT method. The B–N units were obtained from primary crystal information without structure optimization. The polarization anisotropy was acquired from static polarization according to the following formula:

The so-called length-gauge formalism derived by Aversa and Sipe^52,53 was adopted. At a zero frequency, the static second-order nonlinear susceptibilities can be ascribed to the virtual-hole (VH) and virtual-electron (VE) processes. The formulas for calculating the contributions from VE and VH are as follows:⁵⁴

χ⁽²⁾_αβγ = χ⁽²⁾_αβγ(VE) + χ⁽²⁾_αβγ(VH)

where χ⁽²⁾_αβγ(VE) and χ⁽²⁾_αβγ(VH) are computed as follows:

Here, α, β and γ are the Cartesian components, χ_αβγ(VH) and χ_αβγ(VE) denote the contribution from the VE process and the VH process, respectively, v and v′ represent the valence bands, c and c′ represent the conduction bands, and P(αβγ), ℏω_ij and p_ij^α represent the full permutation, the difference of band energy and momentum matrix elements, respectively. Furthermore, the Born effective charges were also obtained using density functional perturbation theory (DFPT) with a linear response method performed using the CASTEP code.

3. Results and discussion

3.1. Crystal and electronic structure

To accelerate the process of advanced material discovery, computer-aided material design and prediction have recently emerged as particularly useful techniques and have exhibited various successful cases.^55,56 In this work, in order to find the target compounds, the nitride borates with alkali and alkaline earth metal cations were screened in terms of the type of FMs with the BN₂ units by investigating the ICSD. In total, 7 structures were screened out, as listed in Table 1.

Table 1 The space group, bandgap, and birefringence of the selected BN₂ compounds

Compounds	Space group	Group	Eg-GGA (eV)	Eg-HSE06 (eV)	Birefringence (@1064 nm)
Li3BN2	P21/c	BN2	3.4	4.58	0.198
Li3BN2	P42/mnm	BN2	3.36	4.57	0.103
Li3BN2	I41/amd	BN2	3.16	4.38	0.116
Na3BN2	P21/c	BN2	1.52	2.76	0.157
Mg3BN3	P63/mcm	BN2	1.5	2.55	0.244
Ca3(BN2)N	P4/mmm	BN2	0.55	1.16	0.411
Ba3(BN2)2	P212121	BN2	2.46	3.46	0.185

---

As we can see, Fig. 1 shows the structure and arrangement of the seven compounds. Obviously, the BN₂ units are all short straight linear groups. The two of Li₃BN₂ and Na₃BN₂, crystallize in the P2₁/c and P4₂/mnm space groups, and are composed of isolated and parallel BN₂ units in opposite directions and A-site Li and Na cations (Fig. 1a, c and d). Mg₃BN₃ and Ca₃(BN₂)N belong to the space groups of P6₃/mcm and P4/mmm, respectively, and the BN₂ units are parallel to each other along the c axis, while the Mg and Ca cations show symmetric distribution. Li₃BN₂ and Ba₃(BN₂)₂ belong to the I4₁/amd and P2₁2₁2₁ space groups, respectively, and the BN₂ units are not only aligned in a parallel manner but also have angles of 172.8°and 170.1°, as shown in Fig. 1c and g.

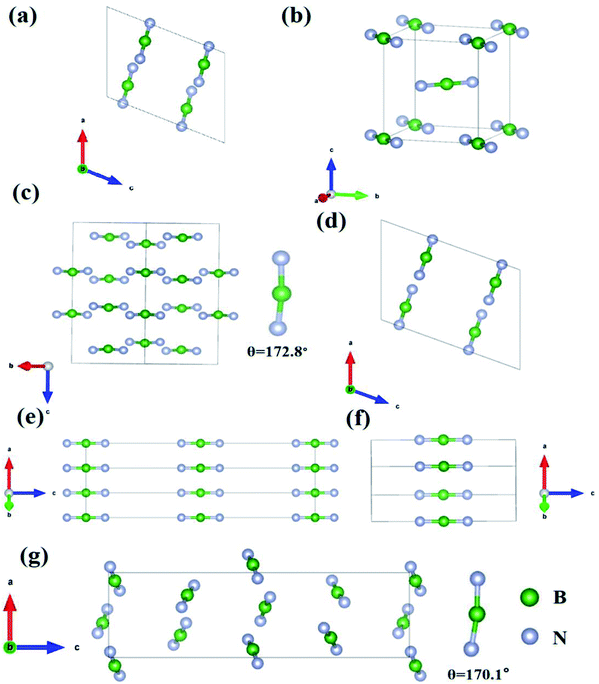Fig. 1 The arrangements of BN₂ in the compounds (a) Li₃BN₂-14, (b) Li₃BN₂-136, (c) Li₃BN₂-141, (d) Na₃BN₂, (e) Mg₃BN₃, (f) Ca₃(BN₂)N and (g) Ba₃(BN₂)₂.

Since there is no data about the experimental bandgap, we employed the HSE06 hybrid functional to accurately predict the bandgaps of these compounds. Most of the title compounds possess a direct bandgap, while Li₃BN₂ (P2₁/c), Li₃BN₂ (P4₂/mnm) and Ba₃(BN₂)₂ possess indirect ones. The calculated bandgaps using the GGA and HSE06 methods are shown in Table 1. The results from the HSE06 hybrid functional are 4.58 eV for Li₃BN₂ (P2₁/c), 4.57 eV for Li₃BN₂ (P4₂/mnm), 4.38 eV for Li₃BN₂ (I4₁/amd), 2.76 eV for Na₃BN₂, 2.55 eV for Mg₃BN₃, 1.16 eV for Ca₃(BN₂)N, and 3.46 eV for Ba₃(BN₂)₂, which are larger than those from GGA because of the discontinuity of the derivative on the exchange-correlation energy within the GGA functional. The GGA bandgaps of those compounds are listed in Fig. S1.†

The partial density of states (PDOS) as well as the orbitals near the Fermi level show the electronic states that are related to the optical properties. The total and partial density of states with the respective atoms was were analyzed to clearly understand the electronic structures of the title compounds, and calculated to analyze the distribution of atomic orbitals in the energy range from −15 to 15 eV, as shown in Fig. S2.† Similar electronic structures demonstrated for the target compounds. It clear to see that the bands of the title compounds near the bandgap are mainly determined by the 2p orbital of the N at the valence bands (VBs) maximum, and the bottom of the conduction bands (CBs) primarily dominated by the B 2p orbital, which means that the B–N group will plays an important role in the optical properties of the title compounds.

To reveal the birefringence-related functions of the BN₂ anionic group, we performed an intensive comparison with BN₃, BO₂ and BO₃. In order to explore these anionic groups, we investigated the electronic structure and optical properties of the BN₂, BN₃, BO₂ and BO₃ anionic groups using DFT implemented by the Gaussian 09 package⁵⁷ at the 6-31G basis set. As is well known to all, the optical property is closely related to the characteristic occupied and unoccupied states near the Fermi level. Fig. 2 shows the corresponding polarizability anisotropy and highest occupied molecular orbital-lowest unoccupied molecular orbital (HOMO–LUMO) gaps of the four anionic groups. The polarizability anisotropy Δα values are 23.7, 13.7, 14.4, 7.0 for BN₂, BN₃, BO₂ and BO₃, respectively. It is obvious that the BN₂ unit possesses the biggest polarizability anisotropy among them. For BN₂, BN₃, BO₂ and BO₃, the HOMO–LUMO gaps are 5.1, 3.1, 9.2 and 8.5 eV, respectively. In particular, the BO₃ unit has been recognized as a birefringence-preferential group, such as in Ca₃(BO₃)₂ (ref. 58) with a large birefringence of 0.104 (at 1064 nm). It was also confirmed that Δα increases with the π-electron population of the conjugated system, which indicates the possibility of large birefringence for the corresponding compounds with B–N units. These calculated results suggest that the BN₂ unit possesses a larger polarizability anisotropy and maintains a moderate HOMO–LUMO gap as well. Thus, we investigated the compounds with BN₂ units and analyzed their optical properties.

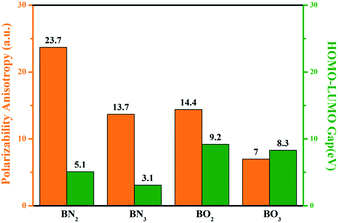Fig. 2 Comparison of the polarizability anisotropy and HOMO–LUMO gap for the BN₂, BN₃, BO₂, and BO₃ anionic groups.

3.2. Optical properties

Using the GGA approach and scissors operator via the calculations with the CASTEP code, the birefringence Δn (Δn = n_max − n_min), which depends on the difference of the maximum and minimum values of the refractive index along the different optical principal axes, was obtained, and the title compounds possessed a large birefringence of about 0.1–0.4 (at 1064 nm). The birefringence values of Li₃BN₂ in different space groups are 0.198 (P2₁/c), 0.103 (P4₂/mnm), and 0.116 (I4₁/amd). For Na₃BN₂, Mg₃BN₃ and Ba₃(BN₂)₂, their birefringence values are 0.157, 0.244, 0.185, respectively. The bandgap was calculated by GGA, and the birefringence of the compounds with BN₂ units is shown in Fig. 3. Simultaneously, the results indicate that the birefringence of the title compounds is much larger than that of the birefringent materials. Ca₃(BN₂)N especially exhibits a gigantic birefringence of about 0.411 at 1064 nm, which is 3.5, 2.5, and 2.0 times those of the most commercially used birefringent crystals α-BaB₂O₄ (Δn = 0.116 at 1064 nm), CaCO₃ (Δn = 0.164 at 1064 nm), and YVO₄ (Δn = 0.208 at 1064 nm), respectively. Meanwhile, in comparison with the chain CNO,⁵⁹ which possesses a birefringence of 0.3–0.4, and the compounds with planar C₃N₃O₃, such as β-Sr₃(C₃N₃O₃)₂ (Δn = 0.36 at 1064 nm) and Ca₃(C₃N₃O₃)₂ (Δn = 0.35 at 1064 nm),^60–62 the birefringence of Ca₃(BN₂)N is also larger than theirs, which indicates that the proposed compounds containing BN₂ units such as Ca₃(BN₂)N are promising candidates for optical applications.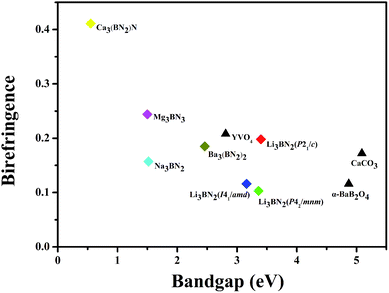

Fig. 3 Bandgap and birefringence (@1064 nm) of the compounds with BN₂ units and birefringent crystal materials.

Since Ba₃(BN₂)₂ belongs to a non-centrosymmetric group, the NLO coefficients were obtained with ab initio electronic structure calculations. Owing to the Kleinman symmetry, the P2₁2₁2₁ space group for the investigated compounds yields three non-zero NLO coefficients. Similar to the calculation of linear optical properties, the same scissors were used to generate the NLO coefficients. At the zero-frequency limit, the calculated largest NLO coefficient d₁₄ is 0.174 pm V⁻¹ (∼0.44 × KDP) for Ba₃(BN₂)₂, and B–N interactions contribute the most to the SHG coefficients (Fig. S4†).

As a post-processing tool, SHG-density (SHG⁶³ stands for second harmonic generation) was performed to further explore the contribution of atoms or groups to the SHG response through the CASTEP package. SHG-density is divided into occupied and unoccupied states of virtual-electron (VE) and virtual-hole (VH), respectively. Then, the distribution of density can be visualized by highlighting the map of SHG-density in the occupied and unoccupied states. For the Ba₃(BN₂)₂ VE and VH processes, VE occupies 57% in the SHG process for d₁₄. Therefore, both of the SHG processes of VE and VH with the occupied and unoccupied states were examined, as shown in Fig. S4.† In Ba₃(BN₂)₂, the density of SHG in the VE occupied and unoccupied states originate from B–N interaction and a small contribution from Ba–N interaction, respectively, while Ba–N interaction plays an important role in the VH process. The result indicates that the atoms in the asymmetric sublattice have an important contribution to the SHG response.⁶⁴

3.3. Optical properties analysis

To the best of our knowledge, the methods of analysis and birefringence estimation can also be employed to evaluate the ability of the functional units, such as the response electron distribution anisotropy (REDA) model,^65,66 real-space atom-cutting (RSAC) technique,⁶⁷ Born effective charge analysis method,⁶⁸ Bader charge integration⁶⁹ and the sum of polarizability anisotropy (SPA).⁷⁰

The optical anisotropy of a crystal depends on the direction of the covalent bond in the anionic groups. Therefore, birefringence is sensitive to the anisotropy of the response electron distribution, corresponding to the REDA index = Σ_g[N_cZ_aΔρ^b/(n₁E_g)] g of the anionic groups contained in the same crystal. Here, N_c is the coordination number of the nearest neighbor cations to the central anion, Z_a is the formal chemical valence of the anion, E_g is the optical bandgap, Δρ^b = ρ^b_max − ρ^b_min, ρ^b_max and ρ^b_min are the maximum and minimum of the covalent electron density of the covalent bond on the optical principal axes of a crystal, and n₁ is the minimum refractive index. Pan et al. proved the rationality of the REDA method, and that the birefringence is proportional to the REDA index. To check the above analysis and quantification, we employed the REDA method to calculate the bonding electron density difference (Δρ^b) of the covalent bonds along the optical principal axes in Li₃BN₂ (P2₁/c, P4₂/mnm, I4₁/amd), Na₃BN₂, Mg₃BN₃, Ca₃(BN₂)N and Ba₃(BN₂)₂. The Δρ^b values of BN₂ are 2.12–4.49 (×10⁻²), and we calculated the Δρ^b values of the remaining anionic groups (Li–N, Na–N, Mg–N, Ca–N and Ba–N), as shown in Table 2. As a result, the BN₂ units contribute the most to Δρ^b, which indicates that the BN₂ units are the main sources of birefringence in the title compounds. As is well known, the Δρ^b value obtained by the REDA method contains the arrangement of anionic groups, and the arrangement of BN₂ units in the title compounds are aligned in a parallel manner; the parallel or antiparallel arrangement is beneficial to the superposition of micro polarizability anisotropy. These results are generally in agreement with the increase of the macro birefringence.

Table 2 Bonding electron density difference (Δρ^b) for anionic groups in compounds calculated by the REDA method

Compounds	Group	Δρ^b (×10^−2) of BN2	Δρ^b (×10^−2) of A (Li, Na, Mg, Ca, Ba) Nn	Birefringence (@1064 nm)
Li3BN2(P21/c)	BN2	3.07	0.09	0.198
Li3BN2(P42/mnm)	BN2	2.51	−0.18	0.103
Li3BN2(I41/amd)	BN2	4.49	1.46	0.116
Na3BN2	BN2	2.15	−0.13	0.157
Mg3BN3	BN2	3.28	−0.77	0.244
Ca3(BN2)N	BN2	2.65	−0.16	0.411
Ba3(BN2)2	BN2	2.12	0.47	0.185

---

Particularly, comparing Mg₃BN₃ and Ca₃(BN₂)N, we find that the birefringence of Ca₃(BN₂)N is about 1.7 times that of Mg₃BN₃, while the values of Δρ^b of BN₂ in Mg₃BN₃ and Ca₃(BN₂)N are 3.28 and 2.65, respectively. Therefore, the BN₂ units contribute about 130% in Mg₃BN₃ and 110% in Ca₃(BN₂)N, which are roughly in agreement. According to the formula of REDA approximation, except for the values of the bandgap, the other indicators in the formula of the two compounds are very close to each other. Consequently, we performed a comparison of Δρ^b(BN₂)/E_g with the birefringence, as shown in Fig. 4. As we can see, the proportion of Δρ^b(BN₂)/E_g is 2.284 in Ca₃(BN₂)N, almost 1.7 times that in Mg₃BN₃ (1.286), which indicates that the tendency is consistent with the variation of birefringence. Simultaneously, there exists a significant difference between the bandgap of the two compounds, which is the main reason that Ca₃(BN₂)N exhibits an extraordinarily larger birefringence than Mg₃BN₃ while they have a similar contribution of BN₂ units.

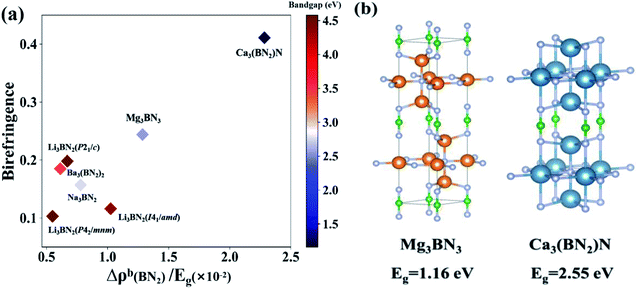Fig. 4 (a) A comparison of Δρ^b(BN₂)/E_g (HSE06) with the birefringence of the selected BN₂ compounds. (b) The structural comparison of Mg₃BN₃ and Ca₃(BN₂)N.

4. Conclusion

In summary, we investigated the birefringence-enhanced FMs in a B–N system, and a linear group BN₂ unit was proposed. Through the investigation based on the Inorganic Crystal Structure Database, seven ternary boron nitrides with the formulas A₃BN₂ (A = Li, Na), A₃BN₃ (A = Mg, Ca), and Ba₃(BN₂)₂ were screened. Their birefringence values are in the range of 0.1–0.4 at 1064 nm, especially the birefringence of Ca₃(BN₂)N, which is 0.411 at 1064 nm, exceeding that of the commercial birefringent materials α-BaB₂O₄, CaCO₃ and YVO₄. Based on the analysis of the REDA and polarizability anisotropy, it was concluded that the large birefringence mainly originates from the BN₂ unit. Hence, the functionality of the BN₂ unit could be utilized in birefringence-enhanced FMs, which exhibits the possibility of applying B–N modules to the birefringent field. This study provides a feasible way to design optical materials with enlarged birefringence.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11664001).

References

1. E. Collett, Field Guide to Polarization, SPIE, Bellingham, 2005.
2. D. H. Goldstein, Polarized Light, CRC, Boca Raton, 2011.
3. J. Hecht, A Short History of Laser Development, Opt. Eng., 2010, 49, 091002.
4. Z. Y. Xie, L. G. Sun, G. Z. Han and Z. Z. Gu, Optical Switching of a Birefringent Photonic Crystal, Adv. Mater., 2008, 20, 3601–3604.
5. M. F. Weber, C. A. Stover, L. R. Gilbert, T. J. Nevitt and A. J. Ouderkirk, Giant Birefringent Optics in Multilayer Polymer Mirrors, Science, 2000, 287, 2451–2456.
6. F. Flossmann, U. T. Schwarz, M. Maier and M. R. Dennis, Polarization Singularities Generated from a Vortex Propagating through a Uniaxial Birefringent Crystal, Phys. Rev. Lett., 2005, 95, 253901.
7. A. Tagaya, H. Ohkita, M. Mukoh, R. Sakaguchi and Y. Koike, Compensation of the Birefringence of a Polymer by a Birefringent Crystal, Science, 2003, 301, 812–814.
8. D. Brida, C. Manzoni and G. Cerullo, Phase-Locked Pulses for Two-Dimensional Spectroscopy by a Birefringent Delay Line, Opt. Lett., 2012, 37, 3027–3029.
9. P. Hlubina, D. Ciprian and L. Knyblova, Interference of White Light in Tandem Configuration of Birefringent Crystal and Sensing Birefringent Fiber, Opt. Commun., 2006, 260, 535–541.
10. M. J. Katz, H. Kaluarachchi, R. J. Batchelor, A. A. Bokov, Z. G. Ye and D. B. Leznoff, Highly Birefringent Materials Designed Using Coordination Polymer Synthetic Methodology, Angew. Chem., Int. Ed., 2007, 46, 8804–8807.
11. L. H. Nicholls, F. J. Rodríguez-Fortuño, M. E. Nasir, R. M. Córdova-Castro, N. Olivier, G. A. Wurtz and A. V. Zayats, Ultrafast Synthesis and Switching of Light Polarization in Nonlinear Anisotropic Metamaterials, Nat. Photonics, 2017, 11, 628–633.
12. M. Li, H. F. Pan, Y. Q. Tong, C. Chen, Y. Shi, J. Wu and H. P. Zeng, All-Optical Ultrafast Polarization Switching of Terahertz Radiation by Impulsive Molecular Alignment, Opt. Lett., 2011, 36, 3633–3635.
13. A. Tudi, S. J. Han, Z. H. Yang and S. L. Pan, Potential Optical Functional Crystals with Large Birefringence: Recent Advances and Future Prospects, Coord. Chem. Rev., 2022, 459, 214380.
14. D. H. Goldstein, L. G. DeShazer, D. B. Chenault, W. G. Egan and M. J. Duggin, Improved Midinfrared Polarizers Using Yttrium Vanadate, Proc. SPIE, 2002, 4481, 10–16.
15. G. Ghosh, Dispersion-equation Coefficients for the Refractive Index and Birefringence of Calcite Anquartz Crystals, Opt. Commun., 1999, 163, 95–102.
16. G. Q. Zhou, J. Xu, X. D. Chen, H. Y. Zhong, S. T. Wang, K. Xu, P. Z. Deng and F. X. Gan, Growth and Spectrum of a Novel Birefringent α-BaB₂O₄ Crystal, J. Cryst. Growth, 1998, 191, 517–519.
17. R. Appel, C. D. Dyer and J. N. Lockwood, Design of a Broadband UV-visible Alpha-Barium Borate Polarizer, Appl. Opt., 2002, 41, 2470–2480.
18. M. J. Dodge, Refractive Properties of Magnesium Fluoride, Appl. Opt., 1984, 23, 1980–1985.
19. Y. M. Cai, X. Z. Wang and H. J. Huang, Design of Wollaston Prism Used for Polarization Illumination System in ArF Lithography Tool, Chin. J. Lasers, 2014, 41, 16002.
20. D. L. Steinrnetz, W. G. Phillips, M. Wirick and F. F. Forbes, A Polarizer for the Vacuum Ultraviolet, Appl. Opt., 1967, 6, 1001–1004.
21. X. L. Chen, B. B. Zhang, F. F. Zhang, Y. Wang, M. Zhang, Z. H. Yang, K. R. Poeppelmeier and S. L. Pan, Designing an Excellent Deep-Ultraviolet Birefringent Material for Light Polarization, J. Am. Chem. Soc., 2018, 140, 16311–16319.
22. T. H. Tong, W. Y. Zhang, Z. H. Yang and S. L. Pan, Series of Crystals with Giant Optical Anisotropy: A Targeted Strategic Research, Angew. Chem., Int. Ed., 2020, 60, 1332–1338.
23. W. Q. Jin, W. Y. Zhang, A. Tudi, L. Y. Wang, X. Zhou, Z. H. Yang and S. L. Pan, Fluorine-Driven Enhancement of Birefringence in the Fluorooxosulfate: A Deep Evaluation from a Joint Experimental and Computational Study, Adv. Sci., 2021, 8, 2003594.
24. W. Y. Zhang, Z. Z. Zhang, W. Q. Jin, R. N. Zhang, M. Cheng, Z. H. Yang and S. L. Pan, From Borophosphate to Fluoroborophosphate: A Rational Design of Fluorine-induced Birefringe-nce Enhancement, Sci. China: Chem., 2021, 64, 1498–1503.
25. Z. H. Yang, A. Tudi, B. H. Lei and S. L. Pan, Enhanced Nonlinear Optical Functionality in Birefringence and Refractive Index Dispersion of the Deep-Ultraviolet Fluorooxoborates, Sci. China Mater., 2020, 63, 1480–1488.
26. B. B. Zhang, G. Q. Shi, Z. H. Yang, F. F. Zhang and S. L. Pan, Fluorooxoborates: Beryllium-Free Deep-Ultraviolet Nonlinear Optical Materials without Layered Growth, Angew. Chem., Int. Ed., 2017, 56, 3916–3919.
27. X. F. Wang, Y. Wang, B. B. Zhang, F. F. Zhang, Z. H. Yang and S. L. Pan, CsB₄O₆F: A Congruent-melting Deep-ultraviolet Nonlinear Optical Material by Combining Superior Functional Units, Angew. Chem., Int. Ed., 2017, 56, 14119–14123.
28. Y. Wang, B. B. Zhang, Z. H. Yang and S. L. Pan, Cation-Tuned Synthesis of Fluorooxoborates: Towards Optimal Deep-Ultraviolet Nonlinear Optical Materials, Angew. Chem., Int. Ed., 2018, 57, 2150–2154.
29. M. Mutailipu, M. Zhang, B. B. Zhang, L. Y. Wang, Z. H. Yang, X. Zhou and S. L. Pan, SrB₅O₇F₃ Functionalized with [B₅O₉F₃]⁶⁻ Chromophores: Accelerating the Rational Design of Deep-ultraviolet Nonlinear Optical Materials, Angew. Chem., Int. Ed., 2018, 57, 6095–6099.
30. J. Y. Guo, A. Tudi, S. J. Han, Z. H. Yang and S. L. Pan, Sn₂B₅O₉Cl: A Material with Large Birefringence Enhancement Activated via Alkaline-earth Metal Substitution by Tin, Angew. Chem., Int. Ed., 2019, 58, 17675.
31. J. Y. Guo, S. C. Cheng, S. J. Han, Z. H. Yan and S. L. Pan, Sn₂B₅O₉Br as an Outstanding Bifunctional Material with Strong Second-Harmonic Generation Effect and Large Birefringence, Adv. Opt. Mater., 2020, 9, 2001734.
32. J. Y. Guo, A. Tudi, S. J. Han, Z. H. Yang and S. L. Pan, Sn₂PO₄I: An Excellent Birefringent Material with Giant Optical Anisotropy in Non π-Conjugated Phosphate, Angew. Chem., Int. Ed., 2021, 60, 24901–24904.
33. J. Lu, Y. K. Lian, L. Xiong, Q. R. Wu, M. Zhao, K. X. Shi, L. Chen and L. M. Wu, How to Maximize Birefringence and Nonlinearity of π-Conjugated Cyanurates, J. Am. Chem. Soc., 2019, 141, 16151–16159.
34. F. Kong, C. L. Hu, M. L. Liang and J. G. Mao, Pb₄(OH)₄(BrO₃)₃(NO₃): An Example of SHG Crystal in Metal Bromates Containing π-Conjugated Planar Triangle, Inorg. Chem., 2016, 55, 948–955.
35. Y. C. Liu, Y. G. Shen and S. G. Zhao, Structure-Property Relationship in Nonlinear Optical Materials with π-conjugated CO₃ Triangles, Coord. Chem. Rev., 2020, 407, 213152–213172.
36. Y. G. Shen, S. G. Zhao and J. H. Luo, The Role of Cations in Second-Order Nonlinear Optical Materials Based on π-conjugated [BO₃]³⁻ Groups, Coord. Chem. Rev., 2018, 366, 1–28.
37. S. Y. Zhang, X. Wu, Y. T. Song, D. Q. Ni, B. Q. Hu and T. Zhou, Growth of Birefringent Ca₃(BO₃)₂ Crystals by the Czochralski Method, J. Cryst. Growth, 2003, 252, 246–250.
38. M. Mutailipu, K. R. Poeppelmeier and S. L. Pan, Borates: A Rich Source for Optical Materials, Chem. Rev., 2021, 121(3), 1130–1202.
39. D. B. Luo, X. J. Qiao and R. Dronskowski, Predicting Nitrogen-Based Families of Compounds: Transition-Metal Guanidinates TCN₃ (T = V, Nb, Ta) and Ortho-Nitrido Carbonates T′₂CN₄ (T′ = Ti, Zr, Hf), Angew. Chem., Int. Ed., 2021, 60, 486–492.
40. L. Kang, F. Liang, Z. S. Lin, F. Liu and B. Huang, Cyano-Based Materials with Giant Optical Anisotropy and Second Harmonic-Generation Effect, Inorg. Chem., 2018, 57, 15001–15008.
41. H. Yamane, S. Kikkawa, H. Horiuchi and M. Koizumi, Structure of a New Polymorph of Lithium Boron Nitride, Li₃BN₂, J. Solid State Chem., 1986, 65, 6–12.
42. H. Yamane, S. Kikkawa, H. Horiuchi and M. Koizumi, High- and Low-Temperature Phases of Lithium Boron Nitride, Li₃BN₂: Preparation, Phase Relation, Crystal Structure, and Ionic Conductivity, J. Solid State Chem., 1987, 71, 1–11.
43. F. E. Pinkerton and J. F. Herbst, Tetragonal I41/amd Crystal Structure of Li₃BN₂ from Dehydrogenated Li–B–N–H, J. Appl. Phys., 2006, 99, 113523.
44. J. Evers, M. Monsterkotter, G. Oehlinger, K. Polborn and B. Sendlinger, Natriumdinitridoborst Mit Dem Linear Gebauten, Symmetrischen BN₂³⁻ – Anion, J. Less-Common Met., 1990, 162, L17–L22.
45. J. Li, J. Ding, B. Ma, Z. Zhao and Y. Wang, Design and Research of a Self-activated Orange Magnesium Boron Nitride Phosphor with Its Application in W-LEDs, Dalton Trans., 2018, 47, 15439–15447.
46. M. Häberlen, J. Glaser and H. J. Meyer, Ca₃(BN₂)N – Eine Fehlende Verbindung im Quasi-Binären System Ca₃N₂-BN, Z. Anorg. Allg. Chem., 2002, 628, 1959–1962.
47. O. Reckeweg, F. J. DiSalvo and M. Somer, Rthorhombic Ba₃[BN₂]₂: a New Structure Type for an Alkaline Earth Metal Nitrido Borate, J. Alloys Compd., 2003, 361, 102–107.
48. L. J. Sham and M. Schluter, Density-Functional Theory of the Energy Gap, Phys. Rev. Lett., 1983, 51, 1888–1891.
49. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
51. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Optimized Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230.
52. C. Aversa and J. E. Sipe, Nonlinear Optical Susceptibilities of Semiconductors: Results with a Length-Gauge Analysis, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636–14645.
53. S. N. Rashkeev, W. R. Lambrecht and B. Segall, Efficient ab initio Method for the Calculation of Frequency-Dependent Second-Order Optical Response in Semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3905.
54. B. B. Zhang, M. H. Lee, Z. H. Yang, Q. Jing, S. L. Pan, M. Zhang, H. P. Wu, X. Su and Z. X. Li, Simulated Pressure Induced Blue-Shift of Phase-Matching Region and Nonlinear Optical Mechanism for K₃B₆O₁₀X (X = Cl, Br), Appl. Phys. Lett., 2015, 106, 031906–031912.
55. X. Dong, A. R. Oganov, A. F. Goncharov, E. Stavrou, S. Lobanov, G. Saleh, G. R. Qian, Q. Zhu, C. Gatti, V. L. Deringer, R. Dronskowski, X. F. Zhou, V. B. Prakapenka, Z. Konk pkov, I. A. Popov, A. I. Boldyrev and H. T. Wang, A Stable Compound of Helium and Sodium at High Pressure, Nat. Chem., 2017, 9, 440–445.
56. B. B. Zhang, X. D. Zhang, J. Yu, Y. Wang, K. Wu and M. H. Lee, First-Principles High-Throughput Screening Pipeline for Nonlinear Optical Materials: Application to Borates, Chem. Mater., 2020, 32, 6772–6779.
57. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
58. S. Y. Zhang, X. Wu, Y. T. Song, D. Q. Ni, B. Q. Hu and T. Zhou, Growth of Birefringent Ca₃(BO₃)₂ Crystals by The Czochralski Method, J. Cryst. Growth, 2003, 252, 246–250.
59. J. Tang, X. H. Meng, F. Liang, K. J. Kang, T. X. Zeng, M. J. Xia, W. L. Yin, Z. S. Lin and B. Kang, Structural Diversity and Giant Birefringence in Cyanates BaCNOX (X = Cl, Br, I, and CNO) Containing Linear π-Conjugated Units: A Combined Experimental and Theoretical Study, Cryst. Growth Des., 2020, 20, 1242–1247.
60. M. J. Kalmutzki, M. Strobele, F. Wackenhut, A. J. Meixner and H. J. Meyer, Synthesis, Structure, and Frequency-Doubling Effect of Calcium Cyanurate, Angew. Chem., Int. Ed., 2014, 53, 14260–14263.
61. M. J. Kalmutzki, K. Dolabdjian, N. Wichtner, M. Ströbele, C. Berthold and H. J. Meyer, Formation, Structure, and Frequency-Doubling Effect of a Modification of Strontium Cyanurate (α-SCY), Inorg. Chem., 2017, 56, 3357–3362.
62. F. Liang, L. Kang, X. Zhang, M. H. Lee, Z. S. Lin and Y. C. Wu, Molecular Construction Using (C₃N₃O₃)³⁻ Anions: Analysis and Prospect for Inorganic Metal Cyanurates Nonlinear Optical Materials, Cryst. Growth Des., 2017, 17, 4015–4020.
63. R. E. Cohen, Origin of Ferroelectricity in Perovskite Oxides, Nature, 1992, 358, 136–138.
64. B. H. Lei, S. L. Pan, Z. H. Yang, C. Cao and D. J. Singh, Second Harmonic Generation Susceptibilities from Symmetry Adapted Wannier Functions, Phys. Rev. Lett., 2020, 125, 187402.
65. B. H. Lei, Z. H. Yang and S. L. Pan, Enhancing Optical Anisotropy of Crystals by Optimizing Bonding Electron Distribution in Anionic Groups, Chem. Commun., 2017, 53, 2818–2821.
66. B. H. Lei, Z. H. Yang, H. H. Yu, C. Cao, Z. Li, C. Hu, K. R. Poeppelmeier and S. L. Pan, Module-Guided Design Scheme for Deep-Ultraviolet Nonlinear Optical Materials, J. Am. Chem. Soc., 2018, 140, 10726–10733.
67. J. Lin, M. H. Lee, Z. P. Liu, C. T. Chen and C. J. Pickard, Mechanism for Linear and Nonlinear Optical Effects in β-BaB₂O₄ Crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13380.
68. Q. Jing, G. Yang, J. Hou, M. Z. Sun and H. B. Cao, Positive and Negative Contribution to Birefringence in a Family of Carbonates: A Born Effective Charges Analysis, J. Solid State Chem., 2016, 244, 69–74.
69. C. S. Lin, A. Y. Zhou, W. D. Cheng, N. Ye and G. L. Chai, Atom-Resolved Analysis of Birefringence of Nonlinear Optical Crystals by Bader Charge Integration, J. Phys. Chem. C, 2019, 123, 31183–31189.
70. X. X. Jiang, S. Y. Luo, L. Kang, P. F. Gong, H. W. Huang, S. C. Wang, Z. S. Lin and C. T. Chen, First-Principles Evaluation of the Alkali and/or Alkaline Earth Beryllium Borates in Deep Ultraviolet Nonlinear Optical Applications, ACS Photonics, 2015, 2, 1183–1191.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated bandgap and PDOS, calculated birefringence, the NLO coefficients, the SHG response origins. See https://doi.org/10.1039/d2ra02135h

---