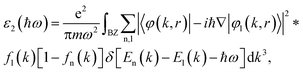Ab initio investigation of electronic structure and optical properties of IrSn₄

Abstract

We have examined the electronic structure and optical properties of intermetallic IrSn₄ for three polymorphic modifications, α-IrSn₄, β-IrSn₄, and γ-IrSn₄, utilizing the first-principles PAW-PBEsol-GGA and FP-LAPW-LSDA methods. The obtained electronic structure data reveal clear-cut differences between α-IrSn₄ and the remaining morphs. This observation may be used to explain the appearance of superconductivity in β-IrSn₄, and also provides reasonable grounds to suspect eventual superconductivity in γ-IrSn₄. Therefore, it is highly desirable to carry out extended measurements on γ-IrSn₄ at lower temperatures.

---

1 Introduction

Nowadays, scientists in the field of modern physics are paying particular attention to issues around superconductors. Various studies have been carried out with the aim of figuring out the mechanism of superconductivity in unconventional, as well as conventional, superconductors, and finally procuring room temperature superconductors.^1,2 Commonly, superconductivity may appear in a material if there are suitable circumstances, for example pressure, magnetic field, temperature, or chemical doping. So, this became to us the important query: what underlying physics lie behind the superconductivity which exists in one morph but not in others?

In this work, by means of first-principles calculations, we study the electronic structure and optical properties of intermetallic IrSn₄. The existence of this compound was reported for the first time by Lang and Jeitschko.³ The material was found to crystallize in a trigonal structure (no. P3₁21), and is denoted by α-IrSn₄ as a low-temperature morph. After that, Nordmark et al.⁴ identified a tetragonal form (no. I4₁/acd) at high temperature and denoted it as β-IrSn₄. Based on the projector-augmented-wave method, the authors ascertained that α-IrSn₄ is more stable than β-IrSn₄. It is known that IrSn₄ can occur in the orthorhombic structure (no. Ccca), denoted as γ-IrSn₄. This morph was announced by the two groups of Larchev et al.⁵ and Künnen et al.,⁶ who studied the crystal structure of IrSn₄ under a high pressure of 6 GPa.

It was surprising enough that superconductivity in the β-IrSn₄ phase was observed by Tran et al.⁷ Based on experimental data, the authors suggested that the presence of superconductivity in β-IrSn₄ is due to a weak electron–phonon pairing, even if the possible existence of d-electrons favors strong correlation.⁷ The discovery of superconductivity in β-IrSn₄ invites further investigation, not only due to the fact that strong correlations are often the origin of many interesting physical phenomena in materials, such as metal–insulator transitions, magnetic ordering, and superconductivity,^8,9 but also owing to the need to answer some crucial questions, e.g.: (i) how does the strong electron correlation affect the superconductivity of β-IrSn₄? (ii) Why the superconductivity is absent in the α-IrSn₄ and γ-IrSn₄ phases? To shed some light on these issues, we compared electronic structures and optical properties between three IrSn₄ morphs. We used the projector-augmented-wave method (PAW),¹⁰ implemented in VASP code,^11,12 to determine several quantities, such as the densities of states (DOS), partial densities of states, electronic band structures (EBS), Fermi surfaces (FS), and electron localization functions (ELFs) of the α-IrSn₄, β-IrSn₄, and γ-IrSn₄ phases. Moreover, we applied the full-potential linearized augmented plane-wave (FP-LAPW) method, executed in ELK program,¹³ to determine the dielectric functions and optical conductivities of these compounds.

2 Computational details

To obtain an optimization of the crystal structure, we relaxed all the structural parameters, starting from the literature data given in Table 1.

Table 1 Crystallographic input parameters of all considered phases of IrSn₄

Phase	a (Å)	b (Å)	c (Å)	V (Å^3)
α-IrSn4 (ref. 3)	6.791	6.791	8.575	395.46
β-IrSn4 (ref. 7)	6.308	6.308	22.739	904.80
γ-IrSn4 (ref. 5)	6.447	11.484	6.426	475.76

---

To achieve a geometry optimization, the calculation was conducted until the difference in energy between self-consistent loops was less than 10⁻⁵ eV and the force approximated 0.01 eV Å⁻¹. Further self-consistent charge density calculations were limited by the plane wave basis set with an energy-cutoff of 210.86 eV. The muffin-tin radii of the atoms were assumed to be R_Ir = 2.600 (a.u) and R_Sn = 3.000 (a.u). We attempted to ascertain the most stable phase amongst the studied polymorphic compounds by a comparison of their total energy. The evaluation will be meaningful if calculations of energy are performed for systems containing similar numbers of atoms, and taking into account the same Monkhorst–Pack grids. The primitive cell of the β-IrSn₄ phase comprises 40 atoms, therefore, we need to construct supercells for α and γ-IrSn₄ to have comparable numbers of atoms. As a result, the supercells of the latter phases possess orthogonal structures of 30 and 40 atoms, respectively. The calculations have been done for a 4 × 4 × 2 grid including 12 k-points for all states. We will scrutinize the total energy per atom given in Table 2. For the electronic structure properties’ calculations, the Brillouin zone was sampled with a 6 × 6 × 4 Monkhorst–Pack grid including 72 k-points for the α-IrSn₄ phase, 24 × 24 × 8 Monkhorst–Pack grid including 312 k-points for β-IrSn₄, and 8 × 4 × 8 Monkhorst–Pack grid including 32 k-points for γ-IrSn₄. The electronic band structure was investigated along the high-symmetry points Γ–M–K–Γ–A–L–H–A|L–M|H–K|Γ–M′–K′–Γ in α-IrSn₄, Γ–X–P–N–Γ–M–S|S₀–Γ|X–R|G–M in β-IrSn₄, and Γ–X–S–Y–Γ–Z–U–R–T–Z|X–U|Y–T|S–R in γ-IrSn₄, in line with proposed paths by Hinuma et al.¹⁴ For the optical investigations, we adopted the full-potential linearized augmented plane-wave (FP-LAPW) method implemented in ELK code.¹³ The Kohn–Sham equations were formalized within the exchange and correlation functional in the local spin density approximation (LSDA). Self-consistency was achieved under the energy convergence of 10⁻⁵ eV. A complex dielectric function ε(ω) = ε₁(ω) + iε₂(ω) was estimated within the random phase approximation (RPA), TDDFT with bootstrap kernel (TDDFT/TB09), and no microscopic contributions. That was calculated in the field polarization direction parallel to the ab-plane. The imaginary dielectric function was derived from the momentum matrix element

where l and n represent the occupied and unoccupied electronic states, e is the charge of an electron, m is the mass of an electron, and f_l(k) and f_n(k) are the associated Fermi distribution functions. Whereas the real part ε₁(ω) is performed through the Kramers–Kronig relations based on the imaginary part,
where P is the principal value of the integral. The optical conductivity tensor σ was computed from the dielectric function,
where σ_αβ(ω) is a component taken from the interband and intraband transition contributions.¹⁵ Although all considered optical properties were calculated in both light polarization directions, perpendicular and parallel to the c-axis, we only obtained the data along the ab-plane due to the limitation of the ELK code within the TDDFT/TB09. The irreducible Brillouin zone was established with 4 × 4 × 4, 4 × 4 × 1 and 4 × 2 × 4 meshes consisting of 16, 6 and 20 k-points for α-IrSn₄, β-IrSn₄, and γ-IrSn₄, respectively. To examine the spatial-division dependence of the optical features, we additionally calculated the dielectric function and optical conductivity of β-IrSn₄ using a 4 × 4 × 2 mesh including 12 k-points. The valence electrons for the constituent elements are Ir: 5d⁷6s² and Sn: 5s²5p². In all calculations, the generalized gradient approximations were employed for the exchange correlation interaction, where the Perdew–Burke–Ernzerhof-type pseudopotential (PBEsol-GGA)¹⁶ was taken into account.

3 Results

The geometry optimization yields lattice parameters, given in Table 2. As one can see, the optimized parameters are slightly modified by around 6% after the structural relaxation.

Table 2 Optimized crystallographic parameters and the calculated total energy of the considered polymorphs of IrSn₄

Phase	a (Å)	b (Å)	c (Å)	Etot (eV at^−1)
α-IrSn4	6.86299	6.86299	8.66819	−8508.6416
β-IrSn4	6.4139	6.4139	23.0127	−8508.6427
γ-IrSn4	6.41178	11.60777	6.39883	−8508.6425

---

In addition to the lattice parameters, the relaxation provides important information in respect of the phase stability of the IrSn₄ phases. The ground state total energy per atom in each morph (given in Table 2) reveals the lowest value of energy in β-IrSn₄ with the differences in E_tot values between α- and β-, and between β- and γ-IrSn₄, of approximately 1.1 meV and 0.2 meV, respectively. Our finding is in contrast to the result of Nordmark et al., who concluded that α-IrSn₄ is the most stable phase.⁴

The total and partial density of states (DOS and PDOS) of IrSn₄ in the energy range −12–6 eV are presented in Fig. 1. One can consider the DOS structure in three different regions, from −12 to −5 eV, from −5 to 0 eV, and that above E_F. The DOS structure in the first region originates from Sn-5s electrons. In the second energy range, the main DOS peaks arise from almost equal contributions of Ir-5d and Sn-5p electrons. This finding implies that Ir-5d orbitals possibly are strongly hybridized with Sn-5p ones. Finally, the valence states in the energy range between 0 and 6 eV exhibit a dominant contribution from the Sn-5p electrons.

Fig. 1 The total density of states and partial density of states of the Ir and Sn atoms in (a) α-IrSn₄, (b) β-IrSn₄ and (c) γ-IrSn₄.

A comparison of the DOS shows a substantial difference in the DOS structure between these polymorphs. A higher and more complicated DOS peak structure just below the Fermi level is found in β-IrSn₄ and γ-IrSn₄ compared to that of α-IrSn₄. Moreover, the highest peak located at −1.2 eV resembles the Van Hove singularity, suggesting an electronic instability, and would involve the mechanism of Cooper pairing.¹⁷

The estimated density of states at the Fermi level N(E_F) and the correspondingly derived Sommerfeld coefficient γ_th of all phases are listed in Table 3. To calculate γ_th, we used the following relation of

where N_A is Avogadro’s number and k_B is Boltzmann’s constant.

Table 3 The density of states at the Fermi level and the Sommerfeld coefficient of all considered phases of IrSn₄

Phase	N(EF) (st eV^−1 f.u.)	γth (mJ K^−2 mol^−1)
α-IrSn4	2.167	5.093
β-IrSn4	1.813	4.259
γ-IrSn4	1.430	3.361

---

A relatively high Fermi level density of states N(E_F), together with electronic instability in β-IrSn₄, allow us to anticipate a superconducting state in this phase, since the conditions required for superconductivity were fulfilled.^17,18 Having the density of states at E_F, we can estimate the Coulomb pseudopotential μ* using the phenomenological Bennemann–Garland formula:¹⁹

μ* = 0.26N(E_F)/(1 + N(E_F)), (2)

Using the theoretical value N(E_F) = 1.813, we obtain the Coulomb pseudopotential μ* = 0.167. Based on the McMillan equation:²⁰

the electron–phonon coupling λ_e–ph would take on a value of 0.503, affirming weak-coupling superconductivity in β-IrSn₄. The Debye temperature Θ_D = 221 K and T_c = 0.9 K are the experimental values taken from ref. 7.

Fig. 2 presents the band structure of the three IrSn₄ phases along the high-symmetry points of the Brillouin zone. The bands crossing the Fermi level are marked by colored lines. We detect only 2 bands crossing the Fermi level in α-IrSn₄ and 3 bands in the γ-IrSn₄ phase, but as many as 6 bands passing through E_F in β-IrSn₄. The observation of many bands located around E_F hints at strong interband scattering in β-IrSn₄. It must be recalled that the pairing mechanism assisted by the interband exchange Coulomb interaction between s and d bands for the mechanism of superconductivity of transition metals was predicted many years ago by Kondo.²¹ A similar mechanism has also been examined by Yamaji in terms of a two-band Hubbard model for high-T_c oxides,²² and by Crépel et al. in the framework of an extended Hubbard model for unconventional superconductivity.²³ Therefore, keeping these theoretical considerations in mind, we believe that the stronger interband scattering observed in β-IrSn₄ favors the creation of superconductivity in this phase.

Fig. 2 Electronic band structures of (a) α-IrSn₄, (b) β-IrSn₄ and (c) γ-IrSn₄. The colored lines denote bands crossing E_F. Insets show enlarged views of the expected Dirac cone points.

The EBS of the three IrSn₄ morphs differ a lot from each other, not only by number of electronic bands crossing E_F but also by different structures near E_F. These bands in β-IrSn₄ (Fig. 2b) and γ-IrSn₄ (Fig. 2c) are closely comparable and they form Dirac-cone-like structures characterized by a small gap of about 13–16 meV (see enlarged figures in the insets). The bands presented in green and yellow (in Fig. 2b), and blue and gray (in Fig. 2c) share the same attribution of Ir-5d and Sn-5p electrons.

One may add that the Dirac cone has been observed in other condensed matter systems, such as topological insulators²⁴ graphene,²⁵ cuprate-based,²⁶ and FeAs-based²⁷ superconductors. There have been several efforts which proved the close relationship between the appearance of Dirac cones and the nature of the spin-density wave (SDW) state in superconductor materials.^28–30

The Fermi surface topology in the primitive Brillouin zone of IrSn₄ is displayed in Fig. 3. The FS illustrate multi-sheet structures and highly anisotropic character in all three morphs. However, one can distinguish several remarkable differences between them. The Fermi surface of α-IrSn₄ is characterized by a 3D topology with a more complex structure, whereas a 2D-like FS is observed in β- and γ-IrSn₄. The two-dimensional Fermi surface topology is an important requirement for superconductivity; e.g., it is often found in HTc FeAs-based superconductors. Therefore, the 2D-FS feature of β-IrSn₄ is not alien to the superconductivity. In addition, the FS of γ-IrSn₄ possesses an almost 2D topology, being a promising factor for superconductivity.

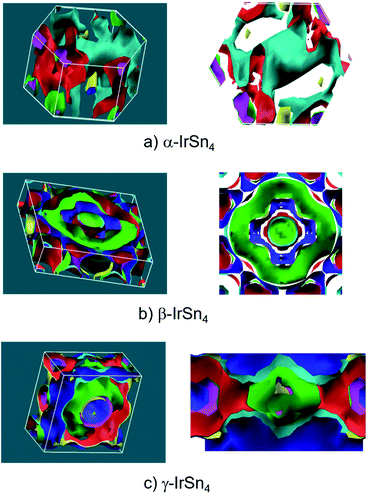Fig. 3 Fermi surfaces in 3D and quasi-2D topology along the 001 configuration of (a) α-IrSn₄, (b) β-IrSn₄ and (c) γ-IrSn₄. The figures are plotted by XCrySDen.³¹

The electron localization function (ELF) describes the spatial distribution of electrons in a chemical compound and it may provide information about the nature of bonding in studied systems. The ELF is defined as

where , , and is the electron density.^32,33 Fig. 4 exhibits the 3D visualizations of the crystal unit cell and the ELF isosurface cut in several different planes. The ELF is restricted between 0 to 1, presented in the color bar from blue to red, corresponding to the change in character of the bonding, from the perfect de-localized to localized one, respectively. The ELF map divulges the high anisotropic distributions of electrons in the considered IrSn₄ phases. The low value of the ELF of about 0.5–0.6 near the Ir atoms suggests the itinerant properties of the Ir-5d electrons, responsible for the metallic character of the material. On the other hand, the quite high ELF value of 0.9 surrounding the Sn atoms points to the highly localized properties of Sn-5p electrons. It is clear that the ELF between Ir and Sn significantly varies, not only within each phase, but also between different phases. The bonding character is also inferred through the analysis of the ELF saddle points between different atoms. The high value of the ELF between Sn atoms is additionally ascribed to the covalent character of the Sn–Sn bond. One recognizes that the ELF value increases in series for the morphs α-IrSn₄–β-IrSn₄–γ-IrSn₄. Accordingly, the character of the covalent bonding develops in the same sequence. Obviously, the atomic bonds between atoms in IrSn₄ are noticeably different between the morphs, which leads to the physical properties of each phase.

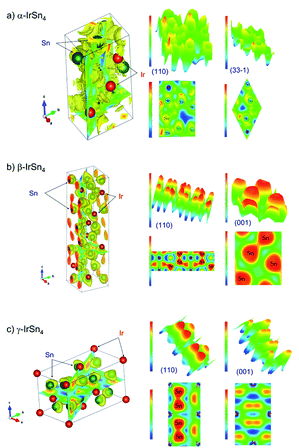Fig. 4 3D visualizations of the crystal unit cells and the ELF isosurfaces cut in several unique planes of (a) α-IrSn₄, (b) β-IrSn₄ and (c) γ-IrSn₄. The figures are plotted by VESTA.³⁴

The nature of the interaction of a material with light can be studied via calculations of optical properties. The frequency-dependent dielectric function ε(ω) = ε₁(ω) + iε₂(ω) yields information on the optical spectra and, furthermore, the inferred optical characteristics. Fig. 5 shows the real (ε₁) and imaginary (ε₂) parts of the dielectric function of all considered IrSn₄ phases calculated for light polarization along the ab-plane in the energy range 0–12 eV. The effect of dielectric field on the polarized degree of materials can be followed by an inspection of the real part of the dielectric functions. The calculated results of ε₁ (Fig. 5a) show the static constants of 83.7, 129.9 and 321.8 at 0 eV in the α-, β-, and γ-IrSn₄ phases, respectively. These values imply that the interaction of IrSn₄ with an electric field, without absorbing energy, increases for this series of compounds in the order of α-, β- and γ-IrSn₄.

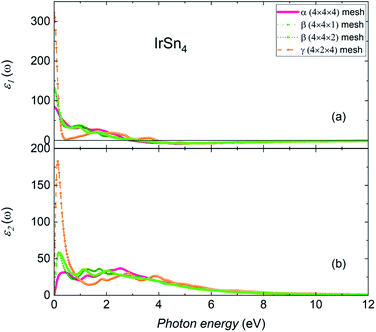Fig. 5 (a) Real and (b) imaginary parts of the dielectric function of α-, β- and γ-IrSn₄ along the ab-plane polarization direction.

Basically, ε₁ in all phases dramatically decreases with increasing energy in the infrared and visible light regions, indicating that the polarization degree is reduced at the high energy range. The change of polarization following the change of photon energy in γ-IrSn₄ is larger than in the remaining phases. The real part of permittivity ε₁ retains a positive value until the photon energy is less than 2.9 eV, 3.2 eV and 3.9 eV in the α-, β- and γ-IrSn₄ compounds, respectively, suggesting a positive phase shift and IrSn₄ is therefore treated as a capacitor.³⁵ In the higher energy ranges, ε₁ decreases to a negative value, meaning that the electric field vector and electric displacement vector arrange in opposite directions, where IrSn₄ displays metallic behavior.^35,36

The spectra of the imaginary part of the dielectric function ε₂ is related to electron excitation, which indicates the ability of materials to absorb energy. The imaginary part of the dielectric constant of IrSn₄ (Fig. 5b) is found to be approximately zero at energies larger than 9 eV but in the low energy range of 0.2–4 eV, ε₂ presents several maxima. Aiming to figure out the contribution of each orbital to the optical transition, we may consider the relationship between the maxima of ε₂ and the partial density of states of Ir and Sn in the α-phase (Fig. 6). The optical spectra in the low energy range are suspected to consist of contributions from excitation of both Ir-d and Sn-p electrons. The peak of ε₂ at 0.2 eV may be assigned to the intraband transitions of Ir-d_x²−y² ↔ Ir-d_x²−y²/d_z²/d_xz and Sn-p_x ↔ p_y. The intraband transitions of Sn-p_y ↔ Sn-s/p_x/p_z, Sn-p_x ↔ Sn-p_x/p_z and Ir-d_z² ↔ Ir-d_yz, and interband transition of Ir-d_z²/d_x²−y² ↔ Sn-s presumably contribute to the peak at 2.5 eV.

Fig. 6 Partial density of states of Ir and Sn in α-IrSn₄.

Upon increasing the k-mesh size from 4 × 4 × 1 to 4 × 4 × 2 in β-IrSn₄, the real and imaginary parts of the dielectric spectra slightly change in the energy range of 0.2–2.2 eV and are preserved in the remaining area. Therefore, the chosen Brillouin zone division is good enough to study the optical properties of β-IrSn₄.

The real parts of optical conductivity σ of α-, β- and γ-IrSn₄ along the ab-plane are presented in Fig. 7. In the infrared and ultraviolet ranges, the σ spectrum of γ-IrSn₄ certainly exhibits a broader spectrum compared to those in the others. This behavior entails more excitation of carriers in this phase. It is remarkable that there are several pronounced peaks in the range 1.5–7 eV; namely, the maxima in the optical conductivity occur at 2.5 eV and 3.2 eV in the α- and β-morphs, respectively. The γ-IrSn₄ spectrum resolves into peaks at 3 and 3.8 eV. It turns out that the electromagnetic response of the γ-morph shows an interesting behavior. Similar to the dielectric behavior under the different k-meshes, the optical conductivity spectra for the β-morph do not change much between the 4 × 4 × 1 and 4 × 4 × 2 meshes.

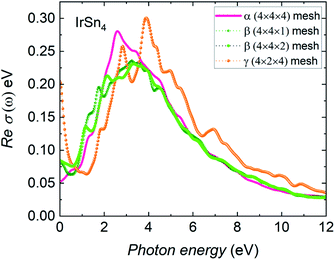Fig. 7 Real part of optical conductivity with RPA of α-, β- and γ-IrSn₄ along the ab-plane polarization direction.

4 Conclusions

We have investigated the electronic and optical properties of three morphs, α-IrSn₄, β-IrSn₄, and γ-IrSn₄. The density of states structure is found to be more complicated with a Van Hove singularity in β-IrSn₄, which reveals the greater instability of electrons in this superconductor. Moreover, the strong interband scattering in this morph is suggested by the numerous bands crossing the Fermi level, corresponding to the 2D-topology of the Fermi surfaces. Meanwhile, the 3D-topology formation is observed in α-IrSn₄.

The electron localization function describes the high itinerant behavior of Ir electrons and the strong covalent bond of Sn–Sn in β-IrSn₄ and γ-IrSn₄. Interestingly, the electronic bands near the Fermi level also form Dirac cone structures in both β-IrSn₄ and γ-IrSn₄. The coincidence of many electronic structures between β-IrSn₄ and γ-IrSn₄ morphs is highly encouraging to verify the possibility of superconductivity in the latter compound.

Concerning the optical properties, the real part of the dielectric function points out that the polarization degree decreases with an increase of energy, and γ-IrSn₄ shows a larger change of polarization than those in other phases. Whereas the high of imaginary part of dielectric function in the infrared and visible light regime seems to be explained by interband and intraband transitions between the valence electrons of Ir-d and Sn-p. In addition, the optical conductivity results indicate a large carrier density, reflected by pronounced maxima in the low energy region.

Author contributions

T. L. Mai: DFT calculations, data analysis, writing and editing. V. H. Tran: conceptualization, validation, writing, and supervision.

Conflicts of interest

We have no conflicts of interest to disclose.

Acknowledgements

T. L. Mai would like to thank the Van Lang University for financial support.

Notes and references

1. H. Kaur, H. Kaur and A. Sharma, Mater. Today: Proc., 2021, 37, 3612–3614.
2. R. Flükiger, Reviews of Accelerator Science and Technology, 2012, vol. 05, pp. 1–23.
3. A. Lang and W. Jeitschko, J. Mater. Chem., 1996, 6, 1897–1903.
4. E.-L. Nordmark, O. Wallner and U. Häussermann, J. Solid State Chem., 2002, 168, 34–40.
5. V. Larchev and S. Popova, J. Less-Common Met., 1984, 98, L1–L3.
6. D. N. B. Künnen and W. Jeitschko, J. Alloys Compd., 2000, 309, 1–9.
7. V. H. Tran, Z. Bukowski, P. Wiśniewski, L. M. Tran and A. J. Zaleski, J. Phys.: Condens. Matter, 2013, 25, 155701.
8. R. M. G. Arti and T. Nandini, Nat. Phys., 2008, 4, 762–765.
9. H. Fukuyama, S. Maekawa and A. P. Malozemoff, Strong Correlation and Superconductivity, Springer, Berlin, Heidelberg, 1989, vol. 89.
10. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
11. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
12. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561.
13. J. K. Dewhurst, et. al., Version 5.2.10, 2018.
14. Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184.
15. G. Grosso and G. Parravicini, Solid State Physics, Academic, San Diego, 2000, https://www.elsevier.com/books/solid-state-physics/grosso/978-0-12-385030-0.
16. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
17. L. Van Hove, Phys. Rev., 1953, 89, 1189–1193.
18. J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175–1204.
19. K. H. Bennemann and J. W. Garland, AIP Conf. Proc., 1972, 4, 103.
20. W. L. McMillan, Phys. Rev., 1968, 167, 331–344.
21. J. Kondo, Prog. Theor. Phys., 1963, 29, 1–9.
22. K. Yamaji and S. Abe, J. Phys. Soc. Jpn., 1987, 56, 4237–4240.
23. V. Crépel, T. Cea, L. Fu and F. Guinea, Phys. Rev. B, 2022, 105, 094506.
24. B. A. Bernevig, T. L. Hughes and S. C. Zhang, Science, 2006, 314, 1757.
25. A. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
26. A. Damascelli, Z. Hussain and Z.-X. Shen, Rev. Mod. Phys., 2003, 75, 473.
27. P. Richard, K. Nakayama, T. Sato, M. Neupane, Y.-M. Xu, J. H. B. G. F. Chen, J. L. Luo, N. L. Wang, X. Dai, Z. Fang, H. Ding and T. Takahashi, Phys. Rev. Lett., 2010, 104, 137001.
28. Y. Ran, F. Wang, H. Zhai, A. Vishwanath and D.-H. Lee, Phys. Rev. B, 2009, 79, 014505.
29. M. Z. Hasan and B. Bernevig, Physics, 2010, 3, 27.
30. D. Hsieh, Y. Xia, L. Wray, D. Qian, K. Gomes, A. Yazdani, G. F. Chen, J. L. Luo, N. L. Wang and M. Z. Hasan, arXiv:0812.2289, 2008, 3,  DOI:10.48550/arXiv.0812.2289.
31. A. Kokalj, Comput. Mater. Sci., 2003, 28, 155–168.
32. A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188.
33. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
34. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
35. J. D. Jackson, Classical Electrodynamics, J. Wiley and Sons, Inc, 1999.
36. K. Sun, J. Xin, Y. Li, Z. Wang, Q. Hou, X. Li, X. Wu, R. Fan and L. C. Kwang, J. Mater. Sci. Technol., 2019, 35, 2463–2469.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra01672a

---