Insight into the exemplary structural, elastic, electronic and optical nature of GaBeCl₃ and InBeCl₃: a DFT study

Abstract

In the scheme of density functional theory (DFT), Structural, elastic, electronic, and optical properties calculations of GaBeCl₃ and InBeCl₃ are carried out using Tran–Blaha modified Becke–Johnson exchange potential approximation (TB-mBJ) installed in Wein2k software. Structurally the compounds of interest are found to be stable. Both compounds possess elastic stability, anisotropy, and ductility determined by the elastic studies. The electronic-band structure analysis shows the semiconductor nature of GaBeCl₃ and InBeCl₃ compounds with indirect band gaps of ∼3.08 eV for GaBeCl₃ and ∼2.04 eV for InBeCl₃ along with the symmetrical points from (X–Γ). The calculated total density of states (TDOS) and partial density of states (PDOS) of these compounds reveal that for the GaBeCl₃ compound, the contribution of Ga (4p) and Cl (3p) orbital states in the valence, as well as the conduction band, is dominant. While for InBeCl₃, the contribution of Cl (3p) states as well as In (5s) is large in the valence band and in that of Cl (3p-states) states in the conduction band. The type of chemical bonding is found to be ionic in both compounds. The optical properties i.e., the real (ε₁(ω)) and imaginary (ε₂(ω)) parts of dielectric function, refractive index n(ω), optical reflectivity R(ω), optical conductivity σ(ω), absorption coefficient α(ω), energy loss L(ω) and electron extinction coefficient k(ω) are also discussed in terms of optical spectra. It is reported that n(ω) and k(ω) exhibit the same characteristics as ε₁(ω) and ε₂(ω) respectively. Efficient application of these materials can be seen in semiconducting industries and many modern electronic devices.

---

Introduction

It is well known that perovskite compounds show significant diversity in mechanical,^1,2 electrical,^3,4 magnetic,⁵ optical,^6,7 and transport properties^8–12 i.e., magnetism, ferroelectricity, multiferroicity, superconductivity, piezoelectricity, colossal magnetoresistance, etc.^8–16 And due to these properties, perovskites are the key materials for several technological applications including optoelectronic, photonic, and spintronic appliances i.e., a promising candidate for radiation detection, photovoltaic absorbance and a laser medium.^17–21 Literally, the flexible crystal structure and elements of which a perovskite is composed of are responsible for some of the characteristics of these perovskites.^22–24 An ideal perovskite having a cubic crystal structure has the general formula ABX₃, in which, “A” (occupying the corners) and “B” (occupying the center) are metallic cations while X (occupying the face centers) is an oxide or halide i.e., Cl, Br, I and F. The cubic perovskites are considered as the most stable. It is observed experimentally and theoretically by many scientists that such type of perovskites exhibit the cubic structure possessing the space group pm̄3m (#221).^25,26

Metal halide perovskites have several similar phenomena, which exist in the oxide perovskites. Although many perovskites have been found experimentally, the huge number of possible combinations of three chemical elements, the perovskites family may be vast, and possibly many systems are still waiting for researcher discovery.

This work is based on the study of the structural, elastic, electronic, and optical properties of GaBeCl₃ and InBeCl₃ perovskites. So far, there has been no experimental or theoretical study on these perovskite materials. Therefore, the work of this paper can be used for reference in the future.

Computational methodology

The following investigation is performed using TB-mBJ in the framework of DFT, implemented in the WIE2K code.²⁷ The TB-mBJ potential is used to investigate the elastic, electronic, and optical properties. Structural properties are computed by fitting the Birch–Murnaghan equation of state (EOS), in which the unit cell volume versus unit cell energy is fitted to attain the ground state parameters. The value of RMT is chosen such that no charge leaks out of the sphere. The energy difference of −6 Ry is taken between the core and valence band. The RMT × K_max cutoff is chosen to be 7. The IRelast package²⁸ is used for the computation of elastic properties. For precise, reliable, and better results, 2000 k-points are taken for computation of all the properties.

Results and discussions

Structural characteristics

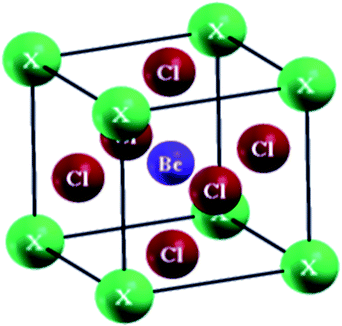
The perovskites compounds XBeCl₃ have an ideal cubic structure exhibiting the space group pm̄3m (#221). The occupied Wyckoff positions in the elementary cell are (0, 0, 0), (0.5, 0.5, 0.5) and (0, 0.5, 0.5) as depicted in Fig. 1. The volume vs. energy is fitted by the Birch–Murnaghan equation of state (EOS) as shown in Fig. 2.²⁹ From this fit, the determined ground state characteristics i–e the lattice constant (a_o), bulk modulus (B), the minimum energy (E_o), and its pressure derivative (B′) are given in the table. No previous experimental or theoretical results are available for the GaBeCl₃ and InBeCl₃ compounds for comparison with the current calculations (Table 1).

Fig. 1 Crystal structure of XBeCl₃ obtained with XCryDen.

Fig. 2 Total energy vs. volume of cubic perovskites XBeCl₃.

Table 1 Calculated a_o (Å), B (GPa), E_o (Ry), B′ (GPa) for cubic perovskites GaBeCl₃ and InBeCl₃

Compounds	ao	B	B′	Eo
GaBeCl3	4.621	65.578	5.371	−6687.0977
InBeCl3	4.586	193.255	42.380	−14565.4784

---

Elastic characteristics

The elastic constants are basic and necessary parameters used to describe the mechanical properties of materials.³⁰ For cubic systems, there are three completely independent elastic constants i–e C₁₁, C₁₂, and C₄₄.³¹ Using these elastic constants, the other parameters e.g. G, ν, A, E, and B/G can be calculated using Voigt–Reuss–Hill eqn (1)–(6).^32–34

The “B” and “G” determine the hardness of the materials.³⁵ Similarly, the material will be brittle, if υ <0.26 and B/G <1.75 otherwise it will exhibit a ductile nature.³⁶ Here both the compounds show the ductile nature. Furthermore, as for isotropic nature, the value of “A” should be equal to 1, if not then the material will have anisotropic nature. Therefore, GaBeCl₃ and InBeCl₃ compounds show anisotropic properties. All the obtained results are summarized in Table 2.

Table 2 Calculated C₁₁(GPa), C₁₂(GPa), C₄₄(GPa), G(GPa), ν, A, E(GPa), and B/G for GaBeCl₃ compounds

Compounds	C11	C12	C44	A	G	E	v	B/G
GaBeCl3	94.9636	48.1999	52.4496	2.2432	38.6754	96.9643	0.3515	1.6956
InBeCl3	332.7265	107.3298	161.7959	1.4356	139.9710	338.2573	0.3582	1.3807

---

Electronic characteristics

To study the electronic properties of the compounds, their energy band structures along the highly symmetrical points in the first Brillouin zone are calculated. Fig. 3(a) and (b) illustrates the band-structures of GaBeCl₃ and InBeCl₃ respectively. It can be observed that in both the compounds, the maximum of the valence band and minimum of the conduction band is located at X and Γ and the two bands do not overlap each other. Therefore, the material GaBeCl₃ can be regarded as semiconducting which possessing an indirect band gap of ∼3.08 eV, while InBeCl₃ possesses a band gap of 2.04 eV and thus a semiconductor.

Fig. 3 Band-structures of XBeCl₃ along with the high symmetry directions. (a) GaBeCl₃ (b) InBeCl₃.

To better understand the electronic properties, the TDOS and PDOS are calculated for both compounds. Fig. 4(a–d) illustrates the TDOS and PDOS for the GaBeCl₃ compound. TDOS is divided into three regions. In the first region from −7 to −1, Cl (p-states) contributes the maximum. In the second region from −1 to 0, the contribution of Ga (4p-states), as well as Cl (3p-states) atoms, is large. These are the regions below the Fermi energy (E_F). Above E_F, again the contribution of Ga (4p-states) and Cl (3p-states) atoms is large. Consequently, in both the valence band as well as the conduction band Ga and Cl, p orbital states are maximum. Similarly, Fig. 4(e–h) shows the TDOS and PDOS for the InBeCl₃ compound. Here the contribution of Cl (3p-states) is large in the energy range of −12 to −3 eV. However, in the region from −3 to 0, In (5s-states) atoms contribution is large. In addition, a Cl (3p-states) atom also makes a certain contribution. Above E_F, in the energy range from 3–8 eV, Cl (3p-states) atoms participation is maximum. Hence the contribution of states in the valence band of InBeCl₃ is due to Cl (3p-states) and In (5s-states) and in that of the conduction band is due to the Cl (3p-states) only. The result of TDOS and PDOS confirms the band structure reports.

Fig. 4 (a–d) TDOS and PDOS of InBeCl₃. (e–h) TDOS and PDOS of GaBeCl₃.

The electronic properties or the band gap varies with the change in A-site, B-site and X-site (halide) ion. As well as when the calculations method is changed. Several examples are listed in Table 3.

Table 3 Calculated bandgaps for some compounds

Compound	LDA	mBJ
CsCaF3 (ref. 37)	6.1	*
CsBaF3 (ref. 31)	5.02	8.78
LiBaF3	7.83	*
BiGaO3 (ref. 38)	*	2.46
BiInO3 (ref. 38)	*	1.05

---

Optical properties

The response of the materials to the incident photons are calculated in the energy range 0–40 eV. The complex dielectric function (eqn (7)) can be separated into two parts i–e real (ε₁(ω)) and imaginary (ε₂(ω)) part.³⁹

ε(ω) = ε₁(ω) + iε₂(ω) (7)

Here ε₁(ω) and ε₂(ω) are related to the absorption and the band structure respectively.^40,41 Fig. 5(a and c) illustrates ε₁(ω) and ε₂(ω) spectrum respectively. From Fig. 5(a) it can be seen that the threshold energy or absorption edge²⁰ for GaBeCl₃ and InBeCl₃ is located at ∼7.178 eV and ∼3.27 eV respectively. Similarly, the static dielectric constant ε₁(0) (5(c)) for GaBeCl₃ and InBeCl₃ is situated at 5.1 and 8.08, while the maximum peaks are found at 4.37 and 3.10 after this a decrease can be seen in both the plots, following another maximum.

Fig. 5 Calculated (a) ε₁(ω), (b) n(ω), (c) ε₂(ω) (d) k(ω) (e) R(ω) (f) σ(ω) (g) L(ω) and (h) α(ω) of XBeCl₃ compounds.

Fig. 5(b) shows n(ω) for both the compounds the static refractive index n(0) is found to be 2.32 and 2.88 for GaBeCl₃ and InBeCl₃ respectively. The value of n(ω) increases and reaches a maximum value of 3.27 at 4.40 and 4.26 at 3.1 eV. This lies in the UV region of the light spectrum. Furthermore, it is observed that behavior of n(ω) and k(ω) is similar to ε₁(ω) and ε₂(ω) for both the compounds.

Fig. 5(e) displays the R(ω) spectra for both the compounds. The results depict the maximum reflectivity of 38% and 48% at 19.24 eV and 3.3 eV for GaBeCl₃ and InBeCl₃ respectively. Similarly, Fig. 5(f–h) depicts (σ(ω), L(ω)) and α(ω) for GaBeCl₃ and InBeCl₃ compounds. The highest conductivity i–e 6.71 Ω⁻¹ cm⁻¹ is obtained at 7.04 eV and 9.98 Ω⁻¹ cm⁻¹ at 10.50 eV for GaBeCl₃ and InBeCl₃ respectively. The resonant energy losses are observed at 23.25 eV and 25.97 eV for both the compounds respectively. In addition, the point at which the material starts absorption is found to be at 2.23 eV and 3.23 eV for GaBeCl₃ and InBeCl₃ compounds respectively.

Conclusion

In summary, the TB-mBJ approximation based on DFT is used to investigate the structural, elastic, electronic, and optical properties of ABeCl₃ (A = Ga, In). It is reported that with the change in cation from Ga to In, the lattice constant and ground state energy decreases while bulk modulus and pressure derivative of bulk modulus increase. The elastic properties confirmed the anisotropic and ductile nature of both the compounds. Furthermore, the studied compounds have mechanical stability which is the key requirement for applications in high-performance electronic devices. The ionic type of chemical bonding is present in the compounds. In addition, the investigated electronic-band structure reveals the narrow band-gap semiconducting nature of the compounds with the indirect gap of ∼3.1 eV along (X–Γ) for GaBeCl₃ and InBeCl₃compounds. The results of TDOS and PDOS for GaBeCl₃ and InBeCl₃ compound shows that in both the valence band as well as the conduction band Ga (4p-states) and Cl (3p-states) atoms contribution are maximum for GaBeCl₃. However, in InBeCl₃ the contribution of Cl (3p-states) and In (5s-states) in the conduction band and that of Cl (3p-states) in the valence band is large. In addition, the optical properties of GaBeCl₃ and InBeCl₃ are calculated in the photon energy range of 0–40 eV. It is reported that n(ω) and k(ω) exhibit the same characteristics as ε₁(ω) and ε₂(ω) respectively. The computed properties of this work must be considered to understand and utilize the possible technical benefits in device manufacturing in semiconducting industries. Optical properties are of great significance in radiation detection and laser technology.

Conflicts of interest

There are no conflicts of interest.

Acknowledgements

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R61) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

References

1. M. S. Ahmad, A. Habib, A. Rauf, M. U. Haq, J. Saddique, M. Nisar, M. U. Rehman and M. Imran, Theoretical investigation, 2020, 1, 1.
2. N. Rahman, M. Husain, J. Yang, G. Murtaza, M. Sajjad, A. Habib, A. Karim, M. U. Haq, A. Rauf and M. Nisar, J. Supercond. Novel Magn., 2020, 33, 3915.
3. N. Rahman, M. Husain, J. Yang, M. Sajjad, G. Murtaza, M. U. Haq, A. Habib, A. Rauf, A. Karim and M. Nisar, Eur. Phys. J. Plus, 2021, 136, 1.
4. S. U. Zaman, N. Rahman, M. Arif, M. Saqib, M. Husain, E. Bonyah, Z. Shah, S. Zulfiqar and A. Khan, AIP Adv., 2021, 11, 015204.
5. M. Husain, M. S. Ahmad, N. Rahman, M. Sajjad, A. Rauf, A. Habib, M. U. Haq, M. Nisar, A. Hussain and M. Imran, Fluoride, 2020, 53, 657.
6. M. Husain, N. Rahman, A. H. Reshak, A. Habib, S. Ali, A. Laref, A. M. Al Bakri and J. Bila, Eur. Phys. J. Plus, 2021, 136, 1.
7. M. Husain, N. Rahman, R. Khan, S. Zulfiqar, S. A. Khattak, S. N. Khan, M. Sohail, A. Iqbal, A. H. Reshak and A. Khan, Int. J. Energy Res., 2022, 46, 2446–2453.
8. T. Y. Ansell and D. P. Cann, Mater. Lett., 2012, 80, 87.
9. M. E. Lines and A. M. Glass, Principles and applications of ferroelectrics and related materials, Oxford university press, 2001.
10. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050.
11. J. Wang, J. Neaton, H. Zheng, V. Nagarajan, S. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. Schlom and U. Waghmare, Science, 2003, 299, 1719.
12. S. Aharon, A. Dymshits, A. Rotem and L. Etgar, J. Mater. Chem. A, 2015, 3, 9171.
13. M. Eibschütz and H. Guggenheim, Solid State Commun., 1968, 6, 737.
14. N. A. Spaldin and R. Ramesh, Nat. Mater., 2019, 18, 203.
15. R. Dubrovin, A. Garcia-Castro, N. Siverin, N. Novikova, K. Boldyrev, A. H. Romero and R. Pisarev, Phys. Rev. B, 2021, 104, 144304.
16. F. Pascale, P. D’arco, V. Lacivita and R. Dovesi, J. Phys.: Condens. Matter, 2021, 34, 074002.
17. D. Sardar, W. Sibley and R. Alcala, J. Lumin., 1982, 27, 401.
18. A. Gektin, I. Krasovitskaya and N. Shiran, J. Lumin., 1997, 72, 664.
19. M. Mortier, J. Gesland and M. Rousseau, Solid State Commun., 1994, 89, 369.
20. A. Mubarak and A. Mousa, Comput. Mater. Sci., 2012, 59, 6.
21. Y. Fu, H. Zhu, J. Chen, M. P. Hautzinger, X.-Y. Zhu and S. Jin, Nat. Rev. Mater., 2019, 4, 169.
22. A. G. Ricciardulli, S. Yang, J. H. Smet and M. Saliba, Nat. Mater., 2021, 1.
23. T. Neumann, S. Feldmann, P. Moser, A. Delhomme, J. Zerhoch, T. van de Goor, S. Wang, M. Dyksik, T. Winkler and J. J. Finley, Nat. Commun., 2021, 12, 1.
24. K. Koteras, J. Gawraczyński, M. Derzsi, Z. Mazej and W. Grochala, Chemistry, 2021, 3, 94.
25. G. Vaitheeswaran, V. Kanchana, R. S. Kumar, A. Cornelius, M. Nicol, A. Svane, A. Delin and B. Johansson, Phys. Rev. B, 2007, 76, 014107.
26. G. Vaitheeswaran, V. Kanchana, R. S. Kumar, A. Cornelius, M. Nicol, A. Svane, N. Christensen and O. Eriksson, Phys. Rev. B, 2010, 81, 075105.
27. R. M. Almeida, A. L. da Rosa, T. Frauenheim and J. S. de Almeida, Phys. Status Solidi B, 2019, 256, 1800380.
28. M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, J. Alloys Compd., 2018, 735, 569.
29. F. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244.
30. K. E. Babu, N. Murali, K. V. Babu, P. T. Shibeshi and V. Veeraiah, Acta Phys. Pol., A, 2014, 125, 1179.
31. M. Harmel, H. Khachai, A. Haddou, R. Khenata, G. Murtaza, B. Abbar, S. B. Omran and M. Khalfa, Acta Phys. Pol., 2015, 128, 34.
32. C.-S. Man and M. Huang, J. Elasticity, 2011, 105, 29.
33. A. Ballato, Voigt-Reuss-Hill moduli for ferroelectric aggregates, 2006 15th ieee international symposium on the applications of ferroelectrics, IEEE, 2006, p. 208.
34. C.-S. Man and M. Huang, J. Elasticity, 2012, 106, 105.
35. M. H. Sadd, Elasticity: Theory, Applications and Numerics, Elsevier Academic Press, Burlington, MA, 2005, pp. 123–259.
36. D. Pettifor, Mater. Sci. Technol., 1992, 8, 345.
37. G. Vaitheeswaran, V. Kanchana, X. Zhang, Y. Ma, A. Svane and N. Christensen, J. Phys.: Condens. Matter, 2016, 28, 315403.
38. R. B. Behram, M. Iqbal, S. Alay-e-Abbas, M. Sajjad, M. Yaseen, M. I. Arshad and G. Murtaza, Mater. Sci. Semicond. Process., 2016, 41, 297.
39. M. Fox, Optical Properties of Solids, Oxford University Press Inc., New York, 2001, p. 25.
40. N. V. Smith, Phys. Rev. B, 1971, 3, 1862.
41. Z. Feng, H. Hu, S. Cui, W. Wang and C. Lu, Open Phys., 2009, 7, 786.

---