Open Access Article
Open Access ArticleSelf-assembled morphologies of polyelectrolyte-grafted nanoparticles directed by oppositely charged polymer matrices†
Qing-Hai Hao *,
Jie Cheng,
Fan Yang and
Hong-Ge Tan
*,
Jie Cheng,
Fan Yang and
Hong-Ge Tan
College of Science, Civil Aviation University of China, Tianjin 300300, China. E-mail: qhhao@cauc.edu.cn
First published on 7th July 2022
Abstract
Self-assembled structure of polymer grafted nanoparticles is an interesting and growing subject in the field of hybrid electronics and high energy density materials. In light of this, the self-assembled morphologies of polyelectrolyte (PE) sparsely grafted nanoparticles tuned by oppositely charged matrix chains are studied using molecular dynamics simulations. Our focus is to elucidate the effect of matrix chain polymerization on modulating the stretching properties of tethered PE layers, on the self-assembled structuring of nanoparticles. Through varying the matrix chain length and stiffness as well as electrostatic interaction strength, rich phase behaviors of PE coated nanoparticles are predicted, including spherical micelle-like structures being preferred with short matrix chains and percolating network morphologies favored with long matrix chains, which is more pronounced with an enhanced matrix chain rigidness. To pinpoint the mechanisms of self-assembled structure formation, the thickness of grafted layers, the gyration radius of tethered chains, and pair correlation functions between nanoparticles are analyzed carefully. Additionally, electrostatic correlations, manifested as the bridging via matrix chains, are examined by identifying three states of matrix PE chains. Our simulation results may be useful for designing smart polymer nanocomposites based on PE coated nanoparticles.
1 Introduction
Precise manipulation of nanoparticle (NP) assemblies would enable one to obtain desired macroscopic properties for different applications that range from structural and biomedical to electronic and optical, and has therefore attracted continuing interest in recent decades.1–3 Specifically, the optimal mechanical performances of polymer nanocomposites (PNCs) are often associated with the spatial organization of NPs within the polymer matrix.4,5 Biological systems in nature, such as teeth and bone, depend on the self-assembled morphologies of “NPs”, collagen and hydroxyapatite, respectively.6,7 Several methods have been developed to tune NP dispersion and their spatial correlation, in particular, the most widely adopted strategy is chemical grafting or physically adsorbing polymer chains onto the NP surface, so as to adjust the enthalpic and entropic interactions between NPs and polymers.8,9 The anisotropic organization of the NPs within polymer hosts can be determined by variables that include: shape and radius of NPs, grafting density, degrees of polymerization (Ng of the grafted chains and Nm of the matrix chains), and so on.10 Because the interactions within these systems are complex and the dynamics are interrelated, a unified picture of how various competing interactions determine the conformations and properties of PNCs remains elusive.5,8Comprehensive understanding and documenting the self-assembled structures of polymer-grafted NPs is essential to predict and control macroscopic properties of PNCs. So far, a series of experimental,11–14 theoretical,15–19 and simulation20–23 studies have investigated the phase behavior of NPs coated by uncharged macromolecules. Akcora et al.11 investigated the self-assembled structure of spherical silicon NPs uniformly coated with polystyrene (PS) chains dispersed in corresponding homopolymer matrix. By varying the grafted and matrix chain length, a series of anisotropic morphologies were observed, such as, dispersed (isolated polymer grafted NPs), long strings, connected/sheet, and spherical aggregates. Xu and coworkers12 demonstrated a rich variety of two- and three-dimensional self-assembled structures through independent adjustment of the core size of Fe3O4 and Au NPs and the molecular weight of densely tethered PS ligands. Choueiri et al.13 developed a new strategy for NP surface patterning, that is, the segregation of a neutral polymer brush into surface pinned patches was triggered by changing solvent quality. And the possible self-assembly structures of these patterned NPs were revealed. Recently, Kumar and coworkers14 systematically compared the dispersion and self-assembly of silica NPs tethered with either a sparse mono-modal PS brush or a bimodal brush comprised of a sparse grafting of long PS chains and a dense carpet of short poly(2-vinypyridine) (P2VP) chains in PS matrices. It was demonstrated that, depending on the PS grafting density and the ratio of grafted/matrix chain length, the NP dispersion states can be tuned from aggregate, thick string and vesicle, clump and string to dispersed phases.
Based on the microscopic polymer reference interaction site model (PRISM) theory, Jayaraman et al.15 studied collective structure and assembly of dense solutions and melts of spherical NPs carrying a single tethered chain. By increasing the total packing fraction and/or particle–particle attraction strength, the strong concentration fluctuations, indicative of aggregate formation and/or a tendency for microphase separation, were observed. In a subsequent literature,16 the same group varied the number of polymer ligands on the NP from 1 to 4, and considered the effect of the location of the grafting points. The coordination number of the NPs increased with increasing particle–particle attraction strength, and decreased as the number of ligands increased. Employing both classical density functional theory (DFT) and self-consistent field theory (SCFT), the structure of polymer-grafted nanorods in homopolymer films were calculated by Frischknecht et al.17 The total interaction free energy between two nanorods was estimated, which can be used to predict the system parameters of dispersed or aggregated states. Combining SCFT and DFT, Zhu et al.18 investigated the self-assembly behavior of spherical NPs functionalized with a single flexible diblock copolymer chain. Ordered hierarchical structures, such as cylinders with cylinders at the interfaces, lamellae with cylinders at the interfaces, and lamellae with cylinders inside a domain, were observed for the chemical neutral NPs. Recently, Ginzburg19 developed a new SCFT describing the phase behavior of one-component polymer-grafted NP system and predicted lamellar, cylindrical, and spherical morphologies as a function of ligand molecular weight and grafting density.
From the simulation side, by means of dissipative particle dynamics (DPD) method, Khani et al.20 conducted a comprehensive study of self-assembled morphology of nanorods (NRs) grafted with a neutral polymer brush in polymer matrices. Three types of structures, such as, dispersion, aggregation, and particle aggregation, were predicted by varying grafting density and ligand chain length. Li et al.21 investigated the structural and mechanical properties of diblock copolymer grafted NPs in a homopolymer matrix by coarse-grained molecular dynamics (MD) simulations. It was reported that the morphology of NPs was shifted from a network structure to an isolated or well dispersed state upon the increase of grafting density. Employing MD simulations, Kumar and coworkers22 studied the self-assembly behavior of grafted NPs mixed with chemical identical homopolymer chains. They pointed out that the phase separation of NPs was driven by the chemical mismatch between the inorganic core and the organic ligands, even though the graft and matrix chains were chemical identical. Very recently, Koski and Frischknecht23 investigated the self-assembly of NPs coated with two neutral immiscible homopolymers (solvophobic and solvophilic chains) in a selective solvent by using Langevin dynamics (LD) simulation. Various well-ordered structures, including double-walled vesicles, were formed when the solvent quality was sufficiently poor for the solvophobic ligands.
In contrast to the most commonly explored morphologies of neutral polymer grafted NPs directed by various parameters, little attention has been paid to study the self-assembled structures of PE coated NPs up to the present. Specifically, the viscosity of PE grafted NPs solutions was investigated using MD simulations by Medidhi and Padmanabhan,24 and they pointed out that the balance between the entanglement of ligand and the electrostatic repulsion governed the viscosity of the solution. Sandberg et al.25 conducted MD simulations to investigate the formation of lateral morphologies of a spherical PE brush in salt-free solutions induced by the electrostatic interaction strength under poor solvent conditions, which provided anisotropic interaction to tune the self-assembly of PE grafted nanoparticles. Cao and Bachmann26 considered the complexation behavior of a spherical PE brush and an oppositely charged linear PE by means of coarse-grained MD simulations. The effects of bending rigidity of the linear PE, the density and lengths of the grafted PEs, and the core radius on the formation and shape of complexes were analyzed. Noting that, the introduce of long-range electrostatic interaction will largely enrich the stimuli-responsive behavior of PNCs, which can provide additional strategies to precise manipulation of NP assemblies. Herein, we focus our attention on the self-assembled morphologies of PE-grafted NPs mixed with oppositely charged polymer matrices by means of coarse-grained MD simulations. The effects of length and stiffness of matrix chains as well as the electrostatic interaction strength on the structures of PE-coated NPs are examined in detail. Our simulation results may help to understand the complicated structure–performance relationship of PNCs with the presence of electrostatic interactions.
2 Model and simulation details
Simulations of PE grafted NPs mixed with oppositely charged matrix chains are carried our by utilizing a well-tested coarse-grained bead-spring model,27,28 which are implemented in the LAMMPS simulation software.29 The NPs with radius Rn = 2.0σ are formed by overlapping a certain number of beads Nb with diameter σ, which are under rigid body constraints during the simulation. The number of beads for constructing the spherical surface of nanoparticle is computed as Nb = 4πRn2/π(0.5σ)2 = 64. To ensure the surface of nanoparticles are arranged densely, we select Nb = 108 in our simulation. Monomers of diameter σ and mass m are bonded to form grafted chains of length Ng and matrix chains of length Nm, and the first bead in the grafted chain is anchored uniformly on a NP surface. The number of ligand PE chains on one NP is chosen as Mg = 8, which is not varied throughout the simulations. Specifically, 4 grafted PE chains are negatively charged, that is, each monomer carries one elementary charge −e, corresponding to a charge fraction of f = 1.0. The positively charged matrix chains are added to the system, which is used to guarantee overall charge neutrality. The counterions of grafted and matrix PE chains are not included in our simulation model mainly due to the consideration of computational resources in charged system. The schematic for our simulation system is shown in ESI (Fig. S1†). The cubic simulation box of size Lx × Ly × Lz is selected, and the periodic boundary condition is applied in the three directions. And an implicit solvent model is chosen in our simulation.The excluded volume interaction between any particle pair is represented by a truncated-shifted Lennard-Jones (LJ) potential,
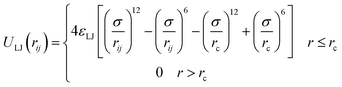 | (1) |
The bonded interactions between the neighbouring monomers are modeled by the finite nonlinear extensible elastic (FENE) potential,27,30
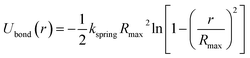 | (2) |
The stiffness of the matrix PE chain is mimicked by using a harmonic angle potential,
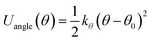 | (3) |
The electrostatic interactions between charged segments are modeled by the Coulomb potential,
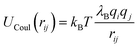 | (4) |
Simulations are carried out in a constant number of particles, volume, and temperature (NVT) ensemble. The Langevin thermostat is applied to maintain the constant temperature T = 1.0. The motion of any bead is described by Langevin equation,
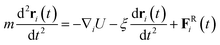 | (5) |
The velocity-Verlet algorithm with a time step of Δt = 0.005τ is used for the integration of the equations of motion. To characterize the role of matrix PE chains more clearly, the length of matrix chains Nm is varied from 1 to 48 in our simulations. Specifically, Nm = 1 corresponds to the case of the coated NPs in monovalent counterions. Furthermore, the effects of the matrix chain rigidness and electrostatic interaction strength on the self-assemble structures are also investigated in our simulations, that is, kθ = 0, 5.0, and 100.0 respectively, λB = 3.0, 10.0, and 20.0 represents the increase of electrostatic interaction. The side lengths of the cubic simulation box are selected as Lx × Ly × Lz = 45.4σ, and the number of grafted NPs is fixed at 36. The total number of beads in our simulation box contains the number of grafted monomers, matrix monomers, and the beads for constructing the spherical surface of nanoparticles, which corresponds to the bead density 0.1σ−3.33,34 The selected bead density can assure that the pressure of system is reasonable.
Simulations are performed in the following procedure. Initially, 36 PE grafted NPs are placed in a simple cubic structure and the grafted chains stretch along the radial direction of the NP. The matrix chains are dispersed randomly in the simulation box. In order to remove any monomer overlaps, an increasingly repulsive soft potential between non-bonded monomers is employed to generate the disordered initial conformation of our system. Then, the full LJ potentials described above take the place of soft potential and the system is equilibrated for 3 × 106 steps. After the equilibrated run, another production run is performed for 4 × 106 steps. During the production run, one configuration is sampled every 2 × 103 steps and 2001 configurations are saved to collect data for analyzing the self-assembled structures by our programs. In addition, all simulation processes are repeated independently three times for statistical consistency.
The relaxation of PE grafted NPs can be investigated by monitoring the fluctuations in the ligand chain parameters. Specifically, to identify a steady state is reached in our simulation, the auto-correlation functions of radius of gyration of grafted PE chains are calculated, which is defined as
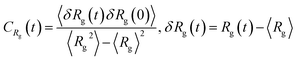 | (6) |
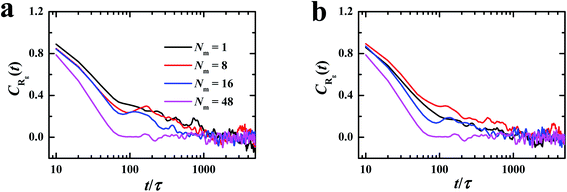 | ||
| Fig. 1 Autocorrelation functions of radius of gyration of the grafted chains with different matrix chain lengths. (a) λB = 3.0 and kθ = 0, (b) λB = 10.0 and kθ = 100.0. | ||
As shown in Fig. 1, it is observed that the autocorrelation functions decay to zero before t = 1000τ (= 2 × 104 steps) in all illustrated cases, which is much shorter than the lasting time of equilibrated run (3 × 106 steps). Therefore, it is convinced that the system approaches the steady state in the production run.
3 Results and discussions
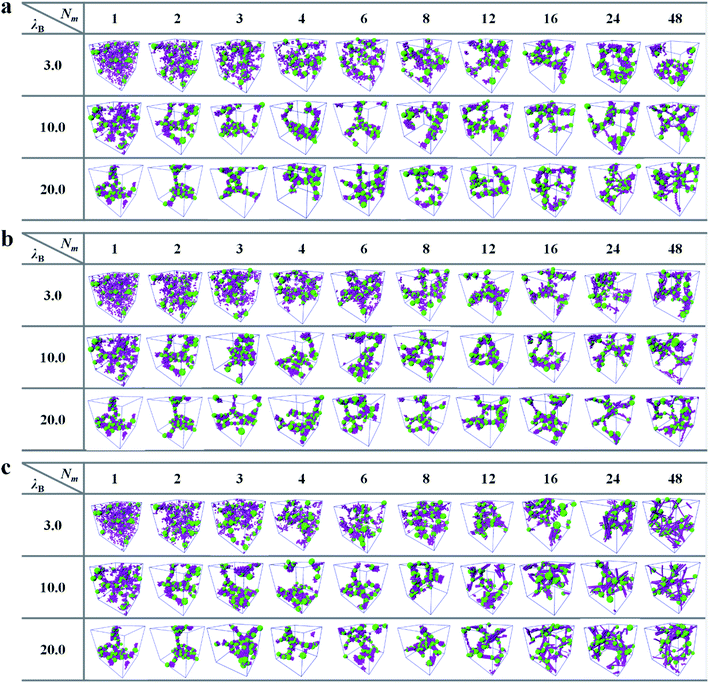
We now turn to the self-assemble structures of PE grafted NPs induced by the oppositely charged matrix chains. The simulation snapshots can provide an visual summary of morphologies of grafted NPs, which are demonstrated in Fig. 2. The effects of length and rigidness of matrix chains as well as the electrostatic interaction strength on the self-assembled structures are explored systematically.For the flexible matrix chains shown in Fig. 2a, we find that, when the electrostatic interaction is weak λB = 3.0, the PE grafted NPs adopt a well-dispersed morphology in the presence of the short matrix chains Nm ≤ 3. Note that Nm = 1 corresponds to the PE coated NPs are immersed in the monovalent counterion solution, which can be understood from the “osmotic brush” regime of PE brushes.35,36 Specifically, a part of counterions are confined in the brush layer due to the electrostatic attraction (see the density distributions along the radial direction of nanoparticles shown in Fig. S3 in ESI†) and other counterions are dissociated outside the brush layer owing to the translational entropy compensation. The electrostatic repulsion of the residual charges on the grafted PE chains renders the grafted corona in a stretched state, which promotes the repulsive interaction of NPs and the formation of a disordered structure. With increasing Nm > 3, the FENE bonds binds several charged monomers in one matrix chain together, which provides the matrix chain an electrostatic correlation effect similar to the multivalent counterions. The electrostatic correlation of oppositely charged matrix chains begins to play the roles of intrachain/interchain bridging. This bridging effect can introduce attractive interactions between PE grafted NPs, and a series of micelle-like aggregates of grafted NPs can be observed with the increase of matrix chain length. This is the manifestation of the electrostatic correlation induced phase separation of PE grafted NPs, which is beyond the description of mean-field theory.37 The similar microphase separations of PE brush systems induced by electrostatic correlation of multivalent counterions were also reported experimentally.38–40 With the increase of electrostatic interaction strength, the most distinguished morphological change is the formation of more micelle-like structures of grafted NPs, even in the case of Nm = 1 (see the third row of Fig. 2a). It was reported that the heterogeneous domains of PE brushes were also formed in the presence of monovalent counterions when the strength of electrostatic interaction is strong enough,41,42 which coincides with our simulation results. The enhanced electrostatic interaction will lead to the closer combination between the positively charged monomers of grafted PE chains and negatively charged monomers of matrix PE chains. The Coulomb screening effect weakens the electrostatic repulsion between charged monomers, which is manifested by the appearance of more compact aggregated structure of grafted NPs. The string-like micelles and the coral-like cylindrical structures are observed in turn with the increase of matrix chain length.
The rigidness of matrix PE chains is a crucial parameter determining the structures and properties of PE grafted NPs. Thus, the self-assembled structures of PE coated NPs induced by the semi-flexible and rigid matrix chains are also investigated, which are plotted in Fig. 2b and c respectively. Since the stiffness of the matrix chain is taken into account through a three-body potential (see eqn (3)), the self-assembled snapshots mediated by semi-flexible and rigid matrix chains for Nm ≤ 2 are consistent with those of flexible matrix chains. With the increase of matrix chain length for Nm ≥ 3, the pronounced bending energy renders the matrix chain to extend relatively. The oppositely charged matrix chains with preferred linear conformations act as the gluing agent to promote aggregation of the grafted NPs in a relatively loose way, which corresponds to the various larger micelle-like morphologies. Very recently, Skandalis et al.43 reported that the spherical cationic micelles comprising hydrophobic cores and mixed coronas prepared by triblock terpolymers could self-assemble in colloidally stable micelleplexes with DNA molecules of different lengths. By means of different experimental characterization methods, they further evidenced that the micelleplexes with short DNA were found to have more spherical morphologies, on the contrary, the micelleplexes with long DNA were preferred to have elongated structures. The similar dependence of aggregated structures of PE grafted NPs on the matrix chain length is also observed in our simulation system, that is, the sphericity of the self-assembled micelles becomes less pronounced with the increase of matrix chain length, especially for the semi-flexible conditions shown in Fig. 2b.
To explore the underlying physical mechanism of self-assembled structures of grafted NPs tuned by PE matrix chain length, the mean thickness of grafted PE chains along the radial direction of the central NPs is calculated, which can be defined as,
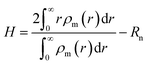 | (7) |
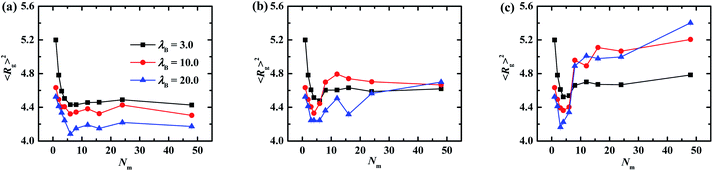
The dependences of the brush thickness on the matrix PE chain length with different chain stiffness are plotted in Fig. 3. In the case of flexible matrix chains depicted in Fig. 3a, the thickness of grafted PE chains demonstrates a pronounced decreasing profile for Nm ≤ 6 regardless of electrostatic interaction strength, which can be attributed to the enhanced electrostatic correlation accompanied by the increasing matrix chain length. It is noted that each relatively short matrix chain is more likely to be adsorbed onto the PE chains tethered on the same NP, which displays the intra-nanoparticle bridging and lowers the brush thickness. Further increasing the matrix chain length Nm > 6, the profile of brush thickness is leveled off at λB = 3.0. On the other side, the grafted corona swells slightly and then levels off at λB = 10.0 and 20.0. The slight increase of brush thickness indicates that the relatively long matrix chains begin to adsorb the PE chains grafted onto different NPs, play the inter-nanoparticle bridging role, and increase the brush thickness. Furthermore, the brush thickness decreases with the increase of electrostatic interaction strength for fixed matrix chain length, which is similar to the height of the PE brush in inorganic salt solutions.44,45 As shown in Fig. 3b and c, when the bending potential energy is introduced into the backbone of the matrix chain, the curves of the brush thickness as a function of the matrix chain length at λB = 3.0 (the solid squares) is consistent with those of the flexible matrix chains, which conveys that the rigidity of matrix chains has slight effect on the self-assembly structures of the grafted NPs under the weak electrostatic interaction strength. However, the brush thickness fluctuates obviously with the increase of the matrix length, which is more pronounced at λB = 20.0 (the filled triangles). These oscillatory profiles corresponds to the transformation of aggregations of PE grafted NPs induced by the matrix chain length, which are also confirmed by the mean number of nanoparticles aggregated in clusters by means of cluster analysis technique.
 | ||
| Fig. 3 The brush thickness of grafted NPs as a function of matrix PE chains with different rigidness. (a) kθ = 0, (b) kθ = 5.0, (c) kθ = 100.0. Error bars are smaller compared to the symbols. | ||
The cluster analysis technique,46,47 is employed for monitoring the self-assembled structures of PE grafted NPs. The inter-nanoparticle distance is used for determining whether a monomer belongs to a cluster, that is, if NP i has an interval less than or equal to rcutoff with any NP already in the cluster, it will be included in this cluster. Here, the rcutoff is equal to the first minimum in the NP–NP pair correlation function. Based on the cluster analysis technique, the mean number of clusters as a function of matrix chain length are calculated, which are shown in Fig. 4.
 | ||
| Fig. 4 The number of NPs aggregated in clusters as a function of matrix chain length with different chain rigidness. (a) kθ = 0, (b) kθ = 5.0, (c) kθ = 100.0. | ||
As observed from Fig. 4, the number of NPs aggregated in clusters also demonstrates an oscillatory profile in the range 3 < Nm < 24 when λB = 10.0 and 20.0 (filled circles and triangles), which confirms that the transformation of aggregations of PE grafted NPs is induced by the matrix chain length.
The global configurations of tethered PE chains are characterized by the radius of gyration Rg, and the results are plotted in Fig. 5. For the case of flexible matrix chains shown in Fig. 5a, the radius of gyration decreases sharply, fluctuates slightly, and then levels off with the increase of matrix chain length, which is almost irrespective with the intensity of electrostatic interaction. The transition point from decreasing to fluctuation locates at Nm = 6 regardless of λB, which can be understood from analyzing the correlation effect of the matrix PE chains. Specifically, the increase of length of matrix chains combined with the increase of charges of one single matrix chain enhances the electrostatic correlation effect, which shrinks the grafted PE chains. From the other side, the increase of polymerization of matrix chains leads to the increase of geometric size of matrix chains, which swells the grafted PE chains. The competition induces the transition point occurred at Nm = 6. As depicted in Fig. 5b and c, the trough located around the first minimum of Rg profile becomes pronounced when the rigidness of matrix PE chains changes from semi-flexible to rigid for fixed electrostatic interaction strength. Furthermore, the location of the first minimum shifts towards to the small Nm side with the increase of λB, which is distinguished with those of flexible matrix conditions shown in Fig. 5a. The value of Rg increase clearly at λB = 10.0 and 20.0 for Nm > 18 and rigid matrix chain condition (see filled circles and triangles in Fig. 5c), however, the brush thickness does not change significantly (see filled circles and triangles in Fig. 3c), which indicates that the grafted PE chains only adjust their configurations in the lateral direction to adapt to the enhancement of matrix chain stiffness. Furthermore, it is observed that the Rg for Nm = 48 is lowest for λB = 20.0 at kθ = 0 (see Fig. 5a) and it is the highest for other kθ values (see Fig. 5b and c). To understand this phenomena, the snapshots of one PE grafted nanoparticle and matrix chains for Nm = 48 for different λB values are shown in Fig. S4.† When the matrix chains are flexible, the grafted PE chains adopt an extended conformation at λB = 3.0, which is manifested as the largest Rg value. For λB = 20.0, the like charged repulsion of grafted PE chains is weakened due to the enhanced electrostatic interaction, which corresponds to the shrink of grafted chains and decrease of Rg. When the matrix chains are rigid, one grafted chain is inclined to be adsorbed tightly to one rigid matrix chain for λB = 20.0 due to the enhanced electrostatic attraction, and the grafted chains are straightened by the rigidness of the matrix chains, which leads to the largest value of Rg for the grafted chains. The similar phenomenon was also reported by Cao and Bachmann26 for one single PE chain complexed with PE grafted nanoparticle.
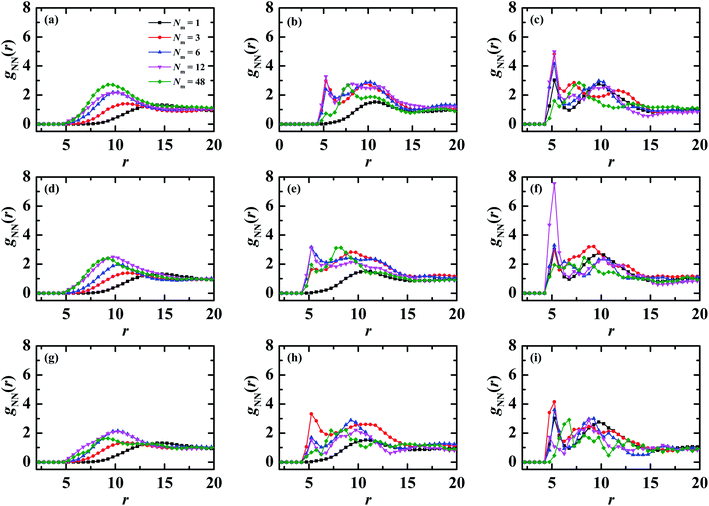
In order to further clarify the local structuring of PE grafted NP systems, we calculate the pair correlation functions (PCF) of NP–NP gNN(r), and the results are plotted in Fig. 6. For clarity, only five different matrix chain lengths are provided. For the flexible matrix chains, it is expected that there exists no correlations between NPs at Nm = 1 in the case of λB = 3.0, which is in fact shown in Fig. 6a (the solid squares). With increasing the matrix chain length Nm, a broad peak is developed in the gNN profile demonstrated in Fig. 6a. The location of this broad peak shifts towards to the small r side for Nm ≤ 6 and is almost unchanged for Nm > 6, which is consistent with the evolution of Rg as a function of matrix chain length shown in Fig. 5a (filled squares). Furthermore, on increasing electrostatic interaction strength, both the nearest neighbor correlation and the long-range correlation become pronounced for fixed matrix chain length without rigidness. For example, at Nm = 3, the profile of gNN demonstrates two apparent peaks at λB = 10.0 (see the filled circles in Fig. 6b), in contrast, three distinct peaks are observed at λB = 20.0 shown in Fig. 6c (the filled circles). This enhancing electrostatic interaction strength induced order has also been reported for the PE brush system with the presence of multivalent counterions.48,49
The nanoparticle–nanoparticle PCFs mixed with semi-flexible and rigid matrix chains are presented in Fig. 6d–f and g–i respectively. One can find that the amplitude of the primary peak demonstrates a nonmonotonic dependence on the matrix chain length, namely, the peak becomes higher firstly and then lower with the increase of matrix chain length, and the transition occurs at different Nm. On the other hand, in PCF of Nm = 12 with the semi-flexible matrix PE chains (the solid down triangles in Fig. 6f), a sharp peak is manifested at r = 5.2, suggesting aggregation of NPs. Moreover, when the two NPs come together bridged by the matrix chains, they push the surrounding grafted chains to the side, which in turn prevent other NPs joining the side of the aggregate, which leads to a formation of sheetlike or string structures. These structures are inclined to form a percolating network (see the second row in Fig. 2b), which is a characteristic of a gel.50,51 Furthermore, for semi-flexible and rigid matrix chains Nm ≥ 12 at λB = 10.0 and 20.0, the primary peak is faded off, however, the secondary and higher order peaks are more distinct, especially for Nm = 48, indicating that oppositely charged matrix chain induced order gets longer with the increasing chain length. And the position of the primary peak in all pair correlation functions as a function of Nm are shown in Fig. S5.†
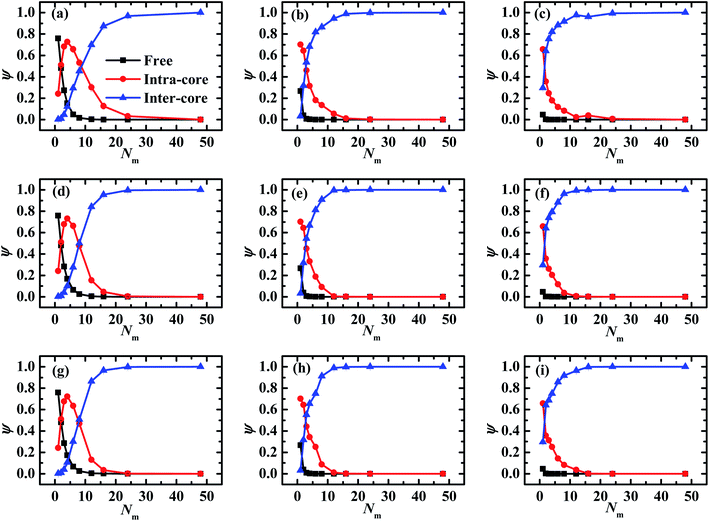
Due to the importance of electrostatic correlation of matrix PE chains in the self-assembled morphologies of PE grafted NPs, we further investigate the states of matrix PE chains by classifying them into three states, namely, the free, the intra-nanoparticle bridging (IAB), and inter-nanoparticle bridging (IEB), respectively.49 The three fractions are defined as the ratios of the number of matrix chains that are in the corresponding states to the total number of matrix chains. The states of matrix PE chains are identified by constructing the neighbor list of grafted monomers for each matrix chain based on a cutoff distance Rc = 21/6, which corresponds to the cutoff distance of the pairwise interactions between monomers of grafted chains and matrix chains. Specifically, if no grafted monomers in the neighbor list, the matrix PE chains are in the free state. If monomers in the neighbor list are grafted onto the single NP, the matrix chain is confirmed in IAB state, however, if the monomers in the neighbor list tethered onto different NPs, the matrix chain is considered in IEB state. The fractions of matrix chains as a function of chain length with different chain rigidness under different electrostatic interaction strength are illustrated in Fig. 7.
As shown in Fig. 7, the fractions of matrix PE chains in the free states (filled squares) demonstrate a sharp decreasing profile and remain a constant with the increase of matrix chain length, however, the fractions of matrix chains on the IEB states (filled triangles) increase significantly and level off with increasing Nm. Specifically, the two fractions ψfree and ψIEB as a function of Nm demonstrate similar profiles regardless of matrix chain stiffness and electrostatic interaction strength, but the magnitude of both fractions decrease clearly with increasing λB especially when Nm < 5. At λB = 3.0 shown in the left panels of Fig. 7, the ψIAB profile demonstrates an apparent peak located at Nm = 4 (see the filled circles) regardless of matrix chain stiffness. When the matrix chains are short Nm = 1, most of matrix chains are in the free state and a small part of matrix chains are in the IAB state due to the relatively weak electrostatic interaction strength at λB = 3.0. The increase of matrix chain length Nm promotes more matrix chains to play the IAB role due to electrostatic attraction firstly, which is manifested as the rapid increase of ψIAB. However, more matrix chains are inclined to play the IEB role once the matrix chain is long enough, which induces increase of ψIEB and the decrease of ψIAB. On the left side of this peak, the fractions of matrix chains in IEB state are much tiny and the effect can be negligible. The increase of fractions of matrix chains in IAB state renders the grafted chains to adopt a relatively compact conformation, which is manifested as the decrease of thickness of grafted brush shown in Fig. 3a. On the right side of the peak, the fraction ψIEB increases sharply and exceeds ψIAB, which causes the PE grafted NPs in a binding-together fashion and promotes the slight re-expansion of brushes. The competition between the intra-nanoparticle bridging and the inter-nanoparticle bridging of matrix chains results a fluctuated profile of brush thickness and radius of gyration illustrated in Fig. 3 and 5. Furthermore, once Nm ≥ 12 (equals to the grafted chain length), the overwhelming majority of matrix PE chains are in the IEB state (filled triangles in Fig. 7), which induce more long-range order in the self-assemble morphologies of grafted NPs.
4 Conclusions
The self-assembled morphologies of PE sparsely grafted NPs tuned by the oppositely charged matrix chain length with different chain rigidness are studied systematically by means of MD simulations. In the presence of charges on the grafted and matrix chains as in the case of PE grafted NPs, the electrostatic interactions between the charged segments will govern the self-assembled structuring of NPs, which are also investigated by varying the electrostatic interaction strength. A series of aggregated structures are predicted, in particular, some of them have been observed experimentally. An increase in matrix PE chain length will result in an enhancement of electrostatic correlations, which will modulate the stretching of the tethered PE chains. The nearest-neighbor distance between NPs is found to be nonmonotonic with the increase of matrix chain length. The self-assemblies of NPs have more spherical micelle-like structures with short matrix chains, however, the network aggregations are preferred due to the long-range order provided by long matrix chains. Our simulation results demonstrate the responses of self-assembled structures of PE grafted NPs to external stimuli, such as, electrostatic interaction strength, volume excluded interaction, as well as stiffness and length of matrix chains, which can serve as a guide to smart polymer nanocomposites design and understanding of PE physics.Author contributions
Hao conceived and designed the simulations. Cheng carried out all simulations. All authors analyzed the data and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support provided by the Tianjin Graduate Scientific Research Innovation Project (Grant No. 2020YJS037) and the Fundamental Research Funds for the Central Universities of China (Grant No. 3122020080).References
- E. J. Bailey and K. I. Winey, Prog. Polym. Sci., 2020, 105, 101242 CrossRef CAS.
- N. J. Fernandes, H. Koerner, E. P. Giannelis and R. A. Vaia, MRS Commun., 2013, 3, 13–29 CrossRef CAS.
- S. Srivastava, J. L. Schaefer, Z. Yang, Z. Tu and L. A. Archer, Adv. Mater., 2014, 26, 201–234 CrossRef CAS PubMed.
- W. R. Lenart and M. J. A. Hore, Nano-Struct. Nano-Objects, 2018, 16, 428–440 CrossRef CAS.
- P. F. Green, Soft Matter, 2011, 7, 7914–7926 RSC.
- J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Polymer, 2010, 51, 3321–3343 CrossRef CAS.
- P. J. M. Smeets, K. R. Cho, R. G. E. Kempen, N. A. J. M. Sommerdijk and J. J. De Yoreo, Nat. Mater., 2015, 14, 394–399 CrossRef CAS PubMed.
- C. Yi, Y. Yang, B. Liu, J. He and Z. Nie Z, Chem. Soc. Rev., 2020, 49, 465–508 RSC.
- H. Heinz, C. Pramanik, O. Heinz, Y. Ding, R. K. Mishra, D. Marchon, R. J. Flatt, I. Estrela-Lopis, J. Llop, S. Moya and R. F. Ziolo, Surf. Sci. Rep., 2017, 72, 1–58 CrossRef CAS.
- S. K. Kumar and N. Jouault, Macromolecules, 2013, 4, 3199–3214 CrossRef.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- X. Ye, C. Zhu, P. Ercius, S. N. Raja, B. He, M. R. Jones, M. R. Hauwiller, Y. Liu, T. Xu and A. P. Alivisatos, Nat. Commun., 2015, 6, 10052 CrossRef PubMed.
- R. M. Choueiri, E. Galati, H. Thérien-Aubin, A. Klinkova, E. M. Larin, A. Querejeta-Fernández, L. Han, H. L. Xin, O. Gang, E. B. Zhulina, M. Rubinstein and E. Kumacheva, Nature, 2016, 538, 79–83 CrossRef CAS PubMed.
- D. Zhao, M. D. Nicola, M. M. Khani, J. Jestin, B. C. Benicewicz and S. K. Kumar, ACS Macro Lett., 2016, 5, 790–795 CrossRef CAS PubMed.
- A. Jayaraman and K. S. Schweizer, J. Chem. Phys., 2008, 128, 164904 CrossRef PubMed.
- A. Jayaraman and K. S. Schweizer, Langmuir, 2008, 24, 11119–11130 CrossRef CAS PubMed.
- A. L. Frischknecht, M. J. A. Hore, J. Ford and R. J. Composto, Macromolecules, 2013, 46, 2856–2869 CrossRef CAS.
- X. Zhu, L. Wang, J. Lin and L. Zhang, ACS Nano, 2010, 4, 4979–4988 CrossRef CAS PubMed.
- V. V. Ginzburg, Macromolecules, 2017, 50, 9445–9455 CrossRef CAS.
- S. Khani, S. Jamali, A. Boromand, M. J. A. Hore and J. Maia, Soft Matter, 2015, 11, 6881–6892 RSC.
- S. Li, Z. Zhang, G. Hou, J. Liu, Y. Gao, P. Coates and L. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 11785–11796 RSC.
- C. Koh, G. S. Grest and S. K. Kumar, ACS Nano, 2020, 14, 13191–13499 CrossRef.
- J. P. Koski and A. L. Frischknecht, Macromolecules, 2021, 54, 5144–5154 CrossRef CAS.
- K. R. Medidhi and V. Padmanabhan, Soft Matter, 2021, 17, 3455–3462 RSC.
- D. J. Sandberg, J.-M. Y. Carrillo and A. V. Dobrynin, Langmuir, 2007, 23, 12716–12728 CrossRef CAS PubMed.
- Q. Cao and M. Bachmann, Soft Matter, 2013, 9, 5087–5098 RSC.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- T. E. Gartner and A. Jayaraman, Macromolecules, 2019, 52, 755–786 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- P. A. Thompson, G. S. Grest and M. O. Robbins, Phys. Rev. Lett., 1992, 68, 3448–3451 CrossRef PubMed.
- M. Murat and G. S. Grest, Macromolecules, 1996, 29, 1278–1285 CrossRef CAS.
- I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- L. Y. Liu, G. Xia, Z. J. Feng, Q. H. Hao and H. G. Tan, Soft Matter, 2019, 15, 3689–3699 RSC.
- L. Y. Liu, Z. X. Yu, L. X. Liu, J. Q. Yang, Q. H. Hao, T. Wei and H. G. Tan, Phys. Chem. Chem. Phys., 2020, 22, 16334–16344 RSC.
- P. Pincus, Macromolecules, 1991, 24, 2912–2919 CrossRef CAS.
- O. Borisov, T. Birshtein and E. Zhulina, J. Phys. II, 1991, 1, 521–526 CrossRef CAS.
- L. Chen, H. Merlitz, S. He, C. Wu and J. U. Sommer, Macromolecules, 2011, 44, 3109–3116 CrossRef CAS.
- Y. Mei, K. Lauterbach, M. Hoffmann, O. V. Borisov, M. Ballauff and A. Jusufi, Phys. Rev. Lett., 2006, 97, 158301 CrossRef PubMed.
- J. Yu, N. E. Jackson, X. Xu, Y. Morgenstern, Y. Kaufman, M. Ruths, J. J. de Pablo and M. Tirrell, Science, 2018, 360, 1434–1438 CrossRef CAS PubMed.
- J. Yu, N. E. Jackson, X. Xu, B. K. Brettmann, M. Ruths, J. J. de Pablo and M. Tirrell, Sci. Adv., 2017, 3, 1497–1506 CrossRef.
- P. Chi, B. H. Li and A. C. Shi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021804 CrossRef.
- P. Chi, Z. Wang, Y. H. Yin and B. H. Li, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042608 CrossRef.
- A. Skandalis, M. Uchman, M. Štěpánek, S. Kereïche and S. Pispas, Macromolecules, 2020, 53, 5747–5755 CrossRef CAS.
- Q. H. Hao, G. Xia, B. Miao, H. G. Tan, X. H. Niu and L. Y. Liu, Macromolecules, 2018, 51, 8513–8521 CrossRef CAS.
- H. G. Tan, G. Xia, L. X. Liu, X. H. Niu and Q. H. Hao, Chin. J. Polym. Sci., 2019, 38, 394–402 CrossRef.
- D. C. Rapaport, The Art of Molecular Dynamics Simulation, Cambridge University Press, 2nd edn, 2004 Search PubMed.
- R. Samanta and V. Ganesan, J. Phys. Chem. B, 2020, 124, 10943–10951 CrossRef CAS.
- H. G. Tan, G. Xia, L. X. Liu and B. Miao, Phys. Chem. Chem. Phys., 2019, 21, 20031–20044 RSC.
- Q. H. Hao, J. Cheng, L. X. Liu, H. G. Tan, T. Wei, L. Y. Liu and B. Miao, Macromolecules, 2020, 53, 7187–7197 CrossRef CAS.
- C. Daniel, C. Dammer and J. M. Guenet, Polymer, 1994, 35, 4243–4246 CrossRef CAS.
- A. Chremos and A. Z. Panagiotopoulos, Phys. Rev. Lett., 2011, 107, 105503 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra00867j |
| This journal is © The Royal Society of Chemistry 2022 |