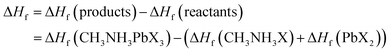Open Access Article
Open Access ArticleRole of metal and anions in organo-metal halide perovskites CH3NH3MX3 (M: Cu, Zn, Ga, Ge, Sn, Pb; X: Cl, Br, I) on structural and optoelectronic properties for photovoltaic applications†
Maliha Nishat *a,
Md. Kamal Hossain
*a,
Md. Kamal Hossain b,
Md. Rakib Hossain
b,
Md. Rakib Hossain c,
Shamima Khanomb,
Farid Ahmedb and
Md. Abul Hossainb
c,
Shamima Khanomb,
Farid Ahmedb and
Md. Abul Hossainb
aDepartment of Physics, Pabna University of Science and Technology, Pabna-6600, Bangladesh. E-mail: malihanishat@pust.ac.bd
bDepartment of Physics, Jahangirnagar University, Dh, aka-1342, Bangladesh
cDepartment of Physics, Bangabandhu Sheikh Mujibur Rahman Science and Technology University, Gopalganj-8100, Bangladesh
First published on 3rd May 2022
Abstract
Methylammonium metal halide perovskites have recently been explored for new uses due to their unique and exciting optoelectronic properties. Their exceptional electronic properties have often been attributed to the overlap between the metal cation s and halogen p states. In this study, density functional theory calculations have been carried out based on the orthorhombic phase of the organometal trihalide perovskite CH3NH3MX3 (M: Cu, Zn, Ga, Ge, Sn, Pb; X: Cl, Br, I) to systematically investigate the effects of the metal cation and halogen anion on the structural, electronic, and optical properties for solar cell applications. The calculated lattice parameters agree well with previously obtained experimental and theoretical results. All of these perovskites are direct band gap compounds at the G symmetry point, except CH3NH3GaX3. The band gap increases from iodide to chloride and also with the metal cation size, from Ge to Pb or Cu to Zn. Furthermore, metal halide perovskites show blue shifts in their optical absorption spectra with an increase in metal cation size. Among the studied examples, CH3NH3GaBr3 and CH3NH3CuCl3 absorb a wide range of light, from UV to the visible region, and possess very unusual high dielectric constants and refractive indices. Our calculations reveal that CH3NH3SnI3, CH3NH3GeI3, and CH3NH3ZnI3 are favorable candidates for lead-free photovoltaic applications.
1 Introduction
In recent years, perovskite-based photovoltaics (PVs) have received tremendous interest, especially when they implement a metal halide perovskite as an absorber material in a hybrid solar cell. The general formula of a halide perovskite compound is ABX3; where the ‘A-site’ involves a large (natural) cation, the ‘B-site’ is filled with considerably divalent metal cations and the ‘X-site’ contains a halide anion. The very first metal halide perovskite to be distinguished was CH3NH3PbI3 by Weber.1 In 2009, Miyasaka and his coworkers2 disclosed it as a remarkable light sensitizer which attracted huge research interest to CH3NH3PbI3. In a couple of years, it showed a tremendous increase in power conversion efficiency (PCE) from 3.8% (in 2009) to more than 22%.3,4 Thus the growth in the field of metal halide perovskites is due to their outstanding optoelectronic properties, including superb charge carrier mobility, long diffusion length, high optical absorption coefficient, tunable band gaps and cheap production cost. So, they have become favorable materials that can easily fit in many other optoelectronic devices like lasers, light-emitting diodes (LED), photo-detectors and field-effect transistors (FETs).5,6 Moreover, because of their natural abundance, these materials result in cheaper and more efficient solar cells than silicon-based photovoltaics.7 In addition, a wide range of diverse processing technologies (like vacuum-based solution techniques and low-temperature solution processes) can be implemented to prepare metal halide perovskites, making them very fascinating.8–10The crystal structure of CH3NH3PbX3 is found to be very responsive to temperature.11,12 CH3NH3PbX3 holds a cubic phase at high temperature, and as the temperature decreases, it transforms into a tetragonal phase and becomes orthorhombic at lower temperature.11–14 Recently orthorhombic CH3NH3PbI3 was determined with its organic CH3NH3 part.11 Many theoretical and experimental investigations have been reported on orthorhombic perovskite CH3NH3PbI3.15–18 Besides, the A, B and X-sites in ABX3-type perovskites can be altered or tuned to improve their performance in perovskite-based photovoltaic devices.
The most famous high-PCE perovskite material has Pb in it, and it is toxic, which is undesirable, and chemically unstable under ambient conditions.19 Hence, lead needs to be replaced for the wider commercialization and application of this type of compound in the photovoltaic and optoelectronic sectors. In this regard, Sn is one of the realistic and possible elements to replace Pb in CH3NH3PbI3 structures as it comes from the same IVA subgroup.19,20 Many experimental and theoretical investigations have been done on Sn-based perovskite systems.19,21,22 Tin is highly sensitive to air, which quickly changes the oxidization state from Sn2+ to Sn4+. This is one of the reasons why Sn-based perovskite have a small PCE while lead-based perovskites possess a high PCE. Ge belongs to group IVA (the same subgroup as Pb and Sn) and Ge-based perovskite shows a comparable optical absorption to Pb-based perovskite.23 Furthermore, it was experimentally confirmed that cation size affects the crystallographic features of Ge-perovskites.24 Thus Ge-based perovskites are an alternative nontoxic choice for photovoltaic material, which is confirmed by research. Both Sn and Ge possess similar chemical composition and valences to Pb as they belong to the same subgroup in the periodic table. So, they can easily replace Pb. Also it is very crucial to analyze the bonding nature of lone-pair electrons25 on these metals (Pb-6s2, Sn-5s2 & Ge-4s2) because they have a vital influence on the electronic properties of these metal-based perovskites.
These days, lead can be supplanted in perovskites with reasonable, alternative, environmentally friendly, earth-abundant elements like transition metals, which may be important in terms of PCE. Pb replacement with transition metals like Cu, Zn or Ga can make novel nontoxic and clean perovskites for solar cells, which can also show an improvement in photovoltaic solar cells. Previously two-dimensional layered copper perovskites were implemented as absorber materials and attained low PCE values (0.51 and 0.63%, respectively).26 Perovskite-based photovoltaics with the suitable addition of Zn2+ can improve the regular PCE from 12.1% to 16.3%, which was reported experimentally.27
In the present work, we perform a systematic simulation on a series of orthorhombic metal halide perovskites to investigate their size (metal cation and halide anion) dependent properties by implementing first-principles density functional theory (DFT) calculations. We took CH3NH3PbI3 as a primary model and then replaced the I− anion with Br− and Cl− anions to make CH3NH3PbX3 compounds where X: Cl, Br, I. A further metal (Pb) cation was also replaced in CH3NH3PbX3 with a sequence of transition metal and post transition metal cations to make CH3NH3MX3 systems where M: Cu, Zn, Ga, Ge, Sn, Pb. The crystal configuration, electronic parameters, optical properties, and the structure–property relationships were explored for all of these perovskite compounds. The essential concern of this study is to understand the size effect of the metal cation and halide anion on the optoelectronic properties of these perovskite compounds. Also, the chemistry of lone pairs of the metal cations and halide anions is a key point for analysis of their impact on the electronic structure and characteristics of these compounds. Further, a proper understanding of the optical parameters is crucial so they can be used in solar cells and other optoelectronic devices like diodes, lasers, etc.
2 Computational details
In this work, ab initio calculations were performed for orthorhombic CH3NH3MX3 by using the framework of density functional theory28 embedded in Cambridge Sequential Total Energy (CASTEP) code29 where the Kohn–Sham equations get solved. The wave functions of the valence electrons are expanded in a basis set of plane waves. Ultra-soft pseudo-potentials can represent the existence of a tightly-bound core electron, and they define the interaction between electron and ion.30 The exchange–correlation potential is treated within the Perdew–Burke–Ernzerhof (1996) version of the generalized gradient approximation (PBE-GGA).31 While Ceperley and Alder developed the local density approximation (LDA), Perdew and Zunger parameterized it.32,33For geometric optimization, a 2 × 3 × 2 Monkhorst–Pack grid34 was employed in the Brillouin zone of the unit cell to produce a uniform grid of k-points along the three axes in reciprocal space. The kinetic cut-off energy was chosen at 280 eV for CH3NH3GeX3, CH3NH3SnX3 and CH3NH3PbX3 (same-group) compounds, whereas it was 400 eV for CH3NH3CuX3, CH3NH3ZnX3 and CH3NH3GaX3 (same-period) compounds. All of the structures become relaxed in their optimized geometry. The structural parameters of CH3NH3MX3 (Pnma (no: 62) space group) were calculated using the BFGS (Broyden–Fletcher–Goldfarb–Shanno) technique, where the following parameters are taken to obtain a converged geometry: stress 0.1 GPa, residual force 0.05 eV Å−1 and energy change per atom less than 2 × 10−5 eV. Optical parameters such as absorption coefficient α(ω), refractive index n(ω), optical conductivity σ(ω), optical reflectivity R(ω) and energy-loss spectrum L(ω) can be calculated by utilizing the complex dielectric function: ε(ω) = ε1(ω) + iε2(ω).
3 Results and discussion
3.1 Geometry optimization
Accurate structural understandings are essential for the better prediction of the optoelectronic characteristics of perovskites. ABX3-type perovskites are sensitive to temperature and change their phase with temperature.11,12 In the present studies, we concentrate on the orthorhombic phase, which is thermodynamically stable, and this is additionally suitable for DFT estimation at zero temperature.35 The optimized unit cell of CH3NH3MX3 (M: Cu, Zn, Ga, Ge, Sn, Pb; X: Cl, Br, I) in the orthorhombic phase is pictured in Fig. 1. A total of eighteen compounds are fully optimized and relaxed in their ground state. This orthorhombic perovskite structure forms with octahedral [BX6] cations that share a corner of the net with halide anions and organic methylammonium [CH3NH3]+ cations situated within the octahedral network.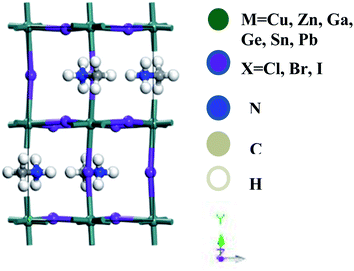 | ||
| Fig. 1 A lattice structural representation of the organometal trihalide perovskite CH3NH3MX3 (M: Cu, Zn, Ga, Ge, Sn, Pb; X: Cl, Br, I) in the orthorhombic phase. | ||
To quantitatively depict the crystal structure, a parameter called the tolerance factor was calculated to define the crystal stability with variations in metal cations and halide anions. It also defines the stability of the perovskite material in solar cells. Analogous to Goldschmidt's early method, the tolerance factors of hybrid organic–inorganic perovskites are calculated with (effective) ionic radii by using the general formula:36
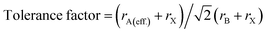 | (1) |
This effective ionic radius of the organic cation was used to modify Goldschmidt's initial approach to calculate the tolerance factor. To calculate the tolerance factors presented in Table 1, the effective radii of the [CH3NH3]+ (methylammonium, 217 pm) were used from ref. 38 and Shannon's ionic radii37 were used for metal cations and halide anions. Another stability parameter is the octahedral factor μ, which is defined by the ratio rB/rX. Both the tolerance factor and the μ parameter can give information about the stability of perovskites within the range of μ > 0.41 and 0.76 < tolerance factor < 1.13.38–41 Most cubic perovskites are formed in the TF range of 0.8–1.0, while a distorted octahedral perovskite TF lies in 0.76–0.90.40 Besides, a TF larger than one forms highly distorted perovskites, and TF > 1.13 results in layered structures with face-sharing octahedra.40 Our calculations found that CH3NH3PbX3 and CH3NH3SnX3 have TF in the range of 0.904–0.938, while CH3NH3GeX3, CH3NH3ZnX3, CH3NH3CuX3 and CH3NH3GaI3 have TF larger than 1 but less than 1.13, which results in distorted perovskites. However, CH3NH3GaBr3 and CH3NH3GaCl3 have TF larger than 1.13, making them non-perovskites but still useful for optoelectronic device applications. It is observed from Table 1 that with an increase in halide size (from Cl to I), both the tolerance factor and μ decrease gradually for all compounds, indicating the stability of the perovskites. On the other hand, with an increase in metal cation size in the same period (from Cu → Zn → Ga) and the same group (Ge → Sn → Pb), the same thing happened (except for CH3NH3GaX3), which may be due to structural distortion. According to the limit of tolerance factor and μ, all of the studied compounds can form stable 3D perovskites except CH3NH3GaX3. The exceptions may be non-perovskites and can be used in other optoelectronic sectors. Fig. 2 displays a structural map of our studied compounds. The areas surrounded by the dotted lines (black and red) represent the boundary limits for the formation of stable perovskites, and the compounds that lie in those areas can form perovskites.
| Material | Tolerance factor | μ | ΔHf |
|---|---|---|---|
| CH3NH3CuCl3 | 1.108 | 0.403 | −205.329 |
| CH3NH3ZnCl3 | 1.104 | 0.409 | −194.149 |
| CH3NH3GaCl3 | 1.158 | 0.343 | −101.868 |
| CH3NH3GeCl3 | 1.108 | 0.403 | −264.494 |
| CH3NH3SnCl3 | 0.929 | 0.674 | −265.276 |
| CH3NH3PbCl3 | 0.938 | 0.657 | −134.925 |
| CH3NH3CuBr3 | 1.086 | 0.372 | −59.736 |
| CH3NH3ZnBr3 | 1.082 | 0.378 | −61.989 |
| CH3NH3GaBr3 | 1.132 | 0.316 | −195.846 |
| CH3NH3GeBr3 | 1.086 | 0.372 | −56.023 |
| CH3NH3SnBr3 | 0.918 | 0.622 | −55.433 |
| CH3NH3PbBr3 | 0.927 | 0.607 | −159.599 |
| CH3NH3CuI3 | 1.055 | 0.332 | −51.256 |
| CH3NH3ZnI3 | 1.051 | 0.336 | −53.492 |
| CH3NH3GaI3 | 1.096 | 0.282 | −187.365 |
| CH3NH3GeI3 | 1.055 | 0.332 | −47.537 |
| CH3NH3SnI3 | 0.904 | 0.555 | −46.941 |
| CH3NH3PbI3 | 0.912 | 0.541 | −169.99 |
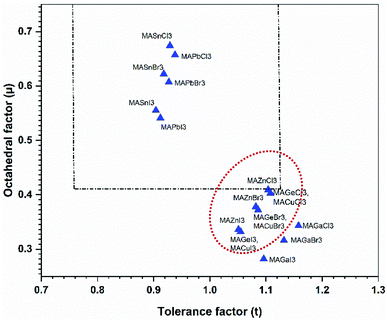 | ||
| Fig. 2 A structural map of CH3NH3MX3 compounds. The dotted lines are the boundary lines mentioned in the text. Compounds in the red dotted circle represent stable perovskites. | ||
Determining the DFT lattice constant was essential for assessing other parameters. Therefore, the obtained values and other available lattice constant and cell volume values from the literature for all of the perovskite compounds are tabulated in Table 2, based on the use of two different functionals. Generally, the value of lattice parameters shows underestimates for LDA and overestimates for GGA.
| Material | Method | Lattice parameter (Å) | Volume (Å3) | Ref. | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| CH3NH3CuCl3 | LDA-CAPZ | 14.749 | 9.204 | 9.599 | 1303.062 | — |
| GGA-PBE | 14.945 | 9.139 | 9.609 | 1314.088 | — | |
| Experiment | 18.8 | 4.23 | 11.11 | 875 | 42 | |
| CH3NH3ZnCl3 | LDA-CAPZ | 12.735 | 7.374 | 12.651 | 1188.029 | — |
| GGA-PBE | 13.453 | 7.870 | 14.935 | 1581.245 | — | |
| CH3NH3GaCl3 | LDA-CAPZ | 11.371 | 9.898 | 10.010 | 1126.620 | — |
| GGA-PBE | 11.480 | 11.610 | 11.545 | 1538.830 | — | |
| CH3NH3GeCl3 | LDA-CAPZ | 14.749 | 9.204 | 9.599 | 1303.062 | — |
| GGA-PBE | 14.945 | 9.139 | 9.609 | 1314.088 | — | |
| Theory | 7.28 | 7.28 | 10.61 | 487.54 | 43 | |
| CH3NH3SnCl3 | LDA-CAPZ | 12.729 | 11.383 | 11.494 | 1665.414 | — |
| GGA-PBE | 11.555 | 11.327 | 11.677 | 1528.326 | — | |
| Experiment | 5.76 | — | 43 | |||
| CH3NH3PbCl3 | LDA-CAPZ | 10.990 | 11.263 | 11.124 | 1376.933 | — |
| GGA-PBE | 11.469 | 11.616 | 11.589 | 1543.932 | — | |
| Experiment | 8.020 | — | 11.260 | — | 44 | |
| Theory | 7.850 | 8.220 | 11.150 | 719.476 | — | |
| CH3NH3CuBr3 | LDA-CAPZ | 7.470 | 9.922 | 8.321 | 616.752 | — |
| GGA-PBE | 9.569 | 10.305 | 8.729 | 860.989 | — | |
| CH3NH3ZnBr3 | LDA-CAPZ | 7.313 | 10.861 | 8.229 | 653.603 | — |
| GGA-PBE | 8.101 | 11.037 | 10.334 | 923.996 | — | |
| CH3NH3GaBr3 | LDA-CAPZ | 7.272 | 11.691 | 7.870 | 669.026 | — |
| GGA-PBE | 7.783 | 11.382 | 8.309 | 736.073 | — | |
| CH3NH3GeBr3 | LDA-CAPZ | 7.459 | 10.849 | 8.041 | 650.687 | — |
| GGA-PBE | 7.842 | 11.485 | 8.449 | 760.919 | — | |
| Theory | 7.64 | 7.64 | 10.91 | 552.01 | 24 | |
| CH3NH3SnBr3 | LDA-CAPZ | 8.089 | 12.324 | 8.728 | 870.029 | — |
| GGA-PBE | 8.0853 | 12.331 | 8.721 | 869.50 | — | |
| Experiment | 5.89 | — | 45 | |||
| CH3NH3PbBr3 | LDA-CAPZ | 7.663 | 11.713 | 8.665 | 777.709 | — |
| GGA-PBE | 8.183 | 12.314 | 8.963 | 903.161 | — | |
| Experiment | 7.94 | 11.85 | 8.59 | 808.73 | 46 | |
| Theory | 7.95 | 12.01 | 8.67 | 830.67 | 46 | |
| CH3NH3CuI3 | LDA-CAPZ | 8.106 | 11.383 | 11.494 | 732.679 | — |
| GGA-PBE | 8.695 | 11.214 | 9.237 | 900.660 | — | |
| CH3NH3ZnI3 | LDA-CAPZ | 8.010 | 11.229 | 7.946 | 830.815 | — |
| GGA-PBE | 8.452 | 12.411 | 9.821 | 1030.201 | — | |
| CH3NH3GaI3 | LDA-CAPZ | 8.080 | 12.022 | 8.116 | 788.305 | — |
| GGA-PBE | 8.572 | 11.966 | 8.913 | 914.136 | — | |
| CH3NH3GeI3 | LDA-CAPZ | 8.265 | 11.442 | 8.404 | 749.742 | — |
| GGA-PBE | 8.683 | 12.349 | 8.769 | 940.184 | — | |
| Experiment | 8.553 | 8.553 | 11.162 | 707.2 | 24 | |
| Theory | 8.20 | 8.20 | 11.34 | 806.58 | 24 | |
| CH3NH3SnI3 | LDA-CAPZ | 8.128 | 12.071 | 8.850 | 868.301 | — |
| GGA-PBE | 8.917 | 12.670 | 9.206 | 1040.079 | — | |
| Theory | 8.556 | 12.428 | 8.326 | 885.400 | 47 | |
| CH3NH3PbI3 | LDA-CAPZ | 8.176 | 12.442 | 8.971 | 912.582 | — |
| GGA-PBE | 8.992 | 13.068 | 9.297 | 1092.467 | — | |
| Experiment (T = 100 K) | 8.866 | 12.629 | 8.577 | 960.338 | 48 | |
| Experiment (T = 100 K) | 8.836 | 12.580 | 8.555 | 951.010 | 11 | |
| Theory | 9.226 | 12.876 | 8.619 | 1023.880 | 49 | |
However, in Table 2, both LDA and GGA overestimate the experimental results. This finding is consistent with the outcomes for traditional semiconductors. However, CH3NH3MCl3 shows overestimated values of the lattice parameters for both LDA (CAPZ) and GGA(PBE) functionals, and this may be due to the lack of van der Waals interactions between the organic part (CH3NH3) and the octahedral [M–Cl] corner.50 If one considers dispersive interactions in a specific form, the obtained lattice parameters can agree well with the experimental data.49,50 On account of the DFT result, the experimental lattice constant was not utilized. The over-restrictive issues in DFT brought about underestimated self-interaction between the charges, which is why the theoretical result becomes smaller than the experimental data. So, our calculated structural parameters are in the acceptable range. In this way, the contrasts between our outcomes and the trial information are as anticipated.
Our obtained lattice parameters also agree well with other theoretical results. It is also observed from Fig. 3 that the cell volume decreases with an increase in the anion size (from Cl to I). Thus the cell volume and the radius of the halide anion share an inverse relationship, while a proportional increase has been shown for the radius of the metal cation. The radius of the metal cation increases from Ge to Pb (same group) and from Cu to Ga (same period), so the lattice of the structure is additionally increasing with a specific end goal of upholding the structural symmetry. According to Fig. 3, the cell volumes of all the perovskites increase with the size of the metal cation (except CH3NH3GaX3).
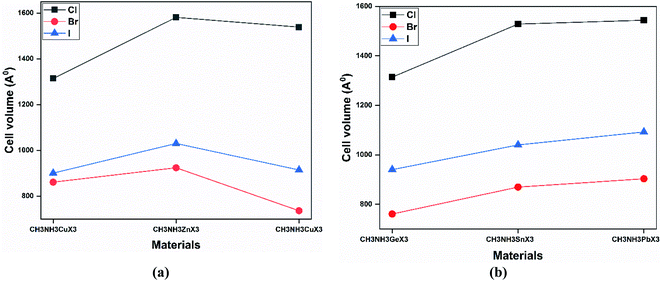 | ||
| Fig. 3 A comparison of the cell volume (in Å) values upon varying the metal and halide at the GGA-PBE level of theory for (a) same-period and (b) same-group perovskite compounds. | ||
The calculated bond lengths are given in Table 3, and this leads to knowledge of the structural alignments and energy gaps of the perovskites. We refer to the six M–X (metal–halide) bond lengths of the MX6 octahedra and other important bonds to observe the variations among the eighteen perovskite compounds. Metal cation and halide anion share six bonds; four bonds are located in the equatorial plane, and the other two bonds are in the axial direction. Interestingly, the M–X bonds are shorter when the atomic size decreases in the same group (from Ga to Cu) and the same period (Pb to Ge). Therefore, all the bond lengths are larger in the equatorial direction than in the axial direction. From Table 3, it is also observed that C–H bond lengths are more significant than the N–H bond length in CH3NH3MX3. As nitrogen has more valence electrons than carbon, it attracts the positively ionized hydrogen atom more strongly and makes a firm bond with it. Also, the N–H ion possesses a larger dipole moment than the C–H ion, which is why the N–H ion is more strongly pulled towards the halogen atoms by the van der Waals forces.
| Material | Bond length (Å) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equatorial plane | Axial plane | ||||||||||||
| M–X1 | M–X2 | M–X3 | M–X4 | N–C | N–H1 | N–H2 | C–H1 | C–H2 | M–X5 | M–X6 | N–H3 | C–H3 | |
| CH3NH3CuCl3 | 2.33 | 2.33 | 2.45 | 2.41 | 1.49 | 1.05 | 1.05 | 1.09 | 1.09 | 2.39 | 2.42 | 1.05 | 1.09 |
| CH3NH3ZnCl3 | 2.22 | 2.22 | 2.30 | 2.30 | 1.49 | 1.05 | 1.04 | 1.09 | 1.09 | 2.40 | 2.40 | 1.05 | 1.10 |
| CH3NH3GaCl3 | 2.37 | 2.37 | 2.36 | 2.36 | 1.46 | 1.06 | 1.05 | 1.10 | 1.10 | 2.51 | 2.50 | 1.05 | 1.10 |
| CH3NH3GeCl3 | 2.33 | 2.33 | 4.43 | 2.37 | 1.51 | 1.04 | 1.04 | 1.10 | 1.09 | 2.70 | 2.83 | 1.04 | 1.09 |
| CH3NH3SnCl3 | 2.83 | 2.83 | 2.98 | 2.98 | 1.49 | 1.05 | 1.04 | 1.09 | 1.09 | 2.93 | 2.91 | 1.04 | 1.09 |
| CH3NH3PbCl3 | 2.91 | 2.83 | 2.83 | 2.90 | 1.49 | 1.05 | 1.05 | 1.09 | 1.09 | 2.93 | 2.91 | 1.05 | 1.09 |
| CH3NH3CuBr3 | 2.32 | 4.16 | 4.16 | 2.32 | 1.49 | 1.05 | 1.05 | 1.09 | 1.09 | 2.58 | 2.58 | 1.05 | 1.09 |
| CH3NH3ZnBr3 | 2.32 | 4.30 | 4.30 | 2.32 | 1.49 | 1.06 | 1.04 | 1.09 | 1.09 | 2.94 | 2.94 | 1.04 | 1.09 |
| CH3NH3GaBr3 | 2.75 | 2.97 | 2.75 | 2.75 | 1.49 | 1.05 | 1.04 | 1.09 | 1.09 | 2.85 | 2.85 | 1.04 | 1.09 |
| CH3NH3GeBr3 | 2.86 | 2.98 | 2.98 | 2.86 | 1.50 | 1.04 | 1.04 | 1.09 | 1.09 | 2.88 | 2.88 | 1.04 | 1.09 |
| CH3NH3SnBr3 | 3.03 | 3.04 | 3.04 | 3.03 | 1.50 | 1.05 | 1.04 | 1.10 | 1.09 | 3.10 | 3.10 | 1.04 | 1.09 |
| CH3NH3PbBr3 | 3.29 | 3.29 | 3.29 | 3.29 | 1.51 | 1.04 | 1.04 | 1.09 | 1.09 | 3.12 | 3.12 | 1.04 | 1.09 |
| CH3NH3CuI3 | 2.54 | 3.83 | 3.83 | 2.54 | 1.49 | 1.05 | 1.04 | 1.09 | 1.09 | 2.81 | 2.81 | 1.04 | 1.09 |
| CH3NH3ZnI3 | 2.56 | 3.95 | 3.95 | 2.56 | 1.49 | 1.06 | 1.04 | 1.09 | 1.10 | 3.11 | 3.11 | 1.04 | 1.10 |
| CH3NH3GaI3 | 3.09 | 3.12 | 3.12 | 3.09 | 1.49 | 1.05 | 1.04 | 1.09 | 1.09 | 3.01 | 3.01 | 1.04 | 1.09 |
| CH3NH3GeI3 | 3.16 | 3.18 | 3.18 | 3.16 | 1.50 | 1.04 | 1.04 | 1.09 | 1.09 | 3.11 | 3.11 | 1.04 | 1.09 |
| CH3NH3SnI3 | 3.06 | 3.08 | 3.08 | 3.06 | 1.50 | 1.05 | 1.03 | 1.09 | 1.09 | 3.06 | 3.06 | 1.03 | 1.09 |
| CH3NH3PbI3 | 3.30 | 3.34 | 3.34 | 3.30 | 1.50 | 1.05 | 1.04 | 1.09 | 1.09 | 3.29 | 3.29 | 1.04 | 1.09 |
Moreover, it is well known that the enthalpy of formation is an essential tool for determining the thermodynamic stability of a material.51,52 Previous studies reported the standard enthalpy of formation of hybrid organic–inorganic perovskites from the corresponding crystalline CH3NH3X and PbX2 salts which form CH3NH3PbX3 and it can be written as:
| CH3NH3X(s) + PbX2(s) → CH3NH3PbX3(s), ΔHf |
Here ΔHf can be calculated with the help of the following equations:
Our calculated formation enthalpies are tabulated in Table 1 and they exhibit negative values for all the compounds, confirming their thermodynamic stability. Besides, the ΔHf values of CH3NH3PbX3 are quite comparable with other theoretical studies.53,54
3.2 Electronic properties
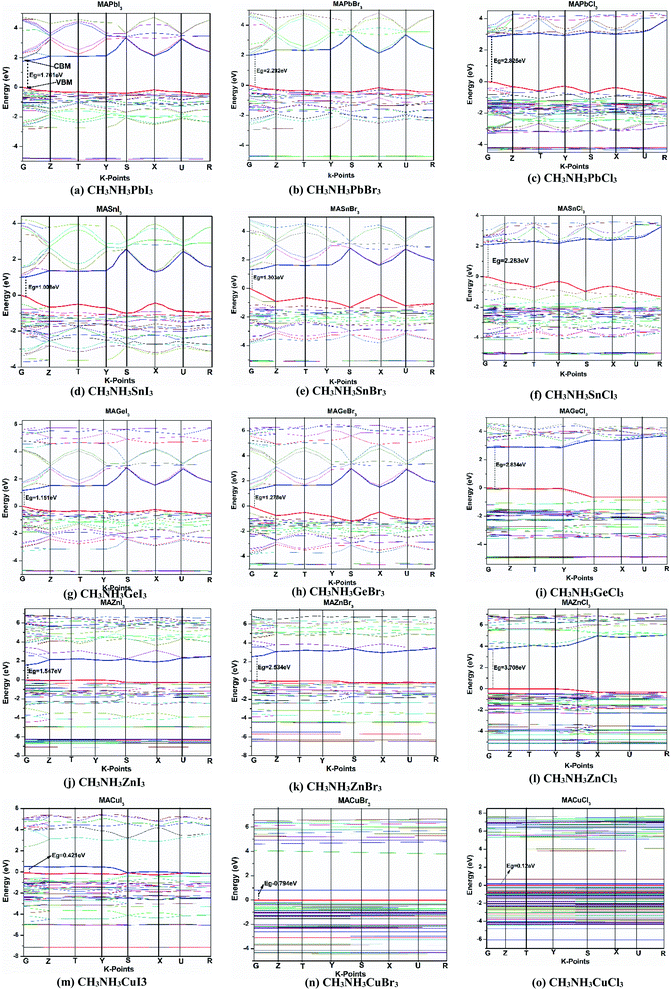
Investigating electronic properties is very important for metal halide perovskites to determine their various prospective applications. In this regard, we have calculated the band structure, density of states (DOS) and projected/partial density of states (PDOS) of orthorhombic CH3NH3MX3 by using the DFT-GGA (PBE) and LDA (CAPZ) level of theory. All calculated band diagrams in the high symmetry zone are depicted in Fig. 4 for CH3NH3MX3 compounds.In the band structures, all energies are relative to the Fermi level, and the top of the valence band indicates the Fermi level for semiconductors. Here it is observed that all the perovskites possess a direct band gap at the G symmetry point except CH3NH3GaX3. All the B-site metal cations (Cu, Zn, Ga, Ge, Sn and Pb) have fully or partially filled valence 3s, 4s, 5s and 6s orbitals, respectively, and these are located under the upper portion of the valence bands (VB) and thus these lone pairs are mainly responsible for the formation of valence band maxima (VBM). Lone-pair electrons directly affect the electronic structure of these metal halide perovskites. If the A-site CH3NH3 cation and X-site halogen anion (for example, iodine, I) are kept fixed and variation is made at the B-site metal, then it is noticed that the increase in the level of lone-pair states (4s1[Cu], 4s2 [Zn], 4s2 [Ge], 5s2 [Sn], 6s2 [Pb]) leads to wider bandgaps for these perovskites. The same thing happened for fixing the X-site as Br− or Cl− anions. Now let us keep the A-site CH3NH3 cation and any metal cation (M: Cu, Zn, Ge, Sn, Pb) fixed and observe variation at the X-site (X: Cl, Br, I). Then we see the reverse case. With an increase in the level of the lone-pair states (3s2[Cl], 4s2[Br], 5s2[I]) of the halide anion, the width of the bandgaps gradually decreased for the studied compounds. The unfilled s-orbitals or lone-pair electrons of these metal cations can introduce unfamiliar properties.55 Herein for all the structures, both the conduction band minima (CBM) and the valence band maxima are isotropic and dispersive (i.e., with a large bandwidths), which indicates minor carrier effective masses and this is useful in photovoltaic sectors. In all the structures, the fluctuations of the bottom conduction band (CB) are more substantial, indicating a quicker passage of photoelectrons. Also, the top VB and bottom CB are broad, which implies non-localized states and long-distance transport of excitons in these materials.
According to Fig. 4, if the halide changes from Cl to I, then the CB and VB, especially an inferior VB, are shifted to the Fermi level. It is also same for metal variation (from Ge to Pb and from Cu to Zn). This happens because the number of lone-pair electrons increases, which lead to more states and bands near the Fermi level.
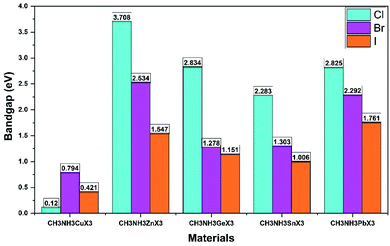
All the calculated fundamental bandgaps at G symmetry points and other available theoretical and experimental values are listed in Table 4. From Table 4, we observe that as the halide changes from Cl to I, the bandgap decreases, and it increases with atomic radius in the same group (Ge to Pb) and in the same period (Cu to Zn). Also, the CH3NH3GeX3 band gaps are quite close to those of CH3NH3PbX3 and larger than those of CH3NH3SnX3, as clearly depicted in Fig. 4. This makes CH3NH3GeX3 a favorable candidate for solar cell applications. Further CH3NH3ZnX3 also possesses a band gap that is quite close to CH3NH3PbX3 and the band gap of CH3NH3ZnI3 is (1.547 eV) very close to that of CH3NH3PbI3 (1.761 eV). This is also a good sign for their application in solar cells. CH3NH3GaX3 show metallic nature, which introduces a new idea for implementing them in other metallic/optoelectronic applications as they are non-perovskite compounds. With a decrease in atomic radius at the B-site, the nucleus gradually increases its electrostatic force on valence electrons. So, the nucleus strongly grasps the valence electrons which lowers the band gap and bonding energy in these materials. This may be one of the reasons why the band gap decreases with a reduction in atomic size. Our calculated band gap is closer to and comparable with experimental results. This trend has furthermore been witnessed in different studies on same-group compounds (CH3NH3GeX3, CH3NH3SnX3, CH3NH3PbX3).58 An exception has been observed for the experimental value of CH3NH3CuCl3 as very little work has been done on it. Also, experiments have been done on different phases and temperatures, which also caused the variation in our calculated results. It is also noticed that the band gaps are very responsive to variation in B-site metal cations in the perovskites and they agree quite well with earlier investigations.21,26 Moreover, the GGA functional containing the Wu–Cohen potential59 is very effective for bandgap investigation in comparison to the results of the LDA functional (Fig. 5).60 Bandgaps that are calculated with DFT give lower values than the experimental data but they can still be accounted for the DFT investigation.28
| Material | GGA-PBE | LDA-CAPZ | Experiment/theory |
|---|---|---|---|
| CH3NH3CuCl3 | 0.120 | 0.090 | 2.60 [exp.]42 |
| CH3NH3ZnCl3 | 3.708 | 4.092 | — |
| CH3NH3GaCl3 | No | No | — |
| CH3NH3GeCl3 | 2.834 | 1.799 | 3.74–3.76 [theory]56 |
| CH3NH3SnCl3 | 2.283 | 2.100 | 2.18 [theory],43 3.69 [exp.],45 1.94 [theory]45 |
| CH3NH3PbCl3 | 2.825 | 2.334 | 3.1 [exp.],57 2.88 [theory]43 |
| CH3NH3CuBr3 | 0.794 | 0.715 | — |
| CH3NH3ZnBr3 | 2.534 | 1.791 | — |
| CH3NH3GaBr3 | No | No | — |
| CH3NH3GeBr3 | 1.278 | 0.532 | 2.76–2.81 [theory]56 |
| CH3NH3SnBr3 | 1.303 | 1.219 | 2.15, 1.04 [exp., theory]45 |
| CH3NH3PbBr3 | 2.292 | 1.746 | 2.31, 2.26 [theory]46 |
| CH3NH3CuI3 | 0.421 | 0.156 | — |
| CH3NH3ZnI3 | 1.547 | 0.460 | — |
| CH3NH3GaI3 | No | No | — |
| CH3NH3GeI3 | 1.151 | 0.626 | 1.9–2.0 [theory]56 |
| CH3NH3SnI3 | 1.006 | 0.350 | 1.21 [exp.]21 |
| CH3NH3PbI3 | 1.761 | 1.441 | 1.6 [exp.]1 |
The electronic band gap can be explicated further by an investigation of the density of states (DOS). The DOS spectra of all the materials are presented in Fig. 6, which shows a comparison among them. All eighteen methylammonium metal halide perovskites possess the same type of total density of states (TDOS) except for MAGaX3 where the VB crosses the Fermi level and they show metallic behavior. However, by changing the cations from Ge to Pb and Zn to Cu, the VB are shifted closer to the Fermi level, as observed in Fig. 6. The same pattern was observed for chloride, bromide and iodide perovskites. This trend is also similar to the band structures which reaffirms the study.
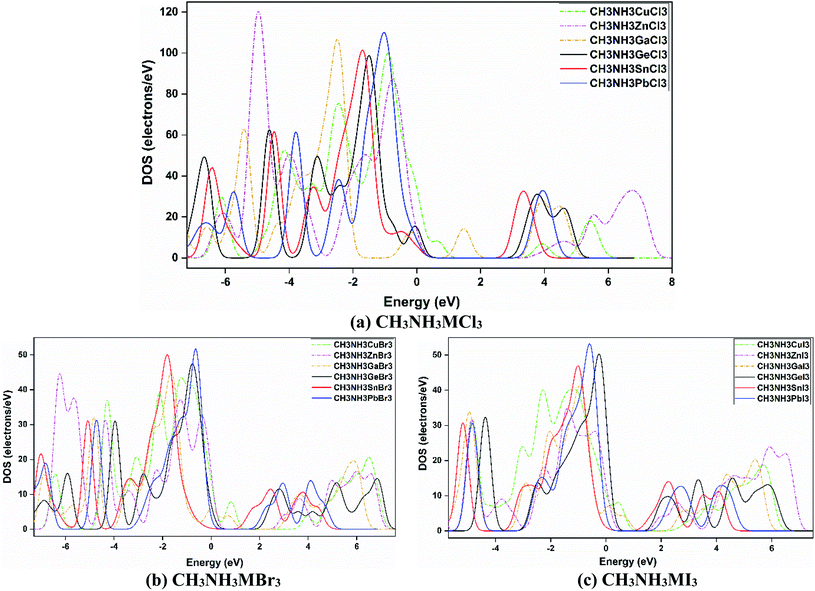 | ||
| Fig. 6 Density of states (DOS) spectra for (a) CH3NH3MCl3, (b) CH3NH3MBr3, and (c) CH3NH3MI3, and a comparison upon varying the metal and halide atoms in those CH3NH3MX3 compounds. | ||
We have further studied the partial/projected density of state (PDOS) of our calculated perovskite compounds, which are shown in Fig. 7. In terms of atomic viewpoint, the main contribution in VB and CB comes from the M-site and X-site atoms and it causes a reduction in band gap of these compounds. The valence electrons of Ge, Sn and Pb are 4s2 3d10 4p2, 5s2 4d10 5p2 and 6s2 5d10 6p2, respectively. From Fig. 7, it can be noted that the PDOS of these valence electrons, especially lone-pair electrons, give the main contribution to the formation of total DOS. For heavy atoms, the energy of the valence lone pair s orbital increases with an increase in metal cation size61,62 in the same period and in the same group which helps to make them defect-tolerant compounds. In the same-group compounds (CH3NH3GeX3, CH3NH3SnX3, CH3NH3PbX3), the main contribution in the conduction band minima (CBM) comes from the partially filled 4p2, 5p2 and 6p2 states of the metal atom, respectively. As the d-orbital is fully filled, its contribution is quite small for this group of perovskites.
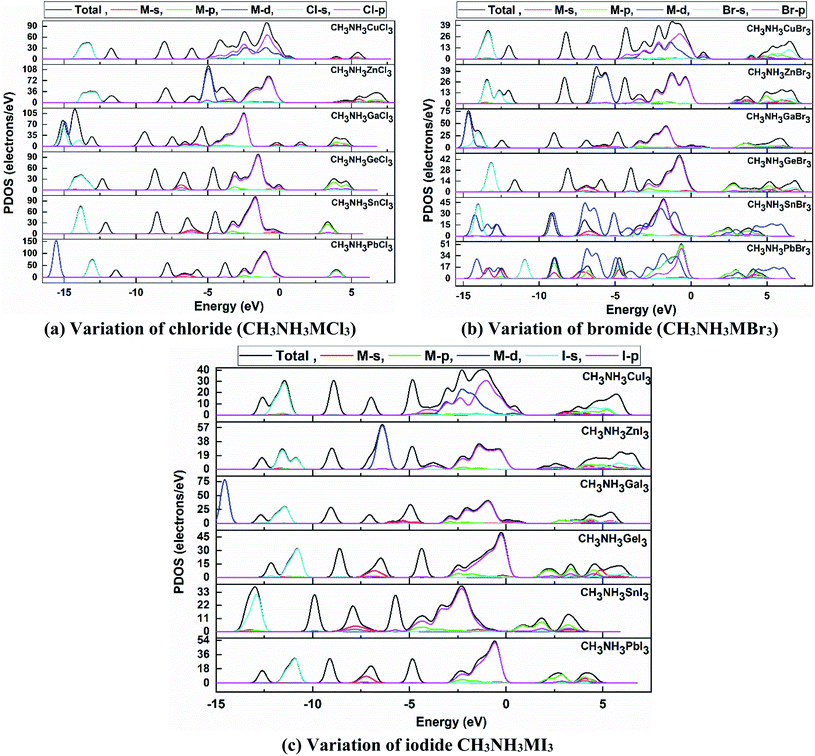 | ||
| Fig. 7 Partial density of states (PDOS) plots of orthorhombic (a) CH3NH3MCl3, (b) CH3NH3MBr3, and (c) CH3NH3MI3 compounds, where the dotted line represents the Fermi level at 0 K. | ||
Mainly the p-orbital and partially the lone-pair s-orbital of the metal atom (lone-pair s–p hybridization) are responsible for the configuration of the CBM. Thus it increases the band gap from Ge to Pb which provided validation of the study. The VBM is dominantly formed by the valence p-orbital of the halide anion and the lone-pair s-orbitals of the metal cation make a partial contribution for these same-group compounds. The lone-pair s–p hybridization of the metal cation and halide anion are greatly related to their band gap and these will lead to making them defect-tolerant compounds, able to tune their electronic attractiveness. The band gap is also linked with the M–X bond lengths of the same-group perovskite compounds and any alteration in the material configuration or bond length of these compounds can alter the band gap. So this elucidates the cause of the reduction in band gap value from CH3NH3PbX3 to CH3NH3GeX3.
Again in the same-period compounds (CH3NH3CuX3, CH3NH3ZnX3, CH3NH3GaX3), the valence electrons of Cu, Zn and Ga are 4s1 3d10, 4s2 3d10 and 4s2 3d10 4p1, respectively. As Cu has a half-filled s-orbital, this affects the TDOS more than for Zn and Ga. Besides the Cu-d orbital contributes mainly to forming the VB near the Fermi level in the CH3NH3CuX3 compounds. In the Cu-group compounds, the valence p-orbital and partial s-orbital of the halogen (X) anion contribute mainly to the VBM. While the main contribution of CBM comes from the s and p orbitals of the metal cation. Thus with an increase in atomic size in the same period (from Cu to Zn), the band gap increases from CH3NH3CuI3 (0.421) to CH3NH3ZnI3 (1.547) and similarly for other halides. Besides, the organic methylammonium part of those perovskite compounds has little impact on the CBM or VBM. Overall, organic CH3NH3 did not participate in the band structure; instead it contributed to the structural cohesion. Here it needs to be mentioned that as we make variations in the metal, the outer shell electrons and lone-pair s–p hybridization are changed and so is their participation in the TDOS as we go from Ge → Sn → Pb and Cu → Zn → Ga.
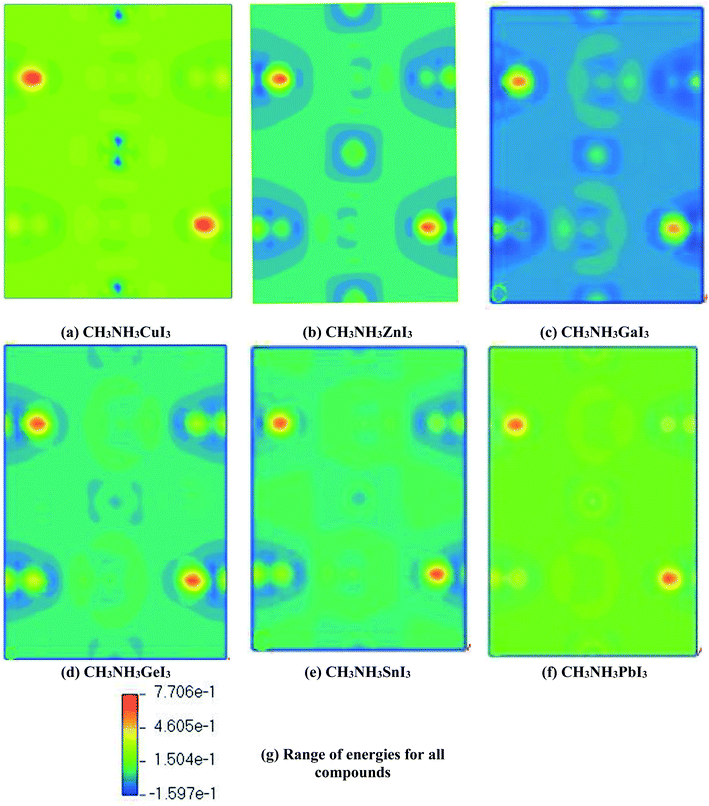
The coupling between the methylammonium cation (organic) and the M–X bond (inorganic) was further inspected with plots of electron charge density. They appear in ESI (Fig. S1†). For a better understanding, we present part of that depiction in Fig. 8 for CH3NH3MI3. Here field representation has been used for plotting electron charge density. According to Fig. 8, we did not observe any electron orbital overlap between the CH3NH3 part and the inorganic M–X bond, which represents a weak coupling between them. So there exists ionic bonding between the organic and inorganic parts. These perceptions indicate the character of the organic molecule for balancing the charge. This also clarifies that bonding between CH3NH3 and M–X is ionic. In this sense, the charges in the metal halide CH3NH3MX3 would show better transport performance.
3.3 Optical properties
Hybrid perovskite compounds become very promising as brilliant light harvesters in photovoltaics because of their organic (CH3NH3) part, which possesses greater optical absorption. Therefore, these compounds receive huge interest in the research community for building more efficient and effective photovoltaic and optoelectronic devices.The optical absorption coefficient of a material is an important parameter that measures the dispersion of light at particular wavelengths before it becomes absorbed.9,21 This is very helpful for providing information related to solar energy conversion efficiency. Thus, this is very relevant for the practical application of a material in photovoltaics.
In Fig. 9, optical absorption coefficient spectra of all eighteen perovskite materials are depicted. For same-group compounds (CH3NH3GeX3, CH3NH3SnX3, CH3NH3PbX3), the peaks of the absorption spectra shift to (right) high energy with the variation in metal from Ge to Pb and also with the changes in halogen from Cl to I. The peak of the absorption spectra was wide for Pb iodide and Sn iodide compounds with a very wide absorption range from far UV to the visible range (174–800 nm) and another peak with a strong absorption coefficient was at 180 nm for the Ge iodide compound. In other words, all the same-group materials within this range possess durable absorption and low electron loss. So it should be pointed that all these same-group compounds were fully transparent in the visible range. Also in going from iodide to chloride compounds, the absorption range decreases gradually from the visible spectrum to near UV. On the other hand, in the same-period compounds (CH3NH3CuX3, CH3NH3ZnX3, CH3NH3GaX3), the peak value shifts to higher energy when Cu is replaced with Zn or Ga, while we observe blue shifts for halogen variation from I to Cl with the total energy range between 125 and 800 nm. Besides, with the decrease in band gap, the absorption spectra of all the perovskites shift to lower energy from Pb to Ge and Ga to Cu in the iodide, bromide and chloride compounds. An exception was observed for CH3NH3GaBr3 and CH3NH3CuCl3 compounds which absorb light over a very wide range (115–800 nm) that make them favorable candidates for diverse optoelectronic devices. Thus optical absorption has a close relationship with electronic structure. As these perovskite compounds absorb UV-Vis light, these types of material show advantages for their application in solar cells as well as in many optical and electronic applications.
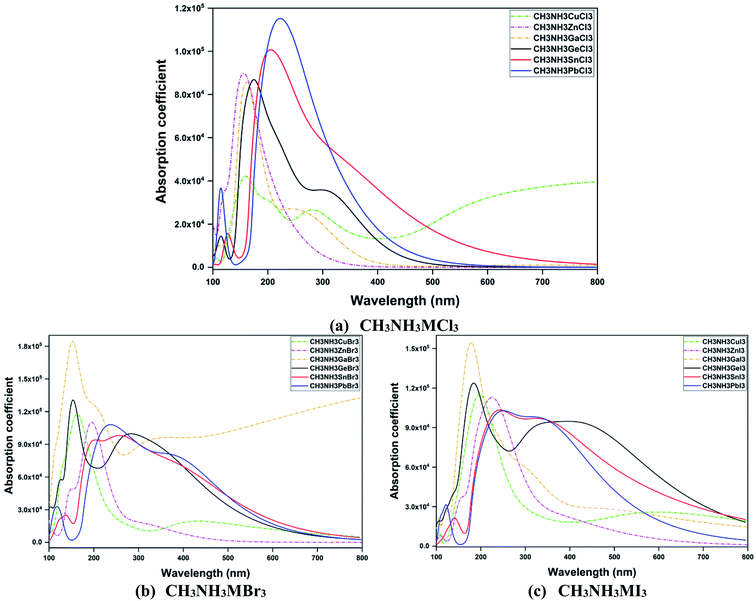 | ||
| Fig. 9 A comparison of the absorption coefficient α(ω) as a function of wavelength (nm) for orthorhombic CH3NH3MX3 compounds. | ||
Other optical properties, including reflectivity, refractive index, complex dielectric function, energy loss function and optical conductivity, of these orthorhombic perovskites have been calculated and are attached in the ESI (Fig. S2†). The zero frequency limit of dielectric function ε1(ω), reflectivity R(ω) and refractive index n(ω) are listed in Table 5. The frequency-dependent real part of the dielectric function, ε1(ω), is shown in Fig. S2.† From the dielectric spectra, we noticed that the compounds move to lower energy when the B-site metal atom changes from Pb to Ge and from Ga to Cu in iodide, bromide and chloride compounds (see Fig. S2†). In these spectra, we noticed a significant quantity which is the zero frequency limit ε1(0). It is considered to be a static dielectric constant. In the spectra the most important quantity is the zero frequency limit ε1(0), which is the electronic part of the static dielectric constant. The values of static ε1(0) are tabulated in Table 5. From Table 5, it is clear that for the same-group compounds, ε1(0) decreases from Ge to Pb and increases for chloride to iodide compounds except for CH3NH3GeCl3. This shows that bandgap and ε1(0) share an inverse relationship. For same-period compounds the value of ε1(0) decreases from Cu to Zn and increases from Zn to Ga based compounds. Also with the variation in halide (from I to Cl), the value of ε1(0) decreases, with the exception of CH3NH3GaBr3 (≈791 eV) and CH3NH3CuCl3 (≈60 eV). These values are unusually high and they also absorb light over a very wide range, as depicted in Fig. 9. This makes these two materials interesting in various optoelectronic device applications.
| Materials | Parameters | ||
|---|---|---|---|
| ε1(0) | R(0) | n(0) | |
| CH3NH3CuCl3 | 60.156 | 0.661 | 7.860 |
| CH3NH3ZnCl3 | 1.613 | 0.014 | 1.270 |
| CH3NH3GaCl3 | 1.658 | 0.016 | 1.288 |
| CH3NH3GeCl3 | 1.951 | 0.027 | 1.397 |
| CH3NH3SnCl3 | 4.389 | 0.125 | 2.095 |
| CH3NH3PbCl3 | 2.430 | 0.048 | 1.559 |
| CH3NH3CuBr3 | 2.591 | 0.055 | 1.610 |
| CH3NH3ZnBr3 | 1.885 | 0.025 | 1.373 |
| CH3NH3GaBr3 | 791.070 | 0.874 | 28.624 |
| CH3NH3GeBr3 | 4.416 | 0.126 | 2.102 |
| CH3NH3SnBr3 | 4.159 | 0.117 | 2.039 |
| CH3NH3PbBr3 | 4.041 | 0.113 | 2.010 |
| CH3NH3CuI3 | 5.077 | 0.149 | 2.254 |
| CH3NH3ZnI3 | 2.586 | 0.054 | 1.608 |
| CH3NH3GaI3 | 11.279 | 0.299 | 3.375 |
| CH3NH3GeI3 | 6.832 | 0.199 | 2.614 |
| CH3NH3SnI3 | 6.688 | 0.196 | 2.586 |
| CH3NH3PbI3 | 4.26 | 0.121 | 2.064 |
It is also noted that R(0) shows similar behavior to ε1(0) in both categories (same group and same period) of compound and also with iodide to chloride compounds. Similar exceptions occurred for CH3NH3GeCl3, CH3NH3GaBr3 and CH3NH3CuCl3. The highest R(0) value was noted for CH3NH3GaBr3 (0.874 eV) which also possesses a very high dielectric function (791 eV). The zero frequency refractive index n(0) further shows analogous behavior to ε1(0) in both categories of compound and also in iodide to chloride compounds.
For same-group compounds, CH3NH3SnCl3 is an exception in n(0) while CH3NH3GaBr3 and CH3NH3CuCl3 are exceptions for same-period compounds. The infrequent high refractive index of CH3NH3GaBr3 (28.624) and CH3NH3CuCl3 (7.860) is far greater than the value for diamond, the natural material with the highest refractive index. Thus CH3NH3GaBr3 and CH3NH3CuCl3 can be turned into artificial and unusual jewel crystals. If the value of the refractive index falls below unity (see Fig. S2†) then it can be able to absorb X-rays, γ-rays and a percentage of UV photons which make these materials superluminescent for these types of rays. So these low values of refractive index (n = c/Vg) imply that Vg swings to the negative realm (as Vg > c) and the medium changes from linear to non-linear which is indicative of the superluminal nature of these materials (CH3NH3GaBr3 and CH3NH3CuCl3).
4 Conclusions
First-principles DFT calculations were performed on orthorhombic hybrid metal halide perovskites of the form CH3NH3MX3 (M: Cu, Zn, Ga, Ge, Sn, Pb; X: Cl, Br and I) to investigate their geometric, electronic, and optical properties and to understand their atomistic origin and the effects of lone-pair orbitals (s–p hybridization) upon varying the metal cations and halogen anions in these perovskite compounds. According to the tolerance factor limit and μ, all eighteen materials may form stable 3D perovskite compounds, except CH3NH3GaX3, which may be a non-perovskite and could be used in other optoelectronic devices. The calculated lattice parameters are directly related to the atomic radii of the metals and are entirely compatible with the experimental values. M–X bonds become more important when the size of the metal cation increases in the same group (Ge to Pb) and the same period (Cu to Ga), and the bond length changes are found to be more significant in the equatorial direction. Also, the calculated M–X bond lengths reduce upon going from I to Cl.According to the electronic band structures, all the hybrid perovskites possess a direct band gap at the G symmetry point. The calculated band gaps of these CH3NH3PbX3 perovskites increase from Cl to I, and they agree well with experimental data. Also, CH3NH3ZnI3 possesses a band gap of 1.547 eV, which is comparable to CH3NH3PbI3 (1.761 eV), making this material (CH3NH3ZnI3) a vital candidate for lead-free solar cell applications. The VBM is mainly contributed to by the p orbital of the halide atom, the CBM comprises the lone-pair s and p orbitals of the metal atom near the Fermi level, and organic CH3NH3 does not contribute to the electronic structure. The impact of the hybridization of the lone-pair (ns2) electrons of the metal cation with the halide anion (lone-pair p-orbital) leads to some unfamiliar properties being shown by these metal halide compounds, which is encouraging for optoelectronic applications. This lone-pair hybridization plays a key role in producing defect-tolerant compounds and is also responsible for suitable band alignments, making these materials perfect absorbers for visible light. Moreover, PDOS plots suggest a relationship between the band gap and the effect of the lone pair (i.e., s–p hybridization) and M–X bonding. Therefore, any alteration at a metal or halogen site can easily affect the band gap values.
From the viewpoint of optical absorption spectra, all the orthorhombic perovskite materials show blue shifting from Pb to Ge and Ga to Cu in iodide, bromide, and chloride compounds. For same-group compounds (CH3NH3GeX3, CH3NH3SnX3, and CH3NH3PbX3), ε1(0), R(0), and n(0) decrease from Ge to Pb and increase when moving from chloride to iodide compounds. Disruptive behavior has been observed for same-period compounds (CH3NH3CuX3, CH3NH3ZnX3, and CH3NH3GaX3). CH3NH3GaBr3 and CH3NH3CuCl3 could be promising nontoxic materials for use in optoelectronic devices as they absorb a wide range of light (from far-UV to visible) and possess very unusual high dielectric functions and refractive indices.
Data availability
Data are available upon request from the authors.Author contributions
Maliha Nishat: Software, Methodology, Formal analysis, Investigation, Writing-Original Draft Md. Rakib Hossain: Writing-Review and Editing, Visualization Md. Kamal Hossain: Conceptualization, Methodology, Validation, Data Curation, Writing-Review and Editing Shamima Khanom: Writing-Review and Editing, Visualization Farid Ahmed: Resources, Project administration, Funding acquisition Md. Abul Hossain: Visualization, Supervision.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge the Higher Education Quality Enhancement Program (HEQEP) subproject CP-3415, University Grant Commission (UGC) of Bangladesh and the World Bank for financial assistance to set up the Computational Physics (CP) Research Lab in the Department of Physics at Jahangirnagar University.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger and A. W. Y. Ho-Baillie, Prog. Photovoltaics Res. Appl., 2018, 26, 3–12 CrossRef.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 221104–67188617 Search PubMed.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS PubMed.
- W. Zhang, G. E. Eperon and H. J. Snaith, Nat. Energy, 2016, 1, 16048 CrossRef CAS.
- B. R. Sutherland, S. Hoogland, M. M. Adachi, P. Kanjanaboos, C. T. O. Wong, J. J. McDowell, J. Xu, O. Voznyy, Z. Ning, A. J. Houtepen and E. H. Sargent, Adv. Mater., 2015, 27, 53–58 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S. J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. Il Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641 RSC.
- Y. Dang, Y. Liu, Y. Sun, D. Yuan, X. Liu, W. Lu, G. Liu, H. Xia and X. Tao, CrystEngComm, 2015, 17, 665–670 RSC.
- L. Chi, I. Swainson, L. Cranswick, J. H. Her, P. Stephens and O. Knop, J. Solid State Chem., 2005, 178, 1376–1385 CrossRef CAS.
- I. P. Swainson, R. P. Hammond, C. Soullière, O. Knop and W. Massa, J. Solid State Chem., 2003, 97–104 CrossRef CAS.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- J. Feng and B. Xiao, J. Phys. Chem. Lett., 2014, 5, 1278–1282 CrossRef CAS PubMed.
- W. Geng, L. Zhang, Y. N. Zhang, W. M. Lau and L. M. Liu, J. Phys. Chem. C, 2014, 118, 19565–19571 CrossRef CAS.
- X. Zhu, H. Su, R. A. Marcus and M. E. Michel-Beyerle, J. Phys. Chem. Lett., 2014, 5, 3061–3065 CrossRef CAS PubMed.
- G. Hodes, Science, 2013, 342, 317–318 CrossRef CAS PubMed.
- L. Lang, J. H. Yang, H. R. Liu, H. J. Xiang and X. G. Gong, Phys. Lett. A, 2014, 378, 290–293 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- T. Ahmed, C. La-O-Vorakiat, T. Salim, Y. M. Lam, E. E. M. Chia and J. X. Zhu, Europhys. Lett., 2014, 108, 67015 CrossRef.
- O. Almora, C. Aranda, E. Mas-Marzá and G. Garcia-Belmonte, Appl. Phys. Lett., 2016, 109, 173903 CrossRef.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed.
- D. H. Fabini, R. Seshadri and M. G. Kanatzidis, MRS Bull., 2020, 45, 467–477 CrossRef.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- R. Chen, D. Hou, C. Lu, J. Zhang, P. Liu, H. Tian, Z. Zeng, Q. Xiong, Z. Hu, Y. Zhu and L. Han, Sustain. Energy Fuels, 2018, 2, 1093–1100 RSC.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys. Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. S. Thind, X. Huang and R. Mishra, Chem. Mater., 2009, 29, 6003–6011 CrossRef.
- S. Sun and A. K. C. Gregor Kieslich, Chem. Sci., 2015, 6, 3430–3433 RSC.
- R. D. Shannon, Acta Crystallogr. A, 1976, 32, 751–767 CrossRef.
- S. Sun and A. K. C. Gregor Kieslich, Chem. Sci., 2014, 5, 4712–4715 RSC.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- M. Becker, T. Klüner and M. Wark, Dalton Trans., 2017, 46, 3500–3509 RSC.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr. Sect. B Struct. Sci., 2008, 64, 702–707 CrossRef CAS PubMed.
- S. S. Ashrafi, K. Hossain, F. Ahmed, A. Hossain and O. Rahman, Adv. Mater. Phys. Chem., 2020, 10, 1–16 CrossRef CAS.
- E. Mosconi, P. Umari and F. De Angelis, Phys. Chem. Chem. Phys., 2016, 18, 27158–27164 RSC.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- F. Chiarella, A. Zappettini, F. Licci, I. Borriello, G. Cantele, D. Ninno, A. Cassinese and R. Vaglio, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045129 CrossRef.
- Z. Yi and Z. Fang, J. Phys. Chem. Solids, 2017, 110, 145–151 CrossRef CAS.
- J. Feng and B. Xiao, J. Phys. Chem. C, 2014, 118, 19655–19660 CrossRef CAS.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- Y. Wang, T. Gould, J. F. Dobson, H. Zhang, H. Yang, X. Yao and H. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 1424–1429 RSC.
- D. A. Egger and L. Kronik, J. Phys. Chem. Lett., 2014, 5, 2728–2733 CrossRef CAS PubMed.
- Y. Pan, S. Chen and Y. Jia, Int. J. Hydrogen Energy, 2020, 45, 6207–6216 CrossRef CAS.
- Y. Pan, Vacuum, 2020, 181, 109742 CrossRef CAS.
- I. L. Ivanov, A. S. Steparuk, M. S. Bolyachkina, D. S. Tsvetkov, A. P. Safronov and A. Y. Zuev, J. Chem. Thermodyn., 2018, 116, 253–258 CrossRef CAS.
- A. Senocrate, G. Y. Kim, M. Grätzel and J. Maier, ACS Energy Lett., 2019, 4, 2859–2870 CrossRef CAS.
- A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428 CrossRef CAS.
- S. F. Hoefler and G. Trimmel, Monatsh. Chem., 2017, 148, 795–826 CrossRef CAS PubMed.
- G. C. Papavassiliou and I. B. Koutselas, Synth. Met., 1995, 71, 1713–1714 CrossRef CAS.
- H. Zhou, Q. Chen, G. Li, S. Luo, T. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546 CrossRef CAS PubMed.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 2–7 Search PubMed.
- B. G. Chae, D. H. Youn, H. T. Kim, S. Y. Maeng and K. Y. Kang, J. Korean Phys. Soc., 2003, 44, 884–888 Search PubMed.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- Z. Xiao, K. Z. Du, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, J. Am. Chem. Soc., 2017, 139, 6054–6057 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1ra08561a |
| This journal is © The Royal Society of Chemistry 2022 |