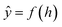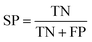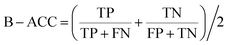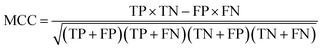Predicting hERG channel blockers with directed message passing neural networks

Abstract

Compounds with human ether-à-go-go related gene (hERG) blockade activity may cause severe cardiotoxicity. Assessing the hERG liability in the early stages of the drug discovery process is important, and the in silico methods for predicting hERG channel blockers are actively pursued. In the present study, the directed message passing neural network (D-MPNN) was applied to construct classification models for identifying hERG blockers based on diverse datasets. Several descriptors and fingerprints were tested along with the D-MPNN model. Among all these combinations, D-MPNN with the moe206 descriptors generated from MOE (D-MPNN + moe206) showed significantly improved performances. The AUC-ROC values of the D-MPNN + moe206 model reached 0.956 ± 0.005 under random split and 0.922 ± 0.015 under scaffold split on Cai's hERG dataset, respectively. Moreover, the comparisons between our models and several recently reported machine learning models were made based on various datasets. Our results indicated that the D-MPNN + moe206 model is among the best classification models. Overall, the excellent performance of the DMPNN + moe206 model achieved in this study highlights its potential application in the discovery of novel and effective hERG blockers.

---

Introduction

The human ether-a-go-go-related gene (hERG) encodes a voltage-gated potassium channel, which plays a major role in cardiac action potential.¹ Blockage of this hERG potassium ion channel will cause a prolonged QT interval and lead to severe cardiotoxicity such as cardiac arrhythmia.² Several marketed drugs, including astemizole,³ terfenadine,⁴ and cisapride,⁵ have been withdrawn due to their unintended hERG-related cardiotoxicity. Consequently, the assessment of hERG-blocking activity is essential in drug discovery projects. Various in vitro and in vivo assays, including fluorescent measurements,⁶ radioligand binding assay,⁷ patch-clamp electrophysiology,⁸ and QTc assays,⁹ have been developed to evaluate the inhibitory effects of small molecules on hERG channel. However, these assays are usually time-consuming and expensive. Thus, it is important to develop reliable in silico methods for the prediction of hERG inhibition in an early stage of the drug discovery and development process. Over the past decade, many in silico models for predicting hERG channel inhibition have been reported.¹⁰ Most of these methods can be categorized as structure-based methods (including quantitative structure–activity relationships (QSAR) and pharmacophore searching) and machine learning methods (such as support vector machine (SVM) and random forest (RF)).^11–13

More recently, as the accumulation of data about hERG inhibition of small molecules or their binding affinity to hERG, several large-scale datasets consisting of thousands of hERG blockers and hERG non-blockers are now publicly available.^14–16 Utilizing these datasets, many machine learning (ML) algorithms have been utilized for predicting hERG blocking activity. For instance, Hou et al. have developed pharmacophore-based models with Naive Bayes (NB) and SVM, and their best SVM model achieved the prediction accuracy of 84.7% for the training set and 82.1% for the external test set.¹⁷ Siramshetty et al. have employed three machine learning methods k-nearest neighbors (kNN), RF, and SVM with different molecular descriptors, and the area under the receiver operating characteristic curve (AUC-ROC) value of the best model reached 0.94.¹⁸ Ogura et al. have established an SVM classification model with the descriptor selected by non-dominated Sorting Genetic Algorithm-II (NSGA-II), and the accuracy reached out to 0.984 for their test dataset.¹⁹ With the development of the deep learning technique, Cai et al. have collected 7889 compounds with well-defined experimental data on hERG, built multi-task deep learning-based prediction models (deephERG) based on the DeepChem²⁰ open-source platform, and obtained accuracy of 0.93 and AUC-ROC of 0.967 for the best model.²¹ In addition, multiple other deep learning-based models have been reported, including Capsule Networks and platforms such as deepHit,²² hERG-Att,²³ hERG-ml,²⁴ and CardioTox net.²⁵ Despite the above substantial progress in hERG blockers prediction, the accuracy performance needs to be further improved in real drug discovery settings.

Recently, Yang et al. have proposed a Directed Message Passing Neural Network (D-MPNN),²⁶ which showed excellent performances across 19 public datasets, including QM7, QM8, QM9, ESOL, FreeSolv, lipophilicity, BBBP, PDBbind-F, PCBA, BACE, Tox21, and ClinTox. Moreover, it is worth noting that Stokes et al. have successfully applied D-MPNN in identifying novel antibacterial compounds from the ZINC15 database, which strongly proved the superiority of D-MPNN.²⁷ In this study, we applied the D-MPNN model on hERG datasets for predicting the hERG blockers. We tested different combinations of D-MPNN with several fingerprints or descriptors (ECFP4,²⁸ ECFP6,²⁸ FCFP4,²⁸ MACCS,²⁹ PubchemFP,³⁰ RDkit 2D normalized,³¹ Mol2vec,³² MOE53,³³ and moe206 ³⁴ (206 2D descriptors generated by MOE)), and found that some of these descriptors can significantly boost the performance of D-MPNN. The best combination is D-MPNN incorporated with moe206 descriptors (D-MPNN + moe206), which obtained AUC-ROC values up to 0.956 ± 0.005 and 0.922 ± 0.015 in the five-fold cross-validation on random split and scaffold split, respectively. Various comparisons were also made between our models and those developed by other machine learning methods on their datasets. All the results confirmed that the D-MPNN + moe206 model is one of the best classification models for predicting hERG blockers.

Experimental section

Dataset

Initially, Cai's hERG dataset²¹ was first used to evaluate the D-MPNN model and search the premium descriptors combinations with the D-MPNN model. It contains a total of 7889 compounds and has 6 thresholds (10 μM, 20 μM, 40 μM, 60 μM, 80 μM, and 100 μM) for distinguishing hERG blockers from non-blockers. To compare the performance of our best model (D-MPNN + moe206) with other machine learning models, we used several other hERG datasets reported by Doddareddy,¹¹ Hou,¹⁷ Ogura,¹⁹ Siramshetty,²⁴ and Karim's.²⁵ Additionally, we conducted principal component analysis (PCA) on Cai's,²¹ Siramshetty's,²⁴ and Hou's¹⁷ datasets in Table S1, Fig. S1 and S2.†

D-MPNN model

Yang et al. have described the directed-message passing neural network (D-MPNN) in detail and built the open-source package Chemprop for implementation of D-MPNN (see more in https://github.com/chemprop/chemprop).²⁶ Similar to other message passing neural networks (MPNN), D-MPNN constructs a learned molecular representation by operating on the graph structure of the molecule. Different from the generic MPNN that uses an atom-dependent neural network to pass a message, D-MPNN uses the edge-dependent neural network to pass a message.

In Chemprop, initially, each SMILES string was converted to their corresponding molecular graph (G) via the open-source package RDKit,³⁵ where the atoms in the chemical structures were described as nodes (v), and the bonds between atoms were considered as edges. Next, node (atom) features x_v and edge (bond) features e_vw were computed. Prior to the first step of message passing, edge hidden states h⁰_vw were initialized with the following equation:

h⁰_vw = τ(W_i cat(x_v, e_vw))

where τ is the rectified linear activation function (ReLU), W_i is a learned matrix, and cat(x_v, e_vw) represents the concatenation of the atom features x_v for atom v and the bond features e_vw for bond vw. Afterward, the D-MPNN functions on hidden states h_vw^t and messages m_vw^t to spread messages based on the graph structure. On each directed message passing step t, each bond's featurization is updated by summing the featurization of neighboring bonds, concatenating the current bond's featurization with the sum. The calculations are according to the following equations:

h_vw^t+1 = τ(h⁰_kv + W_mm_vw^t+1)

where N(v) is the set of neighbors of v in graph G, t ∈ {1, …, T} and T is total steps of the message passing phase, and W_m ∈ R^h×h is a learned matrix. Then each atom representation of the molecule was calculated by aggregating the incoming bond features according to

In the readout phase of D-MPNN, the feature vector h for the whole molecule was obtained by summing the hidden states of all atoms.

Finally, the feature vector h is fed through a feed-forward neural network to generate property predictions.

D-MPNN with molecular characterization

As noted by Yang et al., the original D-MPNN model might not be so efficient at extracting global molecular features, especially for large molecules. To enhance the D-MPNN performance, various molecular features^26,27 could be incorporated into the D-MPNN model.

Here, 9 types of molecular descriptors or fingerprints are used to represent the characteristics of the compounds, including mol2vec,³² RDkit 2d normalized,³¹ MACCS,²⁹ PubChemFP,³⁰ ECFP,²⁸ ECFP6,²⁸ FCFP4,²⁸ MOE53,³³ and moe206.³⁴ The first 8 descriptors or fingerprints were computed by RDkit,³¹ Molmap,³⁶ or mol2vec.³² The last one, moe206, was calculated by Molecular Operating Environment (MOE),³⁴ representing the 206 2D descriptors for each molecule, mainly composed of physicochemical properties, kappa shape index, surface area, atomic and bond number, etc.

The list of descriptors is shown in Table S2.†

Model assessment

The model performance is mainly measured by AUC-ROC. In addition to AUC-ROC, sensitivity (SE), specificity (SP), Negative Predictive Value (NPV), Positive Predictive Value (PPV), Accuracy (ACC), Balanced Accuracy (BA), and Matthews Correlation Coefficient (MCC) were evaluated. The formula for calculating the index is as follow:

True positive (TP): the ratio correctly judged to be positive in all actually positive samples. True negative (TN): a ratio that is correctly predicted to be negative in all actually negative samples. False positive (FP): the rate of being wrongly judged positive in all actually negative samples. False negative (FN): the ratio of false predictions to negative in all actually positive samples.

Hyperparameter optimization

Like other machine learning models, hyperparameter optimization might be an important step for the D-MPNN model. Bayesian hyperparameter optimization³⁷ implemented on chemprop²⁶ was adapted to search the optimum parameters including the number of the model, the hidden size of the neural network, the dropout probability, the number of feed-forward network layers.

Results

Performance on Cai's dataset

Recently, Cai et al. collected an hERG dataset containing 7889 compounds and proposed a deep learning model (deephERG) based on DeepChem module for hERG blockers prediction.²¹ Initially, we compared the performance between the D-MPNN model and the deephERG model. To make a fair comparison, we used the same datasets to train and test the D-MPNN models. Using the same valid dataset and evaluation metric as those reported in Cai's, the D-MPNN model (AUC range from 0.989 to 0.998) showed an improved performance than their deephERG (AUC range from 0.883 to 0.958) (Fig. 1). The distribution of the prediction probabilities by the D-MPNN model for all compounds in Cai's dataset at a threshold of 10 μM were plotted (Fig S3†). It showed that most non-blockers (red color) were predicted as non-blockers whose probabilities are around zero, while a majority of blockers (blue color) have probabilities near 100%.

Fig. 1 Comparison of the AUC-ROC values of D-MPNN and deephERG model across different decoy thresholds on Cai's validation set.

Inspired by the excellent performances of the original D-MPNN, we next evaluated the performance of the D-MPNN model coupled with 9 different molecular descriptors (including ECFP, ECFP4, ECFP6, FCFP4, MACCS, PubchemFP, RDkit 2D normalized, MOE53, moe206, mol2vec, MOE53 + mol2vec, and MOE53 + RDkit 2D normalized). At this time, we also used the same total of 7889 compounds from Cai's dataset but applied a five-fold cross-validation mode instead of using the pre-splitted data for training and testing. In the five-fold cross-validation mode, the whole 7889 compounds were divided into five subsets by random select or scaffold split. In each run, four of the five subsets were selected as the training data, and the remaining subset was used as the testing data for evaluating performance. This process was repeated 5 times until each of the five subsets has used as the testing data once. The average testing result from the five runs was used to calculate the final AUC-ROC.

The five-fold cross-validation results based on the random split are given in Fig. 2A. It is believed that k-fold cross-validation³⁸ can effectively avoid overfitting and underfitting. As expected, D-MPNN using the five-fold cross-validation (set as the control in Fig. 2A) showed a significantly poor performance than the above D-MPNN using pre-split data (AUC-ROC: 0.947 ± 0.005 versus 0.996 ± 0.004). And with the incorporation of the molecular characterizations or their combinations, the D-MPNN performances have about 2% fluctuation (AUC-ROC from 0.935 to 0.956). The D-MPNN coupled with moe206 descriptor (D-MPNN + moe206) provides optimal performance with AUC-ROC reaching 0.956 ± 0.005, which is better than the original D-MPNN (AUC-ROC 0.947 ± 0.005). The combination of D-MPNN with FCFP4 fingerprint provided the worst results.

Fig. 2 (A) Performances of the D-MPNN with the single molecular characterization and the combinations of molecular characterizations (control, ECFP4, ECFP6, FCFP4, MACCS, PubchemFP, RDkit 2D normalized, MOE53, moe206, mol2vec, MOE53 + mol2vec, MOE53 + RDkit 2D normalized) on the validation set under random split. (B) Performances on the validation set under scaffold balanced split.

Similarly, all these models with molecular characterizations were tested using five-fold cross-validation under the scaffold split mode (Fig. 2B). In this circumstance, D-MPNN with MOE53, moe206, and RDkit2D obtained slightly higher performance than others, with AUC-ROC reaching from 0.922 to 0.925. Since AUC-ROC on random split has less fluctuation than that on scaffold split, so the five-fold cross-validation random split mode was chosen for further investigation. D-MPNN + moe206 was considered to be the best incorporated descriptor for D-MPNN.

Performance comparison with other models

To compare the performance of D-MPNN + moe206 with other machine learning methods reported in the literature, we applied the D-MPNN + moe206 model on the same datasets as those methods including Hou et al.,^17,39 Zhang et al.,⁴⁰ and Sun et al.⁴¹ To make a fair comparison, the datasets (including training datasets, valid datasets, and test datasets) were kept the same as the reference methods in each comparison case. AUC-ROC, SE, SP, NPV, PPV, ACC, BA, and MCC were selected as performance indexes. To our delight, D-MPNN + moe206 show generally better or comparable performance over all these models and (Table 1), and it is significantly better than the original D-MPNN in all 6 entries.

Table 1 Comparison the performance of D-MPNN + moe206 model with other best models

	Model	Training set	Test set	AUC-ROC	SE	SP	ACC
a Doddareddy's dataset.b Siramshetty's dataset.c Not available, this value can NOT be found in the original literature.d Hou's training set I and test set I.e Hou's training set II and test set II.f Ogura's training and test dataset. For each D-MPNN model, the average of different folds (N = 5) and the corresponding standard deviation are listed.
1^a	SVM + FCFP	D3 training	D3 test	0.93	0.81	0.89	0.86
	D-MPNN + moe206			0.958 ± 0.005	0.900 ± 0.019	0.913 ± 0.016	0.907 ± 0.010
	D-MPNN			0.955 ± 0.005	0.881 ± 0.032	0.907 ± 0.027	0.896 ± 0.002
2^b	Consensus model	Training	Validation	NA^c	0.74	0.86	NA^c
	D-MPNN + moe206			0.864 ± 0.021	0.808 ± 0.077	0.798 ± 0.039	0.798 ± 0.033
	D-MPNN			0.819 ± 0.012	0.638 ± 0.065	0.844 ± 0.037	0.831 ± 0.031
3^b	Consensus model	Training	FDA-1	0.79	0.71	0.78	NA^c
	D-MPNN + moe206			0.882 ± 0.013	0.613 ± 0.110	0.856 ± 0.023	0.835 ± 0.018
	D-MPNN			0.813 ± 0.032	0.413 ± 0.099	0.884 ± 0.019	0.844 ± 0.013
4^d	SVM	Training I	Test I	0.842	0.907	0.652	0.821
	D-MPNN + moe206			0.871 ± 0.010	0.916 ± 0.014	0.667 ± 0.049	0.832 ± 0.010
	D-MPNN			0.776 ± 0.026	0.907 ± 0.031	0.539 ± 0.065	0.783 ± 0.021
5^e	SVM	Training II	Test II	0.839	0.850	0.745	0.821
	D-MPNN + moe206			0.876 ± 0.015	0.890 ± 0.025	0.676 ± 0.039	0.830 ± 0.010
	D-MPNN			0.806 ± 0.010	0.909 ± 0.037	0.553 ± 0.040	0.808 ± 0.018
6^f	SVM + 72descriptors + ECFP4	Training	Test	0.962	0.670	0.995	0.984
	D-MPNN + moe206			0.968 ± 0.001	0.656 ± 0.033	0.994 ± 0.001	0.983 ± 0.001
	D-MPNN			0.954 ± 0.001	0.627 ± 0.038	0.992 ± 0.001	0.979 ± 0.000

---

Table 1 entry 1 used the dataset from Doddareddy¹¹ et al., since their representative model performed better on Dataset3 (D3), which contains training set (blockers:1004, non-blockers:1385) and test set (blockers:108, non-blockers: 147). The blockers are defined with IC₅₀ values <10 μM, non-blockers are with IC₅₀ values >30 μM, and the optimal model of Doddareddy et al. is the SVM model with Functional Class Fingerprints (FCFP6), which gave the AUC-ROC of 0.93 and ACC of 0.86 under five-fold cross-validation. Our D-MPNN + moe206 model showed improved prediction accuracy under the exact training and test dataset, achieving AUC-ROC of 0.958 ± 0.005 and ACC of 0.907 ± 0.010, respectively. While the original D-MPNN model gave a slightly poor performance with AUC-ROC of 0.955 ± 0.005 and ACC of 0.896 ± 0.002, confirming moe206 descriptor incorporation is important for boosting the prediction power of D-MPNN.

Table 1 entry 2 listed a result from a recent article by Siramshetty²⁴ et al. They combined the best models of RF + RDKit, XGBoost + RDKit, DNN + MorganFP, and long short-term memory (LSTM) + ATN-SMILES with their own merits into a consensus model, providing superior performance. Siramshetty's dataset consists of the training set (blockers: 2164, non-blockers: 5990), prospective validation set (threshold = 30 μM, blockers: 53, non-blockers: 786), and FDA-approved drugs (thresholds = 1 μM, blockers: 15, non-blockers: 162; thresholds = 10 μM, blockers: 46, non-blockers: 131), where the training set comes from Public Domain hERG Bioactivity (ChEMBL) using a binary threshold (1 and 10 μM) and thallium flux assay (NCATS) using a threshold of 30 μM. We run the D-MPNN + moe206 model on the same training dataset as Siramshetty's consensus model and then evaluated performance on Siramshetty's validation dataset and FDA-1 dataset. As shown in Table 1 entry 2, on prediction of Siramshetty's Validation dataset D-MPNN + moe206 performs better in SE (0.808 ± 0.077 versus 0.77), while Siramshetty's consensus model has better SP (0.798 ± 0.039 versus 0.86). For prediction of the FDA-1 dataset (Table 1 entry 3), D-MPNN + moe206 performs much better in AUC-ROC (0.882 ± 0.013 versus 0.79) and SP (0.856 ± 0.023 versus 0.78), but not so good as the consensus model in SE (0.613 ± 0.110 versus 0.71).

The models of entries 4 and 5 in Table 1 are based on Hou's dataset,¹⁷ which contains training set I (blockers: 352, non-blockers: 40), training set II (blockers: 352, non-blockers: 40), test set I (blockers: 175, non-blockers: 20), and test set II (blockers: 175, non-blockers: 20), blockers and non-blockers are distinguished with a threshold of 40 μM. According to Hou's report,¹⁷ the performance of the optimal model SVM reaches the highest AUC-ROC of 0.842 and 0.839 for test I and test II, respectively. Nevertheless, our D-MPNN + moe206 model showed more competitive and superior performance, which gave an AUC-ROC of 0.871 ± 0.010, ACC of 0.832 ± 0.010 for test I, and an AUC-ROC of 0.876 ± 0.015, ACC of 0.830 ± 0.010 for test II.

Entry 6 of Table 1 used Ogura's datasets,¹⁹ which is the largest hERG database so far. It contains a training set (blockers: 6923, non-blockers: 196 918) and a test set (blockers: 2966, non-blockers: 84 395), and as per the criteria of IC₅₀ values ≤10 μM considered to be hERG blockers and IC₅₀ values >10 μM considered to be hERG non-blockers. A prediction model based on the non-dominant sorting genetic algorithm (NSGA-II) was constructed to obtain the maximum prediction performance with 72 selected descriptors and ECFP4 structure fingerprint, reaching an ACC value of 0.984, respectively. D-MPNN + moe206 achieves comparable performance with AUC-ROC of 0.968 ± 0.001 and ACC value of 0.983 ± 0.001 based on the same training and test dataset as Ogura's model.

Very recently Karim et al. proposed a robust predictor based on deep learning meta-feature ensembles called CardioTox net, which showed excellent performance in various classification indexes for three external test sets.²⁵

We tested the performance of D-MPNN + moe206 by comparison with CardioTox using Karim's²⁵ datasets in Table 2, which contains training set (blockers: 6643, non-blockers: 5977), test set-I (blockers: 30, non-blockers: 14), test set-II (blockers: 11, non-blockers: 30), and test set-III (blockers: 30, non-blockers: 710). The blockers are defined with IC₅₀ values <10 μM, and the non-blockers are with IC₅₀ values ≥ 10 μM. As shown in Table 2 entries 1 and 3, D-MPNN + moe206 is comparable to CardioTox on all three dataset. Although D-MPNN + moe206 performance is slightly inferior to CardioTox on test set-I and test set-III which achieved MCC of (0.567 ± 0.061 versus 0.599, 0.214 ± 0.016 versus 0.220) and ACC of (0.800 ± 0.030 versus 0.810, 0.696 ± 0.030 versus 0.746), D-MPNN + moe206 showed improved performance for all metrics except ACC on test set-II, which reaches MCC of 0.470 ± 0.053, NPV of 0.950 ± 0.032, PPV of 0.467 ± 0.020, SP of 0.620 ± 0.030, SE of 0.909 ± 0.064, and B-ACC of 0.764 ± 0.030.

Table 2 Comparison the performance of D-MPNN + moe206 model with Karim's best model

	Model	Evaluation data	AUC-ROC	MCC	NPV	ACC	PPV	SP	SE	B-ACC
a Karim's dataset.b Not available. For each D-MPNN model, the average of different folds (N = 5) and the corresponding standard deviation are listed.
1^a	CardioTox	Test set-I	NA^b	0.599	0.688	0.810	0.893	0.786	0.833	0.810
	D-MPNN + moe206		0.849 ± 0.042	0.567 ± 0.061	0.656 ± 0.044	0.800 ± 0.030	0.890 ± 0.023	0.786 ± 0.051	0.807 ± 0.037	0.796 ± 0.031
2^a	CardioTox	Test set-II	NA^b	0.452	0.947	0.755	0.455	0.600	0.909	0.754
	D-MPNN + moe206		0.810 ± 0.055	0.470 ± 0.053	0.950 ± 0.032	0.698 ± 0.022	0.467 ± 0.020	0.620 ± 0.030	0.909 ± 0.064	0.764 ± 0.030
3^a	CardioTox	Test set-III	NA^b	0.220	0.986	0.746	0.113	0.698	0.794	0.746
	D-MPNN + moe206		0.830 ± 0.010	0.214 ± 0.016	0.986 ± 0.037	0.696 ± 0.030	0.110 ± 0.006	0.692 ± 0.033	0.788 ± 0.064	0.740 ± 0.020

---

According to these comparative analyses, the D-MPNN + moe206 model the D-MPNN + moe206 model showed excellent AUC-ROC, accuracy, MCC, sensitivity, and NPV across different datasets given here, providing one of the best classification tools for predicting potential hERG-induced cardiotoxicity of compounds.

Feature importance with Shapley additive explanations

Why the moe206 descriptors can boost the performance of D-MPNN on predicting hERG blocker? To answer this question, we attempted to analyze the relationship between the moe206 descriptors and the predictive probability of the model through the Shapley additive translation (SHAP) (https://github.com/slundberg/shap),⁴² which would provide rich visualization of an individual feature. Lundberg et al.⁴² proposed SHAP as a unified measure of feature importance and incorporated their algorithm into extreme gradient boosting (XGBoost)⁴³ and Light Gradient Boosting Machine (LightTGBM) in subsequent studies.⁴⁴

We first evaluated the performance of XGBoost based on the moe206 descriptor and ECFP4 fingerprint on Cai's hERG dataset. The results showed that the AUC-ROC of XGBoost on moe206 descriptor is only slightly lower than that of D-MPNN + moe206 (0.950 ± 0.006 versus 0.956 ± 0.005) and significantly better than AUC-ROC of XGBoost on ECFP4 descriptor (0.950 ± 0.006 versus 0.933 ± 0.001) (Fig. 3A). This further confirmed the importance of the moe206 descriptor.

Fig. 3 (A) Comparative prediction performance of XGBoost with D-MPNN under random split through five-fold cross-validation on Cai's dataset. (B) Relative importance and the SHAP values of the 20 highest ranked molecular descriptors of XGBoost with moe206. Each molecule represents a point to form a descriptor line. A molecule with a high (red) SHAP value will increase the probability of being predicted by the model as a blocker.

Next, we did SHAP analysis on the moe206 descriptor. As shown in Fig. 3B, h_pavgQ, logP(o/w), SlogP, vsa_pol, h_logD, and h_pkB are considered to be the six most important descriptors of the model. The higher h_pavgQ, logP(o/w), SlogP and h_logD, and the lower vsa_pol and h_pkB (The list of descriptors is shown in Table S2†), the more likely it is to be predicted as a blocker. According to Honma's research,⁴⁵ positively charged atoms are the main distinguishing factor. Approximately 80% of hERG non-blockers do not have but more than half of the inhibitors contain at least one. The h_pavgQ at the top of the list not only reflects this feature but also reflects the superiority of the model in terms of feature selection. Similarly, the logP (o/w), SlogP and h_logD (ranked second, third and fifth) are related to Log octanol/water partition coefficient, representing those fat-soluble fragments or aromatic heterocycles in the blockers form a Π-stacking interaction with Phe-656 and Tyr-652,⁴⁶ vsa_pol is also related to the hydrophobicity to some extent. Regarding pK_b, on account of a number of hERG blockers have an aromatic ring at the end of the ligand and a basic amine, causing it to protonate readily at physiological pH and creating with cation–π interaction with Tyr652.⁴⁷ In short, the top-ranked descriptors are consistent with the characteristics reported in previous studies that most of the hERG blockers contained positively charged atom, more lipophilic, and more alkaline.^2,48

Discussion

In this study, we establish a series of hERG blocker classifiers based on D-MPNN. Although our model has achieved some relatively better predictive performance compared with previous studies, there are some limitations. The main limitation lies in the collection and selection of datasets.^35,49 Even larger, unbiased and high-quality datasets are required to train the D-MPNN + moe206 model.

Compared to D-MPNN without any descriptors, D-MPNN carries some descriptor prediction performance is even worse, some descriptor values may stay the same, or some descriptors are meaningless to reflect molecular characteristics, etc. It may be due to the fact that some descriptors cannot be used to classify blockers and non-blockers significantly, leading to ineffective work of deep learning, which requires us to intervene in the selection of descriptors. Thus, the complexity of the model is reduced and the generalization ability of the model is improved, and the computational resources and time are saved.⁵⁰

Conclusions

Cardiotoxicity is one of the common side effects of drugs in clinical practice. Since traditional detection methods are time-consuming and laborious, a variety of methods have emerged to establish models in in silico to predict hERG cardiotoxicity in recent years. In this study, we use D-MPNN to build the model based on different datasets, and screen difference descriptors incorporated into D-MPNN to further improve the performance. D-MPNN with moe206 descriptor was found performing better than with other descriptors. Its AUC-ROC value can reach 0.922 ± 0.015 under scaffold split and 0.956 ± 0.005 under random split on Cai's hERG dataset. In addition, we made a quite comprehensive comparison with 5 other recent models reported. All the results showed that the D-MPNN + moe206 model is among the best classification models for evaluating hERG blockers. In conclusion, this study provides a new approach for predicting compounds with potential hERG-induced cardiotoxicity.

Data availability

All datasets and the molecules with the binding data with this paper have been provided in All_datasets.zip file. The dataset used in the paper and script for reproducing these results, can be found at https://github.com/AI-amateur/DMPNN-hERG.

Author's contributions

M. S. and C. J. were the key contributor in drafting the manuscript, designing and conducting computation. J. C. took part in conceiving and directing the project. L.-P. Q., J.-J. Q. and G. C. analysed the results, reviewed and finalized the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Key R&D Program of China (2018YFC1706102) and the Zhejiang Chinese Medicinal University Foundation (2019ZG28).

Notes and references

1. M. C. Sanguinetti, C. Jiang, M. E. Curran and M. T. Keating, Cell, 1995, 81, 299–307.
2. M. C. Sanguinetti and M. Tristani-Firouzi, Nature, 2006, 440, 463–469.
3. Z. Zhou, V. R. Vorperian, Q. Gong, S. Zhang and C. T. January, J. Cardiovasc. Electrophysiol., 1999, 10, 836–843.
4. M. Roy, R. Dumaine and A. M. Brown, Circulation, 1996, 94, 817–823.
5. D. Rampe, M. L. Roy, A. Dennis and A. M. Brown, FEBS Lett., 1997, 417, 28–32.
6. A. Dorn, F. Hermann, A. Ebneth, H. Bothmann, G. Trube, K. Christensen and C. Apfel, J. Biomol. Screening, 2005, 10, 339–347.
7. Z. Yu, E. Klaasse, L. H. Heitman and A. P. Ijzerman, Toxicol. Appl. Pharmacol., 2014, 274, 78–86.
8. S. Stoelzle, A. Obergrussberger, A. Brueggemann, C. Haarmann, M. George, R. Kettenhofen and N. Fertig, Front. Pharmacol., 2011, 2, 76.
9. B. T. Priest, I. M. Bell and M. L. Garcia, Channels, 2008, 2, 87–93.
10. B. O. Villoutreix and O. Taboureau, Adv. Drug Delivery Rev., 2015, 86, 72–82.
11. M. R. Doddareddy, E. C. Klaasse, Shagufta, A. P. Ijzerman and A. Bender, ChemMedChem, 2010, 5, 716–729.
12. A. Cavalli, E. Poluzzi, F. De Ponti and M. Recanatini, J. Med. Chem., 2002, 45, 3844–3853.
13. S. Ekins, W. J. Crumb, R. D. Sarazan, J. H. Wikel and S. A. Wrighton, J. Pharmacol. Exp. Ther., 2002, 301, 427–434.
14. A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis, E. Cibrian-Uhalte, M. Davies, N. Dedman, A. Karlsson, M. P. Magarinos, J. P. Overington, G. Papadatos, I. Smit and A. R. Leach, Nucleic Acids Res., 2017, 45, D945–D954.
15. Y. Wang, S. H. Bryant, T. Cheng, J. Wang, A. Gindulyte, B. A. Shoemaker, P. A. Thiessen, S. He and J. Zhang, Nucleic Acids Res., 2017, 45, D955–D963.
16. M. K. Gilson, T. Liu, M. Baitaluk, G. Nicola, L. Hwang and J. Chong, Nucleic Acids Res., 2016, 44, D1045–D1053.
17. S. Q. Wang, H. Y. Sun, H. Liu, D. Li, Y. Y. Li and T. J. Hou, Mol. Pharm., 2016, 13, 2855–2866.
18. V. B. Siramshetty, Q. Chen, P. Devarakonda and R. Preissner, J. Chem. Inf. Model., 2018, 58, 1224–1233.
19. K. Ogura, T. Sato, H. Yuki and T. Honma, Sci. Rep., 2019, 9, 12220.
20. Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530.
21. C. Cai, P. Guo, Y. Zhou, J. Zhou, Q. Wang, F. Zhang, J. Fang and F. Cheng, J. Chem. Inf. Model., 2019, 59, 1073–1084.
22. J. Y. Ryu, M. Y. Lee, J. H. Lee, B. H. Lee and K. S. Oh, Bioinformatics, 2020, 36, 3049–3055.
23. H. Kim and H. Nam, Comput. Biol. Chem., 2020, 87, 107286.
24. V. B. Siramshetty, D. T. Nguyen, N. J. Martinez, N. T. Southall, A. Simeonov and A. V. Zakharov, J. Chem. Inf. Model., 2020, 60, 6007–6019.
25. A. Karim, M. Lee, T. Balle and A. Sattar, J. Cheminf., 2021, 13, 60.
26. K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388.
27. J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz, N. M. Donghia, C. R. MacNair, S. French, L. A. Carfrae, Z. Bloom-Ackermann, V. M. Tran, A. Chiappino-Pepe, A. H. Badran, I. W. Andrews, E. J. Chory, G. M. Church, E. D. Brown, T. S. Jaakkola, R. Barzilay and J. J. Collins, Cell, 2020, 180, 688–702.
28. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
29. J. L. Durant, B. A. Leland, D. R. Henry and J. G. Nourse, J. Chem. Inf. Comput. Sci., 2002, 42, 1273–1280.
30. https://web.cse.ohio-state.edu/∼zhang.10631/bak/drugreposition/list_fingerprints.pdf.
31. G. Landrum, RDKit: Open-Source Cheminformatics; 2006. https://rdkit.org/docs/index.html, accessed 2019-05-24.
32. S. Jaeger, S. Fulle and S. Turk, J. Chem. Inf. Model., 2018, 58, 27–35.
33. H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 4.
34. C. R. Corbeil, C. I. Williams and P. Labute, J. Comput.-Aided Mol. Des., 2012, 26, 775–786.
35. M. T. RibeiroS. Singh and C. Guestrin 2016 https://arxiv.org/abs/1602.04938.
36. W. X. Shen, X. Zeng, F. Zhu, Y. L. Wang, C. Qin, Y. Tan, Y. Y. Jiang and Y. Z. Chen, Nat. Mach. Intell., 2021, 3, 334–343.
37. B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Proc. IEEE, 2015, 104, 148–175.
38. S. Ounpraseuth, S. Y. Lensing, H. J. Spencer and R. L. Kodell, BMC Res. Notes, 2012, 5, 656.
39. S. Wang, Y. Li, J. Wang, L. Chen, L. Zhang, H. Yu and T. Hou, Mol. Pharm., 2012, 9, 996–1010.
40. C. Zhang, Y. Zhou, S. Gu, Z. Wu, W. Wu, C. Liu, K. Wang, G. Liu, W. Li, P. W. Lee and Y. Tang, Toxicol. Res., 2016, 5, 570–582.
41. H. Sun, R. Huang, M. Xia, S. Shahane, N. Southall and Y. Wang, Mol. Inf., 2017, 36.
42. S. Lundberg and S. I. Lee, 2017, abs/1705.07874.
43. T. Chen and C. Guestrin, 2016, abs/1603.02754.
44. S. M. Lundberg and S. I. Lee, 2017, abs/1706.06060.
45. T. Sato, H. Yuki, K. Ogura and T. Honma, PLoS One, 2018, 13, e0199348.
46. N. Levoin, O. Labeeuw, T. Calmels, O. Poupardin-Olivier, I. Berrebi-Bertrand, J. M. Lecomte, J. C. Schwartz and M. Capet, Bioorg. Med. Chem. Lett., 2011, 21, 5378–5383.
47. D. Fernandez, A. Ghanta, G. W. Kauffman and M. C. Sanguinetti, J. Biol. Chem., 2004, 279, 10120–10127.
48. L. L. Liu, J. Lu, Y. Lu, M. Y. Zheng, X. M. Luo, W. L. Zhu, H. L. Jiang and K. X. Chen, Acta Pharmacol. Sin., 2014, 35, 1093–1102.
49. P. Domingos, Commun. ACM, 2012, 55, 78–87.
50. G. Chandrashekar and F. Sahin, Comput. Electr. Eng., 2014, 40, 16–28.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07956e

‡ Those two authors contribute equally.

---