Donor moieties with D–π–a framing modulated electronic and nonlinear optical properties for non-fullerene-based chromophores

Abstract

Herein, a series of non-fullerene-based substantial chromophores (FHD1–FHD6) with a D–π–A framework was designed from a synthesized non-fullerene compound (FH) via structural tailoring with various donor moieties. The FH and its designed derivatives were optimized with frequency analysis at the M06/6-311G (d,p) level to confirm their true minima on potential energy surfaces. These optimized geometries were utilized to perform further analyses, such as absorption, natural bonding orbital (NBO), frontier molecular orbital (FMO), and nonlinear orbital (NLO) analyses at the aforesaid level. Quantum chemical study revealed that all the designed chromophores exhibited a lower band gap than that of the parent molecule with the exception of FHD3. Furthermore, density of states (DOS) analysis supported the findings from the FMO study, and this agreement revealed that the efficient charge was transferred from the HOMO to the LUMO. The NBO investigations disclosed that all the compounds comprised donor moieties with positive charges and acceptors having negative charges. Interestingly, π-conjugated linkers were also found with positive charges, showing an effective donating property. These NBO findings explicated that FHD1–FHD6 exhibited an efficient push–pull mechanism. The λ_max values of the designed chromophores were observed to be greater than the reference compound. The average polarizability 〈α〉, first hyperpolarizability (β_tot), and second hyperpolarizability 〈γ〉 values of FHD2 were found to be 2.170 × 10⁻²², 3.150 × 10⁻²⁷, and 4.275 × 10⁻³² esu, respectively, while all the other derivatives had been reported in the relevant range. Efficient NLO data revealed that FH-based derivatives may contribute significantly toward NLO technology.

---

Introduction

The promising optoelectronic properties of low-cost, facile-synthesized, fused-structured polycyclic aromatic hydrocarbons (PAHs) have been well explored by many researchers in recent years. These molecules (PAHs) are reported to have significant thermal stability and solubility with a facile synthetic procedure.¹ Although, research in PAHs has primarily been restricted to their synthesis and photoluminescence processes, it is currently being widened to organic electronics and frequently to their use as building block materials for opto-electronics.² Moreover, PAHs are also considered as promising scaffolds based on their various properties, including polarization, molecular wires, liquids crystals, organic electronics, and optical applications.³ A literature review revealed that different classes of polycyclic aromatic hydrocarbons have been computed and they have shown promising nonlinear optical (NLO) and electronic properties.^1–8 In fact, the above-mentioned materials have attracted attention for their strong two-photon absorption properties in recent years. Their absorption properties may be affected by their molecular weight, symmetry, and solubility parameters. Nowadays, an enormous amount of work is devoted to improving the absorption characteristics via employing the sophisticated approach of molecular designing.⁹ Organic compounds with extended π-conjugation displaying excellent NLO, fluorescence emission, and one-photon absorption are being extensively employed in two-photon photodynamic treatment,¹⁰ light-emitting diodes,¹¹ and 3D optical data storage.¹² The designed compounds with proper arrangements of π-conjugation play an important role in improving the NLO response, based on their expanded π-electronic delocalization and enhanced donor to acceptor intramolecular charge transfer via π-spacers.^6,13 The induction of conjugated electron acceptor and donor end groups unsymmetrically may extend their electron-accepting or -donating strength, leading to increased absorption. Their facile synthesis along with structural variation have established a decent core element in organic π-conjugation compounds utilized in NLO devices. These compounds with appropriate geometric structures, one/two-photon physical characteristics, energy levels, and thermodynamic properties have been investigated and have attained promising results, indicating that these compounds have potential as NLO optical materials.¹⁴

Organic materials with established NLO characteristics can enable the modeling of these molecules.¹⁵ Suitable donor, π-spacer, and acceptor parts with enhanced conjugation are needed for attaining the appealing architecture (D–π–A) of NLO materials.¹⁶ Compounds with good NLO properties have been designed based on theoretical/experimental investigations with the following points in focus: planar D–π–A system, bond length alternation approach, heterocyclic compounds auxiliary acceptors/donors model, and twisted π-electronic arrangements.^17,18 In view of the above methodology, NLO responses are simulated upon D or A strength optimization with conjugated bridge enhancement via π-spacer modification. These donor/acceptor electronic associations are sufficient to amplify the oscillator strength of transition matrix substance toward CT transition. Novel D–π–A based non-fullerene compounds were designed that showed a red-shifted absorption spectrum of the type used extensively in organic solar cell (OSC) devices. These acceptors (non-fullerene type) possess a D–π–A structure,^19–21 containing several intrinsic benefits, comprising broader absorption spectra as well as charge transportability.^19–21 The central part (π) and “D” and “A” moieties may play a key role in D–π–A kinds of molecules,²² and provides appropriate access to tune HOMO/LUMO computations and absorption by altering the central “D” or end group “A” moiety, either separately or all together in which the central “D” moiety performs a crucial role regarding the appropriate molecular packing and its morphology. There are numerous efficient approaches that can be employed to alter the donor D moiety to accomplish enhanced absorption, like conjugation length expansion along with π bridge blocks modifications.^23–27

Keeping in view the significant properties of non-fullerene compounds, the compound 2,2′-((2Z,2′Z)-((4,4,7,7,12,12-hexamethyl-7,12-dihydro-4H-thieno[2′′,3′′:1′,2′]indeno [5′,6′:5,6]-s-indaceno[1,2-b]thien-2,9-diyl)bis(methaneylylidene))bis(3-oxo-2,3-dihydro-1H-indene-2,1-diylidene))dimalononitrile (FH) was selected as a reference compound for our NLO study, whose synthetic procedure was reported by Nailiang et al. in 2020.² Such an NLO study for FH and its designed derivatives has not been performed so far. Therefore, a series of compounds named FHD1–FHD6 were designed using FH as the reference molecule. Subsequently, density functional theory (DFT)-based NLO calculations were performed for FH and FHD1–FHD6 for the first time. For the comprehensive understanding of the NLO properties of the aforementioned compounds, theoretical calculations, including the optimization, FMO, TDMs, binding energy (E_b), NBO, density of states (DOS), UV-Vis, and MEP, were performed at the M06 level with the 6-311G(d,p) basis set. The promising DFT-based findings were used to explore the novel designed compounds for their efficient NLO properties. It is expected that the current research work could pay a pivotal role for aiding theoretical as well as experimental researchers in the field of NLO-based technology.

Computational procedure

In this work, different types of electronic analyses, absorption spectra, and NLO parameters of non-fullerene chromophore (FH) and its derivatives were determined by utilizing DFT computations. The quantum chemical studies of the chromophores were performed at the M06/6-311G(d,p) level using the Gaussian 09 program package.²⁸ The NBO 3.1 program package was used for the natural bond orbital (NBO) analysis by applying the above-mentioned level of DFT and the same basis set.²⁹ Time-dependent density functional theory (TDDFT) computations were accomplished at the M06/6-311G (d, p) level for the FMO, MEP, TDM, and UV-Vis spectral investigations. Gauss view 6.0 was used for organizing the input files.³⁰ Moreover, for interpretation of the further results, Avogadro³¹ and Chemcraft³² were utilized. The dipole moment was determined by the following eqn (1).³³

μ = (μ_x²+ μ_y²+ μ_z²)^1/2 (1)

The average polarizability 〈α〉 was determined by eqn (2).³⁴

〈α〉 = 1/3(α_xx + α_yy + α_zz) (2)

Analysis of the Gaussian output file yielded 10 hyperpolarizability tensors as oriented along the x, y, and z directions: β_xxx, β_xyy, β_xzz, β_yyy, β_xxy, β_yzz, β_zzz, β_xxz, β_yyz, and β_xyz. The magnitude of the total first hyperpolarizability (β_tot) was calculated with the help of eqn (3).³⁵

β_total = [(β_xxx + β_xyy + β_xzz)² + (β_yyy + β_yzz + β_yxx)² + (β_zzz + β_zxx + β_xyz)²]^1/2 (3)

The second hyperpolarizability was determined by utilizing eqn (4).³³

〈γ〉 = 1/5[γ_xxxx + γ_yyyy + γ_zzzz +2(γ_xxxx + γ_yyyy + γ_zzzz)] (4)

Results and discussion

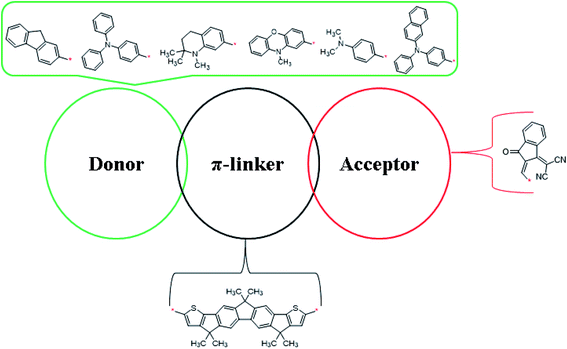
This quantum chemical study was performed for exploration of the NLO properties of non-fullerene chromophore (FH) and its derivatives. The reference chromophore consisted of an A–π–A architecture, and to a create strong push–pull mechanism in the derivatives one terminal acceptor unit was replaced with a donor moiety. By altering the axial donor (D) moieties while keeping the π-linkers and acceptor unit fixed, structural tailoring of all the designed compounds was performed. Therefore, the designed compounds consisted of: (a) (Z)-2-(2-ethylidene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile as the acceptor, (b) 3,3,6,6,10,10-hexamethyl-2,3,6,7,8,10-hexahydro-1H-dicyclopenta[b,h]fluorine as the π-linker, and (c) various donor moieties. The different donor moieties used in designing the compounds were: (i) 9H-fluorene, (ii) triphenylamine, (iii) 1,2,2-trimethyl-1,2,3,4-tetrahydroquinoline, (iv) 10-methyl-10H-phenothiazine, (v) 10-methyl-10H-phenoxazine, and (vi) N,N-diphenylnaphthale-2-amine, as shown in Scheme 1. The optimized structures of the compounds are shown in Fig. S1.†

Scheme 1 Sketch map of the designed compounds with different donor moieties.

The geometries of the chromophores were optimized with analyzing the vibrational frequencies employing the M06/6-311G (d,p) functional. The calculated bond lengths and bond angles are shown in Tables S8–S14.† For FH and FHD1–FHD6, the bond lengths of C1–C2, C1–C6, and C1–C15 were calculated as 1.413, 1.379, and 1.52 Å, respectively. These DFT values of C–C bond lengths were found to be in good agreement with the experimental values of C–C bond lengths.³⁶ Moreover, the bond lengths between the functional group atoms, such as C42–O43 and C50–N51, in FH and FHD1–FHD6 were obtained as 1.213 and 1.156 Å, respectively. All these simulated values of the C–O and C–N bond lengths were in good agreement with the experimentally determined values.³⁶ For the reference compound (FH), the bond angles of C29–C48–C49, C28–C42–O43, C7–C8–C58, and C20–C27–C34 were found to be 123°, 126°, 111°, and 135°, respectively. Moreover, the bond angles of C29–C48–C49, C28–C42–O43, and C7–C8–C58 were examined as 123°, 126°, and 111°, respectively, in all the designed compounds (FHD1–FHD6). The above-mentioned simulated bond angles were observed to be in good agreement with the literature values.³⁷ DFT-based calculations were performed using the optimized geometries of FH and FHD1–FHD6 for exploration of their important quantum chemical properties, such as linear polarizability, first and second hyperpolarizabilities, UV-Vis analysis, frontier molecular orbital (FMO), natural bond orbital (NBO), density of states (DOS), transition density matrix (TDMs), and molecular electrostatic potential (MEP) (Fig. 1).

Fig. 1 The 2D structures of FH and its derivatives.

Electronic structures

The frontier molecular orbital (FMO) theory is an effective tool for determination of the chemical stability, light absorbance, and optical and electronic properties of chromophores.^27,38 The electron-accepting property is determined by the LUMO, while the electron-donating property is determined by the HOMO. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecules orbital (LUMO) analysis plays a vital role in determining the UV-Vis spectra and different types of reaction mechanisms. The parameters for prediction of the chemical reactivity and dynamic stability of molecules can be determined by the HOMO–LUMO energy gap.³⁹ Molecules with a higher value of the HOMO–LUMO energy gap are regarded as chemically stable and may resist to chemical changes,⁴⁰ while molecules with a higher degree of softness are considered to have less stability and exhibit a low HOMO–LUMO energy.⁴¹ Moreover, molecules with a lower HOMO/LUMO energy gap usually show high polarizability and as a consequence yield a promising NLO response.⁴² The E_FMOs of FH and FHD1–FHD6 were calculated at the M06/6-311G (d,p) level of theory and their results are tabulated in Table 1. The other values, like E_HOMO−1, E_LUMO+1, E_HOMO−2, and E_LUMO+2, are collected in Table S15.†

Table 1 E_HOMO, E_LUMO, and energy gap (E_LUMO − E_HOMO) of the studied compounds^a

Compounds	LUMO	HOMO	Band gap
a Units of EHOMO, ELUMO, and energy gaps are shown in eV.
FH	−3.37	−5.930	2.560
FHD1	−3.214	−5.583	2.369
FHD2	−3.211	−5.425	2.214
FHD3	−3.212	−5.417	2.205
FHD4	−3.216	−5.533	2.317
FHD5	−3.212	−5.420	2.208
FHD6	−3.208	−5.515	2.307

---

The band gaps calculated for the reference chromophores was 2.560 eV with −5.930 and −3.37 eV, HOMO/LUMO energies. The data from Table 1 reveal that all the designed chromophores showed a comparable value of energy gap with the parent molecule. Nevertheless, the lowest energy difference between orbitals was seen in FHD3 (2.205 eV), which may be due to the 1,2,2-trimethyl-1,2,3,4-tetrahydroquinoline D moiety. The donor moiety in FHD3 has three electron-donating methyl (–CH₃) groups along with the right conjugation (benzene ring) for creating a strong electron-donating effect with a powerful push–pull architecture (D–π–A), hence leading to a reduction in the band gap. The increasing band gap order of the compounds was FHD3 < FHD5 < FHD2 < FHD6 < FHD4 < FHD1 < FH. The accompanying energies of the orbitals and charge-transfer phenomenon between the orbitals for the studied chromophores is also explained by the FMO investigation, as shown in Fig. 2. In the reference chromophore, the charge density for the HOMO was concentrated largely over the π-bridge and a smaller portion over some atoms of the terminal acceptor unit, while the LUMO was located all over the molecule. Nevertheless, in the derivatives for the HOMO, the electron density mostly occurred on the donor moieties and partially over the π-conjugated linkers. In the LUMO case, the electron density was almost totally presented over the acceptor moieties and a little bit on the π-linkers, which indicated an excellent transfer of charge from D toward A by the π-spacer.

Fig. 2 HOMOs and LUMOs of the studied compounds.

Density of states analysis

The delocalization of electrons exhibited in the HOMO and LUMO orbitals was also supported by a DOS investigation.⁴³ For the studied chromophores, the DOS investigations were performed at the M06/6-311G (d,p) functional and the resulting graphs are illustrated in Fig. 3. As presented in Fig. 2 and 3, charge spreading of the electronic cloud was altered around the LUMO and HOMO because of the strong push and electron withdrawing architecture of the derivatives. As the reference molecule has A–π–A, to understand the DOS, FH was divided into two parts, namely the acceptor and π-linkers, while due to the D–π–A configuration of the derivatives, they were divided into three parts: donor, π-linkers, and acceptor, which are shown by green, blue, and red lines, respectively, in the DOS maps.⁴⁴

Fig. 3 DOS plots of the reference FH and designed compounds.

In the reference compound FH, the acceptor contributes 24.6% to the HOMO and 62.7% for the LUMO. Similarly, π-linkers contributed 75.4% and 37.3% for the HOMO/LUMO, respectively. Among the derivatives, the acceptor contributions to the HOMO were 5.4%, 2.6%, 2.5%, 3.7%, 1.8%, and 3.9%, while the LUMO contributions were 62.7%, 49.6%, 65.9%, 65.8%, 62.3%, 66.0%, and 65.9% from FHD1–FHD6, respectively. In the same way, the π-linkers showed contributions of 68.2%, 40.6%, 40.4%, 68.1%, 50.2%, and 57.6% for the HOMO and 49.2%, 33.5%, 33.6%, 37.6%, 33.8%, and 33.9% for the LUMO from FHD1–FHD6, accordingly. These contributions show that the designing of different compounds by varying different efficient donor moieties play a significant role in the transmittance of the electronic charge in different ways. By these outcomes, it could be examined from the DOS graphs that the HOMOs of all the designed chromophores were largely concentrated on the donor and π-spacers as higher peaks of green and blue color, which were located at nearly −5.6 eV. Similarly, the LUMOs were significantly located on A and minorly on π-spacers in all the derivatives as higher peaks located near 6.5 eV, hence, these graphs significantly support the FMO diagrams (see Fig. 3 and 4). The DOS calculation showed that the charge was efficiently transferred from HOMO to LUMO in all the designed compounds from donor to acceptor through the π-spacers.

Fig. 4 TDM graphs of the studied compounds (FH and FHD1–FHD6).

UV-visible analyses

TD-DFT computations were carried out using the conductor-like polarizable continuum model (CPCM) model³⁴ in dichloromethane solvent at the M06 level with the 6-311G (d,p) basis set in order to have a better understanding of the absorption data.⁴⁵ All the UV-Visible based parameters of FH and FHD1–FHD6 are collected in Table 2, while the absorption spectra are displayed in Fig. S8.†

Table 2 Transition energies, maximum wavelengths, oscillator strengths, and transition contributions of the studied compounds^a

Compounds	DFT λ (nm)	E (eV)	fos	MO contributions
a Units in eV.
FH	650.46	1.91	3.25	H → L (92%)
FHD1	661.96	1.87	1.98	H → L (88%), H-1 → L (8%)
FHD2	683.22	1.81	1.71	H → L (83%), H-1 → L (13%)
FHD3	683.89	1.81	1.70	H → L (82%), H-1 → L (14%)
FHD4	661.60	1.87	1.86	H → L (78%), H-1 → L (16%)
FHD5	676.06	1.83	1.60	H → L (75%), H-1 → L (20%)
FHD6	669.24	1.85	1.81	H → L (80%), H-1 → L (13%)

---

The absorption data from the above table indicated that all the studied chromophores showed absorption in the visible region of the spectrum. The λ_max calculated for the reference molecule was 650.46 nm with 1.91 eV excitation energy. All the derivatives with D–π–A structures exhibited a higher value of the maximum absorption (661.60–683.89 nm) with a lower excitation energy (1.87–1.81 eV) than that of FH due to the strong push–pull configuration. Among the designed chromophores, the lowest values of λ_max were observed for FHD1 and FHD4 as 661.95 and 661.60 nm, with 1.97 and 1.86 f_os, respectively. These λ_max values were further enhanced to 669.24 nm with 1.816 f_os in FHD6 then 676.07 nm with 1.60 f_os in FHD5. Table 2 shows that FHD2 and FHD3 had the maximum red-shifted values at 683.89 nm with 1.70 f_os and 683.22 nm with 1.71 f_os, respectively, among all the designed novel compounds. This might be due to the presence of the benzene ring and three electron-donating (methyl) groups as the D moiety in FHD3 and TPA, which acts as an internal donor unit in a number of hole-transporting amorphous materials due to its significant electron-donating ability in FHD2. These strong D moieties create a strong architecture of pull–push mechanism, which lowers the band gap and broadens the absorption spectra, as shown in Fig. S8† and Table 2. Increased values of the wavelengths were found in the following order: FH < FHD4 < FHD1 < FHD6 < FHD5 < FHD2 < FHD3. A graph was plotted between the wavelengths and molar absorptivity constant values of the studied chromophores and is shown in Fig. S8.† Throughout, this study shows that the absorption spectra of all the designed compounds were obtained reasonably broader as compared to FH, indicating that the D–π–A architecture created a strong pull–push mechanism in the derivatives, which lowered the band gap and allows them to be exploited as promising NLO-active compounds.

Global reactivity parameters

Numerous reactivity parameters were calculated using eqn (S1)–(S7)† and they were determined by FMO study (Table 3).^46–49

Table 3 Computed global reactivity parameters of the studied compounds^a

Compounds	IP	EA	X	H	μ	ω	σ
a Units in Hartree (Eh).
FH	0.217	0.123	0.170	0.047	−0.170	0.310	10.629
FHD1	0.205	0.118	0.162	0.043	−0.161	0.300	11.486
FHD2	0.199	0.118	0.159	0.040	−0.158	0.309	12.291
FHD3	0.199	0.118	0.159	0.041	−0.158	0.310	12.340
FHD4	0.203	0.118	0.161	0.042	−0.161	0.303	11.744
FHD5	0.199	0.118	0.159	0.041	−0.159	0.310	12.324
FHD6	0.202	0.117	0.160	0.042	−0.160	0.303	11.795

---

The energy required to withdraw an electron from the HOMO orbital is equivalent to the ionization potential by which the electron-donating and -accepting abilities of an atom can be calculated.⁵⁰ The electronegativity is a chemical property by which the tendency of interaction of the electronic cloud coming toward an atom is expressed.⁴⁸ The chemical potential of a species helps in understanding the stability and reactivity of the compound. The above data revealed that all the studied chromophores exhibited higher values of ionization potential with lower electron-affinity values, which indicated their electron-acceptance nature. Further, the ionization potential, electron affinity, electronegativity, and global electrophilicity are also related to E_gap. Among all the chromophores, FHD3 exhibit the lowest value of ionization potential, which supported its low E_gap.

The global softness of a molecule refers to the extent of softness of a molecule and is inversely related to the bandgap, i.e. the smaller the bandgap, the softer the molecule will be in nature. Softness of the molecule can also be linked to its reactivity, as a lower bandgap is exhibited by soft molecules, hence their reactivity is greater.⁵¹ Polarizability can also be correlated to the softness, as soft molecules are considered as more polarized. Among the entire designed compounds, the largest value of the softness, i.e.12.340 E_h, was exhibited by FHD3, which showed maximum polarizability along its enhanced reactivity. This value of softness was reduced to 12.324 E_h in FHD5. Further drops in the value were observed in the case of FHD2, FHD6, and FHD4 of 12.291, 11.795, and 11.744 E_h, respectively. The bottom-most value of softness represents the least reactivity with less polarizability and was calculated in FHD1 (11.486 E_h). The decreased order of the softness as examined was: FHD3 > FHD5 > FHD2 > FHD6 > FHD4 > FHD1 > FH. Among all the compounds, the maximum value of hardness (0.047 E_h) was observed for FH, while the minimum value was found to be 0.040 E_h in FHD2. Similar to the hardness, the chemical potential value also seemed to decline in the same manner. Nevertheless, all the studied chromophores had a higher value of global softness (σ = 10.629–12.324 E_h) with the least global hardness (η = 0.040–0.042 E_h). These higher values of softness indicated the higher chemically reactivity of the studied molecules. From all this information, it can be interpreted that the designed chromophores might be active and have substantial NLO properties.

Natural bond orbital (NBO) analysis

Natural bonding orbital (NBO) analysis is frequently used to examine bond interactions and the intermolecular charge transfer (ICT) between orbitals.⁵² NBO is also used to predict the charge transfer between donor and acceptor moieties in D–π–A type organic compounds by calculating the natural charges.⁵³ Therefore, NBO calculations were performed at the M06/6-311G (d, p) level using the optimized structures of FH and FHD1–FHD6 and their results in terms of natural charges for the donor, π-spacer, and acceptor segments are tabulated in Table 4.

Table 4 NBO charges for the donor, π-spacer, and acceptor of the studied compounds

Compounds	Donors	π-Linkers	Acceptors
FHD1	0.0836	0.0736	−0.1572
FHD2	0.0880	0.0707	−0.1587
FHD3	0.0871	0.0715	−0.1587
FHD4	0.0764	0.0790	−0.1555
FHD5	0.0898	0.0674	−0.1572
FHD6	0.1085	0.0516	−0.1601

---

In FH, the acceptor, donor, and acceptor architecture exists, so the natural charges were calculated to be −0.1284, 0.2568, and −0.1284, respectively. The reference compound consisted of an A–D–A configuration, whereas the designed compounds were found to have an effective D–π–A configuration. From Table 4, it could be determined that the positive values of the donor moieties with regard to the NBO charges reveal that all the donors used for the studied compounds have excellent donor properties. Further, the acceptor moieties also have effective withdrawing capabilities in the studied compounds. Moreover, the π-conjugated linkers were determined to have positive values, which show their ability to facilitate charge transfer from the donor to acceptor moieties without any type of charge trapping. Among all the designed compounds, the highest positive value of donors was exhibited by FHD6 as 0.108508. This may be due to the π-electronic cloud and presence of naphthalene as a substituent on the D unit (amine, N,N-diphenylnaphthalen-2-amine). Furthermore, the detailed possible transitions were also calculated at the same level and the representative transitions of all the compounds are tabulated in Table 5.

Table 5 Natural bond orbital (NBO) based transitions of the studied compounds

Compounds	Donor(i)	Type	Acceptor(j)	Type	E^(2)
FH	C28–C30	π	C32–C53	π*	31.51
	C70–N71	π	C72–N73	π*	0.74
	C32–H33	σ	C30–S31	σ*	10.29
	C30–S31	σ	C30–C32	σ*	0.51
	S31	LP(2)	C28–C30	π*	22.51
	S31	LP(1)	C12–C21	σ*	1.05
FHD1	C24–C25	π	C31–C39	π*	32.47
	C50–N51	π	C48–N49	π*	0.77
	C31–H32	σ	C24–S27	σ*	10.41
	C86–H87	σ	C86–C88	σ*	0.51
	S27	LP(2)	C18–C20	π*	29.92
	S30	LP(1)	C12–C21	σ*	0.95
FHD2	C24–C25	π	C31–C39	π*	32.52
	C50–N51	π	C48–N49	π*	0.77
	C31–H32	σ	C24–S27	σ*	10.42
	S30–C85	σ	C22–C23	σ*	0.52
	S27	LP(2)	C	π*	29.93
	S30	LP(1)	C12–C21	σ*	0.95
FHD3	C24–C25	π	C31–C39	π*	32.54
	C44–O45	π	C31–C39	π*	0.74
	C31–H32	σ	C24–S27	σ*	10.44
	C113–H114	σ	C111–C113	σ*	0.50
	S27	LP(2)	C18–C20	π*	29.96
	S30	LP(1)	C12–C21	σ*	0.94
FHD4	C24–C25	π	C32–C40	π*	32.42
	C28–C30	π	C87–C88	σ*	0.74
	C32–H33	σ	C24–S27	σ*	10.42
	C84–N96	σ	C97–H100	σ*	0.5
	S27	LP(1)	C2–C18	σ*	29.96
	S101	LP(2)	C83–C89	π*	0.89
FHD5	C24–C25	π	C32–C40	π*	32.48
	C49–N50	π	C51–N52	π*	0.73
	C32–H33	σ	C24–S27	σ*	10.43
	C19–C73	σ	C73–H76	σ*	0.60
	N97	LP(1)	C84–C85	π*	36.44
	O96	LP(2)	C80–C81	σ*	0.68
FHD6	C24–C25	π	C32–C40	π*	32.62
	C51–N52	π	C49–N50	π*	0.76
	C32–H33	σ	C24–S27	σ*	10.45
	C96–H99	σ	C77–N88	σ*	0.51
	N88	LP(1)	C80–C81	π*	41.21
	N88	LP(1)	C79–C80	σ*	0.51

---

The detailed NBO transitions of the reference and designed compounds are also shown in Tables S16–S22.†

Some dormant π→π* interactions can be noted like: π(C28–C30)→π*(C32–C53), π(C24–C25)→π*(C31–C39), π(C24–C25)→π*(C31–C39), π(C24–C25)→π*(C31–C39), π(C24–C25)→π*(C32–C40), π(C24–C25)→π*(C32–C40) and π(C24–C25)→π*(C32–C40) having greater stabilization energies at 31.51, 32.47, 32.52, 32.54, 32.42, 32.48, and 32.62 kcal mol⁻¹ in FH–FHD6, respectively. Moreover, some other kinds of significant π→π* donor–acceptor intra-molecular charge-transfer (ICT) interplay were also studied, as shown in Tables S16–S22.† The lowest values of stabilization were determined as 0.74, 0.77, 0.77, 0.74, 0.74, 0.73, and 0.76 kcal mol⁻¹ for π (C70–N71)→π*(C72–N73), π(C50–N51)→π*(C48–N49), π(C50–N51)→π*(C48–N49), π(C44–O45)→π*(C31–C39), π(C28–C30)→π*(C87–C88), π(C49–N50)→π*(C51–N52), and π(C51–N52)→π*(C49–N50) transitions in FH–FHD1, respectively (see Tables S16–S22†).

In σ→σ* transitions, larger values of stabilization energies were found to be 10.29, 10.41, 10.42, 10.44, 10.42, 10.43, and 10.45 kcal mol⁻¹ for σ(C32–H33)→σ*(C30–S31), σ (C31–H32)→σ*(C24–S27), σ(C31–H32)→σ* (C24–S27), σ(C31–H32)→σ* (C24–S27), σ (C32–H33)→σ*(C24–S27), σ (C32–H33)→σ* (C24–S27), and σ (C32–H33)→σ* (C24–S27) interactions in FH–FHD6, respectively. Furthermore, some other transitions: σ(C30–S31)→σ*(C30–C32), σ(C86–H87)→σ*(C86–C88) σ(S30–C85)→σ*(C22–C23), σ(C113–H114)→σ*(C111–C113), σ(C84–N96)→σ*(C97–H100), σ(C19–C73)→σ*(C73–H76) and σ(C96–H99)→σ*(C77–N88) with the lowest stabilization energies of 0.51, 0.51, 0.52, 0.50, 0.50, 0.60, and 0.51 kcal mol⁻¹, respectively, were also obtained for FH–FHD6, as shown in Tables S16–S22.† These least energy values were seen due to the emergence of weak interaction between the accepter and donor moieties.

Similar kinds of interaction were also investigated in accordance with resonance. LP2(S31)→π*(C28–C30), LP2(S27)→π*(C18–C20), LP2(S27)→π*(C18–C20), LP2(S27)→π*(C18–C20), LP1(S27)→σ*(C2–C18), LP1(N97)→π*(C84–C85) and LP1(N88)→ π* (C80–C81) with high stabilization energies, i.e. 22.51, 29.92, 29.93, 29.96, 29.96, 36.44, and 41.21 kcal mol⁻¹ for FH–FHD6, respectively. On the other hand, LP1(S31)→σ*(C12–C21), LP1(S30)→σ*(C12–C2), LP1(S30)→σ*(C12–C2), LP1(S30)→σ*(C12–C2), LP2(S101)→ π*(C83–C89), LP2(O96)→σ*(C80–C81), and LP1(N88)→σ*(C79–C80) produced energies of 1.05, 0.95, 0.95, 0.95, 0.89, 0.68, and 0.51 kcal mol⁻¹, respectively which exhibited the lowest electron-donating interaction energies in FH–FHD6 (Tables S16–S22†). The studied chromophores had the highest stability in the span of 32.62 to 0.17 kcal mol⁻¹ for π→π* transitions owing to the extended hyper-conjugation. The increasing stability order of the compounds was noted as: FH < FHD4 < FHD1 < FHD5 < FHD2 < FHD3 < FHD6. All the designed compounds showed a greater stability than the reference compound (Table 5).

TDMs and exciton binding energy (E_b)

TDM analysis is used to determine the charge transfer from a donor to acceptor through a π-bridge.⁵⁴ TDM analysis of the studied chromophores was performed to investigate the behavior of the transitions, essentially from the ground state (S₀) to an excited state (S₁) and the interaction between the donor and acceptor units. For this purpose, the atoms were divided into segments according to their role, i.e. donor (D), π-bridge (π), and acceptor (A). Hydrogen atoms were neglected by default as they do not have much involvement in charge transfer. The TDM heat maps for FH and FHD1–FHD6 are shown in Fig. 4. The DTM heat maps showed the efficient diagonal charge transfer coherence in all the studied chromophores. The larger portion of the electronic cloud was located over the π-bridge, which then successfully transferred through the π-bridge to the acceptor unit, without charge trapping. These heat maps also supported the DOS and FMO investigations, where the same phenomenon of charge transfer was examined. The binding energy is a functional key factor to determine the optoelectronic properties of compounds. The lower the binding energy, the lower the coulombic forces between the hole and electron, in which the excited state provides enhanced exciton dissociation. Actually the binding energy is calculated by the difference between the HOMO–LUMO energy gap and the first exciton energy. The binding energy is calculated by eqn (5) and the results are tabulated in Table 6.

E_b = E_H–L − E_opt (5)

Table 6 The various calculated energies of the studied compounds (FH and FHD1–FHD6)

Compounds	EH–L (eV)	Eopt (eV)	Eb (eV)
FH	2.56	1.906	0.654
FHD1	2.369	1.873	0.496
FHD2	2.214	1.815	0.399
FHD3	2.205	1.812	0.393
FHD4	2.317	1.874	0.443
FHD5	2.208	1.833	0.375
FHD6	2.307	1.852	0.455

---

From Table 6, it is clear that the changing of the donor moieties plays a key role in the good binding energies. The binding energy of the reference compound was noted as 0.654 eV. The E_b values of compounds FHD1–FHD6 were 0.496, 1.497, 0.399, 0.393, 0.443, 0.375, and 0.455 eV, respectively. The binding energy values were noted to be in the increasing order of: FHD5 < FHD3 < FHD2 < FHD4 < FHD6 < FHD1 < FH. Note, molecules having an E_b lower than 1.9 eV are considered as perfect photonic materials with significant NLO responses. Interestingly, our studied chromophores exhibited binding energies smaller than 1.9 eV, illustrating them as perfect NLO materials.

Nonlinear optics (NLO)

NLO compounds are vastly used in the fields of optoelectronics and telecommunication. The optical properties of the molecules are characterized by their electronic analyses of the studied molecule, which supports the nonlinear response (hyperpolarizabilities:β and γ) and linear response (polarizability, α).⁵⁵ Moreover, NLO compounds have been extensively used in optical switches, signal processing, optical memory devices, and communication technology.⁵⁶ Here, the reference compound was reported originally with an A–D–A configuration, which showed a smaller NLO response compared to the designed compounds. The designed compounds (FHD1–FHD6) were found with D–π–A configuration, which was designed by the alteration of the donor moieties and exhibited an excellent push–pull architecture. The effective changes in the band gap and polarizability values were observed by the alternation of different donor moieties.

The electronegativity difference is an effective factor to produce the dipole moment in a molecule. The dipole moment (μ) is directly related with the polarity of a system. The greater the electronegative difference in the molecules, the larger will be the dipole moment values. The μ_total value of the reference compound (FH) was reported as 6.558 D, with tensor values along the x, y, and z axes of 0.0004, 6.5575, and 0.0014 D, respectively. Data from Table 7 show that all the derivatives expressed larger dipole moment values, which indicated that these chromophores have greater polarity than their parent molecule. Among the derivatives, the least value of μ_total was found as 9.352 D in FHD4, which increased to 10.203 and 10.846 D in FHD5 and FHD1, respectively. Further enhancements in the dipole moment were noted as 11.3051, 11.5731, and 13.3253 D in FHD3, FHD2, and FHD6, respectively. The dipole moment values of the investigated compounds were found in decreasing order as: FHD6 > FHD5 > FHD2 > FHD3 > FHD1 > FHD4 > FH (Table 7). Similarly, the linear polarizability 〈α〉 parameter is also considered to be a key factor to determine the electronic properties of organic compounds. For the FH, the value of 〈α〉 was found to be 2.270 × 10⁻²² esu with 4.511 × 10⁻²², 1.723 × 10⁻²², and 5.755 × 10⁻²³ esu along the α_xx, α_yy, and α_zz, respectively. All the designed chromophores exhibited comparable values of linear polarizability in the range of (1.886 × 10⁻²²–2.270 × 10⁻²² esu) with their parent compound. The FHD3 chromophore exhibited a larger value of linear polarizability [〈α〉 = 2.178 × 10⁻²² esu] among all the derivatives. The average polarizability in descending order of the investigated molecules was observed as: FH > FHD3 > FHD2 > FHD4 > FHD1 > FHD5 > FHD6.

Table 7 The computed dipole moment (μ), polarizability 〈α〉, second-order polarizabilities (β), and second-order hyper-polarizability 〈γ〉 of FH and FHD1–FHD6^a

Compounds	μtotal	〈α〉 × 10^−22	βtotal × 10^−27	〈γ〉 × 10^−32
a Units of the dipole moment (μ) in Debye (D) while 〈α〉, (β) and 〈γ〉 are in esu.
FH	6.558	2.270	1.689	3.111
FHD1	10.846	2.021	2.620	3.245
FHD2	11.573	2.170	3.150	4.275
FHD3	11.305	2.178	3.000	4.103
FHD4	9.352	2.053	2.576	3.133
FHD5	10.203	2.018	2.776	3.460
FHD6	13.325	1.886	2.592	2.893

---

Dipole polarizabilities have been found to be a quantitative estimation for assessing the attractive NLO features of species. For instance, the β_total and 〈γ〉 endorsed the estimation of the NLO response of the chromophores, which is then related with the ICT from the D moiety toward an A unit via π-linkers.⁵³ Such kind of interactions for our compounds are displayed in Fig. 2. The interaction of the electron density with the external field increased the dipole moment, resulting in increased first-order hyperpolarizability. The reference compound (FH) exhibited a value of β_total as 1.689 × 10⁻²⁷ esu, with the major contributing tensor values of β_xxx, β_xxy, β_yyz, β_xzz, β_yzz, and β_zzz as 5.841 × 10⁻³², −1.852 × 10⁻²⁸, −1.918 × 10⁻³³, −5.946 × 10⁻³⁵, 2.111 × 10⁻³¹, and −3.321 × 10⁻³⁴ esu., respectively. Interestingly all the designed chromophores expressed larger responses for the second-order polarizabilities (β) as compared to their parent compound. This might be due to that all our derivatives have a D–π–A configuration with a strong pull–push architecture as compared to the parent chromophore, which exhibited an A–π–A structure. This pull–push architecture might decrease the band gap between the orbitals, increase the polarity, and enhance the ICT. Among all the derivatives, a larger value of β_total was examined in FHD2 (3.150 × 10⁻²⁷ esu), which then decreased to 3.000 × 10⁻²⁷ esu in FHD3, and then declined to 2.776 × 10⁻²⁷ esu in FHD5 and further reduced to 2.620 × 10⁻²⁷ and 2.592 × 10⁻²⁷ esu in FHD1 and FHD6, respectively. The minimum value of β_total was studied in FHD4 as 2.576 × 10⁻²⁷ esu among all the derivatives. The hyperpolarizability (β) with a descending order for the investigated molecules was observed as: FHD2 > FHD3 > FHD5 > FHD6 > FHD1 > FHD4 > FH. The detailed values of the dipole moment, linear polarizability, and hyperpolarizability of all the compounds along the x, y, and z axes are tabulated in Tables S30 and S31.†

The second-order hyperpolarizability (γ) also plays an important role in NLO compounds. The reference compound (FH) showed a value of second-order hyperpolarizability as 3.111 × 10⁻³² esu, with tensor values of 3.095 × 10⁻³², 1.452 × 10⁻³⁴, and 6.125 × 10⁻³⁶ esu along the γ_xx, γ_yy, and γ_zz axes, respectively. Among all the studied compounds, the highest second-order hyperpolarizability was observed in FHD2 with tensors γ_xx, γ_yy, and γ_zz as 4.259 × 10⁻³², 1.467 × 10⁻³⁴, and 7.996 × 10⁻³⁶ esu, respectively. The lowest value of second-order hyperpolarizability was noted in FHD6 with tensor values of 2.884 × 10⁻³², 7.584 × 10⁻³⁵, and 9.571 × 10⁻³⁶ esu along the γ_xx, γ_yy, and γ_zz axes, respectively. The values of second-order hyperpolarizability (γ) with descending order of molecules was: FHD2 > FHD3 > FHD5 > FHD1 > FHD4 > FH > FHD6. All the tensors values of the second-order hyperpolarizability (γ) values of all the compounds are collected in Table S30.† A literature review disclosed that the energy gap value influences the polarizability. A smaller bandgap and higher polarizability are clearly associated with stronger hyperpolarizabilities, as evidenced by the substantial NLO values.³⁶ In our studied chromophores, an inverse relationship was observed between the bandgap and NLO response. Among the derivatives, larger values of first-order hyperpolarizability and second-order polarizability were examined in FHD5, FHD3, and FHD2 [(β_total = 2.77 × 10⁻²⁷, 3.00 × 10⁻²⁷, and 3.150 × 10⁻²⁷ esu) (〈γ〉 = 3.46 × 10⁻³², 4.103 × 10⁻³², and 4.275 × 10⁻³² esu)], which expressed a narrow band gap (2.208, 2.205, and 2.214, eV). The decrease in NLO values [(β_total = 2.620 × 10⁻²⁷, 2.576 × 10⁻²⁷, and 2.592 × 10⁻²⁷ esu) (〈γ〉 = 3.245 × 10⁻³², 3.133 × 10⁻³², and 2.893 × 10⁻³² esu)] was been noted as the band gap between orbitals was enhanced (2.369, 2.317, and 2.307 eV) in FHD1, FHD4, and FHD6, respectively.

Fantastically, it was also found that the designed chromophores exhibited a larger value of hyperpolarizability when compared with the standard para-nitroaniline (p-NA). The reported values for the first- and second-order hyperpolarizabilities were 6.46 × 10⁻³⁰ and 7.92 × 10⁻³⁶ esu, respectively.⁵⁷ Interestingly, in all our chromophores, the effective NLO behavior, as three-order magnitude for β_total and four-order magnitude for 〈γ〉, was investigated. This study concluded that by structural tailoring with efficient donor moieties, significant NLO materials could be obtained.

Molecular electrostatic potential (MEP)

MEP mapping is used to visualize the total electron density in a three dimensional framework of systems. The MEP plot performs quite well for its function to explain compound reactivity by predicting various electrophilic and nucleophile sites in chromophores.⁵⁸ The scope of the electrostatic potential in MEP maps is described by different standard colors, namely white (neutral), red (negative), and blue (positive), to denote the electrostatic potential regions,⁵⁹ and their pictorial demonstration is shown in Fig. 5.

Fig. 5 MEP diagrams of the reference FH and designed compounds FHD1–FHD6.

In all the studied chromophores, a negative potential was centered over the oxygen atoms, which can be seen in Fig. 5. The blue color is mainly seen over carbon and hydrogen atoms, signaling the nucleophiles can approach these locations. The green area, which is localized across hydrogen atoms, indicates the average of two absolute values of electrostatic potential (red and blue) and is situated over the S atom in the investigated compounds.

Conclusion

In the present work, a series of chromophores (FHD1–FHD6) with a D–π–A framework was designed via varying the donor moieties consisting of promising electron-donating properties and a fixed π-bridge as well as acceptor groups. The obtained electronic properties showed that the donors have a positive effect on the D–π–A architectures, changing the intact properties of the designed molecules more than the synthetic compound. According to FMO analyses, HOMOs were found over the donor group and its neighboring π-linker, whereas LUMOs were found over the acceptors in all the compounds. The HOMO–LUMO energy gap was reduced from 2.369 eV to 2.205 eV for FHD1–FHD6, respectively. The HOMO–LUMO energy gap of FHD3 was found as 2.205 eV, which was the least among the designed derivatives. DOS and TDM investigations supported the FMO study as a significant ICT was found from the D moiety toward the A unit through the π-spacer. The NBO findings exploited a strong push–pull architecture in the designed chromophores as the donor and π-conjugates expressed positive values, while all the acceptors exhibited negative values. Moreover, the NBO study also revealed that the conjugation in the molecules led to a greater stability of the systems. Incredibly, lower binding energies (0.375–0.496 eV) with greater μ_total (6.558–13.325 D) and global softness (σ = 10.630–12.340 E_h) for the studied molecules were obtained, which predicted higher excitation, dissociation, and larger polarity. Interestingly, significant NLO findings as 〈α〉, β_tot, and 〈γ〉 values were found as 2.170 × 10⁻²², 3.150 × 10⁻²⁷, and 4.275 × 10⁻³² esu, respectively, for FHD2, which were greatest among all the studied chromophores. We can conscript the promising capabilities of our designed compounds for indicating a better NLO response. The FHD1–FHD6 derivatives may attract the attentions of researchers in terms of use in new synthetic approaches. Moreover, from our above-mentioned analyses, it can be concluded that the aforementioned D–π–A based organic NLO compounds may have promising applications in the NLO field.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research work was funded by Institutional Fund Projects under grant no (IFPRC-102-130-2020). Therefore, authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdul aziz University, Jeddah, Saudi Arabia.

References

1. Y. Wang, G. S. He, P. N. Prasad and T. Goodson, Ultrafast dynamics in multibranched structures with enhanced two-photon absorption, J. Am. Chem. Soc., 2005, 127, 10128–10129.
2. F.-X. Wang, M.-H. Chen, X.-Y. Hu, R.-R. Ye, C.-P. Tan, L.-N. Ji and Z.-W. Mao, Ester-modified cyclometalated iridium (III) complexes as mitochondria-targeting anticancer agents, Sci. Rep., 2016, 6, 1–15.
3. G. Walters, B. R. Sutherland, S. Hoogland, D. Shi, R. Comin, D. P. Sellan, O. M. Bakr and E. H. Sargent, Two-photon absorption in organometallic bromide perovskites, ACS Nano, 2015, 9, 9340–9346.
4. E. Walker and P. M. Rentzepis, A new dimension, Nat. Photonics, 2008, 2, 406–408.
5. R. Liu, M. Shu, J. Hu, S. Zhu, H. Shi and H. Zhu, Star-shaped D-π-A compounds with a 1, 3, 5-triazine core and N-aryl chromophore substituted fluorene arms: synthesis, aggregation induced emission and two-photon absorption, Dyes Pigm., 2017, 137, 174–181.
6. T.-C. Lin, Y.-H. Lee, B.-R. Huang, M.-Y. Tsai and J.-Y. Lin, Functionalized tetrafluorenylethylene-type chromophores: Synthesis, two-photon absorption and effective optical power-limiting properties in the visible-to-near IR region, Dyes Pigm., 2016, 134, 325–333.
7. P. Zhou, C. Zhong, X. Chen, J. Qin, I. s. Mariz and E. Maçôas, New kind of hyperbranched conjugated polymers containing alkyl-modified 2, 4, 6-Tris (thiophen-2-yl)-1, 3, 5-triazine unit for enhancing two-photon absorption, Macromolecules, 2014, 47, 6679–6686.
8. A. Qin, J. W. Lam, H. Dong, W. Lu, C. K. Jim, Y. Dong, M. Häussler, H. H. Sung, I. D. Williams and G. K. Wong, Metal-free, regioselective diyne polycyclotrimerization: Synthesis, photoluminescence, solvatochromism, and two-photon absorption of a triphenylamine-containing hyperbranched poly (aroylarylene), Macromolecules, 2007, 40, 4879–4886.
9. M. G. Vivas, D. L. Silva, J. Malinge, M. Boujtita, R. Zaleśny, W. Bartkowiak, H. Ågren, S. Canuto, L. De Boni and E. Ishow, Molecular structure–optical property relationships for a series of non-centrosymmetric two-photon absorbing push-pull triarylamine molecules, Sci. Rep., 2014, 4, 1–11.
10. X. Liu, J. Liang, J. You, L. Ying, Y. Xiao, S. Wang and X. Li, Small molecular hole-transporting and emitting materials for hole-only green organic light-emitting devices, Dyes Pigm., 2016, 131, 41–48.
11. R. Chennoufi, H. Bougherara, N. Gagey-Eilstein, B. Dumat, E. Henry, F. Subra, S. Bury-Moné, F. Mahuteau-Betzer, P. Tauc and M.-P. Teulade-Fichou, Mitochondria-targeted triphenylamine derivatives activatable by two-photon excitation for triggering and imaging cell apoptosis, Sci. Rep., 2016, 6, 1–12.
12. B. H. Cumpston, S. P. Ananthavel, S. Barlow, D. L. Dyer, J. E. Ehrlich, L. L. Erskine, A. A. Heikal, S. M. Kuebler, I.-Y. S. Lee and D. McCord-Maughon, Two-photon polymerization initiators for three-dimensional optical data storage and microfabrication, Nature, 1999, 398, 51–54.
13. Z.-M. Tang, T. Lei, J.-L. Wang, Y. Ma and J. Pei, Star-shaped donor-π-acceptor conjugated molecules: synthesis, properties, and modification of their absorptions features, J. Org. Chem., 2010, 75, 3644–3655.
14. Z. Zhou, H. W. Qiao, Y. Hou, H. G. Yang and S. Yang, Epitaxial halide perovskite-based materials for photoelectric energy conversion, Energy Environ. Sci., 2021, 14, 127–157.
15. M.-S. Yuan, Q. Wang, W.-J. Wang, T.-B. Li, L. Wang, W. Deng, Z.-t. Du and J.-R. Wang, Symmetrical and asymmetrical (multi) branched truxene compounds: Structure and photophysical properties, Dyes Pigm., 2012, 95, 236–243.
16. S. A. Siddiqui, T. Rasheed, M. Faisal, A. K. Pandey and S. B. Khan, Electronic structure, nonlinear optical properties, and vibrational analysis of gemifloxacin by density functional theory, Spectroscopy, 2012, 27, 185–206.
17. L. Shi, M. Horn, S. Kobayashi and H. Mayr, Carbocationic n-endo-trig Cyclizations, Chem.–Eur. J., 2009, 15, 8533–8541.
18. F. Meyers, S. Marder, B. Pierce and J.-L. Bredas, Electric field modulated nonlinear optical properties of donor-acceptor polyenes: sum-over-states investigation of the relationship between molecular polarizabilities (alpha, beta, and gamma) and bond length alternation, J. Am. Chem. Soc., 1994, 116, 10703–10714.
19. W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, Molecular optimization enables over 13% efficiency in organic solar cells, J. Am. Chem. Soc., 2017, 139, 7148–7151.
20. D. He, F. Zhao, J. Xin, J. J. Rech, Z. Wei, W. Ma, W. You, B. Li, L. Jiang and Y. Li, A fused ring electron acceptor with decacyclic core enables over 13.5% efficiency for organic solar cells, Adv. Energy Mater., 2018, 8, 1802050.
21. C. Huang, X. Liao, K. Gao, L. Zuo, F. Lin, X. Shi, C.-Z. Li, H. Liu, X. Li and F. Liu, Highly efficient organic solar cells based on S, N-heteroacene non-fullerene acceptors, Chem. Mater., 2018, 30, 5429–5434.
22. Y. Chen, X. Wan and G. Long, High performance photovoltaic applications using solution-processed small molecules, Acc. Chem. Res., 2013, 46, 2645–2655.
23. W. Ni, M. Li, F. Liu, X. Wan, H. Feng, B. Kan, Q. Zhang, H. Zhang and Y. Chen, Dithienosilole-based small-molecule organic solar cells with an efficiency over 8%: investigation of the relationship between the molecular structure and photovoltaic performance, Chem. Mater., 2015, 27, 6077–6084.
24. S. Dai, F. Zhao, Q. Zhang, T.-K. Lau, T. Li, K. Liu, Q. Ling, C. Wang, X. Lu and W. You, Fused nonacyclic electron acceptors for efficient polymer solar cells, J. Am. Chem. Soc., 2017, 139, 1336–1343.
25. H. Feng, Y. Q. Q. Yi, X. Ke, J. Yan, Y. Zhang, X. Wan, C. Li, N. Zheng, Z. Xie and Y. Chen, New anthracene-fused nonfullerene acceptors for high-efficiency organic solar cells: energy level modulations enabling match of donor and acceptor, Adv. Energy Mater., 2019, 9, 1803541.
26. J. Wang, J. Zhang, Y. Xiao, T. Xiao, R. Zhu, C. Yan, Y. Fu, G. Lu, X. Lu and S. R. Marder, Effect of isomerization on high-performance nonfullerene electron acceptors, J. Am. Chem. Soc., 2018, 140, 9140–9147.
27. T. Li, S. Dai, Z. Ke, L. Yang, J. Wang, C. Yan, W. Ma and X. Zhan, Fused Tris (thienothiophene)-Based Electron Acceptor with Strong Near-Infrared Absorption for High-Performance As-Cast Solar Cells, Adv. Mater., 2018, 30, 1705969.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
29. M. Khalid, H. M. Lodhi, M. U. Khan and M. Imran, Structural parameter-modulated nonlinear optical amplitude of acceptor–π–D–π–donor-configured pyrene derivatives: a DFT approach, RSC Adv., 2021, 11, 14237–14250.
30. R. Dennington, T. A. Keith and J. M. Millam, GaussView, version 6.0. 16, Semichem Inc. Shawnee Mission KS, 2016.
31. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 1–17.
32. G. Zhurko and D. Zhurko, ChemCraft, version 1.6, URL: http://www.chemcraftprog.com, 2009.
33. C. Valverde, S. A. d. L. e Castro, G. R. Vaz, J. L. de Almeida Ferreira, B. Baseia and F. A. Osório, Third-order nonlinear optical properties of a carboxylic acid derivative, Acta Chim. Slov., 2018, 65, 739–749.
34. V. Barone and M. Cossi, Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model, J. Phys. Chem. A, 1998, 102, 1995–2001.
35. Ö. Tamer, D. Avcı and Y. Atalay, Synthesis, X-Ray crystal structure, photophysical characterization and nonlinear optical properties of the unique manganese complex with picolinate and 1, 10 phenantroline: toward the designing of new high NLO response crystal, J. Phys. Chem. Solids, 2016, 99, 124–133.
36. M. Khalid, A. Ali, M. F. U. Rehman, M. Mustaqeem, S. Ali, M. U. Khan, S. Asim, N. Ahmad and M. Saleem, Exploration of noncovalent interactions, chemical reactivity, and nonlinear optical properties of piperidone derivatives: a concise theoretical approach, ACS Omega, 2020, 5, 13236–13249.
37. M. Adnan, M. Y. Mehboob, R. Hussain and Z. Irshad, Banana-Shaped Nonfullerene Acceptor Molecules for Highly Stable and Efficient Organic Solar Cells, Energy Fuels, 2021, 11496–11506.
38. P.-H. Sung and T.-F. Hsu, Thermal stability of NLO sol—gel networks with reactive chromophores, Polymer, 1998, 39, 1453–1459.
39. M. I. Nan, E. Lakatos, G.-I. Giurgi, L. Szolga, R. Po, A. Terec, S. Jungsuttiwong, I. Grosu and J. Roncali, Mono-and di-substituted pyrene-based donor-π-acceptor systems with phenyl and thienyl π-conjugating bridges, Dyes Pigm., 2020, 181, 108527.
40. M. Yoshida and J.-i. Aihara, Validity of the weighted HOMO–LUMO energy separation as an index of kinetic stability for fullerenes with up to 120 carbon atoms, Phys. Chem. Chem. Phys., 1999, 1, 227–230.
41. R. Hussain, F. Hassan, M. U. Khan, M. Y. Mehboob, R. Fatima, M. Khalid, K. Mahmood, C. J. Tariq and M. N. Akhtar, Molecular engineering of A–D–C–D–A configured small molecular acceptors (SMAs) with promising photovoltaic properties for high-efficiency fullerene-free organic solar cells, Opt. Quantum Electron., 2020, 52, 1–20.
42. D. Dini and M. Hanack, Phthalocyanines as materials for advanced technologies: some examples, J. Porphyrins Phthalocyanines, 2004, 8, 915–933.
43. M. Khalid, I. Shafiq, M. Zhu, M. U. Khan, Z. Shafiq, J. Iqbal, M. M. Alam, A. A. C. Braga and M. Imran, Efficient tuning of small acceptor chromophores with A1-π-A2-π-A1 configuration for high efficacy of organic solar cells via end group manipulation, J. Saudi Chem. Soc., 2021, 25, 101305.
44. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
45. M. U. Khan, M. Khalid, M. Ibrahim, A. A. C. Braga, M. Safdar, A. A. Al-Saadi and M. R. S. A. Janjua, First theoretical framework of triphenylamine–dicyanovinylene-based nonlinear optical dyes: structural modification of π-linkers, J. Phys. Chem. C, 2018, 122, 4009–4018.
46. M. Khalid, A. Ali, R. Jawaria, M. A. Asghar, S. Asim, M. U. Khan, R. Hussain, M. F. ur Rehman, C. J. Ennis and M. S. Akram, First principles study of electronic and nonlinear optical properties of A–D–π–A and D–A–D–π–A configured compounds containing novel quinoline–carbazole derivatives, RSC Adv., 2020, 10, 22273–22283.
47. R. G. Parr, L. v. Szentpály and S. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121, 1922–1924.
48. R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, Electronegativity: the density functional viewpoint, J. Chem. Phys., 1978, 68, 3801–3807.
49. N. Kovačević and A. Kokalj, Analysis of molecular electronic structure of imidazole-and benzimidazole-based inhibitors: a simple recipe for qualitative estimation of chemical hardness, Corros. Sci., 2011, 53, 909–921.
50. R. G. Parr, L. v. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
51. H. Chermette, Chemical reactivity indexes in density functional theory, Journal of computational chemistry, 1999, 20, 129–154.
52. S. Tariq, M. Khalid, A. R. Raza, S. L. Rubab, S. F. de Alcântara Morais, M. U. Khan, M. N. Tahir and A. A. C. Braga, Experimental and computational investigations of new indole derivatives: A combined spectroscopic, SC-XRD, DFT/TD-DFT and QTAIM analysis, J. Mol. Struct., 2020, 1207, 127803.
53. M. Ahn, M.-J. Kim, D. W. Cho and K.-R. Wee, Electron Push–Pull Effects on Intramolecular Charge Transfer in Perylene-Based Donor–Acceptor Compounds, J. Org. Chem., 2020, 86, 403–413.
54. G. Dennler, M. C. Scharber, T. Ameri, P. Denk, K. Forberich, C. Waldauf and C. J. Brabec, Design Rules for Donors in Bulk-Heterojunction Tandem Solar Cells Towards 15% Energy-Conversion Efficiency, Adv. Mater., 2008, 20, 579–583.
55. B. S. Mendis and K. N. de Silva, A comprehensive study of linear and non-linear optical properties of novel charge transfer molecular systems, J. Mol. Struct.: THEOCHEM, 2004, 678, 31–38.
56. H. S. Nalwa, T. Watanabe, S. Miyata and J. Rabek, Optical second-harmonic generation in organic molecular and polymeric materials: measurement techniques and materials, Progress in Photochemistry and Photophysics, 1992, 5, 103–185.
57. S. Muhammad, R. A. Shehzad, J. Iqbal, A. G. Al-sehemi, M. Saravanabhavan and M. Khalid, Benchmark study of the linear and nonlinear optical polarizabilities in proto-type NLO molecule of para-nitroaniline, J. Theor. Comput. Chem., 2019, 18, 1950030.
58. M. Akram, M. Adeel, M. Khalid, M. N. Tahir, M. U. Khan, M. A. Asghar, M. A. Ullah and M. Iqbal, A combined experimental and computational study of 3-bromo-5-(2, 5-difluorophenyl) pyridine and 3, 5-bis (naphthalen-1-yl) pyridine: Insight into the synthesis, spectroscopic, single crystal XRD, electronic, nonlinear optical and biological properties, J. Mol. Struct., 2018, 1160, 129–141.
59. F. J. Luque, J. M. López and M. Orozco, Perspective on “Electrostatic interactions of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects”, Theor. Chem. Acc., 2000, 103, 343–345.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07183a

---