Role of imine isomerization in the stereocontrol of the Staudinger reaction between ketenes and imines

Abstract

Computational–experimental analysis has allowed determining that the stereochemistry of the Staudinger reaction between ketenes and imines is strongly associated with the nature of the imine, which affects the two steps of the reaction. The first step, namely the nucleophilic attack of the sp²-hybridized nitrogen atom of the imine on the sp-hybridized carbon atom of the ketene, is affected by the energetically accessible in situ isomerization patterns of the imine. The second step consists of a conrotatory electrocyclization of the zwitterionic intermediate formed in the previous step. This latter pericyclic step depends on the inward/outward torquoelectronic effects generated by the substituents of the imine. The impact of these factors on the stereochemistry of this reaction has been analyzed kinetically by numerical methods. The results of these simulations are compatible with the experimental results and support these conclusions.

---

Introduction

Since its discovery in 1907 (ref. 1) the Staudinger reaction between ketenes and imines has been one of the most useful methods for the convergent and stereocontrolled synthesis of β-lactams² and other valuable compounds³ of biological interest. The versatility of this important reaction is increased by using ketene precursors such as acyl chlorides⁴ or diazo ketones⁵ (Scheme 1). Aside from its practical interest, this reaction is also important from the mechanistic standpoint. As Tidwell⁶ has written, “cycloaddition has remained as the most distinctive, useful and intellectually challenging aspect of ketene chemistry”. In particular, the Staudinger reaction between ketenes and imines constitutes an example of a low energy [2 + 2] thermal cycloaddition, a process for which the least motion supra–supra approach is symmetry forbidden.⁷ Actually, in this process the reactants can avoid the orbital symmetry allowed but geometrically demanding [π₂s + π₂a] thermal pathway by means of a stepwise mechanism.⁸ Thus, the commonly accepted mechanism of the Staudinger reaction involves a sequential formation of the N1–C2 and C3–C4 covalent bonds of the β-lactam ring, according to the reaction path shown in Scheme 1.⁹

Scheme 1 The general mechanism of the Staudinger reaction between ketenes and imines. The possible substituents at the different positions are not shown.

The first step of the reaction consists of a nucleophilic attack of the imine nitrogen on the sp-hybridized carbon atom of the ketene to form, via transition structure TS1, a zwitterionic intermediate denoted as INT in Scheme 1. From this intermediate, the cycloadduct is formed by a conrotatory ring closure associated with transition structure TS2 that can be viewed as an intramolecular Mannich-type reaction of the enolate moiety on the electrophilic iminium part (Scheme 1).^8a

However, it is important to note that the intramolecular nature of this second step and the contributions of the frontier orbitals of the intermediate INT result in a conrotatory motion in the resulting transition structure TS2. Therefore, this latter step of the reaction is subjected to torquoelectronic effects.¹⁰

A major issue of this reaction is the variable stereocontrol achieved depending upon the nature of the substituents or the reaction conditions.¹¹ In 2006, a systematic experimental study on the stereochemistry of the Staudinger reaction was reported by Xu and coworkers.¹² In this important work, formation of trans-cycloadducts was rationalized in terms of rotation about the N1–C4 bond in the corresponding intermediates. This mechanism was also postulated by some of us to understand the formation of trans-4-alkoxy-β-lactams in the Staudinger reaction between ketenes and imidates.¹³ In subsequent papers, Xu et al. explored this mechanism experimentally in photochemical¹⁴ and computationally in thermal Staudinger reactions¹⁵ as well as in closely related sulfa-Staudinger (2 + 2)-cycloadditions.¹⁶

It was reported that the reaction of imines derived from polycyclic aromatic amines and aryloxy ketenes yields exclusively the corresponding trans-cycloadducts instead of the cis-cycloadducts usually found in the reaction between alkoxyketenes and imines derived from substituted anilines.¹⁷ A computational study¹⁸ was performed on these reactions showing that the kinetic distribution in the cis : trans ratio of the corresponding β-lactams can be understood in terms of the initial E/Z isomerization of the starting imines.

Within this context, the aim of the present work is to extend previous experimental-computational studies to different substituents at the three possible positions of the β-lactam ring in order to assess the general character of the previously proposed mechanism by searching computationally all the possible intermediates and transition structures. As relevant case studies we selected ketenes 1a,b and imines 2a–d (Scheme 2). These reagents possess different geometric and electronic features that can shed some light on the factors that determine the stereochemical outcome of this important, but still challenging, reaction. In this work, we confirm the complex nature of the Staudinger reaction in terms of the relevance of the E/Z isomerization of the starting imine, which competes with a similar isomerization in the zwitterionic intermediates. Ultimately, the origins of the cis/trans selectivity of these reactions can be connected with the imine E/Z isomerization.

Scheme 2 Ketenes and imines included in the present study. The corresponding (2 + 2) β-lactam cycloadducts 3 are indicated in Scheme 3.

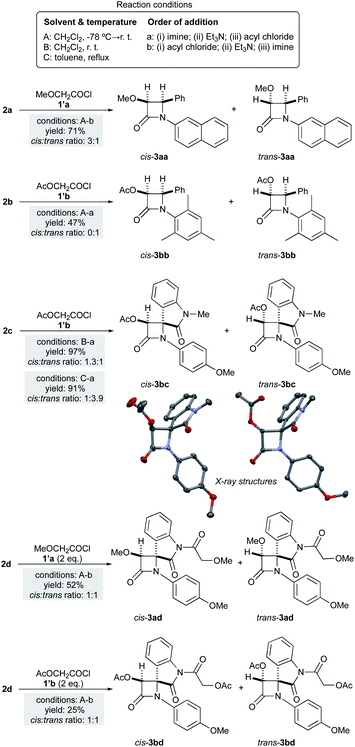
Results and discussion

We first studied the reaction between methoxy- or acetoxyacetyl ketene (1a,b respectively) and (E)-N-2-naphthyl imine 2a, (E)-N-mesityl imine 2b and aryliminoindolones 2c,d. These ketenes were generated in situ from the corresponding methoxyacetyl and acetoxyacetyl chlorides, 1′a and 1′b, respectively (Scheme 3). Different reaction conditions were considered. Given the stepwise nature of the reaction mechanism and the presence of zwitterionic intermediates, dichloromethane at −78 °C → rt (method A) or at room temperature (method B), as well as less polar toluene (method C) were tested. Concerning the order of addition of the reagents, two different protocols were considered: the “imine-first” sequence (method a) and the “acyl chloride-first” protocol (method b). The combination of these reaction conditions should provide information about the in situ generation of the ketene and its reaction with the corresponding imine. The reaction conditions and observed stereochemical outcomes of these reactions are gathered in Scheme 3.

Scheme 3 Staudinger reactions between ketenes 1a,b (generated from the corresponding acyl chlorides 1′a,b) and Schiff bases 2a–d under different conditions. X-ray diffraction structures of cis- and trans-3bc are also given.

As far as (E)-N-2-naphthyl imine 2a is concerned, the reaction yields a 3 : 1 racemic cis- and trans-3aa mixture of isolated diastereoisomers under the A-b protocol. This result complements the trans-preference previously observed in the reaction between methoxyketene 1a and (E)-N-1-naphthyl phenyl imine.¹⁸ In addition, the reaction of acetoxyacetyl ketene 1b and (E)-N-mesityl imine 2b in refluxing toluene under the “imine-first” protocol yields exclusively trans-3bb. In the case of the reaction of acetoxyacetyl ketene 1b and aryliminoindolone 2c, the proportion of cis–trans-products strongly depends on the solvent and reaction temperature used. In that case, cis-3bc is the observed major product (1.3 : 1) when the reaction is carried out at low temperature. Moreover, an increase in the reaction temperature favors the formation of trans-3bc (1 : 3.9). The stereochemistry of racemic cis- and trans-3bc were confirmed by X-ray diffraction analysis.¹⁹ Isatine-derived imine 2d yielded complex reaction mixtures upon reaction with methoxyacetyl chloride under different reaction conditions listed in Scheme 3 as A-b. The corresponding 2-azetidinones could be detected in these reaction mixtures as by-products. Being aware that the amide indolone may interfere with the Staudinger reaction by consuming acid chloride and forming species that may compete with the 2-azetidinone formation, we carried out the reaction of imine 2d with an excess (2.2 equivalents per equivalent of imine) of acid chloride. Under these conditions, excellent yields of the corresponding 2-azetidinones having the isatine amide nitrogen acylated were isolated as 1 : 1 cis–trans mixtures in both cases (Scheme 3). Thus, under the A-b protocol, equimolar ratios of both cis- and trans-3ad,bd cycloadducts were obtained, confirming the low stereocontrol of these Staudinger reactions leading to 4-spiro-β-lactams. Interestingly, an increase of the proportion of the trans-β-lactam 3bc was observed when toluene was used as solvent (C-a conditions, Scheme 3), instead of more polar dichloromethane (B-a conditions).

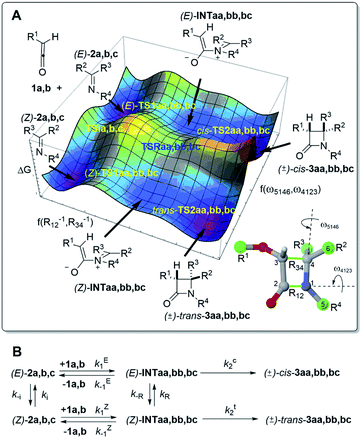
To understand the origins of this stereocontrol, we have performed DFT calculations on the 1a + 2a → 3aa, 1b + 2b → 3bb and 1b + 2c → 3bc reactions at the M06-2X(PCM)/def2-TZVPP level of theory. We have explored the potential energy surfaces associated with all the possible intermediates and transition structures of Staudinger reactions between imines 2a–c and ketenes 1a,b leading to cis- and trans-cycloadducts 3aa,bb,bc. The shape of the scans thus obtained projected on two reaction coordinates related to the pertinent internuclear distances and dihedral angles can be appreciated in Fig. 1A, together with the definition of the kinetic constants corresponding to each elementary step (Fig. 1B). This general picture shows that the stereochemical outcome depends not only on the two steps of the (2 + 2) reaction but also on the E/Z isomerisation of the starting imine 2 or zwitterionic intermediate INT via transition structures TS1 and TSR, respectively. Therefore, a detailed analysis of each elementary step is required.

Fig. 1 (A) General reaction paths for the Staudinger reactions between ketenes 1a,b and imines 2a,b,c to yield cis- and trans-β-lactams 3aa,bb,bc. The reaction coordinates correspond to the formation of the N1–C2 and C3–C4 bonds as well as modifications of the indicated dihedral angles. (B) Definition of the kinetic constants associated with each elementary step.

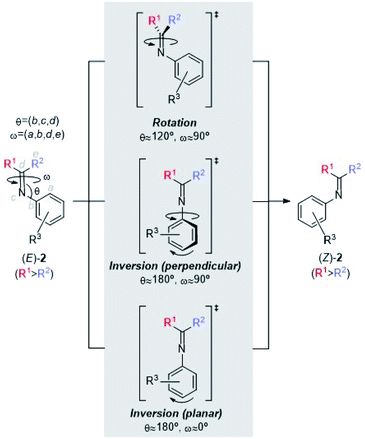
The E/Z isomerization of imines has been studied both experimentally²⁰ and computationally.²¹ According to these studies, at least three mechanisms have been proposed (Scheme 4). The first one consists of a rotation about the C(sp²)=N(sp²) imine moiety. The second and third mechanisms involve inversion of configuration at the nitrogen atom, with a C=N-aryl bond angle of ca. 180 deg. In the second case, this inversion takes place with a concomitant rotation of the aryl group (perpendicular inversion), whereas in the third case this inversion occurs with no rotation of the N-aryl group (planar inversion).

Scheme 4 Rotation and inversion mechanisms for (E)/(Z) isomerization of imines.

In N-benzylideneanilines, the experimental E/Z isomerization barriers range from ca. 14 kcal mol⁻¹ for electron withdrawing groups to ca. 19 kcal mol⁻¹ for electron releasing groups such as dimethylamino or methyl groups.^21a Similar studies on imines stemming from ketones showed E/Z isomerization activation energies of ca. 15 kcal mol⁻¹.^21b,c Hammett plots of these experimental data suggest different mechanisms depending upon the nature of the substituents. In general, the inversion pathways are predominant. In the case of electron-releasing substituents at the N-aryl moiety, the planar mechanism is the less energetic one, whereas electron-withdrawing substituents at the same position promote perpendicular geometries in the corresponding transition structures.²² These data indicate that, in a given Staudinger reaction, the energy barrier associated with E/Z isomerization of the starting imine can compete with the activation energies of the two-step mechanism, in particular with the first step leading to the formation of the C–N bond of INT intermediates. Therefore, the computational studies discussed below will start with this E/Z isomerization step.

We started our study by analyzing the isomerization of imine (E)-2a in dichloromethane and at 195.15 K (−78 °C, A-conditions). The geometry of the transition structure TSia and the relative energies of the two isomers as well as the activation energy for the isomerization reaction are shown in Fig. 2A. According to our results, since the C4–N1–C5 bond angle of TSia is ca. 180 deg., the isomerization mechanism for this imine consists of an inversion of the starting imine. In addition, the β-naphthyl group in TSia is perpendicular to the C6–C4–N1 plane, thus indicating an aza-allenyl structure for this saddle point (Fig. 2B).

Fig. 2 (A) Optimized structure of transition structure TSia, associated with the isomerisation of imine 2a (M06-2X(PCM)/def2-TZVPP level of theory). Relative Gibbs energies, in kcal mol⁻¹, computed at 195.15 K (A-conditions, see Scheme 3) are also given. Bond distances and angles are in Å and deg., respectively. Numbers in parentheses correspond to the calculated bond orders. (B) Several polar resonance forms corresponding to TSia emphasizing its aza-allenyl structure.

Fig. 3 Optimized structure of transition structure TSib, associated with the isomerization of imine 2b (M06-2X(PCM)/def2-TZVPP level of theory). Relative Gibbs energies, in kcal mol⁻¹, computed at 195.15 K (A-conditions, see Scheme 3) and at 298.15 K (in brackets) are also given. Bond distances and angles are in Å and deg., respectively. Numbers in parentheses correspond to the calculated bond orders.

This cumulene structure is stabilized with respect to N-phenyl imines by delocalization of the negative charge along the N-aryl system of TSia (Fig. 2B). This delocalization can be appreciated by inspection of the bond index of the N1–C5 pair (Fig. 2A). Therefore, the isomerization mechanism corresponds to the inversion-perpendicular mode shown in Scheme 4. The calculated activation energy for the isomerization of (E)-2a is ca. 1.3 kcal mol⁻¹ higher than the N-1-α-naphthyl counterpart.¹⁶ As expected, the (Z)-isomer of 2a is calculated to be ca. 4.9 kcal mol⁻¹ less stable than its (E)-isomer.

In the case of N-mesityl imine 2b, our calculations show that the presence of the three methyl groups results in a reduction of the isomerization barrier of ca. 2 kcal mol⁻¹ compared to its unmethylated counterpart.¹⁶ As in the (E)/(Z) transformation of imine 2a, the isomerization mechanism consists of an inversion-perpendicular pathway (vide supra).

The isomerization pattern of imine 2c is slightly different (Fig. 4A). According to our calculations, TSic exhibits C_s symmetry and therefore the isomerization takes place via in-plane inversion with no rotation about the N-PMP bond. Analysis of the Wiberg bond indices and the Kohn–Sham MOs are compatible with Valence Bond (VB) resonance forms shown in Fig. 4B (see ESI† for further information). The aromaticity of the indole moiety in TSic determines the relatively large contribution of different polar forms in which the simultaneous aza-allenic delocalization pattern observed in TSia is not essential. This situation permits to keep the C_s symmetry and leads to a relatively low activation energy compared to the one associated with the isomerization of N-aryl imine 2b. In addition, the energy gap between both isomers is of 1 kcal mol⁻¹ at 298 K (Fig. 4A). Our calculations show that the isomerization process of 2c is feasible via an inversion-planar geometry of the corresponding transition state, a mechanism favored in ketimines with electron-releasing groups at the N-aryl substituent.²² This rapidly cis/trans interconversion at room temperature was found to be characteristic of 3-arylimino-2-indolones. Further analysis under benzene reflux conditions (348.15 K, close to C-conditions) show a reduction of about 0.4 kcal mol⁻¹ on the computed activation barriers, thus favoring the equilibration of both isomers. Moreover, at this temperature, the energy difference between (E)-/(Z)-imines decreases. Remarkably, ¹H-NMR experiments on E/Z mixtures of imine 2c at different temperatures showed fast exchange between the methyl groups signals at 373 K and 393 K (for N-methyl and methoxy moieties, respectively). These temperature values correspond to a Gibbs activation energy of ca. 19.1–19.6 kcal mol⁻¹ (see ESI† for further details), in nice agreement with the theoretical value, thus showing the reliability of the computational study.

Fig. 4 (A) Optimized geometry of TSic and relative Gibbs free energies (M06-2X(PCM)/def2-TZVPP level of theory). Gibbs corrections computed at 298.15 K (room temperature, dichloromethane, B-conditions) and 384.15 K, (refluxing toluene, C-conditions, in brackets) in kcal mol⁻¹, are also given. Bond distances and angles are in Å and deg., respectively. Numbers in parentheses correspond to the calculated bond orders. (B) Several polar resonance forms corresponding to TSic compatible with its C_s symmetry.

We next examined the transition structures, reaction intermediates and products corresponding to the reaction between methoxyketene 1a and both isomers of imine 2a.

The relative energies and geometries of the transition structures are gathered in Fig. 5. Our calculations indicate that (E)-2a is less nucleophilic than its (Z)-isomer. Thus, the calculated nucleophilic values ω⁻ with respect to 1a are 1.58 and 1.85 meV, respectively (see eqn (8) in the Computational methods section). However, the activation energy for the formation of (E)-INTaa via (E)-TS1aa is 0.4 kcal mol⁻¹ lower than that associated with formation of (Z)-INTaa. Both saddle points TS1aa correspond to noncoplanar attacks (see the corresponding ω₄₁₂₃ values in Fig. 5) of the imine nitrogen on the sp-hybridized carbon atom of methoxyketene 1a. It is noteworthy that the activation barriers for the formation of N1–C2 bonds in both intermediates are lower than those computed for the isomerization steps between (E)- and (Z)-2a. In particular, the activation free energy associated with formation of (E)-INTaa from (E)-2a and 1a is 7.5 kcal mol⁻¹ lower than that corresponding to the conversion of (E)-2a into (Z)-2a (Fig. 2 and 5). In addition, (Z)-INTaa is only 0.6 kcal mol⁻¹ more stable than (E)-INTaa because of the lower steric crowding associated with the phenyl group at C4.

Fig. 5 Fully optimized transition structures (M06-2X(PCM)/def2-TZVPP level of theory) associated with formation of β-lactams 3aa from methoxyketene 1a and imine 2a. Bond distances, angles and dihedral angles (as defined in Fig. 1, in absolute values) are given in Å and deg., respectively. Numbers on the arrows are the relative Gibbs energies, in kcal mol⁻¹ and at 195.15 K (dichloromethane, A-conditions).

Conrotatory cyclization of (E)-INTaa to yield cis-3aa has an activation barrier of 5.7 kcal mol⁻¹, a process much faster than isomerization to yield (Z)-INTaa via TSRaa (Fig. 5). The energy barrier associated with this latter isomerization is higher than that calculated for the isomerization of the starting imine. In the former case, the iminium moiety cannot isomerize via the inversion (perpendicular) mechanism and rotation about the C=N(+), more costly in terms of energy, is the only possibility. Therefore, this isomerization postulated for other Staudinger reactions, is not competitive in this specific case. The [π₄c] electrocyclization of (Z)-INTaa has a lower activation barrier compared to its (E)-counterpart. These results agree with the torquoselectivity effects that operate in both saddle points. Thus, in cis-TS2aa the electron-releasing group methoxy group is outward with respect to the C3⋯C4 bond in formation, whereas the electron-releasing group 4-phenyl is inward. Therefore, despite having a methoxy group placed in a favored position, this latter orientation is not favored according to the torquoselectivity theory. In contrast, in trans-TS2aa both substituents occupy outward positions, which results in a less energetic saddle point. Actually, the activation barrier associated with the conrotation of (E)-INTaa via cis-TS2aa is calculated to be 2.5 kcal mol⁻¹ higher in energy than that associated with conrotation of (Z)-INTaa via trans-TS2aa. As far as the relative energies of both β-lactam cycloadducts are concerned, trans-3aa is calculated to be only 0.3 kcal mol⁻¹ more stable than its cis-congener.

The reaction between acetoxyketene 1b and imine 2b in both its (Z)- and (E)-forms was also analysed. The relative energies and the geometries of the relevant transition structures are gathered in Fig. 6.

Fig. 6 Fully optimized transition structures (M06-2X(PCM)/def2-TZVPP level of theory) associated with formation of β-lactams 3bb from acetoxyketene 1b and imine 2b. Bond distances, angles and dihedral angles (as defined in Fig. 1, in absolute values) are given in Å and deg., respectively. Numbers on the arrows are the relative Gibbs energies, in kcal mol⁻¹ at 195.15 K (dichloromethane, A-conditions) and at 298.15 K (dichloromethane, B-conditions, in brackets).

In this case, the activation barrier associated with the N1–C2 bond formation of (Z)-2b is 1.5 kcal mol⁻¹ (A-conditions) or 1.4 kcal mol⁻¹ (B-conditions) lower than that of its (E) counterpart. This is in agreement with the higher computed nucleophilicity ω⁻ of (Z)-2b compared to (E)-2b (1.4 and 6.1 10⁻¹ meV, respectively, see eqn (8) in the Computational methods section). This is a consequence of the presence of the methyl groups in ortho-CMe position, which leads to a rotation about the C6–C4–C5–CMe dihedral angle thus avoiding the expected planar disposition observed in most N-aromatic imines. The final effect is the enhancement of the occupation of the imine lone pair.

Remarkably, in this case the activation barrier associated with the conrotatory step is higher than the one associated with the first step, in contrast with the previous example. Thus, the high steric clash makes the barrier to rise up to 13.0 kcal mol⁻¹ for cis-TS2bb and 8.9 kcal mol⁻¹ for trans-TS2bb. This latter relative lower energy is also in agreement with the 3-out/4-out torquoelectronic effect operating in trans-TS2bb. Our calculations show that trans-3bb is about 2 kcal mol⁻¹ more stable than cis-3bb. In addition, our results indicate that, once the first step of the Staudinger reaction has started, the reaction paths leading to both cycloadducts are independent to each other, since pathways connecting (E)-INTbb and (Z)-INTbb via TSRbb are of much higher energy (Fig. 6). Also in this case, rotation about the C=N(+) bond in INTbb has an activation energy of ca. 36 kcal mol⁻¹, a value that cannot compete with the activation energies associated with conrotatory electrocyclizations leading to cis- and trans-β-lactams 3bb. Therefore, also in this case, formation of trans-3bb via isomerization of zwitterionic intermediate (E)-INTbb to its congener (Z)-INTbb cannot proceed under A- and B-conditions.

Finally, we examined the reaction between acetoxyketene 1b and imine 2c in both (Z)- and (E)-forms. The relative energies and the geometries of the relevant transition structures are gathered in Fig. 7.

Fig. 7 Fully optimized transition structures (M06-2X(PCM)/def2-TZVPP level of theory) associated with formation of β-lactams 3bc from acetoxyketene 1b and imine 2c. Bond distances, angles and dihedral angles (as defined in Fig. 1, in absolute values) are given in Å and deg., respectively. Numbers on the arrows are the relative Gibbs energies, in kcal mol⁻¹ and at 298.15 K (dichloromethane, B-conditions) and at 384.15 K, (refluxing toluene, C-conditions, in brackets).

The computed nucleophilicity ω⁻ of both isomers of imine 2c are 0.74 and 7.91 meV for (E)-2c and (Z)-2c respectively. Similarly, acetoxyketene 1b is more electrophilic than its methoxy analogue 1a. The computed ω⁺ for these ketenes are 41.3 and 45.2 meV, respectively. It is remarkable that in this case the activation energy at 298.15 K, associated with formation of the N1–C2 bond, is lower than the barrier corresponding to the imine isomerization step (see Fig. 4 and 7). Moreover, at the same temperature both (E)-TS1bc and (Z)-TS1bc are reached through a similar activation barrier. In this case, the second step of the reaction, namely the formation of the C3–C4 bond via a conrotatory electrocyclization presents lower energetic barriers than the initial step. Saddle point cis-TS2bc is calculated to be associated with a lower free energy barrier with respect to trans-TS2bc. This is not surprising since in the former conrotatory saddle point the electron-withdrawing amidic C=O moiety occupies the 4-inward position, whereas the electron-releasing phenyl moiety is in an also favored 4-outward disposition. Surprisingly, the activation barrier of the first step increases at higher temperatures (C-conditions), pointing out the relevance of the entropic term in these particular N1–C2 bond formation reactions. In this reaction, the Gibbs energy of transition state TSRbc, associated with rotation about the N1–C2 bond, corresponded to a significantly lower activation energy associated with the conversion of (E)-INTbc into (Z)-INTbc. However, this latter activation energy is much larger than the activation energies associated with conrotatory transition structures TS2bc. Therefore, also in this reaction formation of β-lactam trans-3bc is not predicted to proceed via isomerization of zwitterionic intermediates. Once again, trans-3bc is calculated to be 1.2 or 2 kcal mol⁻¹ thermodynamically more stable than its cis-analogue at 298.15 K (B-conditions) or 384.15 K (C-conditions), respectively.

The computational analysis of these three reactions provide a general picture that involves four aspects: (i) the isomerization of the imine; (ii) the activation energy associated with the formation of the C–N bond; (iii) the relative stability and interconversion of the zwitterionic intermediates; and (iv) the activation energy associated with the formation of the C(3)–C(4) bond. The relative weights of these events can determine the stereochemical outcome of each reaction. Table 1 compiles the most relevant computational data associated with these calculations.

Table 1 Summary of the most relevant computational data^a shown in Fig. 2–7. L and S descriptors denote large and small substituents, respectively

Reaction	1a + 2a → 3aa	1b + 2b → 3bb		1b + 2c → 3bc
Rxn conditions^b	A	A	B	B	C
a Activation (ΔGa), relative (ΔGrel) and reaction (ΔGrxn) free energies calculated at the M06-2X(PCM)/def2-TZVPP level of theory, given in kcal mol^−1.b Temperatures and solvents for conditions A–C are given in Scheme 3.
ΔGa(TSi)	19.4	17.7	17.8	17.9	17.5
ΔGrel[(Z)-2 − (E)-2]	4.9	2.7	2.9	1.0	0.4
ΔGa[(E)-TS1]	11.9	9.6	10.1	15.1	19.6
ΔGa[(Z)-TS1]	12.3	8.1	8.7	15.1	18.4
ΔGrel[(E)-INT − (Z)-INT]	−0.6	−1.4	−1.5	0.0	−1.1
ΔGa(TSR)	22.6	36.1	36.7	9.9	7.6
ΔGa(cis-TS2)	5.7	13.0	12.9	0.2	0.1
ΔGa(trans-TS2)	3.2	8.9	8.6	3.9	1.9
ΔGrxn(cis-3)	−33.9	−26.7	−30.6	−28.8	−32.8
ΔGrxn(trans-3)	−34.2	−67.8	−28.2	−69.0	−30.2

---

We generated the kinetic profiles for 1a + 2a → 3aa, 1b + 2b → 3bb and 1b + 2c → 3bc as we did in the reaction between ketene 1a and the N-(1-napthalen-yl) congener of imine 2a.¹⁶ We performed our simulations assuming that formation of β-lactams 3aa,bb,bc from the corresponding zwitterionic intermediates INT is irreversible. Therefore, the formation of cis- and trans-cycloadducts 3 can be described by means of eqn (1) and (2):

The evolution of intermediates and reactants is described by eqn (3):

where A represents reactants and reaction intermediates in the formand K is the interaction matrix that includes the kinetic constants associated with the different elementary steps:

The meaning of the different kinetic constants is outlined in Fig. 1B. These kinetic constants were calculated from the relative energies reported in Table 1 (see also Fig. 2–7) and using the Eyring equation:

Numerical integration of eqn (1)–(6) led to the time profiles shown in Fig. 8 (the values for these constants can be found in the ESI†). The simulated kinetic profiles associated with the formation of 3aa from 1a and 2a show the preferential formation of cis-3aa under A-conditions (Fig. 8A). This result can be explained in terms of the lower activation barrier associated with the N1–C2 bond formation compared to that associated with the isomerization of the imine 2a (11.9 kcal mol⁻¹ vs. 19.4 kcal mol⁻¹ respectively, Fig. 2 and 5). Therefore, the starting imine (E)-2a would react with methoxyketene 1a to form (E)-INTaa instead of isomerizing to form (Z)-2a. Moreover, the barrier associated with the second step is lower than the isomerization of this intermediate, thus forming β-lactam cis-3aa as the major stereoisomer, in good agreement with the experimental results. In the case of imine 2b, our simulations show a strong dependence on the reaction conditions. At low temperature (195.15 K, A-conditions, Fig. 8B), the imine isomerization takes place slowly. Therefore, despite the ring closure of (E)-INTbb is about 4 kcal mol⁻¹ higher in energy than the ring closure of (Z)-INTbb, a noticeable amount of cis-3bb is formed. At 298.15 K, despite there is no significant difference between the computed imine isomerization activation barriers, the kinetics are one order of magnitude faster. Therefore, initial isomerization of 2b is observed prior to the N1–C2 bond formation step. In this case, the energy difference between the ring closure activation barriers promoted the exclusive formation of trans-2bb. As far as arylaminoindolone 2c is involved, the simulated kinetic profile is strongly dependent of the reaction temperature. At room temperature (B-conditions), preferential formation of cis-3bc is predicted by our simulations (Fig. 8D) whilst at 384.15 K (C-conditions) trans-3bb is the major one (Fig. 8E). This trend towards trans-selectivity at higher temperatures was previously observed by Xu et al.²³ In the former case, the free energy difference between the initial step corresponding to the formation of the N1–C2 bond is of ca. 2 kcal mol⁻¹, which determines the preferential formation of (E)-INTbc compared to (Z)-INTbc (Fig. 7). Moreover, in the case of (E)-INTbc the activation barrier associated with the second step is lower than the one associated with the N1–C2 bond-breaking step leading to the reactants or the isomerization process. This means that the initial equilibrated mixture of imines 2c would react with acetoxyketene 2b to form preferentially (E)-INTbc. This latter intermediate would finally evolve to the kinetically favoured product cis-3bc. On the other hand, at 384.15 K there is a difference in free energy of only 0.4 kcal mol⁻¹ between both imines.

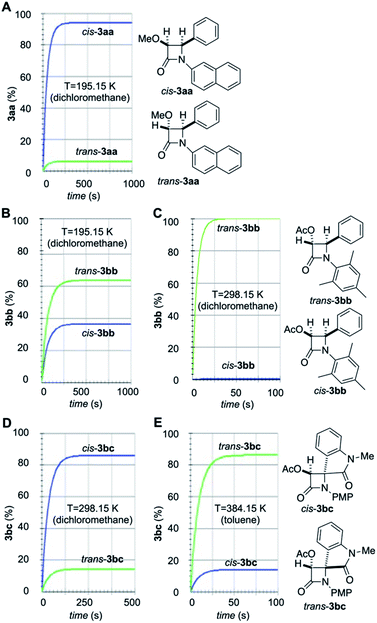Fig. 8 Simulated stereochemical outcomes associated with the reaction between ketenes 1a,b and imines 2a,b,c to yield β-lactams (A) cis- and trans-3aa; (B and C) cis- and trans-3bb; (D and E) cis- and trans-3bc. The distributions of isomers at different temperatures and in the presence of different solvents were obtained from eqn (6)–(11).

In addition, the difference in the activation barrier associated with the reaction of (E)-/(Z)-2c with ketene 1b is of 0 kcal mol⁻¹ (B-conditions) or 1.2 kcal mol⁻¹ (C-conditions). The energetic difference between the ring closure activation barrier and the decomposition of the intermediates towards the reactants is ca. 1 kcal mol⁻¹ higher in the case of (Z)-INTbc. Chemical intuition would suggest the preferential formation of cis-3bc in a less complicated mechanistic scenario. However, due to the exponential nature of the relationship between the kinetic constants and the computed free activation barriers, slightly higher differences in activation barriers do not necessarily implies higher differences in the kinetic constants. In fact, our simulation shows the preferential formation of the most stable β-lactam trans-3bc under C-conditions (Fig. 8E), in qualitative agreement with the experimental findings (vide supra). This result also suggests that a nonpolar solvent such as toluene under refluxing conditions transfers the stereocontrol to the formation of the polar zwitterionic intermediate. It is noteworthy that, in the three cases studied in this work, (E)/(Z) isomerization of intermediates INT has no effect on the respective stereochemical outcomes. Actually, removal of these isomerization processes in the A-matrix of eqn (5) by making k_R = k_−R = 0 yields kinetic profiles identical to those gathered in Fig. 8. However, since the magnitude of the activation energies associated with this isomerization process can vary significantly in magnitude, its relevance in other Staudinger reactions cannot be ruled out.

In summary, our computed kinetic profiles are in qualitative agreement with the observed experimental outcomes, pointing out the complex nature of the reaction mechanism of the Staudinger reaction between ketenes and imines, despite its formal simplicity.

Conclusions

Results above show that the Staudinger reaction is extremely sensitive to multiple factors. In principle, initial (E)/(Z)-imine isomerization in N-polyaromatic imines is difficult and the reaction leads mainly to reaction mixtures in which cis-β-lactams predominate. For these substrates, the stereochemistry of the final four-membered ring is determined by the initial formation of the corresponding zwitterions, and hence from the ratio of (E)/(Z) imines. Isatine-derived imines yield reaction mixtures in which the corresponding trans-2-azetidinone predominates under refluxing toluene conditions. The second step of the reaction, namely the formation of the C3–C4 bond via a conrotatory electrocyclization presents lower energetic barriers than the initial nucleophilic attack of the imine to the ketene. The corresponding trans-β-lactam is exclusively obtained from the imine derived from the bulkier 2,4,6-trimethylaniline and benzaldehyde, 2b. The presence of bulkier substituents in the initial imine can hamper the second step, namely the conrotatory ring closure of the zwitterion intermediate, thus favoring the equilibration of intermediates by regression to the initial reagents.

Moreover, the decomposition of these intermediates increases its relevance at higher reaction temperatures, thus yielding the thermodynamically more stable trans-β-lactam. It is remarkable that, in all the studied cases, the isomerization of the zwitterionic intermediates has no relevance on the stereochemical outcome of the reaction. This isomerization step has been claimed several times as the responsible for obtaining of cis–trans mixtures in the reaction of acid chlorides and imines in the presence of tertiary amines.

It is also noteworthy that all the conrotatory electrocyclic transition structures associated with the second step of the reaction follow the inward/outward torquoelectronic model developed by Houk. However, other factors can determine the observed stereocontrol of the reaction.

To sum up, depending upon the nature of the imine, three different situations may determine the selectivity of the Staudinger reaction: the ability of isomerization of the imine, the formation of the intermediate zwitterions, which is related to the nucleophilicity of the imine and, finally, the inward/outward disposition of the substituents in the conrotatory cyclisation of the zwitterionic intermediates to yield irreversibly the corresponding β-lactams. In the mechanistic model by Xu et al.¹² the isomerization of the zwitterionic intermediates determines the stereochemical outcome. The present study extends this model by including the isomerization of the starting imine, which can be determinant in some cases, such as those reported in the present study.

Experimental methods

General methods for the preparation of β-lactams 3

Method A-a. To a solution of imine 2 (1.79 mmol) and Et₃N (1.97 mmol) in 15 mL of anhydrous CH₂Cl₂ purged with argon and cooled to −78 °C, a solution of acyl chloride (1.79 mmol) in 5 mL of CH₂Cl₂ was dropwise added. The mixture was allowed to reach rt overnight. The crude mixture was washed with saturated NaHCO₃ (3.0 mL) and brine (3.0 mL). The combined organic layers were dried over anh. Na₂SO₄ and the solvent evaporated in vacuo. The crude mixtures were purified by SiO₂ chromatography (EtOAc/Hex mixtures).

Method A-b. A solution of Et₃N (0.27 mmol) in 0.5 mL of CH₂Cl₂ was dropwise added via syringe to a solution of the corresponding acid chloride (0.25 mmol) purged with argon and cooled to −78 °C. The reaction mixture was kept stirring for 20 min at this temperature and a solution of imine 2 (0.22 mmol) in 0.5 mL of CH₂Cl₂ was then dropwise added. The mixture was allowed to reach at rt overnight. The crude mixtures were then diluted with 5.0 mL of CH₂Cl₂, washed with saturated NaHCO₃ (3.0 mL) and brine (3.0 mL). The organic layer was dried over anh. Na₂SO₄ and the solvents evaporated in vacuo. The crude mixtures were purified by SiO₂ chromatography (EtOAc/Hex mixtures). For imine 2d the ratio imine : acid chloride : TEA was 1 : 2.2 : 2.6.

Method B-a. To a solution of imine 2 (1.79 mmol) and Et₃N (1.97 mmol) in 15 mL of anhydrous CH₂Cl₂ purged with argon at rt, a solution of acyl chloride (1.79 mmol) in 5 mL of CH₂Cl₂ was dropwise added. The resulting mixture was stirred at rt for the corresponding time. The crude mixtures were then diluted with 5.0 mL of CH₂Cl₂, washed with saturated NaHCO₃ (3.0 mL) and brine (3.0 mL). The organic layers dried over anh. Na₂SO₄ and the solvents evaporated in vacuo. The crude mixtures were purified by SiO₂ chromatography (EtOAc/Hex mixtures).

Method C-a. To a solution of imine 2 (1.79 mmol) and Et₃N (1.97 mmol) in 15 mL of anhydrous toluene purged with argon, a solution of acyl chloride (1.79 mmol) in 5 mL of anhydrous toluene was dropwise added. The resulting mixture was refluxed for 3 hours. The crude mixtures were then diluted with 5.0 mL of toluene, washed with saturated NaHCO₃ (3.0 mL) and brine (3.0 mL). The combined organic layers were dried over anh. Na₂SO₄ and the solvent evaporated in vacuo. The crude mixtures were purified by SiO₂ chromatography (EtOAc/Hex mixtures).
3-Methoxy-1-(naphthalen-1-yl)-4-phenylazetidin-2-one, 3aa. Methoxyacetyl chloride (98.0 mg, 0.90 mmol), imine 2a (183.0 mg, 0.79 mmol) and Et₃N (98.2 mg, 0.972 mmol) were reacted following Method A-b. After quenching the reaction, a crude mixture with a 3 : 1 cis/trans ratio was obtained and purified by SiO₂ chromatography (Hex/EtOAc 4 : 1) to obtain cis-3aa (125 mg, 0.41 mmol, 52%) and trans-3aa (45 mg, 0.15 mmol, 19%) as white solids.

cis-3aa: mp: 156–157 °C. ¹H NMR (CDCl₃, 300 MHz): δ 7.75 (d, J = 9.1 Hz, 2H), 7.71–7.59 (m, 3H), 7.51–7.31 (m, 7H), 5.35 (d, J = 4.9 Hz, 1H), 4.90 (d, J = 4.9 Hz, 1H), 3.24 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 164.4, 134.6, 133.4, 133.1, 130.5, 129.1, 128.7, 128.6, 127.9, 127.7, 127.4, 126.6, 125.1, 117.4, 114.1, 84.7, 61.8, 58.4. IR (CH₂Cl₂) ν = 1746 cm⁻¹. HRMS (ESI) m/z calc. for C₂₀H₁₇NO₂ [M]⁺: 303.1259, found 303.1268.

trans-3aa: mp: 192–193 °C. ¹H NMR (CDCl₃, 300 MHz): δ 7.75 (d, J = 9.6 Hz, 2H), 7.68 (d, J = 7.5 Hz, 1H), 7.63–7.55 (m, 2H), 7.49–7.32 (m, 7H), 5.06 (d, J = 1.8 Hz, 1H), 4.49 (d, J = 1.8 Hz, 1H), 3.63 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 164.3, 136.3, 134.6, 133.4, 130.5, 129.3, 129.2, 128.7, 127.7, 127.4, 126.6, 125.9, 125.2, 117.5, 114.3, 91.2, 63.4, 58.3. IR (CH₂Cl₂) ν = 1769 cm⁻¹. HRMS (ESI) m/z calc. for C₂₀H₁₇NO₂ [M]⁺: 303.1259, found 303.1323.

1-Mesityl-2-oxo-4-phenylazetidin-3-yl acetate, 3bb. Acetoxyacetyl chloride (244.3 mg, 1.79 mmol), imine 2b (400.0 mg, 1.79 mmol) and Et₃N (200 mg, 1.97 mmol) were reacted following Method A-a. After quenching the reaction, only trans-3bb was observed by NMR in the reaction crude. Pure trans-3bb (272 mg, 47%) was obtained after purification by SiO₂ chromatography (Hex/EtOAc 4 : 1) as a white solid.

trans-3bb: mp: 128–129 °C. ¹H NMR (CDCl₃, 300 MHz): δ 7.31 (s, 5H), 6.82 (s, 2H), 5.84 (d, J = 2.0 Hz, 1H), 5.18 (d, J = 2.0 Hz, 1H), 2.49–2.17 (bs, 6H), 2.23 (s, 3H), 2.22 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ: 169.7, 163.0, 137.9, 135.0, 129.5, 129.3, 128.9, 128.8, 127.0, 79.8, 66.2, 20.8, 20.6, 19.3. IR (CH₂Cl₂) ν = 1758 cm⁻¹. HRMS (ESI) m/z calc. for C₂₀H₂₁NO₃ [M]⁺: 323.1521, found 323.1519.

1-(4-Methoxyphenyl)-1′-methyl-2′,4-dioxospiro[azetidine-2,3′-indol-ine]-3-yl acetate, 3bc. Following Method B-a from acetoxy-acetyl chloride (33.7 mg, 0.25 mmol), imine 2c (66.5 mg, 0.25 mmol) and Et₃N (28.3 mg, 0.28 mmol), a crude mixture (80.0 mg, 0.22 mmol, 87%) with a 1.3 : 1 cis/trans ratio was obtained. Following Method C-a from acetoxy-acetyl chloride (33.7 mg, 0.25 mmol), imine 2c (66.5 mg, 0.25 mmol) and Et₃N (28.3 mg, 0.28 mmol), a crude mixture (75 mg, 0.20 mmol, 82%) with a 1 : 3.9 cis/trans ratio was obtained. Purification by SiO₂ chromatography (Hex–EtOAc 1.5 : 1) of the reaction crudes allowed the obtention of pure cis-3bc and trans-3bc as white solids.

cis-3bc: mp: 197–198 °C. ¹H NMR(CDCl₃, 300 MHz): δ 7.45 (td, J = 7.8, 1.3 Hz, 1H), 7.33 (dd, J = 7.4, 1.2 Hz, 1H), 7.14 (td, J = 7.6, 1.0 Hz, 1H), 7.03–6.97 (m, 1H), 7.02 (d, J = 9.0 Hz, 2H), 6.73 (d, J = 9.0 Hz, 2H), 5.63 (s, 1H), 3.72 (s, 3H), 3.29 (s, 3H), 2.14 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 170.1, 170.0, 160.1, 157.0, 143.5, 131.0, 129.2, 123.5, 123.3, 123.2, 119.1, 114.5, 109.1, 82.6, 66.7, 55.4, 26.8, 20.3. IR (CH₂Cl₂) ν = 1770, 1725 cm⁻¹. HRMS (ESI) m/z calc. for C₂₀H₁₈N₂O₅ [M]⁺: 366.1216, found 366.12128.

trans-3bc: mp: 173–174 °C. ¹H NMR (CDCl₃, 300 MHz): δ 7.43 (t, J = 7.8 Hz, 1H), 7.34 (d, J = 7.1 Hz, 1H), 7.09 (t, J = 7.6 Hz, 1H), 7.02 (d, J = 9.0 Hz, 2H), 6.96 (d, J = 7.8 Hz, 1H), 6.73 (d, J = 9.0 Hz, 2H), 5.74 (s, 1H), 3.70 (s, 3H), 3.33 (s, 3H), 1.86 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 171.8, 168.9, 160.2, 157.0, 144.5, 131.2, 129.2, 125.2, 122.8, 120.4, 118.9, 114.5, 109.1, 80.3, 66.4, 55.3, 26.8, 19.9. IR (CH₂Cl₂) ν = 1761, 1723 cm⁻¹. HRMS (ESI) m/z calc. for C₂₀H₁₈N₂O₅ [M]⁺: 366.1216, found 366.1224.

3-Methoxy-1′-(2-methoxyacetyl)-1-(4-methoxy-phenyl)spiro[azetidine-2,3′-indoline]-2′,4-dione, 3ad. Methoxyacetyl chloride (189.0 mg, 1.74 mmol), Et₃N (208.0 mg, 2.05 mmol) and imine 2d (0.200 g, 0.79 mmol) were reacted following Method A-b. After quenching the reaction, a crude mixture with a 1 : 1 cis/trans ratio was obtained and purified by SiO₂ chromatography (Hex/EtOAc 7 : 3) to obtain cis-3ad (88.0 mg, 0.22 mmol, 28%) and trans-3ad (75.0 mg, 0.19 mmol, 24%) as white solids.

cis-3ad: mp: 169–171 °C. ¹H NMR (CDCl₃, 300 MHz): δ 8.43 (d, J = 8.2 Hz, 1H), 7.58–7.46 (m, 1H), 7.41–7.26 (m, 2H), 7.02 (d, J = 9.0 Hz, 2H), 6.76 (d, J = 9.0 Hz, 2H), 4.83 (s, 1H), 4.76 (d, J = 6.6 Hz, 2H), 3.73 (s, 3H), 3.56 (s, 3H), 3.50 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 171.8, 170.5, 162.3, 157.1, 138.9, 131.3, 128.8, 126.4, 123.8, 122.9, 119.1, 117.4, 114.6, 94.1, 73.7, 68.1, 60.0, 59.6, 55.4. IR (CH₂Cl₂) ν = 1769, 1727 cm⁻¹. HRMS (ESI) m/z calc. for C₂₁H₂₀N₂O₆ [M]⁺: 396.1321, found 397.1319.

trans-3ad: mp: 139–140 °C. ¹H NMR (CDCl₃, 300 MHz): δ 8.42 (d, J = 8.0 Hz, 1H), 7.62–7.47 (m, 2H), 7.36–7.33 (m, 1H), 7.00 (d, J = 9.0 Hz, 2H), 6.75 (d, J = 9.0 Hz, 2H), 4.82 (s, 1H), 4.74 (s, 2H), 3.72 (s, 3H), 3.57 (s, 3H), 3.14 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 174.3, 170.5, 161.7, 157.2, 139.5, 131.4, 129.0, 126.1, 126.1, 121.0, 119.0, 116.9, 114.7, 90.7, 73.8, 67.2, 59.6, 59.3, 55.4. IR (CH₂Cl₂) ν = 1756 cm⁻¹. HRMS (ESI) m/z calc. for C₂₁H₂₀N₂O₆ [M]⁺: 397.1321, found 397.1323.

2-(3-Acetoxy-1-(4-methoxyphenyl)-2′,4-dioxospiro[azetidine-2,3′-indoline]-1′-yl)-2-oxoethyl acetate, 3bd. Acetoxyacetyl chloride (357.6 mg, 2.62 mmol), Et₃N (313 mg, 3.09 mmol) and imine 2d (0.300 g, 1.19 mmol) were reacted following Method A-b. After quenching the reaction, a crude mixture with a 1 : 1 cis/trans ratio was obtained and purified by SiO₂ chromatography (Hex/EtOAc 7 : 3) to obtain cis-3bd (0.135 g, 0.30 mmol, 25%). trans-3bd could not be isolated pure.

cis-3bd: mp: 170–172 °C. ¹H NMR (CDCl₃, 300 MHz): δ 8.32 (d, J = 8.2 Hz, 1H), 7.49 (t, J = 7.8 Hz, 1H), 7.40 (d, J = 7.6 Hz, 1H), 7.30 (d, J = 8.2 Hz, 1H), 7.01 (d, J = 8.9 Hz, 1H), 6.75 (d, J = 8.9 Hz, 1H), 5.58 (s, 1H), 5.32 (d, J = 17.2 Hz, 1H), 5.08 (d, J = 17.2 Hz, 1H), 3.70 (s, 3H), 2.21 (s, 3H), 2.14 (s, 3H). ¹³C NMR (CDCl₃, 75 MHz): δ 171.8, 170.2, 170.1, 167.0, 159.4, 157.3, 139.0, 131.5, 128.4, 126.5, 123.0, 119.1, 117.2, 114.7, 83.9, 67.0, 64.1, 55.3, 20.3, 20.0. IR (CH₂Cl₂) ν = 1767, 1729 cm⁻¹. HRMS (ESI) m/z calc. for C₂₃H₂₀N₂O₈ [M]⁺: 452.1220, found 452.1231.

Computational methods

All the calculations reported in this paper have been performed within density functional theory.²⁴ The different stationary points were optimized using the highly parameterized M06-2X functional,²⁵ that has been demonstrated to be well suited for the treatment of nonbonding interactions and dispersion forces, which can be relevant in densely substituted interacting systems.²⁶ The standard def2-TZVPP basis sets²⁷ as implemented in the GAUSSIAN 16 (ref. 28) suite of programs has been used. In the optimization and characterization of TSR saddle points, open-shell structures were considered in order to describe the possible diradical character of these stationary points associated with rotation about the C=N(+) bond.

Wiberg indices²⁹ B_i were evaluated using the natural bond orbital (NBO) method.³⁰ Zero-point vibrational energy (ZPVE) and Gibbs free energy corrections (TCGFE) were computed at the M06-2X(PCM)/def2-TZVPP level. All the thermodynamic magnitudes were calculated by using thermal corrections computed at 195 K, 298 K or 384 K. Activation Gibbs free energies (ΔG) and reaction Gibbs free energies (ΔG) were computed at the same level considering the initial reagents for the first addition step, and intermediates directly connected to the transition structure for the sing closure step and were corrected in order to consider solvated standard states (see ESI†). This approximate methodology for the evaluation of temperature corrections is based on equations derived from non-interacting particles systems that may introduce some errors in the case of low-lying electronic excited states systems. However, we assume that in our particular scenario these errors are similar in all stationary points and have scarce influence in the computed energetic profiles.

Assfeld et al.³¹ have shown that inclusion of solvent effects is necessary to reproduce correctly the reaction profile of the Staudinger reaction using ab initio methods. We have introduced the solvent effects in our DFT calculations by means of the Polarizable Continuum Model (PCM).³² In all the cases included in this study, the solvents considered were dichloromethane (ε = 8.9) and toluene (ε = 2.27), the ones used in the experimental study. The kinetic treatment of the computed activation Gibbs free energies was performed by means of the FACSIMILE program.³³

Electrophilicities (ω⁺) were computed using eqn (7):³⁴

where μ and η are the chemical potential and hardness of the species under study, respectively. Similarly, the nucleophilicity indexes of imines 2 with respect to electrophilic ketenes 1 were calculated using the following conceptually related expression:³⁵

The chemical potentials and hardnesses of ketenes 1 were calculated within the following approximations:^26a

η₁ = I₁ − A₁ ≈ ε_LUMO(1) − ε_HOMO(1) (10)

In these latter equations, I and A stand for the ionization potential and electron affinity and ε_HOMO and ε_LUMO are the orbital energies of the corresponding frontier orbitals. In the case of imines 2, since the nucleophilic attacks involve the MOs n_N associated with the nitrogen lone pairs, eqn (3) and (4) were adapted accordingly:

η₂ ≈ ε_LUMO(2) − ε_nN(2) (12)

Author contributions

F. P. C.: conceptualization, formal analysis, funding acquisition, methodology, project administration, supervision, visualization, resources, writing – original draft. A. de C.: investigation (computational and experimental results), methodology, software, data curation, validation, supervision, visualization. M. A. S.: conceptualization, formal analysis, funding acquisition, methodology, project administration, supervision, validation, resources, writing – review & editing. L. C.: investigation (experimental results), data curation. J. M.: investigation (experimental results). B. K. B.: conceptualization, funding acquisition, project administration, supervision, resources. D. B.: investigation (experimental results).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support for this work under grants PID2019-108429RB-I00 (to MAS), PID2019-104772GB-I00 (to FPC) and RED2018-102387-TC (Programa Redes Consolider, to FPC and MAS) from the Spanish Ministerio de Ciencia e Innovación, from the Gobierno Vasco/Eusko Jaulariza (IT-1346-19, to FPC), from Fundación Ramón Areces (CIVP18A3938, to MAS), US NIH (to BKB), US NCI and Prince Mohammad Bin Fahd University (to BKB) is gratefully acknowledged. SGI Iker and DIPC are generously acknowledged for generous allocation of computational resources.

Notes and references

1. H. Staudinger, Zur Kenntniss der Ketene. Diphenylketen, Justus Liebigs Ann. Chem., 1907, 356, 51.
2. (a) R. D. G. Cooper, B. W. Daugherty and D. B. Boyd, Chiral control of the Staudinger reaction, Pure Appl. Chem., 1987, 59, 485; (b) T. T. Tidwell, Ketenes, Wiley, New York, 1995, pp. 518–536, and references therein; (c) F. H. Van der Steen and G. van Koten, Syntheses of 3-amino-2-azetidinones: a literature survey, Tetrahedron, 1991, 47, 7503; (d) G. I. Georg and V. T. Ravikumar, in The Organic Chemistry of β-Lactams, ed. G. I. Georg, Verlag Chemie, New York, 1993, pp. 295–398, and references therein; (e) C. Palomo, J. M. Aizpurua, I. Ganboa and M. Oiarbide, Asymmetric Synthesis of β-Lactams by Staudinger Ketene-Imine Cycloaddition Reaction, Eur. J. Org. Chem., 1999, 3223; (f) G. S. Singh, Tetrahedron, 2003, 59, 7631; (g) C. Palomo, J. M. Aizpurua, I. Ganboa and M. Oiarbide, Asymmetric synthesis of beta-lactams through the Staudinger reaction and their use as building blocks of natural and nonnatural products, Curr. Med. Chem., 2004, 11, 1837; (h) M. T. Aranda, P. Pérez-Faginas and R. González-Muñiz, Advances in Organic Chemistry, ed. A. Rahman, Bentham Science Publishers Ltd, Hilversum, The Netherlands, 2013, vol. 6, p. 296.
3. (a) A. R. A. S. Deshmukh, B. M. Bhawal, D. Krishnaswamy, V. V. Govande, B. A. Shinkre and A. Jayanthi, Azetidin-2-ones, Synthon for Biologically Important Compounds, Curr. Med. Chem., 2004, 11, 1889; (b) B. Alcaide and P. Almendros, β-Lactams as Versatile Synthetic Intermediates for the Preparation of Heterocycles of Biological Interest, Curr. Med. Chem., 2004, 11, 1921; (c) M. S. Manhas, S. G. Amin and A. K. Bose, Beta-Lactams as Synthons. Synthesis of Heterocycles via beta-Lactam Cleavage, Heterocycles, 1976, 5, 669; (d) M. S. Manhas, D. R. Wagle, J. Chiang and A. K. Bose, Conversion of Beta-Lactams to Versatile Synthons via Molecular Rearrangement and Lactam Cleavage, Heterocycles, 1988, 27, 1755.
4. T. T. Tidwell, Ketenes, Wiley, New York, 1995, pp. 57–67, and references therein.
5. (a) G. B. Gill, in Comprehensive Organic Síntesis, ed. G. Pattenden, Pergamon, Oxford, 1991, Vol. 3, pp. 887–912; (b) M. A. Miranda and H. Garcia, in The Chemistry of Functional Groups. Supplement B: The Chemistry of Acid Derivatives, ed. S. Patai, Wiley, New York, 1992, vol. 2, pp. 1271–1394.
6. T. T. Tidwell, Ketenes, Wiley, New York, 1995, p. 459.
7. R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Angew. Chem., Int. Ed., 1969, 8, 781.
8. (a) F. P. Cossío, A. Arrieta and M. A. Sierra, The Mechanism of the Ketene−Imine (Staudinger) Reaction in Its Centennial: Still an Unsolved Problem?, Acc. Chem. Res., 2008, 41, 925; (b) A. Arrieta, B. Lecea and F. P. Cossío, Computational Studies on the Synthesis of β-lactams via [2+2] Thermal Conditions, Top. Heterocyl. Chem., 2010, vol. 22, p. 313.
9. (a) F. P. Cossío, J. M. Ugalde, X. Lopez, B. Lecea and C. Palomo, A semiempirical theoretical study on the formation of β-lactams from ketenes and imines, J. Am. Chem. Soc., 1993, 115, 995; (b) F. P. Cossío, A. Arrieta, B. Lecea and J. M. Ugalde, Chiral Control in the Staudinger Reaction between Ketenes and Imines. A Theoretical SCF-MO Study on Asymmetric Torquoselectivity, J. Am. Chem. Soc., 1994, 116, 2085; (c) I. Arrastia, A. Arrieta, J. M. Ugalde, F. P. Cossío and B. Lecea, Theoretical and experimental studies on the periselectivity of the cycloaddition reaction between activated ketenes and conjugated imines, Tetrahedron Lett., 1994, 35, 7825; (d) B. Lecea, I. Arrastia, A. Arrieta, G. Roa, X. Lopez, M. I. Arriortua, J. M. Ugalde and F. P. Cossío, Solvent and Substituent Effects in the Periselectivity of the Staudinger Reaction between Ketenes and α,β-Unsaturated Imines. A Theoretical and Experimental Study, J. Org. Chem., 1996, 61, 3070; (e) J. A. Sordo, J. González and T. L. Sordo, An ab initio study on the mechanism of the ketene-imine cycloaddition reaction, J. Am. Chem. Soc., 1992, 114, 6249; (f) A. Venturini and J. González, A CASPT2 and CASSCF Approach to the Cycloaddition of Ketene and Imine: A New Mechanistic Scheme of the Staudinger Reaction, J. Org. Chem., 2002, 67, 9089.
10. (a) K. N. Houk, in Strain and Its Implications in Organic Chemistry, ed. A. de Meijere and S. Blechert, Kluwer Academic Publishers, Dordrecht, 1989, p. 25; (b) S. Niwayama, E. A. Kallel, D. C. Spellmeyer, C. Sheu and K. N. Houk, Substituent Effects on Rates and Stereoselectivities of Conrotatory Electrocyclic Reactions of Cyclobutenes. A Theoretical Study, J. Org. Chem., 1996, 61, 2813; (c) W. Kirmse, N. G. Rondan and K. N. Houk, Stereoselective substituent effects on conrotatory electrocyclic reactions of cyclobutenes, J. Am. Chem. Soc., 1984, 106, 7989; (d) N. G. Rondan and K. N. Houk, Theory of stereoselection in conrotatory electrocyclic reactions of substituted cyclobutenes, J. Am. Chem. Soc., 1985, 107, 2099; (e) W. R. Dolbier Jr, H. Korionak, K. N. Houk and C. Sheu, Electronic Control of Stereoselectivities of Electrocyclic Reactions of Cyclobutenes: A Triumph of Theory in the Prediction of Organic Reactions, Acc. Chem. Res., 1996, 29, 471; (f) R. López, T. L. Sordo, J. A. Sordo and J. González, Torquoelectronic Effect in the Control of the Stereoselectivity of ketene-Imine Cycloaddition Reactions, J. Org. Chem., 1993, 58, 7036; (g) F. P. Cossío, A. Arrieta, B. Lecea and J. M. Ugalde, Chiral Control in the Staudinger Reaction between Ketenes and Imines. A Theoretical SCF-MO Study on Asymmetric Torquoselectivity, J. Am. Chem. Soc., 1994, 116, 2085; (h) Y. Liang, L. Jiao, S. Zhang, Z.-X. Yu and J. Xu, New Insights into the Torquoselectivity of the Staudinger Reaction, J. Am. Chem. Soc., 2009, 131, 1542; (i) H. Qi, X. Li and J. Xu, Stereoselective control in the Staudinger reaction involving monosubstituted ketenes with electron acceptor substituents: experimental investigation and theoretical rationalization, Org. Biomol. Chem., 2011, 9, 2702.
11. A. Arrieta, B. Lecea and F. P. Cossío, Origins of the Stereodivergent Outcome in the Staudinger Reaction between Acyl Chlorides and Imines, J. Org. Chem., 1998, 63, 5869.
12. (a) L. Jiao, Y. Liang and J. Xu, Origin of the Relative Stereoselectivity of the β-Lactam Formation in the Staudinger Reaction, J. Am. Chem. Soc., 2006, 128, 6060; (b) Y. Wang, Y. Liang, L. Jiao, M.-D. Du and J. Xu, Do Reaction Conditions Affect the Stereoselectivity in the Staudinger Reaction?, J. Org. Chem., 2006, 71, 6983.
13. A. Arrieta, J. M. Ugalde, F. P. Cossío and B. Lecea, Role of the isomerization pathways in the Staudinger reaction. a theoretical study on the interaction between activated ketenes and imidates, Tetrahedron Lett., 1994, 35, 4465.
14. Z. Yiang and J. Xu, Remarkable ketene substituent dependent effect of photo irradiation on the diastereoselectivity in the Staudinger reaction, Tetrahedron Lett., 2012, 53, 786.
15. S. Hou, X. Li and J. Xu, Theoretical studies on selectivities in the Staudinger reaction of vicinal diimines and ketenes, Sci. China: Chem., 2013, 56, 370.
16. Z. Yang and J. Xu, Insights into the β-Sultam Ring Formation in the Sulfa-Staudinger Cycloadditions, J. Org. Chem., 2014, 79, 10703.
17. (a) B. K. Banik and F. F. Becker, Unprecedented stereoselectivity in the Staudinger reaction with polycyclic aromatic imines, Tetrahedron Lett., 2000, 41, 6551; (b) I. Banik, L. Hackfield and B. K. Banik, Cycloaddition of Naphthalenyl and Anthracenyl Imines: Interesting Aspects of the Staudinger Reaction, Heterocycles, 2003, 59, 505.
18. B. K. Banik, B. Lecea, A. Arrieta, A. de Cózar and F. P. Cossío, On the Stereodivergent Behavior Observed in the Staudinger Reaction between Methoxyketene and (E)-N-Benzylidenearyl Amines, Angew. Chem., Int. Ed., 2007, 46, 3028.
19. CCDC 1951437 and 1951438 contain the ESI crystallographic data for compounds cis-3bc and trans-3bc, respectively.†.
20. (a) T. Asano, H. Furuta, H.-J. Hofmann, R. Cimiraglia, Y. Tsuno and M. Fujio, Mechanism of Thermal Z/E Isomerization of Substituted N-Benzylideneanilines. Nature of the Activated Complex with an sp-Hybridized Nitrogen Atom, J. Org. Chem., 1993, 58, 4418; (b) T. W. Swaddle, H. Doine, S. D. Kinrade, A. Sera, T. Asano and T. Okada, High-Pressure 19F NMR Study of the Degenerate Isomerization of Hexafluoroacetone Anils. Evidence for the Existence of Two Different Inversion Transition States, J. Am. Chem. Soc., 1990, 112, 2378; (c) T. Asano, T. Okada and W. G. Herkstroeter, Mechanism of Geometrical Isomerization about the Carbon-Nitrogen Double Bond, J. Org. Chem., 1989, 54, 379; (d) W. G. Herkstroeter, The Mechanism of Syn-Anti Isomerization of Azomethine Dyes, J. Am. Chem. Soc., 1973, 95, 8686; (e) G. E. Hall, W. J. Middelton and J. D. Roberts, Nuclear Magnetic Resonance Spectroscopy. Kinetics of Isomerization of Para-Substituted Hexafluoroacetone N-Phenylimines, J. Am. Chem. Soc., 1971, 93, 4778.
21. (a) H. Yamataka, S. C. Ammal, T. Asano and Y. Ohga, Thermal Isomerization at a C=N Double Bond: How Does the Mechanism Vary with the Substituent?, Bull. Chem. Soc. Jpn., 2005, 78, 1851; (b) H.-J. Hofmann, T. Asano, R. Cimiraglia and R. Bonaccorsi, Structural and Thermal E-Z Isomerization of Substituted 4-Phenylimino-5-pyrazolones and Hexafluoroacetone Anils, Bull. Chem. Soc. Jpn., 1993, 66, 130; (c) H.-J. Hofmann, T. Asano and R. Cimiraglia, On the Conformation of the Inversion State in the The rmal E,Z Isomerization of Aromatic Azomethines, J. Chem. Soc., Chem. Commun., 1991, 295.
22. M. J. Konkel, M. Lagu, L. W. Boteju, H. Jimenez, S. Noble, M. W. Walker, G. Chandrasena, T. P. Blackburn, S. S. Nikam, J. L. Wright, B. E. Kornberg, T. Gregory, T. A. Pugsley, H. Akunne, K. Zoski and L. D. Wise, 3-Arylimino-2-indolones Are Potent and Selective Galanin GAL3 Receptor Antagonists, J. Med. Chem., 2006, 49, 3757.
23. B. Li, Y. Wang, D.-M. Du and J. Xu, Notable and Obvious Ketene Substituent-Dependent Effect of Temperature on the Stereoselectivity in the Staudinger Reaction, J. Org. Chem., 2006, 72, 990.
24. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford, New York, 1989.
25. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2007, 120, 215.
26. (a) Y. Zhao and D. G. Truhlar, Density Functionals with Broad Applicability in Chemistry, Acc. Chem. Res., 2008, 41, 157; (b) J.-L. Chen, J.-T. Hong, K.-J. Wu and W.-P. Hu, The MC-DFT approach to the M06-2X, B2K-PLYP, and B2T-PLYP functionals, Chem. Phys. Lett., 2009, 468, 307.
27. (a) W. J. Hehre, L. Radom, P. v. R. Schleyer and A. J. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986, p. 76; (b) R. Ditchfield, W. J. Hehre and A. J. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724; (c) W. J. Hehre, R. Ditchfield and A. J. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257.
28. M. J. Frisch et al., Gaussian 16, Revision A.03, Gaussian. Inc., Wallingford CT, 2016, full reference in the ESI.†.
29. K. B. Wiberg, Application of the Pople-Santry-Segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083.
30. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899; (b) A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735.
31. X. Assfeld, M. F. Ruiz-Lopez, J. Gonzalez, R. Lopez, J. A. Sordo and T. L. Sordo, Theoretical analysis of the role of the solvent on the reaction mechanisms: one-step versus two-step ketene–imine cycloaddition, J. Comput. Chem., 1994, 15, 479.
32. (a) S. Miertus, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilization of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55, 117; (b) B. Mennucci and J. Tomasi, Continuum solvation models: A new approach to the problem of solutes charge distribution and cavity boundaries, J. Chem. Phys., 1997, 106, 5151; (c) R. Cammi, B. Mennucci and J. Tomasi, Fast Evaluation of Geometries and Properties of Excited Molecules in Solution: A Tamm–Dancoff Model with Application to 4-Dimethylaminobenzonitrile, J. Phys. Chem. A, 2000, 104, 5631.
33. FACSIMILE, v. 3.0.36, UES Software, Inc.
34. (a) R. G. Parr, L. Szentpály and S. Liu, Electrophilicity Index, J. Am. Chem. Soc., 1999, 121, 1922; (b) A. T. Maynard, M. Huang, W. G. Rice and D. G. Covell, Reactivity of the HIV-1 nucleocapsid protein p7 zinc finger domains from the perspective of density-functional theory, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11578.
35. P. Jaramillo, P. Pérez, R. Contreras, W. Tiznado and P. Fuentealba, Definition of a Nucleophilicity Scale, J. Phys. Chem. A, 2006, 110, 8181.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods, energies and Cartesian coordinates of the stationary points discussed in the text, NMR and IR spectra and crystallographic data for compounds cis-3bc and trans-3bc. CCDC 1951437 and 1951438. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra06114c

---