Current-induced hole spin polarization in a quantum dot via a chiral quasi bound state†
V. N.
Mantsevich
 a and
D. S.
Smirnov
a and
D. S.
Smirnov
 *b
*b
aChair of Semiconductors and Cryoelectronics & Quantum Technology Center, Physics department, Lomonosov Moscow State University, 119991 Moscow, Russia
bIoffe Institute, 194021 St. Petersburg, Russia. E-mail: smirnov@mail.ioffe.ru
First published on 5th May 2022
Abstract
We put forward a mechanism for the current-induced spin polarization in semiconductor heterostructures, which is based on the complex structure of the valence band. It takes place for a light hole in a quantum dot side-coupled to a quantum wire with heavy holes. In stark contrast with the traditional mechanisms based on the linear in momentum spin–orbit coupling, an exponentially small bias applied to this structure is enough to create the 100% spin polarization in the quantum dot. Microscopically, this effect is related to the formation of the chiral quasi bound states and the spin-dependent tunneling of holes from the quantum wire to the quantum dot. This new concept is equally valid for the GaAs-, Si- and Ge-based nanostructures.
New conceptsWe put forward a new mechanism for the electrical spin orientation in semiconductor heterostructures, which exploits the complex structure of the valence band. This is an alternative to the old concepts of the current-induced spin polarization, which are based on the momentum-dependent spin–orbit splittings of the conduction and valence bands. The main advantages of the new concept are the possibility to completely polarize hole spin by an exponentially small electric current and its universal applicability to Si-, Ge- and GaAs-based heterostructures. These advantages originate in the formation of the robust chiral quasi bound states of light holes localized in the quantum dot in the vicinity of the quantum wire with heavy holes. This specific structural design is not realized to date, so it represents a promising challenge for the fabrication techniques of the nanoscale heterostructures. |
1 Introduction
With the approach of the quantum computation era1 the localized spins in quantum dots (QDs) remain the most prominent candidates for scalable quantum simulations and quantum information processing.2–4 The electron spins can be already efficiently transferred in chains of QDs using the well-controlled spin–spin interactions, entangled spin states can be generated, and CNOT-gates can be realized with very high fidelity.5–10However, electrical polarization of individual spins in QDs still remains a vital problem. Basically, this can be performed due to the pronounced spin–orbit interaction in most of the semiconductors. Historically, the current-induced spin polarization was first proposed theoretically and realized experimentally for bulk Te, which is a gyrotropic material.11,12 Later the current-induced spin polarization was demonstrated for quantum wells made of GaAs-like semiconductors,13,14 strained bulk semiconductors,15 and epilayers.16,17 However, the maximum degree of current-induced spin polarization is limited to a few percent because of the weakness of the momentum-dependent spin–orbit splitting compared to the Fermi energy.18 Streaming and hopping conductivity regimes can increase the polarization a few times,19,20 but it still remains much smaller than unity.
In this paper we demonstrate that the strong spin–orbit splitting of the valence band can be exploited to create 100% spin polarization of holes localized in QDs in specifically designed structures. This splitting is large; for example, it is of the order of 300 meV in GaAs and Ge and is about 70 meV in Si. Thus, our proposal is equally relevant for high-quality optically-addressable GaAs-based structures,21–23 most technologically advanced Si-based structures,24–26 and emerging Ge-based structures.27–30
Microscopically, the current-induced spin polarization takes place due to the spin-dependent hole tunneling, which leads to the formation of chiral quasi bound states in the continuum.31,32 This represents a new concept that has some similarities to the spin filtering in magnetic fields33 and chiral photonics.34–36 A similar chirality-induced spin selectivity is also used to control spin by non-magnetic means in various molecular systems.37–40
2 System under study
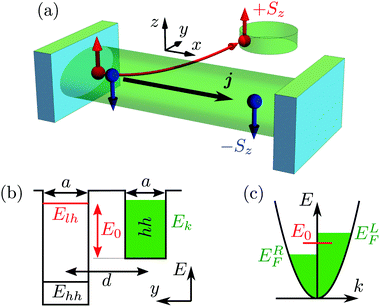
The system under study represents a quantum dot weakly side-coupled to a quantum wire,41–43 see Fig. 1. We assume the structure to be formed electrostatically in a two-dimensional hole gas with a strong splitting between heavy and light hole subbands in the material with the top of the valence band described by Γ8 representation of the Td group or Γ8+ representation of the Oh group. We consider the Fermi energy of heavy holes in the wire to be close to the energy of light hole state localized in the QD, as shown in Fig. 1(b). The heavy hole state in the QD is assumed to be deeply below the Fermi energy, so this state is always doubly occupied. Thus we will take into account only the tunneling between heavy holes in the quantum wire and light holes in the QD.The proposed device is described by the C2v symmetry group. We choose the coordinate frame to have the x axis along the quantum wire and the z axis along the structure growth axis, as shown in Fig. 1(a). Clearly, the electric current jx of heavy holes flowing along the wire can linearly couple to the light hole spin Sz in the QD along the z axis. The symmetry of this effect is the same as that of the Mott scattering or the spin Hall effect, so the spin polarization would change sign for the QD placed at the opposite side of the quantum wire. The current-induced spin polarization does not require any magnetic field or microscopic symmetry reduction, i.e. Rashba or Dresselhaus spin–orbit interactions, and it appears even in the centrosymmetric materials such as Si and Ge along with GaAs. Because of this, a very large degree of spin polarization can be achieved, which we demonstrate below.
The Hamiltonian of the system can be written as follows:
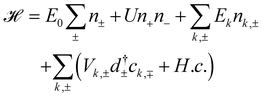 | (1) |
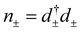 are the occupancies of this state by holes with the spin ±1/2 along the z axis, respectively, with d± being the corresponding annihilation operators, U is the Coulomb interaction energy between the two localized light holes, Ek denotes the energy of a heavy hole in the quantum wire with the wave vector k,
are the occupancies of this state by holes with the spin ±1/2 along the z axis, respectively, with d± being the corresponding annihilation operators, U is the Coulomb interaction energy between the two localized light holes, Ek denotes the energy of a heavy hole in the quantum wire with the wave vector k, 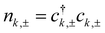 are the occupancies of the states in the wire with the spin ±3/2 with ck,± being the corresponding annihilation operators. We assume the wire to be ballistic and neglect the interaction between holes in it.
are the occupancies of the states in the wire with the spin ±3/2 with ck,± being the corresponding annihilation operators. We assume the wire to be ballistic and neglect the interaction between holes in it.
Most importantly, Vk,± in eqn (1) denote the tunneling matrix elements between the quantum wire and the QD. They are produced by the off-diagonal elements of the Luttinger Hamiltonian44,45 and can be calculated as follows:
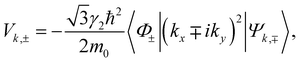 | (2) |
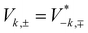 . We note that the heavy hole mass along the wire is given by m = m0/(γ1 + γ2), where γ1 is the first Luttinger parameter, and the dispersion is given by Ek = ħ2k2/(2m). We chose the state with k = 0 to be the energy reference.
. We note that the heavy hole mass along the wire is given by m = m0/(γ1 + γ2), where γ1 is the first Luttinger parameter, and the dispersion is given by Ek = ħ2k2/(2m). We chose the state with k = 0 to be the energy reference.
To be specific, let us consider the Gaussian wave functions:
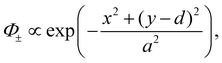 | (3a) |
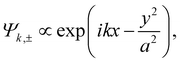 | (3b) |
To calculate the matrix elements Vk,± after eqn (2) we note that kx can be replaced with k, while iky = ∂/∂y. Then we solve the integrals over x and y analytically and obtain
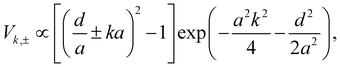 | (4) |
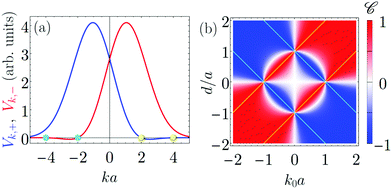 | ||
Fig. 2 (a) Tunneling matrix elements calculated after eqn (2) for d = 3a. (b) Chirality ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) of the quasi bound state calculated after eqn (5). The negative values of d correspond to the location of the QD at the opposite side of the quantum wire. of the quasi bound state calculated after eqn (5). The negative values of d correspond to the location of the QD at the opposite side of the quantum wire. | ||
Intuitively, one can imagine that a hole tunnels from the quantum wire to the quantum dot along a rounding trajectory, as shown in Fig. 1(a). The orbital rotation of the hole in the (xy) plane makes the system chiral and results in an effective magnetic field acting on the hole spin due to the spin–orbit interaction. This field favors tunneling of holes with a certain spin direction and leads to conversion from heavy to light holes.
The single particle states of the Hamiltonian (1) are well known from the studies of Anderson and Fano.46–48 The coupling between the QD and the quantum wire leads to the formation of the quasi bound states at the energy 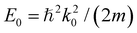 . Their chirality (also termed directionality)
. Their chirality (also termed directionality) ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) can be defined as the difference of the probabilities for a light hole with a given spin to tunnel from the QD to the quantum wire states propagating to the right and to the left:32,34,49
can be defined as the difference of the probabilities for a light hole with a given spin to tunnel from the QD to the quantum wire states propagating to the right and to the left:32,34,49
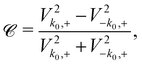 | (5) |
The chirality of the quasi bound state is shown in Fig. 2(b) as a color map. The regions with k0 < 0 and d < 0 show that the chirality is odd under reflection in the (yz) and (xz) planes, respectively. Generally, the absolute value of the chirality is of the order of unity.
Notably, it turns to unity exactly along the four lines given by the equation
| k0a = ±d/a ± 1, | (6) |
As a result, completely chiral bound states in the continuum are formed at certain energies, where the light hole state in the QD couples to the states in the wire propagating only in one direction. These completely chiral bound states in the continuum are robust and appear almost for any choice of the QD and the quantum wire wave functions, as we have checked.
The Gaussian form of the wave functions (3) corresponds to the parabolic localization potential, so at k0a > 2 the coupling to the second size quantized subband of the quantum wire can play a role. Still in the most realistic region of k0a < 2 and d/a ≳ 2 the chirality is very close to unity.
3 Formalism
To calculate the current-induced spin polarization in the nonequilibrium steady state, we use the Keldysh diagram technique.50–52 We start from the bare Hubbard retarded Green's function of an isolated QD:53,54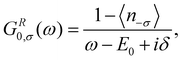 | (7) |
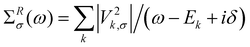 we obtain from the Dyson equation
we obtain from the Dyson equation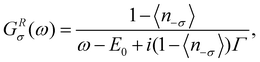 | (8) |
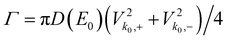 is the width of the quasi bound state with
is the width of the quasi bound state with 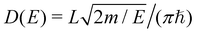 being the total density of states in the quantum wire. This expression includes the suppression of the tunneling rate Γ due to the Coulomb blockade. We assume Γ to be much smaller than the band width E1/a (wide band approximation) and neglect the quasi bound state energy renormalization. Note that for Γ ≪ E1/a the corresponding uncertainty of k is much smaller than 1/a, so the dependence of the tunneling matrix elements on k can be neglected†.
being the total density of states in the quantum wire. This expression includes the suppression of the tunneling rate Γ due to the Coulomb blockade. We assume Γ to be much smaller than the band width E1/a (wide band approximation) and neglect the quasi bound state energy renormalization. Note that for Γ ≪ E1/a the corresponding uncertainty of k is much smaller than 1/a, so the dependence of the tunneling matrix elements on k can be neglected†.
The occupancies of the QD states are given by the lesser Green's function:
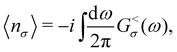 | (9) |
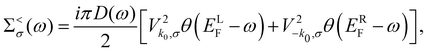 | (10) |
 | (11) |
This set of two equations allows us to find self-consistently the occupancies of the spin states 〈nσ〉. Ultimately, the degree of current-induced spin polarization in the QD is given by P = (〈n+〉 − 〈n−〉)/(〈n+〉 + 〈n−〉).
We note that this approach is valid on one hand for the temperatures below Γ, when the heavy hole distribution functions in the leads can be approximated by the step functions. The role of finite temperature is discussed in the ESI.† On the other hand, the temperature is assumed to be larger than the Kondo temperature TK, so that the high order correlations between holes can be neglected.54 In fact, the retarded Green's function (8) without quasi bound state width renormalization can be obtained from the equations of motion in the Hartree–Fock approximation.55 The Kondo effect at low temperatures can be taken into account, for example, using equations of motion truncated in an appropriate way at the temperatures of the order of TK56,57 or much smaller than it.55 In the Kondo regime the very sharp peak in density of states58 may lead to a strong increase of current-induced spin polarization at small biases. This question, however, deserves a deeper investigation.
4 Results
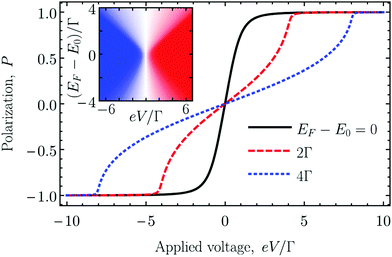
It follows from eqn (11) that the chirality of the quasi bound state![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) produces explicit spin-dependence of the occupancies provided a nonzero bias eV = ELF − ERF is applied to the quantum wire. The current-induced spin polarization is plotted in Fig. 3 as a function of bias for the different positions of the Fermi energy EF = (ELF + ERF)/2 for the completely chiral quasi bound state,
produces explicit spin-dependence of the occupancies provided a nonzero bias eV = ELF − ERF is applied to the quantum wire. The current-induced spin polarization is plotted in Fig. 3 as a function of bias for the different positions of the Fermi energy EF = (ELF + ERF)/2 for the completely chiral quasi bound state, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = 1. Generally, it is an odd function of the applied voltage and for the large voltages its absolute value reaches 100%. For the resonant case, EF = E0, the spin polarization saturates at eV ∼ Γ and for the detuned case it saturates at eV ∼ 2|EF − E0|, as clearly seen from the inset in Fig. 3. Generally, the current-induced spin polarization is the largest when the energy of the quasi bound state E0 lies between the Fermi energies of the left and right leads, as it is shown in Fig. 1(c). In this case the holes flowing from the left can tunnel to the one spin state in the QD only due to its chirality, while the holes flowing from the right at the corresponding energy are absent due to the large bias. For
= 1. Generally, it is an odd function of the applied voltage and for the large voltages its absolute value reaches 100%. For the resonant case, EF = E0, the spin polarization saturates at eV ∼ Γ and for the detuned case it saturates at eV ∼ 2|EF − E0|, as clearly seen from the inset in Fig. 3. Generally, the current-induced spin polarization is the largest when the energy of the quasi bound state E0 lies between the Fermi energies of the left and right leads, as it is shown in Fig. 1(c). In this case the holes flowing from the left can tunnel to the one spin state in the QD only due to its chirality, while the holes flowing from the right at the corresponding energy are absent due to the large bias. For ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) < 1 the shape of this dependence is qualitatively the same.
< 1 the shape of this dependence is qualitatively the same.
Thus the large spin polarization can be induced by the voltages of the order of Γ. It is proportional to the squared tunneling matrix elements, which are given by eqn (4), and contain an exponentially small factor exp[−d2/(2a2)]. As a result, the tunneling rate Γ can be extremely small, which means that the spin polarization can saturate, in principle, at exponentially small bias. The ultimate limit for Γ is set by the spin relaxation time in an isolated QD. In the absence of a magnetic field, the nuclear spin fluctuations lead to the spin relaxation at the nanosecond time scale,59,60 which corresponds to Γ ∼ 1 μeV. However, to achieve this giant spin sensitivity the temperature of the system should be as low as a few millikelvins. Otherwise the applied bias should exceed the thermal energy, see the corresponding analysis in the ESI.†
The spin polarization in the limit of large bias can be found from eqn (11) by setting the first arctangent to π/2 and the second one to −π/2. This gives:
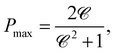 | (12) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) with
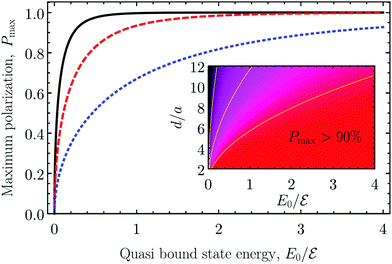
with ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = ħ2/2ma2 corresponds to the energies below the bottom of the second size quantized band of the quantum wire. Generally, the maximum spin polarization decreases with increase of the distance between the quantum wire and the QD because of the chirality decrease shown in Fig. 2(b). However, it is still close to unity almost in the whole range of the quasi bound state energies E0 up to d ∼ 10a. We note that this corresponds to the suppression of the quasi bound state width by a giant factor of ed2/a2. The inset in Fig. 4 explicitly shows the range of parameters where the current-induced spin polarization at large bias exceeds 90%. This range can be even larger for the different form of the wave functions†.
= ħ2/2ma2 corresponds to the energies below the bottom of the second size quantized band of the quantum wire. Generally, the maximum spin polarization decreases with increase of the distance between the quantum wire and the QD because of the chirality decrease shown in Fig. 2(b). However, it is still close to unity almost in the whole range of the quasi bound state energies E0 up to d ∼ 10a. We note that this corresponds to the suppression of the quasi bound state width by a giant factor of ed2/a2. The inset in Fig. 4 explicitly shows the range of parameters where the current-induced spin polarization at large bias exceeds 90%. This range can be even larger for the different form of the wave functions†.
5 Discussion
The current-induced spin polarization can be directly detected optically using the spin-induced Faraday rotation at the related resonances, for example, with the trion optical transitions in the QD. Alternatively, the spin polarization can be detected electrically using ferromagnetic contacts including magnetic microscope tips or using an additional QD weakly coupled to the main one due to the spin blockade effect and exchange interaction between the two QDs.61 There is also an inverse effect: the spin generation in the QD by external means would lead to the spin galvanic effect, e.g. to the current in the wire, which can be measured electrically.We note also that if the two QDs are placed at the opposite sides of the quantum wire, the electric current produces the opposite spin polarizations in them similar to the spin Hall effect, as can be seen from the chirality shown in Fig. 2(b). However, for a single QD the hole spin flips are more efficient in one direction than in the opposite, so the total spin polarization of holes in the system is nonzero in contrast with the spin Hall effect.
We stress that the proposed mechanism of the current-induced spin polarization via the chiral quasi bound states does not require magnetic field or linear in momentum spin–orbit coupling in contrast to the previous approaches. The spin–orbit interaction required here describes the splitting of the valence band exactly at the center of the Brillouin zone. It results in the off-diagonal matrix elements of the Luttinger Hamiltonain [see eqn (2)], which are related to the diagonal ones as γ2/γ1. We stress that this ratio is not parametrically small and amounts, for example, to 0.28, 0.08, and 0.32 in GaAs, Si and Ge, respectively. The close to unity spin polarization is equally possible in all these materials.
To give a specific example of the system parameters to observe the effect, we consider a two-dimensional hole gas in the GaAs/AlGaAs heterostructure.41,43,62–70 The typical parameters of the system are a = 100 nm, Fermi energy EF = 0.2 meV, coupling strength Γ = 10 μeV, and temperature T = 100 mK. The temperature should be low enough to consider a degenerate hole gas. Then at bias larger than 10 μV we predict the possibility of complete current-induced hole spin polarization.
6 Conclusions
We demonstrated that the complex valence band structure leads to chirality of the quasi bound states of light holes in the QD side-coupled to the quantum wire with heavy holes. The current flowing along the quantum wire produces nonequilibrium spin polarization of holes in the QD. This new mechanism of current-induced spin polarization has the following advantages: (i) it takes place for exponentially small applied voltages. (ii) It does not require magnetic fields and can be applied to centrosymmetric materials. (iii) In a broad range of the geometric parameters, the current-induced spin polarization reaches 100%.Author contributions
V. N. M. and D. S. S.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft preparation, and writing – review and editing (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank L. E. Golub, M. M. Glazov, I. V. Krainov, and V. S. Khrapai for fruitful discussions. We acknowledge RF President Grant No. MK-5158.2021.1.2 and the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS”. Analytical calculations by D.S.S were supported by the Russian Science Foundation grant No. 21-72-10035. V. N. M. acknowledges support by a President grant for young scientists MD-781.2021.1 and support from the Interdisciplinary Scientific and Educational School of Moscow University “Photonic and Quantum technologies. Digital medicine”.Notes and references
- M. I. Dyakonov, Will We Ever Have a Quantum Computer?, Springer Nature, 2020 Search PubMed.
- T. F. Watson, S. G.-J. Philips, E. Kawakami, D. R. Ward, P. Scarlino, M. Veldhorst, D. E. Savage, M. G. Lagally, M. Friesen, S. N. Coppersmith, M. A. Eriksson and L. M.-K. Vandersypen, Nature, 2018, 555, 633 CrossRef CAS PubMed.
- J. Yoneda, K. Takeda, T. Otsuka, T. Nakajima, M. R. Delbecq, G. Allison, T. Honda, T. Kodera, S. Oda, Y. Hoshi, N. Usami, K. M. Itoh and S. Tarucha, Nat. Nanotechnol., 2018, 13, 102 CrossRef CAS PubMed.
- C. H. Yang, R. C.-C. Leon, J. C.-C. Hwang, A. Saraiva, T. Tanttu, W. Huang, J. Camirand Lemyre, K. W. Chan, K. Y. Tan, F. E. Hudson, K. M. Itoh, A. Morello, M. Pioro-Ladriére, A. Laucht and A. S. Dzurak, Nature, 2020, 580, 350 CrossRef CAS PubMed.
- K. C. Nowack, F. H.-L. Koppens, Y. V. Nazarov and L. M.-K. Vandersypen, Science, 2007, 318, 1430–1433 CrossRef CAS PubMed.
- D. M. Zajac, A. J. Sigillito, M. Russ, F. Borjans, J. M. Taylor, G. Burkard and J. R. Petta, Science, 2018, 359, 439 CrossRef CAS PubMed.
- F. Basso Basset, M. B. Rota, C. Schimpf, D. Tedeschi, K. D. Zeuner, S. F. Covre da Silva, M. Reindl, V. Zwiller, K. D. Jöns, A. Rastelli and R. Trotta, Phys. Rev. Lett., 2019, 123, 160501 CrossRef CAS PubMed.
- A. R. Mills, D. M. Zajac, M. J. Gullans, F. J. Schupp, T. M. Hazard and J. R. Petta, Nat. Commun., 2019, 10, 1063 CrossRef CAS PubMed.
- H. Qiao, Y. P. Kandel, S. Fallahi, G. C. Gardner, M. J. Manfra, X. Hu and J. M. Nichol, Phys. Rev. Lett., 2021, 126, 017701 CrossRef CAS PubMed.
- S. G. Carter, S. C. Badescu, A. S. Bracker, M. K. Yakes, K. X. Tran, J. Q. Grim and D. Gammon, Phys. Rev. Lett., 2021, 126, 107401 CrossRef CAS PubMed.
- E. L. Ivchenko and G. E. Pikus, JETP Lett., 1978, 27, 604 Search PubMed.
- L. E. Vorob’ev, E. L. Ivchenko, G. E. Pikus, I. I. Farbshtein, V. A. Shalygin and A. V. Shturbin, JETP Lett., 1979, 29, 441 Search PubMed.
- S. D. Ganichev, S. N. Danilov, P. Schneider, V. V. Bel’kov, L. E. Golub, W. Wegscheider, D. Weiss and W. Prettl, J. Magn. Magn. Mater., 2006, 300, 127 CrossRef CAS.
- A. Y. Silov, P. A. Blajnov, J. H. Wolter, R. Hey, K. H. Ploog and N. S. Averkiev, Appl. Phys. Lett., 2004, 85, 5929 CrossRef CAS.
- Y. K. Kato, R. C. Myers, A. C. Gossard and D. D. Awschalom, Phys. Rev. Lett., 2004, 93, 176601 CrossRef CAS PubMed.
- B. M. Norman, C. J. Trowbridge, D. D. Awschalom and V. Sih, Phys. Rev. Lett., 2014, 112, 056601 CrossRef CAS PubMed.
- I. Stepanov, S. Kuhlen, M. Ersfeld, M. Lepsa and B. Beschoten, Appl. Phys. Lett., 2014, 104, 062406 CrossRef.
- S. D. Ganichev, M. Trushin and J. Schliemann, Spin polarization by current in Handbook of Spin Transport and Magnetism, ed. E. Y. Tsymbal and I. Zutic, Chapman & Hall, Boca Raton, 2012, p. 487 Search PubMed.
- L. E. Golub and E. L. Ivchenko, New J. Phys., 2013, 15, 125003 CrossRef.
- D. S. Smirnov and L. E. Golub, Phys. Rev. Lett., 2017, 118, 116801 CrossRef CAS PubMed.
- D. Huber, M. Reindl, Y. Huo, H. Huang, J. S. Wildmann, O. G. Schmidt, A. Rastelli and R. Trotta, Nat. Commun., 2017, 8, 15506 CrossRef CAS PubMed.
- E. A. Chekhovich, S. F.-C. da Silva and A. Rastelli, Nat. Nanotechnol., 2020, 15, 999 CrossRef CAS PubMed.
- D. Najer, I. Söllner, P. Sekatski, V. Dolique, M. C. Löbl, D. Riedel, R. Schott, S. Starosielec, S. R. Valentin, A. D. Wieck, N. Sangouard, A. Ludwig and R. J. Warburton, Nature, 2019, 575, 622 CrossRef CAS PubMed.
- M. Veldhorst, C. H. Yang, J. C.-C. Hwang, W. Huang, J. P. Dehollain, J. T. Muhonen, S. Simmons, A. Laucht, F. E. Hudson, K. M. Itoh, A. Morello and A. S. Dzurak, Nature, 2015, 526, 410–414 CrossRef CAS PubMed.
- X. Mi, J. V. Cady, D. M. Zajac, P. W. Deelman and J. R. Petta, Science, 2017, 355, 156–158 CrossRef CAS PubMed.
- F. Borjans, X. Croot, X. Mi, M. Gullans and J. Petta, Nature, 2020, 577, 195–198 CrossRef CAS PubMed.
- C. Kloeffel, M. Trif and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195314 CrossRef.
- X.-J. Hao, T. Tu, G. Cao, C. Zhou, H.-O. Li, G.-C. Guo, W. Y. Fung, Z. Ji, G.-P. Guo and W. Lu, Nano Lett., 2010, 10, 2956–2960 CrossRef CAS PubMed.
- N. Hendrickx, D. Franke, A. Sammak, G. Scappucci and M. Veldhorst, Nature, 2020, 577, 487–491 CrossRef CAS PubMed.
- F. N.-M. Froning, L. C. Camenzind, O. A.-H. van der Molen, A. Li, E. P.-A. M. Bakkers, D. M. Zumbühl and F. R. Braakman, Nat. Nanotechnol., 2021, 16, 308–312 CrossRef CAS PubMed.
- C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos and M. Soljačić, Nat. Rev. Mater., 2016, 1, 16048 CrossRef CAS.
- A. Overvig, N. Yu and A. Alù, Phys. Rev. Lett., 2021, 126, 073001 CrossRef CAS PubMed.
- M. Vallejo, M. Ladrón de Guevara and P. Orellana, Phys. Lett. A, 2010, 374, 4928–4932 CrossRef CAS.
- F. Spitzer, A. N. Poddubny, I. A. Akimov, V. F. Sapega, L. Klompmaker, L. E. Kreilkamp, L. V. Litvin, R. Jede, G. Karczewski, M. Wiater, T. Wojtowicz, D. R. Yakovlev and M. Bayer, Nat. Phys., 2018, 14, 1043 Search PubMed.
- X. Yin, J. Jin, M. Soljačić, C. Peng and B. Zhen, Nature, 2020, 580, 467 CrossRef CAS PubMed.
- J. Lin, J. P.-B. Mueller, Q. Wang, G. Yuan, N. Antoniou, X.-C. Yuan and F. Capasso, Science, 2013, 340, 331 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250 CrossRef CAS.
- B. P. Bloom, B. M. Graff, S. Ghosh, D. N. Beratan and D. H. Waldeck, J. Am. Chem. Soc., 2017, 139, 9038 CrossRef CAS PubMed.
- S. P. Mathew, P. C. Mondal, H. Moshe, Y. Mastai and R. Naaman, Appl. Phys. Lett., 2014, 105, 242408 CrossRef.
- O. Ben Dor, N. Morali, S. Yochelis, L. T. Baczewski and Y. Paltiel, Nano Lett., 2014, 14, 6042 CrossRef CAS PubMed.
- M. Sato, H. Aikawa, K. Kobayashi, S. Katsumoto and Y. Iye, Phys. Rev. Lett., 2005, 95, 066801 CrossRef PubMed.
- H. Edlbauer, S. Takada, G. Roussely, M. Yamamoto, S. Tarucha, A. Ludwig, A. D. Wieck, T. Meunier and C. Bäuerle, Nat. Commun., 2017, 8, 1710 CrossRef PubMed.
- I. V. Borzenets, J. Shim, J. C.-H. Chen, A. Ludwig, A. D. Wieck, S. Tarucha, H.-S. Sim and M. Yamamoto, Nature, 2020, 579, 210 CrossRef PubMed.
- J. M. Luttinger, Phys. Rev., 1956, 102, 1030–1041 CrossRef CAS.
- E. L. Ivchenko, Optical spectroscopy of semiconductor nanostructures, Alpha Science, Harrow UK, 2005 Search PubMed.
- P. W. Anderson, Phys. Rev., 1961, 124, 41 CrossRef CAS.
- U. Fano, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- M. F. Limonov, M. V. Rybin, A. N. Poddubny and Y. S. Kivshar, Nat. Photonics, 2017, 11, 543 CrossRef CAS.
- P. Lodahl, S. Mahmoodian, S. Stobbe, A. Rauschenbeutel, P. Schneeweiss, J. Volz, H. Pichler and P. Zoller, Nature, 2017, 541, 473–480 CrossRef CAS PubMed.
- J. Rammer and H. Smith, Rev. Mod. Phys., 1986, 58, 323 CrossRef CAS.
- G. Stefanucci and R. van Leeuwen, Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction, Cambridge University Press, 2013 Search PubMed.
- P. I. Arseev, Phys.-Usp., 2015, 58, 1159 CrossRef.
- J. Hubbard and B. H. Flowers, Proc. R. Soc. London, Ser. A, 1963, 276, 238 Search PubMed.
- H. Haug and A.-P. Jauho, Quantum kinetics in transport and optics of semiconductors, Springer, 2008, vol. 2 Search PubMed.
- C. Lacroix, J. Phys. F: Met. Phys., 1981, 11, 2389 CrossRef CAS.
- Y. Meir, N. S. Wingreen and P. A. Lee, Phys. Rev. Lett., 1993, 70, 2601 CrossRef PubMed.
- R. S. Świrkowicz, J. Barnaś and M. Wilczyński, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195318 CrossRef.
- A. C. Hewson, The Kondo problem to heavy fermions, Cambridge university press, 1997 Search PubMed.
- M. M. Glazov, Electron and Nuclear Spin Dynamics in Semiconductor Nanostructures, Oxford University Press, Oxford, 2018 Search PubMed.
- D. S. Smirnov, E. A. Zhukov, D. R. Yakovlev, E. Kirstein, M. Bayer and A. Greilich, Phys. Rev. B, 2020, 102, 235413 CrossRef CAS.
- R. Hanson, L. P. Kouwenhoven, J. R. Petta, S. Tarucha and L. M.-K. Vandersypen, Rev. Mod. Phys., 2007, 79, 1217 CrossRef CAS.
- I. Zailer, J. E.-F. Frost, C. J.-B. Ford, M. Pepper, M. Y. Simmons, D. A. Ritchie, J. T. Nicholls and G. A.-C. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5101–5104 CrossRef CAS PubMed.
- W. R. Clarke, A. P. Micolich, A. R. Hamilton, M. Y. Simmons, K. Muraki and Y. Hirayama, J. Appl. Phys., 2006, 99, 023707 CrossRef.
- S. P. Koduvayur, L. P. Rokhinson, D. C. Tsui, L. N. Pfeiffer and K. W. West, Phys. Rev. Lett., 2008, 100, 126401 CrossRef CAS PubMed.
- J. Shabani, J. R. Petta and M. Shayegan, Appl. Phys. Lett., 2008, 93, 212101 CrossRef.
- S. Sasaki, H. Tamura, T. Akazaki and T. Fujisawa, Phys. Rev. Lett., 2009, 103, 266806 CrossRef CAS PubMed.
- T. Otsuka, E. Abe, Y. Iye and S. Katsumoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195313 CrossRef.
- T. Otsuka, E. Abe, Y. Iye and S. Katsumoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245302 CrossRef.
- J. C.-H. Chen, D. Q. Wang, O. Klochan, A. P. Micolich, K. Das Gupta, F. Sfigakis, D. A. Ritchie, D. Reuter, A. D. Wieck and A. R. Hamilton, Appl. Phys. Lett., 2012, 100, 052101 CrossRef.
- A. Srinivasan, D. S. Miserev, K. L. Hudson, O. Klochan, K. Muraki, Y. Hirayama, D. Reuter, A. D. Wieck, O. P. Sushkov and A. R. Hamilton, Phys. Rev. Lett., 2017, 118, 146801 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed calculation of the tunneling matrix elements and the Keldysh formalism for arbitrary interaction strength and finite temperatures, as well as the detailed analysis of the limits of weak and strong interaction. See DOI: https://doi.org/10.1039/d1nh00685a |
| This journal is © The Royal Society of Chemistry 2022 |