Open Access Article
Open Access ArticleAnnealing post-drawn polycaprolactone (PCL) nanofibers optimizes crystallinity and molecular alignment and enhances mechanical properties and drug release profiles†
Matthew D.
Flamini
 a,
Thamires
Lima
a,
Thamires
Lima
 b,
Kerri
Corkum
a,
Nicolas J.
Alvarez
b,
Kerri
Corkum
a,
Nicolas J.
Alvarez
 b and
Vince
Beachley
b and
Vince
Beachley
 *a
*a
aDepartment of Biomedical Engineering, Rowan University, Glassboro, New Jersey 08028, USA. E-mail: beachley@rowan.edu
bDepartment of Chemical and Biological Engineering, Drexel University, Philadelphia, PA, USA
First published on 9th March 2022
Abstract
Post-drawn PCL nanofibers can be molecularly tuned to have a variety of mechanical properties and drug release profiles depending on the temperature and time of annealing, which has implications for regenerative medicine and drug delivery applications. Post-drawing polycaprolactone (PCL) nanofibers has previously been demonstrated to drastically increase their mechanical properties. Here the effects of annealing on post-drawn PCL nanofibers are characterized. It is shown that room temperature storage and in vivo temperatures increase crystallinity significantly on the order of weeks, and that high temperature annealing near melt significantly increases crystallinity and molecular orientation on the order of minutes. The kinetics of crystallization were assessed using an anneal and quench approach. High temperature annealing also increased the ultimate tensile strength and toughness of the fibers and changed the release profile of a model drug absorbed in PCL nanofibers from first-order to zero-order kinetics.
Introduction
Polycaprolactone (PCL) is a semicrystalline linear aliphatic polyester with a melting point around 60 °C that is commonly used in biomedical applications because it is highly biocompatible and biodegradable. It has been successfully tested in several tissue engineering applications, including for the regeneration of cardiovascular, bone and nerve tissue. It also can be used for controlled release of small molecule and biopharmaceutical drugs. PCL is also readily electrospun into nanofibers, the properties of which can vary greatly depending on spinning and post processing conditions.1For many biomedical applications, such as nerve or ligament regeneration, highly aligned nanofibers are required in order to mimic the aligned collagen fibers found in healthy tissue.2–7 Manufacturing such fibers is typically done by either collecting between two parallel plates,8 or on a rotating mandrel.9 A key strength of electrospinning is that the fibers are drawn in flight before they reach the collector, which can briefly increase the fibers level of molecular alignment. However, the draw is applied while the fibers are not completely free of solvent, which allows chain relaxation to set in upon the cessation of jet velocity when the fiber reaches a collector. This chain relaxation can reverse molecular alignment gains and eliminate this benefit of electrospinning.
Our group has previously demonstrated an automated parallel plate style belt collection system that post-draws electrospun nanofibers at the collector stage. This approach decouples the in-flight drawing and collector stage post-drawing processes.10 It allows for the collection, drying, and drawing of individual fibers, and has resulted in the strongest PCL nanofibers in the literature, due to their high degree of molecular alignment. While post-drawing to increase molecular alignment has yielded high performance fibers, the fibers are still far from their theoretical maximum strength. It has been shown that enhanced molecular alignment via post-drawing can come at the cost of decreasing crystallinity,11 despite the effects of strain induced crystallization. However, we hypothesize that the addition of an annealing step, which is commonly used in textile manufacturing processes to strengthen fibers, can be used to increase the crystallinity of PCL nanofibers and facilitate optimization to specific applications.
It has been demonstrated that the degree of crystallinity and crystalline morphology has a substantial effect on the elastic modulus, elongation, and toughness of PCL nanofibers,12 and that annealing PCL nanofibers increases crystallinity.13–15 Increasing the degree of crystallinity has also been shown to have the desirable effect of extending degradation/drug release kinetics in PCL.16 This effect has been demonstrated in thin films17,18 and microspheres.19 However, the crystallization kinetics, optimal temperature, and overall changes in crystallinity have not been studied in post-drawn nanofibers.
Although much is known about the material properties of bulk PCL, the crystal properties of post-drawn nanofibers and the functional properties affected by them may differ significantly from that of bulk material, and even other electrospun PCL nanofibers. This is due to the highly aligned nature of post-drawn nanofibers, and the spatial confinement of the molecules in the fiber. Despite this knowledge gap, the crystallization of post-drawn PCL nanofibers has not been well studied. The high degree of orientation may simulate the state of recently melted crystals, whose thermal history has not been completely erased. Such molecular structures have been shown to crystallize more rapidly and at lower temperatures than bulk material.20,21 We aim to characterize the isothermal crystallization kinetics by performing an Avrami analysis on annealed fibers.22 Avrami analysis has been shown to be valid for thin confined nano-scale layers of PCL, with the thinnest layers showing significant slowing of crystallization.23 Nanofibers confine an additional dimension, so there is no certainty the Avrami model will extend to nanofibers.
Given the theoretical propensity for crystallization in highly oriented, drawn nanofibers, there is also the possibility of unwanted crystallization that can occur during room temperature storage and handling, and in the body. This could lead to dimensional changes such as shrinking, or changes in mechanical, drug release, or degradation profiles that were not accounted for in the manufacturing process.
Annealing and quenching in water baths has long been used in the textile industry to anneal polymer fibers. We principally aim to characterize the effects these processes have on the molecular structure regarding crystallinity, molecular alignment, and the associated kinetics, while also demonstrating the sort of effects these changes have on material properties of interest for biomedical applications and techniques that can be used. Critically, the study will characterize the crystallinity of the nanofibers in a novel manner: by employing polarized FTIR, which can determine not only crystallinity, but also crystal orientation, and by using a treat and quench strategy to determine crystallization kinetics. We also aim to further understand the degree to which molecular mechanisms, such as crystal growth rate and crystal nucleation, are involved in changes in crystallinity in the nanofibers.
Materials and methods
Electrospinning and preparation of PCL nanofibers
Fibers were electrospun from polymer solutions containing 18% PCL (Mn 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma) in a 3
000, Sigma) in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
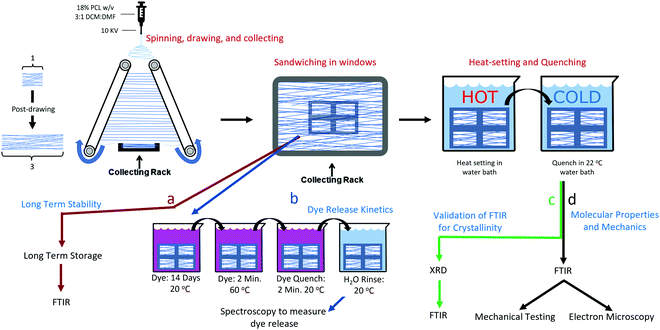
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dichloromethane (DCM, Acros Organics, CAS: 75-09-2) and dimethylformamide (DMF, Acros Organics, CAS: 68-12-2). The PCL solutions were transferred to 5 ml syringes and connected to a 21 gauge blunt tipped needle with polyethylene tubing. The needle tip was connected to a high voltage power source (Gamma High Voltage Research, ES04P-10W) operating at 10 kV, and the solution was extruded from the needle at a rate of 3.0 mL h−1. For aligned fibers, a grounded parallel plate automated track collection system was placed 15 cm below the needle. The system was set to post-draw the fibers at a draw ratio (DR, final length/initial length) of DR3 at a rate of 3 DR min−1. The gap between the two parallel collection points was 5 cm, and the fibers were drawn to a final length of 15 cm. The electrospinning setup is depicted in Fig. 1 and was described by Brennan et al.10
1 dichloromethane (DCM, Acros Organics, CAS: 75-09-2) and dimethylformamide (DMF, Acros Organics, CAS: 68-12-2). The PCL solutions were transferred to 5 ml syringes and connected to a 21 gauge blunt tipped needle with polyethylene tubing. The needle tip was connected to a high voltage power source (Gamma High Voltage Research, ES04P-10W) operating at 10 kV, and the solution was extruded from the needle at a rate of 3.0 mL h−1. For aligned fibers, a grounded parallel plate automated track collection system was placed 15 cm below the needle. The system was set to post-draw the fibers at a draw ratio (DR, final length/initial length) of DR3 at a rate of 3 DR min−1. The gap between the two parallel collection points was 5 cm, and the fibers were drawn to a final length of 15 cm. The electrospinning setup is depicted in Fig. 1 and was described by Brennan et al.10
To obtain unaligned (randomly oriented) nanofibers the fibers were spun onto flat sections of aluminum foil. To collect nanofiber samples in tension, an adhesive frame was used to fix the ends of the fibers after they were drawn. Fibers were collected onto frames so that four windows spanned a single narrow strip of fibers, such that four windows existed for each strip as shown in Fig. S1 (ESI†). This was done so that a direct comparison could be made between the treatments, and because some methods, such as SEM and mechanical tests are destructive, such that a sample can have only one of these tests performed. Framed fibers were used for the mechanical tests, FTIR, SEM, and dye release studies. For all tests other than the long-term kinetics, the fibers were allowed to sit at room temperature for at least two weeks, in order for their crystallinity to stabilize. It has been shown that PCL will continue to crystallize for up to two weeks at room temperature.24 Assessment of the long-term kinetics samples began immediately after spinning.
X-ray diffraction (XRD)
The purpose of taking XRD measurements was to validate an FTIR method for determining the crystallinity25 of PCL nanofibers. In order to compare crystallinity values between XRD and FTIR, three samples from the same electrospinning collection were treated at either 22, 55 or 70 °C. These were chosen because preliminary experiments showed these to be the low, mid and high mark for relative crystallinity as measured by FTIR. The XRD patterns of the three PCL mats (22, 55, and 70 °C) were measured at room temperature using a Rigaku SmartLab (Tokyo, Japan) operating at 40 kV/30 mA with Cu Kα, λ = 1.5406 Å radiation, from 2° ≤ 2θ ≤ 50°, with 0.02° step size, and 1 s per step. The X-ray data were fitted using the Fityk 1.3.1 software.26 The amorphous halos were fitted using Pseudo-Voigt and the crystalline peaks using Lorentzian functions applying Levenberg–Marquardt method. Crystallinity was calculated using eqn (1):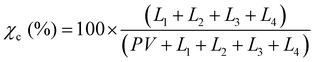 | (1) |
FTIR determination of alignment and crystallinity
FTIR measurements were taken at 8 scans at a resolution of 4 cm s−1, and were done with either no polarization, 0 degree polarization (aligned with fiber axis), or 90 degree polarization (perpendicular to fiber axis). Molecular alignment was obtained by determining the dichroic ratio at the C–O stretching band at ∼1160. Analysis of peak heights for calculating the dichroic ratio was done with custom MATLAB code that removed the baseline trend and measured the height of the peak located at ∼1160 cm−1. The dichroic ratio was calculated according to eqn (2):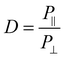 | (2) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching peak at ∼1727 cm−1. The fitting was done using the Fityk 1.3.1 software26 according to a protocol that was adapted from He and Inoue.25 Voigt functions were centered and fixed at 1725.5, 1736, and 1710 cm−1, with all other parameters allowed to change. The fit was performed with a Levenberg–Marquardt algorithm. The percent crystallinity was initially calculated according to eqn (3):
O stretching peak at ∼1727 cm−1. The fitting was done using the Fityk 1.3.1 software26 according to a protocol that was adapted from He and Inoue.25 Voigt functions were centered and fixed at 1725.5, 1736, and 1710 cm−1, with all other parameters allowed to change. The fit was performed with a Levenberg–Marquardt algorithm. The percent crystallinity was initially calculated according to eqn (3):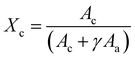 | (3) |
Long-term isothermal crystallization
The control group was placed in a Petri dish in a −20 °C freezer in order to inhibit further crystallization, while the 22 and 37 °C samples were placed in incubators of their respective temperatures. The crystallinity of the 22 and 37 °C samples were assessed using FTIR at days 0, 3, 7, 15, and 35. The −20 °C control was assessed at the first and last time-point.Isothermal crystallization: temperature optimization
Isothermal crystallization experiments were performed for temperatures 22, 37, 55, 60, 65, 70, and 75 °C. All samples were collected on the same day during the same collection period to ensure maximum uniformity between samples. The samples were stored at room temperature for at least 2 weeks to allow for crystallization to plateau. To prevent the samples from absorbing water during the water bath incubation, the framed fibers were placed in a small envelope of plastic film, from which all air was removed. The enveloped fiber samples were submerged into a water bath for 32 minutes and then were quickly transferred to a room temperature bath for at least 10 seconds. They were subsequently removed from the envelopes and their crystallinity and molecular alignment was measured with unpolarized and polarized FTIR, respectively. The temperature that rendered the highest crystallinity was further investigated to determine crystallization kinetics.Isothermal crystallization: kinetics
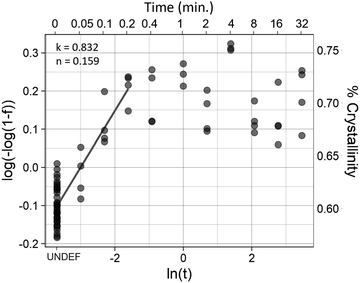
The initial crystallinity of each sample was assessed with polarized FTIR, then the samples were placed in a water bath for 0.05 (3 seconds), 0.10, 0.20, 0.40, 1.00, 2.00, 4.00, 8.00, 16.0, or 32.0 minutes. Samples were then quenched in a room temperature water bath before being measured again with FTIR for crystallinity.The Avrami exponent n and crystallization kinetic constant K at the temperature of maximum crystallization were determined by eqn (4a):
| Y = 1 – exp[–K(t)n] | (4a) |
ln(–ln[1 – Y(t)]) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) K + n K + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t | (4b) |
SEM
SEM images were taken to determine any morphological changes occurring during annealing and in order to assess fiber diameter and collection density, which was used to calculate the total cross-sectional area necessary for generating stress strain curves. ImageJ was used for all quantitative measurements.27Dye release study
To understand the effects of annealing on drug release kinetics, rhodamine B was absorbed into the fibers so as to be used as a model for small molecule drugs.28 Both aligned and random samples in both tension and relaxation, for a total of four groups across two treatment conditions (annealed at 60 °C and 22 °C) were prepared (Table 1). 60 °C was chosen because it had the highest mechanical strength of all the annealed samples, as well as having a balance of increased molecular alignment and crystallinity following annealing.| n | Heat | Tension | Aligned |
|---|---|---|---|
| 6 | x | x | x |
| 6 | x | x | |
| 6 | x | x | |
| 6 | x | ||
| 3 | x | x | |
| 3 | x | ||
| 3 | x | ||
| 3 |
To determine the weight of the nanofibers in tension the weight of the adhesive frame was recorded prior to capturing the nanofibers. This weight was subtracted from the weight of the adhesive frame and nanofibers recorded after capturing the nanofibers. Samples in tension were kept in tension for all dye incubation and heat treatments and rinsing, then cut from their frames right before they were placed in the initial timepoint vial for the release study. The untensioned samples were removed from the windows after collection and prior to dye incubation and heat treatments. A saturated solution of rhodamine B was created by adding 8.00 g rhodamine B to 1 L of PBS. Each nanofiber sample was soaked in 1000 μL of the saturated rhodamine B solutions for 14 days.
For annealing, each sample was placed in individual watertight bags filled with excess rhodamine B solution. The bags were submerged in either 60 °C (treated) or 22 °C water (control) for two minutes. The fibers were then removed from both the water bath and the watertight bags and allowed to quench in a room temperature water bath for an additional two minutes.
For each nanofiber sample, eight microcentrifuge tubes containing 1 mL of PBS were prepared. Directly after annealing and quenching, the samples were rinsed thoroughly in PBS by dipping 100 times. The samples were placed in the first vial for 45 minutes and removed with tweezers, and then moved to vial 2 for 30 minutes, vial 3 for 1.5 hours, vial 4 for 6.25 hours, vial 5 for 16 hours, vial 6 for 24 hours, vial 7 for one week, and vial 8 for one month.
In order to determine the remaining dye in the fibers, they were then removed from vial 8 and placed in 3.5 mL of lipase solution to dissolve. The concentration of dye was determined by spectrophotometry at wavelength 520 nm for all time points and measured against a calibration curve fitted using a 4-parameter logistic regression, including the lipase dissolved endpoint.
Mechanical testing
In order to prepare the samples for mechanical tests, the fibers were freed from the edges parallel to the fibers by cutting along the frame with a razor blade. The cross-sectional area of the samples was calculated by counting the fiber density and multiplying by the average fiber diameter as measured by SEM. Cross-sectional analysis was performed on a matched sample to ensure that the calculated fiber number was representative of the tensile tested sample (Fig. S1, ESI†).The samples were then gripped by the ends of the frame by the mechanical tester, and the sides of the frame removed by cutting. Tensile tests were performed at a rate of 0.2 mm min−1. The relevant mechanical properties were extracted from the stress–strain curves by a custom R script. To assess the effects of annealing and molecular properties on the various mechanical properties, linear or second-degree polynomials were fit to the data. Goodness of fit and statistical significance were assessed by the R2 and p-value of each fit, respectively. To assess the combined effect of crystallinity and alignment, a multivariable linear model was created by standardizing both percent crystallinity and dichroic ratio such that they both had a mean of 0 and a standard deviation of 1.
Results
X-ray diffraction validation of FTIR for crystallinity
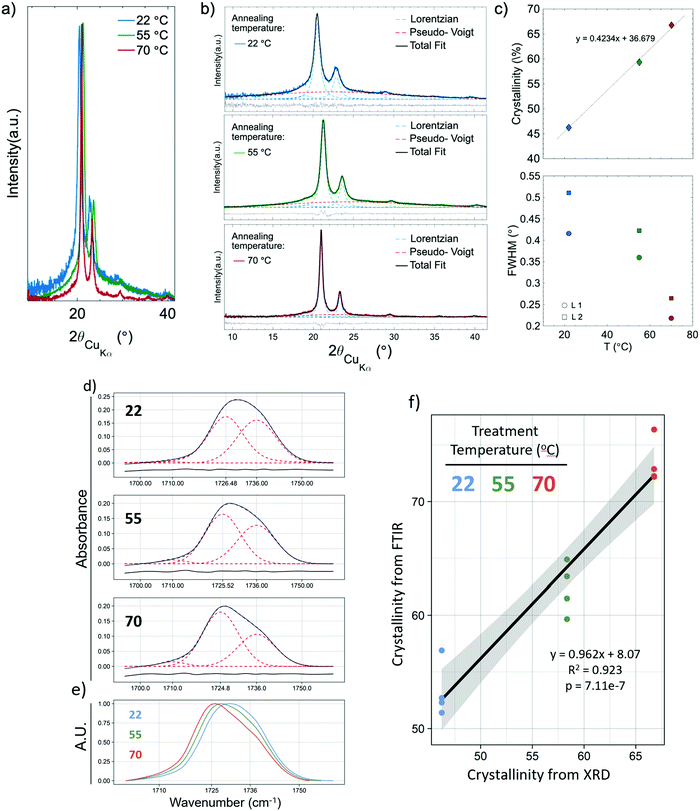
XRD was used to validate and calibrate the FTIR method of obtaining crystallinity. An FTIR method was necessary because it allows for the use of smaller, less dense samples. This vastly increases experimental throughput to levels required to obtain the necessary sample sizes for crystallization kinetics and mechanical experiments. Additionally, the FTIR method was allows the determination of crystallinity orientation via polarized FTIR. There was a strong relationship (p = 7.11 × 10−7, R2 = 0.923) between the two methods. Fig. 2a shows the XRD pattern of the samples that experienced annealing temperatures of 22, 55 and 70 °C. To obtain the crystallinity of each sample, the data were fitted (Fig. 2b) using four Lorentzian functions (crystalline peaks) and one Pseudo-Voigt (PV) curve (amorphous halo) and the percentage of crystallinity was calculated according to eqn (1).Where χc is the percentage of crystallinity, Ln (n = 1, 2, 3 or 4) are the intensities of the Lorentzian functions and PV is the intensity of the Pseudo-Voigt function. Fig. 2c (top) shows percent crystallinity as a function of annealing temperature, which increases from 46.2% to 66.7% for the 22 and 70 °C treated samples, respectively.All crystalline peaks shifted to higher angles with increasing annealing temperature. The two more intensity peaks at 2θ equal to 20.5° and 23° showed a decrease in the full width at half maximum (FWHM) with increasing annealing temperature (Fig. 2c bottom) while the small peaks at 19° and 29.5° presented no significant changes. This decrease on the FWHM is also an indicator of increasing crystallinity.29
The same samples which had their crystallinity analyzed using XRD were also analyzed for crystallinity using FTIR, with each sample being measured in four different locations, giving n = 4 for the FTIR measurements. Fig. 2d shows representative FTIR curves of the samples. An increase in the 1725 cm−1 subpeak occurs as temperature increases, shifting the entire peak to the left (Fig. 2e). Fig. 2f shows the relationship between the crystallinity obtained by XRD and FTIR. The high R2 (0.923) and low p-value (p = 7.11 × 10−7) indicate a strong linear relationship and consistency between the methods. The crystallinity obtained by XRD was 8.07% (absolute percentages) higher as indicated by the y-intercept. XRD is the more regularly used measurement of crystallinity for semicrystalline polymers, therefore all crystallinity measurements taken by FTIR were calibrated to the XRD results by adding 8.07%. It is not surprising that the method of obtaining crystallinity in PCL developed by Hen and Inoue25 performs well but not perfectly. The method was developed using thin anisotropic films, not highly anisotropic nanofibers. The greater internal stresses in drawn fibers and high degree of alignment could change the peak positions slightly.
Long-term isothermal crystallization
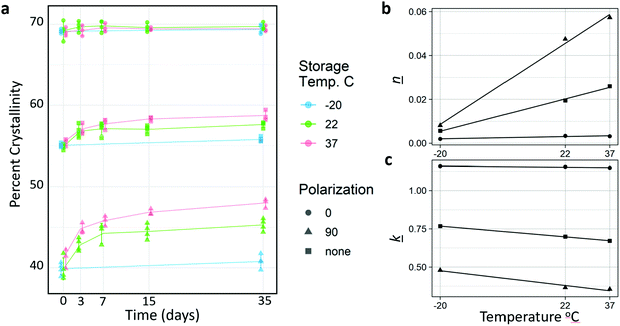
Because the glass transition temperature of PCL (−60 °C) is below storage and body temperatures, we hypothesized that some spontaneous crystallization would occur. Thus, the long-term crystallization of PCL nanofibers at constant temperature (room and body temperature) were assessed prior to discrete annealing experiments. Fig. 3a shows the change in crystallinity for molecules parallel (0°) to the fiber axis, perpendicular (90°) to the fiber axis, and overall. Change in crystallinity increased with increasing temperature, and for molecules that were aligned perpendicular to the fiber axis. Samples kept in the freezer increased their crystallinity marginally, although much of this might be accounted for by the fact that the samples had to be removed from the freezer for testing. It is likely that much if not all the crystallization occurred during this time.Interestingly, despite the fact that increased temperature resulted in higher rates of crystallization, which may have been due to increased chain mobility and crystal growth rate, the Avrami analysis (Fig. 3b and c, Table 2) revealed that the increased crystallization is mediated by an increase in nucleation. This is supported by the increasing Avrami exponent (n), not by an increase in crystal growth rate (k). Surprisingly, k was measured to be lower as temperature increase. This indicates that crystallization in the fibers is likely nucleation limited. Nucleation was likely very rapid for the highly aligned molecules parallel to the fiber axis due to post-drawing, and crystallization in this orientation occurred rapidly, therefore there is little increase in crystallinity in the parallel orientation during sample incubation at room and physiological temperatures. Conversely, time or temperature are required for the more amorphous and more anisotropic regions to nucleate. There was a linear relationship between temperature and both n and k for all orientations (Fig. 3b and c).
| Temp. (°C) | Polarization angle (°) | k (s−1) | n |
|---|---|---|---|
| 22 | 0 | 1.155 | 0.00334 |
| None | 0.699 | 0.01948 | |
| 90 | 0.366 | 0.04745 | |
| 37 | 0 | 1.148 | 0.00317 |
| None | 0.671 | 0.02599 | |
| 90 | 0.355 | 0.05731 |
The k values obtained were comparable to those measured by Ponting et al., who annealed nano-scale PCL films at 40 °C. They measured the k value of bulk PCL at 1.626 s−1, and 900 nm films at 0.6 s−1.23 The nanofibers have an average diameter of approximately 1000 nm, and when annealed at 37 °C and measured with no polarization, a k value of 0.671 s−1 was obtained. The fits for the Avrami analysis are shown in Fig. S2 (ESI†).
Effect of short-term annealing on molecular properties and morphology
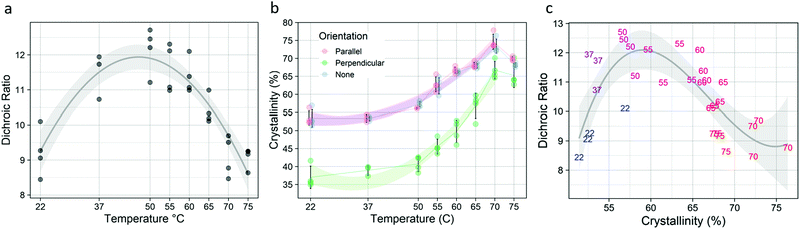
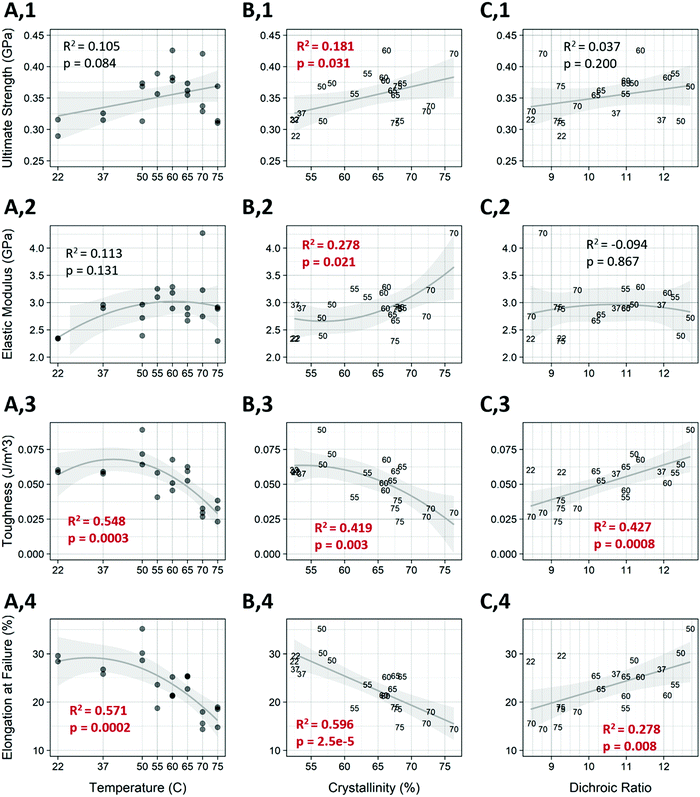
Short term annealing at temperatures from 22–75 °C affected both the molecular alignment and the total crystallinity of the post-drawn PCL nanofibers. Following treatment, fiber macromolecular alignment showed a clear inverted-U relationship (Fig. 4a), with the 22 and 75 °C samples having the lowest level of alignment as measured by dichroic ratio and 50 °C having the highest. The data was fitted to a second-degree polynomial (p < 5.0 × 10−10, R2 = 0.79). Total crystallinity, which is referring to the crystallinity as measured by FTIR with no polarizing filter and represents the crystallinity of molecules in all orientations, was also affected by annealing. Total crystallinity increased with increasing temperatures until 70 °C for all FTIR measurements (Fig. 4b). Total crystallinity (blue) and crystallinity for molecules aligned parallel to the fiber axis (red) increased from approximately 53% to 73%, while molecules that were aligned perpendicular to the fiber axis (green) saw an increase from approximately 36% to 66% (p < 5.0 × 10−13, R2 > 0.92 for all). The parallel and overall crystallinity are nearly identical because most of the molecules in the fiber are aligned to the fiber axis, as determined by the high dichroic ratio. There was also a strong inverted-U relationship between dichroic ratio and crystallinity (Fig. 4c), which was well approximated by a third-degree polynomial (p < 5.0 × 10−5, R2 = 0.523).Fiber morphology was affected by the temperature treatments (Table 3). Untreated fibers existed exclusively as individual fibers, or as unfused bundles. This was also true for temperatures up to 55 °C. At 60 °C, some fibers fused to form fork-like structures or larger fused bundles. At 70 °C, melting occurred, as evidenced by the appearance of a bead-on-string morphology. Representative images of the fibers are shown in Fig. S3 (ESI†).
| Temperature | Individual fibers | Morphology | Fused bundles | Beads on a string |
|---|---|---|---|---|
| Bundles | ||||
| None < few < some < many < most. | ||||
| 22 | Most | Few | Few | None |
| 36 | Most | Few | Few | None |
| 48 | Many | Some | Some | None |
| 54 | Many | Some | Some | None |
| 62 | Some | Many | Many | None |
| 65 | Some | Many | Many | None |
| 70 | Few | Most | Most | Few |
| 80 | Few | Most | Most | Few |
Crystallization kinetics
Isothermal crystallization kinetics were assessed using the temperature that resulted in the highest degree of crystallization (Fig. 4): 70 °C. Avrami analysis of samples treated at 70 °C (Fig. 5) showed that crystal growth is increased for the non-polarized sample, which is a reversal compared to what was seen in the long-term kinetic data, where the crystal growth rate constant (k) decreased with increasing temperature. However, nucleation (n) increased substantially, following the trend established by the long-term data. Although there is an increase in k, the rapid crystallization compared to room and physiological temperatures is mediated almost entirely by the increase in nucleation.Mechanical properties
Annealing was shown to have a significant effect on certain mechanical properties of the fibers (Fig. 6). Temperature alone showed a strong effect on the toughness and elongation at failure of the fibers (Fig. 6, rows 3 and 4), and influences the ultimate strength as well (Fig. 6, row 1), with fiber strength trending upwards up to the 60 °C treatment, followed by a decline in strength as temperature increased further. A student's t-test between the untreated control and the 60 °C treated samples (Fig. 6 A,1) was statistically significant (p = 0.0103) and represented a 30.7 percent increase in strength. This is also the temperature that resulted in the highest elastic modulus. As shown in Fig. 4 temperature has a strong effect on crystallinity and dichroic ratio, which also correlates with the mechanical properties. The percent crystallinity was correlated to all mechanical properties measured (Fig. 6 col. B). As expected, when crystallinity increased the ultimate tensile strength and elastic modulus both increased (p < 0.05). Crystallinity was most highly and significantly correlated with elongation at failure (p = 2.5 × 10−5, R2 = 0.596), while the dichroic ratio (Fig. 6, col. C) was only related to the toughness and elongation at failure. Surprisingly, as the dichroic ratio increased, so did toughness and elongation. It is worth noting that the temperatures tested are not evenly spaced, therefore there is a heavier weighting of higher temperature treatments, which might account for these relationships.A multivariable linear model for each of the mechanical measures was constructed using the crystallinity and dichroic ratio as input variables Fig. S4 (ESI†). The individual loadings for the input variables for each mechanical measure are also shown (Fig. S5, ESI†). Compared to the linear model in Fig. 6, the multivariable model showed increased predictive power for each mechanical measurement. Also of note is that crystallinity was more heavily weighted than dichroic ratio for each of the mechanical properties except toughness, where they were nearly even.
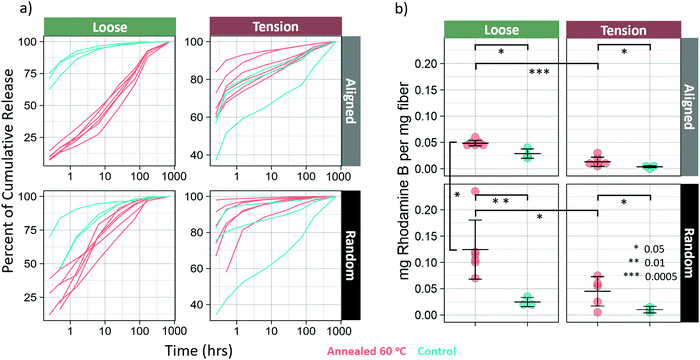
Drug release
Annealing at 60 °C resulted in a marked difference in both release kinetics and loading. Model drug was released much more linearly in the loose-aligned group when annealed samples are compared to control (Fig. 7a). The annealed fibers in this group showed a much slower onset and a much more sustained release of dye that approximates a zero-order release. Not only did that group have a longer, more steady release rate as seen in Fig. 7a, but it also released far more dye than control (Fig. S6, ESI†), which was common for all annealed groups. Drug loading increased for all annealed groups (p < 0.05) (Fig. 7b). Percent increase in loading is shown in Table 4. Both loose groups show a difference in release kinetics with annealing, but the random fibers show a much weaker effect than the aligned. For the loose-random group, all the annealed samples show a slower, more linear release profile than the controls. The groups in tension show an opposite effect, with the annealed groups releasing faster than the controls. The tension-random in particular shows a few samples nearing 100 percent release in the earliest timepoints. This is likely due to much of the dye being washed away during the rinsing, before the time course even began.| Group | Percent increase of drug loading |
|---|---|
| Loose-aligned | 169 |
| Tension-aligned | 351 |
| Loose-random | 0.505 |
| Tension-random | 442 |
Discussion
Effect of annealing on alignment
The increase in molecular alignment following annealing is an expected result. Krigbaum and Roe (1964)30 explained this phenomenon as being due to a conformational selection during nucleation, with the probability of chain segment incorporation into an existing oriented crystal increasing as the chain orientation approaches the crystal orientation. Even before annealing, the fibers are relatively crystalline, and the crystals have high molecular alignment in the orientation parallel to the fiber axis. It is possible that as crystallization occurs, slightly misaligned molecules in the proximity of aligned crystals are incorporated into the crystal structure. The crystals are much larger and constrained in their movement. By contrast, the individual unincorporated chains are much freer to move, especially under elevated temperatures. When these chains are incorporated into the aligned crystals, it serves to increase the overall alignment of the fiber.This explanation, however, is far from complete. Based on this reasoning alone, one would expect to see alignment continue to increase along with crystallinity. However, alignment peaks at 50 °C and begins to dip as temperature increases, while the crystallinity continues to rise. This is possibly due to the temperature approaching the melting point of PCL, which is in the range of 60 °C. The crystals have a higher melting point than the amorphous regions and are tied together by those same amorphous chains. As the temperature increases, the freedom of the crystals to rotate increases. At around 50 °C, this process dominates the chain incorporation process in terms of alignment and explains the inverted-U relationship between temperature and crystallinity. Further studies that look at the precise orientation and size of crystals as a function of temperature should be done to test this hypothesis.
Effect of annealing on crystallization and mechanical properties
As expected, increases in temperature facilitated the formation of crystals in the fibers at all orientations. The ability to control the percent crystallinity in an already spun and drawn fiber gives an additional level of control over the performance of the fiber across several properties. The ultimate tensile strength and elastic modulus were increased by over 30 percent when treated at 60 °C. This was less pronounced than the effect seen by Zhang et al.,13 where electropun PCL nanofiber membranes were annealed at 42 degrees for 12 hours and showed an increase in ultimate strength by over 100%. This is likely due to the membranes also reporting ultimate strength two orders of magnitude less than the current study, giving them much more room to improve. Another study annealed silicone coated PCL nanofiber meshes at 60 °C for 24 hours.14 They saw an improvement of about 14 percent, going from 8.0 MPa to 9.1 MPa. These fibers are also orders of magnitude lower in strength than post-drawn PCL fibers, likely a result of the fibers being randomly oriented and having poor molecular alignment due to the lack of post-drawing. Interestingly, these fibers did not see the same increase in strength reported by Zhang et al., possibly revealing differences in the thermal history due to different spinning parameters, or perhaps an effect of the silicone coating. The current study reports relative increases in strength somewhere between these two studies, but at a vastly different starting strength.Effect of annealing on drug release
Additionally, fibers treated at 60 °C showed an increase in drug loading efficiency, and release kinetics showed a much longer, more sustained zero-order release. This is in line with the results seen by Chiu et al.,18 who showed that solvent vapor annealing resulted in extended release times of spironolactone from annealed PCL nanofibers. Similar results were obtained by J.-C. Jeong et al. who reported that PCL microparticles annealed at 50 °C had a slower release rate than those annealed at lower temperatures. These studies, however did not report differences in loading efficiency for annealed PCL.It may seem that there is a correlation between crystallinity and loading efficiency, however, according to Schultz31 this is actually due to relaxation and transverse alignment of the non-crystalline chains32 that occur during annealing. The transversely aligned chains allow dye to penetrate the fiber more readily. This also accounts for the observation that samples in tension absorbed less drug than those that were loose. The loose samples amorphous regions were allowed to relax, increasing their transverse alignment, while those held in tension did not. It's also the case that the annealed fibers were exposed to the dye at annealing temperature, which should have the effect of increasing the rate of diffusion of the drug into and throughout the nanofibers. The relative contributions of these effects is unclear and requires additional investigation. All drug release was performed at room temperature. Therefore, it would be expected for two identical fibers with differential drug loadings that the fiber with the higher drug loading would release drug faster. However, as is shown in Fig. S6 (ESI†) in the first panel, the loose-aligned annealed fibers released much less drug in the first part of the study compared to the control group, despite having higher loading and ultimately releasing more drug by the conclusion of the time-course. Neither explanation for increased loading also accounts for this difference in drug release profile. Therefore, we hypothesize that it is possible that the dye that was taken up by the fiber before crystallization might have been locked into imperfect regions of crystals, or between crystals, which would slow release by requiring the drug to take a more tortuous path due to increased crystallinity. Evaluation of this mechanism could be the focus of a future study. This protocol, that is to say, loading before and during annealing, allows for both high loading and slow release, which is usually difficult to achieve. Additionally, the proposed mechanism that makes this possible is only applicable for highly oriented, semicrystalline polymers, with high surface areas, leaving nanofibers as an ideal candidate for tunable, high loading efficiency, zero-order release vehicles.
The combination of higher drug loading efficiency, slower, steadier release and degradation kinetics, and increased strength will enable higher-quality cell scaffolds for regenerative medicine applications, such as ligament tissue engineering.
Crystallization kinetics
The results of the Avrami analyses seem anomalous at first glance, due to the low Avrami exponent. Avrami exponents typically range between 2 and 4, with a value of 2 representing growth in 1 dimension, resulting in rod-like crystal growth. In a nanofiber with a high degree of alignment, this is expected. However, the analysis results in an Avrami exponent of less than 1 in all cases. This is likely due to limitations of the method, and some assumptions of the Avrami analysis not being met. As far as limitations are concerned, at the fibers first time-point there is already a high degree of crystallinity. Therefore, we are missing the first three-quarters (or more) of the crystallization curve. Additionally, the amorphous region is not anisotropic. Because molecules parallel to the fiber axis are likely to be incorporated into crystals, the amorphous region is depleted of fibers parallel to the fiber axis, resulting in an amorphous region which likely has some degree of alignment, but in the direction perpendicular to the fiber axis. Therefore, nucleation is more likely to occur than it would in isotropic bulk material, making it reasonable that the Avrami exponent does not fall within the expected range. Further studies will be necessary to further elucidate the crystallization kinetics of the fibers during annealing.Fiber morphology and elevation of melting region
Even though bulk PCL has a melting point of around 60 °C, it was unsurprising to see that the fibers were able to remain intact at temperatures up to 75 °C. Because the fibers were held under tension due to drawing, the fiber experienced sufficiently high stress such that it elevated the melting temperature. Such a phenomena has been described in polypropylene.33Proposed model of crystallization
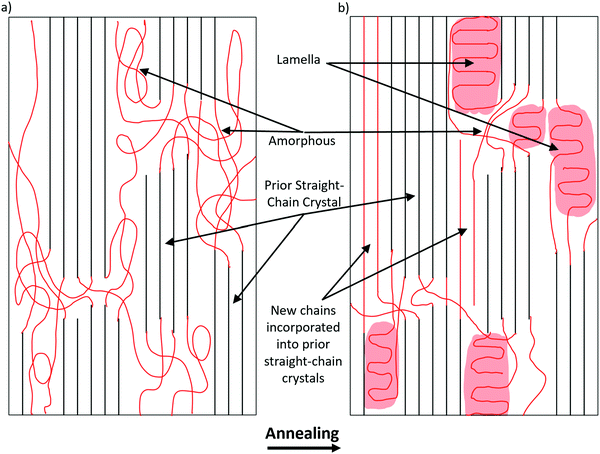
Based on the data presented on the changes in crystallinity and alignment following heat treatment, the following model is hypothesized (Fig. 8). As temperature increases, amorphous chains are either incorporated into the existing straight chain crystals or folded into lamellar crystals. Straight chain incorporation serves to increase the total molecular alignment of the fiber and slightly increase the crystallinity in the oriented direction. This process is dominant until around 50 °C, which is the high point of molecular orientation. Above that temperature, it is possible that some of the less well incorporated molecules are able to leave the straight chain crystals, which recrystallize as lamellar crystals as the fiber cools. The freed chain ends have higher degrees of freedom than when they were incorporated into the straight chain crystals, resulting in a net gain of crystallinity. Much more crystallinity is gained in the transverse direction, where amorphous regions are free to fold into lamellar crystals This also accounts for the deterioration of mechanical strength above 60 °C, which indicates that at this temperature the gains of increased crystallinity are offset by the loss of orientation and straight chain crystals.Conclusion
Post-drawn electrospun PCL nanofibers were annealed in water baths at a range of temperatures from room temperature to melt. The crystallization kinetics at important annealing temperatures were determined, including storage temperature (−20 °C), room temperature (22 °C), physiological temperature (37 °C), and at the temperature that induces maximum crystallinity (70 °C). Isothermal crystallization was also performed on the fibers for temperatures ranging from 22 to 75 °C, and the resulting changes in crystallization, molecular alignment, and mechanical properties were assessed. As stated, the percent crystallinity increased with increasing temperature up until 70 °C. However, the 55 °C resulted in the greatest molecular alignment. This shows that there are two competing processes in the fibers during the annealing process.The associated changes to mechanics were substantial. Annealing at 60 °C resulted in the highest ultimate strength and elastic modulus among all treatments, with an increase of over 30% compared to untreated fibers. As expected, increased crystallinity resulted in lower toughness and elongation at failure as well. Interestingly, dichroic ratio did not correlate with ultimate strength or elastic modulus, but did correlate highly and positively with both toughness and elongation at failure.
The effect of annealing of post-drawn PCL nanofibers were compared to randomly spun fibers in a drug release experiment. Both samples were tested under both tension and loose. The largest effect of annealing was seen for loosely tensioned fibers, which released drug substantially slower compared to the control group. Drug loading was also assessed, and annealed fibers had higher levels of drug loading across the board.
The annealing of post-drawn PCL nanofibers, and polymer nanofibers in general is a promising and easy to perform manufacturing step that can drastically alter the properties of the fibers. With optimization of time and temperature for a specific material, fibers can be engineered with application specific and predictable properties. Additionally, further understanding of the changes in underlying morphology of the fibers is necessary, such as how inter-crystal tie-in molecules and crystal size are affected by the annealing process. Understanding the crystallization kinetics of nanofibers, and how they might differ from bulk material, though technically challenging, is another critical area of research and can be done with FTIR and the treat and quench approach demonstrated in this study. In sum, annealing of PCL nanofibers looks to be a key step in tuning fibers for biomedical engineering applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research was sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-17-2-0227 and by the National Science Foundation (NSF1653329). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes not withstanding any copyright notation herein.References
- G. R. Mitchell, Electrospinning: Principles, Practice and Possibilities, The Royal Society of Chemistry, 2014 Search PubMed.
- D. A. Brennan, A. A. Conte, G. Kanski, S. Turkula, X. Hu, M. T. Kleiner and V. Beachley, Mechanical Considerations for Electrospun Nanofibers in Tendon and Ligament Repair, Adv. Healthcare Mater., 2018, 7, 1–31 CrossRef PubMed.
- S. Han, K. Nie, J. Li, Q. Sun, X. Wang, X. Li and Q. Li, 3D Electrospun Nanofiber-Based Scaffolds: From Preparations and Properties to Tissue Regeneration Applications, Stem Cells Int., 2021, 8790143 CAS.
- O. Bas, E. M. De-Juan-Pardo, M. P. Chhaya, F. M. Wunner, J. E. Jeon, T. J. Klein and D. W. Hutmacher, Enhancing structural integrity of hydrogels by using highly organised melt electrospun fibre constructs, Eur. Polym. J., 2015, 72, 451–463 CrossRef CAS.
- D. Mondal, M. Griffith and S. S. Venkatraman, Polycaprolactone-based biomaterials for tissue engineering and drug delivery: Current scenario and challenges, Int. J. Polym. Mater. Polym. Biomater., 2016, 65, 255–265 CrossRef CAS.
- N. L. Leong, N. Kabir, A. Arshi, A. Nazemi, J. Jiang, B. M. Wu, F. A. Petrigliano and D. R. McAllister, Use of ultra-high molecular weight polycaprolactone scaffolds for ACL reconstruction, J. Orthop. Res., 2016, 34, 828–835 CrossRef CAS PubMed.
- V. Beachley and X. Wen, Polymer nanofibrous structures: Fabrication, biofunctionalization, and cell interactions, Prog. Polym. Sci., 2010, 35, 868–892 CrossRef CAS PubMed.
- D. Li, Y. Wang and Y. Xia, Electrospinning of polymeric and ceramic nanofibers as uniaxially aligned arrays, Nano Lett., 2003, 3, 1167–1171 CrossRef CAS.
- S. Kidoaki, I. K. Kwon and T. Matsuda, Mesoscopic spatial designs of nano- and microfiber meshes for tissue-engineering matrix and scaffold based on newly devised multilayering and mixing electrospinning techniques, Biomaterials, 2005, 26, 37–46 CrossRef CAS PubMed.
- D. A. Brennan, D. Jao, M. C. Siracusa, A. R. Wilkinson, X. Hu and V. Z. Beachley, Concurrent collection and post-drawing of individual electrospun polymer nanofibers to enhance macromolecular alignment and mechanical properties, Polymer, 2016, 103, 243–250 CrossRef CAS.
- D. A. Brennan, K. Shirvani, C. D. Rhoads, S. E. Lofland and V. Z. Beachley, Electrospinning and post-drawn processing effects on the molecular organization and mechanical properties of polyacrylonitrile (PAN) nanofibers, MRS Commun., 2019, 9, 764–772 CrossRef CAS.
- C. T. Lim, E. P. S. Tan and S. Y. Ng, Effects of crystalline morphology on the tensile properties of electrospun polymer nanofibers, Appl. Phys. Lett., 2008, 92, 2006–2009 Search PubMed.
- J. Zhang, H. Liu, J. X. Ding, X. L. Zhuang, X. S. Chen and Z. M. Li, Annealing regulates the performance of an electrospun poly(ε-caprolactone) membrane to accommodate tissue engineering, RSC Adv., 2015, 5, 32604–32608 RSC.
- Y. Il, Ko, Y. Lee, K. Devarayan, B. S. Kim, T. Hayashi and I. S. Kim, Annealing effects on mechanical properties and shape memory behaviors of silicone-coated elastomeric polycaprolactone nanofiber filaments, Mater. Lett., 2014, 131, 128–131 CrossRef.
- J. Kressler, C. Wang and H. W. Kammer, Structure formation in thin poly(ε-caprolactone) films, Langmuir, 1997, 13, 4407–4412 CrossRef CAS.
- G. Sekosan and N. Vasanthan, Morphological changes of annealed poly-ε-caprolactone by enzymatic degradation with lipase, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 202–211 CrossRef CAS.
- M. Fujita, Y. Takikawa, H. Sakuma, S. Teramachi, Y. Kikkawa and Y. Doi, Real-time observations of oriented crystallization of poly(ε- caprolactone) thin film, induced by an AFM tip, Macromol. Chem. Phys., 2007, 208, 1862–1870 CrossRef CAS.
- Y. J. Chiu, Z. Zhang, K. Dziemidowicz, C. G. Nikoletopoulos, U. Angkawinitwong, J. T. Chen and G. R. Williams, The effect of solvent vapor annealing on drug-loaded electrospun polymer fibers, Pharmaceutics, 2020, 12, 1–11 Search PubMed.
- J. C. Jeong, J. Lee and K. Cho, Effects of crystalline microstructure on drug release behavior of poly(ε-caprolactone) microspheres, J. Controlled Release, 2003, 92, 249–258 CrossRef CAS PubMed.
- J. Boon, G. Challa and D. W. van Krevelen, Crystallization kinetics of isotactic polystyrene. II. Influence of thermal history on number of nuclei, J. Polym. Sci., Part A-2, 1968, 6, 1835–1851 CrossRef CAS.
- Y. Deslandes, M. Day, N.-F. Sabir and T. Suprunchuk, Crystallization of poly(aryl-ether-ether-ketone): Effect of thermal history of the melt on crystallization kinetics, Polym. Compos., 1989, 10, 360–366 CrossRef CAS.
- M. Avrami, Kinetics of phase change. I: General theory, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Ponting, Y. Lin, J. K. Keum, A. Hiltner and E. Baer, Effect of substrate on the isothermal crystallization kinetics of confined poly(ε-caprolactone) nanolayers, Macromolecules, 2010, 43, 8619–8627 CrossRef CAS.
- M. M. Coleman and J. Zarian, Fourier-Transform Infrared Studies of Polymer Blends. 11. Poly(eCapro1actone)-Poly(viny1 Chloride) System, J. Polym. Sci., 1979, 17, 837–850 CAS.
- Y. He and Y. Inoue, Novel FTIR method for determining the crystallinity of poly(ε-caprolactone), Polym. Int., 2000, 49, 623–626 CrossRef CAS.
- M. Wojdyr, Fityk: A general-purpose peak fitting program, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- R. Zhang, M. Hummelgrd, G. Lv and H. Olin, Real time monitoring of the drug release of rhodamine B on graphene oxide, Carbon, 2011, 49, 1126–1132 CrossRef CAS.
- K. K. H. Wong, M. Zinke-Allmang and W. Wan, Effect of annealing on aqueous stability and elastic modulus of electrospun poly(vinyl alcohol) fibers, J. Mater. Sci., 2010, 45, 2456–2465 CrossRef CAS.
- W. R. Krigbaum and R.-J. Roe, Diffraction study of crystallite orientation in a stretched polychloroprene vulcanizate, J. Polym. Sci., Part A: Gen. Pap., 1964, 2, 4391–4414 CrossRef CAS.
- J. M. Shultz, in Polymer Crystallization: The Development of Crystalline Order in Thermoplastic Polymers, ed. J. M. Shultz, American Chemical Society, 1st edn, 2001, pp. 232–251 Search PubMed.
- A. S. Abhiraman, Crystallization in oriented polymers: a framework for analysing orientation distributions, J. Polym. Sci., Polym. Phys. Ed., 1983, 21, 583–594 CrossRef CAS.
- J. Militky, in Handbook of Tensile Properties of Textile and Technical Fibres, ed. A. Bunsell, Woodhead Publishing, 1st edn, 2009, pp. 223–314 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma01183a |
| This journal is © The Royal Society of Chemistry 2022 |