Two-dimensional micromodels for studying the convective dissolution of carbon dioxide in 2D water-saturated porous media

Abstract

Convective dissolution is a perennial trapping mechanism of carbon dioxide in geological formations saturated with an aqueous phase. This process, which couples dissolution of supercritical CO₂, convection of the liquid containing the dissolved CO₂, and mixing of the latter within the liquid, has so far not been studied in two-dimensional porous media. In order to do so, two-dimensional (2D) porous micromodels (patterned Hele-Shaw cells) have been fabricated from UV-curable NOA63 glue. NOA63 is used instead of PDMS, which is permeable to CO₂ and does not allow for a controlled no flux boundary condition at the walls. The novel fabrication protocol proposed here, based on the bonding of a patterned photo-lithographed NOA63 layer on a flat NOA63 base, shows good reproducibility regardless of the patterns' typical size, and allows for easy filling of the cell despite the small value of the gap. A pressure chamber allows pressurizing the CO₂ and outside of the flow cell up to 10 bars. Experiments were performed in 11 different porous media geometries. As expected, a gravitational fingering instability is observed upon injection of gaseous carbon dioxide in the cell, resulting in the downwards migration of dissolved CO₂ plumes through the 2D porous structure. The initial wavelength of the fingers is larger in the presence of a hexagonal lattice of pillars. This effect can be correctly predicted from the theory for the gravitational instability in a Hele-Shaw cell devoid of pillars, provided that the permeability of the hexagonal porous medium is considered in the theory instead of that of the Hele-Shaw cell. Fluctuations around the theoretical prediction observed in the data are mostly attributed to a hitherto unknown weak locking of the wavelength on the distance between closest pillars.

---

1 Introduction

It is now generally accepted that the main cause of global warming is increased atmospheric concentrations of greenhouse gases, the main ones found in air being water vapour (2%), carbon dioxide (CO₂, 400 ppm (ref. 1)), and methane (CH₄, 2 ppm). Increases in the atmospheric concentrations of the latter two are associated with human activity in agriculture and deforestation (for CH₄) and with a continuous increase in fossil fuels consumption which is responsible for more than 80% of the CO₂ release to the atmosphere.² Carbon dioxide has been identified as the main target for the reduction of anthropogenic release of greenhouse gases in the atmosphere,³ since it is responsible for about two thirds of the enhanced greenhouse effect.⁴ Consequently, underground storage is for now the only mid-term method that could accommodate the massive amount of CO₂ to be treated annually (32 gigatons of per year).

The storage procedure consists in injecting CO₂ into a porous rock formation that is confined by an impermeable formation, the cap rock, located above it. For a typical geothermal gradient of 30°/km and a surface hydrostatic head, CO₂ exists as a dense, supercritical fluid at a depth of more than about 800 m (relative density with respect to water: ∼0.7). As supercritical CO₂ is less dense than the interstitial fluid (water or brine), it first rises upon injection, then reaches the cap rock, and eventually undergoes lateral buoyancy-driven migration along the base of the caprock. Because CO₂ is partially soluble in water (up to 3 wt% (ref. 5)), dissolution of the supercritical CO₂ into the aqueous phase occurs, resulting in a mixture that happens to be denser than the resident water/brine. Thus, the dissolution at the CO₂/brine interface creates a gravitationally unstable layer of CO₂-enriched water at the top of the brine-saturated pore space. This layer then destabilises to form convective rolls, which subsequently evolve into solutal plumes that migrate towards the bottom of the aquifer.⁶

While other mechanisms are involved in the geological trapping of CO₂ (static structural/stratigraphic trapping, residual gas trapping, mineral/chemical trapping⁶), we focus here on this so-called convective dissolution trapping mechanism. It has been studied experimentally in standard Hele-Shaw cells (fluids only, no porous structure) where pore-scale mixing and the related hydrodynamic dispersion effects are absent,^7,8 or in quasi-3D porous media (thicker Hele-Shaw cells filled with solid beads^2,9–12), where the interstitial flow is no longer bi-dimensional, making the local mixing and dispersion processes difficult to accurately measure and model. Three-dimensional (3D) experiments based on X-ray tomography^13,14 or magnetic resonance imaging¹⁵ allow characterizing the convection structure and convective fingers velocity but do not provide robust measurements of dissolution fluxes, while recent 3D experiments with optical measurements have uncovered a hitherto unknown role of pore scale velocity heterogeneities¹⁶ but do not yet provide precise measurements of the concentration fields. Convective dissolution has also been extensively studied by means of 2D simulations where the physical processes at stake are integrated over a ‘mesoscopic’ Darcy scale;^17–21 a few 3D numerical studies have also been performed,²² including, recently, simulations where hydrodynamic dispersion is accounted for.²³

In this context, the use of patterned Hele-Shaw cells (i.e., quasi-2D porous media) is a method allowing both for heterogeneous pore flow and the pore scale measurement of the concentration field of the dissolved CO₂, and hence, of the dissolution flux. In this article, we depict the design and the manufacturing process of such bi-dimensional porous micromodels (MM) which can allow for a direct and rigorous study of the role of pore scale flow and solute mixing in the solubility trapping of CO₂. Previous micromodel studies on CO₂ trapping have used microfluidic flow cells consisting of fuel silica plates,²⁴ silicon and glass,²⁵ silicon and Pyrex (able to sustain reservoir conditions pressure and temperature),^26,27 or biogenic calcite-functionalized silicon.²⁸ Here, we use a different type of flow cell made of the NOA63 photopolymer. In addition, instead of relying on the strength of the microfluidic cells material(s) to sustain the pressure of the injected CO₂, we use a pressure chamber ensuring that the same pressure is applied homogeneously to the walls of the flow cell from the outside.

Such microfluidic flow cells have been used to study various aspects of CO₂ storage in the subsurface, such as: the impact of the supercritical CO₂-mediated wettability alteration of silica;²⁴ the dew point conditions for CO₂ with impurities;²⁹ residual trapping²⁵ and more generally different regimes of two-phase flows involving an aqueous phase and CO₂ in supercritical or gas phase, which are relevant to residual trapping but mostly reproduce previous general two-phase flow studies in 2D porous media (see ref. 30 for more details); the exsolution of CO₂ from the aqueous phase when pressure decreases,²⁶ the solubility of CO₂ at reservoir pressures and temperature;³¹ and dissolved CO₂-induced precipitation of calcium carbonate in a synthetic porous medium.³² The dissolution of CO₂ into an aqueous phase has been studied in micromodels in conjunction with residual trapping,³³ and the impact of lenses of impermeable material on the convective dissolution of CO₂ inside an aquifer has also been investigated in a patterned Hele-Shaw cell.⁸ However, to the best of our knowledge, convective dissolution has not been studied at the pore scale in 2D porous media. In the following we present such a study performed in the novel NOA63 micromodels, where we characterize the dependence of the most unstable wavelength on the Rayleigh number.

The article is organised as follows. Section 2 describes the methodology, including a detailed description of the microfluidic cells' fabrication. Section 3 presents the data and experimental results. We conclude and presents prospects to this work in section 5.

2 Material and method

Whereas bi-dimensional porous micromodels are generally manufactured by means of standard photolithography or soft lithography techniques (see e.g. ref. 34), or using silica-based microfluidic cells which can sustain reservoir condition temperatures and pressures as discussed above in the Introduction, our flow cells mainly consist of a patterned NOA63 layer bonded on a flat NOA63 base.

2.1 Why use NOA-based cells?

With NOA63, repeatability is much easier to achieve than with etched silicon. Furthermore, with photolithography we can achieve an aspect ratio of the cylindrical pillars that is close to 1 (i.e., pillars whose height is nearly as large as their diameter); it is not the case with silicon-based substrates where the diameter of the pillars is typically 10 times larges than the thickness of the cell. This aspect ratio impacts solute transport properties in the system, which is important for convective dissolution (coupling of natural convection and solute mixing). In addition, the NOA's wetting properties can be tuned continuously in the hydrophilic range, with a wetting angle between 0° and 180°.³⁵ This property is of no use in this particular study (which features natural convection in a single phase), but will be very useful in later studies involving two immiscible fluid phases.

The obtained flow cells are perfectly transparent, which indicates that the roughness of the NOA surfaces are of an amplitude no larger than a few micrometers. This excellent transparency of the cells endures after they have been used between 15 and 20 times. No change in color was observed either, nor any sign of any surface alteration or chemical deposition/precipitation/dissolution. After more than 15 experimental runs, the flow cells appear to have remained entirely unchanged since their fabrication. This indicates that the physico-chemical interaction between the fluids and the flow cell was minimal. Furthermore, when performing the same experiment (with identical experimental parameters) on a given flow cell, just after its fabrication and after many other experiments have been performed using that cell, the results of the two experiments were identical, which confirms the lack of (physico-)chemical interaction between the cell and the fluids.

2.2 Manufacturing process

The manufacture procedure requires a fairly large number of steps which must be precisely calibrated. In this section, we depict the fabrication of the photoresin patterned mould, and the moulding, curing and bonding stages of the NOA63 layers.

2.2.1 Preparation of the SU-8 master. As a preliminary step, a flexible soft plastic photomask with the desired pattern (see e.g.Fig. 1) is designed and printed. The master mould is prepared by superimposing two ∼150 μm layers of photo-reactive SU-8 2050 on a 4 inch silicon wafer – in order to achieve better uniformity in thickness, a two-step process is preferred – leading to a total thickness of ∼300 μm. The manufacturing protocol has been adapted from the manufacturer guideline.³⁶ The key points of the protocol are outlined in Table 1. The spin coating is performed by using a Speciality Coating Systems (G3 model) spin-coater. All the baking stages are carried out on hotplates (Fisher Scientific), while the exposure steps were performed using a collimated LED UV Masker (UV KUB 2, Kloe, France). In order to prevent the strong bonding between polymers and the SU-8 mould during manufacturing of the NOA63 micromodel, a molecular hydrophobic layer is deposited on the wafer: one millilitre of tricholoro-perfluoroctyl-silane is dropped on the wafer, and placed in the vacuum desiccator, where silane vaporizes and eventually settles on the SU-8 coated wafer surface. Each master mould can thus be used repetitively to make multiple NOA63 cells, on average 15 of them.

Fig. 1 Typical patterned photomask used to manufacture the micromodels. White zones are transparent to ultraviolet (UV) light whereas black zones are opaque. As shown in the inset, the radius of the white disks is denoted by R whilst the centre to centre distance is denoted by a. Several types of micromodels with different values for a and R have been manufactured, leading to different values of the permeability and porosity (see Table 3).

Table 1 Main steps in the fabrication protocol of the master SU-8 2050 mould. Steps 1 and 2, which yield a layer of thickness 150 μm are repeated twice to obtain a base SU-8 layer of total thickness of ∼300 μm. As shown in paragraph 2.2.3, the value of the gap thickness E, which is also the height of the porous structure (pillars) in the final NOA63 cell, is marred by a large uncertainty

■ Step 1 (spin coating) – dispense 4 ml of SU-8 2050 at the centre of the wafer/spin at 500 revolution per minute (rpm) for 10 seconds, with acceleration of 100 rpm s⁻¹/spin at 1300 revolution per minute for 30 seconds, with acceleration of 300 rpm s⁻¹

■ Step 2 (soft baking) – bake at 65 °C for 5 minutes/bake at 95 °C for 30 minutes, 10 min cooling period at room temperature

■ Step 3 (UV exposure) – ensure vacuum contact between the mask (printed side) and the coated silicon wafer/expose to UV illumination (365 nm, 600 mJ cm⁻² - i.e. 40 mW cm⁻² for 15 s)

■ Step 4 (post-exposure bake) – bake at 65 °C for 5 min/bake at 95 °C for 18 min (+15 min cooling at room temperature)

■ Step 5 (development) – immerse in SU-8 developer filled tank/rinse out with isopropyl alcohol for 10 s/dry in a direct N₂ stream

■ Step 6 (hard baking) – bake at 150 °C for 5 mn

■ Step 7 (silanisation) – perform 3 hour silanisation (tricholoro-perfluoroctyl-silane, Fisher Scientific) in a vacuum desiccator

---

2.2.2 Fabrication of the NOA63 micromodel. PDMS is unsuitable for the study of convective dissolution in 2D porous micromodels, due to its high permeability to gases (oxygen, CO₂etc.). We utilize instead NOA63, a transparent UV curable photoreactive glue commonly used in the manufacturing of microfuidic systems where gas impermeability is required. The main steps involved in the manufacturing of the NOA63 porous micromodels from the aforementioned SU-8 master mould (see previous section) are as follows. The general method consists in manufacturing separately and partially UV curing the two sides of the cell, and then performing the bonding through a final UV illumination step. The main steps of the manufacturing process are detailed in Table 2 and illustrated in Fig. 2. A direct moulding of the patterned NOA63 layer (direct SU-8/NOA63 moulding, as depicted by Dupont et al.³⁷) turned to be difficult due to the strong bonding between SU-8 and NOA63 consecutive to UV illumination, and the presence of the fragile porous structure. Therefore, a PDMS patterned layer is first made from the SU-8 master mould and subsequently used as an intermediate mould for manufacturing the NOA63 patterned layer. Indeed, once oven cured, the PDMS layer can be easily peeled off from the SU-8 initial mould (if the latter has been silanized, as discussed above), and similarly, the NOA63 layer can be easily removed from the PDMS layer. Note that, because of this intermediate step, the initial SU-8 mould is positive, i.e., its pattern is geometrically similar to that of the final NOA63 layer – whereas the intermediate PDMS layer is a negative of the NOA63 layer. When UV cured (Table 2, step 4), the NOA63/PDMS stack is clamped on the metal plate (not shown in Fig. 2e) to avoid bending due to thermal gradients. After pouring the liquid NOA63 on the intermediate PDMS layers (steps 3 and 6 in Table 2), bubbles were systematically trapped in the vicinity of the pillars. To fix the issue, a heating stage is introduced in the process to decrease the viscosity of the NOA63 and let the bubbles rise by buoyancy.

Table 2 Main steps in the fabrication protocol of the NOA63 porous micromodel. See text for further information and Fig. 2 for illustration

Intermediate PDMS layer (negative mould)

■ Step 1 (PDMS pouring and degassing) – rinse the SU-8 master mould with isopropanol, acetone and distilled water/dry the master mould with N₂ stream/tape the master mould onto a Petri dish and pour 60 ml of a 10 : 1 PDMS base:reagent/put the whole in a vacuum chamber for 30 mn for degassing – see Fig. 2a

■ Step 2 (PDMS curing and peeling) – cure 80 °C for 2 hours/peel the patterned PDMS layer from the SU-8 master mould/rinse the PDMS layer with alcohol and dry with N₂ – see Fig. 2b and c

---

Patterned NOA63 layer

■ Step 3 (NOA63 pouring and heating) – create a NOA63 spacer around the edges of the PDMS layer/dispense 15 ml of NOA63 on the PDMS layer/heat the whole at 60 °C for 12 to 15 minutes

■ Step 4 (two-stage NOA63 partial curing and peeling) – expose the whole to UV power of 3 mW cm⁻² for 30 s/expose the whole to UV power of 3 mW cm⁻² for 70 s/peel the partially cured NOA63 patterned layer from the PDMS negative mould

---

Flat base NOA63/glass layer

■ Step 5 (flat PDMS base) – pour 30 ml of PDMS mixture layer in a second Petri dish/put the Petri dish in a vacuum chamber for 30 mn/cure 80 °C for 2 hours

■ Step 6 (flat NOA layer) – create a NOA63 spacer around the edges of the PDMS layer/dispense 15 ml of NOA63 on the PDMS layer/heat the whole at 60 °C for 5 to 8 minutes

■ Step 7 (glass plate bonding) – rinse a glass plate (60 mm × 60 mm × 1 mm) with alcohol and dry it using nitrogen/clamp the glass plate on top of the NOA63 flat layer/expose the whole stack to a UV light (3 mW cm⁻² for 10 mn)

■ Step 8 (peeling and drilling) – remove the composite layer [glass + NOA63] from the flat PDMS base/drill a 1 mm hole in the glass plate and make a corresponding hole in the NOA64 layer using a punch

---

Final bonding between NOA63 flat and patterned layers

■ Step 9 (UV bonding) – maintain the patterned NOA63 layer and the flat base [glass + NOA63] by means of a heavy transparent weight (thick glass plate)

■ Step 10 (inlet adaptor) – glue the inlet connector onto the glass plate at the location of the 1 mm hole

---

Fig. 2 Manufacturing of the NOA63 porous micromodels (see Table 2). (a–c) Intermediate PDMS layer manufacturing steps; (d–f) patterned NOA63 layer manufacturing steps; (g–j) flat base NOA63 base manufacturing steps; (k and l) final UV bonding. In(k) an auxilliary/additional PDMS layer (manufactured on purpose) is introduced to avoid UV bonding between the heavy glass weight and the upper NOA63 layer.

2.2.3 Actual geometry of the porous micromodels. Eleven different types of porous micromodels with hexagonal patterns have been manufactured in total. The respective dimensions E (thickness of the cell, i.e., distance between the base plates, or equivalently, height of the pillars), a and R (defined in Fig. 1) are listed in Table 3. The code name of each micromodel is chosen as follows: the first three characters inform about the ratio a/R – for instance a3R stands for a = 3R – while the last number is the value of the pillar radius R in microns. A large dispersion was observed on the final thickness E, due to the difficulty of achieving repeatable spin coating, heating and illumination steps. From direct a posteriori optical measurements the average value of the thickness evaluated from the entire set of micromodels is Ē = 227 μm – which has to be compared to an expected value of 300 μm, based on the profiles of the SU-8 master moulds – with a standard deviation of 54 μm. Conversely, the center-to-center distances showed to be consistent with the one expected from the initial mask design. Due to some inevitable collimation defects in the UV illumination, the obtained pillars' radii were systematically smaller by 25 μm than those expected from the initial mask design.

Table 3 Dimensions of the porous micromodels. Figures in blue correspond to the actual methods obtained by means of direct optical measurements and profilometry methods. The values of the porosity and thickness based permeability κ_HS = E²/12 – i.e., the permeability of a standard Hele-Shaw cell of thickness E – are easily calculated. The values of the actual permeability κ_MM of the porous micromodels are inferred from 3D Comsol Multiphysics computations on an elementary cell (see appendix A)

MM type	E (μm)	a (μm)	R (μm)	ϕ	κ HS × 10^10 (m^2)	κ MM × 10^10 (m^2)
a3R200	171	601	176	0.69	24.4	7.9
a3R300	230	900	275	0.66	44.1	16.2
a3R400	227	1202	373	0.65	43.0	14.5
a4R200	255	796	175	0.82	54.2	26.2
a4R400	278	1608	364	0.81	64.4	35.8
a6R200	168	1205	185	0.91	23.5	17.7
a6R400	206	2400	375	0.91	35.4	27.7
a8R200	226	1600	175	0.96	42.6	35.9
a8R400	203	3200	375	0.95	34.3	30.0
a10R200	311	2000	175	0.97	80.6	70.5
a10R400	225	4000	375	0.97	42.2	38.6

---

2.3 Experimental setup and procedure

The experimental setup (side view) is shown in Fig. 3a. At the start of the experimental run, the porous micro model (MM) is placed vertically in a pressure chamber (CH) equipped with four PMMA windows for illumination and visualisation (see next paragraph). The pressure chamber is connected to a reservoir (RES) through a ball valve (V). The chamber, which is connected to a 300 bar nitrogen cylinder (BOC-Linde), can be pressurized up to 10 bars (safety valve is not shown on the figure). The reservoir is connected to the nitrogen cylinder and a 200 bar carbon dioxide cylinder, so that it can be filled with an [N₂ + CO₂] mixture up to a total pressure of 10 bars. The main purpose of the setup is to increase the partial pressure of carbon dioxide in the chamber up to a given value P_CO2 ranging from 1 to 5 bar and trigger a dissolution process of the carbon dioxide into the water through the free water/gas interface at the top of the micromodel (see). The role of the reservoir placed on top of the chamber is to prevent thermal effects due to the adiabatic compression which would occur in the case of a large increase of the total pressure in the chamber.

Fig. 3 Experimental setup. (a) 2D porous micromodel with zoom on the patterned micro-structure. (b) Side view of the whole setup with the 2D micromodel (MM) placed at the center of the pressure chamber (CH). The reservoir (RES), the role of which is to avoid large pressure jumps upon CO₂ release, is connected to the chamber through a ball valve (V). The whole process is monitored by means of several sensors: a pressure sensor (PCH), a differential pressure sensor (PDIF), a thermocouple (TH). (c) Top view of the pH-sensitive dye visualization systems (see paragraph 2.3.1 for further explanations).

Initially, the ball valve (volume V_V ≃ 150 cm³) is closed. The chamber (volume V_C = 743 cm³) is filled with pure nitrogen at a total pressure P. Depending on the targeted partial pressure of carbon dioxide, the reservoir (volume V_R = 1570 cm³) is filled either with pure CO₂ or with a mixture of CO₂ (molar fraction ω) and nitrogen (molar fraction 1 − ω) at a slightly higher total pressure P(1 + ε), with ε ∼ 5%. Upon opening of the valve, the carbon dioxide is convected into the chamber (due to the overpressure ε) and a partial pressure of carbon dioxide

is reached in the whole cavity after about 30 seconds,³⁸ without any large change in the total pressure (and hence, no thermal effects related to adiabatic compression). Note that, in the case where the reservoir is filled with pure CO₂ (ω = 1), and because the initial total pressure in the system before opening the valve cannot be smaller than one atmosphere, the lower bound of the accessible final partial pressure of CO₂ is limited to 0.64 bar by the volume ratio V_R/(V_R + V_V + V_C). Therefore, mixing nitrogen and carbon dioxide – i.e. ω < 1 – would be necessary to achieve values of P_CO2 smaller than 0.64 bar.

2.3.1 pH-sensitive dye and visualisation system. Initially, the porous micromodel is completely filled with Milli-Q water (density ρ₀ = 998 kg m⁻³, viscosity μ ≃ 10⁻⁶ Pa s) and placed vertically in the pressure chamber. Prior to the filling stage, a small amount of pH-sensitive dye (bromocresol purple, Sigma-Aldrich) is diluted in water to obtain an aqueous solution of concentration ∼10⁻³ mol L⁻¹. Upon pressurisation, the carbon dioxide starts dissolving in water, locally increasing the acidity of the medium. With the pH diminishing, the initially purple regions turn yellow, providing a qualitative information about the location of CO₂-enriched zones. The optical system used to visualise the whole cell is shown in Fig. 3c. The white light emitted by a 1 W LED (Thorlabs, model MCWHL7, 930 mW/1370 mW), is partially focused through on a diffuser, which provides a close-to-uniform illumination background. The remaining non-uniformity can be corrected from the images a posteriori.

3 Experimental results

3.1 Description of the dissolution process

A series of pictures showing the convective dissolution of CO₂ in water in a a3R300 micromodel under a partial pressure P_CO2 = 8 bar is displayed in Fig. 4. Upon pressurization, a denser CO₂-enriched region grows purely diffusively beneath the liquid/gas interface (Fig. 4a). Once a critical layer thickness has been reached, this unstable configuration (light fluid surmounted by heavy fluid) destabilises into a natural convection of the denser fluid showing a well defined wavelength (Fig. 4b). The onset of this instability, referred to as linear regime in different numerical and experimental studies (see e.g. ref. 17), is defined as the regime where the perturbation of the concentration field has not yet led to a modification of the CO₂ flux, which still exhibits the same diffusive time evolution. Such an instability eventually turns into a set of downwards propagating solutal plumes which partially merge over time. After the plumes have reached the bottom of the cell, the carbon dioxide rapidly saturates the whole cell. Contrary to what is observed in classic Hele-Shaw cells,^7,39,40 no new plumes appear in the gap left by merged plumes. Indeed, here, the merging process goes along with a strong lateral spreading of the plume, so that no gap is left to be filled, as shown in Fig. 4c–e.

Fig. 4 Snapshots of the convective dissolution process at P_CO2 = 8 bar in an a3R300 NOA63 micromodel (pillar diameter is 200 μm, center-to-center distance is 800 μm). (a) Purely diffusive regime. (b) Onset of instability (linear regime). (c–e) Convection controlled regime, with plume merging. The pH of the blue-colored fluid is 6.8, that of the yellowish-colored fluid 3.5, and the green-colored fluid at the plume front (thin transition zone) is at an intermediate pH ranging between 3 and 5.

3.2 Most unstable wavelength

As previously mentioned, the experiments were performed using 11 different types of micromodels and CO₂ partial pressure ranging from 1 to 5 bar (one single experiment has been performed at 8 bar of partial pressure using an a4R400 micromodel). The values of the HS permeability κ_HS = E²/12 and the actual permeability of each micromodel, computed using Comsol Multiphysics are gathered in Table 3. The exact numerical method used to calculate the permeability, κ_MM, of each micromodel based on the pressure drop across a unit cell of the pattern is detailed in appendix A. It can be observed from Table 3 that, while the difference between κ_HS and κ_MM are moderate for micromodels a6R200, 6R4, 8R2, 8R4, 10R2 and 10R4 (for porosities ϕ > 0.9), that difference is larger for MMs a3R200, a3R400, a3R300, a4R200 and a4R400 (for porosities ϕ < 0.9). Based on their porosity, we therefore (arbitrarily) categorise the micromodels into three different types:

• Low-porosity (red symbols in Fig. 5): a3R200, a3R400, a3R300.

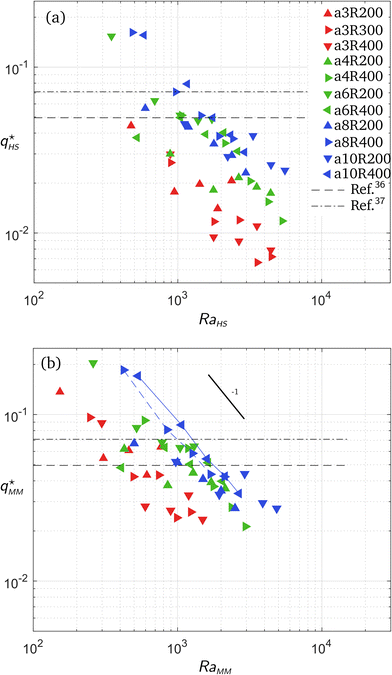Fig. 5 Dimensionless experimental wave number as a function of the Rayleigh number. In (a), the length scale , the dimensionless wave number and the Rayleigh number Ra_HS are defined using the permeability κ_HS of the Hele-Shaw cell as if there were no pillars. In (b), the length scale , the dimensionless wave number 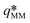and the Rayleigh number Ra_MM, are defined using the true permeability κ_MM of the micromodel. The 2D theoretical predictions from ref. 41 and 42 are plotted with horizontal black dash-dotted and dashed lines, respectively. In (b), for micromodels a10R400 and a8R400, the experimental points are connected by a blue solid and dashed lines, respectively, to emphasize the dependence that reflects a locking of the wavelength by the porous structure (see text for further explanations).

• Intermediate-porosity (green symbols in Fig. 5): a4R200, a4R400, a6R200, a6R400.

• Large-porosity (blue symbols in Fig. 5): a8R200, a8R400, a10R200, a10R400.

For each experimental run, the most unstable wavelength Λ* has been estimated by counting the number of corrugations of the acidic (yellow) front. By most unstable wavelength, we mean the most predominantly visible wavelength that emerges after pressurisation of the chamber, and leads to the solutal plumes in the subsequent (non linear) regime. Aiming at comparing the obtained results with previous theoretical works, a dimensionless framework is adopted in the following. The typical density difference Δρ is considered to be proportional to the saturation concentration as Δρ = αK_HP_CO2, where K_H is Henry's constant and α refers to the solutal expansion coefficient. The product αK_H has been measured by Hebach et al.⁴³ but their results (αK_H = 0.004 ± 0.001 MPa⁻¹) were marred by a 25% uncertainty. Further taking = (Δρgκ/μ), = ϕD/, and = ϕ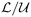 as typical velocity, length and time scales to make the problem dimensionless leads to the natural emergence of the Rayleigh number Ra as the only characteristic dimensionless number in the transport equation for the dissolved CO₂:

This non-dimensional number quantifies the initial strength of the gravitational instability.⁶

In the above expressions for the typical velocity, time, length and time scales, as well as Rayleigh number, the permeability can be chosen to be equal to either the permeability κ_HS = E²/12 of the Hele-Shaw cell of same thickness E, or the actual permeability κ_MM of the micromodel (listed in Table 3). In Fig. 5, the most unstable wavenumber q* = 2π/(/Λ*) has been plotted with respect to the Rayleigh number. In this linear regime the dimensionless wave number is supposed to be independent of the parameters (note that its actual theoretically-predicted value varies amongst the authors^41,42), in particular the Rayleigh number Ra. As shown in Fig. 5(a), the wavenumber is much smaller than predicted when using the permeability κ_HS of the Hele-Shaw cell of same thickness (without microstructure). Conversely, when using the exact permeability κ_MM, the wavenumber is of the expected order of magnitude (see Fig. 5b). Note however that the experimental values vary around the theoretical prediction by a factor 3. The experimental uncertainty is known to be around 20% from previous studies on standard Hele-Shaw cells,³⁸ so this uncertainty alone cannot explain the scattering of the data.

For high porosity micromodels we attribute this data point scattering to a physical locking of the most unstable wave length Λ* at a value equal to multiples of the centre-to-centre distance a of the porous structure. Indeed, for these models the natural wave length of the instability is close to that structural distance. This phenomenon is quite obvious in the case of micromodel a10R400 where the wavelength is locked on the centre-to-centre distance, as shown in Fig. 6. In this case, the natural value of the most unstable wavelength for a homogeneous medium (i.e., without pillars) of same porosity would lie in the range [2.4–11.2 mm], for a centre-to-centre distance a = 4 mm. Thus, for this specific micromodel, we measured Λ* = a in the considered pressure range; in Fig. 5(b), the corresponding dimensionless wave number 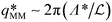scales as Ra_MM⁻¹, since = /Ra_MM⁻¹ in this case. This wavelength locking is also visible in the case of micromodel a8R400 for which a wavelength Λ* ≃ 2a was observed. This locking process is less visible as Λ*/a increases, i.e., for low porosity micromodels where the distance a is about one order of magnitude smaller than the most unstable wavelength.

Fig. 6 Gravitational instability observed in a porous micromodel a10R400 with center-to-center distance a = 4 mm, for P_CO2 = 1 to 5 bar (end of the linear regime, t = 2 min). The real wavelength Λ* does not show obvious dependence on the pressure, so that the dimensionless number is proportional to Ra_MM⁻¹ (see Fig. 5).

The large scattering observed for low CO₂ pressure and/or low porosity is more difficult to interpret as no obvious trend is observed for low porosity micromodels. For the lowest CO₂ pressures, however, the most unstable wavelength is of the same order as the width L and height H of the micromodels. As the vertical extension of the flow (in the linear regime) is supposed to be on the order of the most unstable wavelength, such a vertical constraint could lead to an underestimation of the most unstable wavelength – or equivalently to an overestimation of the wavenumber. In other words, under such conditions, finite size effects impact the measured most unstable wavelength.

4 Discussion – relevance to dissolution trapping of CO₂ in deep aquifers

Injection of CO₂ for subsurface storage is usually performed at depths below 800 m, for which the pressure is typically larger than 10 MPa and the temperature larger than 50 °C. Under such conditions, the injected CO₂ is in its supercritical state. In our experiment, the CO₂ is injected in its gas phase, under injection pressures ranging between 1 and 5 bars. In addition, the deep aquifers used for CO₂ sequestration have permeabilities in the range 10⁻¹⁴ to 10⁻¹² m², and typical pore sizes around 0.1 mm, while our porous media have permeabilities in the range 8 × 10⁻¹⁰ to 7 × 10⁻⁹ m² and typical pore sizes (roughly estimated as a–R) between 0.4 and 3.6 mm. So, to which extent can such analogue experiments be used to draw conclusions relative to natural systems?

4.1 Gas CO₂vs. supercritical CO₂

Convective dissolution occurs within the aqueous phase, and to our knowledge it is not impacted by whether the pure CO₂ phase above the aqueous phase is supercritical or gaseous.

4.2 Pressure and temperature conditions

What controls the gravitational instability and subsequent convection is mostly the non-dimensional Rayleigh number Ra. The pressure and temperature conditions are only relevant in that they impact Ra through the density difference Δρ, the aqueous phases' viscosity μ and the molecular diffusivity of the dissolved CO₂, D. However, it is possible to obtain Rayleigh values in the same range as those encountered in geological formations while working at room temperature and at pressures much lower than in situ pressures. For example two of the best known geological formations in which CO₂ is injected are the Utsira formation at Sleipner and the Krechba formation at In Salah. The corresponding Rayleigh numbers can be computed from eqn (2), based on data for Δρ, κ, ϕ, μ, and D found in ref. 17 and knowing that the Utsira formation consists of nine 20 m thick permeable layers separated by impermeable layers and that the characteristic height H can also be taken to 20 m for Krechba.⁴⁴ We thus infer Ra values of 1.3 × 10⁴ and 140 for Utsira and Krechba, respectively. More generally, the Rayleigh number in natural formations can be as low as 100 and can reach 6 digit numbers in formations which are several hundred of meters thick. Accordingly, theoretical and numerical studies usually consider values in the range 100 or 1000 to 10⁵ or 10⁶.^10,12,18,42 For comparison, the Rayleigh number in our experiments spans the range 150 ≤ Ra ≤ 5 × 10³, hence consistent with conditions in the Krechba formation. Furthermore, using a stronger pressure chamber could allow us to use injection pressures of 50 Pa, and thus, a Rayleigh number larger than 5 × 10⁴, relevant to the conditions in the Utsira formation.

Another non-dimensional characteristic number which is relevant to the convection dissolution dynamics, albeit in a weaker manner than Ra, is the Darcy number Da = κ/H². For Utsira it is smaller than 10⁻¹⁴, while for Krechba is smaller than 10⁻¹⁶. For natural formations, the number 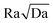is much smaller than 1, which ensures that the most unstable wavelength in the gravitational instability process is much larger than the typical pore size (so-called Darcy regime).This number is smaller than 1.3 × 10⁻³ for Utsira and smaller than 1.4 × 10⁻⁶ for Krechba. In our experiments Da ranges between 8 × 10⁻⁹ and 7 × 10⁻⁸ depending on the flow cell, so that the condition ≪ 1 is valid for Ra < 1100 for the least permeable flow cell, and Ra < 380 for the more permeable one. Note however that the resolution of the optical lithography used to fabricate the cells is on the order of 1 μm, so it is possible to make similar flow cells with smaller permeabilities (i.e., smaller distance between grains and/or smaller grains), allowing the condition to remain valid for larger Rayleigh numbers (but then these Ra values require higher pressures to be reached).

4.3 Pore sizes

In this study, we purposedly chose to consider very permeable porous media to investigate the transition between the behavior observed in a pure Hele-Shaw geometries (without grains) and that observed in a quasi-2D porous media. Reducing the typical pore size to 0.1 mm is very feasible with the fabrication method presented in section 2.2.1. However, as discussed above, in order to obtain results that are relevant to convective dissolution in a given geological formation, one does not necessarily need to consider pore sizes similar to those which are characteristic of that formation.

5 Conclusion and prospects

We have presented a new type of NOA-based microfluidic cell aimed at investigating the impact of solid grains within a Hele-Shaw (HS) cell on the convective dissolution of CO₂ in deep aquifers. The fabrication method allows for precise, gas-tight, two-dimensional (2D) design with a 2D positioning and geometry of the cylindrical pillars that matches the numerical model well and a cell thickness (gap between the two parallel plates of the HS cell) that must be measured a posteriori and is on average 25% smaller than the planned gap. Any 2D porous geometry could be considered, including geometries for which the medium's pores and grains are 10 or 100 times smaller, and of similar size as in geological formations. Note however that, to be conclusive, our experiments do not need to consider a medium whose geometrical features are of identical scale as in the natural medium: invoking the principle of similitude only requires that the characteristic non-dimensional numbers controlling the physics at play be identical in the experiment and in the natural medium. In fact, we have shown that such analogue experiments are well suited to obtaining results that are relevant for geological formations.

The flow cells fabricated in this manner have been used to perform analog experiments of the convective dissolution of CO₂ in gas phase at pressures ranging from 1 to 5 bars. The gaseous CO₂ is put in contact with the porous medium filled with an aqueous phase, where it dissolves, triggering a gravitational convection of the CO₂-enriched gaseous phase. In the linear regime of the gravitational instability that leads to this natural convection, the most unstable wavelength exhibits values that vary by as much as one order of magnitude from the theoretical predictions obtained for a standard Hele-Shaw (without grains). However, when considering in that theory the real permeability of the porous medium instead of that of the pillar-devoid Hele-Shaw cell, this discrepancy is reduced to a factor 3. When the natural wave length of the instability is not very different from a multiple of the centre-to-center distance between pillars, it gets locked onto that multiple of the structural distance, a phenomenon which, to our knowledge, has never been observed in this kind of systems.

Detailed analysis of the linear and non-linear growth of the gravitational instability is out of the scope of this paper, and will be presented in a later study. The fabrication method will also be generalized towards less porous geometries, with the solid pillars occupying a much larger portion of the Hele-Shaw cell's volume, and disordered geometries.

Appendix A: Computation of the permeability

Because measuring the permeability would have required to significantly modify the setup, we resorted to numerical simulations to obtain the flow cells' permeabilities. In order to avoid large computations involving the numerical modelling of an entire micromodel, an elementary cell, such as the one shown in Fig. 7(a), was considered. The cell was taken for x ranging from −a/2 to a/2, y ranging from −E/2 to E/2, and z ranging from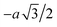 to . The incompressible Navier–Stokes equations was solved in the pore space using the finite element code Comsol Multiphysics. The boundaries were considered periodic in the x and z directions with no-slip boundary conditions on the pillars and on the faces of the Hele-Shaw cell. The mesh contained between 20 000 and 100 000 elements (depending on the geometry of the cell), leading to a number of degrees of freedom ranging from 200 000 to 900 000. A volume force Δρg of amplitude 1 kg m s⁻² was imposed in the z direction; it enforced a steady flow, the streamlines of which are plotted in Fig. 7(b). These streamlines are symmetric in the x and z direction with respect to the center of the cell, while the pressure lobes are antisymmetric with respect to the (x,y)-plane z = 0. This indicates that the fluid viscosity is sufficiently large for the flow to be in the Stokes regime (i.e., no non-linearities). The Darcy permeability was then computed as κ_MM = μQ/EaΔρg, where the volume flow rate Q is evaluated at .

Fig. 7 (a) Geometry of the elementary cell considered for the computation of the actual permeability κ_MM. (b) Numerical streamlines and pressure field obtained in the (x,z)-plane y = 0, for micromodel a6R400.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The French National Research Agency (ANR) is acknowledged for financial support in the framework of the CO2-3D Project (ANR-16-CE06-0001). Two anonymous referees are also gratefully acknowledged for their insightful suggestions towards manuscript improvement.

Notes and references

1. I. IPCC Working Group 1, T. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. Midgley, IPCC, 2013: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge university press technical report, 2013.
2. S. Bachu, Prog. Energy Combust. Sci., 2008, 34, 254–273.
3. R. Oxburgh, Lowest cost decarbonisation for the UK: The critical role of CCS: Report to the Secretary of State for Business, Energy and Industrial Strategy from the Parliamentary Advisory Group on Carbon Capture and Storage (CCS), SCCS, 2016, p. 70.
4. E. Bryant, Climate process and change, Cambridge University Press, Cambridge, 1997, pp. 157–159.
5. R. M. Enick and S. M. Klara, Chem. Eng. Commun., 1990, 90, 23–33.
6. H. E. Huppert and J. A. Neufeld, Annu. Rev. Fluid Mech., 2014, 46, 255–272.
7. A. Vreme, F. Nadal, B. Pouligny, P. Jeandet, G. Liger-Belair and P. Meunier, Phys. Rev. Fluids, 2016, 1, 064301.
8. A. Taheri, O. Torsæter, E. Lindeberg, N. J. Hadia and D. Wessel-Berg, Int. J. Greenhouse Gas Control, 2018, 71, 212–226.
9. T. Menand and A. Woods, Water Resour. Res., 2005, 41, W05014.
10. J. A. Neufeld, M. A. Hesse, A. Riaz, M. A. Hallworth, H. A. Tchelepi and H. E. Huppert, Geophys. Res. Lett., 2010, 37, L22404.
11. C. W. MacMinn, J. A. Neufeld, M. A. Hesse and H. E. Huppert, Water Resour. Res., 2012, 48, W11516.
12. Y. Liang, B. Wen, M. A. Hesse and D. DiCarlo, Geophys. Res. Lett., 2018, 45, 9690–9698.
13. L. Wang, Y. Nakanishi, A. Hyodo and T. Suekane, Int. J. Greenhouse Gas Control, 2016, 53, 274–283.
14. Y. Nakanishi, A. Hyodo, L. Wang and T. Suekane, Adv. Water Resour., 2016, 97, 224–232.
15. Y. Teng, L. Jiang, Y. Fan, Y. Liu, D. Wang, A. Abudula and Y. Song, Magn. Reson. Imaging, 2017, 39, 168–174.
16. C. Brouzet, Y. Méheust and P. Meunier, Phys. Rev. Fluids, 2022, 7, 033802.
17. M. Elenius and K. Johannsen, Comput. Geosci., 2012, 16, 901–911.
18. J. J. Hidalgo, J. Fe, L. Cueto-Felgueroso and R. Juanes, Phys. Rev. Lett., 2012, 109, 264503.
19. H. Emami-Meybodi, Phys. Fluids, 2017, 29, 094102.
20. B. Wen, K. W. Chang and M. A. Hesse, Phys. Rev. Fluids, 2018, 3, 123801.
21. A.-M. Eckel and R. Pini, Phys. Fluids, 2021, 33, 066604.
22. G. Pau, J. Bell, K. Pruess, A. Almgren, M. Lijewski and K. Zhang, Adv. Water Resour., 2010, 33, 443–455.
23. J. Dhar, P. Meunier, F. Nadal and Y. Méheust, Phys. Fluids, 2022, 064114.
24. Y. Kim, J. Wan, T. J. Kneafsey and T. K. Tokunaga, Environ. Sci. Technol., 2012, 46, 4228–4235.
25. M. Buchgraber, A. R. Kovscek and L. M. Castanier, Transp. Porous Media, 2012, 95, 647–668.
26. L. Zuo, C. Zhang, R. W. Falta and S. M. Benson, Adv. Water Resour., 2013, 53, 188–197.
27. S. Morais, N. Liu, A. Diouf, D. Bernard, C. Lecoutre, Y. Garrabos and S. Marre, Lab Chip, 2016, 16, 3493–3502.
28. W. Song, F. Ogunbanwo, M. Steinsbø, M. A. Fernø and A. R. Kovscek, Lab Chip, 2018, 18, 3881–3891.
29. W. Song, H. Fadaei and D. Sinton, Environ. Sci. Technol., 2014, 48, 3567–3574.
30. S. Morais, A. Cario, N. Liu, D. Bernard, C. Lecoutre, Y. Garrabos, A. Ranchou-Peyruse, S. Dupraz, M. Azaroual and R. L. Hartman, et al. , React. Chem. Eng., 2020, 5, 1156–1185.
31. N. Liu, C. Aymonier, C. Lecoutre, Y. Garrabos and S. Marre, Chem. Phys. Lett., 2012, 551, 139–143.
32. C. Zhang, K. Dehoff, N. Hess, M. Oostrom, T. W. Wietsma, A. J. Valocchi, B. W. Fouke and C. J. Werth, Environ. Sci. Technol., 2010, 44, 7833–7838.
33. C. Chang, Q. Zhou, T. J. Kneafsey, M. Oostrom, T. W. Wietsma and Q. Yu, Adv. Water Resour., 2016, 92, 142–158.
34. N. K. Karadimitriou and S. M. Hassanizadeh, Vadose Zone J., 2012, 11, vzj2011.0072.
35. B. Levaché, A. Azioune, M. Bourrel, V. Studer and D. Bartolo, Lab Chip, 2012, 12, 3028–3031.
36. Microchem, SU-8 2000 (2000.5–2015) Permanent epoxy negative photoresist processing guidelines for : SU-8 2000.5, SU-8 2002, SU-8 2005, SU-8 2007, SU-8 2010 and SU-8 2015, 2010.
37. E. P. Dupont, R. Luisier and M. A. Gijs, Microelectron. Eng., 2010, 87, 1253–1255.
38. A. Vreme, PhD thesis, Université De Reims Champagne-Aardenne, 2015.
39. S. Backhaus, K. Turitsyn and R. E. Ecke, Phys. Rev. Lett., 2011, 106, 104501.
40. A. C. Slim, M. M. Bandi, J. C. Miller and L. Mahadevan, Phys. Fluids, 2013, 25, 24101.
41. H. Hassanzadeh, M. Pooladi-Darvish and D. W. Keith, AIChE J., 2007, 53, 1121–1131.
42. A. Riaz, M. Hesse, H. Tchelepi and F. Orr Jr., J. Fluid Mech., 2006, 548, 87–111.
43. A. Hebach, G. Martin, A. Kögel and N. Dahmen, J. Chem. Eng. Data, 2005, 50, 403–411.
44. J. Nijjer, D. Hewitt and J. Neufeld, J. Fluid Mech., 2022, 935, A14.

---