 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the effect of structural changes on slow magnetic relaxation in mononuclear octahedral copper(II) complexes†
Dawid
Marcinkowski‡
 a,
Ariel
Adamski‡
a,
Maciej
Kubicki
a,
Ariel
Adamski‡
a,
Maciej
Kubicki
 a,
Giuseppe
Consiglio
b,
Violetta
Patroniak
a,
Giuseppe
Consiglio
b,
Violetta
Patroniak
 a,
Tomasz
Ślusarski
ac,
Muhammed
Açıkgöz
d,
Daria
Szeliga
e,
Nahir
Vadra
a,
Tomasz
Ślusarski
ac,
Muhammed
Açıkgöz
d,
Daria
Szeliga
e,
Nahir
Vadra
 af,
Mirosław
Karbowiak
af,
Mirosław
Karbowiak
 e,
Ireneusz
Stefaniuk
g,
Czesław
Rudowicz
e,
Ireneusz
Stefaniuk
g,
Czesław
Rudowicz
 a,
Adam
Gorczyński
a,
Adam
Gorczyński
 *a and
Maria
Korabik
*e
*a and
Maria
Korabik
*e
aFaculty of Chemistry, Adam Mickiewicz University, Uniwersytetu Poznańskiego 8, 61-614 Poznań, Poland. E-mail: adam.gorczynski@amu.edu.pl
bDipartimento di Scienze Chimiche, Università di Catania, I-95125 Catania, Italy
cInstitute of Spintronics and Quantum Information, Faculty of Physics, Adam Mickiewicz University, Uniwersytetu Poznańskiego 2, 61-614 Poznań, Poland
dDepartment of Science, The State University of New York (SUNY) Maritime College, New York 10465, USA
eFaculty of Chemistry, University of Wrocław, F. Joliot-Curie 14, 50-383 Wrocław, Poland. E-mail: maria.korabik@chem.uni.wroc.pl
fUniversidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Química Inorgánica, Analítica y Química Física and CONICET – Universidad de Buenos Aires, Instituto de Química Física de los Materiales, Medio Ambiente y Energía (INQUIMAE), Buenos Aires C1428EGA, Argentina
gCollege of Natural Sciences, University of Rzeszow, Rejtana 16a, 35-310 Rzeszow, Poland
First published on 25th July 2022
Abstract
Current advances in molecular magnetism are aimed at the construction of molecular nanomagnets and spin qubits for their utilization as high-density data storage materials and quantum computers. Mononuclear coordination compounds with low spin values of S = ½ are excellent candidates for this endeavour, but knowledge of their construction via rational design is limited. This particularly applies to the single copper(II) spin center, having been only recently demonstrated to exhibit slow relaxation of magnetisation in the appropriate octahedral environment. We have thus prepared a unique organic scaffold that would allow one to gain in-depth insight into how purposeful structural differences affect the slow magnetic relaxation in monometallic, transition metal complexes. As a proof-of-principle, we demonstrate how one can construct two, structurally very similar complexes with isolated Cu(II) ions in an octahedral ligand environment, the magnetic properties of which differ significantly. The differences in structural symmetry effects and in magnetic relaxation are corroborated with a series of experimental techniques and theoretical approaches, showing how symmetry distortions and crystal packing affect the relaxation behaviour in these isolated Cu(II) systems. Our unique organic platform can be efficiently utilized for the construction of various transition-metal ion systems in the future, effectively providing a model system for investigation of magnetic relaxation via targeted structural distortions.
1. Introduction
Molecular nanomagnets (MNMs) are a research focus of scientists due to a variety of potential applications,1–4 including molecular spintronics,1,5,6 high-density information storage,7–9 quantum information processing or sensing.10–16 These systems display magnetic hysteresis below their blocking temperature (TB) and are magnetically bi-stable, exhibiting an energy barrier to spin reversal (Ueff),17–22 ultimately manifested by macroscopic quantum tunneling of magnetization (QTM) and slow relaxation of magnetization. The discovery of the highest TB by Guo et al.,23 for an organometallic Dy(III) complex displaying magnetic hysteresis at temperatures reaching 80 K, could facilitate development of high-temperature SIM devices. In addition, studies of various Dy(III) congeners of this family24–26 indicate the importance of understanding the magnetization relaxation mechanisms and magneto-structural correlations.4,27–33 Still, similar level of performance for d-block MNMs is yet to be achieved.Prerequisites for utilization of 3d complexes as molecular nanomagnets are well-established.3,34 Importantly, the S = ½ systems are excellent candidates for construction of molecular qubits.35,36 Chosen examples based on V(IV),37–41 Fe(V),42,43 Mn(IV),44 Ni(III)45 or Ni(I)46,47 metal ions show how the choice of ligand, electronic configuration of the metal ion and the observed symmetry distortions all affect the magnetic relaxation and its mechanisms, which include combined phonon, direct and Raman processes.48,49 The above compounds are important contributions, nonetheless they are usually pretty unstable at room temperature, which would limit their potential applications. Copper(II) ion on the other hand forms very stable complexes and was demonstrated to be of interest for molecular magnetism studies. Notable examples of S = ½, d9 Cu(II) systems were proposed to act as potential spin qubits with phthalocyanines,50,51 porphyrines52–55 acetylacetonates or dithiocatecholates ligating species.56–58 Recent record value of 1.4 ms coherence time was demonstrated by Dai et al.56 for a (PPh4)2[Cu(mnt)2] (where mnt2− is maleonitriledithiolate), after dilution in isostructural diamagnetic Ni(II) matrix and utilization of dynamic decoupling technique. As for the SIM behavior, the examples of compounds with experimentally determined field-induced slow magnetic relaxation with single d9 Cu(II) ion are rather scarce,59–64 whereas its origin is only partially understood.48,49
To achieve the desired molecular magnetic behavior in S = ½ coordination systems, the following molecular design were proposed: (i) square planar coordination geometry; (ii) coordinating atoms devoid of nuclear spin; (iii) rigidification of the molecular architecture; (iv) minimization of the protons influence above a certain radius from the metal (the concept of spin diffusion barrier).14,54,65,66 Nevertheless, yet undiscovered features may also be important, which can be established through meticulous magneto-structural correlation studies. These can be facilitated by employing modular organic platforms, since they may provide possible predictions of magnetic parameters based on the structure alone.48
Herein, we present a unique example of system, which is suitable for construction of monometallic transition metal complexes, the structure of which can be carefully altered within the ascertained symmetry regime. Stereospecific addition of alcohol to imine ligand leads to pentadentate ligands, which readily coordinate Cu(II) ion to form octahedral complexes (Scheme 1).
 | ||
| Scheme 1 Rationale behind the modular organic platform designed and implemented in the present studies for monometallic magneto-structural correlations. | ||
This framework is close to the N3O square plane, whereas symmetry distortions are then applied through the axial alkoxide moieties. Alterable alcohol appendage and single Cu(II) ionic centre with blocked intermetallic exchange interactions make this platform a suitable starting point for better understanding of relaxation mechanisms and establishing magneto-structural correlations. The effect of the surrounding ligands and symmetry of the polyhedron on the static and dynamic magnetic properties of Cu(II) ions in two systems is investigated. To rationalize our experimental results extensive computational studies are carried out utilizing SHAPE analysis, density functional theory (DFT)/ab initio and semiempirical approaches. This combined strategy enables to draw conclusions on magnetization relaxation mechanisms, magneto-structural correlations, the role of structural distortions, and usefulness of the proposed organic platform for designing new Cu(II) SIMs/qubits.
2. Results and discussion
2.1 Synthesis
Schiff base ligand L was synthesized via condensation of 2,6-pyridinedicarboxaldehyde with 3-amino-5-methylisoxazole as presented in Scheme 2. Although L was isolated and characterized (see Section II in ESI†), its complexation with CuX2 salts in the presence of alcohols leads to unexpected structural transformations. Reactions of L with Cu(ClO4)2·6H2O (1) and Cu(OTf)2 (2) lead to the asymmetric addition of MeOH (1) or EtOH (2) to the imine bond, resulting in the formation of chiral N,O-aminal Lred-1/2, which is unambiguously established via X-ray crystallography of isolated coordination compounds 1 and 2 (Table S1† and Section 2.2). Whereas reduction of the parent ligand L is most plausibly facilitated by the template effect of Cu(II) ions, it is yet to be determined if such reaction is diastereospecific or one of the chiral isomers (here S,S) crystallized in the preferential manner. The solvent as well as the counter ions OTf− and ClO4− does not seem to affect the type of the isomer obtained in both structures. Such chiral N,O-aminal motif is found in a number of natural, pharmaceutical products and valuable synthetic precursors.67–69 Therefore, the development of effective and effortless methods for their synthesis has attracted considerable research effort.70,71 This report is the first on the formation of aldimine-derived N,O-aminals, without the need of applying the external chiral catalyst. Interestingly, only three studies70,72,73 on the use of metallic catalysts in the formation of N,O-aminals from related ketimines were reported so far. Altogether, our approach can be used to form chiral molecules with the N,O-aminals, strategically placed at the 2,6-positions of pyridine, for potential use in construction of more complex systems, particularly of biological or magnetic relevance. | ||
| Scheme 2 Synthetic pathway leading to Schiff base ligand L and its copper(II) complexes; blue sphere represents Cu(II) ion. | ||
2.2 Structural characterization of Cu(II) complexes
Fig. 1a and b shows the perspective views of molecules 1 (a) and 2 (b) together with the numbering schemes. Table S2† lists the relevant geometrical parameters. Structures were refined for the perchlorate analogue at room- (1) and liquid nitrogen-temperature (1′) to unambiguously exclude phase-transition changes. Pentadentate ligands Lred1 (ClO4−; MeOH)and Lred2 (OTf–, EtOH) wrap around copper(II) ions and differ by either methoxy (1) or ethoxy (2) groups attached to the stereogenic center, as a result of the unexpected addition of alcohol to the imine bond (Scheme 2).In both crystal structures complexes exist as dications, with two perchlorate (1) or triflate (2) anions balancing the charge. Cu(II) centers are six-coordinated in distorted octahedral fashion (Fig. 1c). Due to the structure of the ligand the octahedra are elongated along one direction (O7⋯O14), and this elongation is as large as 25% in 1 and slightly smaller in 2 (Fig. 1c and d). Such a geometry is related to the conformation of ligand molecules, in which the ring planes are almost perpendicular one to another (Table S2†). This also results in a nearly square tetradentate plane formed by three nitrogen atoms of the Lred-1/2 ligand and the oxygen atom from the solvent molecule (see SHAPE analysis in Section 2.3). Both compounds crystallize in the triclinic crystal system and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, with two molecules of Cu(II) complex in a unit cell. In the crystal structure of 1, they symmetrically interact with each other through the pyridine–pyridine π–π stacking interactions (C2 relation, smallest Cu⋯Cu distance ca. 8 Å). These form infinite chains of alternate cations and anions connected by the hydrogen bonds, with the second anion threaded to this chain (Fig. 1f and Table S3†). In 2, the main structural motif is a cluster of hydrogen bonded structural fragments: two cations (C2 relation, smallest Cu⋯Cu distance ca. 9.7 Å), four triflate anions, and two solvent-ethanol molecules (Fig. 1g). These principal motifs are connected to form three-dimensional crystal structure by means of electrostatic interactions and weak intermolecular van der Waals forces, thus lacking of the degree of organization present in 1.
space group, with two molecules of Cu(II) complex in a unit cell. In the crystal structure of 1, they symmetrically interact with each other through the pyridine–pyridine π–π stacking interactions (C2 relation, smallest Cu⋯Cu distance ca. 8 Å). These form infinite chains of alternate cations and anions connected by the hydrogen bonds, with the second anion threaded to this chain (Fig. 1f and Table S3†). In 2, the main structural motif is a cluster of hydrogen bonded structural fragments: two cations (C2 relation, smallest Cu⋯Cu distance ca. 9.7 Å), four triflate anions, and two solvent-ethanol molecules (Fig. 1g). These principal motifs are connected to form three-dimensional crystal structure by means of electrostatic interactions and weak intermolecular van der Waals forces, thus lacking of the degree of organization present in 1.
2.3 SHAPE analysis and symmetry considerations
To gain more insight into the local site-symmetry in 1 and 2, calculations using SHAPE software74,75 were performed, which utilize the continuous shape measurements (CShM)76 method. S parameter is therefore introduced, which corresponds to the degree of deviations from the perfect polyhedron with S = 0 corresponding to ideal geometry. Results shown in Table S4† clearly indicate that 1 and 2, as well as magnetically relevant Cu(II) system studied by Boča60 show significant deviations from the octahedral geometry, classified as structurally severe distortions (S > 3).74 Please note that the chemically significant differences were classified to be visible from 0.1 value changes.74Given that investigated systems are heterotopic in terms of ligands nature (N and O donor atoms), we performed additional analysis regarding square planar planes present in the studied octahedra. The aim was to understand: (i) which part of the ligands architecture is responsible for structural anisotropy of relevance to magnetic properties and (ii) why do the observed magnetic properties differ in 1 and 2. Results are gathered in Table S5.† One can discriminate three planes: (A) (N2–N9–N17–MeOH/H2O) which is dependent on the monodentate MeOH (1) or H2O (2) solvent molecules; (B) (MeOH/H2O–N9–O7–O14) and (C) (N2–N17–O7–O14) which are mostly affected by the O7–O14, distortions. Unexpectedly, it appears that plane (A) alone exhibits significantly larger distortions in complex 2 (S-value 2 = 0.308 vs. S-value 1 = 0.077). This could be also dependent on the H-bonding pattern with the perchlorate (1) or triflate (2) counterions. S-Values in planes (B) and (C) favour stronger distortions in 1 than in 2, ascribed to the plane formed by isoxazole/alkoxide moieties.
2.4 DC magnetic properties
The magnetic properties of powdered microcrystalline samples 1 and 2 were studied by measuring the thermal dependence of the magnetic susceptibility in the temperature range of 1.8–300 K and magnetic field of 0.5 T. The field dependences of the magnetization from 0 to 5 T for 1 and 2 were measured at 2 K. In DC magnetic field both compounds show similar properties, typical for non-interacting S = ½ spin system (Fig. S2†). The χmT product values (0.373 ± 0.005 cm3 K mol−1, μeff = 1.73 ± 0.01 B.M.) are practically constant in the whole measured temperature range 1.8–300 K. The 1/χmversus T plots obeys the Curie–Weiss law with Curie constant C = 0.384 and 0.393 cm3 K mol−1 and Weiss constant θ = −0.1 and −0.3 K for 1 and 2, respectively. Simulation of magnetic susceptibility curves using molecular field correction:77,78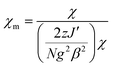 | (1) |
 | (2) |
2.5 AC magnetic properties
Measurements were made at 3 × 10−4 T oscillating field for 16 frequencies, in the temperature range 1.8–10 K. An external magnetic DC field of 0.1 T was chosen from the maximum of out of phase susceptibility χ′′ versus magnetic field relation (Fig. S4 and S5†). Please notice that much stronger field must be applied for complex 2 than for 1, which also correlates with more pronounced character of slow magnetic relaxation in AC field for the latter one (vide infra). The out of phase component χ′′ of 1 and 2 is silent at zero DC field, which indicates that the magnetization relaxation time (τ) is much shorter than ½πν of the AC field. Measurements done under 0.1 T DC field reveal differences in properties of complexes 1 and 2. The in-phase χ′ (Fig. 2a) and out-of-phase χ′′ (Fig. 2b and c) susceptibilities show temperature and frequency dependence with characteristic maxima in 1, indicating slow magnetic relaxation phenomenon. Different types of relaxation mechanisms can be potentially involved in molecular system: Orbach, direct, Raman, and QTM components, respectively.60,61 | (3) |
 | ||
| Fig. 2 Temperature dependence of: (a) the in-phase χ′, (b) the out-of-phase χ′′ susceptibility and (c) χ′′ vs. frequency for complex 1. | ||
In the literature, one can find different approaches to the Arrhenius equation:
 | (4) |
The analysis of the relaxation processes in 1 was carried out using Raman, direct and QTM relaxation mechanisms. The fact that Raman mechanism plays a dominant role in S = ½ system37 and that the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. ln
τ vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T dependence is almost linear (Fig. S6†), suggests that direct relaxation mechanism cannot be ignored.37 A linear fit to the equation ln
T dependence is almost linear (Fig. S6†), suggests that direct relaxation mechanism cannot be ignored.37 A linear fit to the equation ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ = b0 + b1
τ = b0 + b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T was used to determine direct process parameters, which are b0 = −4.50 and b1 = −2.07 and they are comparable to that recently obtained for Cu(II) S = 1/2 system.20 We have also attempted to extract the direct process term from field dependence of τ−1.
T was used to determine direct process parameters, which are b0 = −4.50 and b1 = −2.07 and they are comparable to that recently obtained for Cu(II) S = 1/2 system.20 We have also attempted to extract the direct process term from field dependence of τ−1.
The direct spin relaxation mechanism can be expressed by the following equation:80,81
| τ−1 = AH4T | (5) |
The Cole–Cole plots from the AC magnetic susceptibility data of 1 (Fig. 3b) were fitted by the generalized Debye model (Table S6†).82,83 The α parameters describing the distribution of the relaxation times in a magnetic system were extracted. The limiting value of α = 0 describes a single relaxation process, whereas α = 1 corresponds to an infinitely wide distribution of the relaxation times. The wider the distribution of the relaxation times, the larger the value of α.82 A small value of the distribution coefficient α (0.16 at 4.4 K to 0.25 at 1.8 K) for complex 1 indicates that the relaxation process has a narrow distribution of relaxation time. The τ parameters were extracted from the Debye model (Fig. S6†), with τ = 3.97 ms at 1.8.K. Similar temperature relations and values were presented for vanadium(IV)-based compounds, with S = ½.38
AC susceptibility measurements of complex 2 differ from 1, with no phase shift maxima present in the in-phase χ′ vs. T dependencies (Fig. 4a) and only the slight onset of the out-of-phase signals χ′′ vs. T (Fig. 4b and c) under high external magnetic field frequencies. Despite high structural resemblance of the Cu(II) coordination environment, the properties of 1 and 2 differ significantly and this precluded us from determination of the relaxation parameters for the latter compound.
 | ||
| Fig. 4 Temperature dependence of: (a) the in-phase χ′, (b) the out-of-phase χ′′ susceptibility and (c) χ′′ vs. frequency dependence of the complex 2. | ||
2.6 CW-EPR
Continuous wave electron paramagnetic resonance (CW-EPR) spectra were recorded in X and Q band frequencies to corroborate magnetic phenomena (Sections 2.4 and 2.5) with structural studies (Sections 2.2 and 2.3). For experimental details see EPR Section III in the ESI.† CW-EPR spectra of complexes 1 and 2 in liquid nitrogen (X-band) and helium (Q-band) temperatures with fitting protocols are shown in the ESI (Fig. S7–S16†) with representative ones in Fig. 5. The spectroscopic splitting factors g⊥ and g‖ for all spectra are presented in Table 2 and prove their axial character type (g‖ > g⊥). Transition energy levels at the resonance field Bres are presented in Tables S7 and S8† and their graphical representation in Fig. S17 and S18.† Room temperature X-band EPR spectra of 1 and 2 (Fig. 5a and b) are temperature-independent down to 77 K. For 1 the axial type spectrum is partially, but clearly resolved with the g-factors g⊥ = 2.06, g‖ = 2.28 and parallel hyperfine splitting parameter A‖ = 175 G, resulting from the interaction of the unpaired electron of Cu(II) with the spin of copper nucleus I = 3/2. It is identical for both natural isotopes of 63Cu and 65Cu, so eight hyperfine levels can be expected with four allowed transitions: ΔMS = ±1 and ΔMI = 0 (Fig. S19†).84 The axial EPR spectrum of complex 2 exhibits similar values of the g-factors: g⊥ = 2.06 and g‖ = 2.25 but with no hyperfine structure. | ||
| Fig. 5 X-band EPR spectra of 1 (a) and 2 (b) at RT; solid red line shows temperature independent simulated spectra with parameters presented. The same type of spectrum with the same parameters was observed at 77 K; superposition of Q-band spectra of 1 (c) and 2 (d) at chosen temperature intervals: simulated spectra are in the ESI.† | ||
| Cmpd | 1 | 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| EPR band | X | Q | X | Qa | X | Q | X | Q | |
| (i) | (ii) | ||||||||
| a The SH parameters fitted to Q-band spectra at 10.5 K for: (i) a bimodal signal without constraints yielding the g1 value lower than 2.000 and (ii) for a monomodal signal with constraint of minimum g1 value set at 2.000. For explanations, see text. b All fittings were performed several times for each case, starting from different input data, and as a result, similar final values were obtained with an accuracy of 3%. Hence, the final results were selected taking into account the best fits, i.e. those with the lowest RMSD value. | |||||||||
| T [K] | 300 | 180 | 90 | 10.5 | 10.5 | 300 | 300 | 91 | 11 |
| g 1 | 2.029 | 2.048 | 2.035 | 1.950 | 2.000 | 2.059 | 2.053 | 2.060 | 2.012 |
| g 2 | 2.071 | 2.040 | 2.063 | 2.029 | 2.032 | 2.059 | 2.053 | 2.062 | 2.067 |
| g 3 | 2.259 | 2.258 | 2.258 | 2.289 | 2.267 | 2.32 | 2.307 | 2.185 | 2.349 |
| [g3 − g1] | 0.230 | 0.210 | 0.223 | 0.339 | 0.267 | 0.261 | 0.254 | 0.125 | 0.337 |
| A 1 | −4.79 | 2.739 | −3.33 | 23.34 | 23.35 | −1.756 | −0.0002 | −0.0002 | 36.69 |
| A 2 | −0.37 | −25.47 | 3.2 × 10−5 | −0.116 | 0.0001 | −0.232 | 0.0034 | 0.0002 | −60.04 |
| A 3 | 179.73 | 184.5 | 187.52 | 206.8 | 206.8 | 128.7 | 141.7 | 102.80 | 240.2 |
| Lwpp [mT] | 10.022 | 12.21 | 10.98 | 15.98 | 13.19 | 6.35 | 8.95 | 6.39 | 18 |
| RMSDb | 0.005 | 0.011 | 0.010 | 0.056 | 0.07 | 0.031 | 0.032 | 0.028 | 0.11 |
From spectra in Q-band (Fig. 5c and d) valuable information can be obtained, because the hyperfine structures are more pronounced for both compounds and it can be also observed for complex 2, which was not the case for X-band frequencies.
Down in helium temperatures, formation of a bimodal peak is observed for complex 1 in the range of 1200–1300 mT magnetic field. The second line is an image of transitions in the perpendicular direction (i.e. xy‖B), this effect is clearly observed for sample 1, while for sample 2 it is less apparent due to larger line widths. This phenomenon is even more visible in temperature-dependent EPR spectra (Fig. S7 and S8†). In addition, the LFMA (low field microwave absorption) line, which is an indicator of ferromagnetic interactions, does not occur even up to helium temperatures for both tested samples. This means ferromagnetic interactions are not present in 1 and 2, which is consistent with the DC susceptibility studies (see Section 2.4). While the nature of this phenomenon is yet to be unambiguously established, purity of synthesized samples and the fact that it is manifested in both compounds 1 and 2 (although to a different extent, i.e. sharp vs. broad signal, respectively) excludes the existence of unintentional impurities. Also, the reversibly of this signal can be observed only at very low temperatures (ca. below 25 K). In addition, values of the g-factors below 2.00 (from 1.86–1.99 from 4.5–12.5 K) might suggest formation of radical of different nature i.e., not associated with the Cu(II) ion. Literature survey suggests that this signal may be due to the formation of Cu(I)-NO nitrosyl complexes, which were considered both theoretically and experimentally in zeolite matrices and small molecule complexes.85–88 Formation of small fractions of Cu(I)NO species can be tentatively explained, when we assume that the isoxazole coordinating arms can participate in the Cu(II) > Cu(I) electron transfer. Graphical representation of the origin of the presumed Cu(I)NO nitrosyl-related radicals is depicted in Scheme S1.† Note that electronic structure calculations (Section 2.9.1) also suggest that existence of closely lying states of Cu(I) species may be feasible.
In the S = ½ systems, where the ZFS parameters, e.g. the axial D, are not allowed, the magnetic anisotropy is due only to the anisotropy of the g-factors, i.e. the [gz − gx] difference.60 The values (Table 2) for 1 and 2 are three times higher than for the related system presented in the literature, which indicates that it can be exploited in quantifying the magnetic anisotropy. Nevertheless, since at liquid helium temperatures [gz − gx] values are similar for 1 and 2, it is not the only parameter that should be considered to explain the magnetic behavior (with magnetic relaxation being much longer for 1 than in 2). One can also observe that temperature significantly affects the geff factor (Fig. S20†) and the EPR line width Bpp (Fig. S21†) for both compounds down to the liquid helium temperatures.
2.7 Theoretical calculations of spin Hamiltonian parameters
Using PHI program79 we simulated EPR spectra and variation of electronic levels with external magnetic field for complex 1. To simulate Cu(II) ion we set spin S as ½ and orbital quantum number L as 2. Spin Hamiltonians (SH) parameters (Section 2.9) were calculated using MOLCAS89 and we take gx = 2.0660, gy = 2.0920, gz = 2.3810 from NEVPT2 calculations (Section 2.9). Temperature was set at 300 K, field frequency at 10 GHz (X-band), field was swept from 0.25 to 0.4 Tesla and was directed along the x-, y-, and z-axis of g-tensor as well as powder integration was used. We used anisotropic spectra line widths to get better resemblance to experimental fits. Observed anisotropic broadening (Fig. S23 and S24†) might correspond to unresolved spectral features such as hyperfine coupling90,91 and correlates with the experimentally observed structures.2.8 Optical spectroscopy
To gain more insight into the electronic levels of 1 and therefore the nature of observed slow magnetic relaxation, optical spectroscopy and superposition model (SPM) calculations (Section 2.10) were performed. Fig. S25† shows the absorption spectrum measured at RT for complex 1. The intense bands observed in the range of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are associated with ligand-centered transitions. Electronic transitions of Cu(II) ions are much less intense than those associated with ligand absorption. They appear clearly for a more concentrated sample (blue line) and are observed in the range of 12
000 cm−1 are associated with ligand-centered transitions. Electronic transitions of Cu(II) ions are much less intense than those associated with ligand absorption. They appear clearly for a more concentrated sample (blue line) and are observed in the range of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–21
000–21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Fig. 6 (top) shows the absorption spectrum recorded in the range of Cu(II) electronic transitions at 4.2 K. Two bands at approximately 14
000 cm−1. Fig. 6 (top) shows the absorption spectrum recorded in the range of Cu(II) electronic transitions at 4.2 K. Two bands at approximately 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 and 17
600 cm−1 and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 and a shoulder at approximately 12
300 cm−1 and a shoulder at approximately 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 are clearly visible. Based on the above reasoning (details are in Section IV in ESI†) and the results of ab initio calculations (Section 2.9) the following energy level sequence can be proposed for Cu(II) in 1 assuming approximate C2 symmetry: 2A2(dx2−y2 + dz2) < 2A(dz2 + dx2−y2) < 2A(dxy) < 2B(dxz + dy,z) < 2B(dxz + dy,z) (Fig. 6 (bottom)). Accordingly, to the proposed energy levels structure four bands are expected in absorption spectrum of 1. Deconvolution of the experimental spectrum using four Gaussian functions is presented in the inset in Fig. 6 (top). The obtained bands with maxima at 12
600 cm−1 are clearly visible. Based on the above reasoning (details are in Section IV in ESI†) and the results of ab initio calculations (Section 2.9) the following energy level sequence can be proposed for Cu(II) in 1 assuming approximate C2 symmetry: 2A2(dx2−y2 + dz2) < 2A(dz2 + dx2−y2) < 2A(dxy) < 2B(dxz + dy,z) < 2B(dxz + dy,z) (Fig. 6 (bottom)). Accordingly, to the proposed energy levels structure four bands are expected in absorption spectrum of 1. Deconvolution of the experimental spectrum using four Gaussian functions is presented in the inset in Fig. 6 (top). The obtained bands with maxima at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743, 14
743, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441, 17
441, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 073 and 18
073 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 cm−1 correspond to transitions from the ground 2A2(dx2−y2 + dz2) level to the 2A(dz2 + dx2−y2), 2B(dxz + dy,z), 2B(dxz + dy,z) and 2A(dxy) excited levels. The value of Dq in the Oh approximation can be estimated as the difference between the average energy of levels arising from T2g(Oh) and Eg(Oh) states. This yields a value of Dq ∼ 1015 cm−1, which seems to be reasonably acceptable. For complex 2 the RT absorption spectrum is practically the same as for complex 1 (Fig. S28†). Therefore, for the purpose of present analysis we accepted the same energy level structure for complexes 1 and 2. The determined limiting values of Dq, i.e. 1015 and 1285 cm−1 were used in SPM analysis (Section 2.10).
056 cm−1 correspond to transitions from the ground 2A2(dx2−y2 + dz2) level to the 2A(dz2 + dx2−y2), 2B(dxz + dy,z), 2B(dxz + dy,z) and 2A(dxy) excited levels. The value of Dq in the Oh approximation can be estimated as the difference between the average energy of levels arising from T2g(Oh) and Eg(Oh) states. This yields a value of Dq ∼ 1015 cm−1, which seems to be reasonably acceptable. For complex 2 the RT absorption spectrum is practically the same as for complex 1 (Fig. S28†). Therefore, for the purpose of present analysis we accepted the same energy level structure for complexes 1 and 2. The determined limiting values of Dq, i.e. 1015 and 1285 cm−1 were used in SPM analysis (Section 2.10).
 | ||
| Fig. 6 (top) Absorption spectrum of 1 in the range of Cu(II) electronic transitions at 4.2 K; (bottom) energy level diagrams for Cu(II) ion as a function of symmetry changes. | ||
2.9 Computations using ab initio methods
The ab initio methods cannot explain or provide direct information on magnetic relaxation processes or specific chemical aspects. However, there is a rationale for carrying out the ab initio computations due to three advantages. (1) They may assure that the predicted electronic structure of complexes 1 and 2 as well as so-computed spin Hamiltonian and/or ligand (crystal) field Hamiltonian parameters are compatible with those obtained by other methods. (2) The ab initio computed spin Hamiltonian (SH) parameters (e.g. the g-tensor components) and the crystal/ligand field (CF/LF) ones may be used as starting parameters for fitting of various experimental data. (3) The ab initio computed CF/LF parameters may serve as input for independent modelling of the energy levels and thus SH parameters. Below we present only key results, whereas details of ab initio computations carried out using several methods are provided in Section VI in ESI.†Excited states were computed for complex 1 using TDDFT with long-range corrected exchange–correlation functional CAM-B3LYP. Results of representative multiconfigurational-SCF calculations are provided below, whereas computational details and detailed results are provided in Section VI in ESI.† Calculations were performed using CASSCF method with additional perturbations NEVPT2 to account for dynamic correlations. For Cu(II) ion we choose the active space consisting of five orbitals with major contribution of 3d atomic states with 9 electrons that could occupy them. The self-consistent procedure yields five states well separated from each other in energy scale, i.e. orbital singlets (Table 3).
| Excited state | CASSCF 1 | NEVPT2 1 | CAM-B3LYP TDA 1 | CASSCF 2 | NEVPT2 2 |
|---|---|---|---|---|---|
| 1st | 9699 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 680 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574 574 |
9972 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282 282 |
| 2nd | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255 255 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 547 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 048 |
| 3rd | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212 212 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 186 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 421 421 |
| 4th | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262 262 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 215 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578 578 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 228 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
Calculations for complex 1 show that the ground state consists of total 9 3d electrons in two major configurations: (i) with unpaired 3dz2 electron (∼70%) and (ii) with unpaired 3dx2−y2 electron (∼29%). The 1st excited state is similar to the ground state but proportions are nearly inverted for (ii) with unpaired 3dx2−y2 electron (∼68%) and (i) with unpaired 3dz2 electron (∼29%). Other excited states correspond to the following configurations: 2nd – with unpaired 3dxz electron, 3rd – with unpaired 3dxy electron, and 4th – with unpaired 3dyz electron. Calculations for complex 2 show that the ground state consists of total 9 3d electrons in two major configurations: (i) with unpaired 3dz2 electron (∼77%) and (ii) with unpaired 3dx2−y2 electron (∼22%). The 1st excited state consists of two configurations: (i) with unpaired 3dxz electron (∼51%) and (ii) with unpaired electron 3dx2−y2 (∼39%). The 2nd excited state is similar to the 1st excited state but proportions are different for (ii) with unpaired 3dx2−y2 electron (∼37%) and (i) with unpaired 3dxz electron (∼42%). Other excited states correspond to the following configurations: 3rd – with unpaired 3dyz electron and 4th – with unpaired 3dxy electron. The 3rd and 4th excited state are well separated, suggesting that structure 2 is geometrically more distorted than structure 1.
The effects of the inclusion of NEVPT2 dynamic corrections for the energy levels and the excited states for complex 1 are discussed Section VI in ESI.† Comparative analysis of these effects and the DFT results indicates what follows. The MC-SCF Mulliken occupations of the selected atoms show some differences with respect to DFT results. Most important is the fact that the spin is more strongly localized at the Cu site and electronic charge is closer to nominal charge 2+ (Table S10†). Charges on atoms neighboring with Cu are larger than those obtained from DFT. Spins on these neighboring atoms are very small. This finding is also supported by Loewdin analysis (Table S14†). Nonrelativistic CASSCF excited states are well separated from the ground state and this separation is significantly enlarged with inclusion of dynamic correlations at NEVPT2 level. Consequences of the enlarged separations of states are discussed in Section VI in ESI.†
| g -Tensor | CASSCF 1 | NEVPT2 1 | CASSCF 2 | NEVPT2 2 | B3LYP DFT 1 |
|---|---|---|---|---|---|
| g x | 2.081 | 2.067 | 2.074 | 2.058 | 2.048 |
| g y | 2.115 | 2.093 | 2.113 | 2.087 | 2.054 |
| g z | 2.517 | 2.386 | 2.511 | 2.409 | 2.177 |
Results indicate large difference between gz and (gx, gy), whereas gx and gy differ slightly since our system has C1 symmetry. The main magnetic axes, which correspond to the PAS of Zeeman Hamiltonian,93 do not exactly correspond to the molecular bonds of Cu and neighboring atoms but are lying closely. CASSCF method overestimate the g-factors with respect to NEVPT2 method, so (gi) components derived from the latter one conform well to experimental data for axial symmetry Cu(II) systems.94–97 We have also listed B3LYP results with the basis aug-cc-pVTZ-J and CP(PPP) for Cu atom with extra fineness of the grid to get more accurate values of the g tensor. Products of magnetic susceptibilities and temperature χT = ∂2E/∂B2 for complexes 1 and 2 obtained using NEVPT2 are plotted in Fig. S29.† Plots of EPR spectra (Fig. S23, S24† and Section 2.7) obtained using MOLCAS89 and PHI79 support the conclusion that hyperfine structure might be important in such simulations.
2.10 SPM and MSH analysis
The rationale for employing the two semiempirical modelling approaches, i.e. SPM and MSH, are two-fold. (1) To complement and corroborate (a) the spin Hamiltonian parameters obtained experimentally by EPR (Section 2.6) and computationally by DFT/ab initio approaches (Section 2.9) as well as (b) CF parameters (CFPs) estimated experimentally by optical spectroscopy (Section 2.8). This would enhance reliability of the overall results. (2) To gain more insight into magneto-structural correlations and thus explain differences in magnetic character of compounds 1 and 2. The results of calculations carried out to fulfil rationale (1) are presented below, whereas those concerning rationale (2) are discussed in Section 3.For initial estimation of the gi factors, simplified MSH formulas listed in Section VII† were employed.98,99 The results have indicated general suitability of the MSH approach. For more accurate calculations of SHPs, the MSH formulas for tetragonal (TE)100–106 and orthorhombic107–109 symmetry is applied. To obtain input data for MSH formulas, the CFPs Bkq110–112 are calculated using SPM for Cu(II) centers in 1 and 2 using the structural data for set C2v (Section V in ESI†). The two plausible Dq values ∼1015 cm−1 and ∼1285 cm−1 estimated by us experimentally from optical spectra (Section 2.8) are adopted. Pertinent comments on reliability of usage of SPM/CFP predictions as input data for MSH formulas are provided in Section VII in ESI.† The results listed in Table 5 indicate that after standardization (see Section VII in ESI†) the axial CFP B20 of the highest magnitude and minimal values of B22 and B42 are obtained, while B20 and B22 also change signs along the choice of positive rhombicity ratio built into CST package.113,114
| Complex 1 | Complex 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| CFPs | C 2v | C 2v after OR/STa | C 2v | C 2v after OR/STa | ||||
| a The orthorhombic transformation (OR/ST) defined as S2:109,113,115,116 (X, Y, Z) → (X, −Z, Y) was applied. | ||||||||
| Dq | 1285 | 1015 | 1285 | 1015 | 1285 | 1015 | 1285 | 1015 |
| B 20 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 719 |
−22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651 651 |
−26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
−21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118 118 |
| B 22 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 945 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
−1283 | −1014 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
−2163 | −1708 |
| B 40 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889 889 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 424 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 913 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963 963 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 443 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 239 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
| B 42 | −8102 | −6396 | −1712 | −1351 | −7429 | −5864 | −1279 | −1010 |
| B 44 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082 082 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758 758 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822 822 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701 701 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 958 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 123 |
The relations between the CF energy levels in eqn (S6) and (S7) and those E1 and E2 employed in MSH formulas for tetragonal symmetry in ref. 101 and 104 are as follows:
| E1 = 10Dq = ΔE = (|dx2−y2〉 − |dxy〉) |
| E2 = 10Dq − 3Ds + 5Dt = ΔE = (|dx2−y2〉 − |dyz〉) = ΔE = (|dx2−y2〉 − |dxz〉) | (6) |
In eqn (6)Dq denotes the cubic CFP, whereas Ds and Dt denote the second- and fourth-rank tetragonal CFPs in the conventional notation,117,118 respectively. Depending on the shape of the distorted octahedron (Section 2.3) and thus the strength of tetragonal CFPs, the ground state may be either |dx2–y2〉 or |dz2〉.98,99 This is also evident in our ab initio calculations (Section 2.9). Next, using the CFPs in Table 5 and the conversion relations between the CFPs Bkq and (Ds, Dt) given in ref. 118, the latter CFPs are calculated, and subsequently, the energies E1 and E2 in eqn (6). Finally, the tetragonal SHPs: gi and Ai are calculated by applying the respective MSH formulas.101,104 To calculate the hyperfine structure parameters Ai we employ analogous MSH formulas derived as functions of the gi values and respective CF energies.100–106
For orthorhombic symmetry,107–109 four CF energies Ei (i = 1–4) apply. The corresponding relations are:
| E1 = 10Dq |
| E2 = 10Dq + 3Ds − 5Dt − 3Dξ + 4Dη2 |
| E3 = 10Dq + 3Ds − 5Dt + 3Dξ − 4Dη2 |
| E4 = −4Ds − 5Dt | (7) |
Three important points bearing on interpretation of results in Table S19† must be kept in mind as discussed in Section VII in ESI.† In view of these points, analysis of the results in Table S19† leads to the following conclusions. The SHPs gi and Ai calculated using MSH formulas for the TE case may be directly compared with experimental results in Section 2.3, whereas those for the orthorhombic (OR) case – with the ab initio results in Section 2.9. Results for both cases indicate good mutual consistency, which shows the usefulness of the ascent/descent in symmetry.119–121 Employing the standardized CFP sets in MSH calculations is even more crucial in the TE case than in the OR case, in view of additional approximations involved in the TE case, i.e. omitting the orthorhombic CFPs: B22 and B42.
The values of gi calculated in Table S19† by adopting TE and OR formulas agree well with our experimental ones: g‖ = 2.26 and g⊥ = 2.05 for complex 1 and also with literature data obtained for compounds with axial symmetry Cu-sites, see Table S20.† Since EPR spectra were done on powdered samples, the axes (x, y, z) indicated for the fitted values, i.e. g‖ (z), g⊥ (x, y), may be considered only as the nominal principal axes. Hence, they cannot be related the orientations of any specific axes within the coordination octahedron (Fig. 1c and d). Comparison of the theoretical Ai values in Table S19† with our experimental value A‖ = 175 (G) = 165.8 (10−4 cm−1) for complex 1 and the respective values in Table S20† reveals that all experimental A‖ are positive, whereas theoretical ones are negative. This is due to the limited capabilities of the computer program used, have allowed fitting EPR spectra only with the absolute values of the hyperfine interaction parameters |A|. Since no perpendicular splitting has been observed in EPR spectrum, no accurate value of A⊥ could be determined. Attempts to simulate spectra using A⊥ indicate that this is not a sensitive parameter because any splitting is hidden in the main EPR line. A good match has been obtained with A⊥ equal 1 as well as 20 cm−1. Both formulas: TE and OR ones, yield comparable sets of results and indicate that good agreement may be obtained by appropriate matching of the adjustable parameters. However, overall the Dq value (in cm−1) 1015 seems better than 1285, which yields larger CF energies (Ei). This finding conforms to that obtained in Section 2.8. Comparison of the TE and OR results for sets C2v or both complexes 1 and 2 in Table S19† indicates smaller differences between the respective results than those for sets C2v after OR/ST. This may be due to the approximations involved in the TE case. Since no such approximations are involved in the OR case, the results for sets C2v after OR/ST may be considered as more accurate. Comparison of the results in Table S19† and the respective results obtained by ab initio methods (Section 2.9) also favor the MSH results obtained with lower Dq value for sets C2v after OR/ST. Importantly, the CF energies obtained for sets C2v do not agree as well those for sets C2v after OR/ST. This reinforces the importance of employing orthorhombic standardization.
3. Magneto-structural correlations and outcome
Results provided in Section 2 and in ESI† enable us to extract some information on correlation between the chemical composition of 1 and 2 and their magnetic relaxation properties. The following dependencies were observed in this study. Slow relaxation of magnetization is observed only in the presence of the external magnetic field and it mostly concerns compound 1 [Cu(Lred1)(MeOH)](ClO4)2, while it is much less pronounced in compound 2 [Cu(Lred2)(H2O)](OTf)2. Each metal ion is isolated in its crystal lattice without any exchange interactions, as confirmed by X-ray structures (Cu⋯Cu distances over 8 Å), DC magnetic and EPR studies. This means that observed differences can be related to variations in symmetry of Cu(II) ion in CuLn complex, secondary coordination sphere, and/or additional crystal packing effects.Structural similarity of the [CuN3O3] coordination octahedron (N3O square planar plane and O2 axial elongation – see, Scheme 1) is retained in both complexes, despite differences in the composition of ligands Lred1 and Lred2 and coordinated solvent molecule. Axial octahedral elongation is stronger in 1 than in 2 as determined by SHAPE studies (Section 2.3) and the differences are also observed in temperature-dependent cw-EPR studies (Section 2.6). This phenomenon can be attributed to the Jahn–Teller distortions, which were extensively studied to show structural and electronic consequences of the Jahn–Teller effect.122 Present axial elongation leads to an anisotropic distribution of d-electron spins, which has huge impact on magnetic properties. The N3O plane is more distorted from the pure square planar one in 2 than in 1 (Section 2.3), whereas the excited state calculations also point to this symmetry deviation (Section 2.9.1). Overall, symmetry of compound 1 is akin those of porphyrins/phthalocyanines, which facilitate SIM/qubit behavior for symmetry reasons.50–55 The charge analysis of the ground state of Cu2+ ions in complex 1 and 2, indicates that the CASSCF/NEVPT2 state energies and gi factors are typical for an octahedrally distorted copper(II) complexes. The conclusions drawn from CASSCF calculations are corroborated by TD-DFT and semiempirical results as well as are consistent with level schemes for low symmetries reported in literature.98
To fulfil the rationale (2) of semiempirical calculations (Section 2.10), we examine the dependence of the SPM calculated CFPs on the structural parameters of the complexes, e.g. bond lengths, Ri. This enables to gain insight on how the changes in CFPs affect the MSH calculated SHPs: gi and Ai. An increase in Ri values results in a decrease in Ei values in both TE and OR symmetry cases. This in turn induces a decrease in g⊥ but an increase in g‖ values. Similar trend is also observed for A⊥ and A‖, respectively. Computations also reveal that the reason for the differences in the properties of both complexes 1 and 2 may not be solely related to the immediate surroundings of the Cu(II) ions and other factors, e.g. solid state packing may play a role as discussed below.
In the solid state, both complexes show two molecules of crystallographically equivalent but magnetically inequivalent compounds (C2 inversion axis) in the unit cell. Interestingly, only in 1 they symmetrically interact with each other in antiparallel manner through the pyridine–pyridine π–π stacking interactions (Fig. S22†), similarly as reported.59,123 This ensures the rigid crystal packing, which is otherwise more loose in compound 2, which is related to the effect of the counterion involved in the H-bonded packing (ClO4− in 1, CF3SO3− in 2). The molecular structure of both compounds is not devoid of high-energetic vibrations (C–H, NH) that may also contribute to relaxation mechanisms considered here, i.e. of Raman, direct and QTM origin (Section 2.5). Boča et al.60 showed that octahedral [Cu(pydca)(dmpy)]·0.5H2O (where pydca – pyridine-2,6-dicarboxylate, dmpy – 2,6-dimethanolpyridine) exhibits two relaxation processes with energy barriers estimated as U/kB = 58.6 and 62.7 K. This may be due to existence of two distinct Cu(II) centers in the crystal lattice, each with different local site symmetry Cu(II). Boča's group59 also showed that monometallic octahedral [CuLL′2(H2O)] complex (where L = 2,6-dimethanolpyridine and L′ = 3,5-dinitrocarboxylate) forms dimers that are arranged in the π–π stacking. This leads to 1D-chain and/or ladder structure that also exhibits two relaxation processes through the direct and Raman-like contributions. Cui et al.61 showed that five-coordinate [Cu(12-TMC)Cl][B(C6H5)4] (12-TMC = 1,4,7,10-tetramethyl-1,4,7,10-tetraaza cyclododecane) exhibits only one relaxation process in a distorted square pyramidal geometry of copper(II) ion. Korchagin et al.62 demonstrated that the quasi-one-dimensional Cu(II) complex [Cu(hfac)2(ClTDPO)]n (where hfac – hexafluoroacetylacetonate, ClTDPO – 2,4-di-(tert-butyl)-9-chloro-benzo[5,6][1,4]oxazine[2,3-b]phenoxazine) relaxes through the combination of two-phonon Raman and one-phonon direct processes. Since these examples represent mutually unrelated compounds, more studies of structurally similar monometallic Cu(II) systems are needed to better understand the observed phenomena.
4. Conclusions
Our study provides solid grounds for development of a modular organic platform for controlled formation of magnetically isolated, monometallic Cu(II) systems. This approach would enable better understanding of magnetic relaxation behaviour in S = ½ systems. Herein, the tunable capability of the synthesized complexes comes from: (i) the unique pentadentate Lred-RN,O-aminal ligand family formed by unexpected in situ reduction of the parent Schiff base ligand L; (ii) the chosen solvent/reagent alcohol; (iii) the coordination preferences of the metal salt and its counterion. Since the field-induced SIM coordination compounds with d9 ions are rarely encountered, two structurally similar octahedral Cu(II) compounds were prepared as the case study. The above aspects (i) and (ii) affect modularity most significantly. Both analogues are rare examples of magnetically isolated copper systems that display slow relaxation of magnetisation, with phenomenon being more pronounced for the perchlorate analogue 1 than the triflate 2.48Experimental findings indicate that this behaviour is predominantly the result of: (i) the octahedral structural distortions exerted by the alkoxy groups appended on the Lred-1/2 scaffold; (ii) spatial arrangements of the Cu(II)⋯Cu(II) pairs in the unit cell due to the crystal packing contacts, with anion and π–π interactions being the most important. This translates to the character of the hyperfine structure observed in the EPR spectra as a function of temperature and applied frequencies, related to the interactions of S = ½ electron spin of Cu(II) ion with the nuclear spin I = 3/2. The relaxation of magnetization proceeds through the combination of Raman, direct and QTM processes.
The extensive ab initio ((TD-)DFT, CASSCF, NEVPT2) computations and semiempirical (SPM, MSH) calculations have included the following aspects. Cu(II) electronic states, g-tensor and A-tensor components as well as ligand field parameters were calculated and compared with the experimentally determined values. This enables to gain insight on how the changes in CFPs affect the MSH calculated SHPs: gi and Ai. Such thorough and combined strategy allowed us to probe the effect of geometrical and structural changes on copper(II) electronic states. Consequently, our investigations provided better understanding of the observed magnetic behaviour. The theoretical results corroborate experimental findings and are consistent with level schemes for low symmetries reported in literature.
The thorough and combined strategy, utilized for two Cu(II) ion complexes for the first time, has also helped to delineate advantages and limitations of each of the several experimental techniques and theoretical approaches employed. Hence, this combined strategy may guide development of the design of other potential Cu(II)-based nanomagnets as well. Additional aspects concerning modularity in our study may be invoked, e.g. strongly coordinating counterions. Interestingly, demonstrated modular character of alkoxy groups would allow one to attach perfluorinated arms to evaluate the role of aliphatic CH2 and CH3 vibrations on the relaxation behaviour in the future. These aspects, together with the role of secondary coordination sphere on magnetic relaxation mechanisms are currently of particular interest.124
Author contributions
Dawid Marcinkowski: synthesis of chemical compounds, magneto-structural correlations: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – original draft, writing – review & editing, visualization. Ariel Adamski: synthesis of chemical compounds: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – review & editing, visualization. Maciej Kubicki: crystallographic studies: formal analysis, investigation, data curation, writing – review & editing, visualization. Giuseppe Consiglio: synthesis of chemical compounds: formal analysis, investigation, data curation, writing – review & editing. Violetta Patroniak: methodology, formal analysis, investigation, writing – review & editing, supervision. Tomasz Ślusarski: theoretical studies: DFT/ab initio calculations, formal analysis, investigation, data curation, writing – review & editing, visualization. Muhammed Açıkgöz: theoretical studies: SPM and MSH calculations, formal analysis, investigation, data curation, writing – review & editing, visualization. Daria Szeliga: DC/AC magnetism studies: formal analysis, investigation, data curation, writing – review & editing, visualization. Nahir Vadra: magneto-structural correlations: data curation, writing – review & editing, visualization. Mirosław Karbowiak: spectroscopic and theoretical studies: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – review & editing, visualization. Ireneusz Stefaniuk: EPR studies: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – review & editing, visualization. Czesław Rudowicz: magneto-structural correlations, analysis of SPM, MSH and DFT/ab initio results, conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – review & editing, visualization, supervision, funding acquisition. Adam Gorczyński: SHAPE symmetry studies, magneto-structural analysis and correlations: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – original draft, writing – review & editing, visualization, supervision. Maria Korabik: DC/AC magnetism studies: conceptualization, methodology, formal analysis, investigation, resources, data curation, writing – review & editing, visualization, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dedicated to Professor Stefan Lis on the occasion of his 70th birthday. Technical assistance with EPR measurements from MSc B. Cieniek is much appreciated. This work was mainly supported by: (PI: CZR): UMO-2016/21/B/ST4/02064 from the Polish National Science Center and partially from the budget for science in 2018–2020, as a part of the Polish Ministry of Science and Higher Education project; (PI: DM): Grant No. 0088/DIA/2018/47 in the frame of the “Diamond Grant” programme; (PI: AG): SONATA grant UMO-2020/39/D/ST4/01182 from National Science Centre, Poland. A. G. is a scholarship holder of the Polish Ministry of Education and Science for outstanding young scientists. D. M. is a scholarship holder of the Adam Mickiewicz University Foundation for the academic year 2021/2022. The calculations were made at the Poznań Supercomputing and Networking Center.References
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- C. A. P. Goodwin, Dalton Trans., 2020, 49, 14320–14337 RSC.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- C. E. Jackson, I. P. Moseley, R. Martinez, S. Sung and J. M. Zadrozny, Chem. Soc. Rev., 2021, 50, 6684–6699 RSC.
- R. Mirzoyan, N. P. Kazmierczak and R. G. Hadt, Chem. – Eur. J., 2021, 27, 9482–9494 CrossRef CAS PubMed.
- M. S. Fataftah and D. E. Freedman, Chem. Commun., 2018, 54, 13773–13781 RSC.
- M. Affronte, J. Mater. Chem., 2009, 19, 1731–1737 RSC.
- E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645–659 CrossRef CAS.
- K. Head-Marsden, J. Flick, C. J. Ciccarino and P. Narang, Chem. Rev., 2021, 121, 3061–3120 CrossRef CAS PubMed.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- A. Gaita-Ariño, H. Prima-García, S. Cardona-Serra, L. Escalera-Moreno, L. E. Rosaleny and J. J. Baldoví, Inorg. Chem. Front., 2016, 3, 568–577 RSC.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- C.-J. Yu, S. von Kugelgen, D. W. Laorenza and D. E. Freedman, ACS Cent. Sci., 2021, 7, 712–723 CrossRef CAS PubMed.
- S. E. Crawford, R. A. Shugayev, H. P. Paudel, P. Lu, M. Syamlal, P. R. Ohodnicki, B. Chorpening, R. Gentry and Y. Duan, Adv. Quantum Technol., 2021, 4, 2100049–2100082 CrossRef.
- S. Krastanov, M. Heuck, J. H. Shapiro, P. Narang, D. R. Englund and K. Jacobs, Nat. Commun., 2021, 12, 191 CrossRef CAS PubMed.
- R. S. D. Gatteschi and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- F. L. J. Bartolomé and J. F. Fernández, Molecular Nanomagnets: Physics and Applications, Springer-Verlag Berlin, Heidelberg, 2014 Search PubMed.
- D. G. C. Benelli, Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, Wiley-VCH, Weinheim, 2015 Search PubMed.
- R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH, Weinheim, 2015 Search PubMed.
- P. Z. J. Tang, Lanthanide Single Molecule Magnets, Springer-Verlag Berlin Heidelberg, 2015 Search PubMed.
- E. S. Gao, Molecular Nanomagnets and Related Phenomena, Structure and Bonding, Springer-Verlag Berlin, Heidelberg, 2015 Search PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- M. J. Giansiracusa, A. K. Kostopoulos, D. Collison, R. E. P. Winpenny and N. F. Chilton, Chem. Commun., 2019, 55, 7025–7028 RSC.
- S. E. Stavretis, D. H. Moseley, F. Fei, H.-H. Cui, Y. Cheng, A. A. Podlesnyak, X. Wang, L. L. Daemen, C. M. Hoffmann, M. Ozerov, Z. Lu, K. Thirunavukkuarasu, D. Smirnov, T. Chang, Y.-S. Chen, A. J. Ramirez-Cuesta, X.-T. Chen and Z.-L. Xue, Chem. – Eur. J., 2019, 25, 15846–15857 CrossRef CAS PubMed.
- B. Yin and C.-C. Li, Phys. Chem. Chem. Phys., 2020, 22, 9923–9933 RSC.
- A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486 RSC.
- Y.-Q. Zhai and Y.-Z. Zheng, J. Mater. Chem. C, 2021, 9, 8096–8098 RSC.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- E. Bartolomé, A. Arauzo, J. Luzón, J. Bartolomé and F. Bartolomé, in Handbook of Magnetic Materials, ed. E. Brück, Elsevier, 2017, vol. 26, pp. 1–289 Search PubMed.
- K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396–4415 RSC.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074–2083 RSC.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed.
- A. Albino, S. Benci, L. Tesi, M. Atzori, R. Torre, S. Sanvito, R. Sessoli and A. Lunghi, Inorg. Chem., 2019, 58, 10260–10268 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed.
- J. J. Scepaniak, C. S. Vogel, M. M. Khusniyarov, F. W. Heinemann, K. Meyer and J. M. Smith, Science, 2011, 331, 1049 CrossRef CAS PubMed.
- G. E. Cutsail III, B. W. Stein, D. Subedi, J. M. Smith, M. L. Kirk and B. M. Hoffman, J. Am. Chem. Soc., 2014, 136, 12323–12336 CrossRef PubMed.
- M. Ding, G. E. Cutsail III, D. Aravena, M. Amoza, M. Rouzières, P. Dechambenoit, Y. Losovyj, M. Pink, E. Ruiz, R. Clérac and J. M. Smith, Chem. Sci., 2016, 7, 6132–6140 RSC.
- I. Bhowmick, A. J. Roehl, J. R. Neilson, A. K. Rappé and M. P. Shores, Chem. Sci., 2018, 9, 6564–6571 RSC.
- R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. López, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640–13643 CrossRef CAS PubMed.
- W. Lin, T. Bodenstein, V. Mereacre, K. Fink and A. Eichhöfer, Inorg. Chem., 2016, 55, 2091–2100 CrossRef CAS PubMed.
- R. Boča and C. Rajnák, Coord. Chem. Rev., 2021, 430, 213657 CrossRef.
- C. Rajnák and R. Boča, Coord. Chem. Rev., 2021, 436, 213808 CrossRef.
- M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508 CrossRef CAS PubMed.
- K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC.
- A. Urtizberea, E. Natividad, P. J. Alonso, M. A. Andrés, I. Gascón, M. Goldmann and O. Roubeau, Adv. Funct. Mater., 2018, 28, 1801695 CrossRef.
- C.-J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708 RSC.
- C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Chem. Mater., 2020, 32, 10200–10206 CrossRef CAS.
- S. von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2021, 143, 8069–8077 CrossRef CAS PubMed.
- Y. Dai, Y. Fu, Z. Shi, X. Qin, S. Mu, Y. Wu, J.-H. Su, Y.-F. Deng, L. Qin, Y.-Q. Zhai, Y.-Z. Zheng, X. Rong and J. Du, Chin. Phys. Lett., 2021, 38, 030303 CrossRef CAS.
- M. S. Fataftah, M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny and D. E. Freedman, Chem. Sci., 2019, 10, 6707–6714 RSC.
- S. Lenz, K. Bader, H. Bamberger and J. van Slageren, Chem. Commun., 2017, 53, 4477–4480 RSC.
- D. Valigura, C. Rajnák, J. Titiš, J. Moncoľ, A. Bieńko and R. Boča, Dalton Trans., 2022, 51, 5612–5616 RSC.
- R. Boča, C. Rajnák, J. Titiš and D. Valigura, Inorg. Chem., 2017, 56, 1478–1482 CrossRef PubMed.
- H.-H. Cui, W. Lv, W. Tong, X.-T. Chen and Z.-L. Xue, Eur. J. Inorg. Chem., 2019, 4653–4659 CrossRef CAS.
- D. V. Korchagin, E. P. Ivakhnenko, O. P. Demidov, A. V. Akimov, R. B. Morgunov, A. G. Starikov, A. V. Palii, V. I. Minkin and S. M. Aldoshin, New J. Chem., 2021, 45, 21912–21918 RSC.
- A. Mielcarek, A. Bieńko, P. Saramak, J. Jezierska and A. Dołęga, Dalton Trans., 2019, 48, 17780–17791 RSC.
- M. Dolai, M. Ali, C. Rajnák, J. Titiš and R. Boča, New J. Chem., 2019, 43, 12698–12701 RSC.
- F. Santanni, A. Albino, M. Atzori, D. Ranieri, E. Salvadori, M. Chiesa, A. Lunghi, A. Bencini, L. Sorace, F. Totti and R. Sessoli, Inorg. Chem., 2021, 60, 140–151 CrossRef CAS PubMed.
- L. Gu and R. Wu, Phys. Rev. Lett., 2020, 125, 117203 CrossRef CAS PubMed.
- X. Liang, T.-Y. Zhang, X.-Y. Zeng, Y. Zheng, K. Wei and Y.-R. Yang, J. Am. Chem. Soc., 2017, 139, 3364–3367 CrossRef CAS PubMed.
- G. Huang, B. Kling, F. H. Darras, J. Heilmann and M. Decker, Eur. J. Med. Chem., 2014, 81, 15–21 CrossRef CAS PubMed.
- Y.-Y. Huang, C. Cai, X. Yang, Z.-C. Lv and U. Schneider, ACS Catal., 2016, 6, 5747–5763 CrossRef CAS.
- H. Li, K. M. Belyk, J. Yin, Q. Chen, A. Hyde, Y. Ji, S. Oliver, M. T. Tudge, L.-C. Campeau and K. R. Campos, J. Am. Chem. Soc., 2015, 137, 13728–13731 CrossRef CAS PubMed.
- G. Li, F. R. Fronczek and J. C. Antilla, J. Am. Chem. Soc., 2008, 130, 12216–12217 CrossRef CAS PubMed.
- J. Lu, F. Sha and X.-Y. Wu, Tetrahedron Lett., 2019, 60, 1161–1165 CrossRef CAS.
- T. Arai, K. Tsuchiya and E. Matsumura, Org. Lett., 2015, 17, 2416–2419 CrossRef CAS PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- D. C. M. Llunell, J. Cirera, P. Alemanyand and S. Alvarez, Shape v.2.0, Universitat de Barcelona, 2010 Search PubMed.
- M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582 CrossRef CAS PubMed.
- S. Khan, S. Herrero, R. González-Prieto, M. G. B. Drew, S. Banerjee and S. Chattopadhyay, New J. Chem., 2018, 42, 13512–13519 RSC.
- W. Haase, Ber. Bunsenges. Phys. Chem., 1994, 98, 1208–1208 CrossRef.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- D. Aravena and E. Ruiz, Dalton Trans., 2020, 49, 9916–9928 RSC.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953–9963 RSC.
- R. Boča, C. Rajnák, J. n. Moncol, J. n. Titiš and D. a. Valigura, Inorg. Chem., 2018, 57, 14314–14321 CrossRef PubMed.
- K. Fujisawa, A. Tateda, Y. Miyashita, K.-i. Okamoto, F. Paulat, V. K. K. Praneeth, A. Merkle and N. Lehnert, J. Am. Chem. Soc., 2008, 130, 1205–1213 CrossRef CAS PubMed.
- P. Pietrzyk and Z. Sojka, J. Phys. Chem. A, 2005, 109, 10571–10581 CrossRef CAS PubMed.
- V. Umamaheswari, M. Hartmann and A. Pöppl, J. Phys. Chem. B, 2005, 109, 1537–1546 CrossRef CAS PubMed.
- V. Umamaheswari, M. Hartmann and A. Pöppl, J. Phys. Chem. B, 2005, 109, 10842–10848 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- N. M. Atherton, Principles of electron spin resonance, Prentice Hall, 1993 Search PubMed.
- H. Husein Mor, H. Weihe and J. Bendix, J. Magn. Reson., 2010, 207, 283–286 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- S. K. Misra, Multifrequency Electron Paramagnetic Resonance, erratum, ed. S. K. Misra and C. Rudowicz, Wiley-VCH, Weinheim, 2011, https://www.wiley-vch.de/publish/dt/books/ISBN3-527-40779-0/ Search PubMed.
- P. P. M. Valko, S. Biskupič and M. Mazúr, Chem. Pap., 1990, 44, 805–813 Search PubMed.
- A. Drzewiecki, B. Padlyak, V. Adamiv, Y. Burak and I. Teslyuk, Nukleonika, 2013, 58, 379–385 CAS.
- J. L. Rao, G. Sivaramaiah and N. Gopal, Phys. B, 2004, 349, 206–213 CrossRef CAS.
- R. Ravikumar, R. Komatsu, K. Ikeda, A. Chandrasekhar, B. Reddy, Y. Reddy and P. S. Rao, J. Phys. Chem. Solids, 2003, 64, 261–264 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ion, Clarendon Press, Oxford, 1970 Search PubMed.
- E. Garribba and G. Micera, J. Chem. Educ., 2006, 83, 1229 CrossRef CAS.
- Z. Wen-Chen and W. Shao-Yi, Z. Naturforsch., 2000, 55, 915–917 Search PubMed.
- M.-Q. Kuang, L.-D. Wang and S.-K. Duan, J. Phys. Chem. Solids, 2017, 111, 41–46 CrossRef CAS.
- H.-M. Zhang and X. Wan, J. Non-Cryst. Solids, 2013, 361, 43–46 CrossRef CAS.
- S.-Y. Wu, H.-M. Zhang, P. Xu and S.-X. Zhang, Spectrochim. Acta, Part A, 2010, 75, 230–234 CrossRef PubMed.
- M.-Q. Kuang, S.-Y. Wu, G.-L. Li and X.-F. Hu, Mol. Phys., 2015, 113, 698–702 CrossRef CAS.
- S. Y. WU, J. S. YAO, H. M. ZHANG and G. D. LU, Int. J. Mod. Phys. B, 2007, 21, 3250–3253 CrossRef CAS.
- K. Min-Quan, W. Shao-Yi, H. Xian-Fen and S. Bo-Tao, Z. Naturforsch., A: Phys. Sci., 2013, 68, 442–446 CrossRef.
- L. Chao-Ying, H. Ying and Z. Xue-Mei, Phys. B, 2015, 456, 125–128 CrossRef.
- M.-Q. Kuang, S.-Y. Wu and H.-M. Zhang, Optik, 2012, 123, 1601–1604 CrossRef CAS.
- M.-Q. Kuang, S.-Y. Wu, X.-F. Hu and B.-T. Song, Phys. B, 2013, 417, 13–16 CrossRef CAS.
- D. J. Newman and B. Ng, Rep. Prog. Phys., 1989, 52, 699–762 CrossRef CAS.
- C. A. Morrison, in Crystal Fields for Transition-Metal Ions in Laser Host Materials, ed. C. A. Morrison, Springer Berlin Heidelberg, Berlin, Heidelberg, 1992, pp. 1–2. DOI:10.1007/978-3-642-95686-7_1.
- B. G. Wybourne, Spectroscopic Properties of Rare Earths, Interscience Publishers, 1965 Search PubMed.
- C. Rudowicz, in Computer package CST: conversions, standardization and transformations, ed. B. Ng and D. J. Newman, Cambridge University Press, Cambridge, 2000, p. 259 Search PubMed.
- C. Rudowicz and Q. Jian, Comput. Chem., 2002, 26, 149–157 CrossRef CAS PubMed.
- C. Rudowicz and R. Bramley, J. Chem. Phys., 1985, 83, 5192–5197 CrossRef CAS.
- C. Rudowicz and P. Gnutek, Phys. B, 2010, 405, 113–132 CrossRef CAS.
- J. S. Griffith, The theory of transition-metal ions, Cambridge University Press, 1964 Search PubMed.
- Y. Y. Yeung and C. Rudowicz, Comput. Chem., 1992, 16, 207–216 CrossRef CAS.
- G. W. Burdick and M. F. Reid, Mol. Phys., 2004, 102, 1141–1147 CrossRef CAS.
- M. Karbowiak, C. Rudowicz and P. Gnutek, Opt. Mater., 2011, 33, 1147–1161 CrossRef CAS.
- M. Karbowiak, P. Gnutek and C. Rudowicz, Chem. Phys., 2012, 400, 29–38 CrossRef CAS.
- M. A. Halcrow, Chem. Soc. Rev., 2013, 42, 1784–1795 RSC.
- J. Miklovič, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484–12487 RSC.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental synthetic details, part of magnetic, spectroscopic and theoretical details. CCDC 1965451, 1965452 and 2150965. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt01564a |
| ‡ Dawid Marcinkowski and Ariel Adamski contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |


