Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Free energy predictions for crystal stability and synthesisability
Kasper
Tolborg
 a,
Johan
Klarbring
ab,
Alex M.
Ganose
a,
Johan
Klarbring
ab,
Alex M.
Ganose
 c and
Aron
Walsh
c and
Aron
Walsh
 *a
*a
aDepartment of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bDepartment of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83, Linköping, Sweden
cDepartment of Chemistry, Imperial College London, Exhibition Road, London SW7 2AZ, UK
First published on 12th September 2022
Abstract
What is the likelihood that a hypothetical material—the combination of a composition and crystal structure—can be formed? Underpinning the reliability of predictions for local or global crystal stability is the choice of thermodynamic potential. Here, we discuss recent advances in free energy descriptions for crystals including both harmonic and anharmonic phonon contributions to the vibrational entropy. We critically discuss some of the techniques and descriptors, including data-driven machine learning approaches, being developed to assess the stability and synthesisability of solids. Avenues are highlighted that deserve further attention including thermodynamic and kinetic factors that govern the accessibility of metastable structures away from equilibrium.
Crystal chemical space is vast, and only a fraction of it has been explored. To guide expensive experimental efforts, computational materials design is increasingly applied to screen crystal chemical space to discover elemental compositions and crystal structures with desired functionality. But how many of these are realisable and how can we avoid ‘plausible predictions of fantasy materials’?1
When a certain chemical composition in a crystal structure is predicted to exhibit a desired set of properties, the question one must ask is whether this material will be stable and synthesisable. In virtual materials screening studies, the stability is often defined in terms of athermal internal energies, typically referred to as total energies, and (synthesisable) materials with an energy above the energetic convex hull are termed metastable.
Using this metric, analysis of almost 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 total energies in the Materials Project indicated that 50.5% of experimentally observed structures are metastable with respect to competing phases with a median energy of 15 meV per atom above the convex hull.2 Since 90% of the metastable structures were observed to have energies of less than 67 meV per atom above the convex hull, a metastability window of 100 meV per atom is often assumed for a candidate material to be ‘accessible’.
000 total energies in the Materials Project indicated that 50.5% of experimentally observed structures are metastable with respect to competing phases with a median energy of 15 meV per atom above the convex hull.2 Since 90% of the metastable structures were observed to have energies of less than 67 meV per atom above the convex hull, a metastability window of 100 meV per atom is often assumed for a candidate material to be ‘accessible’.
However, as this accessible window is chemistry dependent, an alternative descriptor has been proposed based on the amorphous limit. Here, only crystalline phases of lower energy than the amorphous ‘polymorph’ of the relevant composition is considered accessible, as the barrier for transformation to an amorphous state must be low.3Fig. 1 illustrates this stability window. Here, two phases are thermodynamically stable at different conditions, one phase is metastable, and potentially synthesisable, since it is of lower energy than the amorphous phase, while the last phase is inaccessible, since it should spontaneously decompose into the amorphous phase.
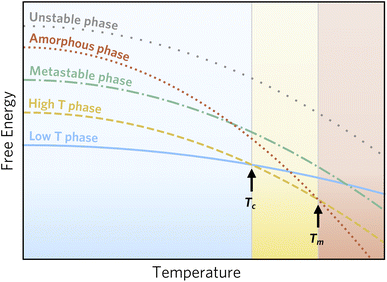 | ||
| Fig. 1 Schematic of phase stability as a function of temperature following Aykol et al.3 Two phases are thermodynamically stable below the melting point, Tm, at low and high temperature, respectively. Furthermore, two phases that are never thermodynamically stable are indicated; one of these can be metastable, whereas the other is unstable at all conditions, since it is of higher energy than an amorphous phase. The amorphous phase is depicted as a continuation of the liquid phase, although small deviations are expected due to differences in the structure of a liquid and an amorphous solid. | ||
The above definition of metastability includes both materials that are thermodynamically stable at some other set of conditions (e.g. high temperature or pressure) and materials that are not thermodynamically stable at any set of equilibrium conditions, but may still be formed under certain synthesis conditions and remain kinetically stable. Thus, it is clear that for a full assessment of stability, we must go beyond metrics based on athermal energies. In this perspective, we assess the current status of the field including advances in free energy descriptions and statistical models to assess crystal stability and synthesisability.
1. Local and global stability
Before assessing how temperature dependent stability metrics can be calculated, a more rigorous definition of stability is warranted. Stability can be defined in many complementary ways, but importantly, we must distinguish between local and global stability.The local stability of a material determines if the material will spontaneously transform into a different structure. Macroscopically, the local stability can be defined in terms of a positive bulk compressability or more precisely using elastic constant relations.4
On a microscopic level, local stability requires that no infinitesimal (collective) atomic displacements result in a decrease in energy. This means that all vibrations should have positive frequencies (ω) to ensure that all deformations of the atomic positions have an energetic penalty. Thus, the phonon frequencies become imaginary, ω2 < 0, for a locally unstable crystal structure.
Note however, that the phonon frequencies are in general dependent on pressure and temperature. Thus, if local stability is examined in a screening study based on its temperature independent (harmonic, see below) phonon dispersion, a material may be deemed unsuitable due to a local instability. Thus, materials that are stable at ambient conditions may be rejected due to low temperature instabilities.
Global stability is defined in terms of thermodynamic potentials, i.e. a material is globally stable if for a set of thermodynamic conditions, it is the global minimum of the relevant thermodynamic potential. For most practical cases, the relevant thermodynamic potential will be the Gibbs free energy, but others may be relevant depending on conditions. When considering global stability, it is important to note that the stability must be considered with respect to all competing phases—i.e. to both polymorphs of the same compositions, and to separation into multiple phases.5
2. Metastability
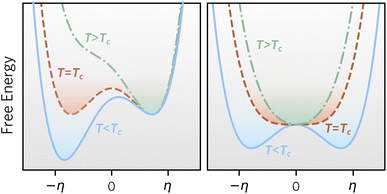
Based on our definitions of local and global stability, we can define metastable materials more generally as materials that are locally stable, but globally unstable at a given set of conditions. Metastable materials can, in principle, transform to a lower energy state, but in many cases, they have sufficient lifetimes for preparation, characterisation, or practical applications. Common examples are anatase TiO2 (ref. 6) and diamond,7 and a more complex recent case is the synthesis of wurtzite-derived β-CuGaO2, which usually adopts a delafossite structure, by ion exchange of NaGaO2.8Fig. 2 illustrates competing phase stability as a function of an order parameter, which for simplicity can be imagined as an atomic displacement. In the left panel, two phases are locally stable at low temperature, and the phase at negative order parameter is globally stable, whereas the other phase is metastable. With increasing temperature, the phase at positive order parameter becomes globally stable. In this case, a first order phase transition with hysteresis is expected between the two phases, since each phase will remain metastable in (part of) the temperature region, where the competing phase becomes globally stable. In the right panel, a phase at zero order parameter is both locally and globally stable at high temperature, whereas the phase at finite order parameter becomes both locally and globally stable at low temperatures. This is expected to result in a second-order phase transition between the phases with no hysteresis. Importantly, only in the case of the left figure, the high temperature phase can be retained to low temperature, since it remains locally stable.
3. Phase competition
To asses the stability of a material, first one has to consider with respect to “what” the material should be stable. This is done in the form of an appropriate chemical reaction.The stability of a crystal (ABC) with respect to atoms
| A(g) + B(g) + C(g) → ABC | (1) |
| A+(g) + B+(g) + C2−(g) → ABC | (2) |
| A(s) + B(s) + C(g) → ABC | (3) |
| ABC → A(s) + BC(s) | (4) |
| 2ABC → A2C(s) + B2C(s) | (5) |
In some cases, it may be appropriate to consider an external environment such as oxygen or water, which can form additional degradation products.9
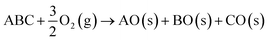 | (6) |
This approach can be generalised to n-component chemical systems using convex hull analysis. An overview of this method for equilibrium phase stability over large chemical spaces has been provided by Bartel.5
4. Thermodynamic potential
To determine whether a material is stable at all, or only under a specific set of conditions, requires a suitable thermodynamic potential to be chosen. Here, we focus on quantities accessible from atomistic modelling, which is widely used to accelerate chemical discovery.4.1. Internal energy (ΔU)
A common choice of energy for prediction of stability is the internal energy of a system, which is the relevant thermodynamic potential to be minimised under constant entropy and volume. These conditions are, however, hardly realisable and the athermal internal energy, typically referred to as the total energy, is more often used as a low-cost approximation to the full free energy.The total energy is fundamental to density functional theory and is readily obtainable from static simulations of the ground state crystal structure. It is a functional of the electron density (n0) as
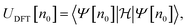 | (7) |
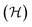 encompasses the range of electron/nuclear interaction terms and Ψ is the electron wavefunction, itself a functional of the electron density.10,11
encompasses the range of electron/nuclear interaction terms and Ψ is the electron wavefunction, itself a functional of the electron density.10,11
In practice, absolute values of internal energy are rarely useful in isolation, and we must focus on energy differences (ΔU) between the different species for balanced chemical reactions such as those considered above. The total energies of different materials cannot be directly compared between codes and a set of common parameters must be chosen for each study. To overcome this limitation, systematic calculations are performed to compile a dataset, e.g. as curated within the Materials Project12 or the Open Quantum Materials Database.13
The internal energy is easily extended to include pressure effects through the enthalpy. The associated PV term is usually negligible for condensed phases at ambient conditions due to the low compressibility of solids, but becomes important at elevated pressures such as those in the Earth's mantle.14
4.2. Free energy (ΔG)
Many materials only appear on phase diagrams at ‘high’ temperature, so a treatment of thermal effects is essential for prediction of materials stability at ambient and elevated temperatures. The central role of entropy in thermodynamics is evident from the Gibbs free energy| G = U + PV − TS = F + PV, | (8) |
For most crystals, the dominant entropy term is vibrational and there are several descriptions to consider.
The vibrational entropy, Svib, can be obtained by appropriately summing the phonon frequencies of a system over bands (ν) and wavevectors (q).17 The associated phonon density of states can be calculated (e.g. lattice dynamics) or measured (e.g. inelastic neutron scattering). Within the harmonic approximation (HA), the vibrational entropy is given by
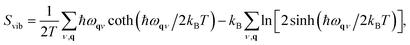 | (9) |
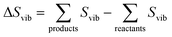 | (10) |
In practice, rather than the vibrational entropy, the vibrational free energy, Fvib, is used for convenience. The expression also includes a correction to the internal energy due to zero-point motion
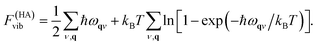 | (11) |
Calculated harmonic phonon information and the associated free energies are becoming increasingly available in materials databases, including PhononDB19 and the Materials Project.20 This paves the way for easier integration of finite temperature free energies in materials screening studies, and gives important data sets for data-driven machine learning studies aimed at predicting finite temperature properties (see below).
Beyond free energies, phonon calculations come with an additional indicator of crystal stability. Displacements that result in a lower energy structure manifest as imaginary phonon frequencies. Thus, a material with no imaginary frequencies is locally stable. If the instability involves a phonon mode away from the centre of the Brillouin zone, this structural transition will require an expansion of the crystallographic unit cell along a particular direction. For example, most cubic perovskites feature instabilities associated with octahedral tilting that require expansions of the unit cell to describe.21–23
In practice, many structures, including a wide range of cubic perovskites, predicted to be dynamically unstable from harmonic phonon theory are in fact stable at finite temperatures. This results from thermal renormalisation of the phonon frequencies, which will be considered in detail below. Furthermore, the vibrational free energy in eqn (11) becomes ill-defined for imaginary modes. Thus, harmonic phonon theory will fundamentally fail to predict the thermodynamic stability of these structures at elevated temperatures—also when the HA is only used to compare free energies. To model such cases, anharmonic contributions are essential.
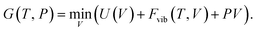 | (12) |
The QHA often gives reasonable predictions of the anharmonic Grüneisen parameter 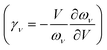 and the thermal expansion in materials—either as a result of negligible intrinsic anharmonic effects or due to a fortuitous cancellation of errors.25,26
and the thermal expansion in materials—either as a result of negligible intrinsic anharmonic effects or due to a fortuitous cancellation of errors.25,26
The change in unit cell volume can have profound impact on phonon frequencies, and thus the free energy. This can affect the relative stability of different phases or polymorphs and lead to more accurate predictions of stability ranges. Indeed, there are many examples of temperature-driven (first-order) phase transitions that are well described within the QHA, including the monoclinic-to-tetragonal phase transition in ZrO2 (ref. 27) and the α-to-β transition in elemental Sn,28 through to more complex hybrid organic-inorganic crystals.18
In recent years, one of the most common applications has been the calculation of mode lifetimes for predictions of lattice thermal conductivity. To a first approximation, thermal conductivity from finite lifetimes due to phonon–phonon scattering can be calculated from perturbation theory on top of the harmonic phonon dispersion, typically based on third-order force constants.30 This perturbative treatment, however, does not result in a correction to imaginary modes or modification of the free energy.
For predictions of crystal stability including anharmonic effects, two approaches can be taken. In the first case, the aim is to obtain temperature renormalised phonon dispersions to predict when a material will become dynamically (and therefore locally) stable. In the second case, the anharmonic vibrational free energy is used to compare the stability of different phases.
Temperature dependent phonon information can be obtained in several ways. The most popular methods are based on the temperature dependent effective potential (TDEP),31 self-consistent phonon theory (SCPH),32,33 stochastic self-consistent harmonic approximation (SSCHA),34 and the velocity auto-correlation function from molecular dynamics trajectories.35 The features of several software packages that employ these approaches are compared in Table 1. These methods have become accessible thanks to increased computing power, as well as novel methods for efficient force constant extraction, such as those based on compressive sensing.36
| Package | Anharmonic phonon method | Force constant extraction | Free energy method |
|---|---|---|---|
| a https://github.com/ttadano/alamode.72 b https://abelcarreras.github.io/DynaPhoPy.35 c https://hiphive.materialsmodeling.org.73 d http://phonopy.sourceforge.net.17 e http://ollehellman.github.io.31 f http://sscha.eu.34 | |||
| Alamodea | Self-consistent phonons | Compressive sensing | Renormalized phonons + higher orders |
| Dynaphopyb | Projected velocity auto-correlation | Molecular dynamics (MD) | Renormalized phonons |
| hiPhivec | Effective harmonic models | Compressive sensing | Harmonic only |
| Phonopyd | Quasi-harmonic approximation | Finite displacements | Harmonic only |
| TDEPe | Effective harmonic models | Stochastic sampling or MD | Renormalised phonons + higher orders |
| SSCHAf | Stochastic self-consistent phonons | Stochastic sampling | Direct minimisation |
The stabilisation of high temperature phases has been reported based on renormalised phonon modes.32,37–39 Temperature dependent phonons are particularly well suited for the description of second order, soft-mode phase transitions, which can be clearly described from the softening of a single phonon mode. Thus, the temperature above which a high temperature (higher symmetry) phase is stable can be predicted from the temperature at which an imaginary mode becomes real. Generally, experimental phase transition temperatures for second-order phase transitions are reproduced with reasonable accuracy using this method, but examples show that care must be taken to include high enough orders of anharmonicity.37,38 It is important to note that several anharmonic phonon methods require all phonon frequencies to be real by definition. Thus when predicting phase transition temperatures from these methods care must be taken to evaluate the frequency as a function of temperature well above the transition temperature, from which the frequency can be extrapolated to zero.32
For predictions of global stability, the anharmonic vibrational free energy is required. The first choice is to use the expression for the harmonic free energy from eqn (11) with the renormalised phonon frequencies instead of the harmonic ones. This allows for calculation of free energies for phases with dynamic instabilities in their harmonic phonon dispersion. However, importantly, an extra correction term must be included to fulfil the first-order cumulant expansion. Within SCPH, the first-order term including the harmonic contributions with renormalised frequencies is given as40
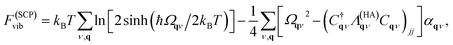 | (13) |
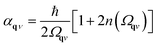 where n(ω) is the Bose–Einstein distribution. The first sum corresponds to a simple rearrangement of eqn (11).
where n(ω) is the Bose–Einstein distribution. The first sum corresponds to a simple rearrangement of eqn (11).
Within TDEP, a slightly different approach is taken, where the free energy reads
| F(TDEP) = U0 + Fvib, | (14) |
Phonon free energies, including the SCPH and TDEP expressions, can be augmented by perturbative corrections.42 These include the so-called bubble correction based on third-order force constants as well as higher order corrections.26,40,43
These free energy methods have seen their merits in predicting thermal expansion beyond the QHA, including the negative thermal expansion of ScF3.26,40,43 For applications to phase stability, TDEP has been used to obtain a phase diagram of SnSe, for which the high temperature Cmcm phase is dynamically unstable,44 and for CrN, for which the vibrational entropy contributes significantly to the magnetic and structural phase transition.45 Two recent examples for phase stability using the SCPH methodology are the pressure induced wurtzite to rocksalt transition in GaN,46 and the relative free energy between four phases of CsPbI3.47
Finally, rather than relying on calculating the free energy based on the phonon dispersion to a given anharmonic order, it is also possible to minimize the free energy during structure optimisation.48–50 This is the approach used in the stochastic self-consistent harmonic approximation (SSCHA) method, where the free energy surface is sampled stochastically.34 It has been successfully employed to predict the ground-state structure of superconducting LaH10 including zero-point anharmonic effects,51 and to study the phase transitions in several materials, including SnSe.39 So far, the main use of this method has been in terms of phase stability for materials with second-order phase transitions but, as it gives access to the free energy directly, predictions of stability between phases that are not related through soft-mode transitions should be straightforward.
A way to include anharmonicity fully in free energy predictions is provided by thermodynamic integration (TI). These set of techniques are based on performing a series of molecular dynamics (MD) simulations where an external parameter (real or artificial) is varied and free energy differences are obtained by integration of a related quantity.
The most common such technique is the so called Kirkwood coupling constant integration, where a parameter λ is used to connect the Hamiltonians of two states, typically in the form 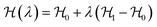 . The free energy difference between these two states is then obtained as52
. The free energy difference between these two states is then obtained as52
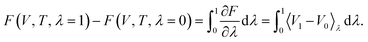 | (15) |
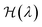 . In practice, the states at λ = 0 and 1 are typically taken as a harmonic system with free energy given by eqn (11) and the fully anharmonic system as given by DFT, respectively. Simulations are then performed at different values of λ (by mixing harmonic and DFT forces) and the free energy is determined through numerical integration.
. In practice, the states at λ = 0 and 1 are typically taken as a harmonic system with free energy given by eqn (11) and the fully anharmonic system as given by DFT, respectively. Simulations are then performed at different values of λ (by mixing harmonic and DFT forces) and the free energy is determined through numerical integration.
There exists several other useful TI variants. These include the free energy shift on changing the temperature from a reference value T0 to T1:
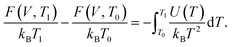 | (16) |
Practically, a set of MD simulations are performed at temperatures varying from T0 to T1, from which the average internal energy U(T) is extracted and the integral in eqn (16) is numerically evaluated. Other TI expressions are also available to obtain the free energy shifts on changing volume or on arbitrary crystal deformations.53,54
TI based approaches have been applied to calculate relative phase stabilities in systems ranging from simple elemental metals to complex molecular crystals or high-entropy alloys.53,55–58 Other applications include defect formation free energies55,56 and melting points.59,60 If the integration is coupled with ab initio molecular dynamics, the computational cost is large. Thus, there is great promise in reducing the burden with modern machine-learned force fields to obtain accurate free energies for more complex crystals.56,58,61
Configurational entropy stabilises disordered crystals and solid-solutions. Mixing ABC and DBC to form (AxD1−x)BC results in a regular solution entropy change assuming random distribution of A and D
ΔSconfig(x) = −kB[x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + (1 − x)ln(1 − x)] x + (1 − x)ln(1 − x)] | (17) |
For organic and hybrid organic-inorganic crystals, molecular orientational disorder, which can be considered a form of configurational disorder, is common and has important implications for phase stability.67 In cases where local order is significant, methods taking such effects into account are needed.68
Degrees of freedom related to electronic and magnetic excitations may also be important for assessing phase stability in certain cases. For metals, there is always an entropic contribution from electronic excitations near the Fermi level. This term is typically small, but must be included when phase competition happens between metallic and insulating phases. Furthermore, effects of electronic entropy are also present in mixed valence compounds, in which it takes a role similar to configurational entropy, but for different charge states of the same element. This has been shown to be of importance in the ionic conductor LixFePO4.69
Another complex entropic stabilisation mechanism is related to ionic conductivity. For superionic conductors, this is considered a partial melting of one sublattice, and analogously to the increased entropy of a liquid, there must be an entropic stabilisation associated with the superionic state. For example, the oxygen sublattice melting in Bi2O3, La2Mo2O9 and Bi4V2O11.70 The entropy of the disordered system can be estimated from simple considerations based on available interstitial sites,71 or more elaborate methods based on thermodynamic integration can be applied.54 As ionic conductors are important for applications in batteries and fuel cells, it will be advantageous if simple but accurate models for prediction of their stability can be established.
There are public databases available with calculated harmonic phonon information, and these serve as useful data sets for learning thermal properties, including the vibrational free energy. A few studies have been dedicated to predicting vibrational free energies (or entropies), including both composition-only based models74 and structure based models.75,76 The currently best performing model gives a mean-absolute-error (MAE) of only 0.0089 meV per K per atom on the out-of-training data for the vibrational entropy at room temperature.76
Other efforts using ML for vibrational properties have focused on predicting the full phonon density of states, from which all integrated thermal properties can be derived.77 Furthermore, one of data sets in the benchmarking test suite, MatBench,78 is related to phonon dispersions, meaning that we should see active development of ML models capable of predicting thermal properties of materials.
As an alternative approach to using calculated vibrational free energies, experimental thermochemical data can also be used for training the ML model. This was done successfully by Bartel et al.79 using the SISSO framework to obtain a closed form analytical expression for the free energy, from which they obtained a test MAE of ∼50 meV per atom over a wide temperature range. Importantly, using experimental training data will naturally include all orders of anharmonicity—at the expense of a smaller data set.
A final approach for decreasing the computational cost of determining free energies is to use ML to decrease the number calculations that should be performed for each material. A common approach is the use of compressive sensing as mentioned above for anharmonic phonons,36 but a similar approach can be used for harmonic phonons as well as for construction of cluster expansion models to include non-vibrational parts of the entropy.80
Integration of ML predicted free energies into a high-throughput materials screening workflow should be relatively straightforward, and recent results show the promise of this method for predicting finite temperature stability.81
5. Synthesisability
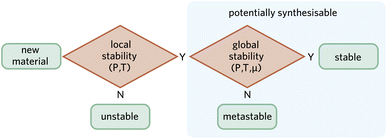
Traditional solid-state synthetic methods take advantage of global stability through a direct reaction of components under equilibrium conditions that favour thermodynamically stable products. However, global stability is not a necessary condition for a material to be synthesised. There are alternative soft chemical methods such as sol–gel synthesis and chemical vapour deposition that provide low temperature processing routes to isolate metastable phases. One notable example is the formation of previously unknown metastable metal nitride semiconductors from high-energy precursors.82While the space of hypothetical materials is infinite, a subset can be defined as locally stable following the criteria previously discussed. We posit that if a material is locally stable, there is a non-zero probability of it being synthesised by a motivated expert—with the caveat indicated in Fig. 1 that phases with a higher energy than a competing amorphous phase are unlikely to be kinetically stable. A synthetic chemist is aided by the diversity of possible synthetic strategies, which can include extreme conditions (e.g. high pressure83,84), non-equilibrium approaches (e.g. plasma-electrochemical methods85), or even nuclear transmutation (e.g. Zn to Cu decay86). Fig. 3 illustrates this suggestion. Note how both local and global stability must be evaluated at the relevant thermodynamic conditions.
Synthesis of metastable crystals can be guided by the free energy methods described above. Traditional equilibrium pressure–temperature methods give access to the global stability and can identify ground state phases at selected synthesis conditions. If these phases are locally stable at ambient conditions, they have the potential to be quenched and persist outside of the synthesis environment where they are no longer the lowest energy phase.
It has been argued that most metastable phases are remnants of phases that were globally stable at another set of thermodynamic conditions during the synthesis process.2 While this may be true for conventional solid-state synthesis, the examples above using high-energy precursors argue that this cannot be generally true for any synthesis route. Indeed organic chemistry is built upon the fact that it is possible to synthesise and stabilise molecules that are unstable with respect to decomposition.
Another approach that has been employed to predict which metastable phases are more likely to be accessible is the concept of basin of attraction.87 As any metastable structure is a local minimum on the energy landscape, they will each form a basin of attraction on the multidimensional configuration coordinate space. Intuitively, the (hyper)volume of the basin could be related to the accessibility of a certain phase, since a larger volume will result in more (random) atomic configurations ending up in that minimum. The concept has been investigated empirically—using athermal internal energies—and results are promising, suggesting that the frequency of occurrence in a random structure search is a better metric for synthesisability than the energy above the convex hull.88
The potential synthesisability of a new compound can be estimated from statistical models trained on data of known compounds. This can be treated as a classification (yes/no) problem or as a regression problem based on probability of success. While there is positive labelled data, i.e. the set of known materials, negative data on ‘unsynthesisable’ materials is generally unavailable. There has been successes in using information from failed experiments,89 but probabilistic models are more generally built from positive and unlabelled data for specific classes of material.90,91 For more universal models, a large amount of diverse data is required. There has been progress in text mining of synthesis information from the literature. Kononova et al.92 extracted 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 recipes for inorganic crystals including a breakdown into precursors, operations, and processing conditions. Such data can then be used to make predictions of optimal crystal synthesis procedures.93
488 recipes for inorganic crystals including a breakdown into precursors, operations, and processing conditions. Such data can then be used to make predictions of optimal crystal synthesis procedures.93
Even if the synthesis of a specific metastable material is possible, a related question is its lifetime before transformation into a lower energy equilibrium configuration. The answer requires knowledge of the free energy landscape and the corresponding barriers and kinetics of the system.94 For molecules and nanoparticles, this is relatively straightforward to explore computationally and a range of techniques are available. However, for extended crystals modelled within periodic boundary conditions it requires prior knowledge of the pathways between two or more structures. For crystals connected by group–subgroup relations this can be straightforward (e.g. from a cubic to tetragonal perovskite95), and the methods from anharmonic phonon theory can be useful to establish the (local) stability range of high temperature phases. However, there are many transitions where no smooth pathway is accessible (e.g. incommensurate polymorphs96).
Enhanced sampling techniques, including parallel tempering, hyperdynamics, and metadynamics, have been developed to probe complex free energy surfaces.97,98 They have traditionally been too expensive to apply to complex crystals. However, longer-timescale simulations enabled by lower-cost force fields and more powerful computer hardware provide a promising direction for expanding their range of applicability to assessing the lifetimes of metastable materials.
6. Conclusion
The predictive modelling of previously unknown materials is now common. Established protocols to filter out implausible candidates include: (i) the absence of imaginary phonons modes as an indicator of local stability; and (ii) endothermic decomposition reactions as an indicator of global stability. These filters are commonly based on harmonic phonon dispersions and athermal internal energies, respectively, which both have known limitations that will result in unreliable predictions.In this perspective, we discussed modern free energy methods beyond the harmonic approximation, which allow one to extend stability predictions to finite temperatures. This gives access to both local and global stability as a function of thermodynamic variables. Thus, these methods can be used to explain and predict relevant synthesis conditions and stability ranges of materials with desired functionalities.
More accurate free energy methods should generally lead to better labelling of potentially synthesisable materials. This will allow one to avoid both false positives, where predicted stable phase only exists at very low temperature, and false negatives where a phase is deemed unstable either locally or globally, but is in fact stable at finite temperature. Exclusion of phases that are locally unstable at athermal conditions, but locally stable at ambient conditions, can be avoided by employing an appropriate anharmonic description of the phonon dispersion and free energy of the system.
Data availability
As this is a perspective article, no primary research results, data, software or code have been included.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. T. acknowledges the Independent Research Fund Denmark for funding through the International Postdoctoral grant (0164-00015B). A. M. G. was supported by EPSRC Fellowship EP/T033231/1. J. K. acknowledges support from the Swedish Research Council (VR) program 2021-00486.References
- A. Zunger, Nature, 2019, 556, 447 CrossRef.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Sci. Adv., 2018, 4, eaaq0148 CrossRef PubMed.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- N. Satoh, T. Nakashima and K. Yamamoto, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- J. C. Angus, Y. Wang and M. Sunkara, Annu. Rev. Mater. Sci., 1991, 21, 221–248 CrossRef CAS.
- H. Nagatani, I. Suzuki, M. Kita, M. Tanaka, Y. Katsuya, O. Sakata, S. Miyoshi, S. Yamaguchi and T. Omata, Inorg. Chem., 2015, 54, 1698–1704 CrossRef CAS PubMed.
- N. M. Twyman, A. Walsh and T. Buonassisi, Chem. Mater., 2022, 34, 2545–2552 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- G. Price, A. Wall and S. Parker, Philos. Trans. R. Soc., A, 1989, 328, 391–407 CrossRef CAS.
- R. H. Fowler, Statistical thermodynamics, CUP Archive, 1939.
- J. D. Dunitz, Curr. Biol., 1995, 2, 709–712 CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- W. Wei, W. Li, K. T. Butler, G. Feng, C. J. Howard, M. A. Carpenter, P. Lu, A. Walsh and A. K. Cheetham, Angew. Chem., 2018, 130, 9070–9074 CrossRef.
- A. Togo, Phonon database at Kyoto University.
- G. Petretto, S. Dwaraknath, H. PC Miranda, D. Winston, M. Giantomassi, M. J. Van Setten, X. Gonze, K. A. Persson, G. Hautier and G.-M. Rignanese, Sci. Data, 2018, 5, 1–12 CrossRef PubMed.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789 CrossRef.
- R. X. Yang, J. M. Skelton, E. L. da Silva, J. M. Frost and A. Walsh, J. Chem. Phys., 2020, 152, 024703 CrossRef CAS PubMed.
- L. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 3520 CrossRef CAS PubMed.
- R. Masuki, T. Nomoto, R. Arita and T. Tadano, Phys. Rev. B, 2022, 105, 064112 CrossRef CAS.
- N. K. Ravichandran and D. Broido, Phys. Rev. B, 2018, 98, 085205 CrossRef CAS.
- A. Kuwabara, T. Tohei, T. Yamamoto and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 064301 CrossRef.
- P. Pavone, S. Baroni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10421–10423 CrossRef CAS.
- M. T. Dove, Am. Mineral., 1997, 82, 213–244 CAS.
- D. A. Broido, M. Malorny, G. Birner, N. Mingo and D. A. Stewart, Appl. Phys. Lett., 2007, 91, 231922 CrossRef.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301(R) CrossRef.
- T. Tadano and S. Tsuneyuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054301 CrossRef.
- T. Tadano and S. Tsuneyuki, J. Phys. Soc. Jpn., 2018, 87, 041015 CrossRef.
- L. Monacelli, R. Bianco, M. Cherubini, M. Calandra, I. Errea and F. Mauri, J. Phys.: Condens. Matter, 2021, 33, 363001 CrossRef CAS PubMed.
- A. Carreras, A. Togo and I. Tanaka, Comput. Phys. Commun., 2017, 221, 221–234 CrossRef CAS.
- F. Zhou, W. Nielson, Y. Xia and V. Ozoliņš, Phys. Rev. Lett., 2014, 113, 185501 CrossRef PubMed.
- T. Tadano and W. A. Saidi, First-Principles Phonon Quasiparticle Theory Applied to a Strongly Anharmonic Halide Perovskite, 2021 Search PubMed.
- J. Klarbring, O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. Lett., 2020, 125, 045701 CrossRef CAS PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef CAS PubMed.
- Y. Oba, T. Tadano, R. Akashi and S. Tsuneyuki, Phys. Rev. Mater., 2019, 3, 033601 CrossRef CAS.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104111 CrossRef.
- D. C. Wallace, Thermodynamics of crystals, Dover Publications, Inc., 1998 Search PubMed.
- N. Benshalom, G. Reuveni, R. Korobko, O. Yaffe and O. Hellman, The dielectric response of rock-salt crystals at finite temperatures from first principles, 2021 Search PubMed.
- A. Dewandre, O. Hellman, S. Bhattacharya, A. H. Romero, G. K. Madsen and M. J. Verstraete, Phys. Rev. Lett., 2016, 117, 276601 CrossRef.
- N. Shulumba, B. Alling, O. Hellman, E. Mozafari, P. Steneteg, M. Odén and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174108 CrossRef.
- B. Sadovyi, M. Wierzbowska, S. Stelmakh, S. Boccato, S. Gierlotka, T. Irifune, S. Porowski and I. Grzegory, Phys. Rev. B, 2020, 102, 235109 CrossRef CAS.
- H.-Y. Gu, W.-J. Yin and X.-G. Gong, Appl. Phys. Lett., 2021, 119, 191101 CrossRef CAS.
- K. De Boer, A. Jansen, R. Van Santen, G. Watson and S. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 826 CrossRef CAS PubMed.
- N. Allan, T. Barron and J. Bruno, J. Chem. Phys., 1996, 105, 8300–8303 CrossRef CAS.
- J. D. Gale, J. Phys. Chem. B, 1998, 102, 5423–5431 CrossRef CAS.
- I. Errea, F. Belli, L. Monacelli, A. Sanna, T. Koretsune, T. Tadano, R. Bianco, M. Calandra, R. Arita, F. Mauri and J. A. Flores-Livas, Nature, 2020, 578, 66–69 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Understanding molecular simulation, Elsevier, 2001, vol. 1 Search PubMed.
- J. B. Haskins, A. E. Thompson and J. W. Lawson, Phys. Rev. B, 2016, 94, 214110 CrossRef.
- J. Klarbring and S. I. Simak, Phys. Rev. Lett., 2018, 121, 225702 CrossRef CAS PubMed.
- B. Grabowski, L. Ismer, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134106 CrossRef.
- B. Cheng, E. A. Engel, J. Behler, C. Dellago and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1110–1115 CrossRef CAS PubMed.
- V. Kapil and E. A. Engel, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1467–1479 CrossRef PubMed.
- B. Grabowski, Y. Ikeda, P. Srinivasan, F. Körmann, C. Freysoldt, A. I. Duff, A. Shapeev and J. Neugebauer, npj Comput. Mater., 2019, 5, 80 CrossRef.
- G. A. de Wijs, G. Kresse and M. J. Gillan, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 8223–8234 CrossRef CAS.
- F. Dorner, Z. Sukurma, C. Dellago and G. Kresse, Phys. Rev. Lett., 2018, 121, 195701 CrossRef CAS PubMed.
- C. Verdi, F. Karsai, P. Liu, R. Jinnouchi and G. Kresse, npj Comput. Mater., 2021, 7, 156 CrossRef CAS.
- A. Cheetham, V. Fender and R. Taylor, J. Phys. C: Solid State Phys., 1971, 4, 2160 CrossRef CAS.
- J. D. Bocarsly, E. E. Levin, C. A. Garcia, K. Schwennicke, S. D. Wilson and R. Seshadri, Chem. Mater., 2017, 29, 1613–1622 CrossRef CAS.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- A. van de Walle, Calphad, 2009, 33, 266–278 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- G. Kieslich, J. M. Skelton, J. Armstrong, Y. Wu, F. Wei, K. L. Svane, A. Walsh and K. T. Butler, Chem. Mater., 2018, 30, 8782–8788 CrossRef CAS.
- M. Habgood, R. Grau-Crespo and S. L. Price, Phys. Chem. Chem. Phys., 2011, 13, 9590 RSC.
- F. Zhou, T. Maxisch and G. Ceder, Phys. Rev. Lett., 2006, 97, 155704 CrossRef PubMed.
- N. L. Allan, S. Conejeros, J. N. Hart and C. E. Mohn, Theor. Chem. Acc., 2021, 140, 1–16 Search PubMed.
- B. Voronin, J. Phys. Chem. Solids, 1995, 56, 839–847 CrossRef CAS.
- T. Tadano, Y. Gohda and S. Tsuneyuki, J. Phys.: Condens. Matter, 2014, 26, 225402 CrossRef CAS PubMed.
- F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184 CrossRef.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220–6227 CrossRef CAS.
- S. A. Tawfik, O. Isayev, M. J. Spencer and D. A. Winkler, Adv. Theory Simul., 2020, 3, 1900208 CrossRef CAS.
- P.-P. De Breuck, G. Hautier and G.-M. Rignanese, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- S. Kong, F. Ricci, D. Guevarra, J. B. Neaton, C. P. Gomes and J. M. Gregoire, Nat. Commun., 2022, 13, 1–12 Search PubMed.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 1–10 CrossRef.
- C. J. Bartel, S. L. Millican, A. M. Deml, J. R. Rumptz, W. Tumas, A. W. Weimer, S. Lany, V. Stevanović, C. B. Musgrave and A. M. Holder, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- T. Mueller and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 024103 CrossRef.
- J. M. Clary, A. M. Holder and C. B. Musgrave, ACS Appl. Mater. Interfaces, 2020, 12, 48553–48564 CrossRef CAS PubMed.
- W. Sun, A. Holder, B. Orvañanos, E. Arca, A. Zakutayev, S. Lany and G. Ceder, Chem. Mater., 2017, 29, 6936–6946 CrossRef CAS.
- J. V. Badding, Annu. Rev. Mater. Sci., 1998, 28, 631–658 CrossRef CAS.
- L. Dubrovinsky, S. Khandarkhaeva, T. Fedotenko, D. Laniel, M. Bykov, C. Giacobbe, E. L. Bright, P. Sedmak, S. Chariton, V. Prakapenka, A. V. Ponomareva, E. A. Smirnova, M. P. Belov, F. Tasnádi, N. Shulumba, F. Trybel, I. A. Abrikosov and N. Dubrovinskaia, Nature, 2022, 605, 274–278 CrossRef CAS PubMed.
- J. Patel, L. Němcová, P. Maguire, W. Graham and D. Mariotti, Nanotechnology, 2013, 24, 245604 CrossRef CAS PubMed.
- E. Wheeler, J. L. Boone, J. Farmer and H. Chandrasekhar, J. Appl. Phys., 1997, 81, 524–526 CrossRef CAS.
- F. Therrien, E. B. Jones and V. Stevanović, Appl. Phys. Rev., 2021, 8, 031310 CAS.
- V. Stevanović, Phys. Rev. Lett., 2016, 116, 075503 CrossRef PubMed.
- P. Raccuglia, K. C. Elbert, P. D. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS PubMed.
- N. C. Frey, J. Wang, G. I. Vega Bellido, B. Anasori, Y. Gogotsi and V. B. Shenoy, ACS Nano, 2019, 13, 3031–3041 CrossRef CAS PubMed.
- G. Gu, J. Jang, J. Noh, A. Walsh and Y. Jung, npj Comput. Mater., 2022, 8, 71 CrossRef.
- O. Kononova, H. Huo, T. He, Z. Rong, T. Botari, W. Sun, V. Tshitoyan and G. Ceder, Sci. Data, 2019, 6, 1–11 CrossRef PubMed.
- H. Huo, C. J. Bartel, T. He, A. Trewartha, A. Dunn, B. Ouyang, A. Jain and G. Ceder, arXiv:2204.08151, 2022.
- D. J. Wales and T. V. Bogdan, Potential energy and free energy landscapes, 2006 Search PubMed.
- W. Zhong, D. Vanderbilt and K. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 6301 CrossRef CAS PubMed.
- R. Cowley and A. Bruce, J. Phys. C: Solid State Phys., 1978, 11, 3577 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- A. F. Voter, Phys. Rev. Lett., 1997, 78, 3908–3911 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |