Automating mix design for 3D concrete printing using optimization methods

Abstract

3D concrete printing technology introduces automation to the construction industry. The wider build customizability is a great advantage of this technology, but it adds complexity to the mix design. The compositions formed are far more complex than in conventional concrete, increasing the difficulty in designing mixtures for 3D concrete printing. As the number of materials in mix design increases, the workload increases exponentially during the development process. In this study, optimization methods are employed to automate the development of mortar mixes. The three objectives are the improvement of workability, buildability, and compressive strength. Eight factors are investigated in total, with three being qualitative and five quantitative. Those factors include cement, sand, and superplasticizer types as well as the water-to-binder ratio, the sand-to-binder ratio, and admixtures dosages. An initial D-optimal set of 18 mixtures is formed to drastically reduce the number of experiments. Feedforward neural networks are used to predict the properties of new mixtures. To increase the accuracy of the models, the genetic algorithm is used to optimize the hyperparameters of each network. Finally, the Pareto-optimization algorithm is used to control the materials and their dosages with the aim of simultaneously optimising the values of the three objectives. The proposed multiobjective approach generated mixtures with improved properties that met all three criteria after only five iterations and twenty-one additional mixtures were formed. The results indicate that this methodology can reduce the required workload while generating mixture compositions with improved properties by following an optimum trend.

---

Introduction

The construction sector is gradually adopting additive manufacturing technology. One of the most significant advantages of this technique is the enhanced build customizability.^1,2 Researchers are looking for the optimum materials to use in mix design to control cement hydration, pumpability, material deposition, and the curing processes. Developing cement-based materials for three-dimensional (3D) printing applications is a complicated process with many conflicting goals.³ High flowability before deposition, extrudability during deposition, buildability and stiffness immediately after the deposition are all desired properties for the printed materials used in this technology.^4,5 The necessity of recycling and reusing building materials adds to the complexity.⁶ A mix design can be made by following a variety of techniques, such as modifying one factor at a time, or following a full-factorial design.^1,7–10 There are various available options for a mix design, but the current mix design approaches reported in the field are often similar. As there are many cement and admixtures available, as well as process variables, articles on mix design strategies are needed, especially to achieve the promise of 3D printing (faster and safer construction, lower embodied carbon in structures, resource efficiency for sustainability). In most studies, the mixture proportion is frequently given directly, with no design method or explanation of how the parameters were obtained.¹¹ The two main methodologies proposed are the empirical mix design, such as the trial-and-error,^12–14 and the mix design following a rheological model.^15,16 These mix design methods are straightforward and effective. However, the number of tests in a mix design grows exponentially as the number of factors or their levels rise, especially when testing cement and admixture types.^17,18 As a result, the main compositions of the mixture remain constant with only a few parameters being treated as independent variables in order to find the best mixture.¹¹ Artificial intelligence can be used to simulate the mixing process and reduce the workload. Many studies in civil engineering have used artificial intelligence.^10,19–23 Artificial neural networks (ANNs) are widely used in the fields of data mining and machine learning.²⁴ Bagging and boosting regression trees, in addition to artificial neural networks, have been shown to be good predictive models for concrete-related issues. The mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R²) are calculated to assess the effectiveness of the models.²⁵ It is difficult to draw definitive conclusions on which predictive algorithm performs better. The performance of any algorithm is frequently dependent on the problem being solved. However, machine learning outperforms linear and quadratic models in terms of predicting concrete mix properties.²⁶ ANNs are used to predict concrete properties, such as the slump, segregation, filling capacity, compressive strength, drying shrinkage, or concrete durability.^26–31 Many scientific and engineering problems have been solved using mathematical approaches, which encompass a wide spectrum of problems. Despite their perfect efficiency, mathematical processes continue to face significant hurdles in tackling optimization problems. Given the increasing complexity of optimization problems, the use of metaheuristic algorithms is the best option.³² Metaheuristic algorithms are nature-inspired algorithms. There is a vast range of algorithms that replicate phenomena such as social behaviour, natural responses or human competitiveness.^33–35 The key aspect of them is the ability to escape from the local optimal point. Swarm-based algorithms simulate species-specific social traits such as labour division or pattern formation during food gathering. Evolution-based algorithms simulate the natural evolution, including the selection of the fittest individuals and their reproduction.^36,37 Recent studies in construction have used approaches that integrate artificial neural networks and metaheuristics. Among other objectives, the studies investigate the compressive strength, which is the most essential mechanical property of the field.^38,39 The recently developed multiobjective Cuckoo Search (CS) algorithm was employed in conjunction with several linear and non-linear regression models for concrete mix design.⁴⁰ The multi-objective grey wolf optimizer, as well as the M5P tree and multi-gene expression programming (MGEP) models, were utilised to find the best rubbercrete mix designs.⁴¹ Finally, to develop asphalt mixes, a feed-forward backpropagation neural network with a single hidden layer was paired with a GA-based optimization model.⁴²

Researchers in 3D concrete printing aim towards mixtures with a high mechanical strength.^43,44 The perpendicular load direction has the maximum compressive strength. The compressive strength of high-performance 3D printed specimens can reach 75 to 102 MPa, while casted moulds have a compressive strength of 107 MPa.⁴⁴ While the final properties are always vital, the early age structural build-up and strength development throughout the dormant period are equally important for this technology.^45–48 The characteristics of fresh-state mortar mixes have been determined using geotechnical experiments, such as the direct shear test. Testing is proposed over a period of 0 to 90 minutes, with 15–30 minutes intervals.⁴⁶ Another study indicates that in the direct shear test, the shear rates have no effect and the cohesiveness of the mixtures is proportional to the binder-to-sand ratio.⁴⁷ Additionally, the maximum printed height before collapsing can be used to assess the mixture's buildability. Along with buildability, flowability is also crucial for 3D concrete printing applications.^14,49,50 The printed region and buildability of the mixtures are defined using slump and flow tests.⁴⁹ Flowability and buildability are affected by the water-to-binder and sand-to-binder ratios. A smooth surface and great buildability are achieved, with mixtures having a slump flow value of 50% to 90%.⁴⁹ Viscosity-modifying agents or silica fume can increase the yield stress. To achieve extrudability and buildability, the material yield stress should be between 1.5 and 2.5 kPa; otherwise, the material's stability and extrudability may be compromised.¹⁴

This study aims to automate the mix design process while reducing the amount of material and time required to generate mixtures with enhanced qualities. Flowability, buildability, and mechanical strength are the three properties considered to choose the optimum mixture. Flowability depends on the extrusion system used. High flowable mixtures will be easier to pump, but at the expense of buildability. For 3D concrete printing, structural build-up in the dormant period is critical. The shear stress should be as high as possible to achieve high printing speeds, although compromises need to be made in terms of the mechanical strength or flowability. As with the buildability, the goal is also to increase the hardened properties to the maximum extent possible. Achieving high-performance cementitious printing mortar enables future applications to use thinner structures with less massive concrete. The proposed testing methods are the ASTM C1437 flow test, the ASTM D3080 direct shear test and the ASTM C109 compressive strength. Starting from the mix design, a D-optimal design was used to generate the initial set of 18 mixtures.⁵¹ This is a non-traditional experimental design that can significantly minimize the number of experiments while producing statistically grounded designs with high-quality results. To identify which admixtures would be included in the D-optimal mix design, a preliminary study was performed using probability plots.⁵² Three types of cement, three types of sand, and five admixtures, including superplasticizers, are chosen in total.⁵¹ Among the eight investigated factors, the qualitative factors are the cement types, the types of sand with different particle size distributions, and the types of superplasticizers. The quantitative factors are the water-to-binder ratio, the sand-to-binder ratio, and the dosages of the selected admixtures. A multiobjective Pareto optimization algorithm guided the procedure. The objective functions are artificial neural networks that are trained using data from lab experiments. To increase the accuracy of the artificial neural networks, the genetic algorithm is used to optimize the hyperparameters of each network. The best networks are then used to predict the properties of the new mixtures proposed during the multiobjective Pareto optimization. Twenty-one new mixture variations are introduced after five iterations of the Pareto optimization process. These mixtures are formed and tested in the lab to determine the fresh and final properties. Section 2 explains the mix design and the materials chosen. Section 3 describes the algorithms and how the optimization tools are connected. Section 4 provides the results gained in terms of both the material properties and the optimization method performance. Finally, Section 5 concludes the study. The results reveal that the Pareto optimization method narrows down the factors and their levels after determining their significance and the optimal doses to concurrently increase the competing objectives while reducing the quantity of material and workload required.

Mix design and database

Binders, sand, and admixtures

Three superplasticizers or admixtures with water-reducer effects are chosen, and two important admixtures were assessed in a prior study.⁵² The two selected admixtures are the biopolymer polysaccharide viscosity modifying agent (B) to control the rheological properties of the mixtures and the calcium silicate hydrate admixture to improve the early and late-age strength development.^39,43 Two out of the three selected superplasticizers are based on synthetic organic polymers, such as polycarboxylate ether (PCE), whereas the third is sulfonated naphthalene polymer based. For cement, the three types are general use Portland cement (GU), binary cement with silica fumes (GUbSF) and Portland cement with a high early strength (HE). For the sand, all three types are fine aggregates with particle sizes below 2.5 mm. Each sand has different characteristics: the first sand is finer, the second is coarser and the third sand is recycled sand that was collected from the residues of the sedimentation basin of truck concrete mixer washing facilities. More details about the selected materials are available in ref. 51.

D-optimal mix design

Initially, there were six factors with three levels each, all related to the selected materials.⁵¹ These factors were the cement type, sand type, water-to-binder ratio, sand-to-binder ratio, superplasticizer type and the use of a second admixture.⁵³ The levels for each factor are presented in Table 1. Here, GU refers to the general use of Portland cement, HE to Portland cement with a high early strength, and GUbSF to binary cement with silica fumes (ASTM C1157). PCEs are superplasticizers based on synthetic organic polymers, and SNPs are sulfonated naphthalene polymer-based water reducers. Finally, B refers to the addition of a biopolymer polysaccharide viscosity modifying agent, and CSH-C refers to the addition of crystalline calcium silicate hydrate. The particle size of all the sand types is below 2.5 mm.

Table 1 Materials selected for the mix design⁵¹

Cement	Sand	Water-binder ratio	Sand-binder ratio	Superplasticizer (Type A & F)	Type S admixtures
GU	Fine	0.32	1.8	PCE-1	—
HE	Coarse	0.345	2	PCE-2	B
GUbSF	Recycled	0.37	2.3	SNP	CSH-C

---

A full factorial plan for the selected number of factors and levels would require 3⁶ = 729 experiments to be made per test. This number of experiments is impractical, even if a fractional factorial plan were used. The benefit of using a D-optimal design is that the required runs, the amount of resources and the time will be drastically reduced. This class of experimental designs selects the best group of design points with respect to a statistical criterion. The designer can choose the number of mixtures that he or she wishes to form. Eighteen mixtures were selected with a D-efficiency equal to 100%.⁵¹ The mixtures are presented in Table 2. The testing methods were the flow test, the direct shear test and the compressive strength. Those three were deemed adequate to start with and to see which can help draw important conclusions regarding the workability and flowability of the material, the early resistance of the mixture during the first few minutes, and its compressive strength.

Table 2 The 18 mixtures from the D-optimal mix design⁵¹

Mix	Cement	Sand	Water:binder	Sand:binder	Superplasticizer (type A & F)	Type S admixtures
1	GU	Coarse	0.320	1.8	PCE-1	—
2	GU	Coarse	0.345	2.0	SNP	B
3	GU	Fine	0.320	2.3	SNP	CSH-C
4	HE	Fine	0.345	2.0	PCE-2	CSH-C
5	HE	Fine	0.370	2.3	PCE-1	—
6	HE	Recycled	0.345	1.8	PCE-1	B
7	GUbSF	Coarse	0.370	2.0	PCE-2	—
8	GUbSF	Recycled	0.320	1.8	PCE-2	CSH-C
9	GUbSF	Recycled	0.370	2.3	SNP	B
10	GU	Fine	0.370	1.8	PCE-2	B
11	GU	Recycled	0.345	2.3	PCE-2	—
12	GU	Recycled	0.370	2.0	PCE-1	CSH-C
13	HE	Coarse	0.320	2.3	PCE-2	B
14	HE	Coarse	0.370	1.8	SNP	CSH-C
15	HE	Recycled	0.320	2.0	SNP	—
16	GUbSF	Coarse	0.345	2.3	PCE-1	CSH-C
17	GUbSF	Fine	0.320	2.0	PCE-1	B
18	GUbSF	Fine	0.345	1.8	SNP	—

---

Optimization approach

After obtaining the D-optimal mixes, tests on the fresh and final properties were performed for each mixture. Feedforward neural networks were trained with the collected data to predict the properties of new mixtures. Feedforward neural networks (FNNs) are one of the most widely used neural networks and have been applied in several applications. Training is the process of determining the best values for a neural network's control parameters. The objective is to discover ideal settings in order to decrease the ANNs' errors and enhance their accuracy; therefore, it may be viewed as an optimization problem. Back propagation is the most commonly used training procedure for FNNs. The coefficient of determination (R²) and the normalized root mean square error (NRMSE) are used to assess the performance of the trained networks.^28,29,54 To help in the training process, a genetic algorithm was used to find the best possible hyperparameters of the networks. The genetic algorithm (GA) is a prominent evolutionary algorithm, belonging to the category of meta-heuristic algorithms. These algorithms compare a subset of solutions that would otherwise be too many to be fully enumerated or investigated. GA is one of the first population-based algorithms, with the primary operators being selection, crossover, and mutation.^17,54,55 The multiobjective Pareto optimization algorithm then used the best three networks, one for each investigated property, as its objective functions. In multiobjective optimization problems, the optimal solution is a combination of solutions with varying trade-offs rather than a single solution. Pareto optimal or non-dominated solutions are terms used to describe these solutions⁵⁶ The definition of the multiobjective problems can be summarized through eqn (1):

Minimize{f₁(x),f₂(x),…,f_i(x)} subject to x ∈ S (1)

where two or more competing objective functions, f_i:Rⁿ → R, where i ≥ 2, need to be simultaneously minimized. The decision variables x, in the form of vectors, belong to the region S ⊂ Rⁿ.

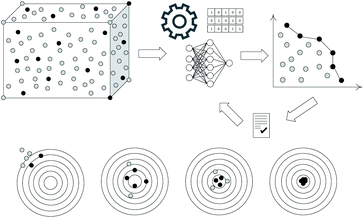
The objective vectors can be deemed optimal if none of their components can be improved without compromising at least one of the others. The output of the Pareto optimization algorithm was a new set of mixtures with properties closer to the desired values by respecting the trade-offs between them. All the Pareto optimal solutions can be considered equally desirable (in the mathematical sense), since arranging the vectors in perfect order is impossible. A decision maker is required to select the most preferred one. The decision maker, for example, is a person who can express preference between the available options.⁵⁶ The properties for those new mixtures were collected in order to verify the predictions, and then they were used to update the networks. This process was repeated five times, which was sufficient to improve the mixtures from the initial set and to acquire mixtures closer to the application needs. The process is depicted in Fig. 1. The population of the solutions is depicted with grey and black dots. The black-coloured solutions represent those solutions that are closer to the goal. In each iteration, the algorithm proposes a new population trying to reach closer to the goal. The end of the process can either be made after a specific number of iterations, after reaching the goal, or if there are no improvements to the current best solutions.

Fig. 1 Representation of the proposed methodology with optimization methods.

In the initial set of the D-optimal mixes, the number of factors was six with three levels each. All of the factors were treated as qualitative factors. The water-to-binder ratio or the sand-to-binder ratio are normally continuous variables and not discrete variables. The selected discrete values were enough to observe the tendency with a design of experiment (DOE) method. However, with the use of optimization algorithms, some of the factors could be treated as quantitative factors. The algorithm used in this study can edit up to eight factors, where three of them are qualitative and the remaining five are treated as quantitative factors. These parameters are the water-to-binder ratio, the sand-to-binder ratio, the dosage of the superplasticizer, the dosage of the biopolymer polysaccharide viscosity modifying agent, and the dosage of crystalline calcium silicate hydrate. The ranges of the values for those quantitative factors are close to the boundaries of the values set in the D-optimal design.⁵¹ Specifically, the water-to-binder ratio can take values between 0.25–0.4% w, the sand-to-binder ratio between 1.7–2.4% w, a superplasticizer dosage of 0.13–0.28% w, the biopolymer polysaccharide viscosity modifying agent dosage range is 0–0.018% w and the crystalline calcium silicate hydrate dosage is between 0–0.4% w.

Genetic algorithm and feedforward neural network

The combination of AI methods with optimization techniques is a promising avenue for predicting the properties of concrete materials. The methodology is similar to that made in a previous study presented in.⁵⁷ Here, the data is divided into training, validation, and testing sets. The proportions of splits are 70% for training, 15% for validation and 15% for testing with the unseen data. The parameters that are investigated to improve the predictive performance of the neural networks are the training method, the number of hidden layers and the neurons of each hidden layer. The goal of the genetic algorithm is to simultaneously maximize the coefficient of determination and minimize the normalized root mean squared error. The maximum number of generations of the genetic algorithm is 100, the number of candidate solutions of the first generation are 80, and at every new generation, the number is increased by 40. The number of maximum epochs of each network is 400. Depending on the cement property being modelled, different parameters can be considered as the best for each individual network. From the training methods in the MATLAB R2022a, the following functions were possible to be selected during the hyperparameter tuning process:

• trainlm: a network training function that updates the weight and bias values according to Levenberg–Marquardt optimization (LM).

• trainrp: a network training function that updates the weight and bias values according to the resilient backpropagation algorithm (Rprop).

• trainscg: a network training function that updates the weight and bias values according to the scaled conjugate gradient method (SCG).

• traincgb: a network training function that updates the weight and bias values according to conjugate gradient backpropagation with Powell-Beale restarts (PB).

• traincgf: a network training function that updates the weight and bias values according to conjugate gradient backpropagation with Fletcher–Reeves updates (FR).

• traincgp: a network training function that updates the weight and bias values according to conjugate gradient backpropagation with Polak–Ribiére updates (PR).

• trainoss: a network training function that updates the weight and bias values according to the one-step secant method (OSS).

• traingdx: a network training function that updates the weight and bias values according to gradient descent momentum and an adaptive learning rate (GDX).

Based on the obtained results, the best training method for the flow is the resilient backpropagation algorithm (Rprop) with one hidden layer. For the compressive strength, the preferred training method is the conjugate gradient backpropagation with Powell-Beale restarts (PB) and two hidden layers. For the shear stress, there are no specific preferences in terms of the number of hidden layers or the training method, but the gradient backpropagation training methods are preferable compared to the other functions. The comparison between the best-performing networks is made based on their performance on the testing dataset. Their performance on the unseen data is not taken into consideration during the training phase. At the end of that phase, the twenty best networks are kept based on their performance on the validation dataset. Then, the performances of those networks are tested in the unseen data, meaning the testing dataset. The best-performing network in all the datasets is used for the prediction. The number of networks that are eventually kept is three in total, one for each property. Those networks are updated after each iteration following the same procedure.

Because the flow test is quite sensitive, even with small adjustments in the dosages of the materials, more data was added for the training of the corresponding network. The fluctuations in the amount of water, sand and superplasticizer can extremely affect the measurement. Apart from the data collected from the 18 formed mixtures, the extra data was the same combinations of materials, but with the absence of water, sand, or superplasticizer. Additionally, the data from the study presented in⁵⁷ was added to improve the accuracy of the predictions.

Multiobjective approach

For 3D printing applications, the optimum material should have high flowability before deposition, high extrudability and buildability at the time of the deposition, and high stiffness immediately after deposition.⁵ Apart from these fresh and crucial properties, the aim is also to achieve the highest possible compressive strength. Various other criteria could be given in a multiobjective approach, but for simplicity's sake and the proof of concept of this methodology, only those criteria are respected. The criteria are kept the same as in the first part of the study.⁵¹ Specifically, the goals that are set are the following:

• Flowability: flowability depends on the extrusion system used.⁵⁸ An increased flowability will be pumped more easily, but it comes in contrast to buildability. The threshold set for this study is a mortar flow above 60%, 5 minutes after the end of the mixing process.

• Shape stability/buildability: structural build-up in the dormant period is crucial. Aimed at high printing speeds, the shear stress should be as high as possible, but compromises will be made for the other two objectives. In this study, a threshold of 16 kPa in 90 minutes after mixing is set.

• Mechanical properties: a threshold of 80 MPa after 28 days is set for the compressive strength of high-performance concrete. As with the buildability and shear stress, the aim is to increase the hardened properties to the greatest extent possible.

Only the mixtures that respect these criteria are considered accepted. The data collected from the initial set of mixtures following the D-optimal mix design are presented in Table 3.

Table 3 Properties of the initial set⁵¹

Mix	Mixture description	Flow in 5 min (%)	Shear stress in 90 min (kPa)	Compressive strength in 28 days (MPa)
1	GU|Coarse|0.32|1.8|PCE-1|—	95	12.0	81.3
2	GU|Coarse|0.345|2.0|SNP|B	65	20.6	66.7
3	GU|Fine|0.32|2.3|SNP|CSH-C	0	—	—
4	HE|Fine|0.345|2.0|PCE-2|CSH-C	80	19.6	83.0
5	HE|Fine|0.37|2.3|PCE-1|—	0	—	—
6	HE|Recycled|0.345|1.8|PCE-1|B	88	12.5	81.1
7	GUbSF|Coarse|0.37|2.0|PCE-2|—	152	6.6	92.3
8	GUbSF|Recycled|0.32|1.8|PCE-2|CSH-C	152	7.6	102.2
9	GUbSF|Recycled|0.37|2.3|SNP|B	73	14.9	70.6
10	GU|Fine|0.37|1.8|PCE-2|B	123	9.3	76.9
11	GU|Recycled|0.345|2.3|PCE-2|—	90	9.3	78.9
12	GU|Recycled|0.37|2.0|PCE-1|CSH-C	111	11.2	78.1
13	HE|Coarse|0.32|2.3|PCE-2|B	56	21.1	80.7
14	HE|Coarse|0.37|1.8|SNP|CSH-C	63	19.1	66.6
15	HE|Recycled|0.32|2.0|SNP|—	0	—	—
16	GUbSF|Coarse|0.345|2.3|PCE-1|CSH-C	70	15.0	90.7
17	GUbSF|Fine|0.32|2.0|PCE-1|B	21	—	—
18	GUbSF|Fine|0.345|1.8|SNP|—	63	16.8	69.8

---

A graphical representation can be seen with the three objectives in Fig. 2. The x-axis is the shear stress at 90 minutes, the y-axis is the compressive strength at 28 days and the z-axis is the flow at 5 minutes after the mixing process. The threshold of each property can be seen as a red dashed line. The new introduced mixtures are in light blue. After evaluating if they respected the criteria, the rejected mixtures are turned yellow and the accepted mixtures are turned green. Among the 18 mixtures proposed by the D-optimal design, mixture 4 with HE, fine sand, a 0.345 water-to-binder ratio, a 2.0 sand-to-binder ratio, PCE-2 superplasticizer, and the addition of CSH-C gave the best results, and it was the only mixture that met the criteria.⁵¹

Fig. 2 Acceptable mixtures from the initial set.

Results and discussion

Optimization process

The optimization process is depicted in Fig. 3. Twenty-one new mixtures were introduced after five iterations of the Pareto optimization process. In total, 39 mixtures were formed, including the initial set of mixes from the D-optimal design. As shown in Fig. 3f, eight mixtures were deemed acceptable.

Fig. 3 Optimization process after 5 iterations (a, b c, d and e) and the final outcome (f).

The composition of the new mixtures can be seen in Table 4. It can be seen that the algorithm showed a preference to specific materials, which was to be expected. Lower values are preferred for the sand-to-binder and water-to-binder ratios. The presence of at least one of the B or CSH-C admixtures is also evident. The PCE-2 superplasticizer is selected in most of the proposed mixtures, with the SNP superplasticizer being eliminated. The HE and GUbSF cement types are preferred instead of the GU. Recycled and coarse sand are preferred instead of finer sand. The preferences made by the algorithm can be explained from the analysis made on the D-optimal mix design.⁵¹ Based on the analysis, the three most important factors are the cement type, the water-to-binder ratio and the superplasticizer type. The low water-to-binder ratio, the addition of the CSH-C admixture, the recycled sand and the GUbSF cement increased the compressive strength. The use of HE, the addition of the B admixture and the coarse sand helped improve the shape stability and the shear stress. On the other hand, the low sand-to-binder ratio, recycled sand, PCE-2 superplasticizer and high water-to-binder ratio helped increase the flowability.

Table 4 Proposed mixtures from the multiobjective optimization algorithm

Mix	Cement	Sand	Water:binder	Sand:binder	Superplasticizer (type A & F)	SP (% w/w)	B (% w/w)	CSH-C (% w/w)
19	GUbSF	Recycled	0.30	2.2	PCE-2	0.25	—	0.23
20	HE	Recycled	0.25	1.9	PCE-2	0.28	0.009	0.30
21	HE	Coarse	0.29	2.1	PCE-2	0.28	0.009	0.25
22	HE	Recycled	0.3	1.7	PCE-2	0.28	0.006	0.40
23	GUbSF	Coarse	0.31	2.1	PCE-2	0.28	—	0.02
24	HE	Coarse	0.35	2.1	PCE-2	0.28	—	0.38
25	GUbSF	Coarse	0.3	1.8	PCE-2	0.26	0.018	—
26	HE	Coarse	0.31	2.1	PCE-2	0.28	0.006	0.02
27	GU	Coarse	0.3	1.7	PCE-1	0.28	0.003	0.33
28	GU	Coarse	0.33	1.8	PCE-1	0.28	—	0.40
29	HE	Fine	0.3	1.7	PCE-1	0.22	—	0.15
30	GU	Fine	0.33	1.8	PCE-1	0.25	—	0.40
31	GUbSF	Fine	0.33	1.8	PCE-1	0.25	—	0.18
32	GUbSF	Recycled	0.3	1.7	PCE-1	0.28	0.013	0.40
33	GUbSF	Recycled	0.3	2.0	PCE-2	0.28	0.013	0.02
34	HE	Coarse	0.3	1.8	PCE-2	0.28	0.013	0.11
35	HE	Recycled	0.3	2.0	PCE-2	0.28	0.013	0.04
36	GUbSF	Recycled	0.3	1.7	PCE-1	0.26	0.008	—
37	HE	Recycled	0.3	1.7	PCE-2	0.28	0.008	0.40
38	GUbSF	Coarse	0.31	2.1	PCE-1	0.28	—	0.02
39	HE	Recycled	0.3	1.7	PCE-2	0.28	0.013	0.11

---

First iteration

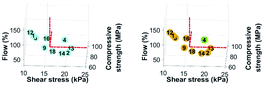
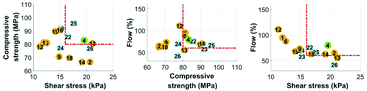
The non-dominant solutions were obtained after 1571 function evaluations with a hypervolume of 42 070, an average distance of 0.0855 and a spread of 0.3565. From the solutions, three unique mixtures were proposed (Table 5). Those three first mixtures that the algorithm proposed had the lowest values for the water-to-binder ratio. At the same time, the algorithm chose the PCE-2 superplasticizer, which gave the highest flow in the mixtures of the initial D-optimal set. However, with a water-to-binder ratio below 0.30% w, the mixtures were too dry to form a flowable mixture.

Table 5 First iteration: set of mixtures proposed by the Pareto algorithm

Mix	Mixture description	Flow (%)	Shear stress (kPa)	Compressive strength (MPa)	Criteria met
19	GUbSF|Recycled|0.30|2.2|PCE-2|0.25|—|0.23	68	14.1	89.6	✓, ✗, ✓
20	HE|Recycled|0.25|1.9|PCE-2|0.28|0.009|0.30	0	—	—	✗, —, —
21	HE|Coarse|0.29|2.1|PCE-2|0.28|0.009|0.25	12	—	—	✗, —, —

---

Mixtures 20 and 21 had a low flowability. As shown in Fig. 4, mixture 19 had an acceptable flowability, and the final strength was above the threshold that was set. However, the mixture did not meet the criteria related to buildability, since the shear stress was below 16 kPa.

Fig. 4 The performance of the proposed mixtures after the first iteration (a, b, c).

Second iteration

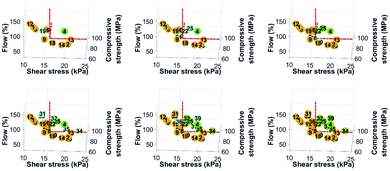
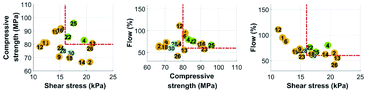
In the second iteration, the non-dominant solutions were obtained after 2162 function evaluations with a hypervolume of 62 103, an average distance of 0.04 and a spread of 0.1978. From the solutions, five new unique mixtures were proposed (Table 6). Mixtures 22 and 25 were able to meet all three criteria at the same time. The water-to-binder ratio and the sand-to-binder ratio at mixtures 22 and 25 were lower than those of the rejected mixes. The presence of HE with the addition of the B admixture helped increase the shear stress, whereas GUbSF and CSH-C increased the compressive strength. With the use of the GUbSF cement type, the compressive strength at 28 days surpassed 90 MPa, and the shear stress remained close to 17 kPa after 90 minutes in mixture 25.

Table 6 Second iteration: set of mixtures proposed by the Pareto algorithm

Mix	Mixture description	Flow (%)	Shear stress (kPa)	Compressive strength (MPa)	Criteria met
22	HE|Recycled|0.30|1.7|PCE-2|0.28|0.006|0.40	76	16.5	85.6	✓, ✓, ✓
23	GUbSF|Coarse|0.31|2.1|PCE-2|0.28|—|0.02	58	15.2	92.0	✗, ✗, ✓
24	HE|Coarse|0.35|2.1|PCE-2|0.28|—|0.38	70	15.1	77.3	✓, ✗, ✗
25	GUbSF|Coarse|0.30|1.8|PCE-2|0.26|0.018|—	67	17.6	95.9	✓, ✓, ✓
26	HE|Coarse|0.31|2.1|PCE-2|0.28|0.006|0.02	42	20.7	77.0	✗, ✓, ✗

---

In Fig. 5, mixtures 22 and 25 were inside the accepted zone for all three criteria. Mixtures 23 and 26 had low flowability, whereas mixture 23 performed better in terms of compressive strength and mixture 26 in terms of shear stress. Mixture 24 had an acceptable flow, but the compressive strength and the shear stress were below the thresholds.

Fig. 5 The performance of the proposed mixtures after the second iteration (a, b and c).

Third iteration

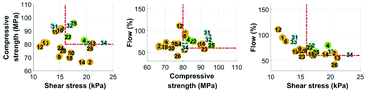
In the third iteration, the non-dominant solutions were obtained after 2709 function evaluations with a hypervolume of 91 704, an average distance of 0.0377 and a spread of 0.1741. The algorithm proposed the use of materials that have not been used in the previous two iterations. Here, four new unique mixtures were proposed, all of which included the PCE-1 superplasticizer (Table 7). GU cement and fine sand were added, the use of a CSH-C admixture was prevalent, and the B admixture was reduced or removed from the majority of the newly proposed mixtures. That was an area that the algorithm has not explored during the previous two iterations. The results of those mixtures showed that these combinations need an increased water-to-binder ratio, from 0.3 to at least 0.33 w%, to acquire enough flowability. The absence of the B admixture also resulted in reduced flowability. The use of GU cement with the PCE-1 and CSH-C admixtures was not sufficient to meet the criteria related to the compressive strength.

Table 7 Third iteration: set of mixtures proposed by the Pareto algorithm

Mix	Mixture description	Flow (%)	Shear stress (kPa)	Compressive strength (MPa)	Criteria met
27	GU|Coarse|0.30|1.7|PCE-1|0.28|0.003|0.33	16	—	—	✗, —, —
28	GU|Coarse|0.33|1.8|PCE-1|0.28|—|0.40	70	15.6	75.2	✓, ✗, ✗
29	HE|Fine|0.30|1.7|PCE-1|0.22|—|0.15	0	—	—	✗, —, —
30	GU|Fine|0.33|1.8|PCE-1|0.25|—|0.40	60	17.1	73.5	✓, ✓, ✗

---

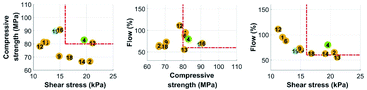
In Fig. 6c, mixture 30 is in the acceptable region since it was able to meet the criteria related to the flow and shear stress. Mixture 28 had sufficient flowability, but its performance in the shear stress was less than the threshold of 16 kPa. The compressive strengths of both mixtures were less than 80 MPa, which can be seen graphically in Fig. 6a and b.

Fig. 6 The performance of the proposed mixtures after the third iteration (a, b and c).

Fourth iteration

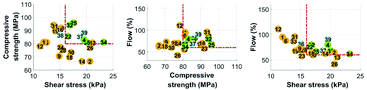
In the fourth iteration, the non-dominant solutions were obtained after 2930 function evaluations with a hypervolume of 18 289, an average distance of 0.0252 and a spread of 0.1892. After exploring different combinations in the third iteration, the algorithm began to become more accurate on its suggestions. Five new mixtures were proposed (Table 8), all of which were able to meet the criteria related to the flow and the compressive strength. Only two mixtures, mixes 31 and 33, did not have a shear stress above the requested threshold of 16 kPa. Mixture 34 had the best shear stress among all the formed mixtures at 23.2 kPa 90 minutes after the mixing procedure.

Table 8 Fourth iteration: set of mixtures proposed by the Pareto algorithm

Mix	Mixture description	Flow (%)	Shear stress (kPa)	Compressive strength (MPa)	Criteria met
31	GUbSF|Fine|0.33|1.8|PCE-1|0.25|—|0.18	96	14.0	93.4	✓, ✗, ✓
32	GUbSF|Recycled|0.30|1.7|PCE-1|0.28|0.013|0.40	80	16.8	94.2	✓, ✓, ✓
33	GUbSF|Recycled|0.30|2.0|PCE-2|0.28|0.013|0.02	87	13.8	94.1	✓, ✗, ✓
34	HE|Coarse|0.30|1.8|PCE-2|0.28|0.013|0.11	62	23.2	81.2	✓, ✓, ✓
35	HE|Recycled|0.30|2.0|PCE-2|0.28|0.013|0.04	68	20.0	81.1	✓, ✓, ✓

---

As shown in Fig. 7b, all of the mixtures are inside the accepted region for the flow and compressive strength. However, only mixtures 32, 34 and 35 met all the criteria and are located inside the accepted area in Fig. 7a, b and c.

Fig. 7 The performance of the proposed mixtures after the fourth iteration (a, b and c).

Fifth iteration

In the fifth iteration, the non-dominant solutions were obtained after 2791 function evaluations with a hypervolume of 38 833, an average distance of 0.034 and a spread of 0.2223. Here, the algorithm proposed four new mixtures (Table 9). Mixtures 37 and 39 were able to meet all three criteria at the same time. Until this iteration, the use of HE cement type was able to increase the shear stress even above 20 kPa after 90 minutes, but the compressive strength at 28 days remained close to 80 MPa. Mixture 39 showed that it is possible to simultaneously acquire a shear stress of 19.6 kPa in 90 minutes, 88.5 MPa in 28 days and a flow of 91% in 5 minutes.

Table 9 Fifth iteration: set of mixtures proposed by the Pareto algorithm

Mix	Mixture description	Flow (%)	Shear stress (kPa)	Compressive strength (MPa)	Criteria met
36	GUbSF|Recycled|0.30|1.7|PCE-1|0.26|0.008|—	82	15.1	86.4	✓, ✗, ✓
37	HE|Recycled|0.30|1.7|PCE-2|0.28|0.008|0.40	69	18.8	85.4	✓, ✓, ✓
38	GUbSF|Coarse|0.31|2.1|PCE-1|0.28|—|0.02	37	9.8	85.7	✗, ✗, ✓
39	HE|Recycled|0.30|1.7|PCE-2|0.28|0.013|0.11	91	19.6	88.5	✓, ✓, ✓

---

As shown in Fig. 8b, all of the mixtures meet the requirements related to the compressive strength. However, only mixtures 37 and 39 met all the criteria and are located inside the accepted area in Fig. 7a, b and c.

Fig. 8 The performance of the proposed mixtures after the fifth iteration (a, b and c).

Analysis and discussion

Among the 18 initial mixtures, only mixture 4 met the three criteria related to the flowability, the compressive strength and buildability/shape stability. Seven more mixtures met the criteria after following the methodology with the optimization algorithms. The algorithm was able to determine which materials performed better and what was the optimum dosage for each one. Table 10 summarizes the results obtained after testing the 39 mixtures of this study. Interestingly, these final mixtures contained recycled fine aggregates. These results are favourable to circulate the fine from the ready-mix concrete truck washing facilities decantation basins.

Table 10 The properties of the 39 mixtures of the study

Mix	Mixture description	Flow in 5 min (%)	Shear stress in 90 min (kPa)	Compressive strength in 28 days (MPa)
1	GU|Coarse|0.32|1.8|PCE-1|—	95	12.0	81.3
2	GU|Coarse|0.345|2.0|SNP|B	65	20.6	66.7
3	GU|Fine|0.32|2.3|SNP|CSH-C	0	—	—
4	HE|Fine|0.345|2.0|PCE-2|CSH-C	80	19.6	83.0
5	HE|Fine|0.37|2.3|PCE-1|—	0	—	—
6	HE|Recycled|0.345|1.8|PCE-1|B	88	12.5	81.1
7	GUbSF|Coarse|0.37|2.0|PCE-2|—	152	6.6	92.3
8	GUbSF|Recycled|0.32|1.8|PCE-2|CSH-C	152	7.6	102.2
9	GUbSF|Recycled|0.37|2.3|SNP|B	73	14.9	70.6
10	GU|Fine|0.37|1.8|PCE-2|B	123	9.3	76.9
11	GU|Recycled|0.345|2.3|PCE-2|—	90	9.3	78.9
12	GU|Recycled|0.37|2.0|PCE-1|CSH-C	111	11.2	78.1
13	HE|Coarse|0.32|2.3|PCE-2|B	56	21.1	80.7
14	HE|Coarse|0.37|1.8|SNP|CSH-C	63	19.1	66.6
15	HE|Recycled|0.32|2.0|SNP|—	0	—	—
16	GUbSF|Coarse|0.345|2.3|PCE-1|CSH-C	70	15.0	90.7
17	GUbSF|Fine|0.32|2.0|PCE-1|B	21	—	—
18	GUbSF|Fine|0.345|1.8|SNP|—	63	16.8	69.8
19	GUbSF|Recycled|0.30|2.2|PCE-2|0.25|—|0.23	68	14.1	89.6
20	HE|Recycled|0.25|1.9|PCE-2|0.28|0.009|0.30	0	—	—
21	HE|Coarse|0.29|2.1|PCE-2|0.28|0.009|0.25	12	—	—
22	HE|Recycled|0.30|1.7|PCE-2|0.28|0.006|0.40	76	16.5	85.6
23	GUbSF|Coarse|0.31|2.1|PCE-2|0.28|—|0.02	58	15.2	92.0
24	HE|Coarse|0.35|2.1|PCE-2|0.28|—|0.38	70	15.1	77.3
25	GUbSF|Coarse|0.30|1.8|PCE-2|0.26|0.018|—	67	17.6	95.9
26	HE|Coarse|0.31|2.1|PCE-2|0.28|0.006|0.02	42	20.7	77.0
27	GU|Coarse|0.30|1.7|PCE-1|0.28|0.003|0.33	16	—	—
28	GU|Coarse|0.33|1.8|PCE-1|0.28|—|0.40	70	15.6	75.2
29	HE|Fine|0.30|1.7|PCE-1|0.22|—|0.15	0	—	—
30	GU|Fine|0.33|1.8|PCE-1|0.25|—|0.40	60	17.1	73.5
31	GUbSF|Fine|0.33|1.8|PCE-1|0.25|—|0.18	96	14.0	93.4
32	GUbSF|Recycled|0.30|1.7|PCE-1|0.28|0.013|0.40	80	16.8	94.2
33	GUbSF|Recycled|0.30|2.0|PCE-2|0.28|0.013|0.02	87	13.8	94.1
34	HE|Coarse|0.30|1.8|PCE-2|0.28|0.013|0.11	62	23.2	81.2
35	HE|Recycled|0.30|2.0|PCE-2|0.28|0.013|0.04	68	20.0	81.1
36	GUbSF|Recycled|0.30|1.7|PCE-1|0.26|0.008|—	82	15.1	86.4
37	HE|Recycled|0.30|1.7|PCE-2|0.28|0.008|0.40	69	18.8	85.4
38	GUbSF|Coarse|0.31|2.1|PCE-1|0.28|—|0.02	37	9.8	85.7
39	HE|Recycled|0.30|1.7|PCE-2|0.28|0.013|0.11	91	19.6	88.5

---

Among the three levels of cement type used in this study, high early strength cement (HE) was most preferred by the algorithm, along with the GUbSF cement type. The use of HE evidently increases the shear stress after 90 minutes. Regarding the compressive strength, the mixtures with GUbSF gave higher values, as expected.^39,59–62 However, the algorithm suggested mixtures that could improve the shear stress and the compressive strength by adjusting the remaining seven factors. The average shear stress of the initial set of mixtures was 14 kPa, which was increased in the proposed mixtures to 16.7 kPa. Regarding the compressive strength, the average value of the initial set of mixtures was 81 MPa and increased to 86 MPa. The best-performing mixes were mixtures 4, 22, 25, 32, 34, 35, 37, and 39 which are marked in bold font in Table 10. Even if the accepted mixtures are not identical, many similarities and patterns can be noticed. For instance, the presence of the type B admixture is evident in all the newly accepted mixtures. This can be explained since the addition of viscosity-modifying agent admixtures increases its workability.⁶⁰ The PCE-2 superplasticizer and the CSH-C admixture are also important to include, since they are present in seven out of eight accepted mixtures. Studies suggest that the presence of CSH-C increases the compressive strength.^60,63 The water-to-binder ratio and the sand-to-binder ratio were kept close to the minimum possible value. The majority of the studies in 3D concrete printing use a sand-to-binder ratio below 2.0. The GU cement type, fine sand and SNP type of the superplasticizer were the levels that performed worse than the other available options, leading the algorithm to avoid them in the proposed mixtures. For the latter, the preference for PCE superplasticizers can be explained by the literature, since the efficiency of the new generation of superplasticizers is better than that of the old generation.^64–66

Conclusion

The proposed methodology allowed for improving the properties of the mixtures following a trend towards a multiobjective optimization. In this study, the three investigated properties were the workability, buildability, and compressive strength. The use of optimization algorithms and artificial intelligence was important due to the high complexity of the mix design. Eight factors were investigated in total. Among the factors, the qualitative factors were three cement types, including high early strength cement, three types of sand with different particle size distributions, including recycled sand, and three types of superplasticizers. The quantitative factors were the water-to-binder ratio, the sand-to-binder ratio, the dosage of the superplasticizer, and the B and CSH-C admixtures. The three investigated properties, i.e., workability, buildability, and compressive strength, were contradictory to one another, with each factor having a positive and negative effect on each property. The Pareto algorithm narrowed down the factors and their levels after identifying the important factors. It also determined the preferred dosages to improve the conflicting objectives. On the other hand, the neural networks helped to visualize the effect of each material. The use of the genetic algorithm contributed to better training of the neural networks for each property. Among the 39 mixtures formed in this study, eight mixtures met the criteria being set. Overall, the approach is promising for improving the wet and final properties of mortar mixes used for 3D concrete printing applications by reducing the material and accelerating the mix design process. The final mixtures contained recycled fine aggregates, which is a positive contribution to a more circular economy. Given the encouraging results obtained, newly proposed optimization algorithms and more design criteria will be added in the next steps of the research.

Data availability

The code and the dataset supporting this article have been uploaded as part of the supplementary material. Data and processing scripts for this paper are also available on GitHub at https://github.com/vsergis/Automating-mix-design-for-3D-concrete-printing-applications.git.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

FRQNT New University Research Grant, the Canada Research Chair Program, and the Natural Sciences and Engineering Research Council of Canada (NSERC) supported this study. Mr Pierre Lacroix and Mr Bruce Labrie are thanked for their discussion on the experimental plan.

References

1. T. Ding, J. Xiao, S. Zou and Y. Wang, Hardened properties of layered 3D printed concrete with recycled sand, Cem. Concr. Compos., 2020, 113 DOI:10.1016/j.cemconcomp.2020.103724.
2. K. L. Geert De Schutter, V. Mechtcherine, V. Naidu Nerella, G. Habert, and I. Agusti-Juan, 2018.
3. D. Marchon, S. Kawashima, H. Bessaies-Bey, S. Mantellato and S. Ng, Hydration and rheology control of concrete for digital fabrication: Potential admixtures and cement chemistry, Cem. Concr. Res., 2018, 112, 96–110,  DOI:10.1016/j.cemconres.2018.05.014.
4. N. Roussel, Rheological requirements for printable concretes, Cem. Concr. Res., 2018, 112, 76–85,  DOI:10.1016/j.cemconres.2018.04.005.
5. G. Ma, L. Wang and Y. Ju, State-of-the-art of 3D printing technology of cementitious material—An emerging technique for construction, Sci. China: Technol. Sci., 2017, 61, 475–495,  DOI:10.1007/s11431-016-9077-7.
6. S. Zou, J. Xiao, T. Ding, Z. Duan and Q. Zhang, Printability and advantages of 3D printing mortar with 100% recycled sand, Constr. Build. Mater., 2021, 273, 121699,  DOI:10.1016/j.conbuildmat.2020.121699.
7. C. Ouellet-Plamondon and G. Habert, Life cycle assessment (LCA) of alkali-activated cements and concretes, in Handbook of Alkali-Activated Cements, Mortars and Concretes, 2015, pp. 663–686.
8. R. A. Buswell, W. R. Leal de Silva, S. Z. Jones and J. Dirrenberger, 3D printing using concrete extrusion: A roadmap for research, Cem. Concr. Res., 2018, 112, 37–49,  DOI:10.1016/j.cemconres.2018.05.006.
9. F. Bos, R. Wolfs, Z. Ahmed and T. Salet, Additive manufacturing of concrete in construction: potentials and challenges of 3D concrete printing, Virtual Phys. Prototyping, 2016, 11, 209–225,  DOI:10.1080/17452759.2016.1209867.
10. M. Charrier and C. M. Ouellet-Plamondon, Artificial neural network for the prediction of the fresh properties of cementitious materials, Cem. Concr. Res., 2022, 156, 106761,  DOI:10.1016/j.cemconres.2022.106761.
11. C. Zhang, V. N. Nerella, A. Krishna, S. Wang, Y. Zhang, V. Mechtcherine and N. Banthia, Mix design concepts for 3D printable concrete: A review, Cem. Concr. Compos., 2021, 122 DOI:10.1016/j.cemconcomp.2021.104155.
12. G. Ma, Z. Li and L. Wang, Printable properties of cementitious material containing copper tailings for extrusion based 3D printing, Constr. Build. Mater., 2018, 162, 613–627,  DOI:10.1016/j.conbuildmat.2017.12.051.
13. Y. Zhang, Y. Zhang, G. Liu, Y. Yang, M. Wu and B. Pang, Fresh properties of a novel 3D printing concrete ink, Constr. Build. Mater., 2018, 174, 263–271,  DOI:10.1016/j.conbuildmat.2018.04.115.
14. A. V. Rahul, M. Santhanam, H. Meena and Z. Ghani, 3D printable concrete: Mixture design and test methods, Cem. Concr. Compos., 2019, 97, 13–23,  DOI:10.1016/j.cemconcomp.2018.12.014.
15. I. Ivanova and V. Mechtcherine, Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete, Materials, 2020, 13(7) DOI:10.3390/ma13071551.
16. K. D. Kabagire, A. Yahia and M. Chekired, Toward the prediction of rheological properties of self-consolidating concrete as diphasic material, Constr. Build. Mater., 2019, 195, 600–612,  DOI:10.1016/j.conbuildmat.2018.11.053.
17. M. Cavazzuti, Optimization Methods: From Theory to Design, Scientific and Technological Aspects in Mechanics, 2013.
18. J. Lawson, Design and Analysis of Experiments with R, CRC Press Taylor & Francis Group, 2015.
19. K. T. Ateş, C. Şahin, Y. Kuvvetli, B. A. Küren and A. Uysal, Sustainable production in cement via artificial intelligence based decision support system: Case study, Case Stud. Constr. Mater., 2021, 15 DOI:10.1016/j.cscm.2021.e00628.
20. S. K. Das, P. Samui and A. K. Sabat, Application of Artificial Intelligence to Maximum Dry Density and Unconfined Compressive Strength of Cement Stabilized Soil, Geotech. Geol. Eng., 2010, 29(3), 329–342,  DOI:10.1007/s10706-010-9379-4.
21. C. W. Lim, K. Tan and X. Zhu, The Framework of Combining Artificial Intelligence and Construction 3D Printing in Civil Engineering, MATEC Web of Conferences, 2018, vol. 206,  DOI:10.1051/matecconf/201820601008.
22. S. Paul, B. Panda, H.-H. Zhu and A. Garg, An Artificial Intelligence Model for Computing Optimum Fly Ash Content for Structural-Grade Concrete, J. ASTM Int., 2019, 8, 1–15,  DOI:10.1520/ACEM20180079.
23. Y. Pan and L. Zhang, Roles of artificial intelligence in construction engineering and management: A critical review and future trends, Autom. Constr., 2021, 122 DOI:10.1016/j.autcon.2020.103517.
24. R. F. Matthew and D. Zeiler, Visualizing and Understanding Convolutional Networks, 2013.
25. D. V. Dao, H. B. Ly, S. H. Trinh, T. T. Le and B. T. Pham, Artificial Intelligence Approaches for Prediction of Compressive Strength of Geopolymer Concrete, Materials, 2019, 12(6) DOI:10.3390/ma12060983.
26. M. A. DeRousseau, J. R. Kasprzyk and W. V. Srubar, Computational design optimization of concrete mixtures: A review, Cem. Concr. Res., 2018, 109, 42–53,  DOI:10.1016/j.cemconres.2018.04.007.
27. H. Van Damme, Concrete material science: Past, present, and future innovations, Cem. Concr. Res., 2018, 112, 5–24,  DOI:10.1016/j.cemconres.2018.05.002.
28. D. Dao, S. Trinh, H.-B. Ly and B. Pham, Prediction of Compressive Strength of Geopolymer Concrete Using Entirely Steel Slag Aggregates: Novel Hybrid Artificial Intelligence Approaches, Appl. Sci., 2019, 9(6) DOI:10.3390/app9061113.
29. H. B. Ly, B. T. Pham, D. V. Dao, V. M. Le, L. M. Le and T. T. Le, Improvement of ANFIS Model for Prediction of Compressive Strength of Manufactured Sand Concrete, Appl. Sci., 2019, 9(18) DOI:10.3390/app9183841.
30. S. Sadati, L. E. Brito da Silva, D. C. Wunsch and K. H. Khayat, Artificial Intelligence to Investigate Modulus of Elasticity of Recycled Aggregate Concrete, ACI Mater. J., 2019, 116(1) DOI:10.14359/51706948.
31. B. A. Young, A. Hall, L. Pilon, P. Gupta and G. Sant, Can the compressive strength of concrete be estimated from knowledge of the mixture proportions?: New insights from statistical analysis and machine learning methods, Cem. Concr. Res., 2019, 115, 379–388,  DOI:10.1016/j.cemconres.2018.09.006.
32. H. Shayanfar and F. S. Gharehchopogh, Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems, Appl. Soft Comput., 2018, 71, 728–746,  DOI:10.1016/j.asoc.2018.07.033.
33. B. Das, V. Mukherjee and D. Das, Student psychology based optimization algorithm: A new population based optimization algorithm for solving optimization problems, Adv. Eng. Software, 2020, 146 DOI:10.1016/j.advengsoft.2020.102804.
34. S. H. Samareh Moosavi and V. K. Bardsiri, Poor and rich optimization algorithm: A new human-based and multi populations algorithm, Eng. Appl. Artif. Intell., 2019, 86, 165–181,  DOI:10.1016/j.engappai.2019.08.025.
35. M. Alimoradi, H. Azgomi and A. Asghari, Trees Social Relations Optimization Algorithm: A new Swarm-Based metaheuristic technique to solve continuous and discrete optimization problems, Math. Comput. Simulat., 2022, 194, 629–664,  DOI:10.1016/j.matcom.2021.12.010.
36. Y. Cao, Q. Wang, Z. Wang, K. Jermsittiparsert and M. Shafiee, A new optimized configuration for capacity and operation improvement of CCHP system based on developed owl search algorithm, Energy Rep., 2020, 6, 315–324,  DOI:10.1016/j.egyr.2020.01.010.
37. W. Zhao, Z. Zhang and L. Wang, Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications, Eng. Appl. Artif. Intell., 2020, 87 DOI:10.1016/j.engappai.2019.103300.
38. D. P. Bentz, Blending different fineness cements to engineer the properties of cement-based materials, Mag. Concr. Res., 2010, 62(5), 327–338,  DOI:10.1680/macr.2008.62.5.327.
39. K. Ghafor, W. Mahmood, W. Qadir and A. Mohammed, Effect of Particle Size Distribution of Sand on Mechanical Properties of Cement Mortar Modified with Microsilica, ACI Mater. J., 2020, 117 DOI:10.14359/51719070.
40. S. P. Boindala and V. Arunachalam, Concrete Mix Design Optimization Using a Multi-objective Cuckoo Search Algorithm, in Soft Computing: Theories and Applications, (Advances in Intelligent Systems and Computing, 2020, ch. 11, pp. 119–126.
41. E. Mohammadi Golafshani, M. Arashpour and A. Kashani, Green mix design of rubbercrete using machine learning-based ensemble model and constrained multi-objective optimization, J. Cleaner Prod., 2021, 327 DOI:10.1016/j.jclepro.2021.129518.
42. H. Sebaaly, S. Varma and J. W. Maina, Optimizing asphalt mix design process using artificial neural network and genetic algorithm, Constr. Build. Mater., 2018, 168, 660–670,  DOI:10.1016/j.conbuildmat.2018.02.118.
43. A. Mohammed and N. T. K. Al-Saadi, Ultra-High Early Strength Cementitious Grout Suitable for Additive Manufacturing Applications Fabricated by Using Graphene Oxide and Viscosity Modifying Agents, Polymers, 2020, 12(12) DOI:10.3390/polym12122900.
44. T. T. Le, S. A. Austin, S. Lim, R. A. Buswell, R. Law, A. G. F. Gibb and T. Thorpe, Hardened properties of high-performance printing concrete, Cem. Concr. Res., 2012, 42(3), 558–566,  DOI:10.1016/j.cemconres.2011.12.003.
45. R. J. M. Wolfs, F. P. Bos and T. A. M. Salet, Triaxial compression testing on early age concrete for numerical analysis of 3D concrete printing, Cem. Concr. Compos., 2019, 104 DOI:10.1016/j.cemconcomp.2019.103344.
46. R. J. M. Wolfs, F. P. Bos and T. A. M. Salet, Early age mechanical behaviour of 3D printed concrete: Numerical modelling and experimental testing, Cem. Concr. Res., 2018, 106, 103–116,  DOI:10.1016/j.cemconres.2018.02.001.
47. R. Jayathilakage, J. Sanjayan and P. Rajeev, Direct shear test for the assessment of rheological parameters of concrete for 3D printing applications, Mater. Struct., 2019, 52 DOI:10.1617/s11527-019-1322-4.
48. J. J. Assaad, J. Harb and Y. Maalouf, Measurement of yield stress of cement pastes using the direct shear test, J. Non-Newtonian Fluid Mech., 2014, 214, 18–27,  DOI:10.1016/j.jnnfm.2014.10.009.
49. Y. W. D. Tay, Y. Qian and M. J. Tan, Printability region for 3D concrete printing using slump and slump flow test, Composites, Part B, 2019, 174 DOI:10.1016/j.compositesb.2019.106968.
50. P. Shakor, J. Renneberg, S. Nejadi and G. Paul, Presented in part at the Proceedings of the 34th International Symposium on Automation and Robotics in Construction, (ISARC), 2017.
51. V. Sergis and C. M. Ouellet-Plamondon, D-optimal design of experiments applied to 3D high-performance concrete printing mix design, Mater. Des., 2022, 218 DOI:10.1016/j.matdes.2022.110681.
52. V. Sergis and C. M. Ouellet-Plamondon, Fractional factorial design to study admixtures used for 3D concrete printing applications, Mater. Lett., 2022, 324, 132697,  DOI:10.1016/j.matlet.2022.132697.
53. Standard Specification for Chemical Admixtures for Concrete, C494/C494M − 17, p. 2018.
54. S. Mirjalili, Evolutionary Algorithms and Neural Networks – Theory and Applications, 2019.
55. G. R. Markus Oberweger, P. Wohlhart, V. Lepetit, Efficiently Creating 3D Training Data for Fine Hand Pose Estimation, 2016.
56. Multiobjective Optimization: Interactive and Evolutionary Approaches, ed. K. D. Jürgen Branke, K. Miettinen and R. Słowinski, 2008.
57. S. Vasileios, M. Charrier and C. M. Ouellet-Plamondon, Prediction of the Yield Stress of Printing Mortar Ink, in Second RILEM International Conference on Concrete and Digital Fabrication, ed. Cham, F. P. Bos, S. S. Lucas, R. J. M. Wolfs and T. A. M. Salet, Springer International Publishing, 2020, pp. 360–369.
58. Y. Chen, S. He, Y. Gan, O. Çopuroğlu, F. Veer and E. Schlangen, A review of printing strategies, sustainable cementitious materials and characterization methods in the context of extrusion-based 3D concrete printing, J. Build. Eng., 2022, 45, 103599,  DOI:10.1016/j.jobe.2021.103599.
59. A. ElNemr, Generating water/binder ratio -to- strength curves for cement mortar used in Masnory walls, Constr. Build. Mater., 2020, 233 DOI:10.1016/j.conbuildmat.2019.117249.
60. M. Benaicha, X. Roguiez, O. Jalbaud, Y. Burtschell and A. H. Alaoui, Influence of silica fume and viscosity modifying agent on the mechanical and rheological behavior of self compacting concrete, Constr. Build. Mater., 2015, 84, 103–110,  DOI:10.1016/j.conbuildmat.2015.03.061.
61. O. Burgos-Montes, M. Palacios, P. Rivilla and F. Puertas, Compatibility between superplasticizer admixtures and cements with mineral additions, Constr. Build. Mater., 2012, 31, 300–309,  DOI:10.1016/j.conbuildmat.2011.12.092.
62. G. A. Rao, Role of water-binder ratio on the strength development in mortars incorporated with silica fume, Cem. Concr. Res., 2001, 31(3), 443–447,  DOI:10.1016/S0008-8846(00)00500-7.
63. V. Kanchanason and J. Plank, Effect of calcium silicate hydrate – polycarboxylate ether (C-S-H–PCE) nanocomposite as accelerating admixture on early strength enhancement of slag and calcined clay blended cements, Cem. Concr. Res., 2019, 119, 44–50,  DOI:10.1016/j.cemconres.2019.01.007.
64. O. Boukendakdji, E.-H. Kadri and S. Kenai, Effects of granulated blast furnace slag and superplasticizer type on the fresh properties and compressive strength of self-compacting concrete, Cem. Concr. Compos., 2012, 34(4), 583–590,  DOI:10.1016/j.cemconcomp.2011.08.013.
65. J. Kruger, S. Zeranka and G. van Zijl, An ab initio approach for thixotropy characterisation of (nanoparticle-infused) 3D printable concrete, Constr. Build. Mater., 2019, 224, 372–386,  DOI:10.1016/j.conbuildmat.2019.07.078.
66. C. A. Anagnostopoulos, T. Chrysanidis and M. Anagnostopoulou, Experimental data of cement grouting in coarse soils with different superplasticisers, Data Brief, 2020, 30, 105612,  DOI:10.1016/j.dib.2020.105612.

---

Footnotes

† PhD Candidate.

‡ Professor, Canada Chairholder on Sustainable Multifunctional Construction Materials.

---