Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Learning the laws of lithium-ion transport in electrolytes using symbolic regression†
Eibar
Flores
 *a,
Christian
Wölke
*a,
Christian
Wölke
 b,
Peng
Yan
c,
Martin
Winter
bc,
Tejs
Vegge
b,
Peng
Yan
c,
Martin
Winter
bc,
Tejs
Vegge
 a,
Isidora
Cekic-Laskovic
a,
Isidora
Cekic-Laskovic
 b and
Arghya
Bhowmik
b and
Arghya
Bhowmik
 *a
*a
aDepartment of Energy Conversion and Storage, Technical University of Denmark, 2800 Kgs. Lyngby, Denmark. E-mail: eibfl@dtu.dk; arbh@dtu.dk
bHelmholtz-Institute Münster (IEK-12), Forschungszentrum Jülich GmbH, Corrensstraße 46, 48149 Münster, Germany
cMEET Battery Research Center, University of Münster, Corrensstrasse 46, 48149 Münster, Germany
First published on 7th June 2022
Abstract
High-throughput experiments (HTE) enable fast exploration of advanced battery electrolytes over vast compositional spaces. Among the multiple properties considered for optimal electrolyte performance, the conductivity is critical. An analytical expression for ionic transport in electrolytes, accurate for practical compositions and operating conditions, would accelerate the process of (i) co-optimizing conductivity alongside other desirable electrolyte properties, and (ii) learning fundamental physical laws from data, which is one of the paramount goals of scientific big-data analytics. Here, we used symbolic regression with an HTE-acquired dataset of electrolyte conductivity and discovered a simple, accurate, consistent and generalizable expression. Notably, despite emerging from a purely statistical approach, the expression reflects functional aspects from established thermodynamic limiting laws, indicating our model is grounded on the fundamental physical mechanisms underpinning ionic transport. We demonstrate the potential of using machine learning with HTE to find accurate and physically-sound models in complex systems without established physico-chemical theories.
Introduction
Non-aqueous aprotic formulations are state-of-the-art electrolytes for Li-ion batteries (LIBs) as they comply with the strict operation requirements for safety, life, reliability and performance. These electrolytes consist of a Li salt dissolved in a mixture of organic solvents, and complemented with performance-enhancing functional additives. Electrolyte formulations balance multiple and often competing properties, among which the ionic conductivity is arguably the most important.1–4 The choice of solvents, conducting salts and their proportion usually aims at achieving electrolytes with an optimum mix of low viscosity and high ion dissociation.1,5–7 However, the conductivity is not the only electrolyte property to tailor: the electrochemical stability window, chemical compatibility with both electrodes, thermal and chemical stability, liquid range, toxicity and costs, are all important factors to consider.7–11 In this multi-objective optimization scenario, researchers in the field would greatly benefit from a predictive, thermodynamic model for electrolyte conductivity, enabling quick exploration of how a promising formulation would affect the electrolytes ionic conductivity without additional experiments. Such a model would ideally be denoted as a simple and universal closed-form expression; i.e., an equation with few algebraic terms, relating easily measurable variables with fundamental physical constants, and without fitting parameters.Despite significant progress in the thermodynamic description of ionic transport,12 such a “utopic” model only exists for highly dilute electrolytes. At infinite dilution, the conductivity is simply directly proportional to the ion concentration in solution c.13,14 However, this model fails at the dilute domain (0 < c < 10−3 mol L−1) since the conductivity depends additionally on a squared root term of the conducting salt concentration.15 Kohlrausch formulated these findings into an empirical law with an adjustable parameter,15,16 later addressed by Onsager by considering that ions are dragged not only by hydrodynamic effects, but also by electrophoretic and relaxation phenomena as in the Debye–Hückel theory. The Debye–Hückel–Onsager (DHO) theory effectively upgrades Kohlrausch's law into a fully theoretical law, without adjustable parameters:17
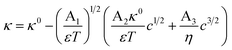 | (1) |
In this work we propose an alternative approach – Symbolic Regression (SR) – to find an explainable and accurate model describing the transport of ions in non-aqueous electrolytes. While machine learning is being increasingly applied to battery research,26–28 SR had remained largely unexplored despite promising results in other areas of materials science.29 In essence, SR simultaneously learns both adjustable parameters and the functional form relating electrolyte conductivity with its formulation. We make use of a HTE setup30 to collect thousands of conductivity measurements of LiPF6-based electrolytes with ethylene carbonate (EC), propylene carbonate (PC) and ethyl methyl carbonate (EMC) as solvents at different temperatures. With a simple SR approach, we train multiple candidate expressions and show that a particular expression emerges as a clear candidate, complying with strict and often competing criteria of accuracy, simplicity and consistency.
Experimental methods
Electrolyte formulation
Lithium hexafluorophosphate (LiPF6), ethylene carbonate (EC), ethyl methyl carbonate (EMC) and propylene carbonate (PC) were used as received from E-Lyte Innovations (battery grade purity) without further purification. As electrolyte solvents, EC, PC and EMC were used, keeping the ratio of cyclic to linear organic carbonates constant at (EC + PC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC 3
EMC 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 by weight. The PC (PC−1 + EC) fraction was varied between 9 and 100 mol%. The concentration of the conducting salt LiPF6 was varied between 0.19 and 2.11 mol kg−1. The composition of the formulations was varied systematically using a fully automated robotic high-throughput screening (HTS) system, operating in a N2-filled glovebox (MBraun, H2O and O2 < 1 ppm).
7 by weight. The PC (PC−1 + EC) fraction was varied between 9 and 100 mol%. The concentration of the conducting salt LiPF6 was varied between 0.19 and 2.11 mol kg−1. The composition of the formulations was varied systematically using a fully automated robotic high-throughput screening (HTS) system, operating in a N2-filled glovebox (MBraun, H2O and O2 < 1 ppm).
Conductivity determination
Conductivity cells (ESI Fig. 1†) were filled with the prepared electrolyte formulations and sealed in the glovebox under N2 atmosphere (MBraun, H2O and O2 < 1 ppm). Cell constants were determined using a 0.01 M solution of KCl at 20 °C (VWR, known conductivity of 1.276 mS cm−1) and averaged over five measurements. Disposable Eppendorf Safe-Lock Tubes (V = 2 mL) were used as sample containers and filled with 750 μL of electrolyte each. Impedance measurements were conducted on a Metrohm Autolab/M204 potentiostat/galvanostat with 12 channels and 8-channel multiplexer for a total of 96 channels in the range of 50 Hz to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz using in-house developed electrodes.31 The conductivity cells were placed in a temperature chamber (Memmert TTC256, 0.1 °C temperature setting accuracy) and each temperature was held for 2 h prior to measurement for equilibration. Ionic conductivities were determined in 10 °C steps in the temperature range from −30 °C to 60 °C. The impedance spectra were fitted using a model specified with set parameters for resistors Rs and Rp, as well as for the constant phase element (CPE) with the Metrohm Nova software. The fit was carried out after each additional measuring point. Electrolyte conductivities were obtained from the quotient of cell constant and determined electrolyte resistance.
000 Hz using in-house developed electrodes.31 The conductivity cells were placed in a temperature chamber (Memmert TTC256, 0.1 °C temperature setting accuracy) and each temperature was held for 2 h prior to measurement for equilibration. Ionic conductivities were determined in 10 °C steps in the temperature range from −30 °C to 60 °C. The impedance spectra were fitted using a model specified with set parameters for resistors Rs and Rp, as well as for the constant phase element (CPE) with the Metrohm Nova software. The fit was carried out after each additional measuring point. Electrolyte conductivities were obtained from the quotient of cell constant and determined electrolyte resistance.
Data pre-processing
The initial dataset was parsed into an array of 3626 measurements with 3 predictors – the electrolyte's temperature [K], salt concentration [mol kg−1] and PC ratio – and the corresponding ionic conductivity [mS cm−1]. Repeated measurements – at the same PC ratio, temperature and conducting salt concentration – were aggregated into mean conductivities and used as target values. The corresponding standard deviations were used as a proxy for measurement uncertainty. Neither imputation nor outlier processing was performed. The 859 data points resulting after aggregation were split into 60% for training (515), 20% for validation (172) and 20% for testing (172). Data correlations and distributions are presented in ESI Fig. 2 and 3,† respectively.Feature generation
For the feature generation step we use the algorithm implemented in the Autofeat library.32 Autofeat constructs an initial pool of thousands of candidate features in multiple feature engineering steps, where the initial predictors are combined and transformed using non-linear operators. The pool is then iteratively reduced during successive selection runs by (i) discarding features not complying with valid physical dimensions, (ii) selecting features that best correlate to the target and (iii) sparsifying coefficients via a Lasso LARS regression. The training data was scaled to unit variance without subtracting the mean, to avoid negative predictor values that cannot be discovered by some operations (e.g. log(x)). Additionally, we specified Kelvin units for temperature and mol kg−1 units for conducting salt concentration, in order to leverage Autofeat's Buckingham's Pi Theorem implementation to filter out terms with non-physical dimensions. From all the operators available in the AutoFeat Library, we did not consider abs(x) since we expect the conductivity to be differentiable; likewise we do not consider neither sin(x) nor cos(x) since we do not expect the conductivity to be periodic with respect to any of the predictors. ESI Table 1† summarizes the hyperparameters used for the feature generation step with Autofeat.Feature selection
Despite Autofeat carrying a rigorous feature selection, it often yielded large candidate expressions; hence we further performed a feature selection step using the Lasso estimator as implemented in the Python package Scikit Learn.33 The Lasso estimator finds a L1 norm solution to the linear model, which not only minimizes the prediction error but also promotes model sparsity. In this step each candidate expression is regressed using Cross-Validated Lasso (ESI Table 3†), choosing the regularization parameter α by the one-standard-deviation rule.34 The chosen α was used to retrain the expression using a simple Lasso estimator and so obtain a sparse solution. Candidate features were discarded when their coefficients βi were statistically insignificant, i.e. when their t-statistic were below 2. The Lasso regression with the chosen α, the thresholding and discarding were all iteratively repeated until arriving to an expression with no discarded terms, which was used as a discovered expression. An additional, physics-based constraint is implemented during the feature selection step: all models are trained constraining the intercept to 0. In this way, the discovered expressions comply with the expected physical behaviour of zero conductivity when all predictors are equal to zero.Results and discussion
Model architecture and training strategy
In our SR approach, we apply non-linear operations to the original predictors to produce more informative candidate features. Formally: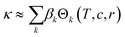 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC molar ratio r. The conductivity is assumed to depend not on all possible candidate features, but on a much-reduced set of these; i.e., the solution of eqn (2) is sparse. Fig. 1 illustrates the methodology, split into feature generation and selection steps. Briefly, the training process involves defining a set of operators (e.g. inverse, logarithms, exponentials), then applying these to the initial predictors to generate a library of candidate features, a few of which are then selected to form a candidate expression.
EC molar ratio r. The conductivity is assumed to depend not on all possible candidate features, but on a much-reduced set of these; i.e., the solution of eqn (2) is sparse. Fig. 1 illustrates the methodology, split into feature generation and selection steps. Briefly, the training process involves defining a set of operators (e.g. inverse, logarithms, exponentials), then applying these to the initial predictors to generate a library of candidate features, a few of which are then selected to form a candidate expression.
The discovered expressions are not unique: candidate features might combine in multiple ways to result in similarly accurate expressions. Consequently, instead of using all training samples, we train on subsamples of 50, 100, 250 and 400 data points, each randomly initialized 5 times to give a total of 20 independent training sessions, in order to evaluate whether a discovered expression is consistent. We use the validation set to evaluate the performance of the discovered expressions and compare them to four benchmark models (ESI, Table 2†) using the three initial predictors, 3rd-order polynomial expansions as in phenomenological models,35 exponential operations as in Arrhenius-based models, and exponential operations on 3rd-order polynomial expansion as in the extended Castel–Amis model.6
Evaluation of models
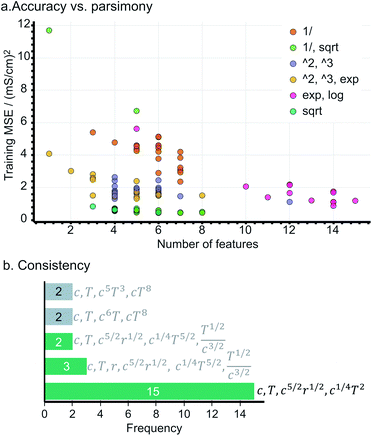
During the evaluation, we search for an expression being not only (i) accurate, i.e., yielding a low mean squared error (MSE), but also (ii) parsimonious, quantified as the number of terms in an expression, and (iii) consistent, represented by the number of times the expression repeats across training sessions. Fig. 2a presents the accuracy vs. complexity trade-off from the expressions found. Each data point represents an expression, whose colour references its parent operator set. As expected, larger expressions fit the data better, however, at the expense of increased model complexity; this is the case of the expressions originating from exponential and logarithmic operations (MSE < 2 but 10+ terms). Interestingly, the expressions populating the Pareto-frontier of the figure originate from sets including square-root operations; i.e., they offer the best compromise between MSE and the number of terms.Note that most expressions only appear once, highlighting these to be highly sensitive to the training subsample and that there is no unique solution. Fig. 2b shows the most frequent expressions across the training sessions, where expressions with square-root operations are highlighted in green. Unlike most expressions, the model:
| κ = β1c + β2T + β3c5/2r1/2 + β4c1/4T2 | (3) |
| Attribute | Value |
|---|---|
| β 1 | −5.11 |
| β 2 | −0.040 |
| β 3 | −0.35 |
| β 4 | 2.73 × 10−4 |
| Training MSE | 1.08 |
| Training R2 | 0.92 |
| Validation MSE | 1.22 |
| Validation R2 | 0.90 |
Model constraints
Enforcing model constraints is an effective way to improve model consistency. To illustrate why, we repeat the 20 training sessions with the same operator sets, this time allowing the intercept to vary freely. The corresponding training errors and stability histograms are shown in ESI Fig. 4 and 5.† Expectedly, removing the intercept constraint results in slightly improved accuracy but significantly deteriorates model consistency, since no viable model repeats more than twice. Our choice of enforcing y0 = 0 has effectively filtered out expressions that became inaccurate under the constraint. We obtained as a result not only a smaller pool of more consistent candidate expressions, but also the guarantee they all comply with the imposed boundary condition y0 = 0. However, constrained models become less expressive, i.e. less capable of capturing the variability of the data. Fig. S6† shows the learning curves of the discovered expression, retrained on subsamples of different sizes with and without the intercept constraint. The unconstrained expression converges to the optimal accuracy already with 100 samples; in contrast, the constrained model fails at almost all samples sizes and only approaches the optimal accuracy when using all 515 training samples. The enforcement of constraints needs to be balanced with the limitations in model expressiveness, especially when modelling the often-small datasets available from experiments.Selected model: accuracy and overfitting
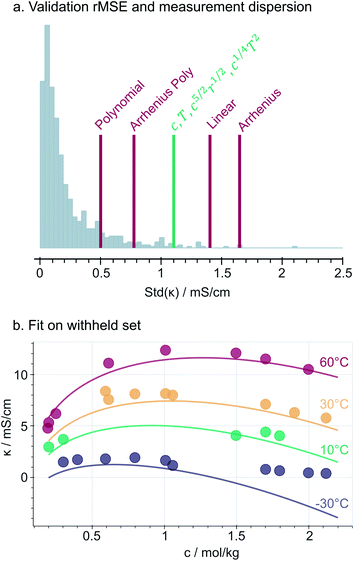
Fig. 3a compares the accuracy of the selected constrained expression on the validation set, relative to the measurement dispersion and along with benchmark models. We use the root mean squared error (rMSE) to describe the prediction accuracy in the same units [mS cm−1] as the conductivity measurements. As expected, the simpler benchmarks such as Linear and Simple Arrhenius models are less accurate. Instead, the more complex models (Polynomial and Arrhenius Polynomial) are prone to overfitting, as their prediction errors are smaller than a non-negligible fraction of measurement dispersion values. Notably, the selected model stands in the middle with a validation-set rMSE of 1.1 mS cm−1, indicating that it is accurate up to the measurement noise and so it does not overfit the dataset. At first glance, eqn (3) seems to yield only a minor improvement (0.3 mS cm−1) compared to the basic linear model; however, (i) the square-root dependence in eqn (3) reproduces the curvature and maxima in the data and (ii) by having no intercept, it complies with the physical constraint of no conductivity at c, T, r = 0.Fig. 3b illustrates that the selected model generally fits well the data not used in the training (i.e., validation and testing sets). However, the fit generally underestimates the measurements. The same expression trained with an intercept (Fig. S7†) fits the withheld data without such bias, indicating that the underestimation in Fig. 3b is a result of imposing the physically-motivated y0 = 0 constraint. However, we highlight that in most of the experimental range, the fit from eqn (3) reproduces the concentration- and temperature-dependent conductivity maxima observed in the data and in previous studies, which is a key attribute for implementing our discovered model as part of multi-target optimization and/or active learning frameworks.25
Selected model: deviations at low temperature and high salt concentration
Fig. 3b also shows that the model is not expressive enough to describe the conductivities measured at −30 °C and concentrations above 1 mol kg−1. Further comparisons between the predicted and measured conductivities (ESI Fig. 8†) show that the model predicts significantly lower conductivities compared to the measurements (down to 2.5 mS cm−1) in concentrated and low temperature regions. Within this regime, the conductivity seems to decay exponentially with concentration (Fig. 3b) instead of following the square-root trends that our expression learned from the rest of the predictors' space. Expectedly, as temperatures drop and salt concentration increases, the electrolyte structure changes significantly36 and its viscosity grows exponentially,37 which overall influence the functional dependency of conductivity. Notably, the effect is especially pronounced in PC-pure solutions (ESI Fig. 8,† top), indicating that our discovered expression missed certain properties of the solvent mixture38 that influence the ionic transport within such viscous regimes. While in this work we assume that a single expression can describe the complete dataset, the observations of several regimes of conduction raises the potential need for either one expression per regime, or for an overarching, more sophisticated symbolic expression that collapses to the right functional behaviour in each regime. Increased accuracy within the viscous regime could be critical for specific applications such as low-temperature electrolyte engineering.39Selected model: interpretations
Assigning a physical meaning to the discovered expression is not straightforward. For one, any comparison to the thermodynamically-derived DHO law would require to explicitly account for the solution's viscosity and dielectric constant, measurements that are not available in the dataset. Second, there are no constraints to avoid unphysical values, like the negative conductivities at sub-zero temperatures and high conducting salt concentrations (Fig. 3b). Third, the solution to our symbolic regression approach is generally not unique, i.e., there are multiple expressions similarly accurate to fit the dataset. Despite these limitations, we observe that expressions sharing square-root operations achieve the best compromise between simplicity and accuracy. Therefore, we believe that our method is learning square-root trends inherent to the data manifold, which indicates that some functional aspects of the DHO law – i.e. its square-root trends on temperature and concentration (see eqn (1)) – are still valid to describe electrolyte conductivity in concentrated formulations.Physical insights can be drawn not only from the expression itself but also from its predictions. Fig. 4 illustrates the conductivity trends from our selected model within the space of electrolyte formulations used for the training. As expected, at higher temperatures, the conductivity increases and the conductivity maxima shift towards higher salt concentrations (0.74 mol kg−1 at −30 °C to 1.70 mol kg−1 at 60 °C). However, the role of the cyclic carbonate is subtler. Note first that all conductivities peak when the electrolyte formulation is EC-pure (PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC ratio = 0). Second, the tails along the salt concentration axis elongate at higher concentrations as the formulations become increasingly EC-pure. From a fundamental standpoint, conductivity depends on a compromise between the ionic mobility, mainly influenced by viscosity, and the number of charge carriers available for migration, mainly controlled by the electrolyte's dielectric constant (c.f. see Bjerrums criterion1 for ionic association).5,6 As EC has a higher dielectric constant compared to PC,40 EC-pure solutions are more effective at preventing ion association and so enhance electrolyte conductivity. This effect should be especially pronounced at high conducting salt concentrations, where ionic association becomes a critical limiting factor for ion transport in the electrolyte.5,41 Such EC-driven improvement of conductivity, which has been observed experimentally,42 is indeed predicted by our selected model as the extended tails along the salt concentration axis in Fig. 4, even if the effect is not evident neither in the correlation maps in ESI Fig. 2† nor the pair-plots ESI Fig. 3.† While eqn (3) performs poorly within the viscous regime, it still manages to capture the subtle effects related to ionic association via the r1/2 term. The predictions in Fig. 4 generally align with our current understanding of the interplay between the solvent's dielectric properties and ionic transport.
EC ratio = 0). Second, the tails along the salt concentration axis elongate at higher concentrations as the formulations become increasingly EC-pure. From a fundamental standpoint, conductivity depends on a compromise between the ionic mobility, mainly influenced by viscosity, and the number of charge carriers available for migration, mainly controlled by the electrolyte's dielectric constant (c.f. see Bjerrums criterion1 for ionic association).5,6 As EC has a higher dielectric constant compared to PC,40 EC-pure solutions are more effective at preventing ion association and so enhance electrolyte conductivity. This effect should be especially pronounced at high conducting salt concentrations, where ionic association becomes a critical limiting factor for ion transport in the electrolyte.5,41 Such EC-driven improvement of conductivity, which has been observed experimentally,42 is indeed predicted by our selected model as the extended tails along the salt concentration axis in Fig. 4, even if the effect is not evident neither in the correlation maps in ESI Fig. 2† nor the pair-plots ESI Fig. 3.† While eqn (3) performs poorly within the viscous regime, it still manages to capture the subtle effects related to ionic association via the r1/2 term. The predictions in Fig. 4 generally align with our current understanding of the interplay between the solvent's dielectric properties and ionic transport.
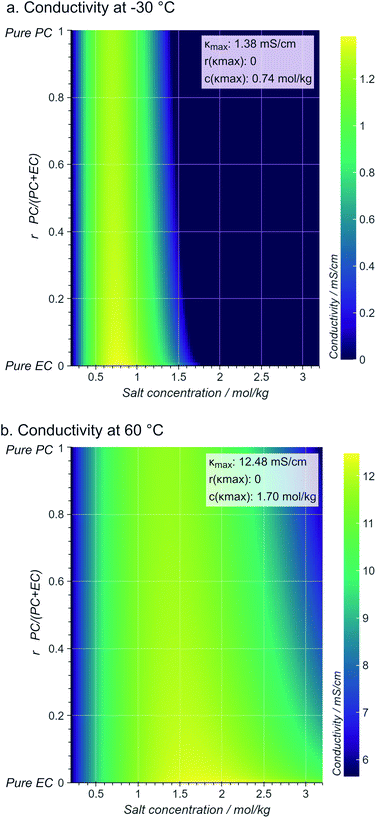 | ||
Fig. 4 Contour maps of electrolyte conductivity versus PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC molar ratio and conducting salt concentration, as predicted by our selected and trained model (eqn.(3)) at (a) low and (b) high operating temperatures. The insets show the maximum conductivity and where is reached. EC molar ratio and conducting salt concentration, as predicted by our selected and trained model (eqn.(3)) at (a) low and (b) high operating temperatures. The insets show the maximum conductivity and where is reached. | ||
At this point, we emphasize we have only implemented two domain-knowledge decisions – (i) exclude non-differentiable and periodic operators and (ii) constrain the intercept to zero – on an otherwise purely statistical approach. Yet, we observe the emergence of an expression clearly outstanding from competing models, for being accurate without overfitting, parsimonious, consistent, with a square-root functional structure resembling the DHO law, and generally agreeing with our understanding of ionic transport. In other words, our expression is not only an appropriate model from a machine-learning standpoint but also seems grounded on the physical-chemical mechanisms underpinning ion transport in electrolytes. Our work opens multiple avenues to pursue further the data-driven discovery of accurate models capable of bridging the existing gap20 in the understanding of concentrated electrolyte formulations. To start with, atomistic descriptors can be incorporated in order to generalize to solvent mixtures other than PC/EC/EMC and conducting salt chemistries beyond conventional Li-ion technology.22 In addition, using other promising SR algorithms43 and implementing domain-knowledge constraints in the feature selection step44 could alleviate the issue with expression consistency and yield physically-sound expressions; i.e. even more rigorous to known boundary conditions (e.g. κ(c = 0) = 0) and to asymptotic behavior on key limits (e.g.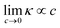 ). These constraints will have to be carefully balanced, given our observations of the inflexible nature of constrained models.
). These constraints will have to be carefully balanced, given our observations of the inflexible nature of constrained models.
Conclusions
In this work we apply symbolic regression as a data-driven method to learn the effects of temperature, conducting salt concentration and solvent composition on the conductivity of a concentrated electrolyte. We use a dataset of 859 experimental measurements on a LiPF6 in EC, PC and EMC electrolyte at temperatures, conducting salt concentrations and EC-to-PC ratios within the practical ranges of operation of Li-based battery electrolytes. Our approach generates thousands of derived features from the initial predictors using a set of non-linear operators. Few of the derived features are then selected using cross-validated Lasso regression to discover candidate expressions, which are then compared in terms of accuracy, parsimony, and consistency. We find that expressions within the accuracy vs. parsimony Pareto-frontier share a square-root functional form, which we believe reflects an underlying data manifold resembling the Debye–Hückel–Onsager equation. Out of these expressions, we singled out a 4-term expression for being not only parsimonious and accurate but also consistent. The discovered expression does not overfit the data, fits the withheld set well, and reproduces the conductivity behaviour expected from similar theoretical and experimental studies. The discovered expression is a promising model to be used in multi-target electrolyte optimization. More broadly, the presented methodology can be used to find analytical models of physicochemical systems where no fundamental, closed-form solution exists. Implementing phenomenological constraints in the feature selection step, while appropriately balancing model expressiveness, would significantly support the search for physically-sound expressions using symbolic regression.Data availability
The data and code to train symbolic regression models, along with examples, are openly available in the Github repository: https://github.com/BIG-MAP/SR-electrolytes. The predictions from the trained model can be further explored in the following web site: https://big-map.github.io/SR-electrolytes/Author contributions
EF: project administration, conceptualization, data curation, formal analysis, investigation, software, validation, visualization, writing – original draft, writing – review and editing. CW, YP and ICL: methodology, resources, writing – original draft, writing – review and editing. MW: writing – review and editing. TV: funding acquisition, writing – review and editing. AB: conceptualization, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation initiative under grants agreement No 957189 (BIG-MAP) and No 957213 (BATTERY 2030+). EF acknowledges Prof. Patrik Johansson and Dr Adam Maximilian Wilson for fruitful discussions.Notes and references
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- R. W. Schmitz, P. Murmann, R. Schmitz, R. Müller, L. Krämer, J. Kasnatscheew, P. Isken, P. Niehoff, S. Nowak, G. V. Röschenthaler, N. Ignatiev, P. Sartori, S. Passerini, M. Kunze, A. Lex-Balducci, C. Schreiner, I. Cekic-Laskovic and M. Winter, Prog. Solid State Chem., 2014, 42, 65–84 CrossRef CAS.
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278 CrossRef CAS.
- D. M. Seo, O. Borodin, D. Balogh, M. O'Connell, Q. Ly, S.-D. Han, S. Passerini and W. A. Henderson, J. Electrochem. Soc., 2013, 160, A1061–A1070 CrossRef CAS.
- M. S. Ding and T. R. Jow, ECS Trans., 2009, 16, 183–214 CrossRef CAS.
- I. Cekic-Laskovic, N. von Aspern, L. Imholt, S. Kaymaksiz, K. Oldiges, B. R. Rad and M. Winter, Top. Curr. Chem., 2017, 375, 1–64 CrossRef CAS PubMed.
- M. Armand, P. Axmann, D. Bresser, M. Copley, K. Edström, C. Ekberg, D. Guyomard, B. Lestriez, P. Novák, M. Petranikova, W. Porcher, S. Trabesinger, M. Wohlfahrt-Mehrens and H. Zhang, J. Power Sources, 2020, 479, 228708 CrossRef CAS.
- K. Xu and A. Von Cresce, J. Mater. Chem., 2011, 21, 9849–9864 RSC.
- S. Nowak and M. Winter, J. Electrochem. Soc., 2015, 162, A2500–A2508 CrossRef CAS.
- N. von Aspern, G. V. Röschenthaler, M. Winter and I. Cekic-Laskovic, Angew. Chem., Int. Ed., 2019, 58, 15978–16000 CrossRef CAS PubMed.
- J.-F. Dufrêche, O. Bernard, S. Durand-Vidal and P. Turq, J. Phys. Chem. B, 2005, 109, 9873–9884 CrossRef PubMed.
- P. Atkins and J. de Paula, in Phyiscal Chemistry, Oxford University Press, Oxford, 8th edn., 2006, pp. 747–790 Search PubMed.
- Y. Matsuda, M. Morita and K. Kosaka, J. Electrochem. Soc., 1983, 130, 101–104 CrossRef CAS.
- L. Martínez, Quim. Nova, 2018, 23, 341 Search PubMed.
- M. I. Duncan A, J. Franklin Inst., 1938, 225, 661–686 CrossRef.
- L. Onsager, Trans. Faraday Soc., 1927, 23, 341 RSC.
- J. Bockris and A. Reddy, in Modern Electrochemistry 1: Ionics, Kluwer Academic Publishers, 2nd edn., 2002, p. 519 Search PubMed.
- A. Anderko, P. Wang and M. Rafal, Fluid Phase Equilib., 2002, 194–197, 123–142 CrossRef CAS.
- G. M. Kontogeorgis, B. Maribo-Mogensen and K. Thomsen, Fluid Phase Equilib., 2018, 462, 130–152 CrossRef CAS.
- R. J. Gilliam, J. W. Graydon, D. W. Kirk and S. J. Thorpe, Int. J. Hydrogen Energy, 2007, 32, 359–364 CrossRef CAS.
- J. Nilsson-Hallén, B. Ahlström, M. Marczewski and P. Johansson, Front. Chem., 2019, 7, 1–6 CrossRef PubMed.
- J. Landesfeind and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, A3079–A3097 CrossRef.
- S. Matsuda, K. Nishioka and S. Nakanishi, Sci. Rep., 2019, 9, 1–8 CrossRef CAS PubMed.
- A. Dave, J. Mitchell, K. Kandasamy, H. Wang, S. Burke, B. Paria, B. Póczos, J. Whitacre and V. Viswanathan, Cell Rep. Phys. Sci., 2020, 1(12), 100264 CrossRef CAS.
- T. Lombardo, M. Duquesnoy, H. El-Bouysidy, F. Årén, A. Gallo-Bueno, P. B. Jørgensen, A. Bhowmik, A. Demortière, E. Ayerbe, F. Alcaide, M. Reynaud, J. Carrasco, A. Grimaud, C. Zhang, T. Vegge, P. Johansson and A. A. Franco, Chem. Rev., 2021 DOI:10.1021/acs.chemrev.1c00108.
- A. Bhowmik, I. E. Castelli, J. M. Garcia-Lastra, P. B. Jørgensen, O. Winther and T. Vegge, Energy Storage Mater., 2019, 21, 446–456 CrossRef.
- A. Bhowmik, M. Berecibar, M. Casas-Cabanas, G. Csanyi, R. Dominko, K. Hermansson, M. R. Palacin, H. S. Stein and T. Vegge, Adv. Energy Mater., 2021, 2102698 Search PubMed.
- Y. Wang, N. Wagner and J. M. Rondinelli, MRS Commun., 2019, 9, 793–805 CrossRef CAS.
- A. N. Krishnamoorthy, C. Wölke, D. Diddens and M. Maiti, ChemRxiv Prepr., 2022, 1–22 Search PubMed.
- H.D. Wiemhöfer, M. Grünebaum, M. M. Hiller, Micro electrode liquid measurement cell, WIPO Utility Patent, No. WO2014139494A1, 2014 Search PubMed.
- F. Horn, R. Pack and M. Rieger, Commun. Comput. Inf. Sci., 2020, 1167, 111–120 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel and M. Blondel, J. Mach. Learn Res., 2014, 39, i–ii Search PubMed.
- T. Hastie, R. Tibshirani and J. Friedman, in The Elements of Statistical Learning, Springer, 2nd edn, 2017, p. 244 Search PubMed.
- L. O. Valøen and J. N. Reimers, J. Electrochem. Soc., 2005, 152, A882 CrossRef.
- E. Flores, G. Åvall, S. Jeschke and P. Johansson, Electrochim. Acta, 2017, 233, 134–141 CrossRef CAS.
- H. Lundgren, M. Behm and G. Lindbergh, J. Electrochem. Soc., 2015, 162, A413–A420 CrossRef CAS.
- O. Borodin, M. Olguin, P. Ganesh, P. R. C. Kent, J. L. Allen and W. A. Henderson, Phys. Chem. Chem. Phys., 2016, 18, 164–175 RSC.
- D. Hubble, D. E. Brown, Y. Zhao, C. Fang, J. Lau, B. D. McCloskey and G. Liu, Energy Environ. Sci., 2022, 15, 550–578 RSC.
- D. S. Hall, J. Self and J. R. Dahn, J. Phys. Chem. C, 2015, 119, 22322–22330 CrossRef CAS.
- D. M. Seo, O. Borodin, S.-D. Han, P. D. Boyle and W. A. Henderson, J. Electrochem. Soc., 2012, 159, A1489–A1500 CrossRef CAS.
- M. S. Ding and T. R. Jow, J. Electrochem. Soc., 2003, 150, A620 CrossRef CAS.
- K. R. Broløs, M. V. Machado, C. Cave, J. Kasak, V. Stentoft-Hansen, V. G. Batanero, T. Jelen and C. Wilstrup, Arxiv Prepr., 2021, 1–18 Search PubMed.
- C. Cornelio, S. Dash, V. Austel, T. Josephson, J. Goncalves, K. Clarkson, N. Megiddo, B. El Khadir and L. Horesh, Arxiv Prepr., 2021, 1–26 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Exploratory data analysis, hyperparameters for feature generation and selection, most accurate expressions, accuracy, simplicity, consistency and fit on the withheld set from unconstrained models, learning curves, deviations on model predictions. See https://doi.org/10.1039/d2dd00027j |
| This journal is © The Royal Society of Chemistry 2022 |