Open Access Article
Open Access ArticleThe resolution-vs.-accuracy dilemma in machine learning modeling of electronic excitation spectra
Prakriti
Kayastha†
,
Sabyasachi
Chakraborty†
and
Raghunathan
Ramakrishnan
 *
*
Tata Institute of Fundamental Research Hyderabad, Hyderabad 500046, India. E-mail: ramakrishnan@tifrh.res.in
First published on 18th August 2022
Abstract
In this study, we explore the potential of machine learning for modeling molecular electronic spectral intensities as a continuous function in a given wavelength range. Since presently available chemical space datasets provide excitation energies and corresponding oscillator strengths for only a few valence transitions, here, we present a new dataset—bigQM7ω—with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 molecules containing up to 7 CONF atoms and report ground state and excited state properties. A publicly accessible web-based data-mining platform is presented to facilitate on-the-fly screening of several molecular properties including harmonic vibrational and electronic spectra. We present all singlet electronic transitions from the ground state calculated using the time-dependent density functional theory framework with the ωB97XD exchange-correlation functional and a diffuse-function augmented basis set. The resulting spectra predominantly span the X-ray to deep-UV region (10–120 nm). To compare the target spectra with predictions based on small basis sets, we bin spectral intensities and show good agreement is obtained only at the expense of the resolution. Compared to this, machine learning models with the latest structural representations trained directly using <10% of the target data recover the spectra of the remaining molecules with better accuracies at a desirable <1 nm wavelength resolution.
880 molecules containing up to 7 CONF atoms and report ground state and excited state properties. A publicly accessible web-based data-mining platform is presented to facilitate on-the-fly screening of several molecular properties including harmonic vibrational and electronic spectra. We present all singlet electronic transitions from the ground state calculated using the time-dependent density functional theory framework with the ωB97XD exchange-correlation functional and a diffuse-function augmented basis set. The resulting spectra predominantly span the X-ray to deep-UV region (10–120 nm). To compare the target spectra with predictions based on small basis sets, we bin spectral intensities and show good agreement is obtained only at the expense of the resolution. Compared to this, machine learning models with the latest structural representations trained directly using <10% of the target data recover the spectra of the remaining molecules with better accuracies at a desirable <1 nm wavelength resolution.
1 Introduction
The future of chemistry research hinges on the progress in data-driven autonomous discoveries.1–3 The performance of intelligent infrastructures necessary for such endeavors, such as chemputers,4 can be tremendously enhanced when augmenting experimental data used for their training with accurate ab initio results.5,6 For designing opto-electronically important molecules such as dye-sensitized solar cells,7,8 sunscreens,9,10 or organic photovoltaics,11,12 the corresponding target properties are excitation energies and the associated spectral intensities. Additionally, successful molecular design also requires information about thermodynamic/dynamic/kinetic stabilities, molecular lifetimes, solubility, and other experimental factors pertaining to molecular characterization. Accelerated discoveries based on molecular design workflows require a seamless supply of accurate theoretical results. To this end, machine learning (ML) models trained on results from ab initio predictions have emerged as their rapid and accurate surrogates.13–15ML models have been shown to accurately forecast a multitude of global13,16,17 and quasi-atomic molecular properties.18–20 For atomization or bonding energies, their prediction uncertainties are comparable to that of hybrid density functional theory (DFT) approximations.14,21–26 They have also successfully modeled non-adiabatic molecular dynamics,27 vibrational spectra,28,29 electronic coupling elements,30 excitons,31 electronic densities,32 excited states in diverse chemical spaces,33–35 as well as excited-state potential energy surfaces (PES).34,36–39 A key difference in the performance of ML in the latter two application domains is that ambiguities due to atomic indices and size-extensivity that affect the quality of structural representations for chemical space explorations40,41 do not arise in PES modeling or dipole surface modeling42–44 resulting in better learning rates.
ML models of global molecular energies (atomization/formation energies, etc.) with a robust structural representation benefit from the well-known mapping between the ground state electronic energy and the corresponding minimum energy geometry established by the Hohenberg–Kohn theorem.45 The Runge–Gross theorem provides a similar mapping between the time-dependent potential and the time-evolved total electron density.46 However, the target quantities in ML modeling of excited states are state-specific stemming from local molecular regions. For quasi-atomic properties such as 13C NMR shielding constants18–20,39 or K-edge X-ray absorption spectroscopy,18,39 a representation encoding the local environment of the query atom results in better learning rates. Similarly, quasi-particle density-of-states—interpreted as intensities in a photo-emission spectrum—have also been successfully modeled.47,48 However, for valence electronic excitations that are also local, the corresponding molecular substructure varies non-trivially across the chemical space. Hence, intensities based on oscillator strengths derived from many-electron excited state wave functions obeying dipole selection rules exhibit slow learning rates.34 Determining the characteristic chromophore responsible for the electronic excitations is non-trivial for chemical space datasets such as QM9 (ref. 49) that exhibit large structural diversity. This complexity, in turn, hinders the development of local descriptors that can map to the composition or structure of the chromophore and its environment. Hence, we are limited to using global structural representations for ML modeling of electronic excited state properties. This limitation becomes evident from the modest performances of ML models of excitation energies,33,34 and their zero-order approximations, the frontier molecular orbital (MO) energies.22,35,50,51
In this study, we: (i) present a high-quality chemical space dataset, bigQM7ω, containing ground-state properties and electronic spectra of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 molecules containing up to 7 CONF atoms modeled at the ωB97XD level with different basis sets. (ii) Demonstrate the resolution-vs.-accuracy dilemma in modeling spectroscopic intensities. (iii) Present ML models trained on the bigQM7ω dataset for an accurate reconstruction of the electronic spectra of allowed transitions in a given wavelength domain.
880 molecules containing up to 7 CONF atoms modeled at the ωB97XD level with different basis sets. (ii) Demonstrate the resolution-vs.-accuracy dilemma in modeling spectroscopic intensities. (iii) Present ML models trained on the bigQM7ω dataset for an accurate reconstruction of the electronic spectra of allowed transitions in a given wavelength domain.
2 Chemical space design
2.1 The bigQM7ω dataset
Pioneering efforts in small molecular chemical space design have culminated in the graph-based generated dataset, GDB11,52,53 containing 0.9 billion molecules with up to 11 CONF atoms. GDB11 provides simplified-molecular-input-line-entry-system (SMILES) string-based descriptors encoding molecular graphs. Larger datasets, GDB13 (ref. 54) and GDB17 (ref. 55) have since been created containing 13 and 17 heavy atoms, respectively. Synthetic feasibility and drug-likeness criteria eliminated several molecules in GDB13 and GDB17. Starting with the SMILES descriptors of GDB13, QM7 (ref. 13) and QM7b (ref. 56) quantum chemistry datasets emerged, provisioning computed equilibrium geometries and several molecular properties. Recently, QM7 has been extended by including non-equilibrium geometries for each molecule resulting in QM7-X.57 Similarly, the QM9 dataset49 used SMILES from the GDB17 library reporting structures and properties of 134 k molecules with up to 9 CONF atoms.In the present work, we explore molecules with up to 7 CONF atoms. We begin with the GDB11 set of SMILES because several important molecules such as ethylene and acetic acid present in GDB11 were filtered out in GDB13 and GDB17. Our new dataset contains 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 883 molecules—almost twice as large as the QM7 sets. The breakdown for subsets with 1/2/3/4/5/6/7 heavy atoms is 4/9/20/80/352/1850/10
883 molecules—almost twice as large as the QM7 sets. The breakdown for subsets with 1/2/3/4/5/6/7 heavy atoms is 4/9/20/80/352/1850/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568. The previous datasets QM7, QM7b, and QM9 have been generated using yesteryear's quantum chemistry workhorses: PBE,58 PBE0,59 and B3LYP.60 Here, we use the range-separated hybrid DFT method, ωB97XD61 that is gaining widespread popularity for its excellent accuracy. Hence, we name this dataset as bigQM7ω, with the last character emphasizing the DFT approximation utilized. The high-throughput workflow used for generating bigQM7ω is shown in Fig. 1 and Table 1 puts the new dataset in perspective by comparing with other popular datasets of similar constitution. While bigQM7ω is smaller than QM9, it provides a better coverage of molecules for the same number of CONF atoms. Further, bigQM7ω also provides excited state data collected at various theoretical levels, hence, comprehensively covering the property domain. A summary of properties of bigQM7ω, made available in the form of structured datasets,62 is provided in Table 2. As unstructured datasets, we provide raw input/output files63 to kindle future endeavors. For example, for ML modeling of forces, properties of non-equilibrium geometries may be extracted from these raw data.
568. The previous datasets QM7, QM7b, and QM9 have been generated using yesteryear's quantum chemistry workhorses: PBE,58 PBE0,59 and B3LYP.60 Here, we use the range-separated hybrid DFT method, ωB97XD61 that is gaining widespread popularity for its excellent accuracy. Hence, we name this dataset as bigQM7ω, with the last character emphasizing the DFT approximation utilized. The high-throughput workflow used for generating bigQM7ω is shown in Fig. 1 and Table 1 puts the new dataset in perspective by comparing with other popular datasets of similar constitution. While bigQM7ω is smaller than QM9, it provides a better coverage of molecules for the same number of CONF atoms. Further, bigQM7ω also provides excited state data collected at various theoretical levels, hence, comprehensively covering the property domain. A summary of properties of bigQM7ω, made available in the form of structured datasets,62 is provided in Table 2. As unstructured datasets, we provide raw input/output files63 to kindle future endeavors. For example, for ML modeling of forces, properties of non-equilibrium geometries may be extracted from these raw data.
| Details | QM7 | QM7b | QM9a | bigQM7ω |
|---|---|---|---|---|
a Contains 3993/22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 molecules with up to 7/8 CONF atoms. Excited state data are available for the 22 786 molecules with up to 7/8 CONF atoms. Excited state data are available for the 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 subset ref. 33. 786 subset ref. 33.
|
||||
| Origin | GDB13 | GDB13 | GDB17 | GDB11 |
| Elements | CHONS | CHONSCl | CHONF | CHONF |
| Size | 7165 | 7211 | 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 885 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 880 |
| Geometry optimization | PBE0/tight tier-2 | PBE/tight tier-2 | B3LYP/6-31G(2df,p) | ωB97XD/3-21G |
| ωB97XD/def2SVP | ||||
| ωB97XD/def2TZVP | ||||
| Frequencies | B3LYP/6-31G(2df,p) | ωB97XD/3-21G | ||
| ωB97XD/def2SVP | ||||
| ωB97XD/def2TZVP | ||||
| Excited states | E 1 | E 1, E2, f1, f2 | All states | |
| GW/tight tier-2 | RICC2/def2TZVP | TDωB97XD/3-21G | ||
| TDPBE0/def2SVP | TDωB97XD/def2SVP | |||
| TDPBE0/def2TZVP | TDωB97XD/def2TZVP | |||
| TDCAMB3LYP/def2TZVP | TDωB97XD/def2SVPD | |||
| PM6 |
|---|
| Equilibrium geometries (Å) |
| All molecular orbital energies (hartree) |
| Total electronic and atomization energies (hartree) |
| ωB97XD/(3-21G, def2SVP, def2TZVP) |
|---|
| Equilibrium geometries (Å) |
| All molecular orbital energies (hartree) |
| Atomization energies (hartree) |
| All harmonic frequencies (cm−1) |
| Zero-point vibrational energy (kcal mol−1) |
| Mulliken charges, atomic polar tensor charges (e) |
| Dipole moment (debye) |
| Polarizability (bohr3) |
| Radial expectation value (bohr2) |
| Internal energy at 0 K and 298.15 K (hartree) |
| Enthalpy at 298.15 K (hartree) |
| Free energy at 298.15 K (hartree) |
| Total heat capacity (cal/mol/K) |
| ZINDO, TDωB97XD/(3-21G, def2SVP, def2TZVP, def2SVPD) |
|---|
| Excitation energy of all states (eV, nm) |
| Oscillator strengths of all excitations (dimensionless) |
| Transition dipole moment of all excitations (a.u.) |
2.2 Computational details
Initial structures of the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 883 molecules in bigQM7ω were generated from SMILES by relaxing with the universal force field (UFF)64 employing tight convergence criteria using OpenBabel.65 As a guideline for quantum chemistry big data generation, a previous study proposed connectivity preserving geometry optimizations (ConnGO) to eliminate structural ambiguities due to rearrangements encountered in automated high-throughput calculations.66 Accordingly, we used a 3-tier ConnGO workflow to generate geometries at the ωB97XD61 DFT level using def2SVP and def2TZVP basis sets.67 Geometry optimizations at the simpler levels such as PM6 and ωB97XD/3-21G were performed without ConnGO, directly starting from the UFF structures. For ωB97XD/def2SVP final geometries, we used HF/STO3G and ωB97XD/3-21G as intermediate tier-1 and tier-2 levels, respectively. Similarly, for ωB97XD/def2TZVP, HF/STO3G and ωB97XD/def2SVP were lower tiers. In each tier, ConnGO compares the optimized geometry with the covalent bonding connectivities encoded in the initial SMILES and detects molecules undergoing rearrangements. For this purpose, we used the ConnGO thresholds: 0.2 Å for the maximum absolute deviation in covalent bond length and a mean percentage absolute deviation of 6%. In DFT calculations, tight optimization thresholds and ultrafine grids were used for evaluating the exchange–correlation (XC) energy. A few molecules required relaxing the optimization thresholds for monotonic convergence towards a minimum. All final geometries were confirmed to be local minima through harmonic frequency analysis. For molecules that are highly symmetric or with multiple triple bonds, converging to minima was only possible with the very tight optimization threshold and superfine grids. At both ωB97XD/def2SVP and ωB97XD/def2TZVP levels, 3 molecules with the SMILES O = c1cconn1, N = c1nconn1, O = c1nconn1, failed the ConnGO connectivity tests. Further investigation revealed these molecules to contain an –NNO– substructure in a 6-membered ring facilitating dissociation as previously noted in ref. 66. After removing these molecules, the size of bigQM7ω stands at 12
883 molecules in bigQM7ω were generated from SMILES by relaxing with the universal force field (UFF)64 employing tight convergence criteria using OpenBabel.65 As a guideline for quantum chemistry big data generation, a previous study proposed connectivity preserving geometry optimizations (ConnGO) to eliminate structural ambiguities due to rearrangements encountered in automated high-throughput calculations.66 Accordingly, we used a 3-tier ConnGO workflow to generate geometries at the ωB97XD61 DFT level using def2SVP and def2TZVP basis sets.67 Geometry optimizations at the simpler levels such as PM6 and ωB97XD/3-21G were performed without ConnGO, directly starting from the UFF structures. For ωB97XD/def2SVP final geometries, we used HF/STO3G and ωB97XD/3-21G as intermediate tier-1 and tier-2 levels, respectively. Similarly, for ωB97XD/def2TZVP, HF/STO3G and ωB97XD/def2SVP were lower tiers. In each tier, ConnGO compares the optimized geometry with the covalent bonding connectivities encoded in the initial SMILES and detects molecules undergoing rearrangements. For this purpose, we used the ConnGO thresholds: 0.2 Å for the maximum absolute deviation in covalent bond length and a mean percentage absolute deviation of 6%. In DFT calculations, tight optimization thresholds and ultrafine grids were used for evaluating the exchange–correlation (XC) energy. A few molecules required relaxing the optimization thresholds for monotonic convergence towards a minimum. All final geometries were confirmed to be local minima through harmonic frequency analysis. For molecules that are highly symmetric or with multiple triple bonds, converging to minima was only possible with the very tight optimization threshold and superfine grids. At both ωB97XD/def2SVP and ωB97XD/def2TZVP levels, 3 molecules with the SMILES O = c1cconn1, N = c1nconn1, O = c1nconn1, failed the ConnGO connectivity tests. Further investigation revealed these molecules to contain an –NNO– substructure in a 6-membered ring facilitating dissociation as previously noted in ref. 66. After removing these molecules, the size of bigQM7ω stands at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880.
880.
We performed vertical excited-state calculations at Zerner's intermediate neglect of differential overlap (ZINDO)68 and TDωB97XD levels. ZINDO calculations were done on PM6 minimum energy geometries, while TDωB97XD with 3-21G, def2SVP, and def2TZVP basis sets, at the corresponding ground state equilibrium geometries. We also performed TDωB97XD calculations with the diffuse function augmented basis set, def2SVPD, on ωB97XD/def2SVP geometries. All electronic structure calculations were performed using the Gaussian suite of programs.69 The number of excited states accessible to the TDDFT formalism is limited by the number of electrons and the size of the orbital basis set. With the finite basis set used in this study, the spectrum is practically discrete. To ensure that all the singlet-type electronic bound states are calculated, we set an upper bound of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the number of states in the TDDFT single point calculations with the keyword nstates = 10
000 for the number of states in the TDDFT single point calculations with the keyword nstates = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For benchmarking the quality of TDDFT excitation spectra, we also performed similarity transformed equation-of-motion coupled cluster with singles doubles excitation (STEOM-CCSD)70 and the aug-cc-pVTZ basis set as implemented in Orca.71,72
000. For benchmarking the quality of TDDFT excitation spectra, we also performed similarity transformed equation-of-motion coupled cluster with singles doubles excitation (STEOM-CCSD)70 and the aug-cc-pVTZ basis set as implemented in Orca.71,72
3 Machine learning modeling of full electronic spectra
Kernel ridge regression (KRR) based ML (KRR-ML) enables accurate predictions through an exact global optimization of a convex model.13,14,73 In KRR-ML the target property, tq, of an out-of-sample query, q, is estimated as the linear combination of kernel (or radial basis) functions, each centered on a training entry. Formally, with a suitable choice of the kernel function, KRR approaches the target when the training set is sufficiently large | (1) |
The coefficients, {ci}, are obtained by regression over the training data. The kernel function, k(·), captures the similarity in the representations of the query, q, and all N training examples. For ground state energetics, the Faber–Christensen–Huang–Lilienfeld (FCHL) formalism in combination with KRR-ML has been shown to perform better than other structure-based representations.22,74 However, for excitation energies and frontier MO gaps, FCHL's performance drops compared to the Spectral London-Axilrod-Teller-Muto (SLATM) representation.75 In this study, we compare the performance of FCHL and SLATM for modeling the full-electronic spectrum. SLATM delivers best accuracies with the Laplacian kernel, k(dq, di) = exp(−|dq − di|1/σ), where σ defines the length scale of the kernel function and |·|1 denotes L1 norm. For the FCHL formalism, we found an optimal kernel width of σ = 5 through scanning and a cutoff distance of 20 Å was used to sufficiently capture the structural features of the longest molecule in the bigQM7ω dataset, heptane.
The kernel width, σ, is traditionally determined through cross-validation. For multi-property modeling σ can be estimated using the ‘single-kernel’ approach,16 where σ is estimated as a function of the largest descriptor difference in a sample of the training set, σ = max{dij}/![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(2). Previous works16,20,76 have shown single-kernel modeling to agree with cross-validated results with in the uncertainty arising due to training set shuffles, especially for large training set sizes. KRR with a single-kernel facilitates seamless modeling of multiple molecular properties using standard linear solvers
log(2). Previous works16,20,76 have shown single-kernel modeling to agree with cross-validated results with in the uncertainty arising due to training set shuffles, especially for large training set sizes. KRR with a single-kernel facilitates seamless modeling of multiple molecular properties using standard linear solvers
| [K + ζI][c1, c2, …] = [p1, p2, …], | (2) |
The property (pi vector in eqn (2)) modeled in this study corresponds to sum of binned oscillator strength of electronic transitions from the ground state. Conventionally, the band intensity due to the k – th excitation is the molar absorption coefficient that is proportional to the corresponding oscillator strength, f![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) k, denoted shortly as fk.79 In order to model a full spectrum in a given wavelength range, one can consider each value of fk (in atomic units, a.u.) as a separate target quantity. However, the number of states is not uniform in a dataset such as bigQM7ω. Further, in practice, one is interested in an integrated oscillator strengths within a small resolution, Δλ. Hence, we uniformly divide the spectral range in powers of 2, Δλ = λspectrum/Nbin, where Nbin = 1, 2, 4, … is the number of bins. For the small organic molecules such as those in bigQM7ω, we set spectral range to λspectrum to 120 nm capturing most of the excitations. For wavelengths >120 nm the bigQM7ω dataset provides too few examples, hence, data in this long wavelength domain is inadequate for ML modeling. The target for ML is the sum of fk in a bin
k, denoted shortly as fk.79 In order to model a full spectrum in a given wavelength range, one can consider each value of fk (in atomic units, a.u.) as a separate target quantity. However, the number of states is not uniform in a dataset such as bigQM7ω. Further, in practice, one is interested in an integrated oscillator strengths within a small resolution, Δλ. Hence, we uniformly divide the spectral range in powers of 2, Δλ = λspectrum/Nbin, where Nbin = 1, 2, 4, … is the number of bins. For the small organic molecules such as those in bigQM7ω, we set spectral range to λspectrum to 120 nm capturing most of the excitations. For wavelengths >120 nm the bigQM7ω dataset provides too few examples, hence, data in this long wavelength domain is inadequate for ML modeling. The target for ML is the sum of fk in a bin
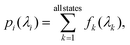 | (3) |
3.1 Mean absolute error
In this study, our target property is the TDωB97XD-level binned oscillator strength defined in eqn (3). Given reference-level TDωB97XD spectra, the error in the spectra predicted with another model (different theory or ML) can be quantified using the standard metric, mean absolute error (MAE):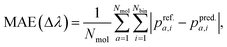 | (4) |
3.2 Accuracy metric for normalized spectra
For the a-th molecule,![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) i,a is the normalized oscillator strength for the i-th bin defined as
i,a is the normalized oscillator strength for the i-th bin defined as 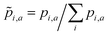 . For two spectra binned at a common resolution, Δλ, the accuracy metric for normalized spectra (Φ) is given by:
. For two spectra binned at a common resolution, Δλ, the accuracy metric for normalized spectra (Φ) is given by: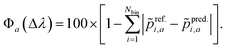 | (5) |
When the reference and target property vectors are the same, the accuracy is maximum, Φ = 100. For a sample with Nmol molecule, an overall prediction accuracy (![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) ) can be obtained as an average
) can be obtained as an average
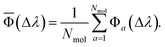 | (6) |
4 Results and discussions
4.1 TDDFT modeling of excited states
A prerequisite for ML modeling is the availability of training data generated with accurate theoretical levels for the properties of interest. In practice, it is also desirable that the theoretical levels offer a sustainable high-throughput rate for data generation. The more recent ‘mountaineering efforts’ have reported extended excited states benchmarks of highly accurate wavefunction methods for carefully selected sets of few hundred molecules.80–82 Another popular dataset for benchmarking excited state properties was developed by Schreiber et al.83 These studies have explored a wide range of correlated excited state methods including the very accurate fourth-order coupled-cluster (CC4) method that approaches the full configuration interaction limit very closely. However, even for the lower order methods such as third-order coupled-cluster (CC3), excited state modeling becomes challenging for a large set of molecules.For the low-lying excited states of small molecules, equations-of-motion coupled cluster with singles doubles (EOM-CCSD)84 and approximate second-order coupled-cluster (CC2) deliver a mean error of 0.10–0.15 eV compared to higher-level wave function methods.59,80–82,85–88 While these methods can be made more economical by using the resolution-of-identity (RI) technique, as in RICC2 (ref. 89) or domain-based local pseudo-natural orbital (DLPNO) variant of EOM-CCSD,90 they have known limitations when modeling the full electronic spectra of thousands of molecules. Formally, the total number of electronic states accounted for by these wave function methods scales as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2oN2v), where No and Nv are the numbers of occupied and virtual MOs. Even for a small molecule such as benzene with a triple-zeta basis set, the size of the resulting electronic Hamiltonian is of the order of millions. It is well known that the iterative eigensolvers used for such large scale problems converge poorly for higher eigenvalues restricting their usage only to the lowest few electronic states.91 Hence, as of now, large scale computations of full electronic spectra across a chemical space dataset are amenable only at the time-dependent (TD) DFT-level92,93 that show an
(N2oN2v), where No and Nv are the numbers of occupied and virtual MOs. Even for a small molecule such as benzene with a triple-zeta basis set, the size of the resulting electronic Hamiltonian is of the order of millions. It is well known that the iterative eigensolvers used for such large scale problems converge poorly for higher eigenvalues restricting their usage only to the lowest few electronic states.91 Hence, as of now, large scale computations of full electronic spectra across a chemical space dataset are amenable only at the time-dependent (TD) DFT-level92,93 that show an ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (NoNv) scaling.
(NoNv) scaling.
While DFT offers a suitable high-throughput data generation rate, its accuracy for geometries and properties is dependent on the exchange-correlation (XC) functional. The chemical space dataset, QM9, was designed using the hybrid generalized gradient approximation (hGGA), B3LYP, with 6-31G(2df, p) basis set because of their use in the Gn family of composite wavefunction methods.94 For thermochemistry energies, B3LYP has an error of 4–5 kcal mol−1.95 A recent benchmark study96 has shown the range-separated hGGAs from the ωB97 family61 to have errors in the 2–3 kcal mol−1 window; their performance is second only to the Gn methods. While curating the QM9 dataset, the dispersion corrected variant of ωB97, namely ωB97XD, predicted high-veracity geometries less prone to rearrangements in automated high-throughput workflows.66 Hence, we resort to ωB97XD for geometry optimization and its time-dependent variant for modeling the complete electronic excitation spectra.
The electronic excitations of the molecules in our dataset are predominantly in the deep-ultraviolet (deep-UV) to X-ray region. Since the popular flavors of TDDFT depend on the adiabatic approximation where the orbitals are relaxed to first-order as a linear response, they often fail to describe the electronic wavefunction of high-lying excited states that can substantially differ from that of the ground state.97 Such effects may be anticipated especially for excitations of long-range charge-transfer character, Rydberg-type98 or excitations of core electrons.99 Additionally, electronic states of doubly excited character are not accessible to the linear-response formalism of TDDFT.100 However, as yet, remedies for improving TDDFT for pathological situations have not been tested over chemical space datasets. Furthermore, some of the new methods such as the orbital optimized DFT also suffer from algorithmic errors resulting in variational collapse to a low-lying state.97
To probe the effect of basis sets on the TDDFT-level excited state properties, we selected the smallest 33 molecules with up to 3 heavy atoms as a benchmark set. Accurate modeling of oscillator strengths and high-lying electronic states require basis sets augmented with diffuse functions in order to achieve semi-quantitative accuracy. Hence, in Fig. 2, we explore ωB97XD's performance for excitation properties computed at def2SVP (SVP), def2TZVP (TZVP), def2SVPD (SVPD), and def2TZVPD (TZVPD). We use the lowest two excitation energies (E1 and E2) and the corresponding oscillator strengths (f1 and f2) with the accurate STEOM-CCSD/aug-cc-pVTZ method as the reference. Unsurprisingly, def2SVP has the largest errors across all excitation properties followed by def2TZVP, def2SVPD, and def2TZVPD. Including diffuse functions results in errors that are almost half of those from basis sets devoid of diffuse functions. The errors for all four properties obtained with the def2SVPD basis set are very similar irrespective of whether the corresponding geometries were determined with def2SVP or def2TZVP basis sets. Even though def2TZVPD offers the best accuracies, we find the computational cost for determining the full spectra of all molecules in bigQM7ω to be very high. Hence, we resort to the def2SVPD basis set that is cost-effective for the excited state calculations. The final target-level data used for training ML models were obtained at the TDωB97XD/def2SVPD level using geometries calculated at the ωB97XD/def2SVP level. While TDωB97XD/def2SVPD level excitation spectra is by no means quantitatively accurate, for high-throughput explorations of medium-sized molecules, it still preserves broad trends that can be learned through structure–property relationships.
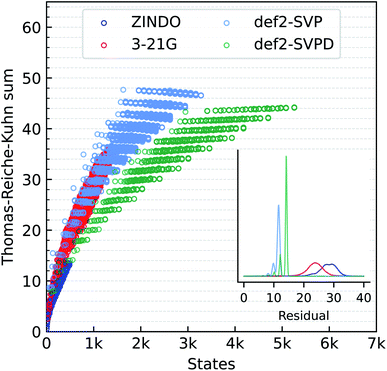
We also compare the performance of different methods for predicting the Thomas–Reiche–Kuhn (TRK) sum, ∑kfk. For an exact excited state method, this sum according to the TRK theorem must converge to the number of electrons.79 In quantum chemistry, unfortunately, this condition is satisfied only at the full-CI limit, when all excitations (singles, doubles, triples, and so on) are accounted for at the basis set limit. ZINDO and the TDωB97XD methods are not expected to satisfy the TRK limit. We illustrate this aspect in Fig. 3 where the TRK-sum is plotted as a function of total number of states accessible. ZINDO deviates the most from the TDωB97XD/def2SVPD target because the number of excited states available is limited by two factors. Firstly, core electrons are not included in ZINDO. Secondly, semi-empirical models are implicitly based on a minimal basis set.
TDDFT modeling with 3-21G improves ∑kfk and the total number of states compared to ZINDO. With the def2SVP and def2SVPD basis sets, ∑kfk quantizes at even numbers with a separation of about 2. For the large basis set, def2SVPD, the number of accessible states increases, while the TRK-sum drops below the def2SVP values. We investigated the reason for this trend using methane and found the def2-basis sets to show somewhat oscillatory convergence with the basis set size. For methane, the def2SVP/def2SVPD values are 8.78/8.12, the larger basis set value agreeing better with the aug-cc-pV5Z basis set limit value of 7.82. Residual errors in ZINDO/TDDFT TRK-sums from total number of electrons are shown in the inset to Fig. 3.
4.2 Resolution-vs.-accuracy trade-off
Typically, uncertainties of hybrid-DFT approximations compared to higher-level wavefunction methods are used as threshold accuracies for gauging the performance of ML models. For the bigQM7ω dataset, along with the conventional MAE metric, we also explore a dimensionless accuracy metric for normalized spectra, Φ (see eqn (5)) and its average. Even though the electronic spectra of molecules in bigQM7ω span a wavelength range until 850 nm, >99% of the spectra lie in the deep UV to X-ray range (10–120 nm). Such a trend has been noted before for small organic molecules.101 Hence in this study, we fix the spectral range (λspectrum) to 0–120 nm and bin oscillator strengths at various wavelength resolutions (Δλ) according to eqn (3). For a given Δλ, we compare MAE and![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) of predictions from ZINDO, ωB97XD/3-21G, or ωB97XD/def2SVP levels with that of the ωB97XD/def2SVPD values (see Fig. 4). For atomization energies and low-lying excitation energies, these values are 3–4 kcal mol−1, and 0.2–0.3 eV,82 respectively. For oscillator strengths, such a threshold has not been established, especially for chemical space datasets.
of predictions from ZINDO, ωB97XD/3-21G, or ωB97XD/def2SVP levels with that of the ωB97XD/def2SVPD values (see Fig. 4). For atomization energies and low-lying excitation energies, these values are 3–4 kcal mol−1, and 0.2–0.3 eV,82 respectively. For oscillator strengths, such a threshold has not been established, especially for chemical space datasets.
 | ||
Fig. 4 Accuracy metrics for binned oscillator strengths in the λ ≤ 120 nm range for all molecules in bigQM7ω: (a) mean absolute error, MAE(Δλ), in atomic units (a.u.) as defined in eqn (4), (b) mean accuracy metric for normalized spectra, ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) (Δλ), as defined in eqn (6). Results are shown for ZINDO, ωB97XD/3-21G and ωB97XD/def2SVP for approximating ωB97XD/def2SVPD level values. (Δλ), as defined in eqn (6). Results are shown for ZINDO, ωB97XD/3-21G and ωB97XD/def2SVP for approximating ωB97XD/def2SVPD level values. | ||
In Fig. 4a, the MAE of ZINDO shows a smaller variation with Δλ. For the extreme case of Δλ = 120 nm, where the oscillator strengths of all states are summed in a bin, ZINDO's MAE saturates to about 27.5 a.u implying a systematic error in ZINDO. For the desired resolution of 0.94 nm, ZINDO's error increases only slightly. The MAEs improve for the spectra calculated with ωB97XD/3-21G. For the single bin case, the 3-21G results also indicate a systematic error albeit of a smaller magnitude compared to ZINDO. The errors are further quenched for the def2SVP basis set, which for a resolution of Δλ = 0.94 nm has an MAE of about 20 a.u. Overall, the MAE-vs-Δλ dependency becomes stronger in the order: ZINDO < ωB97XD/3-21G < ωB97XD/def2SVP. This trend is in agreement with the magnitude of TRK-sum as predicted by these methods, see Fig. 3. In general, a similar trend is noted also for individual oscillator strengths.
As pointed out in Section-3, for the limiting case of Δλ = 120 nm, when all oscillator strengths are summed in one bin, the Φ is 100 for ZINDO, ωB97XD/3-21G, and ωB97XD/def2SVP methods compared to the target ωB97XD/def2SVPD (see Fig. 4b). With increasing resolution, the methods diverge from the target, ZINDO showing the largest deviation from ωB97XD/def2SVPD. For a desirable resolution of 1% of λspectrum, Δλ ≈ 1 nm, 3-21G and def2SVP predictions result in Φs of 30–50 compared to the target, while ZINDO has a worse score ≈10. The reason for poor Φs of ZINDO predictions at small resolution is because core states are absent in ZINDO, limiting the spectral range to >19.8 nm. In contrast, the density of the states at the target TDωB97XD level is high in the short wavelength domain. Applying bin-specific systematic corrections can improve both the accuracy metrics for all three methods: ZINDO, ωB97XD/3-21G, and ωB97XD/def2SVP. However, such corrections may not result in uniform improvement throughout the spectral range. For instance, at short wavelength regions where the TDωB97XD spectra are sharp, ZINDO lacks these lines. However, systematic corrections may result in vanishing MAE for the wrong reason. On the other hand, the effect of such corrections will be less severe for the normalized metric, ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) . Hence, we do not apply bin-specific systematic corrections in this analyses. Overall, at the desired resolution of 0.94 nm, among the methods inspected here, the one with larger MAE has the smaller accuracy metric,
. Hence, we do not apply bin-specific systematic corrections in this analyses. Overall, at the desired resolution of 0.94 nm, among the methods inspected here, the one with larger MAE has the smaller accuracy metric, ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) and vice versa.
and vice versa.
4.3 Reconstruction of electronic spectra with ML models
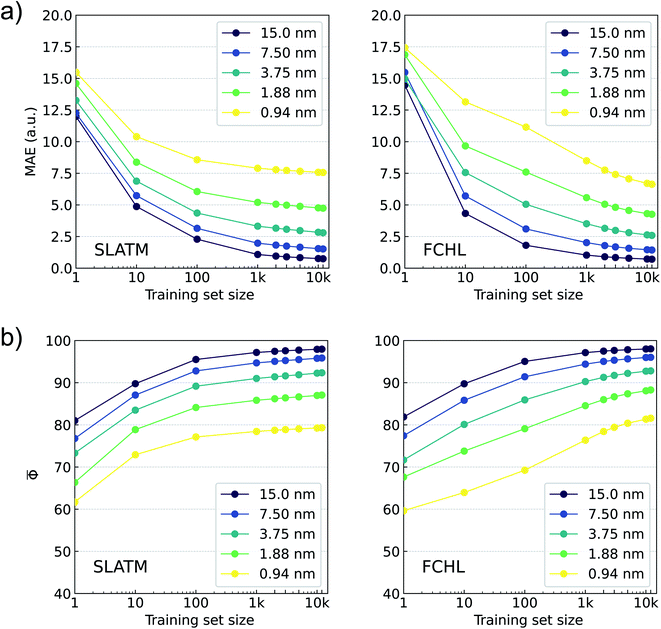
In Fig. 5, we report learning rates based on MAE and Φ for predicting binned oscillator strengths (defined in eqn (3)) using KRR-FCHL and KRR-SLATM models for various training set sizes and spectral resolutions. For poor resolutions, we find small MAEs and large Φs already at the offset of learning curves. For large training set sizes and at all resolutions FCHL slightly outperforms SLATM. While the SLATM model saturates to an MAE of ≈7.5 a.u. and![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/char_e0c1.gif) ≈ 80 for 0.94 nm resolution FCHL model shows improved learning rates, suggesting its scope for modeling full-electronic spectra of larger datasets. These findings indicate that it is possible to employ ML modeling for reconstructing electronic spectra at a high-resolution. Since the ML models were trained on pi (binned oscillator strengths), the predicted spectra can be compared with the reference TDωB97XD spectra similarly binned. The prediction error of the reconstructed spectrum may be quantified either as a sum of absolute differences, or using the accuracy metric upon normalizing the binned intensities. The definitions of the error metric do not influence the ML-reconstruction of the spectra, but they serve merely to quantify the mean prediction accuracy.
≈ 80 for 0.94 nm resolution FCHL model shows improved learning rates, suggesting its scope for modeling full-electronic spectra of larger datasets. These findings indicate that it is possible to employ ML modeling for reconstructing electronic spectra at a high-resolution. Since the ML models were trained on pi (binned oscillator strengths), the predicted spectra can be compared with the reference TDωB97XD spectra similarly binned. The prediction error of the reconstructed spectrum may be quantified either as a sum of absolute differences, or using the accuracy metric upon normalizing the binned intensities. The definitions of the error metric do not influence the ML-reconstruction of the spectra, but they serve merely to quantify the mean prediction accuracy.
The spectra reconstructed with these models do not contain any state-specific information, but rather indicate the intensity of dipole absorption in a finite wavelength window. At the limit of very small Δλ, these bins will correspond to individual transitions. It is worth noting that for a resolution of 0.94 nm, TDωB97XD/def2SVP spectra agree with that of the target-level only with a score of ≈47. The Φ drops even further for TDωB97XD/3-21G (≈29) and ZINDO (≈9) levels. The learning rates in our evaluatory Δ-ML17 calculations using ZINDO, TDωB97XD/3-21G, or even TDωB97XD/def2SVP baseline spectra were inferior than modeling directly on the TDωB97XD/def2SVPD target. Hence, all ML models were trained directly on the target.
In Fig. 6, we present the entire spectrum of an out-of-sample molecule, cyclohexanone, reconstructed using FCHL-ML models with 1 k training examples at three different wavelength resolutions −3.75 nm, 1.88 nm, and 0.94 nm. Since the ML models were trained using geometries at the UFF level, these out-of-sample predictions were performed with in a matter of seconds. As a part of the supplementary material, we provide a sample code for generating the spectrum using a trained FCHL models (see Data Availability). For Δλ = 3.75 nm, the ML-reconstructed spectrum agrees with the target TDωB97XD spectrum with a Φ of 86.5. This accuracy drops for higher resolutions due to the fine details present in the target spectrum. Also, with increase in resolution we note a reduction in the spectral heights in order to conserve the total area under the spectrum. For the desired value of Δλ = 0.94 nm, the spectrum of cyclohexanone is reconstructed with a score of 72.6 which is slightly lower than the mean score reported for out-of-sample predictions in Fig. 5.
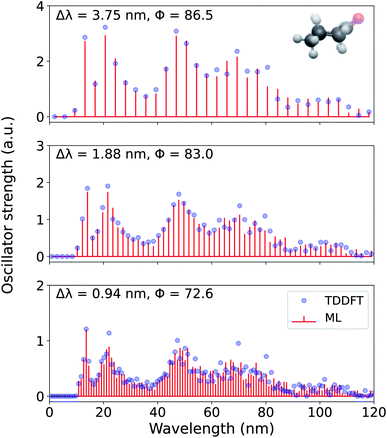 | ||
| Fig. 6 Electronic excitation spectrum of cyclohexanone, reconstructed at 3.75 nm, 1.88 nm, and 0.94 nm resolutions using a 1 k FCHL-KRR-ML model trained on binned oscillator strengths (pi in eqn (3)) at the TDωB97XD/def2SVPD target-level. Accuracy metric for normalized spectra, Φ, compared to TDωB97XD reference values calculated according to eqn (5) are also given. | ||
Further, for the highest resolution explored here, we present the ML reconstructed spectra for three more randomly drawn out-of-sample molecules in Fig. 7. For all these molecules, the prediction is better than for cyclohexanone and are illustrative of the model's mean out-of-sample performance. While the reference TDωB97XD-level binned oscillator strengths are always >0, the predicted values are not bound, hence, we notice small negative intensities for 5,5-dimethyl-4,5-dihydro-1H-pyrazole. For all four out-of-sample molecules considered here, the spectral intensities are low for λ > 100 nm because of the corresponding excitations in this region is sparse. We believe that ML strategy for spectral reconstruction reported in this study will hold even at the interesting long-wavelength domain when these models are trained on adequate examples.
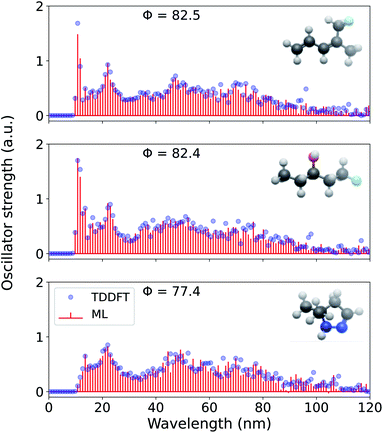 | ||
| Fig. 7 Electronic excitation spectrum of three randomly selected molecules—(3Z)-5-fluoro-4-methylpenta-1,3-diene, 1-fluoropentan-3-ol, and 5,5-dimethyl-4,5-dihydro-1H-pyrazole—reconstructed at 0.94 nm resolution using a 1 k FCHL-KRR-ML. The model was trained on TDωB97XD/def2SVPD electronic spectra in the λ ≤ 120 nm wavelength range. Accuracy metric for normalized spectra, Φ, compared to TDωB97XD reference values calculated according to eqn (5) are also given. | ||
5 Data-mining in MolDis
The dataset collected in lieu of this study, justifies an endeavor to make it accessible to the wider community. While unstructured datasets require an additional step of data extraction, a data-mining platform allows us to rapidly perform multi-property querying and screening. Our data-mining platform MolDis102 is well-suited to cater to such requirements and hence, we are hosting property-oriented mining platforms for minimum energy ground-state structures of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 molecules obtained at the ωB97XD/def2SVP & ωB97XD/def2TZVP levels at https://moldis.tifrh.res.in/datasets.html with both ground-state and excited-state properties.
880 molecules obtained at the ωB97XD/def2SVP & ωB97XD/def2TZVP levels at https://moldis.tifrh.res.in/datasets.html with both ground-state and excited-state properties.
In Fig. 8, we present a representative property query in the MolDis platform and the corresponding results. On accessing the def2SVP tab in the bigQM7ω Datasets page, we arrive at the corresponding query page. As noted in Fig. 8a, there are 11 ground state properties—dipole moment, polarizability, EHOMO, ELUMO, ELUMO–HOMO, zero-point vibrational energy, zero-Kelvin internal energy (U0), room temperature internal energy (U), room temperature enthalpy (H), room temperature Gibbs free energy (G), and constant volume heat capacity (Cv)—with available property ranges reported next to them. For a query, users need to enter values with in the property range with appropriate units selected and click on the Query button. The search can be further customized upon including multiple properties in the query and display them in ascending or descending order with respect to any property from the corresponding drop-down window. We have also enabled an option to query based on composition. In the bottom half of Fig. 8a, users can select either a set of atoms or any valid stoichiometry as listed on the right side of the query page. Upon making a successful query, users are presented with results (Fig. 8b), where the Cartesian coordinates, vibrational and electronic spectra are provided along with the magnitudes of queried properties in desired units. A JSMol applet enables visitors to visualize the structures on their browser upon clicking the “View in JSMol” button. Further, upon a fruitful query, both ground-state and excited-state properties for every molecule is presented to the visitor as downloadable files on the results page (Fig. 8b). This platform allows access to ab initio properties collected via high-throughput chemical space investigations to the community in a user-friendly fashion, hence, widening the applicability scope of the bigQM7ω dataset.
6 Conclusions
In this work we present the new chemical space dataset, bigQM7ω, containing 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 molecules with up to 7 atoms of CONF. Geometry optimizations of the bigQM7ω molecules have been performed with the ConnGO workflow ensuring veracity in the covalent bonding connectivities encoded in their SMILES representation. Minimum energy geometries and harmonic vibrational wavenumbers are reported at the accurate, range-separated hybrid DFT level ωB97XD using def2SVP and def2TZVP basis sets. This level was selected because it has been previously shown to result in efficient geometry predictions for chemical space datasets.66 We report electronic excited state results at the TDωB97XD level using the def2SVPD basis set containing diffuse functions that are necessary for improved modeling of oscillator strengths, and high-lying states in general. Even for the low-lying excited states of the bigQM7ω molecules, we found TDωB97XD/def2SVPD to deliver more accurate results than the ωB97XD/def2TZVP combination when benchmarked against STEOM-CCSD/aug-cc-pVTZ reference values. For all molecules, full electronic spectra are calculated covering all possible excitations allowed by the TDωB97XD framework. For the small molecules H2O, NH3, and CH4 the resulting number of excited states modeled amounts to 188, 156 and 136, respectively, while for large molecules such as toluene or n-heptane the total number of excited states reported is 3222 and 5258, respectively. Our preliminary findings have shown that generating the TDωB97XD results with the even larger basis set def2TZVPD to require several-fold increase in CPU time. However, when aiming at only a few low-lying states, our results can be improved when using approximate correlated methods such as DLPNO-STEOM-CCSD(T) or RI-CC2.
880 molecules with up to 7 atoms of CONF. Geometry optimizations of the bigQM7ω molecules have been performed with the ConnGO workflow ensuring veracity in the covalent bonding connectivities encoded in their SMILES representation. Minimum energy geometries and harmonic vibrational wavenumbers are reported at the accurate, range-separated hybrid DFT level ωB97XD using def2SVP and def2TZVP basis sets. This level was selected because it has been previously shown to result in efficient geometry predictions for chemical space datasets.66 We report electronic excited state results at the TDωB97XD level using the def2SVPD basis set containing diffuse functions that are necessary for improved modeling of oscillator strengths, and high-lying states in general. Even for the low-lying excited states of the bigQM7ω molecules, we found TDωB97XD/def2SVPD to deliver more accurate results than the ωB97XD/def2TZVP combination when benchmarked against STEOM-CCSD/aug-cc-pVTZ reference values. For all molecules, full electronic spectra are calculated covering all possible excitations allowed by the TDωB97XD framework. For the small molecules H2O, NH3, and CH4 the resulting number of excited states modeled amounts to 188, 156 and 136, respectively, while for large molecules such as toluene or n-heptane the total number of excited states reported is 3222 and 5258, respectively. Our preliminary findings have shown that generating the TDωB97XD results with the even larger basis set def2TZVPD to require several-fold increase in CPU time. However, when aiming at only a few low-lying states, our results can be improved when using approximate correlated methods such as DLPNO-STEOM-CCSD(T) or RI-CC2.
For ML modeling of the full electronic spectra, we propose an approach using locally integrated spectral intensities at various wavelength resolutions. We illustrate the existence of a resolution-vs.-accuracy dilemma for comparing full electronic spectra from different methods. The mapping between the electronic spectra and the global molecular structure-based representations improves only when the intensities are binned at a finite resolution. Semi-quantitative agreement between methods is reached only at the expense of resolution. Compared to this, ML models deliver better accuracies at a sub-nm resolution when training on fraction of the dataset. For accurate reconstruction of full electronic spectra across chemical space with a resolution of <1 nm, we recommend FCHL-KRR-ML. Further, it may be possible to improve the ML model's performance in the long wavelength region using varying resolutions at different spectral regions. However, testing this idea requires new datasets comprising adequate data at the desired wavelength domain.
Our goal is to provide a proof-of-concept for ML modeling of binned electronic spectra and demonstrate accurate spectral reconstruction. Unfortunately, the size of the dataset limits the rigor of quantum mechanical methods and basis sets used to estimate the target spectra for ML models. While we used range-separated hybrid DFT with moderately large basis sets containing diffuse functions, inherent deficiencies in the method challenge the accuracy of the target. Further, the small size of the molecules in bigQM7ω implied excitations modeled are in the far UV region. However, ML modeling reproduced target spectra at accuracies lower than that arising from deficiencies in the quantum mechanical methods. This suggests that replacing the target with properties estimated from high-fidelity methods will be adequately captured through ML modeling.
Improvements of ML modeling of excited state requires development of new local descriptors that can map to the chromophores responsible for excitation. For this, an automated protocol to characterize electronic excited-states should be developed for high-throughput chemical space design frameworks. This allows the opportunity to explore chemically diverse photochemically interesting molecules, such as dyes, active in the UV/visible domain and investigate chromophore's/auxochrome's influence on spectra. Another possibility is to cluster the electronic spectral data according to chromophores33,51 or by unsupervised learning.103 However, one must ensure that for generating accurate models, each cluster must be adequately represented in the training set. In order to facilitate further studies, we provide all data generated for this study in public domains.
Data Availability
Structures, ground state properties and electronic spectra of the bigQM7ω dataset are available at https://moldis-group.github.io/bigQM7w, see ref. 62. Input and output files of corresponding calculations are deposited in the NOMAD repository (https://dx.doi.org/10.17172/NOMAD/2021.09.30-1), see ref. 63. A data-mining platform is available at https://moldis.tifrh.res.in/index.html.Author contributions
P. K. and R. R. conceptualised the project and methodology. S. C. and R. R. were involved in writing, reviewing, and editing the manuscript. S. C. and R. R. maintain the project content in GitHub and MolDis. All authors were involved in data generation/curation, analysis and visualization. Software development, resource/funding acquisition were done by R. R. R. R. supervised P. K. and S. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. All calculations have been performed using the Helios computer cluster, which is an integral part of the MolDis Big Data facility, TIFR Hyderabad (https://moldis.tifrh.res.in).Notes and references
- S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson and D. Angelone, et al. , Science, 2019, 363, 1–8 CrossRef PubMed.
- M. Christensen, L. P. Yunker, F. Adedeji, F. Häse, L. M. Roch, T. Gensch, G. dos Passos Gomes, T. Zepel, M. S. Sigman and A. Aspuru-Guzik, et al. , Commun. Chem., 2021, 4, 1–12 CrossRef.
- E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi and I. Foster, et al. , Matter, 2021, 4, 2702–2726 CrossRef.
- P. S. Gromski, J. M. Granda and L. Cronin, Trends Chem., 2020, 2, 4–12 CrossRef CAS.
- X. Li, P. M. Maffettone, Y. Che, T. Liu, L. Chen and A. I. Cooper, Chem. Sci., 2021, 12, 10742–10754 RSC.
- Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063–9071 CrossRef CAS PubMed.
- S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247 CrossRef CAS PubMed.
- B. G. Abreha, S. Agarwal, I. Foster, B. Blaiszik and S. A. Lopez, J. Phys. Chem. Lett., 2019, 10, 6835–6841 CrossRef CAS PubMed.
- D. Sampedro, Phys. Chem. Chem. Phys., 2011, 13, 5584–5586 RSC.
- R. Losantos, I. Funes-Ardoiz, J. Aguilera, E. Herrera-Ceballos, C. García-Iriepa, P. J. Campos and D. Sampedro, Angew. Chem., 2017, 129, 2676–2679 CrossRef.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2015, 25, 6495–6502 CAS.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- R. Ramakrishnan and O. A. von Lilienfeld, Rev. Comput. Chem., 2017, 30, 225–256 CAS.
- O. A. von Lilienfeld, Angew. Chem., Int. Ed., 2018, 57, 4164–4169 CrossRef CAS PubMed.
- R. Ramakrishnan and O. A. von Lilienfeld, Chimia, 2015, 69, 182–186 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- M. Rupp, R. Ramakrishnan and O. A. von Lilienfeld, J. Phys. Chem. Lett., 2015, 6, 3309–3313 CrossRef CAS.
- W. Gerrard, L. A. Bratholm, M. J. Packer, A. J. Mulholland, D. R. Glowacki and C. P. Butts, Chem. Sci., 2020, 11, 508–515 RSC.
- A. Gupta, S. Chakraborty and R. Ramakrishnan, Mach. Learn.: Sci. Technol., 2021, 2, 035010 Search PubMed.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef PubMed.
- Z. Qiao, M. Welborn, A. Anandkumar, F. R. Manby and T. F. Miller III, J. Chem. Phys., 2020, 153, 124111 CrossRef CAS PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Adv. Neural Inf. Process. Syst., 2017, 30, 1–11 Search PubMed.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed.
- O. V. Prezhdo, Acc. Chem. Res., 2021, 54, 4239–4249 CrossRef CAS PubMed.
- J. Lam, S. Abdul-Al and A.-R. Allouche, J. Chem. Theory Comput., 2020, 16, 1681–1689 CrossRef CAS PubMed.
- A. A. Kananenka, K. Yao, S. A. Corcelli and J. Skinner, J. Chem. Theory Comput., 2019, 15, 6850–6858 CrossRef CAS PubMed.
- O. Çaylak, A. Yaman and B. Baumeier, J. Chem. Theory Comput., 2019, 15, 1777–1784 CrossRef PubMed.
- S. Vela, A. Fabrizio, K. R. Briling and C. Corminboeuf, J. Phys. Chem. Lett., 2021, 12, 5957–5962 CrossRef CAS PubMed.
- A. Grisafi, A. Fabrizio, B. Meyer, D. M. Wilkins, C. Corminboeuf and M. Ceriotti, ACS Cent. Sci., 2018, 5, 57–64 CrossRef PubMed.
- R. Ramakrishnan, M. Hartmann, E. Tapavicza and O. A. von Lilienfeld, J. Chem. Phys., 2015, 143, 084111 CrossRef PubMed.
- E. Tapavicza, G. F. von Rudorff, D. O. De Haan, M. Contin, C. George, M. Riva and O. A. von Lilienfeld, Environ. Sci. Technol., 2021, 55, 8447–8457 CrossRef CAS PubMed.
- O. Çaylak and B. Baumeier, J. Chem. Theory Comput., 2021, 17, 4891–4900 CrossRef PubMed.
- J. Westermayr and P. Marquetand, J. Chem. Phys., 2020, 153, 154112 CrossRef CAS PubMed.
- J. Westermayr and P. Marquetand, Chem. Rev., 2020, 121, 9873–9926 CrossRef PubMed.
- P. O. Dral and M. Barbatti, Nat. Rev. Chem., 2021, 5, 388–405 CrossRef CAS.
- C. D. Rankine and T. J. Penfold, J. Phys. Chem. A, 2021, 125, 4276–4293 CrossRef CAS PubMed.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko and K.-R. Muller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- O. A. von Lilienfeld, R. Ramakrishnan, M. Rupp and A. Knoll, Int. J. Quantum Chem., 2015, 115, 1084–1093 CrossRef CAS.
- X. Huang, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2005, 122, 044308 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- S. Manzhos and T. Carrington Jr, Chem. Rev., 2020, 121, 10187–10217 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- C. B. Mahmoud, A. Anelli, G. Csányi and M. Ceriotti, Phys. Rev. B, 2020, 102, 235130 CrossRef.
- J. Westermayr and R. J. Maurer, Chem. Sci., 2021, 12, 10755–10764 RSC.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 1–7 Search PubMed.
- Z. Liu, L. Lin, Q. Jia, Z. Cheng, Y. Jiang, Y. Guo and J. Ma, J. Chem. Inf. Model., 2021, 61, 1066–1082 CrossRef CAS PubMed.
- B. Mazouin, A. A. Schöpfer and O. A. von Lilienfeld, arXiv preprint, arXiv:2110.02596, 2021, 1–12.
- T. Fink, H. Bruggesser and J.-L. Reymond, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS PubMed.
- T. Fink and J.-L. Reymond, J. Chem. Inf. Model., 2007, 47, 342–353 CrossRef CAS PubMed.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, New J. Phys., 2013, 15, 095003 CrossRef CAS.
- J. Hoja, L. M. Sandonas, B. G. Ernst, A. Vazquez-Mayagoitia, R. A. DiStasio Jr and A. Tkatchenko, Sci. Data, 2021, 8, 1–11 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- P. Kayastha and R. Ramakrishnan, bigQM7ω: A high-quality dataset of ground-state properties and excited state spectra of 12880 molecules containing up to 7 atoms of CONF, 2021, https://moldis-group.github.io/bigQM7w.
- P. Kayastha and R. Ramakrishnan, bigQM7ω: Unstructured data on NOMAD repository, 2021, DOI:10.17172/NOMAD/2021.09.30-1.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14 Search PubMed.
- S. Senthil, S. Chakraborty and R. Ramakrishnan, Chem. Sci., 2021, 12, 5566–5573 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, et al., Gaussian 16, 2016 Search PubMed.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- B. Schölkopf, A. J. Smola, F. Bachet al., Learning with kt vector machines, regularization, optimization, and beyond, MIT press, 2002 Search PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951 CrossRef CAS PubMed.
- P. Kayastha and R. Ramakrishnan, Mach. Learn.: Sci. Technol., 2021, 2, 035035 Search PubMed.
- C. F. Van Loan and G. Golub, Matrix computations (Johns Hopkins studies in mathematical sciences), The Johns Hopkins University Press, 1996 Search PubMed.
- A. Christensen, F. Faber, B. Huang, L. Bratholm, A. Tkatchenko, K. Muller and O. von Lilienfeld, QML: A Python toolkit for quantum machine learning, 2017, https://github.com/qmlcode/qml Search PubMed.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern molecular photochemistry of organic molecules, Viva Books University Science Books, Sausalito, 2017 Search PubMed.
- P.-F. Loos, A. Scemama, A. Blondel, Y. Garniron, M. Caffarel and D. Jacquemin, J. Chem. Theory Comput., 2018, 14, 4360–4379 CrossRef CAS PubMed.
- P.-F. Loos, F. Lipparini, M. Boggio-Pasqua, A. Scemama and D. Jacquemin, J. Chem. Theory Comput., 2020, 16, 1711–1741 CrossRef CAS PubMed.
- P.-F. Loos, A. Scemama, M. Boggio-Pasqua and D. Jacquemin, J. Chem. Theory Comput., 2020, 16, 3720–3736 CrossRef CAS PubMed.
- M. Schreiber, M. R. Silva-Junior, S. P. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed.
- T. Korona and H.-J. Werner, J. Chem. Phys., 2003, 118, 3006–3019 CrossRef CAS.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- D. Jacquemin, E. A. Perpete, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed.
- D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS PubMed.
- A. Chrayteh, A. Blondel, P.-F. Loos and D. Jacquemin, J. Chem. Theory Comput., 2020, 17, 416–438 CrossRef PubMed.
- R. Send, M. Kühn and F. Furche, J. Chem. Theory Comput., 2011, 7, 2376–2386 CrossRef CAS PubMed.
- R. Berraud-Pache, F. Neese, G. Bistoni and R. Izsák, J. Chem. Theory Comput., 2020, 16, 564–575 CrossRef PubMed.
- C. W. Murray, S. C. Racine and E. R. Davidson, J. Comput. Phys., 1992, 103, 382–389 CrossRef.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 810–825 CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2005, 123, 124107 CrossRef PubMed.
- S. K. Das, S. Chakraborty and R. Ramakrishnan, J. Chem. Phys., 2021, 154, 044113 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2000, 2, 2117–2121 RSC.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- L. Zheng, N. F. Polizzi, A. R. Dave, A. Migliore and D. N. Beratan, J. Phys. Chem. A, 2016, 120, 1933–1943 CrossRef CAS PubMed.
- S. Krishnan, A. Ghosh, M. Gupta, P. Kayastha, S. Senthil, S. K. Das, S. C. Kandpal, C. Sabyasachi, A. Gupta and R. Ramakrishnan, MolDis: A Big Data Analytics Platform for Molecular Discovery, https://moldis.tifrh.res.in/.
- L. Cheng, J. Sun and T. F. Miller III, arXiv preprint, arXiv:2204.09831, 2022, 1–28.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |